Похожие презентации:
Диаграммы Ламерея. Качественный анализ дискретных ДС
1. Диаграммы Ламерея
ДИАГРАММЫ ЛАМЕРЕЯКачественный анализ дискретных ДС
2. Динамическая система
2Уравнение
Nt+1 = F(Nt ), t = 0,1,...
(1)
может быть использовано для описания динамики популяции с
неперекрывающимися поколениями.
Функция F(N) обладает следующими свойствами:
1) F(N) > 0 допустимого N > 0;
2) F(0) = 0;
3) F(N) возрастает в окрестности точки N = 0;
4) F(N) k = const 0 при N + .
Определение 1. Решением уравнения (1) называется числовая
последовательность
{Nt}t=0,1,2,…., члены которой удовлетворяют
уравнению (1).
3. Основные определения
3Определение 2. Решение уравнения (1) вида Nt = N* = const t = 0,1,2, …
называется стационарным, а точка N* положением равновесия (или
точкой покоя, стационарной точкой).
Все положения равновесия являются корнями уравнения:
F(N) = N
(2)
Определение 3. Стационарное решение Nt = N* t = 0,1,2, … называется
устойчивым, если > 0 > 0, такое, что |Nt N*|< t 0, если
|N0 N*| < .
Определение 4. Если
lim N t - N* 0,
t
когда |N0 N*|< , то решение
Nt = N* t = 0,1,2, … называется асимптотически устойчивым.
4. Диаграмма Ламерея Положения равновесия уравнения Nt+1 = F(Nt)
4y
y=N
y = F(N)
0
N1*
N
N2*
N3*
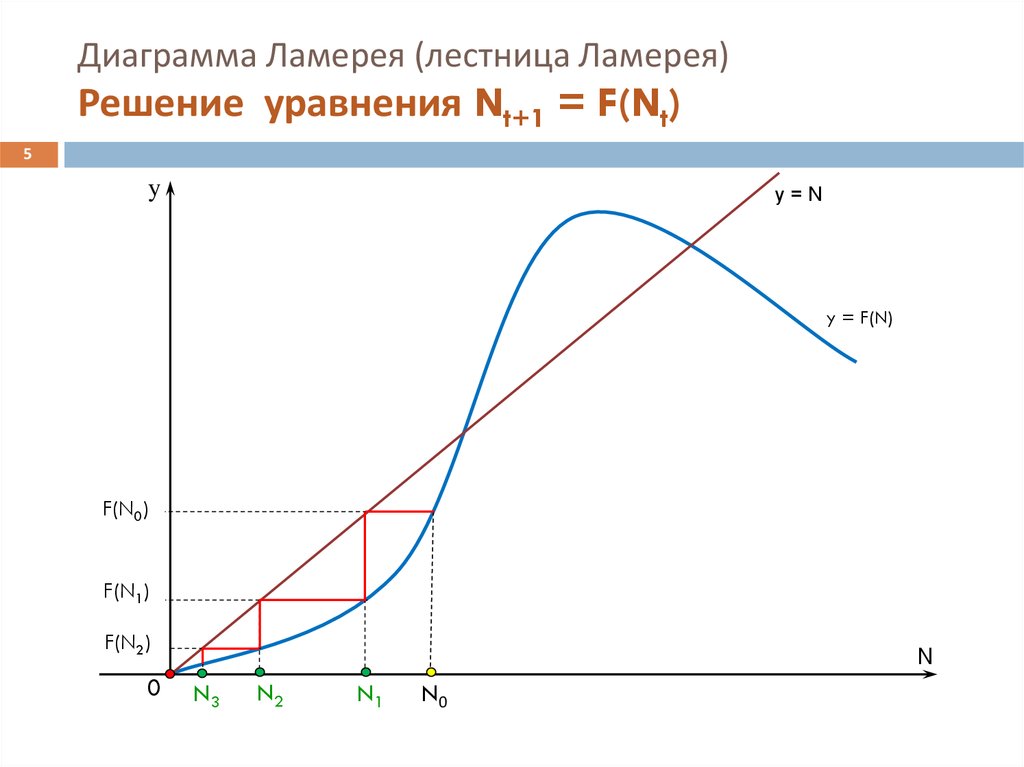
5. Диаграмма Ламерея (лестница Ламерея) Решение уравнения Nt+1 = F(Nt)
5y
y=N
y = F(N)
F(N0)
F(N1)
F(N2)
0
N
N3
N2
N1
N0
6. Траектория
6N
N0
N1
N2
N3
N4
0
1
2
3
4
t
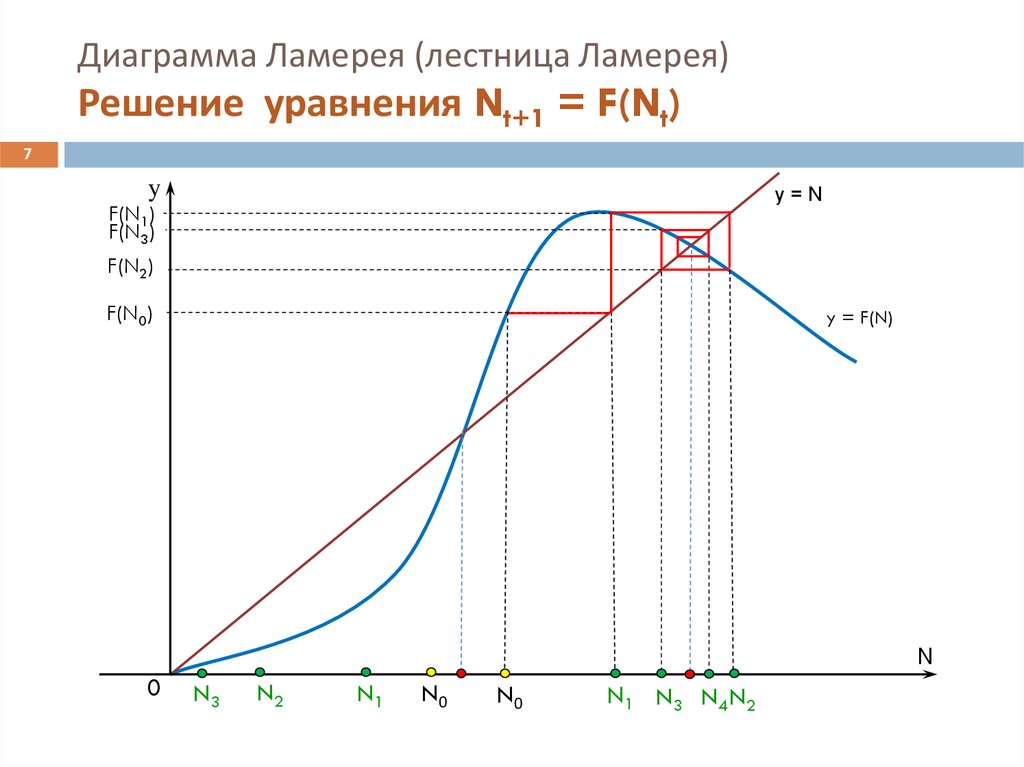
7. Диаграмма Ламерея (лестница Ламерея) Решение уравнения Nt+1 = F(Nt)
7y
y=N
F(N1)
F(N3)
F(N2)
F(N0)
y = F(N)
N
0
N3
N2
N1
N0
N0
N1 N3 N4 N2
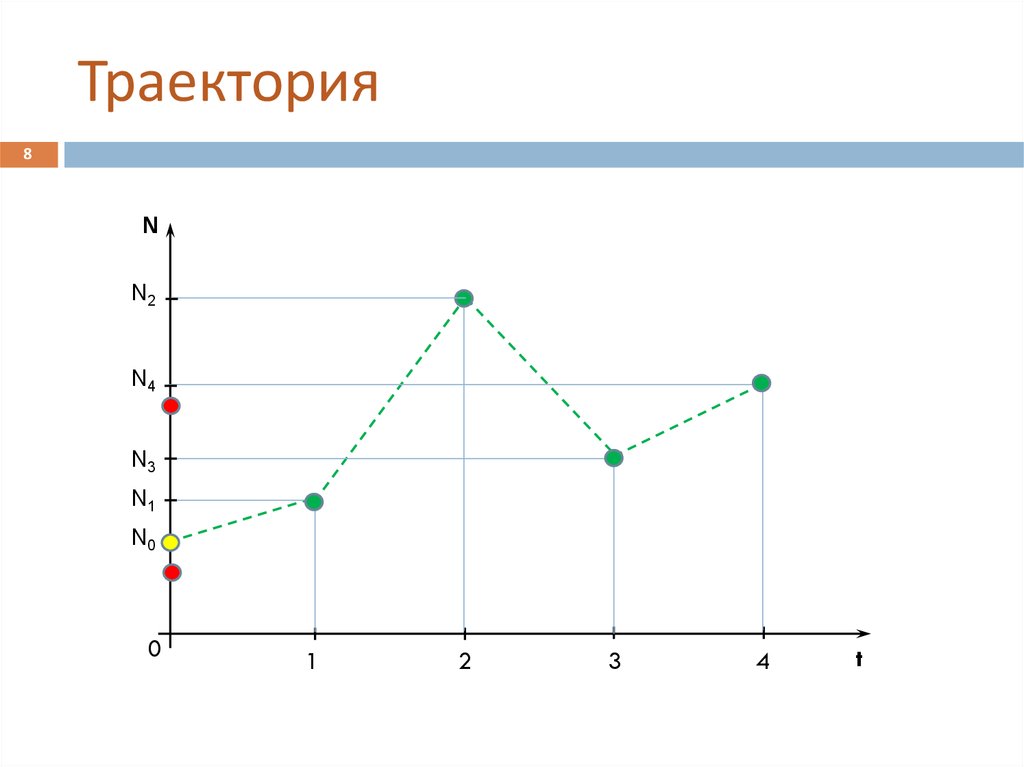
8. Траектория
8N
N2
N4
N3
N1
N0
0
1
2
3
4
t
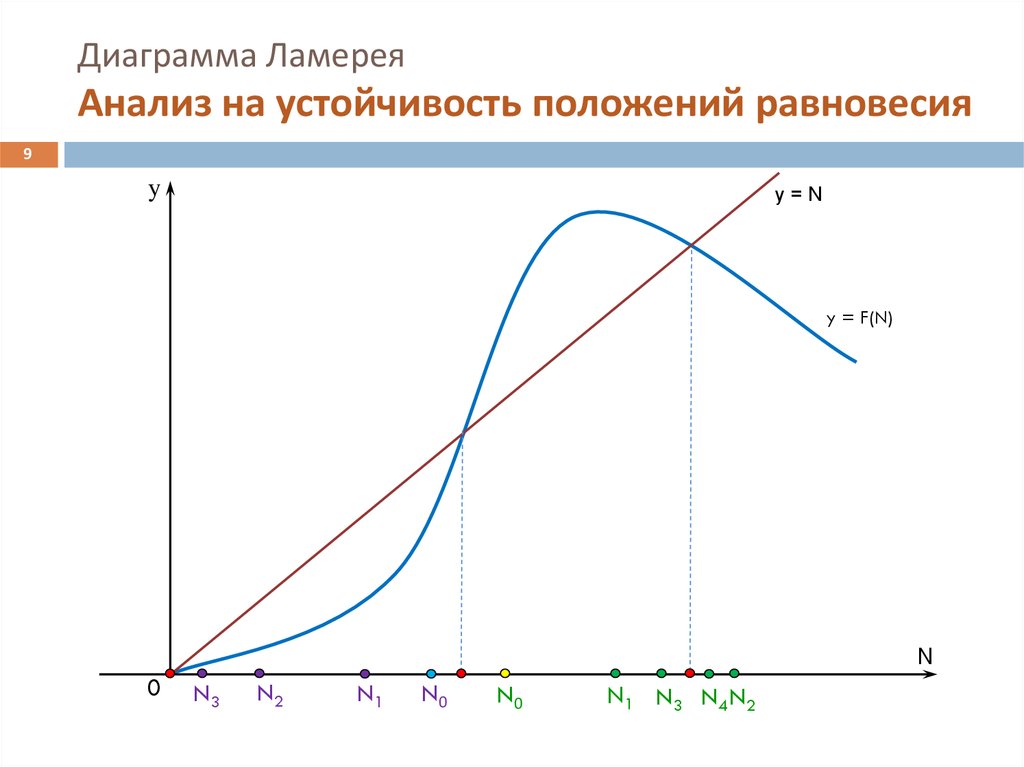
9. Диаграмма Ламерея Анализ на устойчивость положений равновесия
9y
y=N
y = F(N)
N
0
N3
N2
N1
N0
N0
N1 N3 N4 N2
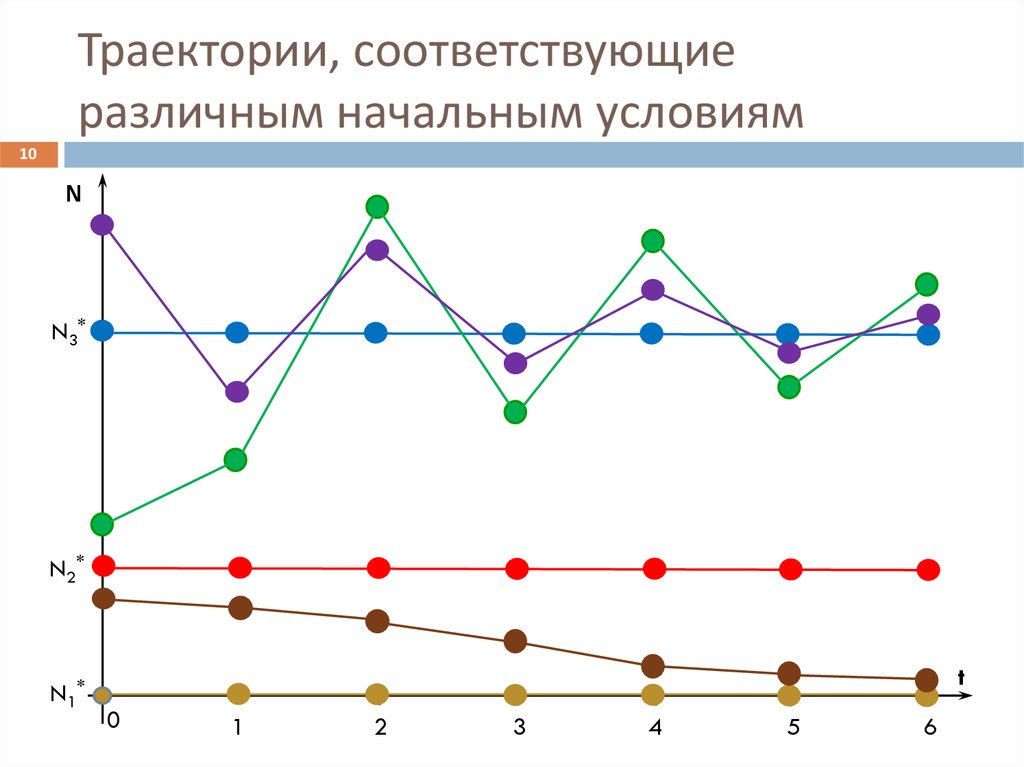
10. Траектории, соответствующие различным начальным условиям
10N
N3*
N2*
N1*
t
0
1
2
3
4
5
6





 Математика
Математика Физика
Физика








