Решите систему уравнений

1.

КР. МА-11. 08.12.09. Запад (без производной)
В1
3
В7
6,5
C1
В2
90
В8
7
В3
4
В9
45
Вариант 14
В4
5
В10
1000
В5
1592,5
В11
5
В6
35
В12
9
Решите систему уравнений
81cos x 12 9cos x 27
0,
log
(1
2
y
)
7
y sin x.
Решение.
Из уравнения 81cos x 12 9cos x 27 0 получаем: 9cos x 9 или 9cos x 3 ,
1
откуда cos x 1 или cos x .
2
1
3
1
.
1) Пусть cos x , тогда либо x 2 n , n , и y sin x
2
2
2
3
3
1
— не дает решения,
либо x 2 n , n , и y sin x
2
2
3
поскольку в этом случае 1 2 y 0 .
2) Пусть cos x 1 , тогда y sin x 0 и, следовательно, log7 (1 2 y) 0 . В
этом случае решений нет.
3
Ответ: x 2 n, n ; y
.
3
2
Содержание критерия
Балл
Решение не соответствует ни одному из критериев,
0
перечисленных ниже.
Получен ответ, возможно, неверный, но только из-за того, что в
решении не учтено, что знаменатель дроби существует и отличен от 1
нуля.
Обоснованно получен правильный ответ.
2
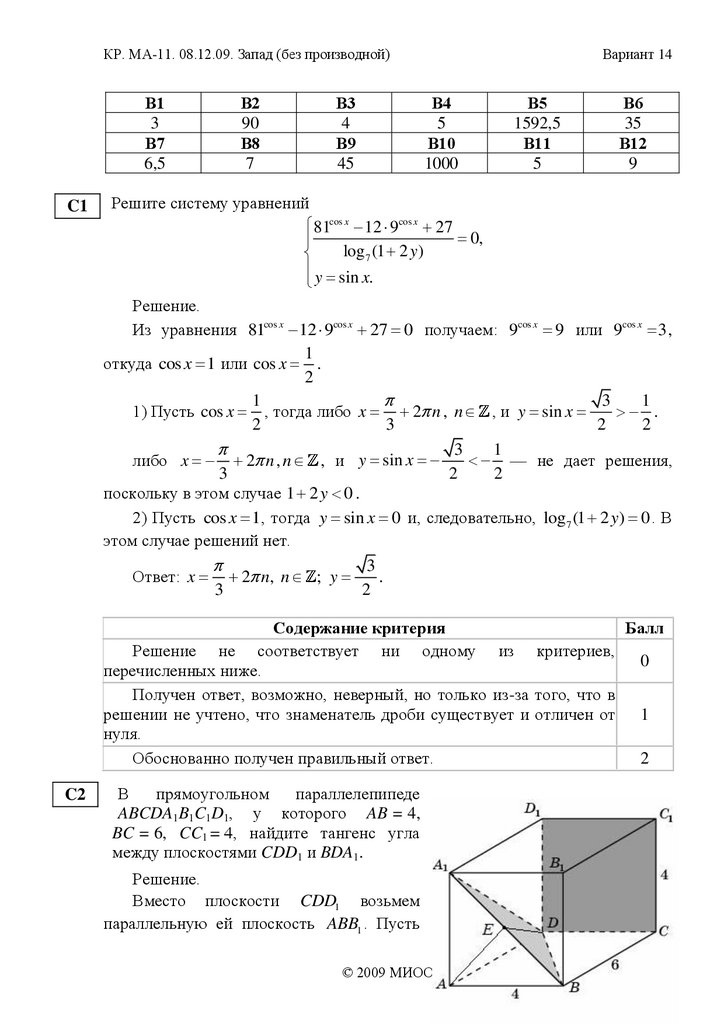
C2
В
прямоугольном
параллелепипеде
ABCDA1B1C1D1, у которого AB = 4,
BC = 6, CC1 = 4, найдите тангенс угла
между плоскостями CDD1 и BDA1.
Решение.
Вместо плоскости CDD1 возьмем
параллельную ей плоскость ABB1 . Пусть
© 2009 МИОО

2.

КР. МА-11. 08.12.09. Запад (без производной)
Вариант 14
E — середина BA1 . DE BA1 , AE BA1 . Значит, угол DEA — линейный
угол искомого угла. Из прямоугольного треугольника DAE находим:
tg DEA
Ответ:
AD
6
3 2
.
AE 2 2
2
3 2
.
2
Содержание критерия
Балл
Решение не соответствует ни одному из критериев,
0
перечисленных ниже.
Способ нахождения искомого угла верен, но получен неверный
1
ответ или решение не закончено.
Обоснованно получен правильный ответ.
2
C3
Решите неравенство
2
2
4
2
2
x
log
x
8
x
16
5
log
x
8
x
16
.
(6 x )
(6 x )
x
Решение.
x 0,
x 6,
6 x 0,
x 0,
Решение неравенства ищем при условиях:
откуда
6 x 1,
x 5,
x 2 8 x 16 0
x 4.
Рассмотрим два случая:
1) log(6 x ) x 2 8x 16 0 , откуда x2 8x 16 1 , т.е. | x 4 | 1 и, значит,
x 3 или x 5 .
Значит, x 3 — решение задачи.
2) log(6 x ) ( x 2 8 x 16) 0 , откуда x2 8x 16 1 . Разделив обе части
неравенства
на
log (6 x ) x 2 8 x 16 ,
2
получим:
x
4
5,
x
( x 1)( x 4)
0 . Решим это неравенство: 0 x 1, x 4 .
x
С учетом ограничений получаем 0 x 1, x 3, 4 x 5, 5 x 6 .
Ответ: 0 x 1, x 3, 4 x 5, 5 x 6 .
© 2009 МИОО
откуда

3.

КР. МА-11. 08.12.09. Запад (без производной)
Вариант 14
Содержание критерия
Балл
Решение не соответствует ни одному из критериев,
0
перечисленных ниже.
Решение содержит верные преобразования, но в ответе либо
потеряны верные промежутки, либо приобретены лишние 1
промежутки.
Ответ или отличается от верного конечным числом точек, или
2
при правильном рассуждении неверен из-за арифметической ошибки.
Обоснованно получен правильный ответ.
3
C4
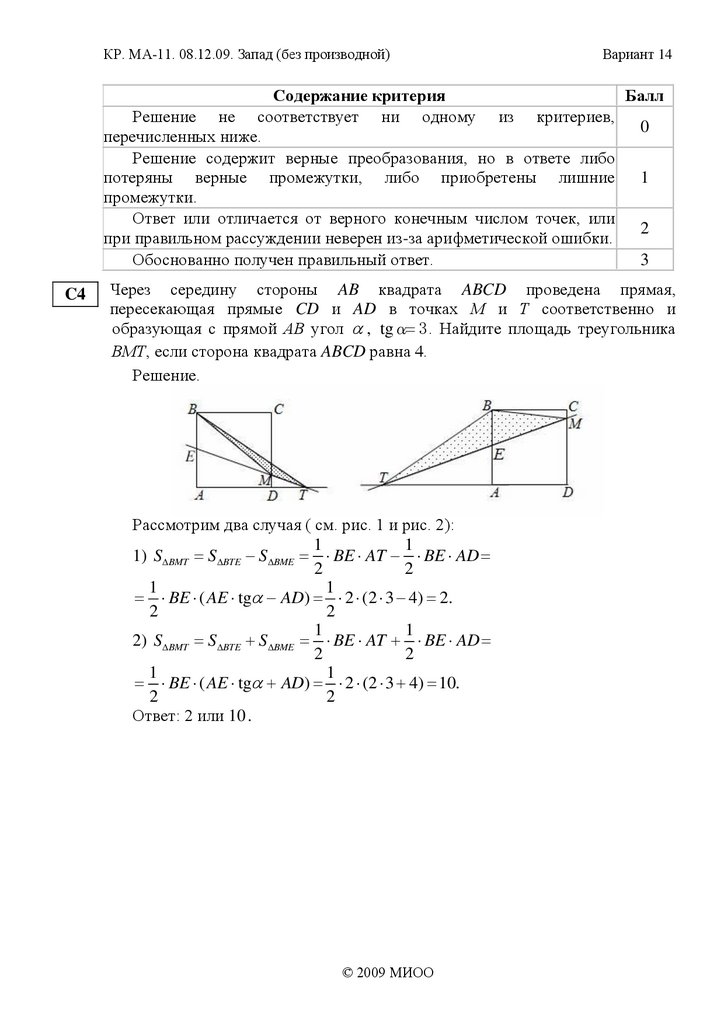
Через середину стороны AB квадрата ABCD проведена прямая,
пересекающая прямые CD и AD в точках М и Т соответственно и
образующая с прямой АВ угол , tgα 3 . Найдите площадь треугольника
ВМТ, если сторона квадрата ABCD равна 4.
Решение.
Рассмотрим два случая ( см. рис. 1 и рис. 2):
1
1
1) S BMT S BTE S BME BE AT BE AD
2
2
1
1
BE ( AE tg AD) 2 (2 3 4) 2.
2
2
1
1
2) S BMT S BTE S BME BE AT BE AD
2
2
1
1
BE ( AE tg AD) 2 (2 3 4) 10.
2
2
Ответ: 2 или 10 .
© 2009 МИОО

4.

КР. МА-11. 08.12.09. Запад (без производной)
Вариант 14
Содержание критерия
Балл
Решение не соответствует ни одному из критериев,
0
перечисленных ниже.
Рассмотрена хотя бы одна возможная геометрическая
конфигурация, в которой получено значение искомой величины,
1
неправильное из-за арифметической ошибки.
Рассмотрена хотя бы одна возможная конфигурация, в которой
2
получено правильное значение искомой величины.
Рассмотрены все возможные геометрические конфигурации, и
3
получен правильный ответ.
C5
Найдите все значения a , при каждом из которых решения неравенства
| 3x a | 2 | x 4 | образуют отрезок длины 1.
Решение.
Перенесем двойку: | 3x a | | x 4 | 2 .
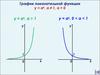
Построим схематично графики функций y | 3x a | и y | x 4 | 2 .
На рисунке видно, что неравенство имеет решения только при
a
6.
3
© 2009 МИОО
a
2 или
3

5.

КР. МА-11. 08.12.09. Запад (без производной)
Вариант 14
a 6,
a 6,
a 6
a 2
,
1)
3x a x 2, x
|
3
x
a
|
x
2;
4
3x a x 2;
a 2
x
.
2
a 2 a 2
1 , откуда a 2 .
Решения образуют отрезок длины 1, если
4
2
a 18,
a 18,
a 18,
a 6
,
2)
3x a x 6, x
|
3
x
a
|
x
6;
2
3x a x 6;
a 6
x
.
4
a 6 a 6
1, откуда a 22 .
Решения образуют отрезок длины 1, если
2
4
Ответ: a 2, a 22 .
Содержание критерия
Балл
Все ситуации, отличные от описанных ниже.
0
Ответ, возможно, отсутствует или неверен, но в решении с
помощью верного рассуждения найдены некоторые из искомых 1
значений параметра.
Ответ, возможно, отсутствует или неверен, но в решении с
помощью верного рассуждения найдено хотя бы один верный 2
интервал значений параметра.
Либо получен верный ответ, но при его обосновании допущены
ошибки, либо обоснованно получен ответ, отличный от верного
3
только из-за потери (приобретения) одного–двух искомых значений
параметра.
Обоснованно получен верный ответ.
4
© 2009 МИОО

6.

КР. МА-11. 08.12.09. Запад (без производной)
C6
Вариант 14
Найдите все пары ( x; y) целых чисел, удовлетворяющие системе неравенств:
x 2 y 2 18 x 20 y 166,
2
2
32 x y x 12 y 271.
Решение.
Выделяя полные квадраты, получаем:
( x 9) 2 ( y 10) 2 15,
2
2
( x 16) ( y 6) 21,
x, y .
Из первого и второго неравенств системы:
( x 9)2 15, 6 x 12,
x 12 .
2
( x 16) 21; 12 x 20;
Подставляя x 12 в систему, получаем:
( y 10) 2 6,
( y 6) 2 5,
y ;
2 y 10 2,
2 y 6 2,
y ;
12 y 8,
8 y 4, y 8 .
y ;
Ответ: (12; 8) .
Содержание критерия
Балл
Решение не соответствует ни одному из критериев,
0
перечисленных выше.
Решения ищутся прямым перебором с ошибками. Ответ
1
отсутствует или неверен.
Ответ неверен, однако есть попытка провести перебор с
2
использованием геометрических или аналитических соображений.
Ответ неверен из-за арифметической ошибки, но правильно
обозначена идея перебора основанная на выделении полного 3
квадрата.
Обоснованно получен правильный ответ.
4
© 2009 МИОО