Статистические ряды распределения

1. Статистические ряды распределения

2. Большинство встречающихся на практике величин принимают неодинаковые значения у различных членов совокупности

Статистический
ряд
распределения – это
упорядоченное распределение
единиц совокупности на группы
по определенному
варьирующемуся признаку (стаж
работы, возраст, пол и т.д.)

3. С помощью статистического ряда распределения:

Характеризуют состав (структуру),
изучаемого явления
Рассматривают вопрос об однородности
совокупности
Рассматривают вопрос о границах
варьирования единиц совокупности и
закономерностях ее распределения

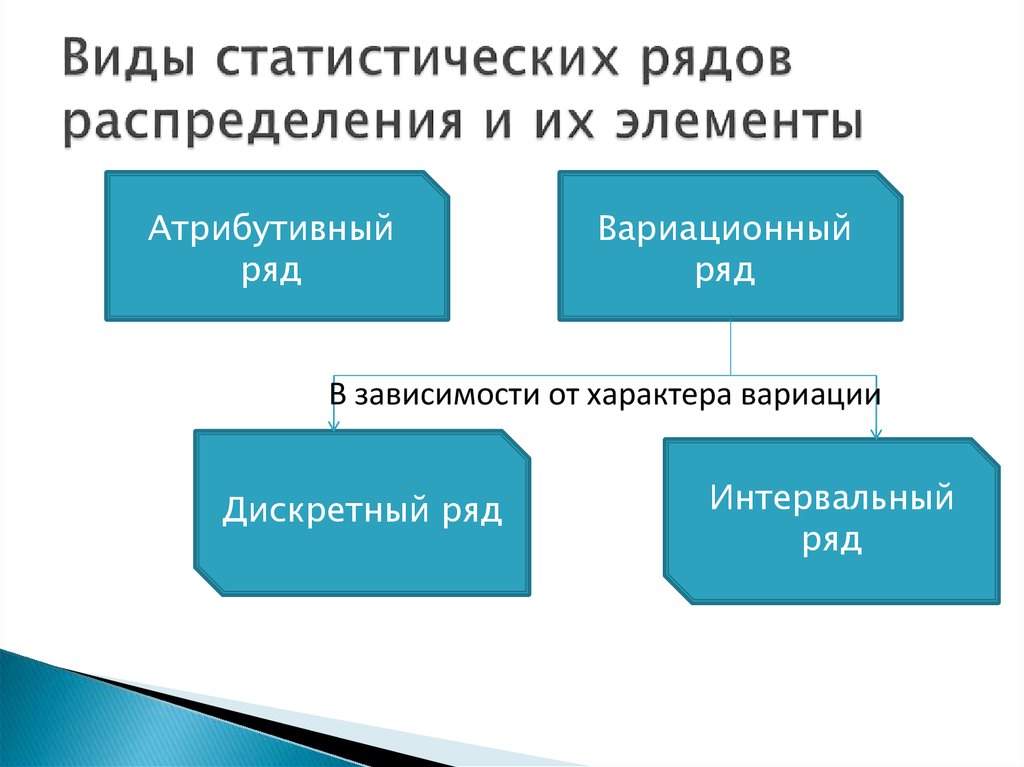
4. Виды статистических рядов распределения и их элементы

Атрибутивный
ряд
Вариационный
ряд
В зависимости от характера вариации
Дискретный ряд
Интервальный
ряд

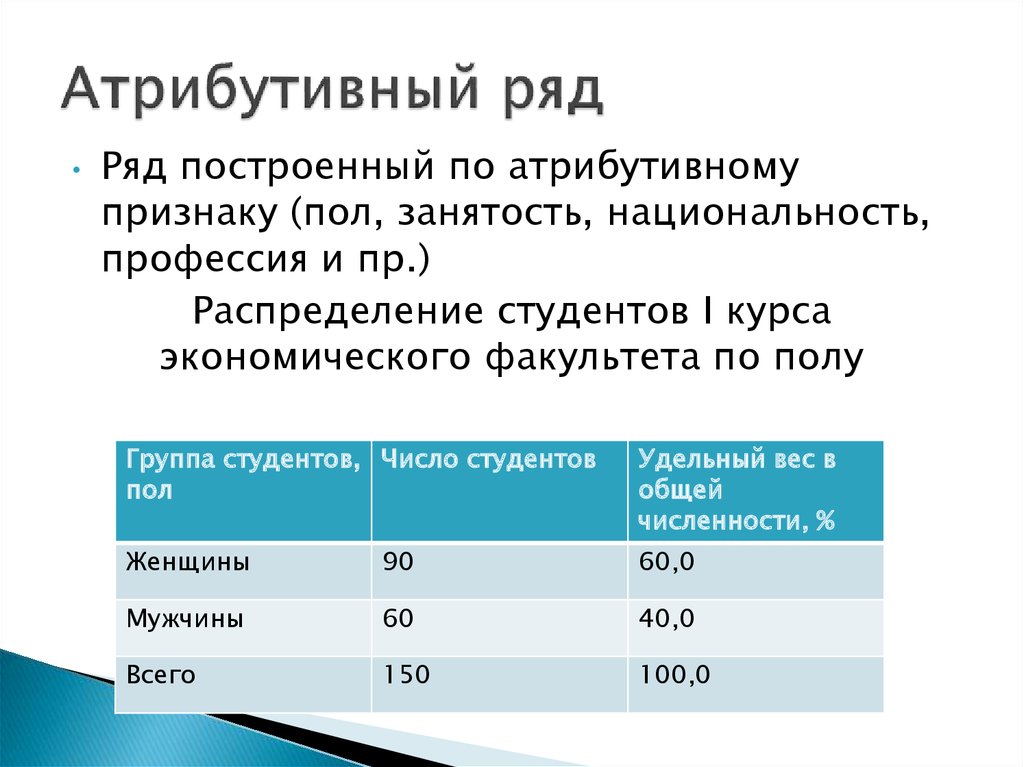
5. Атрибутивный ряд

Ряд построенный по атрибутивному
признаку (пол, занятость, национальность,
профессия и пр.)
Распределение студентов I курса
экономического факультета по полу
Группа студентов, Число студентов
пол
Удельный вес в
общей
численности, %
Женщины
90
60,0
Мужчины
60
40,0
Всего
150
100,0

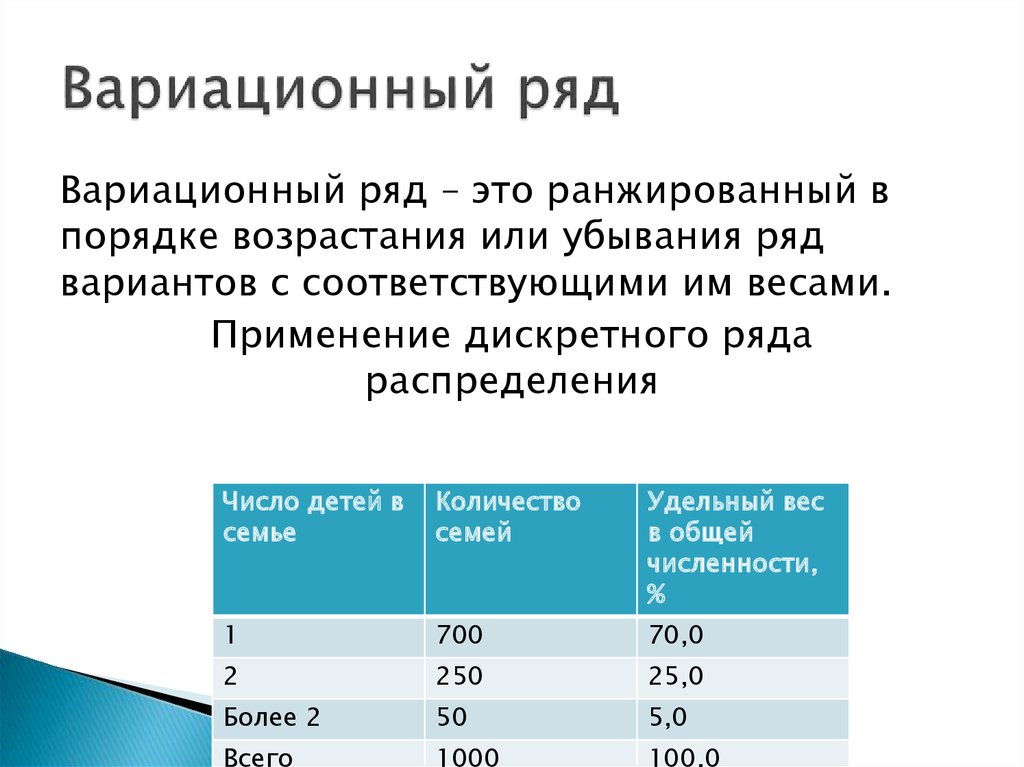
6. Вариационный ряд

– это ранжированный в
порядке возрастания или убывания ряд
вариантов с соответствующими им весами.
Применение дискретного ряда
распределения
Число детей в
семье
Количество
семей
Удельный вес
в общей
численности,
%
1
700
70,0
2
250
25,0
Более 2
50
5,0
Всего
1000
100,0

7. Характеристики вариационных рядов:

1. Варианты – это числовые значения
количественного признака в вариационном
ряду распределения (положительные,
отрицательные, относительные, абсолютные)
2. Частоты – это численности отдельных
вариантов или каждой группы вариационного
ряда, т.е. числа, показывающие насколько
часто встречаются те или иные варианты в ряду
распределения
Сумма всех частот называется объемом
совокупности и равна числу элементов всей
совокупности

8. Характеристики вариационных рядов:

3. Частости – это частоты, выраженные в виде
относительных величин (долях или
процентах)
Сумма частостей равна 1 или 100%
Замена частот частостями позволяет
сравнивать ряды с разным число наблюдений

9. Дискретный вариационный ряд

В основе этого ряда лежит дискретный
(прерывный) признак, т.е. значения
признака отличаются друг от друга не
менее чем на некоторую постоянную
величину

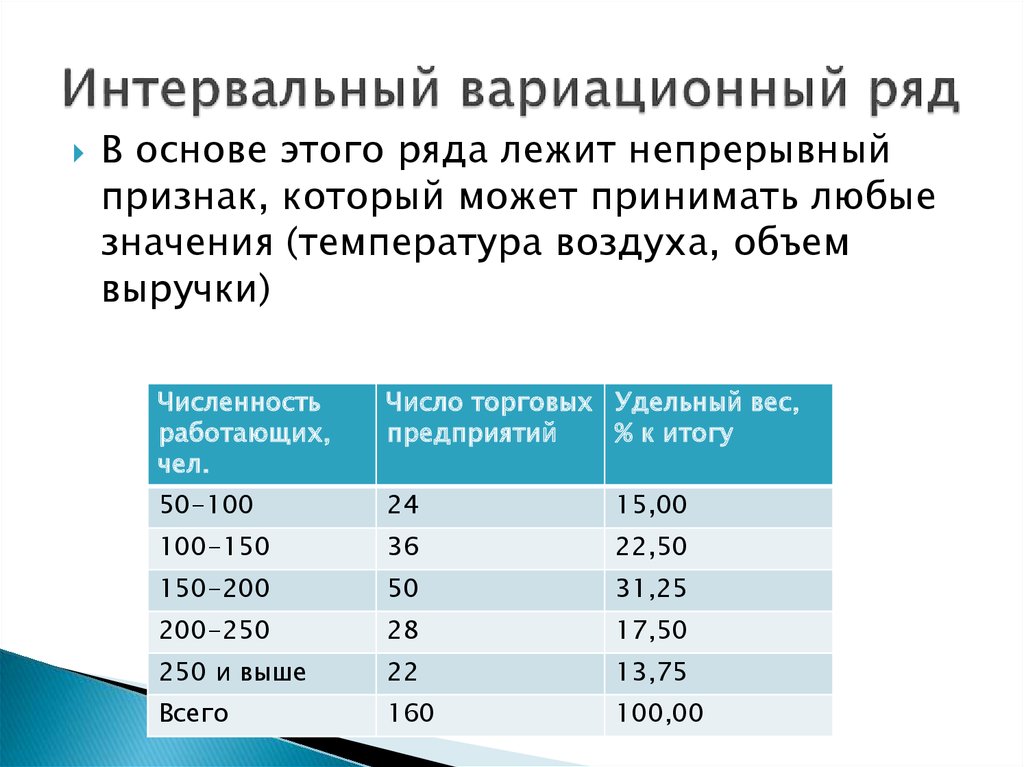
10. Интервальный вариационный ряд

В основе этого ряда лежит непрерывный
признак, который может принимать любые
значения (температура воздуха, объем
выручки)
Численность
работающих,
чел.
Число торговых Удельный вес,
предприятий
% к итогу
50-100
24
15,00
100-150
36
22,50
150-200
50
31,25
200-250
28
17,50
250 и выше
22
13,75
Всего
160
100,00

11. Первый шаг построения вариационного ряда распределения

Ранжирование – расположение всех вариантов в
возрастающем или убывающем порядке
Например стаж работы рабочих бригады:
2, 4,
5,3,15,6,5,9,7,14,8,5,9,10,11,4,2,3,4,6,5,13,10,1
Ранжированный ряд:
1,2,2,3,3,4,4,4,5,5,5,5,6,6,6,7,8,9,9,10,10,11,13,14
,15

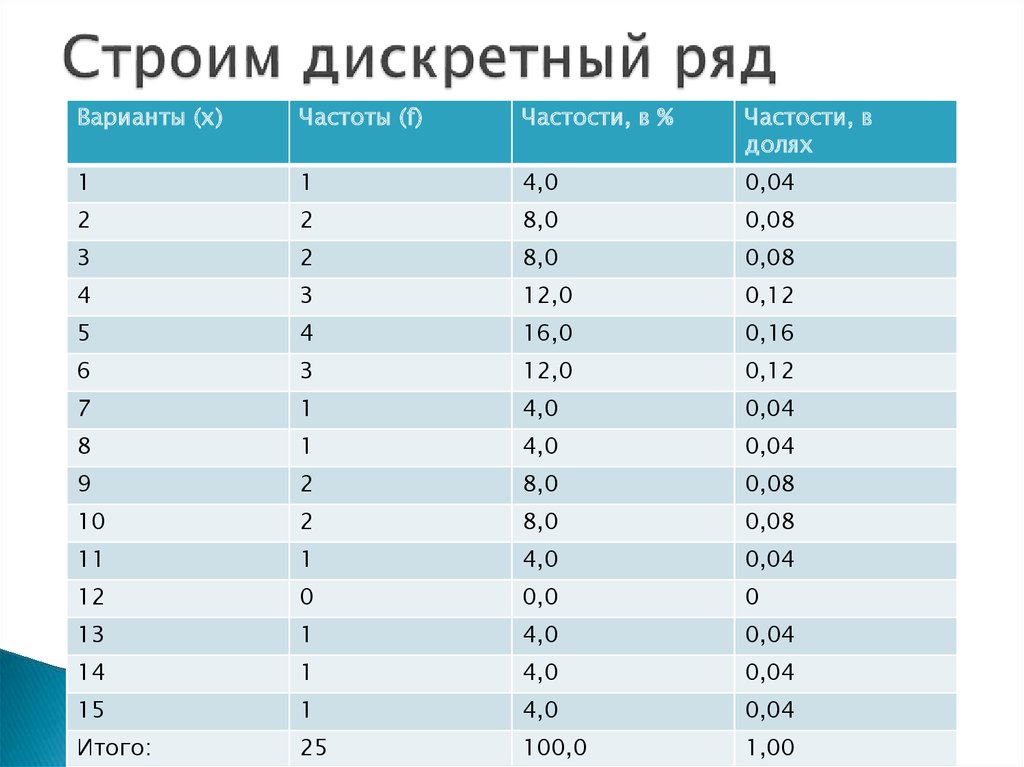
12. Строим дискретный ряд

Варианты (х)
Частоты (f)
Частости, в %
Частости, в
долях
1
1
4,0
0,04
2
2
8,0
0,08
3
2
8,0
0,08
4
3
12,0
0,12
5
4
16,0
0,16
6
3
12,0
0,12
7
1
4,0
0,04
8
1
4,0
0,04
9
2
8,0
0,08
10
2
8,0
0,08
11
1
4,0
0,04
12
0
0,0
0
13
1
4,0
0,04
14
1
4,0
0,04
15
1
4,0
0,04
Итого:
25
100,0
1,00

13. Строим интервальный ряд (как группировку)

Вычисляем количество интервалов по
формуле Стерджесса
n 1 3.322 lg( N )
Вычисляем величину интервала
Строим таблицу:
n=1+3,322lg25=5,6 примерно 5
h=(15-1)/5=2,8 примерно 3
x
До 3 лет
3-6 года
6-9 лет
9-12 лет
12-15
лет
f
3
9
5
5
3

14. Графическое изображение рядов распределения

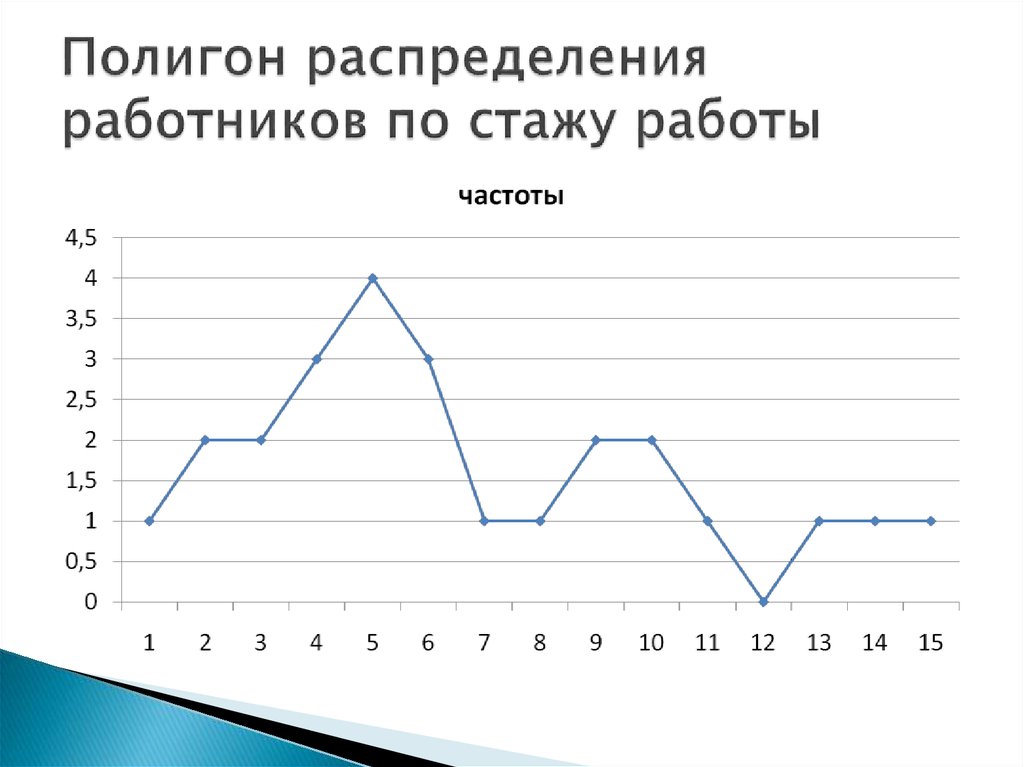
Полигон – графическое изображение
вариационных дискретных рядов:
Ось абсцисс – ранжированные значения
вариационного признака
Ось ординат – выражение численности
каждого варианта (величины частот)

15. Полигон распределения работников по стажу работы

16.

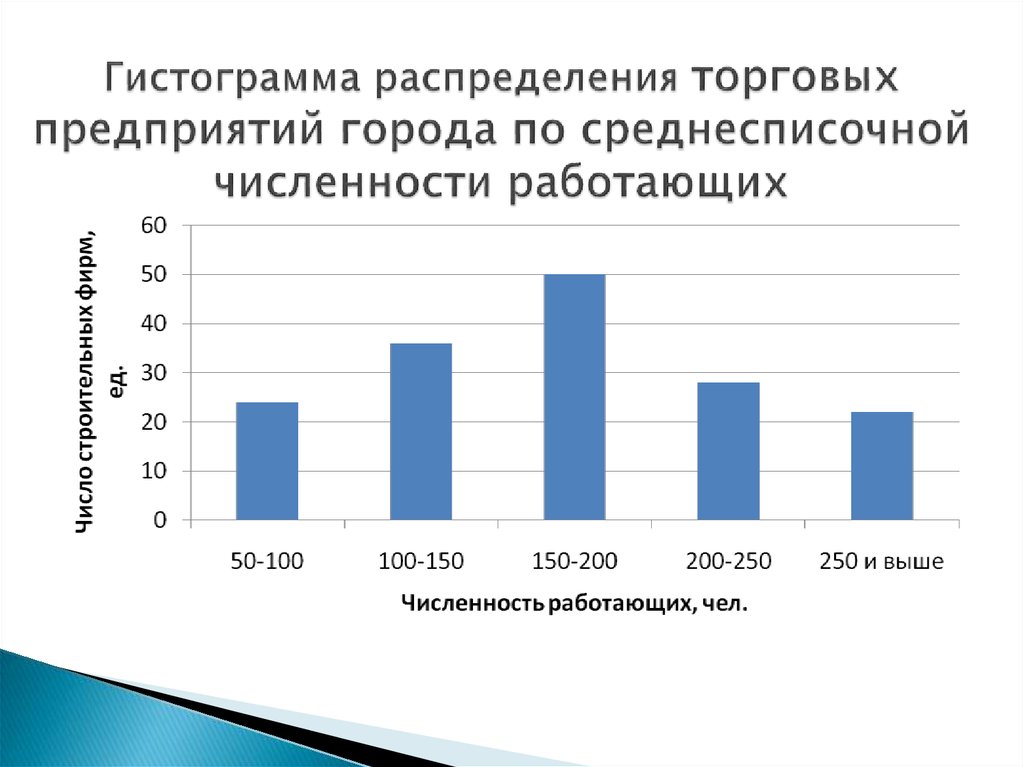
Гистограмма - графическое изображение
вариационных интервальных рядов
Ось абсцисс – отображение величин
интервалов
Частоты описываются прямоугольниками,
построенными на соответствующих
интервалах, высота которых
пропорциональна частотам

17. Гистограмма распределения торговых предприятий города по среднесписочной численности работающих

18. Формы статистических распределений

Распределение называется симметричным
если веса любых вариантов,
равноотстоящих от среднего, равны между
собой.
Умеренно ассиметричные – это
распределения у которых частоты,
находящиеся по одну сторону от
наибольшей, больше (или меньше) частот,
находящихся по другую сторону

19.

Крайне ассиметричными называются
распределения, у которых частоты или все
время возрастают, или все время убывают
При U- образном распределении частоты
сначала убывают, а затем возрастают.

20. Эмпирическая функция распределения

Эмпирической функцией распределения
(функция распределения выборки)
называетсяF*(x), определяющую для каждого
значения x относительную частоту события X<x.
F*(x)>nx/n; nx – число вариант, меньше x,
n – объем выборки.

21. Свойства функции распределения

значения F*(x) [0;1]
*
*
*
F (x) – функция неубывающая: F (x2)> F (x1),
если x2> x1
*
если x1 – наименьшая варианта, F (x1)=0
если xk – наибольшая, то F*(x1)=1.

22. Графическое представление

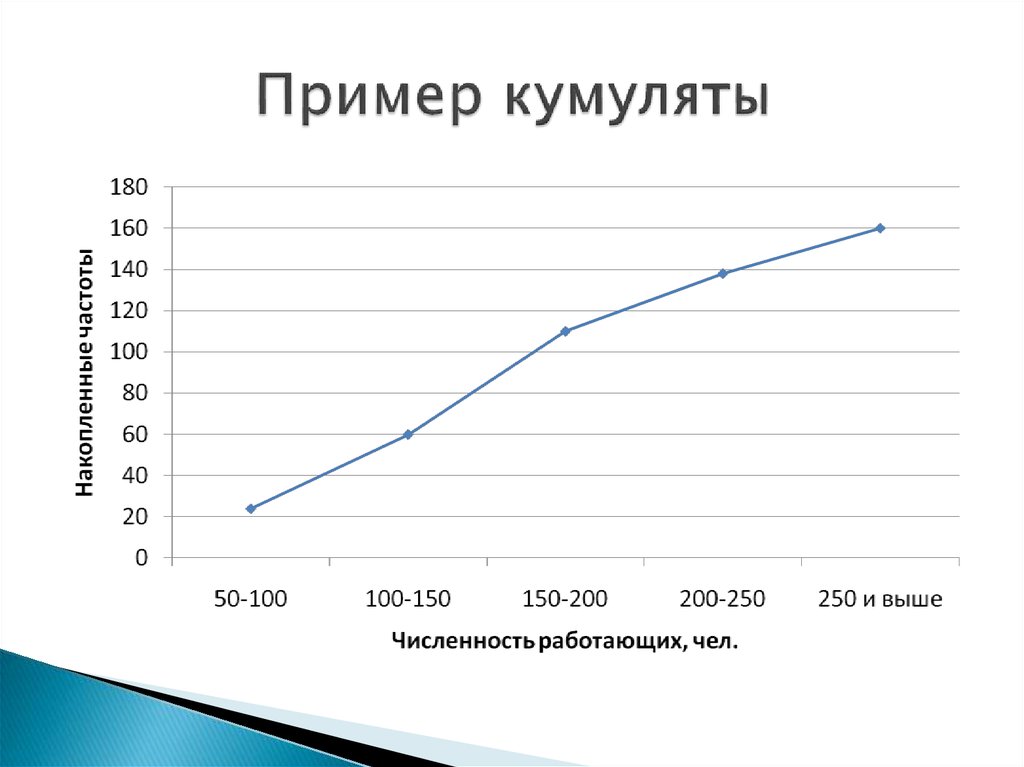
Кумулята – для изображения ряда
накопленных частот
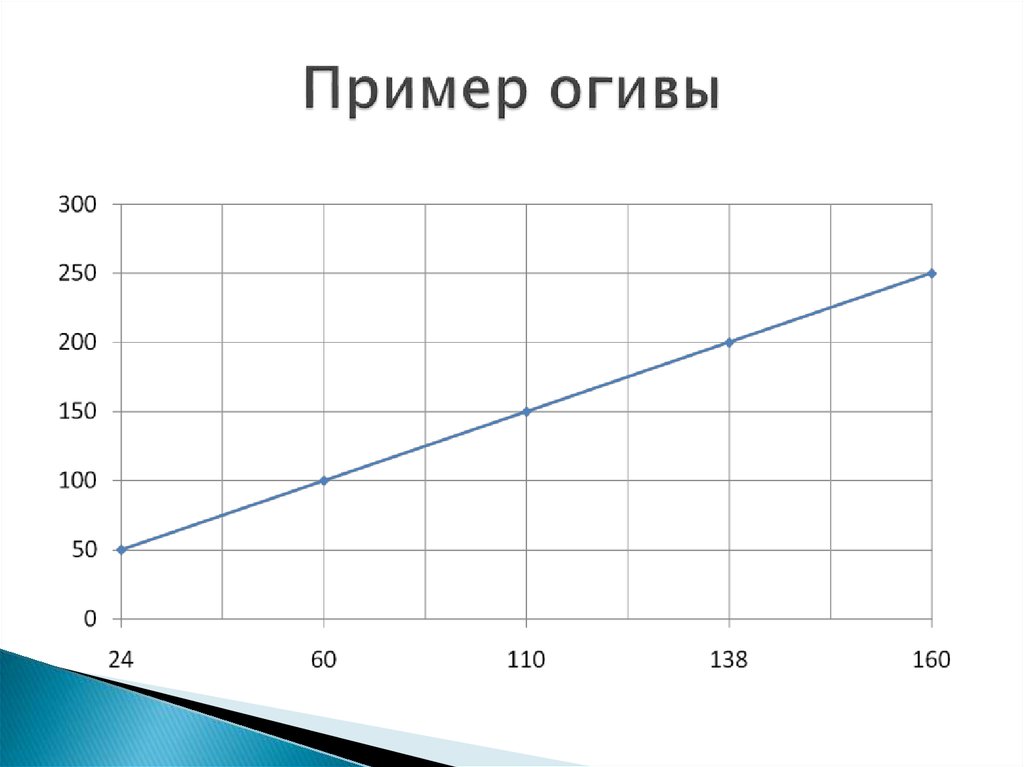
Огива – это кумулята, в которой оси
поменяны местами

23. Пример кумуляты

24. Пример огивы

25. Меры уровня, или средние

Наиболее употребительными в статистических
исследованиях являются три вида средних:
средняя арифметическая, мода и медиана.
средняя арифметическая:
. Если вместо частоты заданы частости qi, то формула имеет вид

26. Меры уровня

Медианой (обозначим Mе) называется такое
значение варьирующего признака, которое
приходится на середину вариационного ряда.
При нахождении медианы дискретного
вариационного ряда могут возникнуть два
случая: 1) число вариант нечетно (k=2m+1), 2)
число вариант четно (k=2m). В первом случае
Me=xm+1, т. е. медиана равна центральной
(срединной) варианте ряда, во втором случае
Me,=(xm+xm+1)/2, т.е. медиана принимается
равной полу сумме находящихся в середине
ряда вариант.

27. Меры уровня

Модой (обозначим Мо) называется варианта,
наиболее часто встречающаяся в данном
вариационном ряду

28. Показатели вариации

Размах вариации показывает разность
между наибольшим и наименьшим
значениями признака (R=xmax-xmin).
Достоинством этого показателя является
простота расчета. Однако возможности его
применения ограничены, так как эта
характеристика является наиболее грубой
из всех мер рассеяния.

29. Показатели вариации

Дисперсия, или средний квадрат
отклонения (обозначим σ2) есть средняя
арифметическая из квадратов отклонений
вариант от их средней арифметической, т.
е. в математической записи

30. Показатели вариации

Часто для исследования удобно представлять
меру рассеяния в тех же единицах
измерения, что и варианты. Тогда вместо
дисперсии используют среднее квадратичное
отклонение, которое является квадратным
корнем из дисперсии, т. е. среднее
квадратичное отклонение вычисляется по
формуле

31. Генеральная совокупность и выборка

Вся подлежащая изучению совокупность
объектов называется генеральной
совокупностью
Та часть объектов которая попала на
проверку или исследование называется
выборочной совокупностью или выборкой.
Число элементов в генеральной
совокупности и в выборке называется
объемом.

32. Типы выборок

Собственно-случайная
Механическая выборка (члены из
генеральной совокупности отбираются
через определенный интервал)
Типическая (генеральная совокупность
разбита на непересекающиеся группы, а
затем образуются собственно-случайные
выборки из каждой группы)

33. Характеристики генеральной и выборочной совокупности

Средняя арифметическая распределения признака
генеральной совокупности называется генеральной
средней, а дисперсия этого распределения –
генеральной дисперсией
m
x0
xi Ni
i 1
N
m
02
2
(
x
x
)
i 0 Ni
i 1
N

34. Характеристики генеральной и выборочной совокупности

Средняя арифметическая распределения
признака в выборочной совокупности
называется выборочной средней, а дисперсия
этого распределения – выборочной
дисперсией
m
x0
xi ni
i 1
n
m
02
2
(
x
x
)
i 0 ni
i 1
n

35. Характеристики генеральной и выборочной совокупности

Генеральной долей p признака А называется
отношение числа M членов генеральной
совокупности с признаком А к ее объему
M
p
N
Выборочной долей признака А называется
отношение числа m членов выборочной
совокупности с признаком А к ее объему
m
n

36. Случайные величины

Случайной называют величину, которая в результате испытания примет одно и
только одно возможное значение, наперед неизвестное и зависящее от
случайных событий, которые заранее не могут быть учтены.
Обозначения случайных величин: X, Y, Z; значения — x, y, z.
Дискретной (прерывной) называется случайная величина, которая принимает
отдельные, изолированные возможные значения с определенными
вероятностями.
Число возможных значений дискретной случайной величины может быть как
конечным, так и бесконечным (счетным).
Для задания дискретной случайной величины недостаточно перечислить все ее
возможные значения,
нужно еще указать их вероятности.

37.

Законом распределения дискретной случайной величины называют
соответствие между возможными значениями и их вероятностями. Его
можно задать в виде таблицы, аналитически и графически.
При табличном задании закона распределения дискретной случайной
величины первая строка таблицы содержит возможные значения (как
правило, в порядке возрастания), а вторая строка — их вероятности.
Х x1 x2 … xk -1 xk
Р р1 р2 … рk -1 рk
Поскольку в одном испытании случайная величина принимает одно и только
одно возможное
значение, заключаем, что события X = x1, X = x2, …, X = xk, образуют полную
группу,
следовательно, сумма вероятностей этих событий равна единице:
k
k
P
(
X
x
)
pi 1
i
i 1
i 1

38.

Числовые характеристики
дискретных случайных величин
Математическое ожидание дискретной случайной величины
Математическим ожиданием дискретной случайной величины Х называется
сумма произведений всех ее возможных значений на соответствующие
вероятности
k
M ( X ) xi pi xi pi x2 p2 xk pk
i 1
Замечание. Из определения следует, что математическое ожидание
дискретной случайной величины есть неслучайная (постоянная) величина.

39.

Вероятностный смысл математического
ожидания
Пусть проведено n испытаний, в которых случайная величина Х приняла m1
раз значение х1, m2 раз значение х2, …, mk раз значение хk, причем m1 + m2 +
… + mk = n. Тогда сумма всех значений, принятых Х равна m1х1 + m2 х2 + … +
mkхk. Среднее арифметическое всех значений, принятых этой случайной
величиной
X
x1m1 x2 m2 xk mk
m
m
m
x1 1 x2 2 xk k
n
n
n
n
Заметим, что mi/n = wi — относительной частоте значения хi. допустим, что
число испытаний велико. Тогда wi ≈ pi. Заменяя в последнем выражении
относительные частоты вероятностями, получим
X x1 p1 x2 p2 xk pk
X M (X )
Замечание.
Математическое ожидание приближенно равно (тем точнее, чем больше
число испытаний) среднему арифметическому наблюдаемых значений
случайной величины.
xi pi
xC
pi 1 xC M ( X )
pi

40.

Свойства математического ожидания
1. Математическое ожидание постоянной величины С равно самой постоянной:
М(С) = С.
Доказательство. Рассмотрим постоянную величину С как дискретную
случайную величину, которая имеет одно возможное значение С и принимает
его с вероятностью р = 1. Следовательно, М(С) = С ∙ 1 = С.
2. Постоянный множитель можно выносить за знак математического ожидания:
М(СХ) = С ∙ М(Х).
Доказательство.
СХ Сx1 Сx2 … Сxk
Р р1 р2 … рk
M (CX ) Cx1 p1 Cx2 p2 Cxk pk C ( x1 p1 x2 p2 xk pk ) CM (X )
3. Математическое ожидание произведения двух независимых
случайных величин равно произведению их математических ожиданий:
М(ХY) = М(Х) ∙ М(Y).
Доказательство.
ХY x1y1 x1y2 x2y1 x2y2
Р р1g1 р1g2 р2g1 р2g2
M ( XY ) x1 y1 p1g1 x1 y2 p1g 2 x2 y1 p2 g1 x2 y2 p2 g 2
y1g1 ( x1 p1 x2 p2 ) y2 g 2 ( x1 p1 x2 p2 ) ( x1 p1 x2 p2 )( y1g1 y2 g 2 ) M ( X )M (Y )

41.

4. Математическое ожидание суммы двух случайных величин равно
сумме математических ожиданий слагаемых: М(Х + Y) = М(Х) + М(Y).
Доказательство.
Х+Y x +y x +y x +y x +y
Р
1
р11
1
1
р12
2
2
р21
1
2
р22
2
M ( X Y ) ( x1 y1 ) p11 ( x1 y2 ) p12 ( x2 y1 ) p21 ( x2 y2 ) p22
x1 ( p11 p12 ) x2 ( p21 p22 ) y1 ( p11 p21 ) y2 ( p12 p22 )
Докажем, что р11 + р12 = р1.
Событие {Х = х1}влечет за собой событие {Х + Y = (х1 + y1 или х1 + y1)} и
обратно
P( X x1 ) p1
Аналогично,
P X Y ( x1 y1 или x1 y2 ) p11 p12
p1 p11 p12
p2 p21 p22 , g1 p11 p21, g 2 p12 p22 .
M ( X Y ) ( x1 p1 x2 p2 ) ( y1g1 y2 g 2 ) M ( X ) M (Y )

42.

Дисперсия дискретной случайной
величины
Пусть Х — случайная величина и М(Х) — ее математическое ожидание.
Отклонением называют случайную величину Х - М(Х) , возможные значения
которой равны разностям между возможными значениями случайной величины
и ее математическим ожиданием, а вероятности величины Х - М(Х) равны
вероятностям величины Х.
Х x1 x2 … xk
Х – М(Х) x1– М(Х) x2– М(Х) … xk– М(Х)
Р р1 р2 … рk
Р
р1
р2
…
рk
Теорема. Математическое ожидание отклонения равно 0: М[Х - М(Х) ] = 0.
Дисперсией (рассеянием) дискретной случайной величины называют
математическое ожидание
квадрата отклонения случайной величины от ее математического ожидания:
D( X ) M [ X M ( X )]2
Х x1 x2 … xk
Р р1 р2 … рk
[Х – М(Х)]2 [x1– М(Х)]2 [x2– М(Х)]2 … [xk– М(Х)]2
Р
р1
р2
…
рk
D( X ) M [ X M ( X )]2 xi M ( X ) 2 pi

43.

Теорема. Дисперсия равна разности между математическим ожиданием
квадрата случайной величины Х и квадратом ее математического
ожидания: D(X) = М(Х 2) – [М(Х)]2.
Доказательство. Поскольку математическое ожидание М(Х) — есть
величина постоянная, то 2 М(Х) и [М(Х)]2 — также постоянные величины.
Поэтому
D( X ) M [ X M ( X )]2 M [ X 2 2 X M ( X ) M 2 ( X )] M ( X 2 ) 2M ( X ) M ( X ) M 2 ( X )
= М(Х 2) – [М(Х)]2.
Пример. Найти дисперсию случайной величины Х, заданной законом
распределения
Х 1 2 5
Р 0,3 0,5 0,2
Решение. Математическое ожидание: М(Х) = 1 ∙ 0,3 + 2 ∙ 0,5 + 5 ∙ 0,2 = 2,3.
Закон распределения квадрата случайной величины
Х2 1
Р 0,3
4
0,5
25
0,2
Математическое ожидание квадрата случайной величины: М(Х) = 1 ∙ 0,3 + 4∙
0,5 + 25 ∙ 0,2 = 7,3.
Дисперсия: D(X) = 7,3 – 2,32 = 2,01.

44.

1. Дисперсия постоянной величины С равна нулю: D(С) = 0.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в
квадрат: D(CX) = C2D(X).
3. Дисперсия суммы двух независимых случайных величин равна сумме
дисперсий этих величин: D(X + Y) = D(X ) + D(Y).
4. Дисперсия разности двух независимых случайных величин равна
сумме дисперсий этих величин:
D(X - Y) = D(X ) + D(Y).
св во
3
св во
2
D( X Y ) D( X ( Y )) D( X ) D( Y ) D( X ) ( 1) 2 D(Y ) D( X ) D(Y )

45.

Среднее квадратическое отклонение
Дисперсия имеет размерность квадрата случайной величины. Для того чтобы
иметь показатель рассеяния случайной величины той же размерности, что и
размерность случайной величины, извлекают корень квадратный из
дисперсии.
Средним квадратическим отклонением случайной величины Х называют
квадратный корень из дисперсии
( X ) D( X ).
Теорема. Среднее квадратическое отклонение суммы конечного числа
взаимно независимых случайных величин равно
квадратному корню из суммы квадратов средних квадратических отклонений
этих величин
( X1 X 2 X n ) 2 ( X1 ) 2 ( X 2 ) 2 ( X n ).

46.

Начальные и центральные теоретические
моменты
Х 1 2
5 100
Р 0,6 0,2 0,19 0,01
M ( X ) 1 0,6 2 0,2 5 0,19 100 0,01 2,95
Х2 1 4 25 10000
Р 0,6 0,2 0,19 0,01
M ( X ) 1 0,6 4 0,2 25 0,19 10000 0,01 106,15
Начальным моментом порядка k случайной величины Х называют
математическое ожидание
k
величины X k : k M ( X )
2 и т.д. D ( X ) 2 12 .
M
(
X
)
1 M ( X ), 2
В частности,
Центральным моментом порядка k случайной величины Х называют
математическое ожидание величины (Х – М (X))k :
k M X M ( X ) k
В частности,
1 M X M ( X ) 0,
2 M X M ( X ) 2 D(X )
2 2 12 , 3 3 3 2 1 2 13 , 4 4 4 3 1 6 2 12 3 14 .

47.

Функция распределения
Функцией распределения называют функцию F(x), определяющую
вероятность того, что случайная величина Х в результате испытания примет
значение, меньшее х, т.е.
F(x) = P(X < x).
Свойства функции распределения
1. Значения функции распределения принадлежат отрезку [0; 1]:
0 ≤ F(x) ≤ 1.
2. Функция распределения непрерывна слева.
3. F(x) — неубывающая функция, т.е. F(x1) ≤ F(x2), если x1 < x2.
Доказательство. Пусть x1 < x2.
(**)
{X < x2} = {X < x1 и x1 ≤ X < x2}
P(X < x2) = P(X < x1) + P(x1 ≤ X < x2)
P(X < x2) - P(X < x1) = P(x1 ≤ X < x2)
F(x2) – F(x1) = P(x1 ≤ X < x2)
lim F ( x) 0; lim F ( x) 1.
x
x
Поскольку P(x1 ≤ X < x2) ≥ 0, то
F(x1) ≤ F(x2)

48.

Итак, каждая функция распределения является неубывающей, непрерывной
слева и удовлетворяющей условиям F(- ) = 0, F(+ ) = 1.
Верно и обратное: каждая функция, удовлетворяющая указанным условиям,
может рассматриваться как функция распределения некоторой случайной
величины.
Для дискретной случайной величины, заданной законом распределения
Х x1 x2 … xk
Р р1 р2 … рk
функция распределения F(х) задается равенством
F ( x) pi .
xi x
Таким образом, функция распределения дискретной случайной величины
является
ступенчатой функцией со скачками высотой pi в точках xi.

49.

Непрерывная случайная величина
Случайная величина называется непрерывной, если существует
неотрицательная функция р(х), удовлетворяющая при любых х равенству
x
F ( x) p( z )dz.
Функция р(х) называется плотностью распределения вероятностей.
Если F(x) абсолютно непрерывна, а тем более, дифференцируема при всех х,то
ее производная и является плотностью распределения:
F ( x) p( x).
Функция распределения иногда называется интегральной,
а плотность — дифференциальной функцией распределения.
Если возможные значения случайной величины принадлежат интервалу [a, b],
то
b
p ( x)dx 1.
a
Если возможные значения случайной величины принадлежат всей
числовой оси, то
p( x)dx 1.

50.

Свойства функции распределения непрерывной случайной величины
1. Вероятность того, что непрерывная случайная величина Х примет одно
определенное значение равно 0.
Доказательство. Положим в (**) x2 = x1 + x. Тогда
P(x1 ≤ X < x1 + x) = F(x1 + x) – F(x1).
Пусть x 0. Тогда, в силу непрерывности F(x)
F(x1 + x) – F(x1) 0
P(X = x1) = 0.
P(a ≤ X < b) = P(a < X < b) = P(a < X ≤ b) = P(a ≤ X ≤ b).
2. Если возможные значения непрерывной случайной величины принадлежат
интервалу (a, b), то
а) F(x) = 0 при x ≤ a;
б) F(x) = 1 при b ≤ x.

51.

Вероятность попадания непрерывной
случайной величины в заданный интервал
Теорема. Вероятность того, что непрерывная случайная величина Х примет
значение, принадлежащее интервалу (a, b), равна определенному интегралу
от плотности распределения, взятому в пределах от a до b:
b
P (a x b) p ( x)dx.
Доказательство.
a
Воспользуемся соотношением (**):
P(a ≤ X < b) = F(b) – F(a)
По формуле Ньютона-Лейбница
b
b
a
a
F (b) F (a ) F ( x)dx p ( x)dx
Таким образом,
b
P (a x b) p ( x)dx.
a
Поскольку P(a ≤ X < b) = P(a < X < b), то
b
P(a x b) p( x)dx.
a

52.

Числовые характеристики непрерывных случайных величин
Математическим ожиданием непрерывной случайной величины Х,
возможные значения которой принадлежат интервалу [a, b], называют
определенный интеграл
b
M ( X ) xp ( x)dx.
a
Если возможные значения случайной величины принадлежат всей
числовой оси, то
M (X )
xp ( x)dx.
(предполагается, что несобственный интеграл сходится абсолютно, т.е.
существует интеграл
x p( x)dx.

53.

Дисперсией непрерывной случайной величины называют
математическое ожидание квадрата ее отклонения.
Если возможные значения случайной величины принадлежат интервалу [a, b],
то
b
D ( X ) [ x M ( x)]2 p ( x)dx.
a
Если возможные значения случайной величины принадлежат всей числовой
оси, то
D( X ) [ x M ( x)]2 p ( x)dx.
b
Замечание.
D ( X ) x p ( x)dx [ M ( x)] .
a
2
2
D( X )
x
2
p ( x)dx [ M ( x)]2 .
Среднее квадратическое отклонение непрерывной случайной величины
( X ) D( X ).
Медианой непрерывной случайной величины называется такое ее значение m,
при котором F(m)=0,5;другими словами,
P( X m) P( X m) 0,5.
Квантилью порядка р (0 < р < 1) называется корень уравнения F(х) = р.
Если случайная величина непрерывна, то модой распределения называют то
значение аргумента, при котором плотность достигает максимума.
Модой дискретной случайной величины называют ее наиболее вероятное
значение.

54.

Равномерное распределение вероятностей
Распределение вероятностей называется равномерным, если на интервале,
которому принадлежат все возможные значения случайной величины,
плотность распределения сохраняет постоянное отличное от нуля значение:
р
0 при x a,
p( x) C при a x b,
0 при b x.
Замечание.
p( x) C f ( x)
1
b a
b
1
a
f ( x)dx
C f ( x)dx 1 С b
a
b
Cdx 1 С b
1
С
dx
a
1
b a
a
0
1
p ( x)
b a
0
при
x a,
при
a x b,
0
a
b
х
при b x.
Числовые характеристики равномерно распределенной случайной величины
b
1 b
M ( X ) xp ( x)dx
xdx
b aa
a
M (X )
a b
2
2
1 b 2
a b
D ( X ) x p ( x)dx [ M ( x)] .
x dx
b
a
2
a
a
b
2
2
(b a) 2
D( X )
12

55.

Нормальное распределение
Нормальным называется распределение вероятностей непрерывной
случайной величины, которое описывается плотностью
0 ( x )
1
e
2
( x a )2
2 2
Нормальное распределение определяется двумя параметрами: а и .
1
M ( X ) x 0 ( x)dx
x e
2
( z a)e
2
2
z
2
( x a )2
2 2
ze
2
dz
dx
2
z
2
dz
x a
dx dz
z
a
e
2
2
z
2
dz
ze
2
z
2
dz 0,
M (X ) a
1
D( X )
( x a) 2 e
2
( x a )2
2 2
dx
2
x a
2
z
2
2
z ze dz
2
dx dz
z
D( X ) 2
(X )
e
2
z
2
dz
2 a.

56.

Общим называется нормальное распределение с произвольными
параметрами а и . Нормированным называется нормальное распределение
с параметрами а = 0 и = 1. Таким образом, если Х — нормальная величина,
то U = (х – а)/ — нормированная нормальная величина, причем M(U) = 0,
D(U) = 1.
Плотность нормированного распределения (нормированная функция Гаусса)
x2
2
1
( x)
e .
2
График плотности нормального распределения называют нормальной
кривой (кривой Гаусса)
y
a=
0
= 0,5
a>
0
=1
=2
0
x=a
x

57.

1. Функция F0(x) общего нормального распределения
и функция F(х) нормированного распределения
связаны соотношением
F0 ( x)
F ( x)
x
1
e
2
x
1
e
2
z2
2
( z a )2
2 2
dz
dz
x a
F0 ( x) F
.
2. Вероятность попадания нормированной нормальной величины Х в интервал
(0, х) вычисляется при помощи функции Лапласа:
x
1 x z22
P (0 X x) ( z )dz
e dz (x).
2
0
0
0
3. ( x)dx 1
( x)dx
1
1
1
P( X 0) F ( x) ( x)
2
2
2

58.

Вероятность попадания в заданный интервал нормальной
случайной величины
P ( X ) p ( x)dx
P ( X )
1
e
2
( x a )2
2 2
dx
a
a
x a x z a, dx dz;
x
z
x
z
,
z
,
2
2
1
1
P ( X )
a
1
e
2 a
z2
2
1
dz
2
a
e
0
z2
2
0
1
dz
e
2 a
z2
2
dz 1
2
a
a
a
P( X )
0
e
z2
2
dz
1
2
a
e
0
z2
2
dz

59.

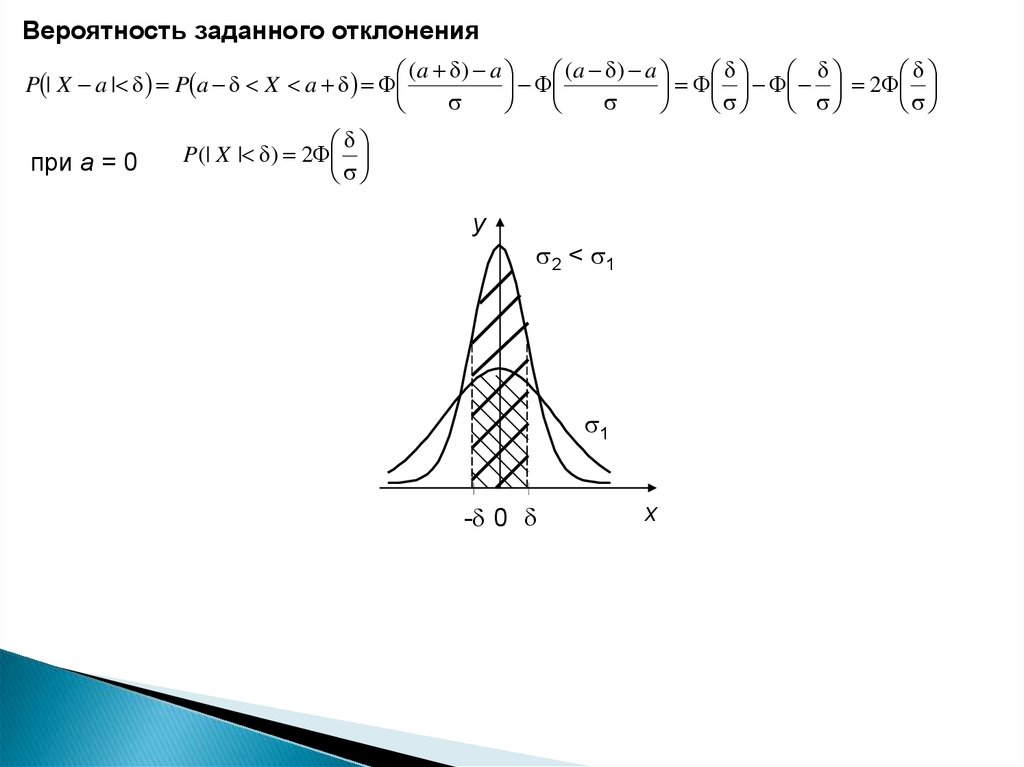
Вероятность заданного отклонения
(a ) a
(a ) a
P | X a | P a X a
2
при а = 0
P(| X | ) 2
y
2 < 1
1
- 0
x

60.

Правило «трех сигм»
P | X a | 2
t
P | X a | t 2 t
t 3
P | X a | 3 2 3 2 0,49865 0,9973
P | X a | 3 0,9973 P | X a | 3 0,0027
Вероятность того, что отклонение по абсолютной величине будет
меньше утроенного среднего квадратического отклонения, равна 0,9973.
Другими словами, вероятность того, что абсолютная величина отклонения
превысит утроенное среднее квадратическое отклонение очень мала, а
именно равна 0,0027.
Это означает, что такое может произойти лишь в 0,27% случаев.
Такие события исходя из принципа невозможности маловероятных событий
можно считать практически невозможными.
В этом и состоит сущность правила трех сигм:
если случайная величина распределена нормально, то абсолютная
величина ее отклонения от математического ожидания не превосходит
утроенного среднего квадратического отклонения.

61.

При изучении распределений, отличных от нормального, возникает
необходимость качественно оценить это различие. С этой целью вводят
специальные числовые характеристики, в частности, асимметрию и эксцесс.
Для нормального распределения эти характеристики равны нулю. Поэтому
небольшие значения асимметрии и эксцесса дают возможность предположить,
что такое распределение близко к нормальному; большие значения указывают
на значительное отклонение от нормального распределения.
Можно показать, что для симметричных распределений каждый центральный
момент нечетного порядка равен нулю. Для несимметричных распределений
такие моменты отличны от нуля. Поэтому центральный момент третьего
порядка используется для оценки асимметрии.
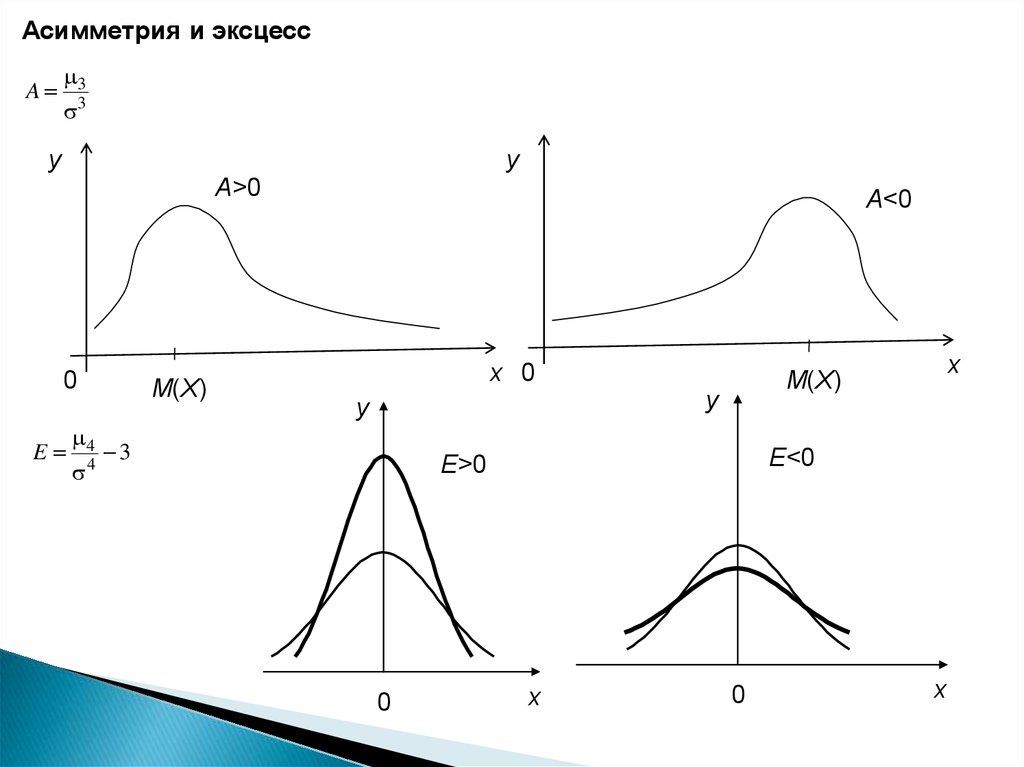
Асимметрия положительна, если более пологая часть кривой распределения
расположена справа от математического ожидания и отрицательна, если
слева.
Для оценки «крутизны» подъема распределения по сравнению с нормальным
используется характеристика, называемая эксцессом.
Если эксцесс больше нуля, то кривая такого распределения имеет более
высокую и острую вершину, чем нормальная кривая, если эксцесс меньше
нуля, то сраниваемая кривая имеет более низкую и плоскую вершину, чем
нормальная.

62.

Асимметрия и эксцесс
A
3
3
у
у
А>0
0
E
M(X)
4
4
А<0
х 0
y
y
3
E<0
E>0
0
х
M(X)
x
0
x

63.

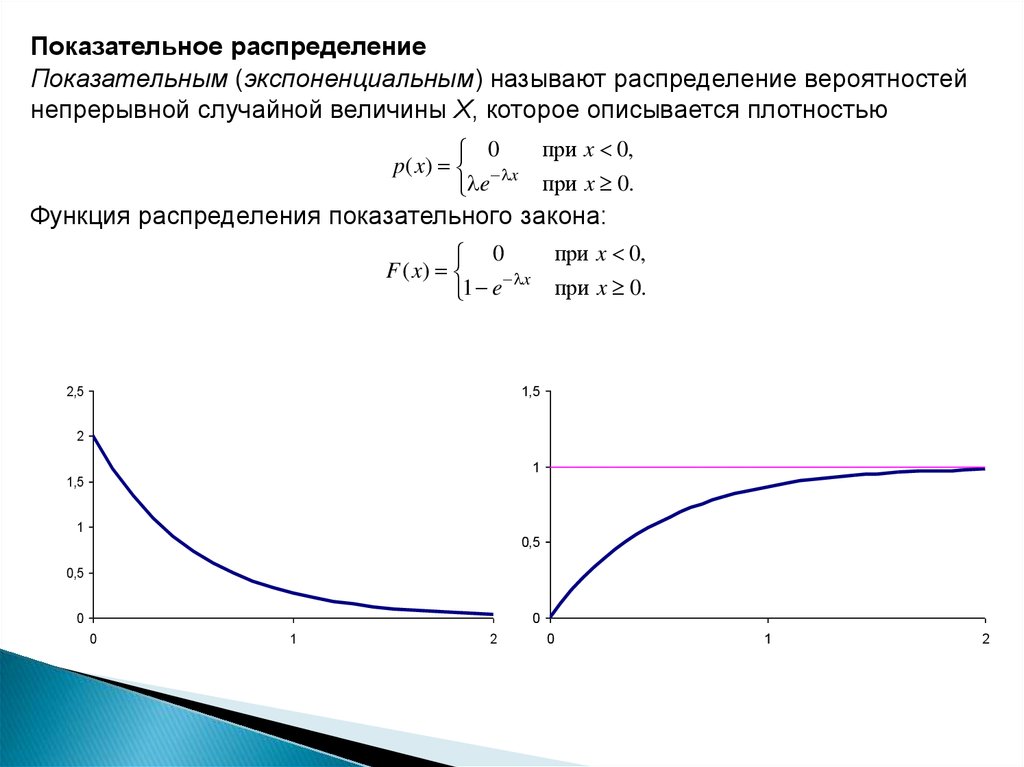
Показательное распределение
Показательным (экспоненциальным) называют распределение вероятностей
непрерывной случайной величины Х, которое описывается плотностью
при x 0,
0
p ( x ) x
e
при x 0.
Функция распределения показательного закона:
при x 0,
0
F ( x)
x
1 e
2,5
при x 0.
1,5
2
1
1,5
1
0,5
0,5
0
0
0
1
2
0
1
2

64.

Вероятность попадания в заданный интервал
показательно распределенной случайной величины
Воспользуемся формулой P(a < X < b) = F(b) – F(a).
F ( x ) 1 e x ,
Учитывая, что при х ≥ 0
получаем
F (b) 1 e b ,
F ( a ) 1 e a ,
P ( a x b ) e a e b .
Числовые характеристики показательного распределения
Пусть случайная величина Х распределена по показательному закону
0
p ( x ) x
e
Математическое ожидание
Дисперсия
D( X )
x
x
2
M (X )
при x 0,
при x 0.
x
x
x
xp ( x)dx xe dx
x
2 x
p ( x)dx [ M ( X )] x e
2
D( X )
2
M (X )
1
x
2
1
dx ; x 2e x dx 2
1
2
Среднее квадратическое отклонение
1
( X ) .

65.

66. Система двух случайных величин

Закон распределения двумерной случайной величины
Кроме одномерных случайных величин изучают случайные величины,
возможные значения которой определяются двумя, тремя, …, n числами.
Такие величины называют соответственно двумерными, трехмерными, и т.д.
Двумерную случайную величину будем обозначать (X, Y ).
Каждую из величин X, Y называют составляющей (компонентой) двумерной
случайной величины.
Аналогично n-мерная случайная величина определяется как система
n случайных величин.

67.

Закон распределения двумерной случайной величины
Законом распределения дискретной двумерной случайной величины называют
перечень возможных значений этой величины, т.е. пар (xi, yj) и их вероятностей
pij = p (xi, yj) (i = 1, …, n; j = 1, …, m).
Обычно закон распределения двумерной дискретной случайной величины
задают в виде таблицы.
Y
X
P(Y = yj)
x1
x2
… xi … xn
y1
p(x1, y1)
p(x2, y1) … p(xi, y1) … p(xn, y1) P(Y y ) p( x , y )
n
1
…
…
…
yj
p(x1, yj)
…
…
ym
p(x1, ym)
…
…
…
1
p(x2, yj) … p(xi, yj) … p(xn, yj)
…
…
…
…
…
p(x2, ym) …p(xi, ym)… p(xn, ym)
1
2
m
m
1
i
…
P(X = xi) P( X x ) P( X x )
p( x , y ) p( x , y )
j 1
i 1
j
j 1
2
j
∑ ∑ p(xi, yj) = 1
∑ P(X = xi) = 1
∑ P(Y = yj) = 1
События {X = xi, Y = yj} образуют полную группу
Событие {X = x1=} ({X = x1; Y = y1или
} или {X = x1; Y = y)m}
} {X = x1; Y = y2…

68.

Функция распределения двумерной случайной величины
Рассмотрим двумерную случайную величину (X, Y) (дискретную или непрерывную).
Функцией распределения двумерной случайной величины (X, Y) называют
функцию F (x, y), определяющую для каждой пары чисел (x, y)
вероятность того, что X примет значение, меньшее x, Y примет значение меньше y:
F (x, y) = P (X < x, Y < y)
x 1 1
x 1
1
F
(
x
,
y
)
arctg
arctg
y
Пример.
2 2
3 2
(x, y)
Найти Р(Х < 2, Y < 3).
Решение.
2 1 1
3 1 9
1
P( X 2,Y 3) F (2,3) arctg arctg
2 2
3 2 16
x
Свойства функции распределения двумерной случайной величины
1. 0 ≤ F (x, y) ≤ 1.
2. F (x2, y) ≥ F (x1, y), если x2 ≥ x1;
F (x, y2) ≥ F (x, y1), если y2 ≥ y1.
3. F(-∞, y) = 0;
F(x, -∞) = 0;
F(-∞, -∞) = 0;
F(∞, ∞) = 1.
4. F(x, ∞) = F1 (x);
F(∞, y) = F (y).

69.

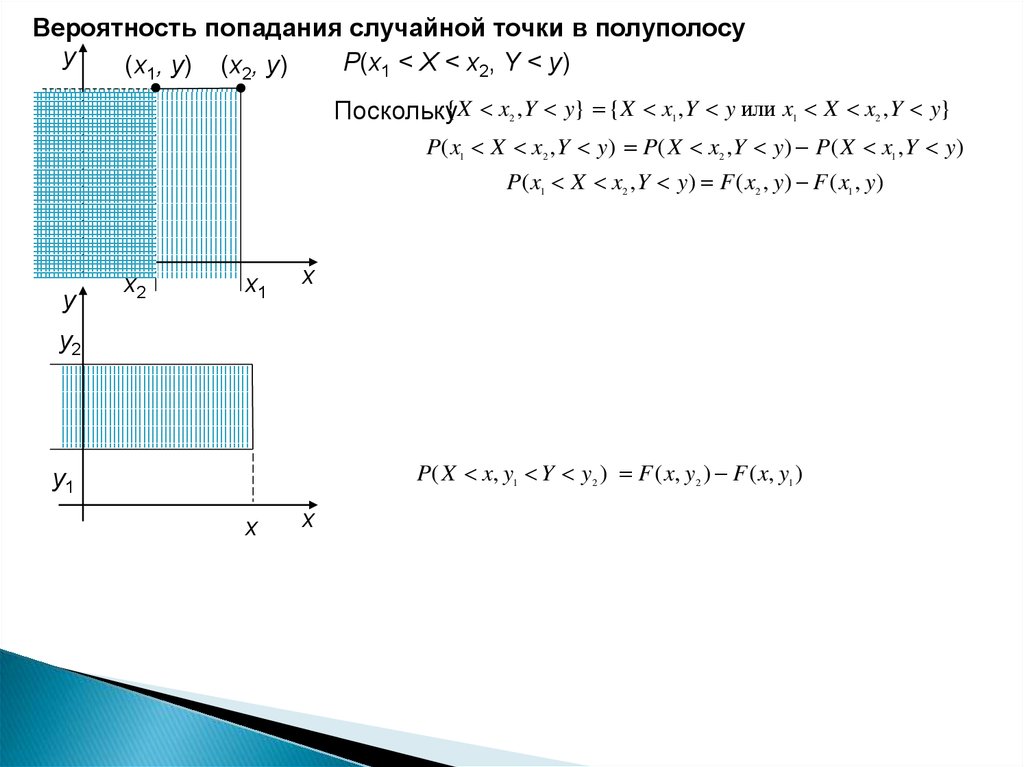
Вероятность попадания случайной точки в полуполосу
y
P(x1 < X < x2, Y < y)
(x1, y) (x2, y)
Поскольку{ X x ,Y y} { X x ,Y y или x X x ,Y y}
2
1
1
2
P( x1 X x2 , Y y) P( X x2 ,Y y) P( X x1 , Y y)
P( x1 X x2 ,Y y) F ( x2 , y) F ( x1 , y)
y
x2
x1
x
y2
P( X x, y1 Y y2 ) F ( x, y2 ) F ( x, y1 )
y1
x
x

70.

Вероятность попадания случайной точки в прямоугольник
y
A(x1, y2)
B(x2, y2)
C(x1, y1)
D(x2, y1)
x
P( x1 X x2 , y1 Y y2 ) P( x1 X x2 ,Y y2 ) P( x1 X x2 , Y y1 )
P( x1 X x2 , y1 Y y2 ) [ F ( x2 , y2 ) F ( x1 , y2 )] [ F ( x2 , y1 ) F ( x1 , y1 )]

71.

Плотность совместного распределения вероятностей двумерной случайной в
Будем предполагать, что функция распределения F(x, y) непрерывна
и имеет почти всюду непрерывные частные производные второго порядка.
Плотностью совместного распределения вероятностей p(x, y)
двумерной непрерывной случайной величины называют F ( x, y)
p( x, y )
вторую смешанную производную от функции распределения:
x y
Зная плотность совместного распределения, можно найти функцию распределения
F ( x, y ) f ( x, y )dxdy
по формуле
2
y x

72.

Вероятность попадания случайной точки в двумерную область
P( x1 X x2 , y1 Y y2 ) [ F ( x2 , y2 ) F ( x1 , y2 )] [ F ( x2 , y1 ) F ( x1 , y1 )]
x2 x1 x;
y
A(x1, y1 + y)
B(x1 + x, y1 + y)
y2 y1 y.
PABCD Fxy ( , ) x y p( , ) x y
x1 x1 x, y1 y1 y
D(x1 + x, y1)
C(x1, y1)
x
y
n m
P(( X ,Y ) D ) p( i , i ) x y
i 1 j 1
x 0, y 0
y
Di
P(( X ,Y ) D) p( x, y)dxdy
D
x
x

73.

Свойства двумерной плотности вероятности
1. Двумерная плотность вероятности неотрицательна: p(x, y) ≥ 0.
2. p( x, y )dxdy 1
Отыскание плотностей вероятности составляющих двумерной случайной вел
Пусть известна плотность совместного распределения вероятностей
системы двух случайных величин p(x, y).
Найдем плотность распределения составляющей X.
dF ( x)
Обозначим через F1(x) функцию распределения составляющей Х.
p X ( x) 1
По определению плотности распределения одномерной случайной величины
dx
F ( x, y )
y
x
p( x, y )dxdy
F1 ( x) F ( x, )
F1 ( x)
x
p( x, y )dydx
p X ( x)
dF1 ( x)
p ( x, y )dy
dx
p( x, y )dy
pY ( y )
p( x, y )dx
Плотность распределения одной из составляющих равна несобственному интеграл
с бесконечными пределами от плотности совместного распределения системы,
причем переменная интегрирования соответствует другой составляющей.

74.

Условные законы распределения составляющих системы дискретных случай
Для того чтобы охарактеризовать зависимость между составляющими случайной в
введем понятие условного распределения.
Рассмотрим дискретную двумерную случайную величину (X, Y).
Пусть возможные значения составляющих таковы: x1, x2, …, xn, y1, y2, …, ym.
Допустим, что в результате испытания величина Y приняла значение yj: Y = yj;
при этом Х примет одно из возможных значений x1, или x2, … или xn.
Обозначим p(xi | yj) вероятность того, что случайная величина Х примет значение xi
при условии, что Y = yj. Эта вероятность, вообще говоря, не будет равна
безусловной вероятности p(xi).
Условным распределением составляющей X при Y = yj называют совокупность
условных вероятностей p(x1 | yj), p(x2 | yj), …, p(xn | yj), вычисленных в предположени
что событие {Y = yj} уже наступило.
Аналогично определяется условное распределение составляющей Y.
Зная закон распределения двумерной случайной величины, можно, пользуясь фор
условной вероятности, вычислить условные
p( xi , y j ) законы распределения составляющих
( xi | y j )
,X,(iв предположении,
1,..., n)
Например, условный закон pраспределения
что событие Y = yj
p( y j )
p( xi , y j )
может быть найден по формуле
p
(
y
|
x
)
, ( j 1,..., m)
Аналогично, условные законы распределения составляющей
Y:
j
i
p( xi )
Замечание. Сумма вероятностей условного распределения равна 1:
n
m
i 1
j 1
при фиксированном ypj ( xi | y j ) 1, при фиксированном xip( y j | xi ) 1

75.

Пример. Дискретная двумерная случайная величина задана следующим законом р
Y
x1
X
x2
x3
y1
0,10
0,30
0,20
0,60
y2
0,06
0,18
0,16
0,40
P(Y = yj)
Найти условные законы распределения составляющей X.
Решение. Найдем закон распределения составляющей Y:
3
3
i 1
i 1
P(Y y1 ) p ( xi , y1 ) 0,10 0,30 0,20 0,60. P(Y y2 ) p( xi , y2 ) 0,06 0,18 0,16 0,40.
p( xi , y j )
p
(
x
|
y
)
:
Далее, по формуле i j
p( y j )
0,30 1
p( x1, y1 ) 0,10 1
,
p( x1 | y1 )
, p( x2 | y1 )
0,60 2
p( y1 )
0,60 6
p( x3 | y1 )
0,20 1
,
0,60 3
3
p( xi | y1 ) 1;
i 1
3
0,16 2
p( x2 , y2 ) 0,06 3 p( x | y ) 0,18 9 ,
p( x3 | y2 )
, p ( xi | y2 ) 1.
p( x2 | y2 )
,
2
2
0,40 20
0,40 5 i 1
p ( y2 )
0,40 20

76.

Условные законы распределения составляющих системы непрерывных слу
Пусть (X, Y) — непрерывная случайная величина.
Условной плотностью (x | y) распределения составляющей X при данном значен
называют отношение плотности совместного распределения p(x, y) системы (X, Y)
к плотности распределения pY(y) составляющей
Y:
p( x, y)
( x | y)
pY ( y)
.
Отличие условной плотности (x | y) от безусловной pX(x) состоит в том,
что функция (x | y) дает распределение Х при условии Y = y;
функция pX (x) дает распределение х независимо от того,
какие из возможных значений приняла составляющая Y.
Аналогично определяется условная плотность
p( x, y ) составляющей Y при данном значе
( y | x)
p X ( x)
.
Если известна плотность совместного распределения p(x, y),
то условные плотности составляющих могут быть вычислены по формулам
( x | y )
p ( x, y )
, ( y | x)
p( x, y )dx
p ( x, y )
.
p( x, y )dy
Умножая безусловный закон распределения одной из составляющих на
условный закон распре- деления другой составляющей, найдем закон
распределения системы случайных
p( x, y) pY ( y)величин:
( x | y) p X ( x) ( y | x)
( x | y) 0, ( x | y )dx 1, ( y | x) 0, ( y | x)dy 1.
Свойства:

77.

Пример. Двумерная случайная величина (X, Y) задана плотностью совместного рас
1
f ( x, y ) r 2
0
при x 2 y 2 r 2 ,
при x 2 y 2 r 2 .
Найти условные законы распределения составляющих.
Решение.p( x, y)
( x | y)
pY ( y)
При x y r
2
2
.
r2 y2
2
| x | r 2 y 2
1
1
r 2
( x | y)
2 r 2 y2 2 r2 y2
r 2
1
2
2
( x | y) 2 r y
при | x | r 2 y 2
0 при | x | r 2 y 2
1
2
2
( y | x ) 2 r x
при | y | r 2 x 2
0 при | y | r 2 x 2
pY ( y )
r2 y2
1
r
2
dx
2 r2 y2
r 2

78.

Условное математическое ожидание
Условным математическим ожиданием дискретной случайной величины Y при X =
(x — определенное возможное значение Х)
называют сумму произведений возможных
m значений Y на их условные вероятности
M (Y | X x) yi p( yi | x).
i 1
M (Y | X x) y ( y | x)dy,
Для непрерывных величин
где (y | x) — условная плотность случайной величины Y при X = x .
Условное математическое ожидание M(Y | x) есть функция от х: M(Y | x) = f(x),
которую называют функцией регрессии Y на X.
Аналогично определяется условное математическое ожидание случайной величин
и функция регрессии Х на Y: M(Х | y) = (y).

79.

Пример. Задана двумерная случайная величина:
Y
y1 = 3
y2 = 6
X
x1 = 1
0,15
0,30
x2 = 3
0,06
0,10
x3 = 4
0,25
0,03
x4 = 8
0,04
0,07
Найти условное математическое ожидание составляющей Y при х1 = 1.
Решение.p( x1 ) 0,15 0,30 0,45
Найдем условное распределение вероятностей величины Y при Х = 1:
p( y1 | x1 )
p( x1, y1 ) 0,15 1
p( x1, y2 ) 0,30 2
; p( y2 | x1 )
.
0,45 3
p( x1 )
0,45 3
p( x1 )
M (Y | X x1 )
2
y j p( y j | x1 )
J 1
1
2
3 6 5.
3
3

80.

Зависимые и независимые случайные величины.
Две случайные величины X и Y называются независимыми, если закон распределе
не зависит от того, какие возможные значения приняла другая величина.
Условные распределения независимых величин равны их безусловным распределе
Теорема 1. Для того чтобы случайные величины X и Y были независимыми,
необходимо и достаточно, чтобы функция распределения системы (X , Y)
была равна произведению функций распределения составляющих:
F(x, y) = F1 (x) F2 (y).
Теорема 2. Для того чтобы случайные величины X и Y были независимыми,
необходимо и достаточно, чтобы плотность совместного распределения системы (X
была равна произведению плотностей распределения составляющих:
p(x, y) = pХ (x) pY (y).

81.

Корреляционный момент. Коэффициент корреляции.
Корреляционным моментом xy случайных величин X и Y называют
математическое ожидание произведения отклонений этих величин:
xy M {[ X M ( X )] [Y M (Y )]}
xy M ( XY ) M ( X ) M (Y )
n m
xy [ xi M ( X )][ y j M ( y )] p( xi , y j )
i 1 j 1
xy [ x M ( X )][ y M ( y )] p( x, y )dxdy
Корреляционный момент служит для характеристики связи между величинами X и
Теорема 1. Корреляционный момент двух независимых случайных величин X и Y р
xy M {[ X M ( X )] [Y M (Y )]} M [ X M ( X )] M [Y M (Y )] 0.
Доказательство.
| xy | Dx Dy
Теорема 2.
Коэффициентом корреляции rxy случайных величин X и Y называют отношение
корреляционного момента к произведению средних квадратических отклонений
xy
этих величин
rxy
x y
Теорема 3. |rxy| ≤ 1.
Замечание. Пусть дана случайная величина
Нормированная
Х.
случайная величина
X M (X )
, M ( X ' ) 0, D( X ' ) 1
x
rxyи Y
x 'y '
Для двух случайных величин X
X

82.

Коррелированность и зависимость случайных величин
Две случайные величины X и Y называют коррелированными, если их коэффициент
(или корреляционный момент) отличен от нуля;
случайные величины X и Y называют некоррелированными, если их корреляционны
Две коррелированные величины также зависимы.
Обратное предположение не верно, т.е. если две величины зависимы, то они могут
как коррелированными, так и некоррелированными.
Пример. Двумерная случайная величина (X, 2Y) задана
плотностью распределения
2
1
x
y
при
1,
6
9
4
p ( x, y )
2
2
0 при x y 1.
9
4
Доказать, что X и Y — зависимые некоррелированные величины.
(внутри эллипса)
Решение. Вычислим плотности
распределения составляющих
2
b
p X ( x) p ( x, y )dy
a
12
6
1 x / 9
dy
2 1 x 2 / 9
2
9 x2
9
pY ( y )
1
4 y2
2
p X ( x) pY ( y) p( x, y) X и Y — зависимые величины
xy [ x M ( X )][ y M ( y )] p ( x, y )dxdy
Поскольку pX(x) и pY(y) симметричны относительно Ох и Oy, то M(X) = M(Y) = 0.
xy
1
1
xy dxdy
ydy xdx 0. X и Y — некоррелированные величины
6 D
6

83.

Нормальный закон распределения на плоскости
Нормальным законом распределения на плоскости называют распределение веро
двумерной случайной величины, определяемое плотностью
f ( x, y)
1
2
2 x y 1 rxy
1
exp
2
2 1 rxy
x a1 y a2
( x a1 ) 2 ( y a2 ) 2
2rxy
2
2
x
y
y
x
Нормальный закон на плоскости задается пятью параметрами:
а1, а2 — математические ожидания;
x, y — средние квадратические отклонения;
rxy — коэффициент корреляции величин Х и Y.
Положив rxy = 0, получим
2
2
1
1 ( x a1 ) ( y a2 )
exp
f ( x, y )
2 x y
2 2x
2y
1
x
( y a )2
1
( x a1 ) 2
2 f ( x) f ( y )
exp
X
Y
exp
2
2
y 2
2
2
2
y
x
Таким образом, видим, что если составляющие нормально распределенной случа
некоррелированы (rxy = 0), то ее составляющие — независимы [f(x, y) = fX(x) fY(y)].
Можно показать, что если двумерная случайная величина распределена по норма
то и ее составляющие также распределены но нормальному закону.

84.

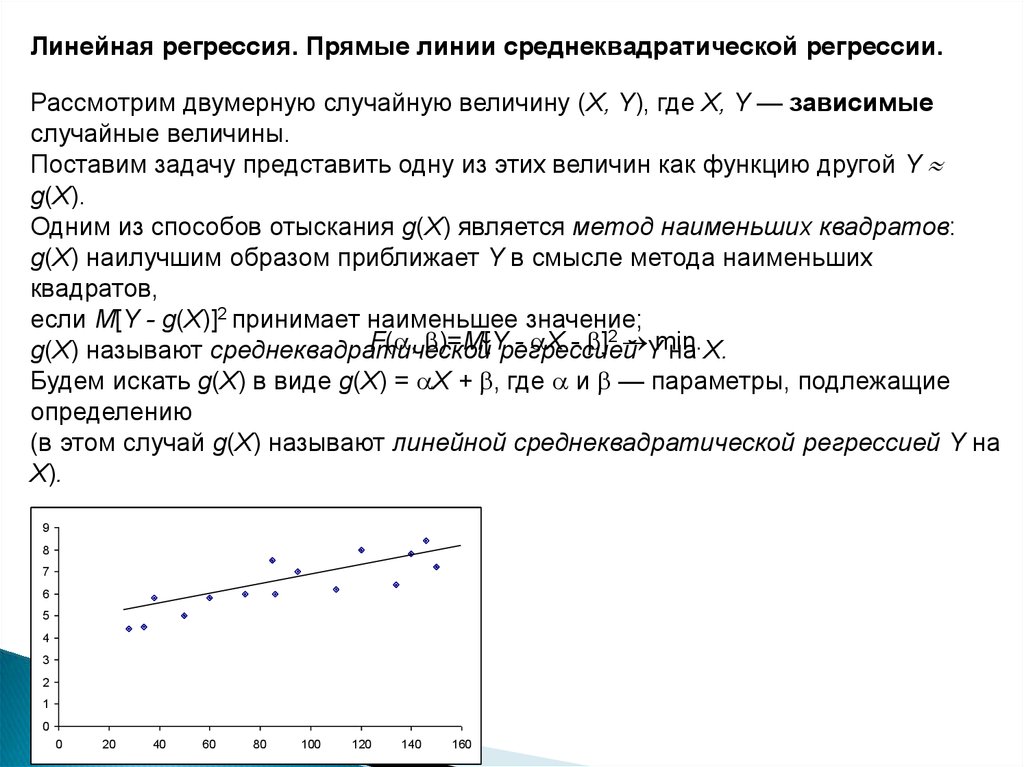
Линейная регрессия. Прямые линии среднеквадратической регрессии.
Рассмотрим двумерную случайную величину (X, Y), где X, Y — зависимые
случайные величины.
Поставим задачу представить одну из этих величин как функцию другой Y
g(X).
Одним из способов отыскания g(X) является метод наименьших квадратов:
g(X) наилучшим образом приближает Y в смысле метода наименьших
квадратов,
если M[Y - g(X)]2 принимает наименьшее значение;
F( , )=M[Yрегрессией
- X - ]2 Ymin.
g(X) называют среднеквадратической
на X.
Будем искать g(X) в виде g(X) = Х + , где и — параметры, подлежащие
определению
(в этом случай g(X) называют линейной среднеквадратической регрессией Y на
X).
9
8
7
6
5
4
3
2
1
0
0
20
40
60
80
100
120
140
160

85.

Линейная средняя квадратическая регрессия Y на X имеет вид
g ( X ) my r
y
x
( X mx ),
xy
m
M
(Y
),
r
.
m
M
(
X
),
D
(Y
)
,
x D(X ) , y
y
где x
y
y
x y
r
m
r
m
.
— коэффициент регрессии Y наyX,
x
x
x
y
y my r
( x mx ) — прямая среднеквадратической регрессии Y на Х.
x
min F ( , ) 2y (1 r 2 ) — остаточная дисперсия случайной величины Y относительно
которая характеризует величину ошибки при замене Y линейной функцией g(X) = Х
При r = ±1 остаточная дисперсия равна 0.
Другими словами, при r = ±1 Y и Х связаны линейной зависимостью.
x
mx rвид( y m y )
Прямая среднеквадратической регрессии Х на Y xимеет
Здесьr
x
— коэффициент регрессии X на Y,
y
y
2x (1 r 2 ) — остаточная дисперсия случайной величины X относительно Y.
Если r = ±1, то обе прямые регрессии совпадают.
Обе прямые регрессии проходят через точку (mx; my), которая называется
центром совместного распределения X и Y.