Отношения

1.

2.

Элементы множества могут находиться в некоторых
отношениях R между собой, с элементами других множеств
или с самими множествами.
Пусть даны два множества – X = {1, 2, 3, 4, 5, 6} и Y = { 1, 2, 3}.
а) 1 X; б) 1 Y - отношения принадлежности R = « ».
в) Y X - отношение включения: R = « ».
Элементы множества X могут находиться в отношениях:
R = « > » — «больше», R = « < » — «меньше»,
R = « » — «больше или равно»,
R = « » — «меньше или равно»,
R = « = » — «равно», R = « » — «не равно».

3.

Например, пусть x, y X и x = 2, y = 4.
Если xRy, т.е. 2R4, то это выражение будет справедливо при
R = « < » или R = « ».
Отношения между парами объектов называют бинарными.
В общем виде бинарное отношение может быть записано как
xRy, где R – отношение, устанавливающее связь между
элементом x X и элементом у Y.

4.

Бинарное отношение R — это подмножество декартова
произведения множеств X и Y: R X Y
X = {x1, x2, x3} = {1, 2, 3}
Y = {y1, y2} = {1, 2}
X Y = {(x1, y1), (x1, y2), (x2, y1), (x2, y2), (x3, y1), (x3, y2)} =
={(1, 1), (1, 2), (2, 1), (2, 2), (3, 1), (3, 2)}.
Отношение R = « » будет равно:
R = { x1y1, x1y2, x2y2} = {(1, 1), (1, 2), (2, 2)}.
Для отношения R = « = » получим: R = { x1y1, x2y2} = {(1, 1), (2, 2)}.

5.

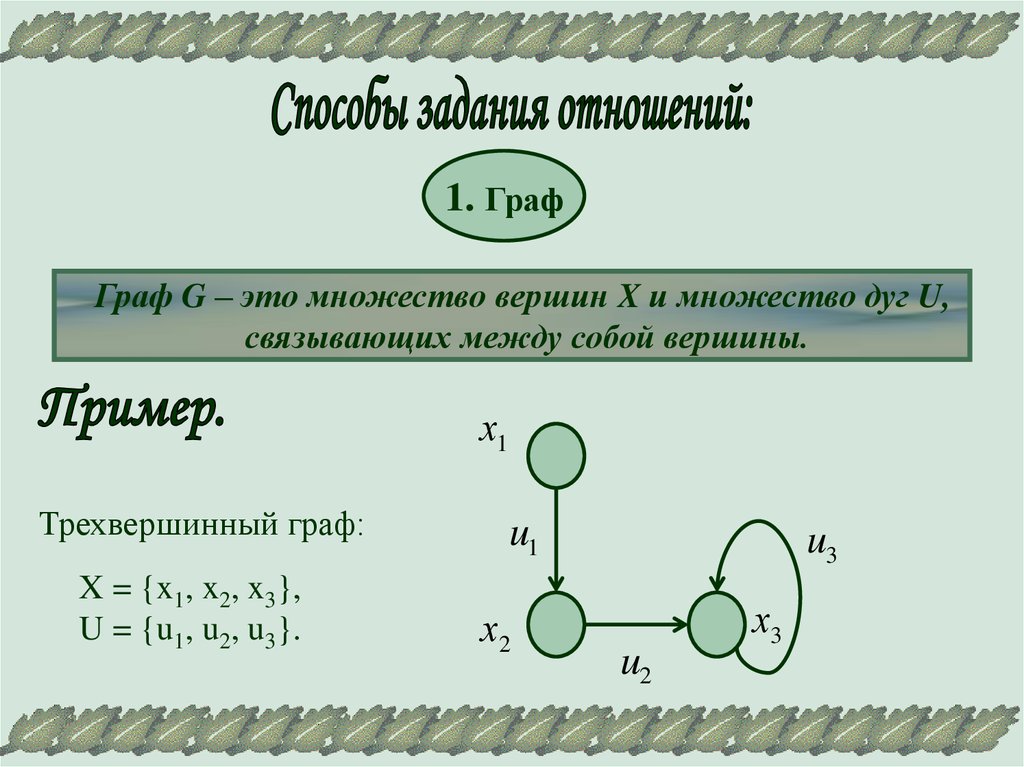
1. Граф
Граф G – это множество вершин X и множество дуг U,
связывающих между собой вершины.
х1
Трехвершинный граф:
X = {x1, x2, x3},
U = {u1, u2, u3}.
u1
х2
u3
u2
х3

6.

Так как каждая дуга соединяет две вершины, то
U = {u1, u2, u3}= {х1х2, x2x3, x3x3}.
Запишем декартово произведение Х Х :
Х Х х1 , х2 , х3 х1 , х2 , х3
х1 х1 , х1 х2 , х1 х3 , х2 х1 , х2 х2 , х2 х3 , х3 х1 , х3 х2 , х3 х3 ,
U Х Х
Если на множестве X для вершин x Х , y X
задать бинарное отношение R: R = «x и y связаны дугой»,
то граф G может быть определен как G = (X, R).

7.

2. Перечисление
3. Описание
(по аналогии с описанием множеств)
4. Матрица

8.

Матрица бинарного отношения R на множестве X
|X| = n – это квадратная матрица C порядка n,
в которой каждый элемент cij, стоящий в i - й строке
и j - ом столбце, определяется как:
1, если хi Rx j ,
0, в др. случаях

9.

Дано множество X = {1, 2, 3, 4, 5, 6}, на котором задано
отношение R = « ». Матрица отношений:
1
2
3
4
5
6
1
1
1
1
1
1
1
2
0
1
1
1
1
1
3
0
0
1
1
1
1
4
0
0
0
1
1
1
5
0
0
0
0
1
1
6
0
0
0
0
0
1

10.

Дано множество X = {1, 2, 3, 4, 5, 6}, на котором задано
отношение R = «x и y являются чётными числами»,
матрица отношений:
1
2
3
4
5
6
1
0
0
0
0
0
0
2
0
1
0
1
0
1
3
0
0
0
0
0
0
4
0
1
0
1
0
1
5
0
0
0
0
0
0
6
0
1
0
1
0
1