Похожие презентации:
Финансовый менеджмент
1. ФИНАНСОВЫЙ МЕНЕДЖМЕНТ
Автор курса:М.C. Гринчук, доцент, ISMA
2. Введение
Финансовый менеджмент - вид профессиональной деятельности, направленный надостижение целей предприятия (фирмы) путем эффективного использования всей
системы финансовых взаимосвязей, фондов и резервов, формирующих финансовый
механизм деятельности предприятия в условиях рыночной экономики.
Цель финансового менеджмента - максимизация прибыли и стоимости предприятия с
помощью рациональной финансовой политики.
Задачи финансового менеджмента:
• Обеспечение наиболее эффективного использования финансовых ресурсов.
• Оптимизация денежного оборота.
• Оптимизация расходов.
• Обеспечение минимизации финансового риска на предприятии.
• Оценка потенциальных финансовых возможностей предприятия.
• Обеспечение рентабельности предприятия.
• Задачи в области антикризисного управления.
• Обеспечение текущей финансовой устойчивости предприятия.
3. Раздел 1: МЕНЕДЖМЕНТ СТОИМОСТИ ПРЕДПРИЯТИЙ
Одним из критериев эффективной деятельности коммерческого предприятия является главныйисточник финансирования - чистая прибыль (NI) (бухгалтерская прибыль):
NI S TC
где:
S = нетто оборот (выручка);
TC = общие расходы.
Необходимо понимать, что бухгалтерская прибыль имеет ряд упущений. Основой недостаток в
том, что она не учитывает объем капиталовложений и требуемую доходность инвесторов.
Экономическая прибыль служит критерием эффективности использования ресурсов. Её
положительное значение показывает, что предприятие заработало больше, чем требуется для
покрытия стоимости используемых ресурсов, следовательно, была создана дополнительная
стоимость для инвесторов, учредителей.
В случае обратной ситуации — это свидетельствует о том, что организация оказалась неспособна
покрыть стоимость использования привлечённых ресурсов. Отсутствие экономической
прибыли может стать причиной оттока капитала из предприятия.
С точки зрения оценки эффективности, показатель экономической прибыли позволяет получить
более полное, по сравнению с показателем бухгалтерской прибыли, представление об
эффективности использования предприятием имеющихся активов, в силу того, что сравнивает
финансовый результат, полученный конкретным предприятием, с результатом который
обеспечит ему реальное сохранение вложенных средств.
4. Экономическая прибыль
Формула расчета экономической прибыли (EP):EP IC ( ROIC r
)
WACC
где:
IC = инвестированный в предприятие капитал (чистый операционный капитал) ;
ROIC = рентабельность инвестированного капитала (%);
rWACC = средневзвешенная стоимость капитала (%).
Рентабельность инвестированного капитала определяется по формуле:
ROIC
NOPAT
IC
где:
NOPAT = чистая операционная прибыль после уплаты налогов
Если ROIC > rWACC, предприятие получает добавленную стоимость. При таком соотношении
финансовый результат деятельности компании выше, чем издержки финансирования.
Компания в состоянии удовлетворить ожидания владельцев (акционеров) и кредиторов
и создает добавленную стоимость.
Чем выше экономическая прибыль, тем более привлекательна компания для финансового
капитала. В инвестиционной модели экономики rWACC выступает как минимальное
значение (нижняя граница) рентабельности использования капитала компании.
5. Экономическая прибыль
Пример 1.1:Предприятие было основано год назад.
Заемный капитал (кредитные обязательства) – €4,000,000
Собственные средства – €4,000,000
Средневзвешенная стоимость капитала – 8%
Стоимость собственного капитала – 10%
Финансовые показатели на конец года:
Чистая операционная прибыль после уплаты налогов – €1,000,000
Процентные платежи – €240,000
Определить экономическую прибыль предприятия.
Решение:
NOPAT = 1,000,000
IC = 8,000,000
ROIC = NOPAT / IC = 1,000,000 / 8,000,000 = 0.125 = 12.5%
rWACC = 8%
EP = IC × ( ROIC – rWACC ) = 8,000,000 (0.125 – 0.08) = €360,000
6. Экономическая добавленная стоимость
Экономическая добавленная стоимость (Economic Value Added) — альтернативный метод,при помощи которого можно определить экономическую прибыль предприятия:
EVA EBIT (1 t ) IC rWACC
где:
EBIT = прибыль до уплаты процентов и налогов;
t = подоходный налог с предприятия;
IC = инвестированный в предприятие капитал (чистый операционный капитал);
WACC = средневзвешенная стоимость капитала.
Экономическая добавленная стоимость (EVA) — аналитический показатель представляющий собой прибыль компании от
текущей деятельности за вычетом налогов, уменьшенную на величину платы за весь инвестированный в компанию
капитал. Используется для оценки эффективности компании с позиции ее собственников.
Свободный денежный поток (Free Cash Flow)
Для текущих и потенциальных инвесторов, вкладывающих средства в активы той или иной
фирмы, основной интерес представляет способность ее менеджмента генерировать
положительные денежные потоки от их эксплуатации, которые не только покрывают
все необходимые затраты, но и обеспечивают прирост благосостояния. Поэтому в
процессе принятия решений инвесторы уделяют основное внимание не валовому или
чистому, а свободному денежному потоку фирмы, который может быть направлен в их
распоряжение.
7. Свободный денежный поток
Свободный денежный поток (FCF) – денежный поток, которым располагает предприятиепосле финансирования всех инвестиций, которые оно находит целесообразным
осуществить:
FCFt NOPATt IC
где:
NOPATt = чистая операционная прибыль после налогов (за период t). Определяется как:
NOPATt EBITt (1 t )
где:
EBITt = прибыль до уплаты процентов и налогов (операционная прибыль) за период t;
ΔIC = ICt – ICt-1 = нетто инвестиции в операционный капитал (прирост за период t).
IC NOWC OLTA C A / R INV ( A / P Accr ) OLTA
где:
NOWC = чистый операционный рабочий капитал;
OLTA = операционные долгосрочные активы (напр., основные средства);
C = денежные средства;
A/R = дебиторская задолженность;
INV = запасы;
A/P = кредиторская задолженность;
Accr = накопленные обязательства.
8. Свободный денежный поток
Свободный денежный поток – средства доступные для всех инвесторов предприятия(акционеров и кредиторов).
Свободный денежный поток может быть использован для следующих целей:
1) погашение процентов и основной суммы по кредиту,
2) выплата дивидендов акционерам,
3) выкуп акций,
4) краткосрочные финансовые инвестиции,
5) инвестиции в средства не связанные с основной деятельностью предприятия.
Свободные денежные потоки являются основным объектом инвестиционного анализа и
при оценке стоимости предприятия. Методика расчета этого показателя наглядно
показывает, каким образом менеджмент может увеличивать стоимость предприятия.
Основными рычагами роста этого показателя являются:
увеличение операционной прибыли EBIT посредством снижения затрат и
наращивания выручки;
оптимизация налогообложения;
минимизация операционных и основных активов за счет более эффективного их
использования;
рационализация капитальных вложений и т. п.
9. Расчет экономической добавленной стоимости и свободного денежного потока
Пример 1.2:Определить экономическую добавленную стоимость (ЕVА) и свободный денежный поток
(FCF) за 2014 – 2015 г. используя финансовые отчеты предприятия.
Средневзвешенная стоимость капитала предприятия – 11.0%.
10. Расчет экономической добавленной стоимости и свободного денежного потока
Баланс, 31 дек., 2015$ ‘000
Актив
2015
2014
Оборотные средства
Денежные средства и их эквиваленты
10
80
Дебиторская задолженность
375
315
Запасы
615
415
1,000
810
Здания и оборудование
1,000
870
Итого активы
2,000
1,680
Итого оборотные средства
Oсновные средства
11. Расчет экономической добавленной стоимости и свободного денежного потока
Пассив2015
2014
Обязательства
Кредиторская задолженность
60
30
Накопленные обязательства
140
130
Краткосрочный долг
110
60
Итого краткосрочные обязательства
310
220
Долгосрочные займы
750
580
1,060
800
Обыкновенные акции (50 млн.)
130
130
Удержанная прибыль
810
750
Итого акционерный капитал
940
880
2,000
1,680
Итого обязательства
Акционерный капитал
Итого обязательства и акционерный
капитал
12. Расчет экономической добавленной стоимости и свободного денежного потока
Отчет о прибыли и убытках,$ ‘000
2015
Нетто оборот
Операционные издержки (искл. износ и
амортизацию)
Износ и амортизация
Итого операционные расходы
Прибыль до уплаты процентов и налогов
(EBIT)
Расходы по процентам
Прибыль до уплаты налогов
Подоходный налог с предприятия (40%)
Чистая прибыль
2014
3,000
2,850
2,616.2
2,497
100
90
2,716.2
2,587
283.8
263
88
60
195.8
203
78.3
81.2
117.5
121.8
13. Расчет экономической добавленной стоимости и свободного денежного потока
Объем капиталовложений: $1,800Кредиторская задолженность ($60) и накопленные обязательства ($140) исключаются.
EBIT = 283.8
rWACC = 11.0%
IC = 1,800
t = 40%
Краткосрочный долг
Долгосрочные займы
Собственный капитал
Инвестированный капитал (IC)
110
750
940
1,800
EVA2015 = EBIT(1 – t) – IC × WACC = 283.8 (1 – 0.4) – 1,800 × 0.11 = 170.3 – 198 = – $27.7
EVA2014 = EBIT(1 – t) – IC × WACC = 263 (1 – 0.4) – 1,520 × 0.11 = 157.8 – 167.2 = – $9.4
FCF2015 = NOPAT2015 - Δ IC = EBIT2015 (1 – t) – (IC2015 – IC2014)
IC2015 = (NOWC + OLTA)2015 = [(C + A/R + INV) – (A/P + Accr) + OLTA]2015 = (10 + 375 + 615) –
(60 + 140) + 1,000 = 800 + 1,000 = 1,800
IC2014 = (NOWC + OLTA)2014 = [(C + A/R + INV) – (A/P + Accr) + OLTA]2014 = (80 + 315 + 415) –
(30 + 130) + 870 = 650 + 870 = 1,520
FCF2015 = EBIT2015 (1 – t) – (IC2015 – IC2014) = 283.8 (1 – 0.4) – (1,800 – 1,520) =
= 170.3 – 280 = – $109.7
14. Раздел 2: ОСНОВЫ ФИНАНСОВОЙ МАТЕМАТИКИ
Финансовым менеджерам предприятий часто приходится сталкиваться с расчетами
процентных платежей, расчетами денежных потоков, финансовых рент и
инвестиционными решениями.
К основным видам финансовых расчетов можно отнести:
Наращение капитала (compounding)
Дисконтирование капитала (discounting)
Существуют два метода начисления процентов:
Простые проценты;
Сложные проценты.
Основное отличие между методами - база начисления процентов. Для простых процентов
базой начисления выступает начальная сумма капитала. Для сложных процентов база
начисления - уже накопленный за какой-либо период капитал.
На практике простые проценты используются крайне редко, в большинстве случаев для
краткосрочных капиталовложений со сроком до одного года. Расчет сложных
процентов применим для долгосрочных капиталовложений.
15. Наращение капитала
Наращение капитала при сложном проценте определяется при помощи следующейбазовой формулы:
FVn PV (1 r ) n
где:
FV = наращенная (будущая) сумма капитала (future value);
PV = начальная сумма капитала (present value);
r = процентная ставка;
n = период наращения капитала.
Доход по процентам In за весь период наращения капитала n можно определить составив
следующее уравнение:
I n FV PV PV (1 r ) n PV
Преобразовав уравнение получаем формулу:
I n PV [(1 r ) n 1]
16. Наращение капитала
Пример 2.1:Номинальная процентная ставка по банковскому депозиту – 6%. Клиент открыл
сберегательный счет и внес сумму в размере €100. Какой величины достигнет вклад
a) через год;
b) через 2 года,
если процент начисляется ежегодно (по сложной ставке)?
Решение:
a) FV1 = PV x (1 + r)n = €100 × (1+ 0.06)1 = €106;
b) FV2 = PV x (1 + r)n = €100 × (1+ 0.06)2 = €112.36
17. Наращение капитала
Временная линияБудущую стоимость капитала можно отобразить при помощи временной линии:
Чем выше r и N, тем выше FV при равной PV.
Задача 2.1:
Какую сумму составит долг в размере €750,000 через 12 лет, при процентной ставке 7%
годовых (сложные проценты)?
Ответ: FV12 = €1,689,143.69
Задача 2.2:
Стоимость земельного участка на момент покупки составила €20,000. В последствии
стоимость повышалась в среднем на 15% в год. Определить стоимость участка в конце
5 года. Какую прибыль получил владелец земельного участка, продав его через 5 лет,
если доля расходов (включая налоги) составила 30% от всего дохода? (сложные
проценты)
18. Наращение капитала
Решение:1) FV5 = 20,000 (1 + 0,15)5 = €40,227.14
2) I5 = 20,000 [(1 + 0,15)5 – 1] = €20,227.14
3) Расчет расходов:
20,227.14 × 0,3 = €6,068.14
4) Расчет прибыли:
20,227.14 – 6,068.14 = €14,159
19. Дисконтирование капитала
Дисконтирование капитала можно рассматривать как процесс противоположный
наращению.
• По сути, дисконтирование – это поиск решения для следующей задачи:
Каким должен быть размер вклада PV сегодня, чтобы в будущем иметь на счету
определенную сумму FV, при условии начисления процентов при ставке r:
r = 10% (сложный процент)
1
n=0
PV = ?
Задачу можно решить по формуле:
PV
FVn
(1 r ) n
2
3
FVn = €1,300
20. Дисконтирование капитала
Пример 2.2:Инвестиционный фонд предлагает доход 8.5% годовых. Какую сумму необходимо вложить
инвестору, чтобы через 3 года иметь на счету €50,000?
Решение:
FV = 50,000
r = 8.5% = 0.085
n=3
PV - ?
PV
FV3
50,000
€39,145.40
3
3
(1 r )
(1 0.085)
21. Расчет FV и PV при плавающих процентных ставках
Вследствие нестабильности на финансовых рынках могут применяться плавающие
процентные ставки.
В этом случае, будущую и современную стоимость капитала можно определить по
следующим формулам:
FVn PV (1 r1 )(1 r2 )...(1 rn )
n
или
FVn PV (1 rk )
k 1
PV
FVn
n
(1 r )
k
k 1
Пример 2.3:
Вкладчик разместил €200,000 на депозитном счету. Определить накопленную сумму
вклада в конце третьего года при процентых ставках 2%, 3.5% и 4% годовых.
Решение:
FV3 = 200,000 * (1 + 0.02) * (1 + 0.035) * (1 + 0.04) = €219,585.60
22. Расчет FV и PV при плавающих процентных ставках
Пример 2.4:Кредит на сумму €100,000 выдан на 5 лет. В кредитном договоре предусматриваются
следующие ежегодные процентные ставки: первые два года – 10%, третий и четвертый
год – 15%, пятый год – 20%.
1. Определить сумму погашения кредита.
2. Среднюю сложную ежегодную процентную ставку .
Решение:
1. FV5 = 100,000 (1 + 0.1)2(1 + 0.15)2(1 + 0.2) = €192,027
2. x = средняя ежегодная процентная ставка
FV5 = 100,000 (1 + x)5
192,027 = 100,000 (1 + x)5
1.92027 = (1 + x)5
x = 0.1394 = 13.94%
23. Начисление процентов m раз в год
Обычно проценты начисляются несколько раз в год. В этом случае расчет проводится с
условием того, что n будет обозначать теперь количество периодов начисления, а r –
периодическую процентную ставку.
Например, если проценты начисляются в течении 5 лет ежеквартально, то n = 5 x 4 = 20
• Практически все финансовые и кредитные учреждения (напр. банки, эмитенты
финансовых инструментов) предлагают ежегодную процентную ставку и сообщают о
периодичности начисления процентов.
Например, банк сообщает, что процентная ставка по депозитам составляет 4% годовых с
ежеквартальным начислением, или эмитент облигаций сообщает, что номинальная
ставка по облигациям – 8% при полугодовой выплате процентных платежей. Практически
это означает, что банк будет начислять проценты по ставке 1% (4% / 4), а эмитент по
ставке 4% (8% / 2).
Если проценты начисляются m раз в год, наращение капитала происходит быстрее, чем при
одноразовом начислении процентов в год. По этой причине формулы для расчета
будущей и современной стоимости капитала необходимо представить как:
nm
rs
FVn PV 1
m
nm
r
PV FVn 1 s
m
где::
rs = номинальная процентная ставка;
m = количество начислений процентов за год;
n = количество лет;
nm = количество периодов начисления;
rs / m = периодическая процентная ставка
24. Начисление процентов m раз в год
Пример 2.5:Номинальная процентная ставка по депозиту – 4.5%. Какую сумму необходимо вложить
сегодня, чтобы через 8 лет иметь накопления на счету в размере €10,000 при начислении
процентов
a) раз в год,
b) ежемесячно.
Решение:
a) rs = 4.5% = 0.045
FVn
10,000
m=1
PV
€7,031.85
nm
8 1
rs
0,045
n=8
1
1
1
m
FV8 = 10,000
PV - ?
b) m = 12
n=8
периодическая процентная ставка (rs / m) = 0.045 / 12 = 0.375%
PV
FVn
rs
1
m
nm
10,000
0,045
1
12
8 12
€6,981.46
25. Расчет периода времени n и процентной ставки r
При планировании и анализе капиталовложений часто возникает необходимость в
вычислении периода наращения или дисконтирования капитала.
Период времени n определяется по формуле:
FVn
ln
PV
n
ln(1 r )
Пример 2.6:
Через какой период времени начальный капитал удвоится, если ежегодная доходность
составит 10%?
Решение:
FVn / PV = 2
r = 10% = 0.1
n
ln 2
0.6930
7.27( лет )
ln(1 0.1) 0.0953
26. Расчет периода времени n и процентной ставки r
Пример 2.7:Объем начальных инвестиций – €75,000. Через какой период времени инвестированный
капитал достигнет €200,000, при доходности 8% годовых?
Решение:
200
75 0.982 12.75( лет )
n
ln(1 0.08) 0.077
ln
Процентная ставка r (или темп роста g) определяется по формуле:
r
n
FVn
1
PV
Пример 2.8:
Какой должна быть ежегодная доходность, чтобы за 5 лет объем начальных инвестиций в
размере €100,000 вырос до €150,000? (сложный процент)
Решение:
r 5
150,000
1 0.0845 8.45%
100,000
27. Потоки платежей
До сих пор рассматривались случаи финансовых операций, состоящих из отдельного
разового платежа, например получение и погашение долгосрочного займа. Вместе с
тем погашение такого займа возможно не только единовременным платежом, но и
множеством распределенных во времени выплат. В финансовой литературе ряд
распределенных во времени выплат и поступлений называется потоком платежей
(cash flows).
Примеры потоков платежей:
Плановое погашение кредитной задолженности;
Регулярные денежные поступления на депозитный счет;
Арендные платежи за использование объекта недвижимости;
Денежные поступления в инвестиционный фонд;
Страховые выплаты;
Начисление процентов по облигациям.
Потоки платежей являются неотъемлемой частью всевозможных финансовых операций: с
ценными бумагами, в управлении финансами предприятий, при осуществлении
инвестиционных проектов, в кредитных операциях, при оценке бизнеса, при оценке
недвижимости, выборе альтернативных вариантов финансовых операций и т. п.
Потоки платежей могут быть регулярными (размеры платежей постоянные или следуют
установленному правилу, предусматривающему равные интервалы между платежами)
и нерегулярными.
Члены потоков могут быть положительными (поступления) и отрицательными (выплаты).
28. Параметры финансовой ренты
Финансовая рента (аннуитет)Поток платежей, все члены которого — положительные величины, а временные интервалы
между платежами одинаковы, называют финансовой рентой, или просто рентой, или
аннуитетом.
Ренты часто встречаются на практике. Их примером являются взносы по погашению
потребительского кредита, пенсия, регулярная выплата процентов по банковскому
депозиту или по ценным бумагам и т. д.
Параметры финансовой ренты
Рента описывается следующими параметрами:
• суммарный годовой платеж — R — размер суммы, которая переходит от одного
владельца к другому в течение года;
• количество поступлений отдельных платежей в течение года — р;
• член ренты — размер отдельного платежа — РМТ (payment) = R/p (PMT = R, если p = 1);
• период — временной интервал между двумя соседними платежами;
• срок потока платежей — n — время от начала первого периода ренты до конца
последнего;
• процентная ставка — r — ставка, используемая при наращении или дисконтировании
отдельных платежей, из которых состоит поток;
• количество раз m в году начисления процентов исходя из годовой ставки r.
29. Виды финансовых рент
По количеству выплат членов ренты на протяжении года ренты делятся:• на годовые (выплата раз в году);
• на p-срочные (p — количество выплат в году).
По числу раз начислений процентов на протяжении года различают:
• ренты с ежегодным начислением;
• с начислением m раз в году;
• с непрерывным начислением.
Моменты начисления процентов необязательно совпадают с моментами выплат членов
ренты.
По величине отдельных платежей ренты делятся:
• на постоянные (с одинаковыми размерами члена ренты);
• на переменные.
Очень важным является различие по моменту выплат платежей в пределах периода ренты:
• если платежи осуществляются в конце этих периодов, то соответствующие ренты
называют обыкновенными, или постнумерандо (postnumerando);
• если же платежи производятся в начале периодов, то их называют пренумерандо
(prenumerando).
30. Рента постнумерандо и пренумерандо
Рента постнумерандо0
r%
1
2
3
500
500
500
1
2
3
500
500
Рента пренумерандо
0
r%
500
31. Наращенная сумма для постоянных рент постнумерандо
Наращенная стоимость аннуитета FVA (future value of annuity) — это сумма всехпоследовательных платежей с начисленными на них процентами к концу срока
операции.
Пример 2.9:
Параметры и особенности потоков платежей:
Постоянная рента постнумерандо;
Количество поступлений отдельных платежей в течение года — 1 платеж (p = 1);
Ограниченный, определенный период времени;
Проценты начисляются один раз в год (m = 1);
Размер отдельного платежа (PMT) = €100, n = 3 года, r = 10%
Определим наращенную стоимость для постоянной ренты постнумерандо (FVA, Future
value of ordinary annuity)
n=0
PMT =
r = 10%
1
100
100(1+0.1)2
2
3
100
100(1+0.1)
Постнумерандо
100
110
121
FVA3 = €331
Проценты начисляются
для всех платежей
кроме последнего
32. Наращенная сумма FVAn для постоянных рент постнумерандо
Наращенную стоимость для постоянной ренты постнумерандо можно также вычислить поформуле:
(1 r ) n 1
FVAn PMT
r
где:
PMT = размер отдельного платежа;
r = процентная ставка
n = срок потока платежей
[(1 + r)n – 1] / r = коэффициент наращения ренты (future value interest factor of annuity,
FVIFA)
(1 0.1) 3 1
FVA3 100
100(3.31) €331
0.1
Задача 2.3:
Для обеспечения будущих расходов создается фонд, средства в который поступают в виде
постоянных ежегодных платежей. Платежи поступают в конце каждого года в течении 5
лет. Размер разового платежа – €50,000. На поступившие взносы начисляются
проценты по ставке 12% годовых.
Определить величину фонда на конец срока.
Ответ: €317,642
33. Наращенная сумма FVAn для постоянных рент постнумерандо, если m > 1
Наращенная сумма FVAn для постоянных рент постнумерандо, если m > 1Если проценты начисляются более одного раза в год (m > 1), наращенная стоимость для
постоянной ренты постнумерандо образуется следующим образом:
m
r
r
FVAn PMT PMT 1 s PMT 1 s
m
m
2m
r
... PMT 1 s
m
После математических преобразований получаем формулу:
nm
rs
1 1
m
FVAn PMT
m
rs
1 1
m
где:
PMT = размер отдельного платежа;
rs = номинальная процентная ставка;
m = количество начислений процентов в год;
n = количество лет;
rs / m = периодическая процентная ставка
( n 1) m
34. Наращенная сумма FVAn для постоянных рент постнумерандо, если m > 1
Наращенная сумма FVAn для постоянных рент постнумерандо, если m > 1Пример 2.10:
Для обеспечения будущих расходов создается особый фонд, средства в который поступают в
виде постоянных ежегодных платежей. Платежи в размере €2,000 будут поступать в конце
каждого года в течении 3 лет. Номинальная норма доходности фонда – 12%.
Определить сумму накопленного капитала в конце 3 года если проценты по вкладам
начисляются:
1) раз в год (m = 1);
2) ежеквартально (m = 4)?
Решение:
1) Наращенная сумма платежей формируется след. образом:
FVAn PMT PMT (1 r )1 PMT (1 r ) 2 ... PMT (1 r ) n 2 PMT (1 r ) n 1
FVA3 2,000 2,000(1 0.12)1 2,000(1 0.12) 2 2,000 2,240 2,508.8 €6,748.80
n=0
PMT =
1
r = 12%
2,000
2
3
2,000
2,000
2,000(1+0.12)1
2,000(1+0.12)2
2,240
2,508.8
FVA3 = €6,748.80
35. Наращенная сумма FVAn для постоянных рент постнумерандо, если m > 1
Наращенная сумма FVAn для постоянных рент постнумерандо, если m > 1Также по формуле:
(1 0.12) 3 1
FVA3 2,000
€6,748.80
0
.
12
2) При ежеквартальном начислении процентов (m = 4) наращенная сумма платежей
формируется след. образом:
m
( n 1) m
2m
r
r
r
FVAn PMT PMT 1 s PMT 1 s ... PMT 1 s
m
m
m
4
8
0.12
0.12
FVA3 2,000 2,000 1
2,000 1
2,000 2,251.02 2,533.54 €6,784.56
4
4
n=0
PMT =
1
r = 3%
2,000
2
3
2,000
2,000
2,000(1+0.03)4
2,000(1+0.03)8
2,251.02
2,533.54
FVA3 = €6,784.56
36. Наращенная сумма FVAn для постоянных рент постнумерандо, если m > 1
Наращенная сумма FVAn для постоянных рент постнумерандо, если m > 1Также по формуле:
0.12 3 4
1
1
4
€6,784.56
FVA3 2,000
4
0.12
1 4 1
Чем чаще происходит начисление процентов, тем выше наращенная сумма капитала.
37. Наращенная сумма FVAn для постоянных рент постнумерандо, если p > 1
Наращенная сумма FVAn для постоянных рент постнумерандо, если p > 1p-срочная рента
Особенности ренты:
Размер отдельного платежа – R/p, где: R = суммарный годовой платеж;
p = количество поступлений отдельных платежей в течение года.
Платежи поступают p раз в год (p > 1), т.е. временной интервал между платежами меньше
года;
Количество платежей = np, интервал между платежами = 1/p.
Проценты могут начисляться:
a) раз в год (m = 1);
b) соответственно количеству поступления платежей в год (m = p);
c) не соответствуя количеству платежей в год (m ≠ p).
Если платежи поступают в конце периода (постнумерандо) и проценты начисляются раз в
год (m = 1), наращенная сумма для постоянной ренты формируется след. образом::
1
2
1
n
R R
R
R
p
p
FVAn (1 r ) (1 r ) ... (1 r ) p
p p
p
p
После математических преобразований получаем формулу:
n
R (1 r ) 1
FVAn
1
p
p
(1 r ) 1
38. Наращенная сумма FVAn для постоянных рент постнумерандо, если p > 1
Наращенная сумма FVAn для постоянных рент постнумерандо, если p > 1Пример 2.11:
Для обеспечения будущих расходов создается особый фонд сроком на 3 года. Каждый год
в фонд поступают средства на сумму €2,000, причем платежи вносятся в конце каждого
полугодия в размере €1,000. Номинальная норма доходности фонда – 12%. Проценты
начисляются ежегодно.
Определить сумму накопленных средств по истечении срока.
Решение:
p =2; m = 1; n = 3; R = 2,000; рента постнумерандо; FVA - ?;
Сумма накопленных средств формируется след. образом:
1
2
1
n
R R
R
R
p
p
FVAn (1 r ) (1 r ) ... (1 r ) p
p p
p
p
FVA3 1,000 1,000(1 0.12) 0.5 1,000(1 0.12)1 1,000(1 0.12)1.5 1,000(1 0.12) 2
1,000(1 0.12) 2.5 1,000 1,058.30 1,120 1,185.30 1,254.40 1,327.53 €6,945.53
39. Наращенная сумма FVAn для постоянных рент постнумерандо, если p > 1
Наращенная сумма FVAn для постоянных рент постнумерандо, если p > 1Ситуацию можно отобразить графически:
n=0
R/p =
r = 12%
1
1,000
1,000
1,000
2
3
1,000
1,000
1,000
1,000(1+0.12)0.5
1,000(1+0.12)1
1,000(1+0.12)1.5
1,000(1+0.12)2
1,000(1+0.12)2.5
1,058.30
1,120.00
1,185.30
1,254.40
1,327.53
FVA3 = €6,945.53
Также по формуле:
FVA3 1,000
(1 0.12) 3 1
1
2
(1 0.12) 1
€6,945.53
40. Наращенная сумма FVAn для постоянных рент постнумерандо, если p = m
В рассмотренной выше ситуации платежи поступали p раз в году и предполагалось, чтоm = 1. Рассмотрим ситуацию, в которой количество поступлений отдельных платежей в
течение года совпадает с количеством начислений процентов в год, т.е. p = m.
Для расчета необходимо преобразовать базовую формулу для постоянной ренты
постнумерандо, заменив r периодической ставкой rs/m, а n на np. Принимая во
внимание, что p = m, получаем формулу:
(1 r ) n 1
FVAn PMT
r
где:
PMT = размер отдельного платежа;
rs = номинальная процентная ставка;
m = количество начислений процентов в год;
n = количество лет;
rs / m = периодическая процентная ставка
Также используя параметр R:
где:
R = суммарный годовой платеж
rs nm
1 1
m
FVAn PMT
rs
m
rs nm
1 1
R
m
FVAn
rs
m
m
41. Наращенная сумма FVAn для постоянных рент постнумерандо, если p = m
Пример 2.12:Создан накопительный фонд сроком на 3 года. Ежегодно в фонд поступают средства на сумму €2,000, причем
платежи вносятся в конце каждого квартала в размере €500. Номинальная норма доходности фонда – 12%.
Проценты начисляются ежеквартально. Определить сумму накопленных средств по истечении срока.
Решение:
p = m = 4; n = 3; R = 2,000; PMT = R/p = 500; rs = 12%; rs/m = 3%; рента постнумерандо; FVA - ?
n=0
r = 3%
1
2
PMT = 500
500
500
500
500
500
500
500
500
500
3
500
500
500(1+0.03)1 515
500(1+0.03)2
530.45
500(1+0.03)3
500(1+0.03)4
500(1+0.03)5
500(1+0.03)6
500(1+0.03)7
500(1+0.03)8
500(1+0.03)9
500(1+0.03)10
500(1+0.03)11
546.36
562.75
579.64
597.03
614.94
633.38
652.39
671.96
692.12
FVA3 = €7,096.02
42. Наращенная сумма FVAn для постоянных рент постнумерандо, если p = m
Также по формуле:rs nm
0.12 3 4
1
1 1
1
m
4
500
€7,096.02
FVAn PMT
rs
0
.
12
4
m
43. Наращенная сумма FVAn для постоянных рент постнумерандо, если p ≠ m
Бывают ситуации, в которых количество ежегодных платежей не совпадает с количествомначислений процентов в год (p ≠ m). В таком случае наращенная сумма для постоянной
ренты формируется след. образом:
FVAn
R R rs
1
p p m
m
1
p
R rs
1
p m
m
2
p
...
R rs
1
p m
1
m n
p
Преобразовав сумму элементов прогрессии, будущую стоимость периодических платежей
можно выразить след. образом:
nm
r
1 s 1
R
m
FVAn
m
p
rs p
1
1
m
При условии, что p > 1 un m > 1.
44. Наращенная сумма FVAn для постоянных рент постнумерандо, если p ≠ m
Пример 2.13:Создан накопительный фонд сроком на 3 года. Ежегодно в фонд поступают средства на
сумму €2,000, причем платежи вносятся в конце каждого квартала в размере €500. На
поступающие взносы начисляются проценты по ставке 12%. Проценты начисляются
каждые полгода. Определить сумму накопленных средств по истечении срока.
Решение:
p = 4; m = 2; n = 3; R = 2,000; PMT = R/p = 500; rs = 12%; rs/m = 6%; рента постнумерандо;
FVA - ?
nm
3 2
r
0
.
12
s
1 1
1
1
R
m
2000
2
FVAn
€7,078.42
m
2
p
4
rs p
0.12 4
1
1
1
1
m
2
45. Наращенная сумма FVAn для постоянных рент постнумерандо, если p ≠ m
Денежные потоки показаны на временной линии:n=0
r = 6%
PMT = 500
500
1
500
2
500
500
500
500
3
500
500
500
500
500
500(1+0.06)0.5
514.78
500(1+0.06)1
530.00
500(1+0.06)1.5
500(1+0.06)2
500(1+0.06)2.5
500(1+0.06)3
500(1+0.06)3.5
500(1+0.06)4
500(1+0.06)4.5
500(1+0.06)5
500(1+0.06)5.5
545.67
561.80
578.41
595.51
613.11
631.24
649.90
669.11
688.89
FVA3 = €7,078.42
46. Наращенная сумма FVAn для постоянных рент постнумерандо: Выводы
Обобщив результаты примеров 2.10 – 2.13 можно получить след. неравенствa:FVAn ( p 1; m 1) FVAn ( p 1; m 1) FVAn ( p 1; m 1) FVAn ( p m 1)
FVAn ( p m 1) FVAn (m p 1)
Данные неравенства можно использовать в процессе выбора инвестиционных объектов и
заключения финансовых договоров, т.к. они дают возможность уже на начальной
стадии процесса планирования получить представление об условиях конкретной
финансовой ренты и обозначить приоритеты при выборе той или иной ренты.
Например, можно уже заранее без расчетов сделать вывод о том, что платежи с условием
p = 2 и m = 4 обеспечат большую сумму наращенного капитала, чем платежи с условием
p = 1 и m = 2, при прочих равных условиях.
47. Наращенная сумма FVAn для постоянных рент пренумерандо
Аннуитет (рента) пренумерандо (annuity due) — рента при которой выплата
осуществляется в начале периода.
Пример 2.14:
Параметры и особенности потоков платежей:
Постоянная рента пренумерандо;
Временной интервал – один год;
Ограниченный, определенный период времени;
Проценты начисляются один раз в год (m = 1);
Размер отдельного платежа (PMT) = €100, n = 3 года, r = 10%
Определим наращенную стоимость для постоянной ренты пренумерандо (FVA, Future
value of annuity due)
n=0
PMT = 100
1
r = 10%
100
2
3
100
110
121
133.1
FVA3 = €364.1
Пренумерандо
48. Наращенная сумма FVAn для постоянных рент пренумерандо
Наращенная сумма постоянной ренты пренумерандо в (1 + r) раз превышает наращеннуюсумму аналогичной ренты постнумерандо. Следовательно, формула для расчета
будущей стоимости ренты пренумерандо имеет след. вид:
(1 r ) n 1
FVAn PMT
(1 r )
r
(1 0.1) 3 1
FVA3 100
(1 0.1) €364.1
0.1
Пример 2.15:
Какой объем средств будет накоплен в течении 20 лет при процентной ставке 4% годовых,
если размер ежегодных взносов, вносимых в начале каждого года, составит €300?
Решение:
(1 0.04) 20 1
FVA20 300
(1 0.04) €9,290.76
0.04
49. Наращенная сумма FVAn для постоянных рент пренумерандо, если m > 1
Наращенная сумма FVAn для постоянных рент пренумерандо, если m > 1При дополнительном условии, что m > 1, будущая стоимость аннуитета пренумерандо
определяется по формуле:
rs nm
m
1 1
r
m
1 s
FVAn PMT
rs m
m
1 1
m
Пример 2.16:
Для обеспечения будущих расходов создается особый фонд, средства в который
поступают в виде постоянных ежегодных платежей. Платежи в размере €2,000 будут
поступать в начале каждого года в течении 3 лет. Номинальная норма доходности
фонда – 12%.
Определить сумму накопленного капитала в конце 3 года если проценты по вкладам
начисляются поквартально.
Решение:
0.12 3 4
1
4
1
0
.
12
4
1
FVA3 2,000
2,000(3.392279)(1.125509) €7,636.08
4
4
0.12
1 4 1
50. Наращенная сумма FVAn для постоянных рент пренумерандо, если m > 1
Наращенная сумма FVAn для постоянных рент пренумерандо, если m > 1Ситуация отображена на рисунке:
n=0
PMT =
2,000
1
2,000
r = 3%
2
3
2,000
2,000(1+0.03)4
2,000(1+0.03)8
2,000(1+0.03)12
2,251.02
2,533.54
2,851.52
FVA3 = €7,636.08
51. Наращенная сумма FVAn для постоянных рент пренумерандо, если p > 1
Наращенная сумма FVAn для постоянных рент пренумерандо, если p > 1Рассмотрим ренту пренумерандо с условием, что платежи поступают p раз в год (p > 1). По
аналогии с рентой постнумерандо существуют 3 варианта:
m = 1; p = m; p ≠ m.
Если m = 1, наращенная стоимость постоянной ренты пренумерандо определяется след.
образом:
n
1
R (1 r ) 1
FVAn
1 r p
1
p
(1 r ) p 1
Если p = m:
rs nm
1 1
m
1 rs
FVAn PMT
rs
m
m
Если p ≠ m:
nm
r
m
1 s 1
R
m
rs p
FVAn
1
m
p
m
rs p
1 m 1
52. Наращенная сумма FVAn для постоянных рент пренумерандо, если p > 1
Наращенная сумма FVAn для постоянных рент пренумерандо, если p > 1Пример 2.17:
На банковском счету предприятия – €90,000. Предприятие планирует за 2 года накопить
денежные средства на покупку производственного оборудования – по крайней мере
€400,000. Какую сумму денег необходимо вносить на банковский счет в начале каждого
квартала, при процентной ставке 9% годовых и поквартальном начислении процентов?
Решение:
Для накопления средств для покупки предприятие может вложить сегодня €90,000 при
ставке 9% (m=4), а оставшуюся часть обеспечить периодическими денежными взносами
на депозитный счет. При внесении денежных сумм (PMT), наращенная стоимость
потока платежей генерируется по формуле:
rs nm
1 1
m
1 rs
FVAn PMT
rs
m
m
Составим уравнение:
Рента пренумерандо,
p=m>1
0.09 2 4
1
2 4
1
4
0.09
1 0.09
400,000 90,000 1
PMT
0.09
4
4
4
400,000 107,534.80 PMT 8.853993
PMT 33,032.01
53. Наращенная сумма FVAn для постоянных рент пренумерандо, если p > 1
Наращенная сумма FVAn для постоянных рент пренумерандо, если p > 1Денежные потоки представлены на рисунке:
r = 2.25%
n=0
1
2
PV = 90,000
90,000(1+0.0225)8
107,534.80
FV2 = €107,534.80
r = 2.25%
n=0
PMT =
33032
33032
33032
33032
1
33032
2
33032
33032
33032
...
...
33,775.23
34,535.17
33032(1+0.0225)3
33032(1+0.0225)4
33032(1+0.0225)5
33032(1+0.0225)6
33032(1+0.0225)7
33032(1+0.0225)8
35,312.22
36,106.74
36,919.14
37,749.82
38,599.19
39,467.68
FVA2 = €292,465.20
Σ = €400,000
54. Современная (текущая) стоимость постоянной ренты постнумерандо
Современная (текущая) стоимость постоянной ренты постнумерандо (present value of
ordinary annuity, PVA) находит широкое применение в разнообразных финансовых
расчетах: планирование погашения долгосрочных займов, реструктурирование долга,
оценка и сравнение эффективности производственных инвестиций и т. п.
Пример 2.18:
Параметры и особенности потоков платежей:
Постоянная рента постнумерандо;
Количество поступлений отдельных платежей в течение года — 1 платеж (p = 1);
Ограниченный, определенный период времени;
Проценты начисляются один раз в год (m = 1);
Размер отдельного платежа (PMT) = €100, n = 3 года, r = 10%
Определим современную стоимость для постоянной ренты постнумерандо (PVA, Present
value of ordinary annuity):
n=0
PMT =
90.91
82.64
75.13
PVA3 = €248.68
100(1+0.1)-1
1
r = 10%
100
2
3
100
100(1+0.1)-2
100(1+0.1)-3
Рента постнумерандо
100
55. Современная (текущая) стоимость постоянной ренты постнумерандо
Текущая стоимость аннуитета постнумерандо формируется след. образом:PMT
PMT
PMT
PMT
PMT
PVAn
...
n 1
(1 r ) (1 r ) 2 (1 r ) 3
(1 r )
(1 r ) n
В конечном итоге сумма имеет вид:
1
1
(1 r ) n
PVAn PMT
r
где:
PMT = размер отдельного платежа;
r = процентная ставка;
n = срок потока платежей;
(1 - (1 + r)-n)/r = коэффициент дисконтирования аннуитета (Present value interest factor of
annuity, PVIFA).
1
1
(1 0.1) 3
PVA3 100
100(2.4868) €248.68
0.1
56. Современная (текущая) стоимость постоянной ренты постнумерандо
Пример 2.19:Какую сумму необходимо внести на депозитный счет сегодня, при процентной ставке 5.5%
годовых, чтобы иметь возможность в течении 8 лет снимать со счета в конце каждого
года сумму в размере €300? Предполагается, что после последней операции по снятию
средств, баланс депозитного счета будет равен нулю.
Решение:
r = 5.5% = 0.055
n=8
PMT = 300
рента постнумерандо
1
1
(1 0.055) 8
PVA3 300
300(6.334566) €1,900.37
0
.
055
57. Современная стоимость постоянной ренты постнумерандо, если m > 1
Современная стоимость постоянной ренты постнумерандо, если m > 1Если проценты начисляются m раз в год, формула расчета текущей стоимости постоянной
ренты постнумерандо принимает вид:
1
1
nm
r
1 s
m
PVAn PMT
m
rs
1 1
m
PVAn
где:
PMT = размер отдельного платежа;
rs = номинальная процентная ставка;
m = количество начислений процентов в год;
n = количество лет;
rs / m = периодическая процентная ставка
При условии, что m > 1 un p = 1.
PMT
PMT
PMT
...
(1 rs / m) m (1 rs / m) 2 m
(1 rs / m) nm
58. Современная стоимость постоянной ренты постнумерандо, если m > 1
Современная стоимость постоянной ренты постнумерандо, если m > 1Пример 2.20:
Какой должна быть сумма вклада, чтобы на протяжении 5 лет в конце каждого года можно
было снимать со счета по €500, при номинальной процентной ставке 4.5% годовых и
капитализации процентов раз в полгода?
Решение:
rs= 4.5% = 0.045
n=5
m=2
p=1
PMT = 500
рента постнумерандо
1
1
5 2
0.045
1
2
0.19949
PVA5 500
500
€2,191.90
0.045 2
0.045506
1
1
2
59. Современная стоимость постоянной ренты постнумерандо, если m > 1
Современная стоимость постоянной ренты постнумерандо, если m > 1Денежные потоки показаны на временной линии:
r = 2.25%
n=0
PMT =
478.24
457.42
437.51
418.47
400.26
PVA5 = €2,191.90
1
500
2
500
3
500
4
500
5
500
500(1+0.0225)-2
500(1+0.0225)-4
500(1+0.0225)-6
500(1+0.0225)-8
500(1+0.0225)-10
60. Современная стоимость постоянной ренты постнумерандо, если p > 1
Современная стоимость постоянной ренты постнумерандо, если p > 1Если платежи поступают p раз в году (p > 1), и m = 1, текущая стоимость аннуитета
постнумерандо определяется по формуле:
1
1
R (1 r ) n
PVAn
1
p
p
(
1
r
)
1
PVAn
R
R
R
...
p(1 r )1/ p p(1 r ) 2 / p
(1 r ) np / p
где:
R = суммарный годовой платеж;
p = количество периодических платежей за год;
r = процентная ставка;
n = количество лет
Пример 2.21:
Какой должна быть сумма вклада, чтобы на протяжении 5 лет ежегодно можно было
снимать со счета сумму в размере €500, снимая по €250 в конце каждого полугодия,
при номинальной банковской процентной ставке 4.5% годовых и капитализации
процентов раз в год?
61. Современная стоимость постоянной ренты постнумерандо, если p > 1
Современная стоимость постоянной ренты постнумерандо, если p > 1Решение:
r = 4.5%
n=0
PMT =
244.56
239.23
234.03
228.93
223.95
219.07
214.31
209.64
205.08
200.61
PVA5 = €2,219.41
1
250
...
250
2
250
250
3
250
250
4
250
250
5
250
250
...
...
250(1+0.045)-2
250(1+0.045)-2.5
250(1+0.045)-3
250(1+0.045)-3.5
250(1+0.045)-4
250(1+0.045)-4.5
250(1+0.045)-5
1
1
1
1
R (1 r ) n 500 (1 0.045) 5
0.197549
PVAn
250
€2,219.41
1
1
p
2
0
.
022252
(1 0.045) 2 1
p
(
1
r
)
1
62. Современная стоимость постоянной ренты постнумерандо, если p = m
Если количество ежегодных платежей совпадает с количеством начислений процентов вгод, т. е. p = m, при условии, что p > 1 и m > 1, текущая стоимость аннуитета
постнумерандо определяется по формуле:
1
1
nm
rs
1
m
PVAn PMT
rs
m
где:
PMT = размер отдельного платежа;
rs = номинальная процентная ставка;
m = количество начислений процентов в год;
n = количество лет;
rs / m = периодическая процентная ставка
63. Современная стоимость постоянной ренты постнумерандо, если p = m
Пример 2.22:Какой должна быть сумма вклада, чтобы на протяжении 5 лет в конце каждого полугодия
можно было снимать со счета по €250, при номинальной процентной ставке 4.5%
годовых и капитализации процентов раз в полгода?
Решение:
rs= 4.5% = 0.045
n=5
m=2
p=2
PMT = 250
рента постнумерандо
1
1
1
1
nm
5
2
rs
0
.
045
1
1
m
2
250
250 0.19949 €2,216.55
PVAn PMT
rs
0.045
0.0225
2
m
64. Современная стоимость постоянной ренты постнумерандо, если p = m
Денежные потоки представлены на временной линии:r = 2.25%
n=0
PMT =
244.50
239.12
233.86
228.71
223.68
218.76
213.94
209.23
204.63
200.13
PVA5 = €2,216.55
1
250
...
250
2
250
250
3
250
250
4
250
250
5
250
250
...
...
250(1+0.045)-4
250(1+0.045)-5
250(1+0.045)-6
250(1+0.045)-7
250(1+0.045)-8
250(1+0.045)-9
250(1+0.045)-10
65. Современная стоимость постоянной ренты постнумерандо, если p ≠ m
Если количество ежегодных платежей не совпадает с количеством начислений процентов вгод, т. е. p ≠ m, при условии, что p > 1 и m > 1, текущая стоимость аннуитета
постнумерандо формируется следующим образом:
PVAn
R
1
1
...
p 1 rs / m m / p 1 rs / m 2 m / p
Формула для расчета имеет вид:
1
1
nm
rs
1
R
m
PVAn
m
p
1 rs p 1
m
где:
R = суммарный годовой платеж;
p = количество периодических платежей за год;
66. Современная стоимость постоянной ренты постнумерандо, если p ≠ m
Пример 2.23:Какой должна быть сумма вклада, чтобы на протяжении 5 лет ежегодно можно было
снимать со счета сумму в размере €500, снимая по €250 в конце каждого полугодия,
при номинальной банковской процентной ставке 4.5% годовых и ежемесячном
начислении процентов?
Решение:
rs= 4.5% = 0.045
n=5
m = 12
p=2
R = 500
PMT = 500 / 2 = 250
рента постнумерандо
1
1
1
1
nm
5
12
r
0.045
1 s
1
R m 500
12
0.201148
PVAn
250
€2,214.11
m
12
p
2
0.022712
1 rs p 1
1 0.045 2 1
m
12
67. Современная стоимость постоянной ренты постнумерандо, если p ≠ m
Денежные потоки представлены на временной линии:r = 0.375%
n=0
PMT =
244.45
239.02
233.71
228.52
223.45
218.48
213.63
208.89
204.25
199.71
PVA5 = €2,214.11
1
250
...
250
2
250
250
3
250
250
4
250
250
5
250
250
...
250(1+0.00375)-18
250(1+0.00375)-24
250(1+0.00375)-30
250(1+0.00375)-36
250(1+0.00375)-42
250(1+0.00375)-48
250(1+0.00375)-54
250(1+0.00375)-60
68. Современная стоимость постоянной ренты постнумерандо: Выводы
Сравнение результатов полученных в примерах 2.21. – 2.23. свидетельствует о том, чтотекущая стоимость постоянной ренты постнумерандо зависит от частоты платежей p и
интенсивности начисления процентов m.
Отношения можно представить в виде неравенств:
PVAn ( p m 1) PVAn ( p m 1) PVAn (m p 1)
Эти неравенства можно пременять при выборе инвестиционных объектов, заключении
финансовых договоров, т.к. они позволяют уже на стадии планирования получить
представление об определенных разновидностях финансовых рент, условиях
дисконтирования, а также обозначить приоритет в их использовании исходя из
конкретной ситуации.
Например, можно заранее определить, что, при прочих равных условиях, финансовая
рента с параметрами p = 2 и m = 4 имеет более низкую текущую стоимость, чем рента с
параметрами p = 4 и m = 1.
69. Современная (текущая) стоимость постоянной ренты пренумерандо
Расчет текущей стоимости постоянной ренты пренумерандо:Пример 2.24:
Предположим, что PMT = €100, n = 3 года, r = 10%. Платежи поступают в начале года.
Денежные потоки представлены на временной линии:
n=0
1
r = 10%
2
3
Рента пренумерандо
PMT =
100
90.91
82.64
100
100
100(1+0.1)-1
100(1+0.1)-2
PVA3 = €273.55
Современная стоимость постоянной ренты пренумерандо (Present value of annuity due,
PVA) определяется по формуле:
1
1
(1 r ) n
PVAn PMT
(1 r )
r
1
1
3
(1 0.1)
PVA3 100
(1 0.1) €273.55
0
.
1
70. Современная стоимость постоянной ренты пренумерандо, если m > 1
Современная стоимость постоянной ренты пренумерандо, если m > 1Если m > 1, при условии, что p = 1, современная стоимость постоянной ренты
пренумерандо определяется по формуле:
1
1
nm
r
1 s
m
m rs
PVAn PMT
1
m
m
r
1 s 1
m
где:
PMT = размер отдельного платежа;
rs = номинальная процентная ставка;
m = количество начислений процентов в год;
n = количество лет;
rs / m = периодическая процентная ставка
71. Современная стоимость постоянной ренты пренумерандо, если p > 1
Современная стоимость постоянной ренты пренумерандо, если p > 1Рассмотрим ренту пренумерандо с условием, что платежи поступают p раз в год (p > 1). По
аналогии с рентой постнумерандо существуют 3 варианта: m = 1; p = m; p ≠ m.
Если m = 1, текущая стоимость постоянной ренты:
1
1
R (1 r ) n
1/ p
PVAn
1
r
1
p
p
(
1
r
)
1
При p = m:
При p ≠ m:
1
1
nm
rs
1
m rs
PVAn PMT
1
m
rs
m
1
1
nm
rs
1
m/ p
rs
R
m
PVAn
1
m
p
m
1 rs p 1
m
72. Задачи на лизинг
Лизинг – договор, согласно которому одна сторона – лизингодатель (владелец)предоставляет другой стороне – лизингополучателю (арендатору) права на
использование собственности на определенный срок, при соблюдении определенных
условий. Обычно в течении срока лизингополучатель вносит арендную плату. По
окончании срока аренды собственность остается у владельца, либо арендатор ее
выкупает. Таким образом, лизинговые операциии представляют собой денежный поток.
Часто возникает вопрос: что выгоднее, аренда или покупка собственности? Предпочтение
отдается той сделке, которая, при определенной цене капитала, характеризуется более
низкой текущей стоимостью денежного потока.
Пример 2.25:
Предприниматель может взять в аренду производственное оборудование. Срок аренды –
36 месяцев, ежемесячный платеж составит €800.
Данное оборудования можно также купить по цене €25,000. Какая альтернатива является
приемлемой при цене капитала 12% годовых?
Решение:
PMT = 800; n = 3; p = m = 12; рента постнумерандо
Текущая стоимость лизинговых платежей при процентной ставке 12% годовых:
1 (1 rs / m) nm
1 (1 0.12 / 12) 3 12
PVAn PMT
800
€24,086
rs / m
0.12 / 12
Оборудование выгоднее взять в аренду
73. Задачи на лизинг
Пример 2.26:Аренда или покупка?
Стоимость оборудования – €1,000,000. Оборудование можно взять в аренду или купить.
Условия аренды:
Срок аренды – 4 года;
Ежемесячный платеж – €21,000 (оплата в начале месяца);
Ремонтные расходы покрывает пользователь.
Условия покупки:
Цена - €1,000,000;
Аванс - €200,000;
На оставшуюся часть берется кредит сроком на 5 лет при процентной ставке 6% годовых;
Погашение кредита равными выплатами в конце каждого года;
Остаточная стоимость оборудования к концу 5 года – €400,000;
Ремонтные расходы покрывает пользователь.
Альтернативная цена капитала – 8% в год.
74. Задачи на лизинг
Решение:Необходимо сравнить текущие стоимости денежных потоков для каждой из альтернатив:
1) В случае аренды
PMT = 21,000; n = 4; p = m = 12; рента пренумерандо
1
1
1
1
nm
4
12
r
0.08
1 s
1
m rs
12
1 0.08 €865,930
PVAn PMT
1 21,000
m
rs
0.08
12
12
m
2) В случае покупки определим сначала величину кредитного платежа PMT:
PVA5 = 800,000; n = 5; p = m = 1; r = 0.06; рента постнумерандо
1
1
(1 0.06) 5
800,000 PMT
PMT €189,920
0
.
06
1 1.08 5
PV 200,000 189,920
400,000 1.08 5 €686,060
0.08
Оборудование целесообразнее купить
75. Современная стоимость вечной ренты
Под вечной рентой (perpetuity) понимается ряд платежей, количество которых неограничено — теоретически она выплачивается в течение бесконечного числа лет. На
практике иногда сталкиваются со случаями, когда есть смысл прибегнуть к такой
абстракции, например, когда предполагается, что срок потока платежей очень большой
и конкретно не оговаривается.
Классический пример — облигация Великобритании (консоль) — бессрочный долговой
инструмент (ценная бумага), с периодическими фиксированными купонными
платежами, не имеющий срока погашения.
Формула для расчета современной стоимости вечной ренты (PVP):
PVP
PMT
r
Пример 2.27:
Предполагается, что на протяжении длительного срока чистый доход с одного гектара
земли составит €50 в год. Определить стоимость гектара земли, если альтернативная
цена капитала - 11%.
Решение:
Чистый доход с одного гектара земли можно рассматривать как вечную ренту.
Современная стоимость ренты (теоретическая рыночная стоимость):
PVP
50
€454.55
0.11
76. Будущая и современная стоимость переменной ренты
Для расчета будущей стоимости переменной ренты необходимо определить будущуюстоимость для каждого единичного потока CF, а затем полученные результаты сложить:
n
FVn CFt (1 r ) n t
t 1
Пример 2.28:
n=0
CF =
r = 10%
1
2
100
3
150
4
200
5
230
6
200
7
0
1,000
0
200(1+0.1)2
230(1+0.1)3
200(1+0.1)4
150(1+0.1)5
100(1+0.1)6
242.00
306.13
292.82
241.58
177.16
FV7 = €2,259.68
77. Будущая и современная стоимость переменной ренты
Для расчета современной стоимости переменной ренты необходимо определитьдисконтированную стоимость для каждого единичного потока CF, а затем полученные
результаты сложить:
1
PV CFt
t 1
1 r
n
t
r = 10%
Пример 2.29:
n=0
CF =
100(1+0.1)-1
90.91
123.97
1
2
100
3
150
4
200
5
230
6
200
7
0
150(1+0.1)-2
200(1+0.1)-3
150.26
230(1+0.1)-4
157.09
200(1+0.1)-5
124.18
0(1+0.1)-6
0
513.16
PV = €1,159.57
1,000(1+0.1)-7
1,000
78. Погашение кредита равными платежами
Кредитные расчеты (погашение кредита):Пример 2.30:
Банк выдает кредит на сумму €100,000. Срок погашения кредита - 5 лет, процентная ставка
— 10% годовых. Кредит будет погашаться равными платежами, которые будут поступать
в конце каждого года. Определить величину ежегодного платежа и составить план
погашения кредита (амортизационный план).
Отобразим ситуацию на временной линии:
n=0
- 100,000
1
PMT
2
PMT
r = 10%
PMT
3
4
PMT
5
PMT
r = 10%, n = 5, PVA5 = €100,000, Необходимо найти платеж PMT. Для определения размера
регулярного платежа воспользуемся формулой современной стоимости ренты
постнумерандо при m = p = 1:
1
1
(1 r ) n
PVAn PMT
r
79. Погашение кредита равными платежами
Составим уравнение:1
1
(1 0.1) 5
100,000 PMT
0
.
1
100,000 PMT 3.790787
PMT 26,379.75
Таким образом, можно составить общую формулу для погашения кредита равными
платежами PMT:
PMT
PVAn r
1 (1 r ) n
Амортизационный план погашения кредита (loan amortization schedule) влкючает в себя
след. позиции:
• начальный баланс кредита;
• платежи получателя кредита;
• проценты по кредиту;
• основная сумма кредита;
• конечный баланс кредита
80. Погашение кредита равными платежами
Амортизационный план погашения кредита, €Год
Начальный
баланс
кредита
Платеж
Процент по
кредиту*
Погашение
основной
суммы
кредита
Конечный
баланс
кредита
1.
100,000.00
26,379.75
10,000.00
16,379.75
83,620.25
2.
83,620.25
26,379.75
8,362.03
18,017.72
65,602.53
3.
65,602.53
26,379.75
6,560.25
19,819.50
45,783.03
4.
45,783.03
26,379.75
4,578.30
21,801.44
23,981.59
5.
23,981.59
26,379.75
2,398.16
23,981.59
0.00
Итого 131,898.74
31,898.74
100,000.00
* При условии, что r = 10%, процент начисляется с начального баланса кредита.
Например,, 100,000 × 0.1 = 10,000; 83,620.25 × 0.1 = 8,362.03 и т.д.
81. Погашение кредита равными платежами
Сущность расчета не меняется при ситуации, когда интервалами погашения кредитавыступают не годы, а месяцы (напр., при лизинговых платежах), кварталы или
полугодия. В таких случаях, в базовую формулу для расчетов нужно внести
корректировки для параметров r и n.
Пример 2.31:
Определить размер полугодового платежа для кредита на сумму €200,000, который выдан
на срок 8 лет при годовой процентной ставке 11.5%.
Решение:
Если PMT — полугодовой платеж, тогда r = 0.115 / 2 = 0.0575 и n = 16.
0.115
2
PMT
€19,452.06
2 8
0
.
115
1 1
2
200,000
Задача 2.4:
Предприятие способно выплачивать €4,000 в месяц по кредиту. Какую сумму кредита
сроком на 10 лет при номинальной процентной ставке 9% может позволить себе
предприятие?
82. Погашение кредита равными платежами
Решение:n = 10;
m = 12;
p = m;
rs = 9% = 0.09;
PMT = 4,000;
PVA - ?
1
1
1
1
nm
10
12
r
0.09
1 s
1
m
12
€315,766.77
PVAn PMT
4,000
rs
0.09
12
m
83. Раздел 3: АНАЛИЗ ФИНАНСОВОЙ ОТЧЕТНОСТИ ПРЕДПРИЯТИЯ
Финансовый анализ представляет собой процесс исследования финансового состояния иосновных результатов финансовой деятельности предприятия с целью выявления резервов
повышения его рыночной стоимости и обеспечения дальнейшего эффективного развития.
Цель финансового анализа — определение финансового состояния предприятия.
Основные задачи финансового анализа:
Анализ активов;
Анализ источников финансирования;
Анализ платежеспособности (ликвидности);
Анализ финансовой устойчивости;
Анализ финансовых результатов и рентабельности;
Анализ деловой активности (оборачиваемости);
Анализ денежных потоков;
Анализ вероятности банкротства.
Комплексная оценка финансового состояния.
Подготовка выводов и рекомендаций.
При анализе финансового состояния предприятия используют след. информацию:
• Приложения к документации отчетности;
• Бухгалтерские данные;
• Отчет о прибыли и убытках;
• Баланс;
• Отчет о движении денежных средств.
84. Показатели используемые при анализе
Финансовые показатели можно разделить на след. группы:1. Показатели ликвидности (liquidity ratios) – характеризуют способность предприятия
выполнять краткосрочные обязательства.
2. Показатели деловой активности (activity ratios) – показывают насколько эффективно
предприятие использует средства, находящиеся в его распоряжении.
3. Показатели платежеспособности (solvency ratios) – отражают соотношение собственных
и заемных средств в источниках финансирования компании, т.е. характеризуют степень
финансовой независимости предприятия от кредиторов.
4. Показатели рентабельности (profitability ratios) – показывают, насколько прибыльна
деятельность предприятия.
85. Методы финансового анализа
Методы используемые в финансовом анализе:• горизонтальный анализ;
• вертикальный анализ;
• анализ финансовых коэффициентов.
Горизонтальный анализ – берется показатель (строка) баланса или отчета о прибыли и
прослеживается его изменение в течение двух или более периодов.
Анализ этих данных позволяет определить тенденцию развития предприятия.
Вертикальный анализ – позволяет сделать вывод о структуре баланса и отчета о прибыли
в текущем состоянии, а также проанализировать динамику этой структуры.
Технология вертикального анализа состоит в том, что общую сумму активов предприятия
(при анализе баланса) и выручку (при анализе отчета о прибыли) принимают за 100%, и
каждую статью финансового отчета представляют в виде процентной доли от принятого
базового значения.
86. Горизонтальный анализ
Пример 3.1:ОБОРОТНЫЕ СРЕДСТВА
Отклонение, Отклонение,
€
%
2015
2014
5,853,982
6,097,654
-243,672
-4.00
Авансовые платежи за товар
61,068
78,846
-17,778
-22.55
Итого запасы
5,915,050
6,176,500
-261,450
-4.23
Задолженности покупателей и заказчиков
1,623,238
1,514,639
108,599
7.17
Задолженность связанных предприятий
2,048,543
1,509,320
539,223
35.73
Прочие дебиторы
67,125
50,983
16,142
31.66
Расходы будущих периодов
25,329
31,628
-6,299
-19.92
Hакопленные доходы
85,135
63,323
21,812
34.45
3,849,370
3,169,893
679,477
21.44
227,306
78,608
148,698
189.16
9,991,726
9,425,001
566,725
6.01
Запасы
Готовые изделия и товары на продажу
Дебиторы
Итого дебиторы
Денежные средства и их эквиваленты
ИТОГО ОБОРОТНЫЕ СРЕДСТВА
87. Вертикальный анализ
Пример 3.2:2015
14,926,948
Структура 2015 г., Структура 2014 г.,
2014
%
%
15,189,408
-
Нетто оборот
Затраты на производство и реализацию
продукции
(13,132,234) (13,071,647)
Брутто прибыль
1,794,714
2,117,761
Расходы на продажу
(155,366)
(712,013)
Административные расходы
(686,703)
(637,293)
Прочие доходы от хоз. деятельности
Прочие расходы от хоз. деятельности
Прочие процентные и тому подобные
доходы
Процентные платежи и тому подобные
расходы
Доход или убытки до уплаты
налогов
Подоходный налог с предприятия
Отложенный налог
Прочие налоги
Прибыль или убытки отчетного года
Отклонение,
проц. пункты
-
87.98
12.02
1.04
4.60
86.06
13.94
4.69
4.20
1.92
-1.92
-3.65
0.40
259,658
(326,990)
229,455
(522,139)
1.74
2.19
1.51
3.44
0.23
-1.25
819
1,485
0.01
0.01
0.00
(64,457)
(52,778)
0.43
0.35
0.08
821,675
(103,209)
(28,868)
(191)
689,407
424,478
(136,711)
41,768
(191)
329,344
5.50
0.69
0.19
0.00
4.62
2.79
0.90
0.27
0.00
2.17
2.71
-0.21
-0.08
0.00
2.45
88. Базовые принципы анализа финансовых коэффициентов
Анализ финансовых коэффициентов заключается в сравнении их значений с базиснымивеличинами (benchmarking), а также в изучении их динамики за отчетный период и ряд
лет (trend analysis).
В качестве базисных величин используются:
1. Общепринятые параметры;
2. Среднеотраслевые показатели;
3. Аналогичные показатели прошлых лет;
4. Показатели конкурирующих предприятий.
89. Показатели ликвидности
ЛиквидностьВ краткосрочной перспективе критерием оценки финансового состояния предприятия
выступает его ликвидность и платежеспособность. Термин «ликвидный»
предусматривает беспрепятственное преобразование имущества в средства платежа.
Чем меньше время, необходимое для превращения отдельного вида активов, тем выше
его ликвидность. Таким образом, ликвидность предприятия — это его способность
превратить свои активы в денежные средства платежа для погашения краткосрочных
обязательств.
Оценку ликвидности предприятия выполняют с помощью системы финансовых
коэффициентов, которые позволяют сопоставить стоимость текущих активов, имеющих
различную степень ликвидности, с суммой текущих обязательств. К ним относятся:
1. Коэффициент общей ликвидности (current ratio);
2. Коэффициент быстрой ликвидности (quick ratio);
3. Коэффициент абсолютной ликвидности (cash ratio).
При расчете коэффициентов ликвидности используются данные баланса предприятия.
90. Структура баланса
Активы балансаДолгосрочные
вложения
Оборотные
средства
Нематериальные вложения
Запасы
Основные средства
Дебиторы
Долгосрочные финансовые
вложения
Краткосрочные финансовые вложения
Денежные средства
Пассивы баланса
Собственный
капитал
Кредиторы
Основной капитал
Долгосрочные кредиторы
Добавочный капитал
Краткосрочные кредиторы
Резервы
Нераспределенная прибыль
91. Структура баланса
92. Оценка ликвидности
Коэффициент текущей ликвидности (current ratio):CR
CA
CL
где:
CA = оборотные средства;
CL = краткосрочные кредиторы (обязательства).
Коэффициент отражает способность компании погашать текущие (краткосрочные)
обязательства за счёт только оборотных средств.
Чем показатель больше, тем лучше платежеспособность предприятия.
Нормальным считается значение коэффициента 2 и более (в мировой практике считается
нормальным от 1.5 до 2.5, в зависимости от отрасли).
Значение ниже 1 говорит о высоком финансовом риске, связанном с тем, что предприятие
не в состоянии стабильно оплачивать текущие счета.
93. Оценка ликвидности
Коэффициент быстрой ликвидности (quick ratio):CCE A / R
QR
CL
где:
CCE = денежные средства и их эквиваленты;
A/R = дебиторская задолженность;
CL = краткосрочные кредиторы (обязательства).
Коэффициент быстрой ликвидности характеризует способность организации погасить свои
краткосрочные обязательства за счет продажи ликвидных активов. При этом в
ликвидные активы в данном случае включаются как денежные средства и
краткосрочные финансовые вложения, так и краткосрочная дебиторская
задолженность).
Запасы считаются наименее ликвидные активами, считается, что их труднее всего
перевести в деньги (т.е. реализовать), поэтому они не участвуют в расчете.
Чем выше коэффициент быстрой ликвидности, тем лучше финансовое положение
компании. Нормой считается значение 1.0 и выше. В то же время, значение может
отличаться для разных отраслей. При значении коэффициента менее 1 ликвидные
активы не покрывают краткосрочные обязательства, а значит существует риск потери
платежеспособности, что является негативным сигналом для инвесторов.
94. Оценка ликвидности
Коэффициет абсолютной ликивидности (cach ratio):KR
CCE
CL
где:
CCE = денежные средства и их эквиваленты;
CL = краткосрочные кредиторы (обязательства).
Коэффициент показывает отношение самых ликвидных активов организации – денежных
средство и краткосрочных финансовых вложений – к краткосрочным обязательствам.
Коэффициент отражает достаточность наиболее ликвидных активов для быстрого расчета
по текущим обязательствам, характеризует "мгновенную" платежеспособность
организации.
Нормальное значение коэффициента: 0.3 – 0.7.
Пример 3.3:
Дать оценку ликвидности предприятия используя данные балансовых отчетов.
Отрасль: Оптовая торговля запчастями и оборудованием для грузовых автомобилей
(NACE код: 45.31)
95. Оценка ликвидности
Баланс предприятия за 2011 - 2015 г.АКТИВЫ
ДОЛГОСРОЧНЫЕ ВЛОЖЕНИЯ
Нематериальные вложения
Лицензии, концессии и патенты, товарные знаки и
подобные права
ИТОГО
Oсновные средства
Земельные участки, здания и строения
Долгосрочные арендуемые основные средства
Технологическое оборудование и машины
Прочие основные средства и инвентарь.
Создание основных средств
Авансовые платежи за основные средства
ИТОГО
Долгосрочные финансовые вложения
Прочие ценные бумаги и вложения
Отложенный налоговый актив
ИТОГО
ИТОГО ДОЛГОСРОЧНЫЕ ВЛОЖЕНИЯ
2015
2014
6,795
6,795
2013
1,964
1,964
2012
3,027
3,027
2,250
2,250
0
22,079
128,549
182,446
63,053
725
28,448
80,645
219,306
63,053
396,127
392,177
0
398,377
0
392,177
23,968
138,227
165,234
17,641
191,514
207,091
327,429
416,246
16,416
108,798
159,130
91,862
34,201
410,407
11,000
4,538
15,538
349,762
11,000
33,407
44,407
462,617
0
413,434
ОБОРОТНЫЕ СРЕДСТВА
Запасы
Готовые изделия и товары на продажу
Авансовые платежи за товар
ИТОГО
Дебиторы
Задолженности покупателей и заказчиков
Задолженность связанных предприятий
Прочие дебиторы
Расходы будущих периодов
Накопленные доходы
ИТОГО
Денежные средства и их эквиваленты
ИТОГО ОБОРОТНЫЕ СРЕДСТВА
2015
ИТОГО АКТИВЫ
2014
2011
2013
2012
2011
5,853,982
61,068
5,915,050
6,097,654
78,846
6,176,500
4,046,268
85,121
4,131,389
3,602,567
45,063
3,647,630
3,405,158
143,977
3,549,135
1,623,238
2,048,543
67,125
25,329
85,135
3,849,370
227,306
9,991,726
1,514,639
1,509,320
50,983
31,628
63,323
3,169,893
78,608
9,425,001
1,114,925
590,318
151,284
12,057
14,838
1,883,422
108,084
6,122,895
1,249,033
648,293
121,965
10,470
14,484
2,044,245
99,536
5,791,411
768,380
669,874
208
8,931
8,942
1,456,335
43,768
5,049,238
10,341,488
9,887,618
6,536,329
6,189,788
5,441,415
96. Оценка ликвидности
ПАССИВЫСОБСТВЕННЫЙ КАПИТАЛ
Долевой капитал
Резервы:
резервы, установленные в уставе
прочие резервы
Нераспределенная прибыль:
a) нераспределенная прибыль прошлых лет
b) нераспределенная прибыль отчетного года
2015
458,563
2014
458,563
2013
322,280
2012
322,280
2011
322,280
7,067
7,454
1,733,986
689,407
1,839,642
329,344
1,429,438
179,856
1,138,799
440,639
664,090
460,188
2,881,956
2,627,549
1,931,574
1,901,718
1,461,079
2015
124,085
124,085
2014
118,274
118,274
2013
КРЕДИТОРЫ
Долгосрочные кредиторы
Займы в кредитных учреждениях
Обязательства по финансовому лизингу
Другие займы
Обязательства по отложенному налогу
ИТОГО
Краткосрочные кредиторы
Займы в кредитных учреждениях
Другие займы
Обязательства по финансовому лизингу
Авансы, полученные от покупателей
Задолженности поставщикам и подрядчикам
Задолженность связанным предприятиям
Налоги и взносы госуд. соцстрахования
Прочие кредиторы
Невыплаченные дивиденды
Накопленные обязательства
ИТОГО
ИТОГО КРЕДИТОРЫ
ИТОГО НАКОПЛЕНИЯ И КРЕДИТОРЫ
2015
2014
2013
ИТОГО ПАССИВЫ
ИТОГО СОБСТВЕННЫЙ КАПИТАЛ
НАКОПЛЕНИЯ
Прочие накопления
ИТОГО НАКОПЛЕНИЯ
493,092
71,105
2012
62,446
62,446
2011
39,955
39,955
2012
34,091
34,091
2011
302,458
48,602
242,579
14,417
248,619
21,964
316,210
564,197
351,060
5,876
262,872
6,191
276,774
2,435,089
1,826,416
33,601
4,275
3,952,068
15,969
222,773
51,410
980,760
529
29,090
1,621
2,202,336
99,423
132,041
20,021
56,065
6,771,250
7,335,447
7,459,532
36,667
219
4,143,305
14,496
231,473
44,801
53,000
440,358
6,790,735
7,141,795
7,260,069
1,022,441
4,167
20,926
411
2,494,765
22,362
135,848
31,919
546,598
4,279,437
4,542,309
4,604,755
505,520
3,971,341
4,248,115
4,288,070
142,411
17,318
293,220
18,814
3,610,093
3,946,245
3,980,336
10,341,488
9,887,618
6,536,329
6,189,788
5,441,415
19,942
336,152
1,116,993
23,955
6,099
1,991,283
97. Оценка ликвидности
Среднеотраслевые показателиисточник: lursoft.lv
98. Оценка ликвидности
CR20159,991,726
1.48
6,771,250
2015
9,991,726
6,771,250
1.48
Итого оборотные средства
Итого краткосрочные кредиторы
Коэффициент текущей ликвидности
2014
2013
2012
2011
9,425,001 6,122,895 5,791,411 5,049,238
6,790,735 4,279,437 3,971,341 3,610,093
1.39
1.43
1.46
1.40
2,40
2,20
2,00
1,80
1,60
1,40
1,46
1,43
1,39
1,48
1,40
1,20
1,00
2011
2012
2013
2014
2015
Выше чем в среднем по отрасли (1.22).
Likviditātes kopējais
koeficients
99. Оценка ликвидности
QR2015227,306 3,849,370
0.60
6,771,250
Итого дебиторы
Денежные средства и их эквиваленты
ИТОГО
Итого краткосрочные кредиторы
Коэффициент быстрой ликвидности
0,65
2015
3,849,370
227,306
4,076,676
6,771,250
0.60
2014
3,169,893
78,608
3,248,501
6,790,735
0.48
2013
1,883,422
108,084
1,991,506
4,279,437
0.47
0,60
0,60
0,54
0,55
0,50
0,45
0,47
0,48
Likviditātes
starpseguma
koeficients
0,42
0,40
0,35
0,30
2011
2012
2013
2014
2015
Cоответствует среднеотраслевому показателю (0.59).
2012
2,044,245
99,536
2,143,781
3,971,341
0.54
2011
1,456,335
43,768
1,500,103
3,610,093
0.42
100. Оценка ликвидности
KR2015227,306
0.03
6,771,250
Денежные средства и их эквиваленты
Итого краткосрочные кредиторы
Коэффициент абсолютной ликвидности
2015
227,306
6,771,250
0.03
2014
78,608
6,790,735
0.01
2013
108,084
4,279,437
0.03
2012
2011
99,536
43,768
3,971,341 3,610,093
0.03
0.01
101. Анализ управления активами
Показатели деловой активности – группа коэффициентов, показывающая интенсивностьиспользования активов или обязательств.
Деловая активность в финансовом аспекте проявляется в скорости оборота средств.
Оборачиваемость товарно-складских запасов (inventory turnover ratio):
COGS
INV T / O
INV
где:
COGS = pасходы на производство проданной продукции
INV = cредн. величина запасов
Оборачиваемость запасов показывает, сколько раз за анализируемый период организация
использовала средний имеющийся остаток запасов.
Чем выше оборачиваемость запасов компании, тем более эффективным является
производство и тем меньше потребность в оборотном капитале для его организации.
102. Анализ управления активами
Оборачиваемость дебиторской задолженности (accounts receivable turnover ratio):S
A/R T / O
A/ R
где:
S = нетто оборот;
A/R = средн. величина дебиторской задолженности.
Коэффициент оборачиваемости дебиторской задолженности показывает, сколько раз за
период (год) организация получила от покупателей оплату в размере среднего остатка
неоплаченной задолженности. Показатель измеряет эффективность работы с
покупателями в части взыскания дебиторской задолженности, а также отражает
политику организации в отношении продаж в кредит.
Снижение данного показателя может свидетельствовать о росте числа неплатежеспособных
клиентов и других проблемах сбыта, но может быть связано и с переходом компании к
более мягкой политике взаимоотношений с клиентами, направленной на расширение
доли рынка. Чем ниже оборачиваемость дебиторской задолженности, тем выше будут
потребности компании в оборотном капитале для расширения объема сбыта.
103. Анализ управления активами
Период оборачиваемости дебит. задолженности (days sales outstanding):DSO
A/ R
365
S
где:
S = нетто оборот;
A/R = средн. величина дебиторской задолженности.
Сокращение сроков оборачиваемости в динамике рассматривается как положительная
тенденция. Тем не менее, показатели оборачиваемости целесообразно сравнивать с
нормативными показателями.
Увеличение
периода
оборачиваемости
дебиторской
задолженности
может
свидетельствовать об ухудшении условий оплаты продукции (услуг) по договорам,
финансовых затруднениях у потребителей. Но подходить к оценке данного показателя
прямолинейно - совершенно недопустимо. Очень часто компании для увеличения
объемов продаж в борьбе за покупателей идут на значительные отсрочки платежа.
Поэтому интерпретировать полученные цифровые значения необходимо с учетом
отраслевой ситуации, покупательной способности клиентов и т.д.
104. Анализ управления активами
Оборачиваемость основных средств (fixed asset turnover ratio):S
FA T / O
FA
где:
S = нетто оборот;
FA = средн. остаток основных средств.
Этот показатель, называемый также коэффициентом фондоотдачи, характеризует
эффективность использования предприятием основных средств.
Чем выше значение коэффициента, тем эффективнее предприятие использует основные
средства.
Низкий уровень фондоотдачи свидетельствует о недостаточном объеме продаж или о
слишком высокой величине капитальных вложений.
Следует заметить, что данный коэффициент имеет сильно выраженную отраслевую
специфику. Кроме того, значение этого показателя во многом зависит от способов
начисления амортизации и практики оценки стоимости активов. Вполне возможна
ситуация, при которой предприятие, использующее изношенные основные средства,
имеет коэффициент фондоотдачи более высокий, чем модернизированное
предприятие.
105. Анализ управления активами
Оборачиваемость активов (total asset turnover ratio):TA T / O
S
TA
где:
S = нетто оборот;
TA = cреднегодовая стоимость активов.
Оборачиваемость активов (ресурсоотдача) – позволяет определить число оборотов
капитала за период времени.
Коэффициент оборачиваемости активов позволяет оценить эффективность использования
всех активов предприятия вне зависимости от источника их образования. Коэффициент
ресурсоотдачи показывает, сколько евро прибыли получает предприятие с каждого
евро, вложенного в активы.
От скорости оборота вложенных средств напрямую зависит финансовое состояние
предприятия, его платежеспособность и ликвидность.
Определенного норматива для показателей оборачиваемости не существует, поскольку
они зависят от отраслевых особенностей организации производства. В капиталоемких
отраслях оборачиваемость активов будет ниже, чем в торговле или сфере услуг.
Низкая оборачиваемость может свидетельствовать о недостаточной эффективности
использования активов.
Пример 3.4:
Используя данные отчета о прибыли и убытках, дать оценку эффективности управления
активами.
106. Анализ управления активами
Отчеты о прибыли и убытках за 2011 - 2015 г.Нетто оборот
Расходы на производство проданной
продукции
Брутто прибыль или убытки
Расходы на продажу
Административные расходы
Прочие доходы от хоз. деятельности
Прочие расходы от хоз.деятельности
Прочие процентные и тому подобные
доходы
Процентные платежи и тому подобные
расходы
Доход или убытки до уплаты налогов
Подоходный налог с предприятия
Отложенный налог
Прочие налоги
Прибыль или убытки отчетного года
2015
14,926,948
2014
15,189,408
2013
10,752,406
2012
9,988,126
2011
8,940,985
(13,132,234)
1,794,714
(155,366)
(686,703)
259,658
(326,990)
(13,071,647)
2,117,761
(712,013)
(637,293)
229,455
(522,139)
(9,198,380)
1,554,026
(802,521)
(475,956)
157,101
(186,186)
(8,438,988)
1,549,138
(706,285)
(340,060)
205,284
(138,106)
(7,527,207)
1,413,778
(649,216)
(146,581)
107,843
(125,177)
819
1,485
(64,457)
821,675
(52,778)
424,478
(33,254)
213,210
(44,362)
525,609
(51,926)
548,721
(103,209)
(28,868)
(191)
689,407
(136,711)
41,768
(191)
329,344
(33,534)
315
(135)
179,856
(78,640)
(6,191)
(139)
440,639
(88,226)
(307)
460,188
107. Анализ управления активами
INV T / 0 201513,132,234
2.2
(5,915,050 6,176,500) / 2
Расходы на производство проданной продукции
Средн. величина запасов
Оборачиваемость товарно-складских запасов
2015
2014
13,132,234 13,071,647
6,045,775 5,153,945
2.2
2.5
2013
9,198,380
3,889,510
2.4
2012
2011
8,438,988 7,527,207
3,598,383
N/A
2.3
N/A
Ниже чем в среднем по отрасли (3.02).
A/R T / 0 2015
14,926,948
4.25
(3,849,370 3,169,893) / 2
2015
Нетто оборот
Средн. величина дебиторской задолженности
Оборачиваемость дебиторской задолженности
Отрицательная динамика.
2014
2013
2012
14,926,948 15,189,408 10,752,406 9,988,126
3,509,632 2,526,658 1,963,834 1,750,290
4.25
6.01
5.48
5.71
2011
8,940,985
N/A
N/A
108. Анализ управления активами
DSO20153,509,632
365 86(дней)
14,926,948
2015
Период оборачиваемости дебит. задолженности
2014
86
2013
61
2012
67
2011
64
N/A
Значительно выше чем в среднем по отрасли (40.57). Тенденция роста.
FA T / 0 2015
14,926,948
40.1
(327,429 416,246) / 2
Нетто оборот
Итого основные средства
Средний остаток основных средств
Оборачиваемость основных средств
2015
2014
2013
14,926,948 15,189,408 10,752,406
327,429
416,246
410,407
371,838
413,327
403,267
40.1
36.7
26.7
Тенденция роста. Среднеотраслевые данные отсутствуют.
2012
9,988,126
396,127
394,152
25.3
2011
8,940,985
392,177
N/A
N/A
109. Анализ управления активами
TA T / 0 201514,926,948
1.48
(10,341,488 9,887,618) / 2
2015
Нетто оборот
Средний остаток активов
Оборачиваемость активов
2014
2013
14,926,948 15,189,408 10,752,406
10,114,553 8,211,974 6,363,059
1.48
1.85
1.69
2012
9,988,126
5,815,602
1.72
Cоответствует среднеотраслевому показателю (1.48), но сохраняется негативная динамика
ввиду снижения оборачиваемости запасов и дебиторской задолженности.
110. Анализ структуры капитала и платежеспособности
Структура капитала компании характеризуется отношением долгосрочных заемныхсредств и собственных средств. Эта важнейшая пропорция, определяющая рост и
финансовый риск для компании, устанавливается на долгосрочный период.
Финансовая устойчивость (платежеспособность) — составная часть общей устойчивости
предприятия, сбалансированность финансовых потоков, наличие средств, позволяющих
организации поддерживать свою деятельность в течение определенного периода
времени, в том числе обслуживая полученные кредиты и производя продукцию.
111. Показатели платежеспособности
Отношение всех обязательств к суммарным активам (total liabilities to assets ratio):L/ A
TL
TA
где:
TL = сумма обязательств (итого кредиторы и накопления);
TA = суммарные активы.
Коэффициент показывает удельный вес обязательств в структуре капитала.
Отношение всех обязательств к собственному капиталу (total liabilities to equity ratio):
TL
L/E
TE
где:
TL = сумма обязательств (итого кредиторы и накопления);
TE = собственный капитал.
Коэффициент характеризует финансовую автономию (независимость). Высокий показатель
(напр., L/E > 1.0) означает, что значительную часть финансирования составляют
обязательства.
Обычно кредиторы отдают предпочтение более низкому показателю.
112. Показатели платежеспособности
Отношение кредитных обязательств к собственному капиталу (debt to equity ratio):D/E
D
TE
где:
D = кредитные обязательства (кратк. и долг. займы);
TE = собственный капитал.
Сумма обязательств по кредиту включает в себя займы в кредитных учреждениях и прочие
займы, предусматривающие погашение кредита.
Обычно кредиторы отдают предпочтение более низкому показателю, т.к. высокий
удельный вес заемного капитала подразумевает более высокий риск
неплатежеспособности.
Отношение кредитных обязательств к суммарным активам (debt to assets ratio):
D/ A
D
TA
D = кредитные обязательства (кратк. и долг. займы);
TA = суммарные активы.
Показывает какую часть активов составляют займы.
113. Показатели платежеспособности
В сфере кредитных учреждений широко применяется показатель способности предприятияобслуживать свои долговые обязательства - коэффициент покрытия процентов. Важность
данного индикатора заключается в том, что если его величина ниже установленной банком
нормативы, предприятие может столкнуться с трудностями в получении дополнительного
финансирования.
Коэффициент покрытия процентов (times interest earned):
TIE
EBIT
IX
где:
EBIT = прибыль до уплаты процентов и налогов;
IX = проценты к уплате.
Коэффициент
характеризует способность предприятия обслуживать свои долговые
обязательства. Показатель сравнивает прибыль до уплаты процентов и налогов (EBIT) за
определенный период времени (обычно один год) и проценты по долговым обязательствам
за тот же период.
Фактически коэффициент показывает, во сколько раз прибыль до уплаты процентов и налогов
превышает расходы на уплату процентов. Чем меньше коэффициент покрытия процентов, тем
тем выше вероятность наступления банкротства. Коэффициент ниже 1.5 ставит под вопрос
возможность фирмы обслуживать свой долг. Критическим считается коэффициент менее 1.0
(т.е. EBIT превышает проценты к уплате), который означает, что приток денежных средств
недостаточен для выплаты процентов кредиторам.
114. Показатели платежеспособности
Пример 3.5:Расчет коэффициентов платежеспособности:
L / A2015
7,459,532
0.72
10,341,488
2015
Итого накопления и кредиторы
Итого активы
Отношение обязательств к суммарным активам
L / E2015
2014
7,459,532 7,260,069
10,341,488 9,887,618
0.72
0.73
2013
4,604,755
6,536,329
0.70
2012
2011
4,288,070 3,980,336
6,189,788 5,441,415
0.69
0.73
7,459,532
2.59
2,881,956
2015
Итого накопления и кредиторы
Итого собственный капитал
Отношение обязательств к собственному капиталу
2014
7,459,532 7,260,069
2,881,956 2,627,549
2.59
2.76
2013
4,604,755
1,931,574
2.38
2012
2011
4,288,070 3,980,336
1,901,718 1,461,079
2.25
2.72
Обязательства составляют 72% от суммы баланса. Большая часть обязательств —
задолженности поставщикам и подрядчикам.
115. Показатели платежеспособности
D / E20152,982,181
1.02
2,881,956
Итого займы в кредитных учреждениях и
прочие займы
Итого собственный капитал
Отношение кредитных обязательств к
собственному капиталу
D / A2015
2015
2014
2013
2012
2011
2,928,181
2,881,956
2,128,874
2,627,549
1,269,187
1,931,574
1,229,908
1,901,718
1,477,100
1,461,079
1.02
0.81
0.66
0.65
1.01
2,928,181
0.28
10,341,488
2015
Итого займы в кредитных учреждениях и
прочие займы
Итого активы
Отношение кредитных обязательств к
суммарным активам
2014
2013
2012
2011
2,928,181
10,341,488
2,128,874
9,887,618
1,269,187
6,536,329
1,229,908
6,189,788
1,477,100
5,441,415
0.28
0.22
0.19
0.20
0.27
Займы составляют 28% от суммы баланса.
116. Показатели платежеспособности
TIE2015886,132
13.7
64,457
Прибыль до уплаты налогов (EBT)
Процентные платежи и тому подобные расходы
Прибыль до уплаты процентов и налогов
Коэффициент покрытия процентов
2015
2014
2013
2012
2011
821,675
64,457
886,132
13.7
424,478
52,778
477,256
9.0
213,210
33,254
246,464
7.4
525,609
44,362
569,971
12.8
548,721
51,926
600,647
11.6
Предприятие располагает достаточным уровнем операционной прибыли для покрытия
процентных платежей. Коэффициент покрытия процентов за 2015 год показывает, что
прибыли до уплаты процентов и налогов полученной в 2015 достаточно, чтобы покрыть
процентные расходы начисленные за год свыше 13 раз.
Текущее финансовое положение компании можно характеризовать как относительно
устойчивое.
117. Показатели рентабельности
Рентабельность — относительный показатель экономической эффективности.Рентабельность комплексно отражает степень эффективности использования
материальных, трудовых и денежных ресурсов. Коэффициент рентабельности
рассчитывается как отношение прибыли к активам, ресурсам или потокам, её
формирующим.
В общем смысле рентабельность продукции подразумевает, что производство и
реализация данного продукта приносит предприятию прибыль.
Уровень рентабельности определяется с помощью относительных показателей —
коэффициентов.
Показатели рентабельности можно условно разделить на две группы (два вида):
• рентабельность продаж и
• рентабельность активов и собственного капитала.
Рентабельность продаж предприятия
В мировой практике финансового анализа, к показателям рентабельности продаж относят:
чистую рентабельность продаж,
валовую рентабельность продаж и
операционную рентабельность продаж.
118. Показатели рентабельности продаж
Чистая рентабельность продаж (net profit margin):NI
NPM
S
где:
NI = чистая прибыль (или убытки);
S = нетто оборот.
Чистая рентабельность продаж — коэффициент рентабельности, который показывает долю
чистой прибыли в каждом заработанном евро. Обычно рассчитывается как отношение
чистой прибыли (прибыли после налогообложения) за определённый период к
выраженному в денежных средствах объёму продаж за тот же период.
Показывает эффективность менеджмента в производстве, реализации продукции и
использовании привлеченных финансовых ресурсов.
119. Показатели рентабельности продаж
Операционная рентабельность продаж (operating profit margin):OPM
EBIT
S
где:
EBIT = прибыль до уплаты процентов и налогов;
S = нетто оборот.
Операционная рентабельность продаж учитывает как расходы связанные с реализацией
продукции так и прочие операционные издержки, исключая расходы по процентам и
налогам.
Валовая рентабельность продаж (gross profit margin):
GPM
GP
S
где:
GP = валовая прибыль;
S = нетто оборот.
Валовая рентабельность продаж показывает насколько эффективно (прибыльно) фирма
производит каждую единицу продукции
120. Показатели рентабельности продаж
Пример 3.6:Расчет показателей рентабельности продаж:
NPM 2015
689,407
0.046 4.6%
14,926,948
2015
Нетто оборот
Прибыль отчетного года
Чистая рентабельность продаж
14,926,948
689,407
4.6%
2014
15,189,408
329,344
2.2%
2013
10,752,406
179,856
1.7%
2012
2011
9,988,126
440,639
4.4%
8,940,985
460,188
5.1%
2012
2011
9,988,126
569,971
5.7%
8,940,985
600,647
6.7%
Положительная тенденция.
OPM 2015
886,132
0.059 5.9%
14,926,948
2015
Нетто оборот
Прибыль до уплаты процентов и налогов
Операционная рентабельность продаж
Положительная тенденция.
14,926,948
886,132
5.9%
2014
15,189,408
477,256
3.1%
2013
10,752,406
246,464
2.3%
121. Показатели рентабельности продаж
GPM 20151,749,714
0.12 12%
14,926,948
2015
Нетто оборот
Валовая прибыль
Валовая рентабельность продаж
14,926,948
1,794,714
12.0%
2014
2013
15,189,408 10,752,406
2,117,761 1,554,026
13.9%
14.5%
Наблюдается незначительное снижение показателя.
Показатель ниже среднеотраслевого (15.05%).
2012
9,988,126
1,549,138
15.5%
2011
8,940,985
1,413,778
15.8%
122. Рентабельность активов
Рентабельность активов характеризует степень эффективности использования активовпредприятия в рамках получения прибыли.
Рентабельность активов (return on assets):
ROA
NI
TA
где:
NI = чистая прибыль (или убытки);
TA = средняя сумма активов.
Рентабельность активов – финансовый коэффициент, характеризующий отдачу от
использования всех активов предприятия, эффективность использования имущества,
позволяющий оценить качество работы финансовых менеджеров.
Показывает, сколько чистой прибыли в расчете на денежные единицы приносит каждая
единица активов, имеющихся в распоряжении предприятия.
123. Рентабельность активов
Пример 3.7:Расчет рентабельности активов:
ROA2015
689,407
0.068 6.8%
10,114,553
2015
Прибыль отчетного года
Средняя сумма активов
Рентабельность активов
689,407
10,114,553
6.8%
2014
2013
2012
329,344
8,211,974
4.0%
179,856
6,363,059
2.8%
440,639
5,815,602
7.6%
Положительная динамика. Показатель значительно выше среднеотраслевого
(-0.14%), что может свидетельствовать о прочной позиции предприятия в отрасли.
124. Рентабельность капитала
Рентабельность капитала показывает, как эффективно были вложены в предприятие денежныесредства инвесторов.
Рентабельность общего капитала:
NI IX
ROTC
TE D
где:
NI = чистая прибыль (или убытки);
IX = процентные расходы;
TE = средний остаток собственного капитала;
D = средний остаток заемного капитала.
Показывает, какой была бы рентабельность собственного капитала при отсутствии внешнего
кредитования.
Рентабельность собственного капитала (return on equity):
NI
ROE
TE
где:
NI = чистая прибыль (или убытки);
TE = средний остаток собственного капитала.
Характеризует эффективность использования не всего капитала (или активов) предприятия, а только
той части, которая принадлежит его собственникам.
125. Рентабельность капитала
Пример 3.8:Расчет рентабельности капитала:
ROTC2015
689,407 64,457
0.143 14.3%
2,754,753 2,528,528
Прибыль отчетного года
Процентные платежи и тому подобные расходы
Cредний остаток собственного капитала
Cредний остаток заемного капитала
Рентабельность общего капитала
2015
689,407
64,457
2,754,753
2,528,528
14.3%
2014
329,344
52,778
2,279,562
1,699,031
9.6%
2013
179,856
33,254
1,916,646
1,249,548
6.7%
2012
440,639
44,362
1,681,399
1,353,504
16.0%
Если задействованный капитал был бы собственным, рентабельность собственного
капитала составила 14.3%.
ROE2015
689,407
0.25 25%
2,754,753
2015
Прибыль отчетного года
Cредний остаток собственного капитала
Рентабельность собственного капитала
689,407
2,754,753
25.0%
2014
329,344
2,279,562
14.4%
2013
2012
179,856
1,916,646
9.4%
440,639
1,681,399
26.2%
Положительная динамика. Показатель значительно выше среднеотраслевого (-4.17%).
126. Модель Дюпона
Модель Дюпона (DuPont Analysis)Модель Дюпона и ее модификации в трех- и пятифакторные формулы позволяет
предприятию оценить степень влияния различных факторов на формирование
рентабельности собственного капитала (ROE).
Трехфакторная модель Дюпона
ROE
NI S TA
S TA TE
где:
NI / S = чистая рентабельность продаж (NPM);
S / TA = оборачиваемость активов (TA T/O);
TA / TE = коэффициент капитализации (коэффициент финансового рычага).
Модель Дюпона используется для выявления влияния различных факторов на
формирование рентабельности и ее изменение. Рентабельность продаж NPM
характеризует операционную деятельность. Ресурсоотдача TA T/O характеризует
деловую активность. Коэффициент финансовой зависимости TA/TE характеризует
структуру капитала.
Изучая изменения компонентов за ряд отчетных периодов, финансовый менеджер может
выяснить, какие параметры финансовой деятельности фирмы в наибольшей степени
повлияли на изменение рентабельности собственного капитала.
127. Роль трехфакторной модели Дюпона
Трехфакторная модель Дюпона показывает, что менеджмент предприятия может повыситьрентабельность собственного капитала следующим образом:
1. Увеличив показатель чистой рентабельности продаж
Рентабельность продаж обычно возрастает при увеличении оборота, что может быть
связано со снижением цены. Снижение цены может сопровождаться увеличением
объема физической реализации при изменении рыночной ситуации. При этом
рентабельность
продаж
можно
также
повысить
благодаря
снижению
производственных издержек (при закупке нового и эффективного производственного
оборудования, более дешевых сырьевых материалов).
Для увеличения рентабельности продаж необходимо учитывать:
возможности повышения, снижения цен;
обеспечение деятельности предприятия на более благоприятных рынках;
производство и продажа новых и более рентабельных видов продукции;
поиск новых решений по минимизации расходов.
2. Ускорив оборачиваемость всех активов
Оборачиваемость активов можно ускорить засчет снижения объема активов (ликвидируя
ненужные основные средства, оборотные средства и дебиторскую задолженность) или
увеличения нетто оборота. Чем выше оборачиваемость активов, тем меньше капитала
необходимо для достижения определенного уровня доходности.
128. Роль трехфакторной модели Дюпона
3. Изменив структуру капиталаПри изменении структуры капитала финансовый менеджер определяет оптимальное
отношение между заемным и собственным капиталом. Для поиска оптимальной
структуры капитала необходимо учесть два аспекта:
рентабельность;
риск.
Взаимодействие между структурой капитала, рентабельностью и риском можно показать
при помощи формул:
NI ROTC TE ( ROTC k d ) D
где:
NI = чистая прибыль;
ROTC = рентабельность общего капитала;
TE = средний остаток собственного капитала;
kd = стоимость заемного капитала;
D = средний остаток кредитных обязательств.
D
ROE ROTC ( ROTC k d )
TE
где:
ROE = рентабельность собственного капитала.
129. Роль трехфакторной модели Дюпона
Если разница между рентабельностью общего капитала и процентной ставкой по кредитувыше нуля (ROTC – kd > 0), при увеличении соотношения между заемным и собственным
капиталом (D / TE), рентабельность собственного капитала увеличивается.
Если разница между рентабельностью общего капитала и процентной ставкой по кредиту
ниже нуля (ROTC – kd < 0), при увеличении соотношения между заемным и собственным
капиталом, рентабельность собственного капитала снижается. Если D/TE превышает
определенный уровень, дальнейшее привлечение заемных средств приносит убытки.
Таким образом, увеличение заемного капитала приводит к повышенной степени риска.
Чем выше соотношение D/TE,тем выше риск.
130. Модель Дюпона (пример)
Пример 3.9:Выясним, какие параметры финансовой деятельности предприятия в наибольшей степени
повлияли на изменение рентабельности собственного капитала за последние 3 года.
Для этой цели можно применить трехфакторную модель Дюпона:
ROE
NI S TA
S TA TE
где:
NI / S = чистая рентабельность продаж (NPM);
S / TA = оборачиваемость активов (TA T/O);
TA / TE = отношение активов к собственному капиталу (коэффициент финансового рычага).
2015
Чистая рентабельность продаж
Оборачиваемость активов
Отношение активов к собственному капиталу
Рентабельность собственного капитала (ROE)
2014
4.62%
1.48
3.67
25.0%
2013
2.17%
1.85
3.60
14.4%
1.67%
1.69
3.32
9.4%
За последние годы рентабельность собственного капитала существенно возрасла.
Основной причиной роста является увеличение рентабельности продаж. Вторая причина –
изменение структуры капитала, т.е., увеличение заемных средств, о чем свидетельствует
повышение коэффициента финансового рычага.
С другой стороны, снижение оборачиваемости активов оказало негативное влияние на
показатель рентабельности собственного капитала.
131. Отношение между ROE и D/TE (пример)
Пример 3.10:Проанализируем взаимосвязь между структурой капитала, рентабельностью и риском на
примере нашего предприятия.
Отношение между рентабельностью собственного капитала и структурой капитала можно
выразить след. образом:
ROE ROTC ( ROTC k d )
D
TE
где:
ROE = рентабельность собственного капитала;
ROTC = рентабельность общего капитала;
kd = средняя процентная ставка по кредиту (стоимость заемного капитала);
D = средний остаток кредитных обязательств;
TE = средний остаток собственного капитала;
D/TE = отношение объема займов к собственному капиталу.
Анализируемые финансовые отчеты не дают информации о фактических процентных
ставках кредитования. Тем не менее, среднюю стоимость заемного капитала можно
определить след. образом:
kd
IX
D
где:
IX = процентные расходы;
D = средний остаток кредитных обязательств.
132. Отношение между ROE и D/TE (пример)
Например, проведем расчет средней стоимости заемного капитала за 2015 год.Информация о кредитных обязательствах (см. баланс предприятия):
КРЕДИТНЫЕ ОБЯЗАТЕЛЬСТВА
2015
2014
2013
2012
2011
Долгосрочные кредиторы
Займы в кредитных учреждениях
Прочие займы
Краткосрочные кредиторы
Займы в кредитных учреждениях
Прочие займы
D2015
493,092
302,458
242,579
316,210
19,942
2,435,089
1,826,416
1,022,441
4,167
493,092 302,458 2,435,098 1,826,416
2,528,528
2
2
Расчет процентых платежей (см. отчет о прибыли предприятия):
IX 2015 64,457
k d , 2015
248,619
64,457
0.0255 2.55%
2,528,528
980,760
529
1,116,993
23,955
133. Отношение между ROE и D/TE (пример)
Проведем расчет рентабельности собственного капитала и определим взаимосвязь данногопоказателя со структурой капитала и риском:
ROE2015 0.143 (0.143 0.0255) 0.92 0.25 25%
Рентабельность общего капитала (ROTC)
D/TE
Средняя стоимость заемного капитала
Рентабельность собственного капитала (ROE)
2015
14.3%
0.92
2.55%
25.0%
2014
9.6%
0.75
3.11%
14.4%
2013
6.7%
0.65
2.66%
9.4%
2012
16.0%
0.80
3.28%
26.2%
Рентабельность общего капитала превышает среднюю стоимость заемного капитала
(среднюю процентную ставку кредитования) (ROTC – kd > 0). В результате этого, при
повышении отношения между заемным и собственным капиталом рентабельность
собственного капитала увеличивается.
Это означает, что у менеджеров предприятия есть возможность повысить рентабельность
собственного капитала засчет увеличения кредитных обязательств, при условии быстрой
оборачиваемости активов и ситуации, при которой рентабельность общего капитала
превышает стоимость заемных средств. Однако, если предприятие функционирует в
среде повышенного риска, необходимо, чтобы удельный вес собственного капитала в
общей структуре капитала был выше, т.к. при увеличении пропорции заемного капитала
повышается риск.
134. Пятифакторная модель Дюпона
Пятифакторная модель ДюпонаПомимо влияния чистой рентабельности продаж, оборачиваемости активов и финансовой
структуры на формирование рентабельности собственного капитала, пятифакторная
модель учитывает роль налогового и процентного бремени.
NI EBT EBIT S TA
ROE
EBT EBIT S TA TE
где:
NI / EBT = коэффициент налогового бремени (tax burden);
EBT / EBIT = коэффициент процентного бремени (interest burden);
EBIT / S = операционная рентабельность продаж;
S / TA = оборачиваемость активов (TA T/O);
TA / TE = коэффициент капитализации (коэффициент финансового рычага).
Таким образом рентабельность собственного капитала (ROE) предприятия формируется за
счет: налоговой ставки, процентов по заемному капиталу, эффективности продаж,
результативности инвестиционной деятельности и финансового риска.
В частности, показатель налогового бремени характеризует налоговую нагрузку по налогу
на прибыль. Увеличение данного показателя возможно за счет сокращения налоговых
обязательств посредством использования различных схем налоговой минимизации.
Показатель процентного бремени отражает относительную стоимость привлечения
заемных средств. Увеличение данного показателя возможно за счет формирования
кредитного портфеля с минимально возможной средней процентной ставкой.
135. Раздел 4: АНАЛИЗ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ
Капиталовложения в долгосрочные активы один из факторов, влияющих на стоимостьпредприятия.
Капиталовложения (инвестиции) – вложение средств предприятия в приобретение
активов с целью получения доходов.
Предприятия в основном осуществляют два вида инвестиций:
реальные (прямые) инвестиции – долгосрочные вложения в конкретное предприятие под
конкретную инвестиционную программу (развитие и модернизация предприятия,
совершенствование технологий, выпуск нового продукта);
портфельные (финансовые) инвестиции – вложения в ценные бумаги с целью получения
дохода в виде дивидендов или курсовой разницы при покупке и продаже.
В данном разделе рассматриваются реальные инвестиции.
Капиталовложение является эффективным если:
Чистый доход от инвестиционного проекта превышает доходность другого
альтернативного проекта;
Уровень отдачи от вложенных средств превышает уровень инфляции;
Инвестиционный проект соотвествует стратегии и профилю риска предприятия.
136. Взаимодействие между проектами
Различают две категории инвестиционных проектов:1. Независимые проекты (independent projects)
когда решение о принятии одного проекта не влияет на решение о принятии другого. Для
того, чтобы инвестиционный проект А был независим от проекта В, должны
выполняться два условия:
• должны быть возможности (технические, технологические) осуществить проект А вне
зависимости от того, будет или не будет принят проект В;
• на денежные потоки, ожидаемые от проекта А, не должно влиять принятие или отказ от
проекта В.
2. Альтернативные (взаимоисключающие) проекты (mutually exclusive projects)
когда два или более анализируемых проектов не могут быть реализованы одновременно,
и принятие одного из них автоматически означает, что оставшиеся проекты не могут
быть реализованы.
Например, предприятие в рамках модернизации производства может приобрести
оборудование A либо оборудование B – принятие одного из этих проектов
автоматически делает невозможным осуществление другого.
137. Критерии эффективности инвестиционных проектов
При принятии решений о вложении средств в реальные инвестиции необходимопроизвести анализ эффективности таких вложений.
Чаще всего на практике изпользуются следующие показатели эффективности инвестиций:
срок окупаемости (PP);
чистая приведенная стоимость (NPV);
индекс рентабельности (PI);
внутренняя норма доходности (IRR).
138. Срок окупаемости
Срок окупаемости (PP)Срок окупаемости (payback period) — период времени, необходимый для того, чтобы
доходы, генерируемые инвестициями, покрыли затраты на инвестиции.
Например, если инвестиционный проект требует инвестиций в €2,000,000 и эти
инвестиции будут возвращаться по €1,000,000 в год, то можно говорить, что срок
окупаемости проекта составляет два года.
Показатель срока окупаемости является приоритетным, если инвестор ставит задачей как
можно быстрей вернуть вложенные инвестиции.
Преимущества метода
• простота расчета;
возможность наглядно оценить реальный период возврата вложенных средств.
Недостатки метода
• Игнорирует денежные поступления впоследствии истечения срока окупаемости. Так,
по проектам с длительным сроком окупаемости после всего периода возврата
инвестиций может быть получен больший результат.
• Не учитывает вероятность реинвестирования доходов.
• Проекты с одинаковым сроком окупаемости, но различной временной структурой
доходов признаются равноценными.
139. Расчет срока окупаемости
Пример 4.1:Рассматриваются 2 альтернативных проекта, A и B. Денежные поступления и расходы,
связанные с каждым проектом отображены в таблице:
Год
0. год (начальные инвестиции)
1. год (денежные поступления)
2. год (денежные поступления)
3. год (денежные поступления)
4. год (денежные поступления)
5. год (денежные поступления)
5. год (ликвидационная стоимость)
Проект A
(EUR)
–70,000
15,000
35,000
30,000
25,000
15,000
10,000
Проект B
(EUR)
–165,000
45,000
65,000
45,000
35,000
35,000
20,000
Предприятие отклоняет проекты срок окупаемости которых превышает 4 года.
Используя критерий PP, оценить проекты в рамках срока окупаемости. Какой из проектов
является более приемлемым с позиции ликвидности?
140. Расчет срока окупаемости
Решение:Год
0. год
1. год
2. год
3. год
4. год
Проект A, EUR
Ежегодный
денежный
поток
Сальдо
–70,000
15,000
35,000
30,000
X
Проект A
–70,000
–55,000
–20,000
10,000
X
Проект B, EUR
Ежегодный
денежный
поток
Сальдо
–165,000
45,000
65,000
45,000
35,000
–165,000
–120,000
–55,000
–10,000
25,000
Проект B
Начальные инвестиции окупаются Начальные инвестиции окупаются в
в третьем году
четвертом году
Срок окупаемости:
Срок окупаемости:
2 года+ (20,000 / 30,000) ≈ 2.6 года 3 года + (10,000 / 35,000) ≈ 3.3 года
Проект А предпочтительней, т.к. имеет более короткий срок окупаемости.
141. Расчет срока окупаемости
Пример 4.2:Выбрать один из двух альтернативных проектов используя информацию в таблице:
Название позиции
Расходы по закупке основных
средств (начальные инвестиции)
Прибыль (до отчисления износа)
1. год
2. год
3. год
4. год
5. год
Проект C
(EUR)
Проект D
(EUR)
75,000
75,000
30,000
40,000
50,000
55,000
70,000
60,000
35,000
10,000
10,000
10,000
Начальные инвестиции проекта C покрываются в третьем году.
Проект D окупается уже во втором году. Используя исключительно метод PP в оценке
инвестиций выбирается проект D. Однако прибыль для проекта C значительно выше,
чем для проекта D:
— вложив €75,000 в проект C, в течении 5-ти лет можно заработать €245,000;
— вложив €75,000 в проект D, в течении 5-ти лет можно заработать только €125,000.
В оценке инвестиций, при использовании критерия PP, необходимо также учитывать
суммарный объем прибыли.
142. Метод дисконтирования денежных потоков (DCF)
Дисконтирование денежных потоков (discounted cash flow approach) - математическийметод, используемый в оценке эффективности инвестиционных проектов. Метод
учитывает временную стоимость денежных средств и общую рентабельность проекта.
На основе метода DCF используются 2 базовых критерия при оценке эффективности
инвестиционных проектов:
1. Чистая приведенная стоимость (NPV);
2. Внутренняя норма доходности (IRR).
Базовые правила при принятии инвестиционных решений
1. Определение проблемы
Оценку надо начинать с того, что должна дать данная инвестиция (больший объем продаж,
новый продукт, снижение затрат и т. д.).
2. Оценка будущих затрат и выгод
Необходимо учесть неопределеннось (риск) будущих затрат и выгод.
3. Дополнительные денежные потоки
Обоснование вложения капитала основано на дополнительных изменениях денежных
потоков после налогообложения (приростных величинах), вытекающих из решений по
инвестированию. Любые доходы и расходы, которые останутся постоянными как до, так
и после совершения инвестиций, несущественны для целей анализа. Любые
бухгалтерские операции, относящиеся к инвестиционному решению, но не
затрагивающие денежных потоков несущественны для целей обоснования проектов.
143. Базовые правила при принятии инвестиционных решений
4. Необратимые затратыВ процессе поиска решений прошлые затраты не имеют значения. Эти необратимые
затраты (невозвратные) представляют собой ранее произведенные и невозместимые
расходы, которые при принятии решений игнорируются.
5. Издержки упущенных возможностей
При анализе учитывают отказ от возможных выгод, связанных с неиспользованием
инвестиций в альтернативных проектах. Эти издержки добавляют к первоначальным
расходам по проекту.
6. Стоимость денег во времени
Все будущие денежные потоки следует "привести" к настоящему времени с помощью
дисконтирования.
Чтобы оценить привлекательность инвестиционного проекта следует рассмотреть 4
элемента:
объем затрат – чистые инвестиции;
потенциальные выгоды – чистый денежный приток от деятельности;
период, в котором проект будет обеспечивать доход – жизненный цикл инвестиций;
любое высвобождение капитала в конце срока экономической жизни проекта –
ликвидационная стоимость.
144. Метод чистой приведенной стоимости (NPV)
Метод чистой приведенной стоимости (NPV)Метод чистой приведенной стоимости (net present value) получил широкое применение при
бюджетировании капитальных вложений и принятии инвестиционных решений. Также NPV
считается лучшим критерием отбора для принятия или отклонения решения о реализации
инвестиционного проекта, поскольку основывается на концепции стоимости денег во
времени. Другими словами, чистая приведенная стоимость отражает ожидаемое изменение
благосостояния инвестора в результате реализации проекта.
Чистая приведенная стоимость проекта является суммой настоящей стоимости всех денежных
потоков (как входящих, так и исходящих). Формула расчета выглядит следующим образом:
n
CFn
CFt
CF1
CF2
NPV CF0
...
1
2
n
t
(1 r ) (1 r )
(1 r )
t 0 (1 r )
где:
CF0 = начальные инвестиции;
CFt = ожидаемый чистый денежный поток (разница между входящим и исходящим денежным
потоком) за период t;
n = срок реализации проекта;
r = ставка дисконтирования (альтернативная цена капитала).
Важно понимать, что при выборе ставки дисконтирования (r) должна быть учтена не только
концепция стоимости денег во времени, но и риск неопределенности ожидаемых денежных
потоков. По этой причине в качестве ставки дисконтирования рекомендуется использовать
средневзвешенную стоимость капитала (weighted average cost of capital, rWACC),
привлеченного для реализации проекта. Другими словами, rWACC является требуемой нормой
доходности на капитал, инвестированный в проект. Следовательно, чем выше риск
неопределенности денежных потоков, тем выше ставка дисконтирования, и наоборот.
145. Метод чистой приведенной стоимости (NPV)
NPV: Критерий отбора проектовЕсли...
Это означает, что...
Поэтому...
NPV > 0
инвестиции увеличивают стоимость
предприятия
проект можно принять
NPV < 0
инвестиции снижают стоимость предприятия
проект следует отклонить
NPV = 0
инвестиции не влияют на стоимость
предприятия
принятие проекта не принесет ни прибыли, ни
убытка.
Правило принятия решения об отборе проектов при помощи NPV метода довольно
прямолинейно. Нулевое пороговое значение говорит о том, что денежные потоки
проекта позволяют покрыть стоимость привлеченного капитала. Таким образом,
критерии отбора можно сформулировать следующим образом:
Отдельно взятый независимый проект должен быть принят при положительном
значении чистой приведенной стоимости или отклонен при отрицательном. Нулевое
значение является точкой безразличия для инвестора.
Если инвестор рассматривает несколько независимых проектов, принять следует те из
них, у которых наблюдается положительный NPV.
Если рассматривается ряд взаимоисключающих проектов, выбрать следует тот из них,
у которого будет максимальная чистая приведенная стоимость.
146. Расчет NPV
Пример 4.3:Предприятие рассматривает инвестиционный проект, при осуществлении которого
ожидаются следующие денежные потоки:
Год
0. год (начальные инвестиции)
Денежный поток (EUR)
–150,000
1. год
70,000
2. год
90,000
3. год
50,000
4. год
40,000
Стоимость капитала предприятия — 15%
Определить чистую приведенную стоимость проекта. Является ли проект приемлемым?
Решение:
NPV 150,000
70,000
90,000
50,000
40,000
€34,668.44
1
2
3
4
(1 0.15) (1 0.15) (1 0.15) (1 0.15)
Чистый дисконтированный доход превышает расходы на €34,668.44.
NPV > 0. Проект можно принять.
147. Расчет NPV
Пример 4.4:Дать оценку эффективности инвестиционному проекту, если стоимость капитала — 9.5% и
инфляция составит 5% в год.
Прогнозируемый чистый денежный
доход в год, тыс. €
Инвестиции, тыс. €
1.год
50,000
2.год
20,000
20,000
3.год
25,000
Для оценки проекта воспользуемся критерием NPV.
1. Рассмотрим проект без учета инфляции:
20,000
20,000
25,000
€3,986.41
1 0.095 (1 0.095) 2 (1 0.095) 3
Не принимая во внимание инфляцию, проект можно принять.
NPV1 50,000
2. Рассмотрим проект с учетом инфляции:
NPV2 50,000
20,000
20,000
1 0.095 (1 0.05) (1 0.095) 2 (1 0.05) 2
25,000
€1,026.83
(1 0.095) 3 (1 0.05) 3
Принимая во внимание инфляцию, проект необходимо отклонить, т.к. NPV2 < 0
148. Метод внутренней нормы доходности (IRR)
Внутренняя норма доходности (IRR)Внутренняя норма доходности (рентабельности) (internal rate of return) — cтавка
дисконтирования, при которой суммарная приведенная стоимость доходов от
осуществляемых инвестиций равна стоимости этих инвестиций.
IRR определяет максимальную стоимость привлекаемого капитала, при которой
инвестиционный проект остается выгодным. В другой формулировке, это средний
доход на вложенный капитал, обеспечиваемый данным инвестиционным проектом.
IRR рассчитывается как значение ставки дисконтирования r, при которой NPV = 0:
n
CFt
t
t 0 (1 IRR)
NPV 0
Если величина IRR проекта больше стоимости капитала для предприятия (напр., rWACC), то
проект следует принять.
Для расчета IRR можно применить:
• метод интерполяции (в этом случае можно определить только приближенное
значение);
• MS Excel функцию IRR .
149. Расчет IRR
Приближенное значение IRR можно получить используя метод интерполяции.Для расчета необходимо два значения NPV, наиболее близко лежащие к нулю: одно –
положительное значение, второе – отрицательное значение, а также соответствующие
каждому из NPV нормы дисконта:
IRR r1
(r2 r1 ) NPV1
( NPV1 NPV2 )
где:
r1 = дисконтная норма, при которой NPV1 > 0;
r2 = дисконтная норма, при которой NPV2 < 0.
150. Расчет IRR
Пример 4.5:Предприятие рассматривает возможность покупки технологического оборудования,
стоимость которого составляет €80,000. Использование оборудования даст экономию
средств в размере €20,000 в год на протяжении 5-ти лет. В конце срока эксплуатации
планируется продать оборудование по цене €15,000. Стоимость капитала – 10%.
Определить IRR. Является ли проект рентабельным?
Решение:
Определим NPV при норме дисконтирования 10%:
Год
Денежный поток Дисконтированная
(EUR)
стоимость (EUR)
0. год
1. год
2. год
3. год
4. год
5. год
Конец 5-го года
NPV1
NPV1 80,000
–80,000
20,000
20,000
20,000
20,000
20,000
15,000
–80,000.00
18,181.82
16,528.93
15,026.30
13,660.27
12,418.43
9,313.82
5,129.56
20,000
20,000
20,000
20,000
20,000
(1 0.1)1 (1 0.1) 2 (1 0.1) 3 (1 0.1) 4 (1 0.1) 5
15,000
€5,129.56
5
(1 0.1)
151. Расчет IRR
Т.к. полученный результат – положительное число, фактическая внутренняя нормарентабельности выше 10%.
Определим NPV при норме дисконтирования 15%:
Год
0. год
1. год
2. год
3. год
4. год
5. год
Конец 5-го года
NPV2
Денежный поток Дисконтированная
(EUR)
стоимость (EUR)
–80,000
20,000
20,000
20,000
20,000
20,000
15,000
–80,000.00
17,391.30
15,122.87
13,150.32
11,435.06
9,943.53
7,457.65
–5,499.25
r1 = 10%, NPV1 = 5,129.56
r2 = 15%, NPV2 = -5,499.25
NPV2 – отрицательное число. Из этого следует, что фактическая IRR выше 10%, но ниже 15%.
IRR 10%
(15% 10%) 5,129.56
12.41%
(5,129.56 ( 5,499.25))
IRR > цена капитала (10%), проект можно принять.
IRR 11.86% (MS Excel)
152. Оценка проектов связанных с расширением деятельности предприятия
Чаще всего инвестиции осуществляются с целью расширения деятельности предприятия.При расширении предприятия, как правило, растут потребности в оборотном капитале
и новых основных средствах, повышаются операционные издержки и прибыль всвязи с
увеличением нетто оборота. Если проект принимается, увеличение данных позиций
затрагивает финансовую отчетность фирмы и означает изменение объема денежных
поступлений и расходов. Эти изменения необходимо учитывать при расчетах
прогнозируемых чистых денежных потоков.
Денежные потоки инвестиционного проекта можно разделить на три категории:
1. Начальные инвестиции в основные и оборотные средства.
Денежные расходы, связанные с инвестициями в основные средства, как правило,
следующие:
а) закупочная стоимость;
б) доставка и инсталляция основного средства.
При принятии проекта увеличивается объем оборотных средств, т.к. в большинстве случаев
рост выручки (в результате расширения деятельности предприятия) приводит к
увеличению дебиторской задолженности, товарно-складских запасов и счетов к оплате
(т.е. кредиторской задолженности).
Данные изменения затрагивают баланс предприятия.
153. Оценка проектов связанных с расширением деятельности предприятия
Таким образом, объем чистых инвестиций в оборотные средства (net working capital investments)можно представить в виде формулы:
NWCInv CA CL
где:
ΔCA = увеличение объема оборотных средств (денежные средства исключаются);
ΔCL = увеличение объема краткосрочных кредиторов (займы в кредитных учреждениях не
учитываются).
Например, если в результате принятия проекта ожидаются изменения в объеме запасов,
дебиторской задолженности и задолженности поставщикам и подрядчикам, объем чистых
инвестиций в оборотные средства можно представить как:
NWCInv ( INV A / R) A / P
где:
ΔINV = увеличение объема товарно-складских запасов;
ΔA/R = увеличение объема дебиторской задолженности;
ΔA/P = увеличение объема кредитных обязательств перед поставщиками и подрядчиками.
Если NWCInv – положительное число, это означает, что необходимо финансирование (исходящий
денежный денежный поток). Если NWCInv – отрицательная величина, происходит экономия
денежных средств (входящий денежный поток).
Также предпологается, что к концу жизненного цикла произойдет высвобождение оборотного
капитала. Это условие необходимо учесть в расчете потока на момент закрытия проекта.
154. Оценка проектов связанных с расширением деятельности предприятия
Таким образом, объем начальных капиталовложений можно определить по формуле:CF0 FCInv NWCInv
где:
FCInv = инвестиции в основные средства (fixed capital investments);
NWCInv = инвестиции в оборотные средства (net working capital investments);
2. Операционный денежный поток после отчисления налогов.
Изменения происходят в отчете о прибыли, т.к. при принятии проекта как правило
увеличиваются доходы и операционные издержки.
Операционный денежный поток после налоговых отчислений (after-tax operating cash flow)
определяется по формуле:
ATOCFt (St Ct Dt ) (1 t ) Dt
где:
St = доход от реализации продукции (в денежном эквиваленте) за отчетный период t (cash
sales);
Ct = операционные издержки за отчетный период t (cash operating expenses);
t = налоговая ставка;
Dt = расходы по износу основных средств за отчетный период t;
155. Оценка проектов связанных с расширением деятельности предприятия
3. Ликвидационный денежный поток .В конце жизненного цикла проекта предприятие может продать задействованные в проекте
основные средства (входящий денежный поток). При продаже разница между
рыночной и балансовой стоимостью основного средства облагается налогом
(исходящий денежный поток). Оборотный капитал высвобождается (обычно входящий
денежный поток).
Таким образом денежный поток поступающий на момент закрытия проекта можно
определить след. образом:
TNOCFT SVT NWCInv t ( SVT BVT )
где:
SVT = средства полученные при реализации основного средства по рыночной цене (salvage
value);
NWCInv = инвестиции в оборотный капитал (высвобождение средств);
t = налоговая ставка;
BVT = балансовая стоимость основного средства в момент продажи (book value);
T = жизненный цикл проекта (годы).
Расчеты денежных потоков основываются на прогнозах, т.е. используются ожидаемые
будущие денежные расходы и доходы связанные с проектом. Долгосрочное
прогнозирование потоков является сложной экономической задачей, особенно трудно
прогнозировать влияние цен и спроса.
156. Оценка проектов связанных с расширением деятельности предприятия
Чистая приведенная стоимость инвестиционного проекта определяется след. образом:NPV CF0
ATOCF1 ATOCF2 ATOCF3
ATOCFT TNOCFT
...
(1 r )1
(1 r ) 2
(1 r ) 3
(1 r )T
где:
CF0 = начальные капиталовложения в основные и оборотные средства;
ATOCF = прогнозируемый операционный денежный поток после отчисления налогов;
TNOCF = ликвидационный денежный поток;
r = норма дисконтирования (стоимость капитала).
Если NPV > 0, проект можно принять.
Если NPV < 0, проект необходимо отклонить.
157. Оценка проектов связанных с расширением деятельности предприятия
Пример 4.6:Предприятие планирует расширить свою деятельность и внедрить в производство новую
продукцию. У предприятия есть возможность купить производственное здание по цене
€24,000. Также планируется приобрести новое технологическое оборудование по цене
€16,000. В момент закупки основных средств предприятие планирует выделить
финансирование для оборотных средств в размере €12,000.
Срок проекта - 4 года.
Прогнозируемая стоимость основных средств в конце 4 года:
Основные средства
Рыночная цена
(EUR)
Производственное здание
Оборудование
Балансовая стоимость
(EUR)
15,000
4,000
21,816
2,720
Предполагается, что доход от реализации новой продукции составит €80,000 в год, а
переменные издержки составят 60% от выручки, т.е. €48,000; постоянные издержки €10,000 в год (исключая износ). Таким образом, общие операционные издержки
составят €58,000 в год. Подоходный налог с предприятия - 40%. Стоимость
привлеченного капитала - 12%.
Информация по износу основных средств:
Год
1.год
2.год
3.год
4. год
Расходы по износу
3,512
5,744
3,664
2,544
К концу срока проекта предприятие планирует
продать основные средства по рыночной цене и
высвободить оборотные средства.
Определить NPV и IRR для данного проекта. Является
ли проект рентабельным?
158. Оценка проектов связанных с расширением деятельности предприятия
Решение:1) Начальные инвестиции:
CF0 FCInv NWCInv (24,000 16,000) 12,000 52,000
2) Операционный денежный поток после отчисления налогов (для каждого года):
ATOCFt (St Ct Dt ) (1 t ) Dt
ATOCF1 (80,000 58,000 3,512) (1 0.4) 3,512 14,605
ATOCF2 (80,000 58,000 5,744) (1 0.4) 5,744 15,498
ATOCF3 (80,000 58,000 3,664) (1 0.4) 3,664 14,666
ATOCF4 (80,000 58,000 2,544) (1 0.4) 2,544 14,218
3) Ликвидационный денежный поток (в конце 4 года):
TNOCF 4 SV4 t ( SV4 BV4 ) NWCInv
TNOCF4 [15,000 0.4 (15,000 21,816)]
[4,000 0.4 (4,000 2,720)] 12,000 33,214
159. Оценка проектов связанных с расширением деятельности предприятия
4) Чистая приведенная стоимость проекта:NPV CF0
ATOCF1 ATOCF2 ATOCF3
ATOCFT TNOCFT
...
(1 r )1
(1 r ) 2
(1 r ) 3
(1 r )T
NPV 52,000
14,605
15,498
14,666
14,218 33,214
€13,978
(1 0.12)1 (1 0.12) 2 (1 0.12) 3
(1 0.12) 4
CF0 – отрицательная величина, т.к. инвестиции в основные средства и оборотный капитал исходящий денежный поток.
Используя MS Excel, IRR = 21.9%
5) Проект можно принять, т.к. NPV > 0 и IRR > 12%.
Решение задачи при помощи таблиц:
160. Оценка проектов связанных с расширением деятельности предприятия
Год0
1
2
3
4
Atrisinājums (izmantojot tabulu):
Начальные инвестиции:
в основные средства
– 40,000
в оборотные средства
– 12,000
– 52,000
Операционный денежный поток после отчисления налогов
Доход от реализиции продукции
80,000
80,000
80,000
80,000
Операционные издержки
58,000
58,000
58,000
58,000
3,512
5,744
3,664
2,544
18,488
16,256
18,336
19,456
7,395
6,502
7,334
7,782
11,093
9,754
11,002
11,674
3,512
5,744
3,664
2,544
14,605
15,498
14,666
14,218
Расходы по износу
Операционная прибыль до налогов
Налоги
Операционная прибыль после уплаты налогов
(+) расходы по износу
Операционный денежный поток после налогов
Ликвидационный денежный поток:
Средства полученные при продаже осн. cредств с
учетом налогов
21,214
Высвобождение оборотных средств
12,000
Ликвидационный денежный поток (TNOCF)
33,214
Итого денежный поток после отчисления налогов
– 52,000
NPV (12%)
13,978
IRR
21.9%
14,605
15,498
14,666
47,432
161. Оценка проектов связанных с модернизацией основных средств
В результате модернизации основных средств происходит замена существующих основныхсредств на более новые и эффективные.
В этом случае, анализ денежных потоков представляет собой более сложную задачу, т.к.
необходимо сравнить денежные потоки, формирующиеся в результате модернизации
основного средства, с потоками, которыми предприятие располагало бы при отсутствии
проекта. Это означает, что при оценке инвестиционного проекта должен соблюдаться
базовый принцип:
При анализе эффективности проекта, необходимо сравнивать денежные потоки,
формирующиеся в результате принятия проекта, с денежными потоками
формирующимися без проекта.
Пример 4.7:
Предприятие планирует заменить существующее технологическое оборудование на более
новое и эффективное. Информация об основных средствах:
Существующее оборудование
Текущая балансовая стоимость
Текущая рыночная цена
Срок эксплуатации
Прогнозируемый доход за год
Операционные издержки (в денежн.экв.)
Расходы по износу (за год)
Балансовая стоимость к концу срока проекта
Прогноз. рыночная стоимость к концу проекта
Новое оборудование
€400,000
€600,000
10 лет
€300,000
€120,000
€40,000
€0
€100,000
Текущая рыночная цена
Срок эксплуатации
Прогнозируемый доход за год
Операционные издержки (в денежн.экв.)
Расходы по износу (за год)
Балансовая стоимость к концу срока проекта
Прогноз. рыночная стоимость к концу проекта
€1,000,000
10 лет
€450,000
€150,000
€100,000
€0
€200,000
162. Оценка проектов связанных с модернизацией основных средств
Призамене оборудования на более новое, потребуются дополнительные
капиталовложения в оборотные средства в размере €80,000. Налоговая ставка - 15%.
Стоимость капитала - 8%. Определить NPV.
Решение:
1) Начальные инвестиции можно определить по формуле:
CF0 FCInv NWCInv SV0 t (SV0 BV0 )
где:
FCInv = инвестиции в основные средства (напр. стоимость нового основного средства) ;
NWCInv = инвестиции в оборотные средства;
SV0 = текущая рыночная цена существующего основного средства;
t = налоговая ставка;
BV0 = балансовая стоимость существующего основного средства.
Денежный поток CF0 формируется след. образом:
a) При принятии проекта существующее (заменяемое) основное средство продается по рыночной цене
(входящий денежный поток);
b) Разница между полученным доходом с продаж старого основного средства и его балансовой
стоимостью облагается налогом (исходящий денежный поток);
c) Осуществляются необходимые инвестиции в оборотные средства (исходящий денежный поток);
d) Денежные средства используютя для покупки нового основного средства (исходящий денежный
поток).
CF0 1,000,000 80,000 600,000 0.15 (600,000 400,000) €510,000
163. Оценка проектов связанных с модернизацией основных средств
2) Рассчитаем операционный денежный поток с учетом налогообложения. В расчетахнеобходимо учесть, что в результате модернизации произойдут изменения в
следующих позициях:
доходы от реализации продукции;
операционные издержки, и
расходы по износу.
Формула для расчета:
ATOCFt ( St Ct Dt ) (1 t ) Dt
где:
ΔATOCFt = прирост операционного денежного потока после отчисления налогов (за год);
ΔSt = увеличение доходов от реализации продукции (выручки) (за период t);
ΔCt = увеличение операционных издежек (за период t);
ΔDt = увеличение расходов по износу (за период t);
t = налоговая ставка.
Для каждого из основных средств износ начисляется по линейному методу, поэтому:
ΔATOCF1 = ΔATOCF2 = ... = ΔATOCF10 :
ATOCF1, 2...10 [(450,000 300,000) (150,000 120,000) (100,000 40,000)] (1 0.15)
(100,000 40,000) (150,000 30,000 60,000) (1 0.15) 60,000 €111,000
164. Оценка проектов связанных с модернизацией основных средств
3) Теперь определим величину ликвидационного денежного потока:TNOCFT SVT NWCInv t ( SVT BVT )
где:
ΔSVT = разница между рыночной ценой нового и существующего (заменяемого) основного
средства (в момент ликвидации проекта);
NWCInv = возврат (освобождение) капиталовложений в оборотные средства;
ΔBVT = разница между балансовой стоимостью нового и заменяемого основного средства (в
конце проекта);
t = налоговая ставка.
TNOCF10 (200,000 100,000) 80,000 0.15 [(200,000 100,000 (0 0)] €165,000
4) Рассчитаем чистую приведенную стоимость проекта:
10
111,000
165,000
€311,245.96
t
10
(
1
0
.
08
)
(
1
0
.
08
)
t 1
NPV 510,000
5) Модернизация основного средства целесообразна, т.к. NPV > 0.
165. Взаимоисключающие проекты с различными жизненными циклами
Если проекты взаимоисключающие и имеют неравные сроки действия, рекомендуетсяиспользовать метод эквивалентного аннуитета (equivalent annual annuity, EAA).
Процедура метода:
1. Найти NPV для каждого проекта;
2. Найти EAA для каждого проекта по следующей формуле:
r NPV
EAA
1
1
(1 r ) n
где:
NPV = чистая приведенная стоимость проекта;
r = периодическая норма дисконтирования для проекта;
n = количество периодов.
3. Выбрать проект с максимальным показателем EAA.
166. Взаимоисключающие проекты с различными жизненными циклами
Пример 4.8:Предприятие рассматривает два взаимоисключающих проекта.
Стоимость капитала – 12%.
Жизненный цикл проекта А – 6 лет. Жизненный цикл проекта B – 3 года. Данные о чистых
денежных потоках, NPV и IRR отображены на временных линиях:
Проект A
r = 12%
0
1
2
3
4
5
6
– 20,000
4,000
7,000
6,500
6,000
5,500
5,000
NPV = €3,245.47; IRR = 17.5%
Проект B
r = 12%
0
1
2
3
– 10,000
3,500
6,500
6,000
NPV = €2,577.44; IRR = 25.2%
Какой из проектов является наиболее приемлемым?
167. Взаимоисключающие проекты с различными жизненными циклами
Решение:Определим EAA для каждого из проектов:
EAAA
EAAB
0.12 (3,245.47)
€789.38
1
1
(1 0.12) 6
0.12 (2,577.44)
€1,073.12
1
1
(1 0.12) 3
Рекомендуется принять проект B, т.к. EAAB > EAAA
168. Оценка риска инвестиционных проектов
Для оценки риска инвестиционных проектов используются следующие методы:1. Анализ чувствительности (sensitivity analysis)
2. Анализ сценариев (scenario analysis)
Анализ чувствительности
Анализ чувствительности (sensitivity analysis) — заключается в оценке влияния изменения
исходных параметров проекта на его конечные характеристики, в качестве которых,
обычно, используется внутренняя норма рентабельности или NPV. Техника проведения
анализа чувствительности состоит в изменении выбранных параметров в определенных
пределах, при условии, что остальные параметры остаются неизменными. Чем больше
диапазон вариации параметров, при котором NPV остается положительной величиной,
тем устойчивее проект.
Анализ чувствительности проекта позволяет оценить, как изменяются результирующие
показатели реализации проекта при различных значениях заданных переменных,
необходимых для расчета. Этот вид анализа позволяет определить наиболее критические
переменные, которые в наибольшей степени могут повлиять на осуществимость и
эффективность проекта.
169. Анализ чувствительности
Пример 4.9:Предприятие рассматривает инвестиционный проект. Прогнозируемые данные указаны в
таблице:
Базовый сценарий
Цикл проекта
3 года
Физический объем реализации (в год)
1,500 ед.
Цена за единицу продукции
€50.00
Переменные издержки (за единицу продукции)
€20.00
Постоянные издержки (в год)
€5,000
Инвестиции в основные средства
€60,000
Износ основных средств начисляется по линейному методу в течении 3-х лет до
балансовой стоимости 0.
Инвестиции в оборотные средства
€15,000
Денежные средства с продаж основных средств в
конце 3-го года
€10,000
Налоговая ставка
15%
Стоимость капитала
15%
170. Анализ чувствительности
1. Определить NPV и IRR проекта для базового сценария.2. Провести анализ чувстительности показателей эффективности проекта к изменению
критических факторов, повышая и понижая определенный параметр на 20%, при
условии, что остальные факторы остаются неизменными.
3. Определить критические переменные, к изменениям которых показатели NPV и IRR
наиболее чувствительны.
Решение:
1. Определим объем начальных инвестиций:
CF0 FCInv NWCInv 60,000 15,000 €75,000
Прогнозируемый денежный доход от реализации продукции:
S Q P 1,500 50 €75,000
Прогнозируемые операционные издержки:
C TVC FC (20 1,500) 5,000 €35,000
Расходы по износу (по линейному методу):
D
60,000
€20,000
3
171. Анализ чувствительности
Определим операционные денежные потоки после отчисления налогов и ликвидационныйденежный поток на момент закрытия проекта:
ATOCF1 ATOCF2 ATOCF3 ( S C D) (1 t ) D
(75,000 35,000 20,000) (1 0.15) 20,000 €37,000
TNOCF3 SV3 NWCInv t ( SV3 BV3 )
10,000 15,000 0.15 (10,000 0) €23,500
Чистая приведенная стоимость проекта определяется след. образом:
3
37,000
23,500
€24,930.96
t
3
(1 0.15)
t 1 (1 0.15)
NPV 75,000
IRR 32.5% (MS Excel)
172. Анализ чувствительности
2. Результаты анализа чувствительности представлены в таблице:Переменные
Объем продаж (в год)
– 20%
NPV
IRR
Цена за единицу продукции
NPV
IRR
Переменные издержки (за ед. продукции)
NPV
IRR
Постоянные издержки (в год)
NPV
IRR
Денежные средства с продаж основных
средств в конце 3 года
NPV
IRR
€7,464
20.3%
– €4,180
12.0%
€36,575
40.4%
€26,872
33.8%
€23,813
31.8%
Базовый сценарий
€24,931
32.5%
€24,931
32.5%
€24,931
32.5%
€24,931
32.5%
€24,931
32.5%
+ 20%
€42,398
44.4%
€54,042
52.1%
€13,287
24.4%
€22,990
31.2%
€26,049
33.2%
3. Показатели эффективности проекта наиболее чувствительны к изменениям цены
продукции. Если цена снизится на 20%, NPV проекта будет отрицательной (–€4,180) и
внутренняя норма рентабельности будет ниже стоимости капитала.
173. Анализ сценариев
Анализ сценариевПо существу, анализ сценариев представляет собой развитие методики анализа
чувствительности – одновременному изменению подвергается вся группа переменных
проекта, проверяемых на риск.
Обычно рассматриваются три сценария развития проекта:
• пессимистический;
• базовый (основной);
• oптимистический.
Одновременно изменяя величину существенного фактора на x %, для каждого из сценариев
определяется показатели NPV и IRR, и устанавливается нижний и верхний порог
чувствительности для этих показателей.
Недостаток метода в том, что он не учитывает вероятности развития сценариев.
174. Анализ сценариев
Пример 4.10:Используя данные из примера 4.9., проанализируем три возможных сценария развития
проекта. Определим нижнюю и верхнюю границу для показателей NPV и IRR.
Переменные
Сценарий
Пессимистический
Базовый
Оптимистический
Объем продаж (в год)
– 20%
1,500
+ 20%
Цена за единицу продукции
– 20%
€50.00
+ 20%
Переменные издержки (за ед.
продукции)
+ 20%
€20.00
– 20%
Постоянные издержки (в год)
+ 20%
€5,000
– 20%
Денежные средства с продаж
основных средств в конце 3 года
– 20%
€10,000
+ 20%
NPV
– €28,199
€24,931
€94,363
IRR
– 6.2%
32.5%
78.1%
175. Анализ сценариев с учетом вероятностей
Пример 4.11:Продолжим пример 4.10. Предположим, что пессимистический сценарий – это ухудшение
всех показателей на 20%, оптимистический – улучшение на 20%. Также предположим, что
известна вероятность развития сценариев. Возможные варианты NPV проекта и
вероятность развития сценариев представлены в таблице:
Сценарий
Вероятность
NPV
Пессимистический
0.25
– €28,199
Базовый
0.50
€24,931
Оптимистический
0.25
€94,363
Ожидаемую чистую приведенную стоимость, E(NPV), рассчитаем используя формулу
математического ожидания:
n
E ( NPV ) NPVi pi
i 1
где:
NPVi – чистая приведенная стоимость при i-ом исходе событий;
pi – вероятность наступления i-го исхода событий;
n – количество исходов событий.
E ( NPV ) ( 28,199) (0.25) (24,931) (0.5) (94,363) (0.25) €29,007
176. Анализ сценариев с учетом вероятностей
Если значение E(NPV) < 0, то проект следует отклонить.Рассчитаем среднее квадратическое отклонение NPV проекта (средневзвешенное по
вероятности отклонение от ожидаемой величины) по формуле:
n
2
(NPV
E
(
NPV
))
( pi )
i
i 1
NPV ( 28,199 29,007 ) 2 0.25 (24,931 29,007 ) 2 0.5 (94,363 29,007 ) 2 0.25 43,523
Определим коэффициент вариации (показатель риска на единицу дохода), CV (coefficient of
variation) по формуле:
CV
CV
NPV
E (NPV )
43,523
1.50
29,007
Следующий этап оценки риска – сравнение коэффициента вариации данного проекта
предприятия с соответствующим коэффициентом среднего проекта. Например, если у
среднего проекта коэффициент вариации равен 1.40, то рассматриваемый проект имеет
более высокую степень риска.
177. Раздел 5: СТРУКТУРА КАПИТАЛА
Понятие структуры капиталаКапитал – основной елемент в управлении финансами предприятия. Для обеспечения
деятельности необходимы ресурсы для инвестиций в активы и производства продукции
(оказания услуг). С позиции предприятия, эти ресурсы представляют собой капитал.
Вопросы управления структурой капитала являются ключевыми в области финансового
управления предприятием. Недостаток капитала может препятствовать финансированию
рентабельных инвестиционных проектов, с другой стороны, переизбыток заемного
капитала может привести к снижению финансовой независимости.
Для финансирования своей деятельности предприятие использует:
заемный капитал и
собственный капитал.
Компании, обеспеченные недорогим долгосрочным капиталом, имеют больше
возможностей для роста и завоевания рынка по сравнению со своими конкурентами. В то
же самое время важно не только привлечь достаточно средств для развития компании,
но и правильно определить подходящую для нее структуру капитала. Так, наиболее
дешевым источником является заемный капитал, однако, привлекая займы и кредиты,
компания увеличивает финансовые риски. Финансирование деятельности за счет
собственного капитала менее рискованно, однако, является более дорогостоящим.
Поэтому только сбалансированная структура капитала компании может обеспечить ей
устойчивое развитие.
В общем виде, под структурой капитала обычно понимается соотношение собственного и
заемного капитала предприятия, которое соответствует его долгосрочной
стратегии развития.
178. Источники финансирования
Источники финансирования предприятияДва основных источника финансирования предприятия – заемный и собственный капитал,
которые обеспечиваются соответственно:
кредиторами и
собственниками (акционерами).
Позиция кредиторов и собственников характеризуется определенным и, в то же время,
отличающимся профилем риска и доходности.
Профиль риска и доходности кредиторов
Кредиторы имеют меньше контроля над предприятием, однако получают доход в виде
фиксированных процентов и, в случае неплатежеспособности, пользуются приоритетом в
получении выплат. Таким образом, этой группе инвесторов, в сравнении с акционерами
(собственниками), характерен более низкий уровень риска и доходности.
Профиль риска и доходности ацкионеров
В свою очередь, выплаты по дивидендам не несут постоянный характер, цена акции может
существенно колебаться, что означает повышенный уровень риска для собственников.
Неопределенность связанная с получением прибыли обуславливает более высокую
требуемую норму доходности по акционерному капиталу. Также, в случае
неплатежеспособности предприятия, акционеры получают выплаты после кредиторов.
179. Источники финансирования
Налоговая экономия при использовании заемного финансированияРиски связанные с использованием заемного капитала снижаются благодаря налоговой
экономии (tax shield). По законодательству большинства стран, выплачиваемые проценты
вычитаются при расчете налога, что снижает фактическую стоимость займа. Для
предприятия это означает дополнительный денежный поток, т.к. процентные платежи по
заемному капиталу (напр., банковскому кредиту) исключаются из налогооблагаемой
базы. Численно величина налоговой экономии может быть найдена как произведение
процентных платежей по заемному капиталу за период и ставки налога на прибыль.
Собственный капитал
Собственный капитал и резервы включают вложенный капитал и накопленную прибыль.
Вложенный капитал — это капитал, инвестированный собственником (уставный капитал,
добавочный капитал, целевые поступления). Собственный капитал предприятия —
нераспределенная прибыль, резервный капитал, различные фонды.
Накопленная (нераспределенная) прибыль — это прибыль за вычетом налогов и дивидендов,
которую предприятие заработало в предшествующий и настоящий период.
Заемный капитал (обязательства предприятия)
Заемный капитал в структуре капитала предприятия состоит из кратко- и долгосрочных
обязательств.
Долгосрочные обязательства — это кредиты и займы со сроком погашения более года.
Краткосрочные обязательства — это обязательства со сроком погашения менее 1 года
(например, краткосрочные кредиты и займы, кредиторская задолженность).
180. Признаки собственного и заемного капитала
Различия между собственным и заемным капиталом предприятияПризнак
Собственный
Заемный
Непосредственное право на участие в
управлении предприятием
Дает такое право
Не дает
такого права
Отношение к финансовому риску
Увеличение доли
собственного капитала
снижает финансовый риск
Увеличение доли
заемного капитала
увеличивает финансовый
риск
Право на получение прибыли
По остаточному принципу
Первоочередные
Очередность удовлетворения требований при
банкротстве
По остаточному принципу
Первоочередные
Срок и условия оплаты и возврата капитала
Однозначно не
установлены
Четко определены
кредитным соглашением
Основное направление финансирования
Долгосрочные активы
Краткосрочные активы
Снижение налога на прибыль за счет
отнесения финансовых издержек на затраты
Такая возможность
отсутствует
Такая возможность
присутствует
Связь дохода владельца капитала с
прибыльностью предприятия
Доход владельца
капитала
непосредственно связан с
финансовым результатом
Доход владельца
капитала не связан с
финансовым
результатом
181. Признаки собственного и заемного капитала
В современных условиях, при наличии множества источников финансирования, иногда сложноидентифицировать принадлежность конкретного источника финансирования собственному или
заемному капиталу.
В представлении А. Дамодарана (2011), оснобенности собственного и заемного капитала (см. рис.
5.1.) следующие:
Рис. 5.1. Признаки заемного и собственного капитала
Низкий приоритет
Отсутствие налоговой
экономии
Отсутствие определенного
срока
Право контроля
Фиксированный платеж
Высокий приоритет
Налоговая экономия
Определенный срок
Нет права контроляs
s
Заемный
капитал
Гибриды (комбинации
собственного и заемного капитала)
Собственный
капитал
К основным типам гибридных инструментов относятся конвертируемые облигации, облигации со
встроенными опционами и привилегированные акции.
Например, привилегированная акция не дает права владельцу на управление акционерным обществом через
участие в собрании акционеров. За отказ от этого права привилегированные акции предоставляют
владельцам ряд льгот:
- право на получение фиксированного дивиденда вне зависимости от прибыли АО;
- право на получение определенной части имущества АО в случае его ликвидации до того, как оно будет разделено
между владельцами обыкновенных акций.
182. Средневзвешенная стоимость капитала
Средневзвешенная стоимость капиталаэто средняя процентная ставка по всем источникам финансирования компании. При расчете
учитывается удельный вес каждого источника финансирования в общей стоимости.
Показатель характеризует относительный уровень общей суммы расходов по
обеспечению
каждого
источника
финансирования
и
представляет
собой
средневзвешенную цену капитала.
Рассчитывается по формуле:
D
E
rWACC rd (1 t ) re
V
V
где:
D = рыночная стоимость заемного капитала;
E = рыночная стоимость собственного капитала;
D + E = V;
V = рыночная стоимость предприятия;
D/V = удельный вес заемного капитала;
E/V = удельный вес собственного капитала;
rd = стоимость заемного капитала;
re = стоимость собственного капитала;
t = ставка налога на прибыль для предприятия.
183. Оценка стоимости заемного капитала и собственного капитала
Оценка стоимости заемного капиталаДля определения стоимости заемного капитала предприятия, можно изпользовать рыночную
процентную ставку по текущим кредитным обязательствам предприятия (займ в
кредитных учреждениях) и доходность к погашению (по облигациям, выпущенным
предприятием).
Оценка стоимости собственного капитала
Стоимость собственного (акционерного) капитала - норма доходности, компенсирующая
владельцев за риски, которые они берут на себя при вложении собственных средств.
Многие инвесторы используют модель ценообразования долгосрочных активов (Capital
Asset Pricing Model, CAPM) для этой цели.
184. Оценка стоимости заемного капитала и собственного капитала
Модель ценообразования долгосрочных активов (CAPM)Модель CAPM была создана У.Шарпом (1964) и Дж. Линтером (1965) и позволяет
спрогнозировать будущее значение доходности акции (актива) на основании линейной
регрессии. Модель отражает линейную взаимосвязь планируемой доходности с уровнем
рыночного риска, выраженного коэффициентом бета.
Модель оценки долгосрочных активов имеет следующий вид:
re RF i ( E ( RM ) RF )
где:
RF — безрисковая ставка доходности;
βi — коэффициент чувствительности актива i к изменениям рыночной доходности RM;
E(RM) — ожидаемая доходность рыночного портфеля;
(E(RM) — RF ) — премия за риск вложения в акции, равна разнице ставок рыночной и
безрисковой доходности.
Доходность по безрисковому активу, на практике, берется
государственным ценным бумагам.
Для расчета рыночной доходности используют доходность индекса.
как
доходность
по
185. Оценка стоимости заемного капитала и собственного капитала
Бета-коэффициент акции (βi) является мерой рыночного риска акции, показываетизменчивость доходности акции к доходности на рынке в среднем (применяется для
оценки риска вложений в ценные бумаги).
cov( Ri , RM )
i
2 ( RM )
где:
β – коэффициент бета, мера систематического риска (рыночного риска);
Cov (Ri, RM) – ковариация доходности i-ой акции и доходности рынка;
Ri – доходность i-й акции (инвестиционного портфеля);
RM – рыночная доходность;
σ2M – дисперсия рыночной доходности.
Коэффициент бета показывает рыночный риск акции и отражает чувствительность
изменения акции по отношению к изменению доходности рынка.
В таблице ниже показана оценка уровня риска по коэффициенту бета. Коэффициент бета
может иметь как положительный, так и отрицательный знак, который показывает
положительную или отрицательную корреляцию между акцией и рынком.
Положительный знак отражает, что доходность акций и рынка изменяются в одном
направлении, отрицательный – разнонаправленное движение.
186. Оценка стоимости заемного капитала и собственного капитала
Интерпретация бета коэфициентаЗначение показателя
β>1
β=1
0<β<1
-1 < β < 0
Уровень риска акции
Высокий
Умеренный
Низкий
Низкий
Направление изменения
доходности акции
Однонаправленное
Однонаправленное
Однонаправленное
Разнонаправленное
β < 0 – доходность акции демонстрирует разнонаправленное движение с доходностью портфеля
или индекса рынка, интерпретация осуществляется по абсолютному значению.
β = 0 – отсутствует корреляция между доходностью акции и доходностью портфеля или индекса
рынка.
0 < β < 1 – доходность акции и портфеля (индекса рынка) демонстрируют однонаправленное
движение, однако волатильность доходности акций ниже, чем волатильность доходности
портфеля.
β = 1 – доходность акции и портфеля (индекса рынка) демонстрируют однонаправленное движение,
при этом волатильность доходности акции равна волатильности доходности портфеля.
β > 1 – доходность акции и портфеля (индекса рынка) демонстрируют однонаправленное движение,
при этом волатильность доходности акции выше волатильности доходности портфеля.
187. Методы определения оптимальной структуры капитала
Оптимальная структура капитала - отношение заемного капитала к собственному, прикотором минимизируется стоимость капитала и максимизируестся стоимость
предприятия.
Методы определения оптимальной структуры капитала (А. Дамодаран, 2011):
• Метод средневзвешенных затрат на капитал (cost of capital approach)
Оптимальная структура капитала достигается при минимальной стоимости капитала;
Улучшенный метод средневзвешенных затрат на капитал (enhanced cost of capital
approach)
Оптимальная структура капитала достигается при минимальной стоимости капитала и
максимальной прибыли;
Метод скорректированной приведенной стоимости (adjusted present value approach)
Оптимальная структура капитала достигается при максимальной рыночной стоимости
предприятия;
Использование отраслевых показателей (sector approach)
Оптимальная структура достигается в соответствии со среднеотраслевыми показателями
структуры капитала;
188. Теории структуры капитала
Теории структуры капитала дают представление о влиянии структуры капитала нафинансовые показатели предприятия. Основная цель заключается в поиске оптимальной
структуры капитала.
Оптимальная структура капитала - сочетание источников финансирования, которое
позволяет максимизировать стоимость предприятия.
Оптимизация структуры капитала компании является одной из ключевых и, в то жe время,
сложных задач, решаемых в области корпоративных финансов.
Существует ряд методов, применяемых для этой цели, которые можно представить в
хронологическом порядке следующим образом:
Традиционный подход;
Теория Миллера и Модильяни;
Теория иерархии;
Статическая компромиссная теория;
Динамическая компромиссная теория;
Агентские модели;
Теория отслеживания рынка.
189. Традиционный подход
Традиционный подходСогласно данной теории у предприятия существует определенная оптимальная структура
капитала, которая максимизирует стоимость предприятия и минимизирует
средневзвешенную стоимость капитала.
Традиционалисты считали, что в любом случае собственный капитал дороже заемного
капитала. Кроме того, предполагалось, что в некоторых пределах наличие заемных
средств незначительно влияет на доходность (стоимость) собственного капитала. Поэтому
вначале с ростом доли заемных средств в совокупном капитале (D/V) средневзвешенная
стоимость (rWACC) будет снижаться, а рыночная стоимость фирмы (V) расти. Однако после
того, как доля заемного капитала достигнет определенного значения, дальнейшее ее
увеличение приведет к возрастанию финансового риска, что в конечном итоге вызовет
увеличение стоимости заемных средств (rd) и требуемой доходности собственного
капитала (re). Соотношение собственных и заемных средств, при котором
средневзвешенная стоимость капитала компании становится минимальной, и будет
определять ее оптимальную структуру капитала (рис. 5.2., 5.3.).
190. Традиционный подход
Рис. 5.2. Зависимость стоимости капитала от удельного веса заемного капитала (D/V) – традиционныйподход
Стоимость капитала
re
rWACC
rd
1
2
D*/V
3
D/V
191. Традиционный подход
Рис. 5.3. Зависимость стоимости предприятия (V) от удельного веса заемного капитала (D/V) –традиционный подход
V
V = max
1
2
3
D*/V
D/V
rWACC = min
В соответствии с традиционным подходом, структура капитала оказывает влияние на рыночную
стоимость предприятия. Стоимость предприятия максимизируется при оптимальном
соотношении собственного и заемного капитала, т.е. при минимальной средневзвешенной
стоимости капитала.
192. Традиционный подход
Пример 5.1.:Рассмотрим предприятие А, которое использует заемные средсва и предприятие B,
деятельность которого финансируется исключительно собственными средствами.
Предположим, что операционная прибыль предприятий (EBIT) будет одинаковой и
составит €900,000 в год без ограничения по времени, т.е. прогнозируемые потоки
предприятий рассматриваются как вечная рента. Предполагается, что предприятия имеют
одинаковую степень риска.
При отсутствии налогов, операционная прибыль (EBIT) распределяется между владельцами
капитала. Стоимость собственного капитала – 30%. Стоимость заемного капитала – 20%.
Рассчитаем стоимость предприятия А по формуле:
I EBIT I
V D E
rd
re
где:
D = рыночная стоимость заемного капитала;
E = рыночная стоимость собственного капитала;
I = процентные платежи;
EBIT = прибыль до уплаты процентов и налогов;
rd = стоимость заемного капитала;
re = стоимость собственного капитала.
193. Традиционный подход
Если сумма кредита (D) = €1,000,000, процентные платежи (I) можно рассчитать как:I D rd 1,000,000 0.2 €200,000
Стоимость предприятия А:
VA
I EBIT I 200,000 900,000 200,000
1,000,000 2,333,333 €3,333,333
rd
re
0.2
0.3
Средневзвешенная стоимость капитала для предприятия А:
1,000,000
2,333,333
D
E
rWACC , A rd (1 t ) re
0.2 (1 0)
0.3 0.27 27%
3
,
333
,
333
3
,
333
,
333
V
V
Предприятие B не использует внешнее кредитование (D = 0, I = 0). Стоимость предприятия B:
VB
EBIT I 900,000 0
€3,000,000
re
0.3
Средневзвешенная стоимость капитала для предприятия = 30%, т.к. D = 0 и E = V.
Стоимость предприятия А выше стоимости предприятия B и его средневзвешенная стоимость
капитала ниже.
194. Теория Миллера и Модильяни, при t = 0
При традиционном подходе предполагалось, что до определенного уровня коэффициентазадолженности значения стоимости акционерного и заемного капитала не меняются и
рыночная оценка фирмы А в рассмотренном выше примере оказывается выше. В модели
ММ утверждается, что это непостоянная ситуация.
Теория Миллера и Модильяни (MM)
В противоположности традиционному подходу, теория Миллера и Модильяни доказывает,
что при условии совершенных рынков капитала и отсутствии налогообложения, структура
капитала не оказывает влияния на стоимость предприятия. Перовое исследование,
опубликованное в 1958 году, без учета налогообложения, основывается на следующих
утверждениях:
Утверждение 1:
Цена капитала и рыночная стоимость предприятия не зависят от структуры капитала.
Это означает, что два предприятия, структура капитала которых отличается, при всех равных
условиях, будут иметь одинаковую рыночную стоимость:
EBIT EBIT
VL VU
rWACC
r0
rWACC r0
где:
VL = стоимость финансово зависимого предприятия;
VU = стоимость финансово независимого предприятия;
EBIT = прибыль до уплаты процентов и налогов;
rWACC = cредневзвешенная стоимость капитала ;
r0 = цена капитала финансово независимого предприятия.
195. Теория Миллера и Модильяни, при t = 0
Утверждение 2:При увеличении доли заемного капитала (D/E), увеличивается стоимость собственного
капитала (re), т.к. акционеры требуют дополнительную премию за повышенный
финансовый риск. Увеличение стоимости собственного капитала компенсируется более
низкой ценой заемного капитала (rd), таким образом, средневзвешенная стоимость
капитала и рыночная стоимость предприятия остаются неизменными.
Цена капитала
re
r0
D
re r0 (r0 rd )
E
rWACC
rd
D/E
Рис. 5.4. Зависимость между ценой капитала и D/Е – теория Миллера и Модильяни при t = 0
196. Теория Миллера и Модильяни, при t = 0
Пример 5.2.:Изменения структуры капитала и ее влияние на стоимость капитала, средневзвешенную
стоимость капитала и рыночную стоимость предприятия.
Единственный источник финансирования предприятия C – собственный капитал.
Прогнозируется, что операционная прибыль предприятия (EBIT) составит €10,000
ежегодно без ограничения по времени. Средневзвешенная стоимость капитала
(стоимость собственного капитала) – 10%. Налоговая ставка – 0%.
При данном условии, рыночную стоимость предприятия можно определить след. образом:
V
EBIT 10,000
€100,000
rWACC
0.1
Предприятие планирует изменить структуру капитала, выпустив облигации на сумму €25,000
при процентной ставке (доходности по облигациям) 6% годовых.
Одновременно планируется выкупить акции предприятия на открытом рынке на сумму
€25,000.
Ежегодные процентные платежи с суммы займа – €1,500 (т.е., €25,000 × 0.06).
В результате финансовых операций, стоимость собственного капитала (Е) снизится до 100,000
– 25,000 = €75,000.
На основе второго утверждения теории ММ (t = 0), стоимость (требуемая доходность)
собственного капитала увеличится до 11.33%:
re r0 (r0 rd )
D
25,000
0.1 (0.1 0.06)
0.1133 11.33%
E
75,000
197. Теория Миллера и Модильяни, при t = 0
Стоимость предприятия останется неизменной:V
I EBIT I 1,500 (10,000 1,500)
25,000 75,000 €100,000
rd
re
0.06
0.1133
Средневзвешенная стоимость капитала также останется неизменной:
D
E
rWACC rd (1 t ) re 0.25 (0.06) (1 0) 0.75 (0.1133) 0.1 10%
V
V
198. Теория Миллера и Модильяни, при t > 0
Теория Миллера и Модильяни, при t > 0Во втором исследовании (1963) рассматривалось воздействие налоговой нагрузки на
структуру капитала и рыночную стоимость предприятия.
Основным положением усовершенствованной модели стала гипотеза, что рыночная оценка
компании, использующей финансовый рычаг (VL), будет выше, чем рыночная оценка
компании, не использующей финансовый рычаг (VU), на размер налоговой экономии tD.
Основанием для такого утверждения является возможность отнесения процентов за
использование заемного капитала на расходы, что приводит к возникновению налоговой
экономии. Эта зависимость может быть описана следующим уравнением:
VL VU t D
Также при увеличении удельного веса заемного капитала в структуре капитала, цена
собственного капитала увеличивается, но темп роста ниже, чем при отсутствии
налогообложения:
D
re r0 (r0 rd ) (1 t )
E
По этой причине, средневзвешенная стоимость капитала снижается, а рыночная стоимость
предприятия увеличивается (см. рис. 5.5.).
199. Теория Миллера и Модильяни, при t > 0
Теория Миллера и Модильяни, при t > 0Цена капитала
D
re r0 (r0 rd ) (1 t )
E
re
r0
rd
rWACC
D/E
Рис. 5.4. Зависимость между ценой капитала и D/Е – теория Миллера и Модильяни при t > 0
200. Теория Миллера и Модильяни, при t > 0
Теория Миллера и Модильяни, при t > 0Пример 5.3.:
Изменения структуры капитала и ее влияние на стоимость капитала, средневзвешенную
стоимость капитала и рыночную стоимость предприятия.
Продолжив пример 5.2., предположим, что подоходный налог для предприятия – 15%.
Определим стоимость финансово независимого предприятия:
VU
EBIT (1 t ) 10,000 (1 0.15)
€85,000
rWACC
0.1
Предположим, что предприятие выпустит облигации на сумму €25,000 при процентной
ставке (обещанной доходности) 6% годовых. Полученные средства будут использованы
для выкупа акций на открытом рынке. В результате данной операции рыночная
стоимость предприятия увеличится до:
VL VU t D 85,000 3,750 €88,750
D €25,000
V €88,750
E V D 88,750 25,000 €63,750
На основе утверждения теории ММ (t > 0), стоимость (требуемая доходность) собственного
капитала увеличится до :
25,000
D
re r0 (r0 rd ) (1 t ) 0.1 (0.1 0.06) (1 0.15)
0.1133 11.33%
E
63,750
201. Теория Миллера и Модильяни, при t > 0
Теория Миллера и Модильяни, при t > 0Основываясь на утверждении теории ММ (t > 0), средневзвешенная стоимость капитала
снижается:
25,000
63,750
D
E
rWACC rd (1 t ) re
(0.06) (1 0.15)
(0.1133) 9.58%
V
V
88,750
88,750
Следует отметить, что стоимость финансово зависимого предприятия можно также
определить след. образом:
VL
I ( EBIT I ) (1 t ) 1,500 (10,000 1,500) (1 0.15)
€88,750
rd
re
0.06
0.1133
где:
I = процентные платежи; I D rd
Или:
VL
EBIT (1 t ) 10,000 (1 0.15)
€88,750
rWACC
0.09577
Выводы:
В результате использования заемного капитала, рыночная стоимость предприятия выросла с
€85,000 до €88,750 по причине более низкой стоимости заемного капитала в сравнении
со стоимостью собственного капитала (rd < re) и налоговой экономии.
202. Статическая компромиссная теория
Статическая компромиссная теорияСогласно статической компромиссной теории (static trade-off theory) предприятие ищет
компромисс между выгодой от использования заемного капитала (налоговой экономии)
и издержками, связанными с убыктками от возможного банкротства.
Налоговая экономия
По причине того, что начисленные проценты по кредиту снижают облагаемую налогом
прибыль, формируется так называемый налоговый щит (tax shield) который увеличивает
рыночную стоимость предприятия. При отсутствии роста финансового риска, рыночная
стоимость предприятия достигла бы максимального объема, если структура капитала
включала бы исключительно заемный капитал. На практике это допущение не является
возможным, т.к. по мере роста кредитных обязательств увеличивается риск
неплатежеспособности и расходы, связанные с убытками от возможного банкротства.
Издержки банкротства
Издержки финансового банкротства (costs of financial distress) можно классифицировать как:
• прямые издержки и
• косвенные издержки.
Прямые издержки включают в себя юридические издержки, связанные с банкротством,
расходы по реструктуризации и др.
Косвенные издержки имеют отношение к потере репутации покупателей и поставщиков,
падение лояльности персонала и др.
Чем выше удельный вес заемного капитала, тем выше вероятность того, что предприятие столкнется с издержками
банкротства. При большом финансовом рычаге вероятность банкротства увеличивается, и налоговые преимущества
могут не покрывать растущих издержек банкротства.
203. Теория агентских издержек
Теория агентских издержекТеория агентских издержек основывается на предположении, что интересы и цели
кредиторов, акционеров и менеджеров отличаются.
Это означает, что какая-либо сторона пытается максимизировать собственную выгоду.
Данное явление называют конфликтом интересов. Существуют два вида конфликта
интересов:
конфликт между акционерами и менеджерами и
• конфликт между акционерами и кредиторами.
Агентские издержки (agency costs of equity) - расходы, связанные с конфликтом интересов
между акционерами и менеджерами.
Акционеры желают максимизации своего благосостояния, а менеджеры должны действовать
в интересах акционеров. Но зачастую менеджеры могут преследовать иные интересы,
например, расширение компании или улучшение своей репутации.
Главный аргумент теории агентских издержек заключается в том, что использование
заемного капитала позволяет дисциплинировать менеджеров предприятия, чтобы они
более рационально использовали денежные ресурсы предприятия.
204. Иерархическая теория структуры капитала
Иерархическая теория структуры капиталаИерархическая теория (pecking order theory) основывается на принципе асимметрии
информации. Асимметрией информации называется неравномерность распределения
информации между участниками рынка при принятии ими экономических решений и
совершении сделок. Неравномерность распределения информации возникает, когда
один субъект рынка располагает более полной, либо более качественной информацией,
необходимой для принятия решений, чем другие субъекты.
С. Майерс и Н. Мэйлаф (1984) показали, что асимметрия информации влияет на
формирование структуры капитала компаний.
Согласно теории, менеджеры предприятия отдают предпочтение внутренним источникам
финансирования, нежели внешним.
Теория иерархии предполагает, что у отдельно взятой фирмы не существует какого-либо
определённого планового коэффициента долговой нагрузки. Компания всегда будет
стремиться привлечь сначала источник высшей иерархии, который будет обладать
наименьшей ценой привлечения и наименьшим риском.
Таким образом, вначале фирма исчерпает внутренние источники финансирования, затем
прибегает к займам, и лишь потом выпускает гибридные ценные бумаги
(конвертируемые облигации, привилегированные акции) и только в крайнем случае –
обыкновенные акции.
Внутренние
ресурсы
Займы
Гибридные
инструменты
Эмиссия
акций
205. Структура капитала: Задания
Задание 5.1.:Предприятие планирует покупку активов на сумму €500,000. Есть возможность взять кредит при
процентной ставке 8% годовых, либо использовать собственный капитал. Налоговая ставка –
15%.
Если предприятие берет кредит, рассчитать:
1) ежегодную величину налоговой экономии;
2) стоимость заемного капитала с учетом налогообложения.
Решение:
1) Сначала рассчитаем размер процентного платежа:
I = D0 × rd = 500,000 (0.08) = €40,000
Начисленные проценты по кредиту снижают прибыль, облагаемую налогом. Налоговая экономия в
год – €6,000 (40,000 × 0.15).
2) Стоимость заемного капитала без учета налогообложения – 8%.
Издержки заемного финансирования с учетом налогообложения = 40,000 (процентные платежи)
– 6,000 (налоговая экономия) = €34,000. Цена заемного капитала = 34,000 / 500,000 = 0.068 =
6.8%.
Или:
Издержки заемного финансирования с учетом налогообложения = rd (1 – t) = 0.08 (1 – 0.15) = 0.068 =
6.8%
206. Структура капитала: Задания
Задание 5.2.:ММ Теория: взаимосвязь между налоговой нагрузкой и ценой собственного капитала
Предприятие не имеет долговой нагрузки. Цена капитала – 13%. Предприятие планирует
расширить свою деятельность и рассматривает возможность взять кредит. Процентная
ставка по кредиту – 9% годовых. В результате кредитования, отношение кредитных
обязательств к собственному капиталу составит 0.5.
Рассчитать стоимость собственного капитала, если:
1) подоходный налог с предприятия – 0%;
2) подоходный налог с предприятия – 32%.
Решение:
1) re = r0 + (r0 – rd)(D/E) = 0.13 + (0.13 – 0.09)(0.5) = 0.15 = 15%
2) re = r0 + (r0 – rd)(1 – t)(D/E) = 0.13 + (0.13 – 0.09)(1 – 0.32)(0.5) = 0.1436 = 14.36%
На основе утверждений теории ММ (t = 0 и t > 0), стоимость собственного капитала
увеличивается как в первом, так и во втором случае. Однако, во втором случае, темп
прироста ниже.
207. Структура капитала: Задания
Задание 5.3.:Предприятие открывает новый филиал. Требуются средства на сумму €3,000,000.
Необходимо найти оптимальное решение для финансирования филиала, при котором
стоимость привлечения средств будет минимальной. Руководство рассматривает три
сценария финансирования:
1. кредитные обязательства – 0%, собственные средства – 100%;
2. кредитные обязательства – 50%, собственные средства – 50%;
3. кредитные обязательства – 80%, собственные средства – 20%.
Подоходный налог с предприятия – 15%. Информация по стоимости капитала:
Цена капитала
Цена собств. капитала
Цена заемного капитала
Сценарии
Займы: 50%
Соб. средства: 50%
Займы: 0%
Соб. средства: 100%
Займы: 80%
Соб. средства: 20%
13.5%
18%
28%
-
9%
18%
Какой способ финансирования обеспечит минимальную стоимость привлечения средств?
208. Структура капитала: Задания
Решение:Рассчитаем средневзвешенную стоимость капитала для каждого сценария:
D
E
rWACC rd (1 t ) re
V
V
rWACC ,1 13.5%
rWACC , 2 0.5 0.09 (1 0.15) 0.5 0.18 0.1283 12.83%
,
rWACC ,3 0.8 0.18 (1 0.15) 0.2 0.28 0.1784 17.84%
,
Второй вариант финансирования
(кредитные обязательства – 50%) обеспечивает
минимальную стоимость капитала.
209. Раздел 6: ЭФФЕКТ РЫЧАГА И АНАЛИЗ БЕЗУБЫТОЧНОСТИ
Понятие рычагаРычаг (leverage) – финансовый механизм, при помощи которого удельный вес постоянных
издержек в структуре общих издержек предприятия может воздействовать на
рентабельность и степень риска предприятия.
Постоянные издержки можно классифицировать как:
• постоянные операционные издержки (напр., аренда, расходы по износу основных
средств);
• постоянные финансовые издержки (напр., процентные платежи).
Постоянные издержки возникают в независимости от объема реализуемой продукции.
Эффект рычага:
Чем выше уровень рычага, тем выше степень колебания (волатильность) чистой прибыли,
кредитный риск и дисконтная норма, используемая при оценке стоимости предприятия.
Предприятие с высоким показателем рычага может понести значительные убытки при
неблагоприятной конъюнктуре рынка.
Рычаг увеличивает риск и потенциальную доходность.
210. Структура расходов
Структура расходовСтепень рычага зависит от структуры издержек предприятия. Общие издержки включают в
себя постоянные и переменные:
TC FC VC
где:
TC = общие издержки;
FC = постоянные издержки;
VC = переменные издержки.
Постоянные издержки не зависят от физического объема реализации:
• расходы по износу основных средств;
• арендная плата за офисное помещение;
• расходы по страхованию (страховые премии);
• процентные платежи;
• зарплата сотрудникам, получающим оклады.
В свою очередь переменные издержки напрямую зависят от объема продукции:
расходы, связанные с реализацией продукции;
затраты на сырье и материалы, энергию, топливо;
• заработная плата рабочих.
211. Операционные и финансовые издержки
Понятие операционных издержек:Операционные издержки (operating expenses, OPEX) – издержки, возникающие в результате
основной (операционной) деятельности предприятия. Могут влючать в себя:
расходы по закупке сырья и запасов;
расходы по износу ОС;
арендные платежи;
маркетинговые расходы;
оплата труда;
страховые выплаты;
прочие расходы, связанные с основной деятельностью предприятия.
Операционная прибыль (прибыль до уплаты процентов и налогов) (EBIT) – разница между
нетто оборотом предприятия (доходом от реализации проданной продукции или
оказания услуг) и операционными издержками (OPEX):
EBIT S OPEX
Понятие финансовых издержек:
Финансовые издержки возникают в результате кредитования предприятия (напр., банковский
кредит, выпуск облигаций). К финансовым издержкам относят процентные платежи по
кредиту и купонные платежи по облигациям.
212. Эффект рычага (пример)
Пример 6.1.:Эффект рычага
Информация о фин. показателях предприятий Альфа и Бета представлена в таблице:
Альфа (€)
Бета (€)
Физический объем производства и реализации (Q)
200,000
200,000
Цена одной единицы продукци
20
20
Переменные издержки (за ед. продукции)
7
14
Постоянные операционные издержки (в год)
1,000,000
200,000
Постоянные финансовые издержки (в год)
800,000
200,000
Альфа (€)
Бета (€)
Доход от реализации проданной продукции (S)
4,000,000
4,000,000
Операционные издержки (постоянные + переменные)
2,400,000
3,000,000
Операционная прибыль (EBIT)
1,600,000
1,000,000
Финансовые издержки
800,000
200,000
Чистая прибыль (NI)
800,000
800,000
Чистая прибыль
предприятий
одинаковая(€800,000),
но структура расходов
существенно
отличается. Альфа
имеет более высокий
удельный вес
постоянных издержек
в общих издержках. У
предприятия Бета
преобладают
переменные издерзки
в структуре расходов.
213. Эффект рычага (пример)
Предположим три сценария объема производства и реализации. Оценим влияние структурырасходов на чистую прибыль.
Если:
Oбъем производства и
реализации – 150,000 ед.
Oбъем производства и
реализации – 200,000 ед.
Oбъем производства и
реализации – 250,000 ед.
Альфа
Бета
Альфа
Бета
Альфа
Бета
Доход от реализации
проданной продукции
3,000,000
3,000,000
4,000,000
4,000,000
5,000,000
5,000,000
Операционные
издержки
2,050,000
2,300,000
2,400,000
3,000,000
2,750,000
3,700,000
Операционная
прибыль (EBIT)
950,000
700,000
1,600,000
1,000,000
2,250,000
1,300,000
Финансовые издержки
800,000
200,000
800,000
200,000
800,000
200,000
Чистая прибыль
150,000
500,000
800,000
800,000
1,450,000
1,100,000
81%
38%
Чистая прибыль (%
изменения)
- 81%
- 38%
Выводы:
В структуре расходов предприятия Альфа доминируют постоянные издержки (как
операционные, так и финансовые). В результате этого, повышенный уровень рычага
приводит к большим процентуальным изменениям чистой прибыли. Например, при
уменьшении объема реализации на 25%, чистая прибыль снижается на 81%. В случае
предприятия Бета, чистая прибыль снижается только на 38%.
214. Эффект операционного рычага
Структура расходов влияет на риск предприятия. Чем выше уровень постоянных издержек вструктуре расходов, тем выше риск.
Структура расходов зависит главным образом от отрасли, в которой функционирует
предприятие. Однако предприятия могут изменять (контролировать) структуру своих
расходов, применяя различные методы производства. Предприятию с высоким
соотношением постоянных издержек к переменным труднее приспосабливаться к
изменениям объема реализации.
Наличие постоянных затрат у предприятия как раз и обуславливает возникновение
операционного рычага. Поскольку в определенных пределах их величина остается без
изменений, то величина общих затрат на единицу продукции будет снижаться по мере
роста объема реализации, и, наоборот, увеличиваться при его снижении. Это приводит к
тому, что величина операционной прибыли (EBIT) будет изменяться быстрее, чем объем
реализации.
Эффект операционного рычага
При высоком удельном весе постоянных операционных издержек, процентуальное
изменение нетто оборота приводит к повышенному изменению операционной прибыли.
Степень чувствительности операционной прибыли к изменениям объема реализации
можно определить при помощи коэффициента операционного рычага (degree of
operating leverage) (DOL):
DOL
% EBIT
% S
где:
%ΔEBIT = процентуальное изменение операционной прибыли;
%ΔS = процентуальное изменение объема продаж
215. Эффект операционного рычага (пример)
Пример 6.2.:Эффект операционного рычага
Используя данные предприятия Альфа (см. пример 6.1.), рассмотрим влияние степени
операционного рычага на операционную прибыль, при увеличении физического объема
реализации на 10%:
Oбъем производства и реализации
%
изменения
200,000
220,000
€4,000,000
€4,400,000
10.00%
Переменные издержки (-)
1,400,000
1,540,000
10.00%
Постоянные издержки (-)
1,000,000
1,000,000
0.00%
€1,600,000
€1,860,000
16.25%
Доход от реализации
Операционная прибыль (EBIT)
При увеличении оборота на 10%, операционная прибыль повышается на 16.25%.
216. Вычисление коэффициента операционного рычага DOL
Коэффициент операционного рычага рассчитывается по формуле:DOL
Q (P V )
Q (P V ) F
где:
Q = физический объем реализации;
P = цена за одну единицу продукции;
V = переменные издержки за одну единицу продукции;
F = постоянные операционные издержки.
Пример 6.3.:
Определим DOL для предприятия Альфа при базовом объеме реализации – 200,000 единиц:
DOLA, 200, 000
200,000 (20 7)
1.625
200,000 (20 7) 1,000,000
Вывод:
При объеме реализации 200,000 единиц, увеличение оборота на 1% приводит к увеличению
операционной прибыли на 1.625%.
217. Вычисление коэффициента операционного рычага DOL
Определим DOL для предприятия Альфа при базовом объеме реализации – 400,000 единиц:DOLA, Q 400, 000
400,000 (20 7)
1.238
400,000 (20 7) 1,000,000
При объеме реализации 400,000 единиц, увеличение оборота на 1% приводит к увеличению
операционной прибыли на 1.238%.
Вывод:
При изменении физического объема реализации (Q), степень операционного рычага
изменяется. При большем объеме продаж, степень чувствительности операционной
прибыли к изменению оборота снижается.
Следует заметить, что операционная прибыль наиболее чувствительна к изменению объема
реализации при показателе близком к нулю (т.е., EBIT ≈ 0).
218. Вычисление коэффициента операционного рычага DOL
Показатель DOL также зависит от структуры расходов предприятия.Пример 6.4.:
Определим показатель DOL для предприятия Бета, которому характерен более низкий
уровень постоянных операционных издержек в сравнении с предприятием Альфа.
Предположем, что базовый физический объем реализации составляет 200,000 единиц:
DOLB , Q 200, 000
200,000 (20 14)
1.2
200,000 (20 14) 200,000
При объеме реализации 200,000 единиц, увеличение оборота на 1% приводит к увеличению
операционной прибыли на 1.2%.
При Q = 200,000, показатель DOL предприятия Бета ниже, чем у Альфа. Это означает, что
чувствительность операционной прибыли к изменению оборота для предприятия Бета
ниже.
При большем обьеме реализации Q, коэффициенты операционного рычага для двух
предприятий существенно не отличаются.
Предприятия с высоким значением коэффициента операционного рычага уязвимы даже к
незначительным снижениям в объемах продаж. Другими словами, снижение продаж на
несколько процентов может привести к потере существенной части операционного
дохода или даже к операционному убытку. С одной стороны, такие компании должны
тщательно управлять и своими постоянными расходами и точно предсказывать
изменения объема реализации. С другой стороны, в благоприятных рыночных условиях
они обладают более высоким потенциалом роста операционного дохода.
219. Эффект финансового рычага
Эффект финансового рычагаФинансовый рычаг возникает в результате того, что проценты по долговым обязательствам
носят постоянный характер, поэтому при изменении объема реализации чистая прибыль
(и прибыль на акцию) будет изменяться более высокими темпами.
Последствия финансового рычага для предприятия
Увеличение заемного капитала приводит к увеличению объема процентных платежей и росту
финансового риска предприятия. С другой стороны, увеличивается рентабельность
собственного капитала (ROE) при условии, что рентабельность активов превышает
стоимость заемного капитала (ROA > rd).
Для компаний с высоким финансовым рычагом зачастую характерна высокая волатильность
чистой прибыли или денежных потоков (см.пример 6.5.).
Экономические спады деловой активности, такие как рецессии и депрессии, могут быть
более трудными для этих компаний, поскольку постоянные затраты (т.е. финансовые
затраты) должны быть профинансированы независимо от уровня текущего дохода.
220. Эффект финансового рычага (пример)
Пример 6.5.:Эффект финансового рычага
Предприятие U использует только собственный капитал для финансирования. Предприятие L
использует как собственный капитал, так и заемный капитал.
Предприятие U (без кредитных обязательств)
Оборотные средства
50 Займы
Основные средства
50 Собственный капитал
Итого активы
0
100 Итого пассивы
100
100
Сценарий
Оптимистический
Доход от реализации
Пессимистический
100.00
82.50
Операционные издержки
70.00
80.00
Операционная прибыль (EBIT)
30.00
2.50
0.00
0.00
Прибыль до уплаты налогов
30.00
2.50
Налоги (40%)
12.00
1.00
Чистая прибыль
18.00
1.50
18.00%
1.50%
Процентные платежи
Рентабельность собств. капитала (ROE)
221. Эффект финансового рычага (пример)
Оптимистическийсценарий:
Пессимистический
сценарий :
ROEU
NI 18
18%
TE 100
ROEL
13.5
27%
50
ROEU
NI 1.5
1.5%
TE 100
ROEL
3
6%
50
Предприятие L (+ кредитные обязательства)
Оборотные средства
50 Займы (rd = 15%)
50
Основные средства
50 Собственный капитал
50
Итого активы
100 Итого пассивы
100
Сценарий
Оптимистический
Доход от реализации
Пессимистический
100.00
82.50
Операционные издержки
70.00
80.00
Операционная прибыль (EBIT)
30.00
2.50
7.50
7.50
22.50
(5.00)
9.00
(2.00)
13.50
(3.00)
27.00%
(6.00%)
Процентные платежи
Прибыль до уплаты налогов
Налоги (40%)
Чистая прибыль
Рентабельность собств. капитала (ROE)
222. Вычисление коэффициента финансового рычага DFL
Коэффициент финансового рычага DFLЭффект финансового рычага DFL (degree of financial leverage) можно представить след.
образом:
% NI
DFL
% EBIT
где:
%ΔNI = процентуальное изменение чистой прибыли;
%ΔEBIT = процентуальное изменение операционной прибыли
Фомулы для вычисления:
DFL
[Q ( P V ) F ] (1 t )
[Q ( P V ) F ]
[Q ( P V ) F C ] (1 t ) [Q ( P V ) F C ]
где:
Q = физический объем реализации;
P = цена за одну единицу продукции;
V = переменные издержки за одну единицу продукции;
F = постоянные операционные издержки.
C = постоянные финансовые издержки (напр., процентные платежи);
t = налоговая ставка.
223. Вычисление коэффициента финансового рычага DFL
Для удобства расчета с точки зрения подачи информации в финансовой отчетности формулаэффекта финансового рычага может быть представлена как:
DFL
EBIT
EBIT IX
где:
EBIT = прибыль до уплаты процентов и налогов за отчетный период (операционная
прибыль);
IX = обязательства по процентам за отчетный период
224. Вычисление коэффициента финансового рычага DFL
Пример 6.6.:Продолжая пример 6.1., рассмотрим реакцию чистой прибыли Альфа на изменение
операционной прибыли при разных уровнях постоянных финансовых издержек.
Базовый сценарий:
EBIT = €1,600,000.
Альтернативный сценарий: EBIT увеличивается на 20%.
Для упрощения, налоговая нагрузка не учитывается.
Постоянные финансовые издержки = €800,000
Операционная прибыль (EBIT)
Изменения(%)
1,600,000
1,920,000
20.00%
Процентные платежи
800,000
800,000
0.00%
Чистая прибыль
800,000
1,120,000
40.00%
Постоянные финансовые издержки = €1,200,000
Изменения(%)
Операционная прибыль (EBIT)
1,600,000
1,920,000
20.00%
Процентные платежи
1,200,000
1,200,000
0.00%
400,000
720,000
80.00%
Чистая прибыль
Вывод:
При повышенном уровне постоянных финансовых издержек (€1,200,000) изменение
операционной прибыли на 20% приводит к более высокому темпу роста чистой прибыли.
225. Вычисление коэффициента финансового рычага DFL
Пример 6.7.:Вычислим коэффициент финансового рычага для предприятия Альфа при операционной
прибыли – €1,600,000 и постоянных финансовых издержках – €800,000.
DFLA, EBIT 1.6m
200,000 (20 7) 1,000,000
2.0
400,000 (20 7) 1,000,000 800,000
Или:
DFLA, EBIT 1.6m
1,600,000
2.0
1,600,000 800,000
При операционной прибыли – €1,600,000 и постоянных финансовых издержках – €1,200,000:
DFLA, EBIT 1.6m
200,000 (20 7) 1,000,000
4.0
400,000 (20 7) 1,000,000 1,200,000
Очевидно, что эффект финансового рычага зависит от объема операционной прибыли и
структуры расходов.
226. Эффект общего рычага
Эффект общего рычагаЭффект общего рычага (degree of total leverage) является результатом совокупного влияния
операционного и финансового рычага компании. Он возникает в результате того, что
часть расходов компании носит постоянный характер. Показывает насколько процентов
изменится чистая прибыль при изменении выручки на 1%.:
% NI
DTL
% S
где:
%ΔNI = процентуальное изменение чистой прибыли;
%ΔS = процентуальное изменение выручки от реализации
Фомулa для вычисления:
DTL
Q (P V )
DOL DFL
[Q ( P V ) F C ]
где:
Q = физический объем реализации;
P = цена за одну единицу продукции;
V = переменные издержки за одну единицу продукции;
F = постоянные операционные издержки.
C = постоянные финансовые издержки (напр., процентные платежи)
227. Эффект общего рычага (пример)
Пример 6.8.:Продемонстрируем эффект общего рычага на примере предприятия Альфа, при изменении
оборота на 10%.
Oбъем производства и реализации Q
180,000
200,000
220,000
Доход от реализации (S)
3,600,000
4,000,000
4,400,000
Переменные затраты (-)
1,260,000
1,400,000
1,540,000
Постоянные операционные затраты (-)
1,000,000
1,000,000
1,000,000
Операционная прибыль (EBIT)
1,340,000
1,600,000
1,860,000
Расходы по процентам
800,000
800,000
800,000
Чистая прибыль
540,000
800,000
1,060,000
Относительно объема производства и реализации – 200,000 ед.
Изменение выручки (%)
– 10.00%
10.00%
Изменение операционной прибыли (%)
– 16.25%
16.25%
Изменение чистой прибыли (%)
– 32.50%
32.50%
228. Эффект общего рычага (пример)
Пример 6.9.:Определим коэффициент DTL для предприятия Альфа по формуле:
DTLA, Q 200,000
200,000 (20 7)
3.25
200,000 (20 7) 1,000,000 800,000
Или:
DTL A, Q 200,000 1.625 2 3.25
Коэффициент показывает, что при начальном обьеме Q = 200,000 ед., увеличение выручки на
1% приводит к увеличению чистой прибыли на 3.25%.
Эффект общего рычага является своего рода показателем, характеризующим чувствительность
компании к изменению объемов продаж. При этом, чем выше его значение, тем быстрее будет
изменяться такой показатель как прибыль на акцию.
Знание точного значения эффекта финансового рычага важно не только для менеджеров компании,
но и для ее акционеров, кредиторов и потенциальных инвесторов. Каждой из этих групп данная
информация необходима, чтобы оценить перспективы бизнеса в случае различных вариантов
развития событий. Для инвесторов и кредиторов это важно с той точки зрения, поскольку им
необходимо удостовериться, смогут ли они вернуть вложенные средства и получить доход от
своих вложений. Для менеджеров компании важно учесть пессимистичный сценарий развития
событий, чтобы разработать мероприятия для смягчения негативных последствий. Акционерам
важно знать эффект общего рычага, чтобы иметь возможность оценить размер чистой прибыли
компании, от которого будет зависеть размер дивидендов.
229. Анализ безубыточности
Анализ безубыточностиАнализ безубыточности (breakeven analysis) является процессом, который позволяет
компании принять решение относительно того, сколько необходимо произвести и
реализовать продукции QBE, чтобы полностью покрыть свои постоянные и переменные
затраты.
Точка безубыточности (breakeven quantity) QBE показывает какое количество единиц
продукции, товаров или услуг необходимо реализовать, чтобы покрыть общие затраты.
Пример 6.10.:
На графике показана точка безубыточности для предприятия Альфа::
Сумма затрат и выручки, €
8 000 000
Выручка от
реализации
7 000 000
6 000 000
5 000 000
Общие
затраты
4 000 000
3 000 000
QBE = 138,461
2 000 000
1 000 000
Q
0
0
40 000
80 000 120 000 160 000 200 000 240 000 280 000 320 000 360 000
230. Точка безубыточности
При производстве одного вида продукции расчет точки безубыточности в натуральномвыражении имеет следующий вид:
QBE
F C
P V
где:
F = общие постоянные операционные затраты;
C = постоянные финансовые издержки;
P = цена за одну единицу продукции;
V = переменные издержки за одну единицу продукции.
Пример 6.11.:
Определим точку безубыточности для предприятия Альфа и Бета:
QBE , A
1,000,000 800,000
138,461
20 7
QBE , B
200,000 200,000
66,666
20 14
Предприятию Альфа необходимо производить и реализовывать больший объем продукции
(138,461 ед.), чтобы покрывать более высокий объем постоянных затрат. Однако, при
достижении точки безубыточности, для Альфа потенциал наращения прибыли при
большем объеме реализации Q значительно выше, чем для Бета (см. рис.):
231. Точка безубыточности
АЛЬФАСумма затрат и выручки, €
8 000 000
Прибыль
7 000 000
Выручка от
реализации
6 000 000
5 000 000
Общие
затраты
Убытки
4 000 000
3 000 000
QBE = 138,461
2 000 000
1 000 000
Q
0
0
БЕТА
40 000
80 000
120 000 160 000 200 000 240 000 280 000 320 000 360 000
Сумма затрат и выручки, €
8 000 000
Прибыль
7 000 000
6 000 000
Выручка от
реализации
Общие
затраты
5 000 000
4 000 000
Убытки
3 000 000
2 000 000
QBE = 66,666
1 000 000
Q
0
0
40 000
80 000
120 000 160 000 200 000 240 000 280 000 320 000 360 000
232. Раздел 7: ФИНАНСОВЫЕ РЫНКИ
Структура финансового рынкаФинансовый рынок включает денежный рынок и рынок капиталов.
Под денежным рынком понимается рынок краткосрочных кредитных операций (до одного
года).
Участниками денежного рынка являются с одной стороны лица, предоставляющие деньги
(кредиторы), а с другой стороны — лица заимствующие деньги на определённых
условиях (заёмщики).
В качестве кредиторов и заёмщиков на денежном рынке выступают:
Банки;
Предприятия и организации различного типа — юридические лица;
Физические лица;
Государство в лице определённых органов и организаций;
Международные финансовые организации;
Другие финансово-кредитные учреждения.
Одной из категорий участников рынка являются финансовые посредники.
В качестве финансовых посредников на денежном рынке выступают:
Банки;
Профессиональные участники фондового рынка:
Брокеры;
Дилеры
Другие финансово-кредитные учреждения.
233. Денежный рынок
Интересы участников денежного рынка состоят в получении дохода от операций сразличными финансовыми инструментами денежного рынка. Кредиторы получают доход
в виде процента на переданную сумму. Заёмщики получают доход в виде
дополнительной прибыли, полученной от использования заимствованных денежных
средств. Финансовые посредники получают доход в виде комиссионного вознаграждения
или разницы между процентными ставками привлечения и размещения средств.
Инструментами денежного рынка являются:
1. Различные краткосрочные ценные бумаги:
Казначейские (правительственные) векселя (Treasury bills)
Муниципальные векселя (Municipal bills)
Коммерческие векселя (юридических лиц) (Commercial bills)
Банковские векселя;
Коммерческие бумаги (Commercial paper)
Депозитные сертификаты (Certificate of deposit, CD)
2. Kраткосрочные кредиты
Межбанковские кредиты;
Коммерческие кредиты;
Сделки РЕПО (Repurchase agreements) — продажа ценных бумаг с условием обратного
выкупа.
Особенностью инструментов денежного рынка является низкий финансовый риск.
234. Рынок капитала
Рынок капиталa охватывает средне- и долгосрочные кредиты, а также акции и облигации.Он подразделяется на рынок ценных бумаг (фондовый рынок) и рынок средне- и
долгосрочных банковских кредитов. Рынок капиталов служит важнейшим источником
долгосрочных инвестиционных ресурсов для правительств, корпораций и банков.
Рынок капитала - часть финансового рынка, на котором обращаются денежные средства со
сроком обращения более года.
Если денежный рынок предоставляет высоколиквидные средства в основном для
удовлетворения краткосрочных потребностей, то рынок капиталов обеспечивает
долгосрочные потребности в финансовых ресурсах.
Формы обращения денежных средств (финансовых ресурсов) на рынке капиталов могут быть
различными:
банковские займы (ссуды);
акции;
облигации;
финансовые деривативы.
Деривативами (финансовыми деривативами) называются производные финансовые инструменты, в основе
которых лежат другие, более простые финансовые инструменты — акции, облигации.
Основными видами финансовых деривативов являются:
опционы (дающие их владельцу право продавать или покупать акции),
свопы (соглашения об обмене денежными платежами в течение определенного периода времени),
фьючерсы (контракты на будущую поставку, в том числе валюты, по зафиксированной в контракте цене).
235. Государство и финансовый рынок
Государство и финансовый рынокВзаимоотношения государства и финансового рынка многоплановы. Государство может
выступать кредитором и заемщиком, устанавливать общие правила функционирования
рынка и осуществлять повседневный контроль за ним, проводить через рынок
официальную денежно-кредитную политику и даже более широкие экономические
мероприятия.
Денежно-кредитная политика
Денежно-кредитная (монетарная или кредитно-денежная) политика (monetary policy) — это
макроэкономическая политика денежных властей, комплекс мер, направленных на
управление совокупным спросом через условия денежного рынка (краткосрочная
процентная ставка, номинальный валютный курс или уровень текущей ликвидности
банковского сектора) для достижения комбинации конечных целей, в которые могут
входить ценовая стабильность, сохранение устойчивого валютного курса, финансовая
стабильность и содействие сбалансированному экономическому росту.
Общие инструменты кредитно-денежной политики
Общими инструментами регулирования выступают:
1. регулирование учетной ставки (дисконтная политика, осуществляемая центральным
банком);
2. установление и изменение размеров минимальных резервов, которые финансовые
институты страны обязаны хранить в центральном банке;
3. операции государственных учреждений на рынке ценных бумаг, такие как эмиссия
государственных обязательств, торговля ими и погашение. При помощи этих
инструментов государство стремиться изменить соотношение спроса и предложения на
финансовом рынке (рынке ссудных капиталов) в желаемом направлении.
236. Цели и инструменты кредитно-денежной политики
1. Учетная политика.Одна из функций центрального банка — предоставление ссуд коммерческим банкам. По этим
ссудам взимаются процентные платежи по определенным ставкам. Ставка, по которой
центральный банк выдает кредиты коммерческим банкам, называется учетной ставкой
(если кредиты предоставляются в форме учета векселей) или ставкой рефинансирования
(при других формах кредитования).
При повышении учетной ставки коммерческие банки сокращают размеры заимствований у
центрального банка, повышается величина процента по кредитам, выдаваемым
коммерческими банками. Все это приводит к сокращению кредитования бизнеса и
населения, уменьшению денежного предложения. Снижение учетной ставки действует в
обратном направлении.
2. Проведение операций на открытом рынке.
В настоящее время основным инструментом регулирования денежного предложения в
развитых странах являются операции на открытом рынке. Операции на открытом рынке
— покупка и продажа центральным банком государственных ценных бумаг.
При продаже центральным банком государственных ценных бумаг сокращаются избыточные
резервы коммерческих банков, возможности для кредитования и создания новых денег.
Денежное предложение сокращается, а процентная ставка (цена заемных денежных
средств) повышается.
При покупке центральным банком государственных ценных бумаг идет обратный процесс.
237. Цели и инструменты кредитно-денежной политики
3. Установление норм, обязательных резервов коммерческих банков.Центральный банк изменяет объем денежного предложения путем регулирования
избыточных резервов коммерческих банков. Резервы коммерческих банков — денежный
капитал, который может быть отдан в кредит. Обязательные резервы коммерческих
банков — часть резервов, которую коммерческие банки должны хранить на специальных
счетах центрального банка. От размеров избыточных резервов зависит способность
коммерческих банков создавать деньги и увеличивать денежное предложение.
Норма обязательных резервов — процент обязательных отчислений коммерческих банков от
привлеченных ресурсов на резервный счет в центральном банке. Нормы обязательных
резервов устанавливаются в процентах от объемов депозитов. Эти деньги не могут
использоваться для проведения активных операций, и прежде всего кредитования.
Обязательные резервы представляют собой минимальный размер резервов, которые
должны иметь коммерческие банки. Они, во-первых, должны обеспечивать
необходимый уровень ликвидности, наличия денежных ресурсов коммерческих банков
для выполнения платежных обязательств, а во-вторых, являются инструментом
центрального банка для регулирования объема денежной массы. Банки могут хранить и
избыточные резервы, например для непредвиденных случаев увеличения потребности в
ликвидных средствах. Избыточные резервы коммерческих банков — резервы банка
минус обязательные резервы. Чем выше устанавливает центральный банк норму
обязательных резервов, тем меньшая доля средств может быть использована
коммерческими банками для активных операций. Увеличение нормы резервов
уменьшает денежный мультипликатор и ведет к сокращению денежной массы.
238. Цели и инструменты кредитно-денежной политики
Селективные инструменты кредитно-денежной политикиОбщие инструменты кредитно-денежной политики влияют на рынок ссудных капиталов в
целом. Селективные инструменты кредитно-денежной политики регулируют конкретные
виды кредита или кредитование отдельных отраслей, крупных фирм и т. д.
Селективными методами регулирования являются:
1. Контроль по отдельным видам кредитов.
Этот контроль часто применяется в отношении кредитов под залог биржевых ценных бумаг,
ипотечного кредита, потребительских ссуд на покупку товаров в рассрочку. Здесь
центральный банк может дать указание финансовым учреждениям делать специальные
депозиты в центральный банк в случае увеличения названных видов кредита.
2. Регулирование риска и ликвидности банковских предприятий.
Существует множество правительственных положений, регулирующих операционную
деятельность банков. Основное внимание в этих положениях уделяется риску и
ликвидности банковских операций. Риск банковской деятельности определяется не через
оценку финансового положения должников, а через соотношение выданных кредитов и
суммы собственных средств банка.
239. Цели и инструменты кредитно-денежной политики
3. Предписываемая законом маржа.Фондовая биржа — необходимый институт рыночных экономических отношений. Фондовые
биржи представляют собой рынки ценных бумаг компаний. Однако безудержная
спекуляция на финансовом рынке доставляет экономике серьезные проблемы. Падение
курса акций может привести к разорению как предприятий, так и частных лиц, что, в свою
очередь, приведет к сокращению инвестиций и потребительского спроса и подтолкнет
экономику к спаду.
В качестве меры против излишней спекуляции на фондовой бирже используют
предписываемую законом маржу. Маржа — минимальная пропорция стоимости
покупаемых ценных бумаг, которая оплачивается из собственных средств покупателя.
Например, при марже в 60%, приобретая пакет ценных бумаг на сумму в 1 млн. евро,
покупатель должен своими деньгами заплатить 600 тыс. евро и только 400 тыс. евро
могут составлять средства, полученные в кредит. Маржа повышается, когда желательно
ограничить спекулятивную скупку акций, и понижается — для оживления рынка.
4. Увещевания.
Руководящие кредитно-денежные институты могут «настоятельно рекомендовать»
коммерческим банкам следовать определенной политике. Например, ограничить
ежегодное расширение кредита, поскольку это может иметь негативные последствия для
банковской системы и экономики в целом.
240. Раздел 8: ОБЛИГАЦИИ И ИХ ОЦЕНКА
ОблигацииОблигация (bond) — эмиссионная долговая ценная бумага, владелец которой имеет право
получить от лица, её выпустившего (эмитента облигации), в оговорённый срок её
номинальную стоимость деньгами или в виде иного имущественного эквивалента. Также
облигация может предусматривать право владельца (держателя) на получение процента
(купона) от её номинальной стоимости либо иные имущественные права.
Общим доходом по облигации являются сумма выплачиваемых процентов (купонов) и
размер дисконта при покупке.
Облигации служат дополнительным источником средств для эмитента, являясь эквивалентом
займа. Иногда их выпуск носит целевой характер — для финансирования конкретных
программ или объектов, доход от которых в дальнейшем служит источником для
выплаты дохода по облигациям.
Все
платежи по облигации обеспечиваются имуществом
обязательными и приоритетными по сравнению с акциями.
Экономическая суть облигаций очень похожа на кредитование.
должника
и
являются
241. Виды облигаций
Виды облигацийСуществуют следующие виды облигаций:
В зависимости от эмитента
государственные — выпускаются федеральным правительством;
муниципальные — выпускаются местными органами государственной власти;
корпоративные — выпускаются юридическими лицами;
иностранные – выпускаются иностранными эмитентами, могут быть как частными, так
и государственными.
По сроку действия
Облигации с оговоренной датой погашения :
краткосрочные (до года);
среднесрочные (1-5 лет);
долгосрочные (5-30 лет).
Облигации без фиксированного срока погашения:
• бессрочные (consols);
• отзывные (callable bonds) — могут быть востребованы (отозваны) эмитентом до
наступления срока погашения. Такие облигации повышают риск инвестора, поэтому
эмитенты, чтобы сделать их более привлекательными, либо делают выкуп выше
номинала, либо продают по более низкой цене;
• с правом погашения (putable bonds) — предоставляют право инвестору на возврат
облигации эмитенту до наступления срока погашения и получения за нее номинальной
стоимости. Повышают риск эмитента, поэтому продаются обычно дороже;
242. Виды облигаций
В зависимости от способа получения доходакупонные (coupon bonds) — выплачивается процент (купон);
бескупонные или облигации с нулевым купоном или чистые дисконтные облигации (zerocoupon bonds) — доход инвестора составляет только дисконт. Дисконт — это разница
между ценой погашения облигации (номиналом) и ценой приобретения.
По способу выплаты купонного дохода
купонные или твердопроцентные — с фиксированной процентной ставкой, то есть
установленным заранее процентом, рассчитываемым, как часть номинальной стоимости
облигации;
с плавающей процентной ставкой или переменным купоном (floating rate notes) — доход
изменяется в зависимости от изменения ставок денежного рынка;
индексируемые (index-linked bonds)— индексируется не только купон, но и номинал
облигации;
с равномерно возрастающей процентной ставкой (step-up notes);
смешанного типа – часть срока выплачивается фиксированный процент, а часть срока –
плавающий.
По способу погашения номинала (выкупа облигации):
разовым платежом (bullet bonds);
распределенными во времени погашениями оговоренных долей номинала;
последовательным погашением доли общего количества облигаций.
243. Характеристики долговых инструментов
Срок погашенияСроком погашения долгового обязательства считается количество лет, по истечении которых
эмитент должен выполнить свои обязательства. На дату погашения эмитент обязан
погасить все оставшиеся долговые обязательства.
Номинальная стоимость
Номинальной стоимостью облигации (M) считается сумма, которую эмитент обязуется
выплатить держателю финансового инструмента (облигации) на дату погашения.
Облигации могут иметь любую номинальную стоимость. Цену долгового инструмента
принято выражать в процентах от его номинальной стоимости.
Купонная ставка
Купонная, или номинальная ставка (rc), - это процентная ставка, по которой эмитент/заемщик
обязуется производить ежегодные выплаты. Денежное выражение выплаты, называемое
также купонным (процентным) платежем (C), вычисляется как произведение купонной
ставки на номинальную стоимость долгового инструмента:
C rc M
Например, выплата процентов по долговому инструменту с купонной ставкой 7% и
номинальной стоимостью €1,000 составляет €70 (7% от €1,000). Частота выплаты
процентов зависит от типа долгового инструмента.
244. Структура денежных потоков облигации
Пример 8.1.:Рассмотрим структуру денежных потоков купонной облигации, погашение номинала которой
осуществляется разовым платежем в конце срока облигации.
Предприятие выпустило купонную облигацию, срок до погашения которой - 5 лет.
Номинальная стоимость облигации - €1,000. В момент выпуска, купонная ставка 8% равна
рыночной требуемой норме доходности по облигации. Предполагается, что требуемая
доходность по облигации останется неизменной на протяжении всего периода
погашения. Составим график платежей по облигации:
Облигация, rc = 8%, M = 1,000
Год
Денежные потоки
эмитента
Процентные
платежи
Выплата
основной суммы
кредита
Конечный баланс
основной суммы
кредита
0
€1,000.00
1,000.00
1
–80.00
80.00
0.00
1,000.00
2
–80.00
80.00
0.00
1,000.00
3
–80.00
80.00
0.00
1,000.00
4
–80.00
80.00
0.00
1,000.00
5
–1,080.00
80.00
1,000.00
0.00
• Купонный (процентный) платеж = 0.08 × 1,000 = €80
• Последний платеж= последний купон + номинал = 80 + 1,000 = €1,080
245. Рейтинг облигаций
На рынке капиталов инвесторы могут использовать рейтинг облигаций в качестве ориентиракредитоспособности их эмитента.
Большинство инвесторов и эмитентов прибегают к услугам профессиональных посредников –
рейтинговых агентств, крупнейшими из которых являются Standard & Poor's (S&P),
Moody's и Fitch Ratings и, которые, в частности, предоставляют услуги присвоения
кредитного рейтинга облигаций. Каждое из агентств имеет свою унифицированную
шкалу, согласно которой ранжируются эмитенты по уровню их кредитоспособности.
Сравнительная таблица долгосрочных кредитных рейтингов имеет следующий вид:
Долгосрочный рейтинг облигаций не ниже BBB- по шкале S&P и Fitch
Ratings, Baa3 по шкале Moody’s считаются инвестиционным уровнем.
Агентства обоснованно предполагают, что эмитенты с таким
уровнем кредитоспособности будут в состоянии выполнить свои
обязательства, невзирая на неблагоприятные экономические
условия. Поэтому их облигации рассматриваются инвесторами как
относительно безопасная инвестиционная возможность, однако, и
купонная ставка по таким облигациям будет довольно низкой. Для
эмитента, в свою очередь, от рейтинга облигаций будет зависеть
стоимость привлечения заемного капитала.
Облигации с рейтингом ниже инвестиционного уровня часто
упоминаются как «мусорные облигации» (junk bonds). Их эмиссиям
присваивается долгосрочный рейтинг BB+ и ниже по шкале S&P и
Fitch Ratings, Ba1 по шкале Moody’s. Риски, связанные с
осуществлением инвестиций в облигации неинвестиционного
уровня значительно выше, чем у облигаций с рейтингом
инвестиционного уровня. Поэтому эмитенты таких ценных бумаг
предлагают потенциальным инвесторам более высокую доходность,
которая может быть в несколько раз выше, чем у первоклассных
облигаций с рейтингом «AAA» или «Aaa». Агентства обоснованно
полагают, что эмитенты облигаций с рейтингом неинвестиционного
уровня уязвимы к неблагоприятным экономическим и бизнес
условиям, что может негативно сказаться на выполнении их
долговых обязательств.
246. Базовые принципы оценки стоимости облигаций
Базовые принципы оценки стоимости финансового инструментаЦена любого финансового инструмента равна текущей стоимости ожидаемого денежного
потока от этого финансового инструмента. Таким образом, для определения его цены
необходимо:
1. Оценить ожидаемый денежный поток.
2. Оценить соответствующую требуемую доходность.
Ожидаемые денежные потоки одних финансовых инструментов вычислить просто, для
других это сделать сложнее. Требуемая доходность (required yield, required rate of return)
является оценкой доходности финансовых инструментов со сравнимым риском, так
называемых альтернативных инструментов.
Оценка облигаций
Первым шагом в вычислении цены облигации является определение ее денежного потока.
Например, денежный поток для облигации, которую эмитент не может отозвать до
установленной даты погашения (т.е. облигации без права досрочного погашения, или
безотзывной облигации), состоит из:
1. Периодических купонных выплат до даты погашения.
2. Выплаты номинала в дату погашения.
Требуемая доходность определяется путем исследования доходностей, предлагаемых на
рынке по сравнимым облигациям. Требуемая доходность обычно выражается в виде
годовой процентной ставки. Если платежи поступают раз в полгода, на рынке принято
соглашение использовать 1/2 годовой процентной ставки в качестве процентной ставки
за купонный период, с помощью которой дисконтируется денежный поток.
247. Базовые принципы оценки стоимости облигаций
Если известны денежные потоки и требуемая доходность, то мы обладаем всейинформацией, необходимой для оценки облигаций. Поскольку цена облигации — это
приведенная стоимость денежного потока, то она определяется путем сложения
следующих двух значений:
1. Приведенной стоимости (PV) купонных выплат.
2. Приведенной стоимости номинала (или суммы погашения).
Математическая модель оценки денежной стоимости облигаций основана на
дисконтировании денежных потоков, выплачиваемых на протяжении всего срока до
погашения. Стоимость облигации в настоящий момент времени равна дисконтированной
сумме всех денежных потоков, с ней связанных.
В общем случае цена облигации может быть вычислена с помощью следующей формулы:
N
C
M
k
(1 r ) N
k 1 (1 r )
P
где:
C = ежегодный купонный (процентный) платеж;
М = номинал облигации;
N = количество лет до погашения;
r = норма требуемой доходности по облигации;
k = номер года, в который поступает купонный платеж.
248. Оценка стоимости купонной облигации
Пример 8.2.:Инвестор приобрел облигацию номиналом €1,000 с купонной ставкой 10%, которая
соответствует ежегодной выплате €100. Предположим, что требуемая в данный момент
инвестором ставка доходности для этого типа облигаций составляет 20%, а срок до
погашения - 3 года. Определить стоимость облигации.
Решение:
M = 1,000; rc = 0.1; C = 1,000 * 0.1 = 100; r = 0.2; N = 3.
P
100
100
100
1,000
€789.35
(1 0.2)1 (1 0.2) 2 (1 0.2) 3 (1 0.2) 3
Таким образом, норма доходности в 20% по данной операции будет обеспечена при покупке
облигации по цене, приблизительно равной €789.35.
Очевидно, что равномерные выплаты купонных платежей представляют собой аннуитет
постнумерандо (т.е. равные купонные платежи поступают в конце каждого периода).
Таким образом, приведенную стоимость купонных платежей (PVC) можно определить как:
1
1
(1 r ) N
PVC C
r
249. Оценка стоимости купонной облигации
Из этого следует, что формулу для расчета стоимости купонной облигации, платежи покоторой поступают ежегодно, можно представить след. образом:
1
1
(1 r ) N
P PVC PVM C
r
M
N
(
1
r
)
где:
PVC = приведенная стоимость купонных выплат;
PVM = приведенная стоимость суммы погашения долга (номинала);
C = ежегодный купонный (процентный) платеж;
М = номинал облигации;
N = срок до погашения;
r = норма требуемой доходности по облигации.
1
1
3
(1 0.2)
1,000
P 100
210.65 578.70 €789.35
3
0
.
2
(
1
0
.
2
)
250. Оценка стоимости купонной облигации
Задача 8.1.:Hоминальная стоимость купонной облигации – €1,000. Срок до погашения составляет 16 лет.
Номинальная процентная ставка – 14%. Купонные платежи по облигации поступают
ежегодно. Способ погашения номинальной стоимости – разовый платеж в конце срока
облигации. Определить теоретическую стоимость облигации, если требуемая норма
доходности – 12%.
(P = 1,139.5)
251. Оценка стоимости купонной облигации
Начисление процентов по облигации m раз в годуЕсли проценты по облигации начисляются m раз в году, формула для расчета стоимости
облигации будет следующей:
C
m N
M
m
P
k
m N
r
r
k 1
1
1
m
m
где:
m = количество начислений процентов (выплат по облигации) в год;
N = количество лет до погашения;
mN = количество периодов до погашения;
C/m = размер периодического купонного (процентного) платежа;
М = номинал (сумма погашения);
r = норма требуемой доходности по облигации;
r/m = процентная ставка за купонный период;
k = период времени, когда производится выплата.
252. Оценка стоимости купонной облигации
Пример 8.3.:Рассмотрим 20-летнюю 10%-ную облигацию с номиналом $1,000. Предположим, что
требуемая доходность по облигации равна 11%. Денежный поток по этой облигации
будет следующим:
1. 40 полугодовых купонных выплат по $50.
2. $1,000 номинала через 40 полугодовых купонных периодов от настоящего момента.
r = 0.11; m = 2; r/m = 0.11/2 = 0.055; N = 20; M = 1,000; C = 0.1*1,000 = 100.
Полугодовая процентная ставка, или процентная ставка за купонный период (требуемая
доходность за период), равна 5,5% (11%, деленные на 2).
Стоимость облигации определяется как сумма приведенной стоимости купонных платежей и
приведенной стоимости номинала:
P PVC PVM
C
40
M
50
1,000
m
P
802.31 117.46 $919.77
k
m N
k
40
(1 0.055)
r
r
k 1
k 1 1 0.055
1
1
m m
m N
Поскольку полугодовые купонные выплаты эквивалентны постоянной ренте постнумерандо,
то их приведенная стоимость может быть найдена по следующей формуле:
253. Оценка стоимости купонной облигации
11
m N
r
1
C m
PVC
r
m
m
Из этого следует, что формулу для расчета стоимости купонной облигации с полугодовым
начислением купона можно представить след. образом:
1
1
m N
r
1
C
m
P PVC PVM
r
m
m
M
m N
r
1
m
Соотвественно, цена облигации:
1 (1.055) 40
1,000
P 50
802.31 117.46 $919.77
40
0.055
(1.055)
254. Оценка стоимости купонной облигации
Задача 8.2.:Hоминальная стоимость купонной облигации – $1,000. Срок до погашения составляет 16 лет.
Номинальная процентная ставка – 14%. Купонные платежи по облигации осуществляются
на полугодовой основе (каждые 6 месяцев). Способ погашения номинальной стоимости –
разовый платеж в конце срока облигации. Определить теоретическую стоимость
облигации, если требуемая норма доходности – 12%.
(P = 1,140.84)
255. Соотношение цены и доходности облигаций
Фундаментальное свойство облигации состоит в том, что ее цена изменяется в направлении,противоположном
направлению
изменения
соответствующей
доходности.
Действительно, цена облигации — это приведенная стоимость денежного потока. При
возрастании требуемой доходности приведенная стоимость потока снижается, а
следовательно, снижается и цена. Верно и обратное: в случае снижения требуемой
доходности возрастает приведенная стоимость потока и, следовательно, цена облигации
возрастает.
Пример 8.4.:
Рассмотрим 20-летнюю 10%-ную облигацию с номиналом $1,000. Купонные платежи по
облигации осуществляются каждые полгода. Теперь предположим, что требуемая
доходность по облигации равна не 11%, а 6.8%. Тогда цена облигации будет равна
$1,347.04, что видно из следующих вычислений.
Приведенная стоимость купонных выплат с использованием процентной ставки за период,
равной 3,4% (6,8%/2), составляет:
1
1
m N
r
1
C m
PVC
r
m
m
1
1
2 20
0.068
1
2
$1,084.51
50
0.068
2
256. Соотношение цены и доходности облигаций
Приведенная стоимость номинала $1,000 с получением через 40 шестимесячных периодов отнастоящего момента, дисконтированных по ставке 3,4%, равна:
PVM
M
r
1
m
m N
1,000
$262.53
(1 0.034) 40
Тогда цена облигации равна:
P PVC PVM 1,084.51 262.53 $1,347.04
Можно показать, что если требуемая доходность равна купонной ставке (10%), то цена
облигации будет равна ее номиналу $1,000.
257. Соотношение купонной ставки, требуемой доходности и цены
Соотношение между купонной ставкой, требуемой доходностью и ценой может бытьвыражено следующим образом:
Купонная ставка < Требуемая доходность -> Цена < Номинал (облигация с дисконтом).
Купонная ставка = Требуемая доходность -> Цена = Номинал (облигации, котирующиеся по
номиналу).
Купонная ставка > Требуемая доходность -> Цена > Номинал (облигация с премией).
Если доходность на рынке в некоторый момент времени поднялась выше купонной ставки, то цена
облигации приводится в соответствие с ней таким образом, что инвестор может получить
дополнительный доход. Это происходит за счет падения цены ниже номинала. Выигрыш в разности
цен покупки и погашения (если инвестор держит облигацию до погашения) дает инвестору
дополнительный доход, компенсирующий недостаточный по сравнению с требуемой доходностью
уровень купонной ставки.
Когда облигация продается по цене ниже номинала, говорят, что она продается с дисконтом (discount). В
наших примерах вычислений цены облигации мы видели, что если требуемая доходность выше
купонной ставки, цена облигации всегда ниже номинала ($1,000).
Если требуемая доходность ниже купонной ставки, то облигации должны продаваться по цене выше
номинала. Это происходит из-за того, что инвесторы, имеющие возможность покупать облигации по
номиналу, получали бы купонный доход выше диктуемого рынком. В результате повышенный спрос
на такие облигации поднял бы их цену, поскольку высокая доходность привлекательна для
инвесторов.
Очевидно, что цена будет подниматься до того уровня, при котором доходность облигации сравняется с
рыночной. Про облигации с ценой выше номинала говорят, что они продаются с премией (premium).
258. Изменения цены облигации
Соотношение цены облигации и срока до погашения в случае неизменных процентных ставокДля облигации, продающейся по номиналу, купонная ставка равна требуемой доходности.
При приближении к дате погашения облигация по-прежнему будет продаваться по
номиналу. Однако цена облигации, продающейся с дисконтом или премией, не будет
оставаться неизменной. Цена дисконтной облигации при приближении к погашению
возрастает (при предположении, что требуемая доходность не изменяется).
Противоположное происходит с облигацией, продающейся с премией. Для обеих этих
облигаций в момент погашения цена будет равна номиналу.
Причины изменения цены облигации
Цена облигации может измениться вследствие одной или нескольких из трех причин:
1. Происходит изменение требуемой доходности из-за изменения кредитного рейтинга
эмитента. То есть требуемая доходность изменяется из-за того, что рынок выравнивает
доходность данной облигации с доходностями других облигаций с тем же кредитным
рейтингом.
2. Происходит изменение цены облигации, продающейся с премией или с дисконтом без
каких-либо изменений требуемой доходности, просто вследствие приближения к дате
погашения.
3. Происходит изменение требуемой доходности, вызванное изменением доходности по
сравнимым облигациям, т.е. изменяются рыночные процентные ставки.
259. Основные риски облигаций
Основные риски облигацийФактические доходы, связанные с облигацией, по тем или иным причинам могут сильно
отличаться от ожидаемых, и именно это различие между ожидаемыми и фактическими
доходами является характеристикой риска.
Чем больше абсолютная величина отклонения фактической доходности облигации от ее
ожидаемого значения, тем выше степень риска.
По факторам, обусловливающим появление этих отклонений, все риски корпоративных
облигаций могут быть классифицированы следующим образом:
процентный риск;
реинвестиционный риск;
риск досрочного отзыва;
риск дефолта;
риск снижения рейтинга облигации;
инфляционный риск;
валютный риск;
риск ликвидности.
260. Основные риски облигаций
Процентный рискФундаментальным свойством облигаций является изменение цены в направлении,
противоположном изменению требуемой доходности по ним. Это свойство объясняется
тождеством цены облигации значению приведенной стоимости предполагаемых
денежных потоков облигации:
N
C
M
P
k
N
(
1
r
)
(
1
r
)
k 1
Из формулы следует, что при возрастании процентной ставки r цена облигации снижается и у
держателя облигации возникает убыток. Наоборот, при снижении процентной ставки
цена облигации растет и у владельца облигации возникает дополнительный прирост
капитала.
Именно этот возможный прирост или убыток делает инвестиции в облигации рискованными,
даже если эмитент гарантирует инвесторам выплату купонных платежей и основной
суммы долга по облигации.
Процентный риск облигации (interest rate risk) определяется чувствительностью ее стоимости
к изменению рыночной процентной ставки.
На практике, для измерения процентного риска облигации используют дюрацию.
261. Основные риски облигаций
Реинвестиционный рискРиск реинвестиций (reinvestment risk) — это снижение доходности облигации, обусловленное
тем, что полученные по облигации проценты (купонные платежи) или полученные при
погашении облигации средства будут реинвестированы под меньшую процентную ставку.
Риск досрочного отзыва
Риск досрочного отзыва (call risk) возникает в том случае, если эмитент воспользуется правом
досрочного исполнения обязательств (правом отзыва). Как правило, эмитент отзывает
облигации в двух случаях. В первом случае, при снижении уровня процентных ставок,
облигации с фиксированным доходом отзываются для рефинансирования долга. Эмитент
выкупает облигации, чтобы выпустить новые под более низкий процент и таким образом
уменьшить финансовое бремя обслуживания долга.
Риск держателя облигации состоит в том, что, получив средства за выкупленную облигацию,
он сможет реинвестировать их только под более низкий процент, поскольку процентные
ставки на рынке упали.
Риск дефолта
Риск дефолта (default risk) — это вероятность того, что эмитент облигации может оказаться не
в состоянии вовремя произвести выплаты основной суммы долга или процентов по нему
или выполнить другие обязательства, которые вытекают из условий выпуска облигации.
Обычно риск дефолта по облигации измеряют с помощью рейтинга, присваиваемого
рейтинговой компанией.
262. Основные риски облигаций
Риск снижения рейтинга облигацииРиск снижения рейтинга облигации — это вероятность недополучения дохода владельцем
облигации в результате понижения ее рейтинга. Этот вид риска связан с тем, что
кредитоспособность эмитента постоянно изменяется во времени и ее ухудшение может
быть отмечено рейтинговым агентством путем понижения рейтинга облигации. Если
рейтинг облигации снизился, то премия за риск по этой облигации должна быть
увеличена, что может привести к падению цены облигации.
Таблица иллюстрирует, что с понижением рейтинга облигации премия за риск и вероятность
дефолта возрастают, причем для облигаций спекулятивного уровня (уровень ВВ и ниже)
значительно больше, чем премия для облигаций инвестиционного уровня (уровень ВВВ и
выше):
263. Основные риски облигаций
264. Основные риски облигаций
Инфляционный рискИнфляционный риск (inflation risk) — это вероятность снижения реальной доходности
облигации в результате превышения фактического уровня инфляции над ожидаемым
уровнем, на который ориентировался инвестор в момент приобретения облигации.
Инфляционный риск связан с тем, что в момент выплаты по облигации уровень инфляции
будет отличаться в большую сторону от уровня инфляции в момент покупки облигации.
Валютный риск
Валютный риск (exchange-rate risk) заключается в потере стоимости евро облигации,
деноминированной в иностранной валюте.
Риск ликвидности
Риск ликвидности (liquidity risk) возникает в том случае, когда облигацию не удается быстро
реализовать по справедливой цене.
Чем больше неопределенность в отношении времени, затрачиваемого на покупку или
продажу облигации, и величина уступки в цене, тем большим является риск ликвидности.
Риск ликвидности облигации измеряется отклонением цены, по которой куплена или
продана облигация, от ее справедливой цены.
265. Раздел 9: АКЦИИ И ИХ ОЦЕНКА
АкцииАкция (share) — эмиссионная ценная бумага, доля владения компанией, закрепляющая права
её владельца (акционера) на получение части прибыли акционерного общества в виде
дивидендов, на участие в управлении акционерным обществом и на часть имущества,
остающегося после его ликвидации, пропорционально количеству акций, находящихся в
собственности у владельца.
Дивиденд
Дивиденд — часть прибыли акционерного общества, распределяемая между акционерами,
участниками в соответствии с количеством и видом акций, долей, находящихся в их
владении.
Величина и порядок выплаты дивидендов определяются собранием акционеров, участников
и уставом акционерного или иного общества.
Дивиденды могут выплачиваться несколько раз в год, а могут и не выплачиваться вообще.
Выплата дивидендов уменьшает капитализацию и требует накоплений, недопущенных к
реинвестированию или изъятых из него.
Акционерный капитал
Акционерный капитал — это собственный капитал (ownership equity, net worth) акционерного
общества. Он равен её совокупным активам (assets) за вычетом совокупных обязательств
(liabilities).
266. Пакет акций
Пакет акцийПакет акций — количество акций одного акционерного общества (АО), находящееся в одних
руках или под единым контролем.
Блокирующий пакет акций
Блокирующий пакет акций — доля акций, позволяющая их владельцам накладывать вето на
решения совета директоров акционерного общества. Обычно блокирующий пакет
составляет более четверти (25%) всех акций — то есть владение таким количеством
акций, которое позволяет блокировать любое принимаемое акционерным обществом
решение, если оно не устраивает такого акционера. Теоретически доля акций,
необходимая для блокирования, 25 %, но на практике она меньше.
Контрольный пакет акций
Контрольный пакет акций — доля акций, дающая их владельцу возможность самостоятельно
принимать решения в вопросах функционирования акционерного общества, в том числе
назначать руководящий состав. Безусловным контрольным пакетом является 50 % + 1
акция. Но в большинстве компаний решение на общем собрании принимают
большинством голосов от присутствующих. Чем крупнее компания и чем более
распространены её акции среди миноритарных акционеров, тем выше вероятность, что
на общем собрании не будет присутствовать значительная часть акционеров. В такой
ситуации большинство голосов может обеспечить значительно меньший пакет.
Миноритарный пакет акций
Миноритарный пакет акций — не контрольный пакет акций.
267. Обыкновенные акции
Категории акцийРазличают обыкновенные и привилегированные акции.
Обыкновенные акции
Обыкновенные акции (common shares) являются ценными бумагами, которые подтверждают
участие в собственном капитале компании. В иерархии прав их владельцы имеют самый
низкий приоритет, уступая кредиторам компании (держатели облигаций, банки,
поставщики) и владельцам привилегированных акций.
Например, в случае объявления процедуры банкротства или ликвидации компании, в первую
очередь в полном объеме должны быть удовлетворены интересы всех кредиторов. Если
после этого остались какие-либо средства, то право на получение возмещения в полном
объеме получают владельцы привилегированных акций. Оставшиеся средства, если
таковые имеются, будут распределены между владельцами обыкновенных акций
пропорционально их участию в собственном капитале.
Свойства обыкновенных акций
Можно выделить ряд свойств, которые характерны для обыкновенных акций практически в
любой юрисдикции:
1. Право на получение дивидендов.
Владельцы обыкновенных акций имеют право на получение части чистой прибыли компании
пропорционально своему участию в собственном капитале в форме дивидендов. Однако
их выплата не является обязательной для компании и зависит от решения совета
директоров. Следует отметить, что владельцы привилегированных акций имеют
первоочередное право на получение дивидендов, как правило, фиксированных. Другими
словами, по обыкновенным акциям дивиденды будут выплачены только после того, как
будут удовлетворены все обязательства по привилегированным.
268. Обыкновенные акции
2. Право на получение части активов компании в случае ее ликвидации.Владельцы простых акций имеют право на получение части средств, вырученных от продажи
активов компании, в случае ее ликвидации. При этом они занимают самое низкое место в
иерархии прав, после держателей облигаций, кредиторов компании и владельцев
привилегированных акций.
3. Право голоса.
В отличии от привилегированных акций обыкновенные дают их владельцам право голоса при
назначении совета директоров и по другим фундаментальным вопросам таким как
внесение изменений в устав компании, слияние, продажа части активов, ликвидация.
Следует отметить, что некоторые классы обыкновенных акций могут не иметь права
голоса, что должно быть прописано в уставе и разрешено законодательством в данной
юрисдикции.
4. Право на получение возмещения в случае слияния или поглощения компании.
Если совет директоров и собрание акционеров одобряют решение о слиянии или
поглощении компании, владельцы обыкновенных акций имеют право на компенсацию,
которая может быть осуществлена в форме выкупа принадлежащих им акций, либо в
форме акций новой компаний.
5. Право ликвидности.
Владельцы обыкновенных акций имеют право продать их в любой момент времени на
открытых торгах или путем частной сделки.
269. Обыкновенные акции
Эмиссия обыкновенных акцийЭмиссия обыкновенных акций, как правило, проводится с целью привлечения
дополнительного капитала.
Преимущество этого способа состоит в том, что в отличии от эмиссии облигаций, он не
приводит к росту риска дефолта эмитента. Другими словами, обязательства перед
держателями облигаций должны быть выполнены в полном объеме и в сроки,
предусмотренные условиями эмиссии. Их невыполнение будет автоматически означать
дефолт эмитента. Выплата дивидендов по обыкновенным акциям, напротив, не является
обязательной, а зависит от решения совета директоров. Однако и их кредитный рейтинг
будет ниже, чем у привилегированных акций и облигаций этой же компании.
Обращение обыкновенных акций
Размещение новой эмиссии обыкновенных акций осуществляется на первичном рынке
(primary market) путем проведения первичного публичного предложения (Initial Public
Offering, IPO) либо через профессиональных посредников.
Проведение IPO характерно для крупных публично торгуемых компаний, которые
преследуют цель заинтересовать максимальный круг потенциальных инвесторов.
Мелкие и средние компании, как правило прибегают к услугам профессиональных
посредников, к которым относятся брокерские компании, инвестиционные банки,
инвестиционные фонды. Следует отметить, что средства, вырученные в результате
первичного размещения, идут на формирование собственного капитала компании.
270. Обыкновенные акции
Однако наибольшее количество сделок с обыкновенными акциями происходит на вторичномрынке (secondary market), поскольку они могут перепродаваться теоретически
неограниченное количество раз.
При этом сам вторичный рынок делится на два сегмента:
• биржевой и
• внебиржевой рынок (OTC).
Биржевой рынок
На биржевом рынке сделки по покупке продаже обыкновенных акций происходят на
торговой площадке фондовой биржи (stock exchange). Однако для большинства компаний
этот рынок является недоступным, поскольку биржи устанавливают достаточно жесткие
требования для включения в листинг. Поэтому к торгам, как правило, допускаются акции
только крупнейших публично-торгуемых компаний.
Внебиржевой рынок
На внебиржевом рынке обращаются обыкновенные акции компаний, которые не могут быть
включены по тем или иным причинам в листинг биржи. Сделки на нем осуществляются
через профессиональных посредников, в роли которых, как правило, выступают
брокерские компании.
Потенциальные инвесторы в обыкновенные акции
Как объект инвестиций обыкновенные акции
институциональным инвесторам.
интересны
как
частным
так
и
271. Привилегированные акции
Привилегированные акцииПривилегированные акции (preference shares) являются гибридным финансовым
инструментом, который одновременно объединяет в себе как характеристики
обыкновенных акций, так и облигаций. С точки зрения финансового учета они относятся к
собственному капиталу, как и обыкновенные акции, а не к обязательствам, как
облигации. С точки зрения иерархии предоставляемых прав они относятся к старшим
ценным бумагам, находясь в ней выше обыкновенных акций, но ниже облигаций.
Свойства привилегированных акций
Компании-эмитенты могут сами определять, какие дополнительные права или привилегии
они будут предоставлять владельцам привилегированных акций, если это не
противоречит законодательству конкретной юрисдикции. Для этого финансового
инструмента, характерен следующий ряд свойств:
1. Преимущественное право на получение дивидендов.
При распределении чистой прибыли владельцы привилегированных акций получают
первоочередное право на выплату дивидендов. Это не означает полной гарантии их
выплаты, но обязывает компанию в первую очередь выполнить обязательства перед их
владельцами, а затем перед владельцами простых акций.
2. Фиксированный размер дивидендов.
Как правило, размер дивидендов по привилегированным акциям фиксируется в твердой
денежной сумме или в процентах к номинальной стоимости.
272. Привилегированные акции
3. Кумулятивные дивиденды.В некоторых случаях дивиденды по привилегированным акциям могут быть кумулятивными.
Например, если их размер установлен на уровне €5 в квартал, а компания в отчетном
квартале смогла выплатить только €3, то невыплаченные €2 будут перенесены на
следующий период. То есть, в следующем квартале компания должна будет выплатить
уже €7, из которых €5 – это очередные дивиденды, а €2 – накопленные за предыдущие
периоды.
4. Преимущественное право на получение части активов компании в случае ее ликвидации.
В случае принятия решения о ликвидации активов компании интересы держателей
привилегированных акций стоят выше интересов держателей обыкновенных акций, но
ниже держателей облигаций.
5. Возможность конвертации в обыкновенные акции.
Условии эмиссии могут включать пункт, дающий право держателю привилегированных акций
осуществить их конвертацию в обыкновенные.
6. Возможность обратного выкупа.
В некоторых случаях компании может предусмотреть пункт, который дает ей возможность
осуществить обратный выкуп привилегированных акций. При этом выкуп будет
осуществлен по номинальной стоимости, если другое не оговорено в условиях эмиссии.
7. Отсутствие права голоса.
Как правило, все привилегированные акции лишены права голоса. Тем не менее, в условиях
эмиссии или уставе компании оговаривается исчерпывающий перечень чрезвычайных
событий, в которых они получают специальное право голоса.
273. Оценка стоимости обыкновенных акций
Метод дисконтирования дивидендовВ большинстве случаев дивиденды характерезуются более высокой стабильностью чем
чистая прибыль или свободный денежный поток и, поэтому, являются важной формой
денежного потока. Для определения стоимости акции, денежные потоки (дивиденды)
дисконтируются с учетом требуемой нормы доходности для акции предприятия и
соответствующего временного интервала.
Для использования модели дисконтирования дивидендов (dividend discount model) при
оценке стоимости акции, необходимы следующие условия:
• предприятие имеет историю выплаты дивидендов и прозрачную дивидендную политику;
• синхронизация прибыли и дивидендных выплат;
• инвестор владеет миноритарным («неконтролирующим») пакетом акций.
Модель дисконтирования дивидендов (DDM) имеет следующий общий вид (Джон Бэрр
Уильямс, 1938):
Dn
Dt
D1
V0
...
...
V
0
t
(1 r )1
(1 r ) n
(
1
r
)
t 1
где:
Dt = дивиденд по обыкновенной акции, полученный в конце периода t;
r = дисконтная норма (требуемая норма доходности по акционерному капиталу).
274. Модель постоянного роста дивидендов
Применяемые методы дисконтирования дивидендов различаются в зависимости отпредположений о темпе роста дивидендов.
Модель постоянного роста
Модель постоянного роста дивидендов (Gordon Growth Model) (Гордон, 1962) предполагает
неизменный темп роста дивидендов и прибыли на акцию. Коэффициет выплаты
дивидендов (DPR) также остается неизменным:
DPR
DPS
const
EPS
где:
DPS = дивиденды на акцию;
EPS = прибыль на акцию.
Модель подразумевает, что компания на сегодняшний день выплачивает дивиденды в
размере D0, которые в будущем будут увеличиваться с неизменной ставкой g:
D1 D0 (1 g )
D2 D0 (1 g ) 2
D3 D0 (1 g ) 3
Dt D0 (1 g ) t
g const
275. Модель постоянного роста дивидендов
С учетом этого допущения формула для оценки стоимости обыкновенной акции принимаетвид:
D0 (1 g )1 D0 (1 g ) 2
D0 (1 g ) n
V0
...
...
1
2
n
(1 r )
(1 r )
(1 r )
После алгебраических упрощений формула принимает следующий вид:
D0 (1 g )
V0
(r g )
или
D1
V0
(r g )
Mодель предполагает что:
• r > g, в противном случае цена акции становится неопределенной.
• Предприятие должно выплачивать дивиденды регулярно, в противном случае модель
неприменима. Более того, требование неизменности величины g означает, что компания
направляет на выплату дивидендов всегда одну и ту же долю своего дохода (неизменный
коэффициент выплаты дивидендов)
• Компоненты доходности r (дивидендная доходность и доходность по приросту капитала)
будут неизменными на протяжении всего времени.
Модель используется для предприятий, темпы роста которых равны номинальному темпу роста экономики (т.е. реальный
рост ВВП + долгосрочная ожидаемая ставка инфляции) или ниже данного роста экономики, при этом у этих компаний
есть определенная политика выплаты дивидендов, которую они намерены проводить и в будущем.
276. Модель постоянного роста дивидендов
Пример 9.1.:Последний выплаченный предприятием дивиденд — €7.50, ожидаемый темп роста
дивидендов постоянен и составит 4% в год. Используя модель дисконтирования
дивидендов, определить стоимость акции предприятия, если требуемая норма
доходности акционерного капитала — 13.5%.
Решение:
D0 = 7.50; g = 0.04 = const; r = 0.135
V0
D0 (1 g )
7.50(1.04)
€82.11
(r g )
(0.135 0.04)
277. Оценка долгосрочного темпа роста дивидендов
Оценка долгосрочного темпа роста дивидендовДля определения темпа роста дивидендов g, можно использовать:
средний по отрасли темп роста, и
внутренний темп роста (sustainable growth rate), определяемый по формуле:
g b ROE
где:
b = коэффициент удержания (retention ratio);
ROE = рентабельность собственного капитала.
Внутренний темп роста - это максимальный темп роста, который может развить компания
без внешних источников финансирования
Коэффициент удержания рассчитывается как отношение разности между величиной чистого
дохода и выплаченных дивидендов к величине чистого дохода:
b
NI DIV
NI
Например, если компания в текущем периоде принесла чистую прибыль в размере €350,000
и выплатила дивидендов на сумму €75,000, то нераспределенная прибыль составит
€275,000. При этом коэффициент удержания будет равен (350,000-75,000)/350,000 =
78,57%.
278. Оценка долгосрочного темпа роста дивидендов
Цель большинства компаний состоит в том, чтобы сохранить максимально высокийкоэффициент удержания, сохранив при этом выплату дивидендов, размер которых будет
привлекательным для инвесторов. Когда компания в состоянии достигнуть этого баланса,
в ее распоряжении появляется больше денег, которые можно вложить в улучшение
существующей деятельности, расширение бизнеса, выход на новые рынки,
финансирование научно-исследовательской деятельности.
Рентабельность собственного капитала (ROE) можно представить в виде трехфакторной
модели Дюпона:
NI S TA
ROE
S TA TE
где:
NI / S = чистая рентабельность продаж (NPM);
S / TA = оборачиваемость активов (TA T/O);
TA / TE = коэффициент капитализации (коэффициент финансового рычага).
Таким образом, внутренний темп роста g можно определить при помощи следующей модели
(PRAT model):
g
NI DIV NI S TA
NI
S TA TE
279. Двухфазная модель дисконтирования дивидендов
В зависимости от типа рассматриваемой компании и предполагаемой динамики выплатдивидендов различают следующие типы моделей: двухэтапную, H-модель и трехэтапную.
Двухэтапная модель дисконтирования дивидендов (2-stage DDM):
Модель предпологает две фазы роста дивидендов:
1. дивиденды имеют высокий краткосрочный темп роста (gS) в течении периода n;
2. после периода n, дивиденды имеют постоянный нормированный темп роста gL.
Модель расчета стоимости обыкновенной акции имеет следующий вид:
D0 (1 g S ) t D0 (1 g S ) n (1 g L )
V0
t
(1 r )
(1 r ) n (r g L )
t 1
n
где:
r = требуемая норма доходности акционерного капитала
D0 = последний выплаченный дивиденд
gS = краткосрочная норма прироста дивидендов
gL = долгосрочная норма прироста дивидендов (gL= const)
280. Двухфазная модель дисконтирования дивидендов
Пример 9.2.:Предприятие выплатило по дивидендам €2.00 за последний год. В течение ближайших трех
лет темп роста дивидендов составит 8%. В последующие годы (без ограничений по
времени) дивиденды будут расти с темпом 5%. Определить стоимость обыкновенной
акции предприятия, если требуемая норма доходности по акционерному капиталу для
данного предприятия составляет 13%.
Решение:
D0 = 2.00; gS = 0.08; gL = 0.05; n = 3; r = 0.13
n D0 (1 g s ) t D0 (1 g s ) n (1 g L ) 3 2(1 0.08) t 2(1 0.08) 3 (1 0.05)
V0
t
n
t
3
t 1 (1 r ) (1 r ) (r g L ) t 1 (1 0.13) (1 0.13) (0.13 0.05)
2(1 0.08)1 2(1 0.08) 2 2(1 0.08) 3 2(1 0.08) 3 (1 0.05)
V0
1
2
3
3
1.13
1.13
1.13
(1 0.13) (0.13 0.05)
2.16 2.33 2.52 2.52(1.05)
V0
1.91 1.82 1.75 22.92 €28.40
1
.
13
1
.
28
1
.
44
1
.
44
(
0
.
08
)
281. Двухфазная модель дисконтирования дивидендов
Представим решение задачи графически:t=0
gs = 8%
1
2.16
gs = 8%
2
2.33
gs = 8%
3
2.52
2.16(1+0.13)-1
1.91
2.33(1+0.13)-2
1.82
2.52(1+0.13)-3
1.75
PVD = €5.48
t=0
1
2
3
gL = 5%
4 gL = 5%
...
2.645
PVV3= €22.92
Σ = €28.40
33.067(1+0.13)-3
V3
D4
2.645
€33.067
(r g L ) (0.13 0.05)
282. Н-модель
H-модель (H-model)Н-модель (Фуллер и Хсиа, 1984) – это разновидность двухэтапной модели, в основании
которой стоит допущение о том, что темпы роста в прогнозном периоде n снижаются
линейно, постепенно стремясь к постпрогнозному стабильному значению роста, напр., к
среднеотраслевому.
Модель расчета стоимости обыкновенной акции имеет следующий вид:
V0
D0 (1 g L ) D0 H ( g S g L )
r gL
где:
r = требуемая норма доходности акционерного капитала
D0 = последний выплаченный дивиденд
gS = краткосрочная норма прироста дивидендов
gL = долгосрочная норма прироста дивидендов (gL= const)
H = ½ продолжительности прогнозного периода
Предполагается, что на момент оценки предприятие достигло критического темпа роста. В дальнейшем
подразумевается снижение темпов роста, причем обязательно линейное (каждый год на одно и то же
количество процентных пунктов). Это снижение длится ровно 2H периодов (лет), после чего темп
прироста будет постоянным и равным, например, среднеотраслевому темпу прироста (или
номинальному росту ВВП).
Таким образом, начиная с года 2Н к оценке акций компании можно применить модель Гордона. Авторы
модели подчеркивают, что общая стоимость акции складывается из двух компонентов: стоимости при
стабильном росте и стоимости при ненормированном росте, длящимся 2H периода.
283. Н-модель
H-модель наиболее приемлема для предприятий, которые росли до настоящего моментаочень быстро, но к моменту t=0 достигли большого размера, и темп их роста
замедляется.
Пример 9.3.:
Предприятие выплатило по дивидендам €1.37 за последний год. Изначальный темп роста
дивидендов составляет 24%. Предполагается, что в течении 12-ти лет данный темп роста
будет линейно снижаться и достигнет долгосрочного постоянного роста на уровне 6%.
Требуемая норма доходности акционерного капитала – 10%. Используя Н-модель,
определить теоретическую стоимость акции предприятия.
Решение:
D0 = 1.37; gS = 0.24; gL = 0.06; 2H = 12; H = 6; r = 0.10.
V0
D0 (1 g L ) D0 H ( g S g L ) 1.37(1.06) 1.37(6)(0.24 0.06)
€73.30
r gL
0.10 0.06
284. Трехфазные модели дисконтирования дивидендов
Трехэтапные моделиВ отличие от двухфазных моделей, в трехфазной предполагается деление жизненного цикла
компании на три стадии. Например:
1-я стадия: стабильный и быстрый рост компании, но при этом выплаты дивидендов
отсутствуют или минимальны (чаще всего используется остаточный принцип начисления
дивидендов);
2-я стадия: понижающийся рост компании, сопровождающийся сокращением
инвестиционной программы и увеличением доли чистой прибыли, выплачиваемой в
виде дивидендов, однако дивиденды определяются на каждый период по-разному;
3-я стадия: стабильный и невысокий темп роста компании, высокие и постоянные
дивидендные выплаты.
Пример 9.4.:
Предприятие выплатило по дивидендам €1.60 за последний год. Требуемая норма
доходности – 12%. Прогнозируется ежегодное увеличение дивидендных выплат на 14% в
течении 2-х лет. Затем норма прироста дивидендов составит 12% в год в течении 5-ти лет,
а в последствии – 10.2% в год без ограничения по времени.
Дать инвестиционную оценку акции на основе трехфазной модели дисконтирования
дивидендов.
285. Трехфазные модели дисконтирования дивидендов
Решение:Год
Стоимость
Вычисление
1
D1
1.60(1.14)
€1.8240
€1.6286
2
D2
1.60(1.14)2
2.0794
1.6577
3
D3
1.60(1.14)2(1.12)
2.3289
1.6577
4
D4
1.60(1.14)2(1.12)2
2.6083
1.6577
5
D5
1.60(1.14)2(1.12)3
2.9214
1.6577
6
D6
1.60(1.14)2(1.12)4
3.2719
1.6577
7
D7
1.60(1.14)2(1.12)5
3.6645
1.6577
7
V7
1.60(1.14)2(1.12)5(1.102) /
(0.12 – 0.102)
224.3515
101.4852
Итого
Dt или Vt
Приведенная
стоимость
Dt / (1.12)t или
Vt / (1.12)t
€113.0600
286. Доходность и риск акций
ДоходностьИсточниками дохода по финансовым активам для инвестора (например, при вложении в
акции и облигации) могут являться:
• Периодическая доходность (дивиденды и доход по процентам);
• Доход (убытки) по приросту капитала, появляющиеся в результате изменения рыночной
цены актива.
Доходность за период владения активом
Доходность за период владения активом (HPR) — доходность инструмента инвестирования
за определенный период, которая вычисляется путем деления суммы прироста
капитала (или убытков) и текущего дохода, полученных в течение периода владения
активом, на первоначальную стоимость инвестиций.
Для акций доходность можно вычислить по след. формуле:
Pt Pt 1 Dt Pt Pt 1 Dt
HPR
Pt 1
Pt 1
Pt 1
где:
Pt = цена акции в конце периода
Pt−1 = цена акции в начале периода
Dt = дивиденд выплаченный в конце периода
287. Доходность за период владения
Пример 9.5.:Инвестор купил акцию предприятия за €100, получил дивиденд в размере €5 и продал
акцию за €110 через 9 месяцев. Определите доходность за период владения активом
(HPR).
Решение:
HPR
110 100 5
0.10 0.05 0.15 15%
100
100
Доходность за период владения активом (HPR) можно также определить для нескольких
периодов, наращивая доходности отдельных периодов:
HPR [(1 R1 ) (1 R2 ) ... (1 RN )] 1
где:
R1 , R2 , R3 , … RN = доходность за отдельный период
Пример 9.6.:
Стоимость акции увеличилась на 10% в течении первого года и на 8% в течении второго
года. В течении третьего года стоимость ации упала на 6%. Определить доходность
полученную инвестором за три года.
Решение:
HPR [(1 0.10)(1 0.08)(1 0.06)] 1 0.1167 11.67%
288. Средняя арифметическая доходность
Средняя арифметическая доходностьСреднеарифметическая доходность может быть рассчитана путем суммирования
периодических значений доходности и деления полученной суммы на число этих
значений T:
Ri1 Ri 2 RiT 1 RiT 1 T
Ri
Rit
T
T t 1
Применяя формулу средней арифметической, предполагают, что объем инвестиций
оставался неизменным в течение всех периодов, то есть по сути рассчитывается
средний базисный темп прироста, что неверно. Рассчитывать средний цепной темп
прироста следует по формуле средней геометрической, так как начальная сумма
инвестиций меняется от периода к периоду.
Среднеарифметическая доходность всегда выше среднегеометрической и эта разница
увеличивается по мере усиления разброса исходных показателей.
289. Средняя геометрическая доходность
Средняя геометрическая доходностьДоходность со сложным начислением, которая уравнивает исходную и конечную
стоимости. Среднегеометрическая доходность равна корню T-й степени от наращенного
дохода, где T — число периодов расчета накопленного наращенного дохода:
RGi T 1 Ri1 1 Ri 2 1 RiT 1 1 RiT 1
T
T 1 Rit 1
t 1
Поскольку геометрическая доходность дает возможность учета сложного процента
(реинвестирования денежных потоков), она является более приемлемой для оценки
инвестиционной деятельности.
290. Средняя геометрическая доходность
Пример 9.7.:Определить среднюю арифметическую и среднюю геометрическую доходности. Какой
показатель доходности является наиболее приемлемым?
Период
Доходность за
период (HPR)
Коэффициент
наращения
1
10%
1.10
2
30%
1.30
3
-20%
0.80
4
0%
1.00
5
20%
1.20
Средняя арифметическая доходность:
RA = (0.1 + 0.3 + (-0.2) + 0.0 + 0.2) / 5 = 0.08 = 8%
Средняя геометрическая доходность:
RG = [(1.10)(1.30)(.80)(1.00)(1.20)]1/5 – 1 = 0.0654 = 6.54%
Для нахождения приемлемой доходности, предположим, что начальный объем инвестиций
составил €1,000. Определим размер конечной стоимости инвестиции с учетом
реинвестирования (т.е. наращения стоимости):
291. Средняя геометрическая доходность
ПериодДоходность за
период (HPR)
Стоимость
инвестиции
1
10%
€1,100
2
30%
1,430
3
-20%
1,144
4
0%
1,144
5
20%
1,373
Через 5 лет будущая наращенная стоимость инвестиции с учетом средней арифметической
доходности составит:
FV5 = €1,000 (1.08)5 = €1,469
Через тот же период времени будущая наращенная стоимость инвестиции с учетом
средней геометрической доходности составит:
FV5 = €1,000 (1.0654)5 = €1,373
Очевидно, что геометрическая доходность является наиболее приемлемой мерой
доходности для инвестора.
292. Аннуализированная доходность
Расчет годовой доходности за период меньше годаНезависимо от того, насколько коротким или длинным является фактический период
инвестирования, доходность обычно выражают в годовом или аннуализированном
выражении. Делается это потому, что доходность инвестиций гораздо легче сравнивать,
если их временые периоды приведены к общему знаменателю.
Аннуализированная (т.е. в годовом выражениии) доходность:
rA (1 rper ) N 1
где:
rper = доходность за период
N = количество периодов в год
293. Аннуализированная доходность
Пример 9.8.:Финансовый менеджер располагает следующей информацией:
Инвестиция 1 предлагает доход в размере 5.5% за 120 дней;
Инвестиция 2 предлагает доход в размере 6.2% за 16 недель;
Инвестиция 3 предлагает доход в размере 7.3% за 4 месяца.
Определить доходность в годовом эквиваленте для каждого варианта.
Решение:
rA,1 (1 0.055) 365 / 120 1 17.69%
rA, 2 (1 0.062) 52 / 16 1 21.59%
rA,3 (1 0.073)12 / 4 1 23.54%
294. Номинальная и реальная норма доходности
Номинальная и реальная норма доходностиРеальная норма доходности - ежегодная доходность от инвестиций в процентах, которая
приспособлена к изменениям в ценах из-за инфляции или других внешних эффектов.
Этот метод выражает номинальную норму прибыли в реальном выражении, которая
сохраняет покупательную способность для данного уровня капитала постоянной в
течение долгого времени.
Корректировка номинальной нормы доходности, чтобы дать инвесторам компенсацию за
факторы, такие как инфляция, позволяет инвесторам определять, сколько из их
номинальной доходности они фактически получают.
Пример 9.9.:
Банк выплачивает предприятию 5% в год от фондов, находящихся на его сберегательном
счете. Если уровень инфляции составляет 3% в год, то реальная доходность от
сбережений предприятия приближенно составляет 2%. Другими словами, реальная
ценность сбережений предприятия увеличивается только на 2% за год.
295. Ожидаемая доходность
Ожидаемая доходностьВ сфере инвестирования ожидаемая доходность представляет собой процентную ставку
или сумму, которую инвестор ожидает получить в течение определенного периода
времени от вложений в определенный актив. С практической точки зрения этот
показатель может быть рассчитан исходя из полного набора вероятностей, либо на
основе исторических данных о доходности актива.
Ожидаемая доходность на основе вероятностных данных
В случае, если заранее известен полный набор вероятностей, то есть вероятности всех
возможных вариантов исхода событий, ожидаемую доходность можно рассчитать
использовав следующую формулу:
n
R ( Ri )( Pi )
i 1
где:
Pi – вероятность наступления i-го исхода событий;
Ri – доходность при i-ом исходе событий;
n – количество исходов событий.
296. Ожидаемая доходность
Пример 9.10.:Предположим, что инвестор рассматривает возможность покупки акций нового
предприятия, исторические данные которого недостаточны для прогнозирования
будущей доходности. Инвестор располагает сведениями о четырех возможных
состояниях экономики: ускоренный рост, стабильный рост, небольшой спад и глубокий
спад. Каждое состояние экономики имеет одинаковую вероятность, равную 25%. В
случае ускоренного роста, ожидаемая доходность акции составляет 30%, при
стабильном росте доходность составляет 16%, а при небольшом спаде - 8%. В случае
глубокого спада, прогнозируемые убытки составляют 10%.
Определить ожидаемую доходность на основе вероятностных данных.
Решение:
Событие
Вероятность
Доходность
Взвешенная
доходность
Ускоренный рост
0.25
30%
7.5%
Стабильный рост
0.25
16%
4.0%
Небольшой спад
0.25
8%
2.0%
Глубокий спад
0.25
-10%
-2.5%
Взвешенная сумма =
11.0%
R (0.25)(0.3) (0.25)(0.16) (0.25)(0.08) (0.25)( 0.1) 0.11 11%
297. Ожидаемая доходность
Ожидаемая доходность на основе исторических данныхВ условиях реального финансового рынка инвестор, как правило, принимает решение на
основании имеющейся информации об исторической доходности ценной бумаги.
В этом случае ожидаемая доходность рассчитывается как среднеарифметическое:
n
R
R
i 1
i
n
где:
Ri – доходность ценной бумаги в i-ом периоде;
n – количество наблюдений.
298. Оценка риска
Оценка риска – это количественное измерение величины риска.Понятие риска существует в трех формах:
риск отдельной ценной бумаги;
риск портфеля ценных бумаг (риск совокупности ценных бумаг, находящихся в
собственности данного владельца);
рыночный риск, т. е. риск, свойственный рынку ценных бумаг в целом.
Дисперсия доходности
В статистике дисперсия или вариация является показателем, который используется для
оценки разброса значений случайной величины относительно ее математического
ожидания. В финансовой теории дисперсия доходности является мерой риска,
связанного с инвестированием в определенный актив или портфель активов.
Если известен полный набор вероятностей исхода события, для расчета величины
дисперсии ценной бумаги (напр., акции) используется следующая формула:
n
(R i R) ( Pi )
2
2
i 1
Модель применима для субъективной оценки риска
доходности ценной бумаги и базируется на мнениях
экспертов относительно вероятности развития по тому
или иному сценарию.
где:
Ri – доходность ценной бумаги или актива при i-ом варианте исхода событий;
R – ожидаемая доходность ценной бумаги или актива;
Pi – вероятность i-го варианта исхода событий.
299. Дисперсия доходности
В реальной практике инвестирования обычно доступны исторические данные о доходностиценной бумаги или актива. Если доступен полный массив информации, т.е. дисперсия
оценивается на основании генеральной совокупности данных, необходимо
использовать следующую формулу:
n
2
(R
i 1
i
)2
Модель применима для объективной оценки риска
доходности и базируется на фактических данных
предыдущих периодов
n
где:
Ri – i-ое значение доходности ценной бумаги;
μ – средняя доходность ценной бумаги;
n – количество наблюдений.
Однако чаще оценку риска проводят на основании некоторой выборки из генеральной
совокупности данных. В этом случае формула будет выглядеть следующим образом:
n
s2
(R
i 1
i
R)
n 1
2
Чем выше значение дисперсии, то есть чем выше разброс
доходности актива или портфеля активов относительно
его ожидаемой доходности, тем выше будет уровень
риска. Напротив, низкие значения этого показателя
свидетельствуют о низком уровне риска, связанного с
осуществлением инвестиций.
300. Стандартное отклонение доходности
Стандартное отклонение доходностиСтандартное отклонение (standard deviation) доходности ценных бумаг используется для
оценки меры риска. Стандартное отклонение – квадратный корень от дисперсии.
Если известно точное распределение дискретной случайной величины, а именно, известно
ее значение при каждом исходе и может быть оценена вероятность каждого исхода, то
формула расчета среднеквадратического отклонения будет выглядеть следующим
образом.
n
2
(R
R
)
( Pi )
i
i 1
Модель применима для субъективной оценки риска
доходности ценной бумаги и базируется на мнениях
экспертов относительно вероятности развития по тому
или иному сценарию.
где:
Ri – доходность ценной бумаги или актива при i-ом варианте исхода событий;
R – ожидаемая доходность ценной бумаги или актива;
Pi – вероятность i-го варианта исхода событий.
При этом ожидаемая доходность ценной бумаги или актива рассчитывается по формуле:
n
R ( Ri )( Pi )
i 1
301. Стандартное отклонение доходности
Для оценки риска можно использовать также исторические данные по фактическойдоходности ценной бумаги. Если доступен полный массив исторической информации,
необходимо использовать следующую формулу:
n
(R
i 1
)2
i
n
где:
Ri – i-ое значение доходности ценной бумаги;
μ – средняя доходность ценной бумаги;
n – количество наблюдений.
Если используется не вся генеральная совокупность данных, а только выборка из нее,
стандартное отклонение доходности вычисляется как:
n
s
(R
i 1
i
R)
n 1
2
Стандартное отклонение доходности используется в качестве
меры волатильности. Чем выше его значение, тем выше риск,
связанный с инвестициями в финансовый актив, и наоборот. При
прочих равных параметрах, предпочтение следует отдавать тому
активу, у которого этот показатель будет минимальным.
302. Стандартное отклонение доходности
Пример 9.11.:Вычисление стандартного отклонения доходности на основе вероятностных данных
Инвестор предполагает, что возможная ежегодная доходность по обыкновенной акции
представлена в первых двух колонках таблицы, отображающей вероятностное
распределение ежегодной нормы доходности. Определить ожидаемую доходность и
стандартное отклонение для акции.
Вероятность
варианта исхода
события, Pi
Расчет ожидаемой
доходности
Расчет дисперсии (σ2)
( Ri )( Pi )
( Ri R) 2 ( Pi )
– 0.10
0.05
– 0.005
(– 0.10 – 0.09)2(0.05)
– 0.02
0.10
– 0.002
(– 0.02 – 0.09)2(0.10)
0.04
0.20
0.008
(0.04 – 0.09)2(0.20)
0.09
0.30
0.027
(0.09 – 0.09)2(0.30)
0.14
0.20
0.028
(0.14 – 0.09)2(0.20)
0.20
0.10
0.020
(0.20 – 0.09)2(0.10)
0.28
0.05
0.014
(0.28 – 0.09)2(0.05)
Σ = 1.00
Σ = 0.090 = R
Возможная
доходность, Ri
Σ = 0.00703 = σ2
Стандартное отклонение (σ) = (0.00703)0.5 = 0.0838
303. Стандартное отклонение доходности
Применение стандартного (среднеквадратичного) отклоненияЧем выше стандартное отклонение, тем выше разброс (вариация) доходности и, таким
образом, выше вероятность того, что ожидаемая доходность не будет соответствовать
фактической.
Стандартное отклонение – мера компактности вероятностного распределения. Чем ниже
стандартное отклонение, тем компактнее вероятностное распределение доходности, и,
соответственно, ниже риск финансового актива. Например, применительно к акциям
среднеквадратическое отклонение используется в качестве показателя их
волатильности.
Стандартное отклонение применяется также в оценке вероятности исхода событий,
связанных с доходностью актива. Для этой цели необходимо предположить каким будет
вероятностное распределение доходности.
Вероятностное распределение доходности акций
Доходность акции является непрерывной случайной величиной и подчиняется
нормальному распределению. Нормальное распределение возникает в том случае,
когда на случайную величину оказывает влияние множество факторов, каждый из
которых не имеет определяющего значения.
График кривой нормального распределения (график плотности вероятности) случайной
величины представлен на рис.:
304. Нормальное распределение
Нормальное распределениеГрафик кривой нормального распределения симметричен относительно среднего значения
случайной величины (математическому ожиданию случайной величины). Сама
случайная величина может принимать любые отрицательные и положительные
значения.
Нормальное распределение полностью определяется двумя характеристиками случайной
величины – ее математическим ожиданием и стандартным отклонением. Стандартное
отклонение характеризует степень рассеяния возможных значений случайной
величины вокруг ее среднего значения. Кроме того, оно говорит о вероятности того, что
значение случайной переменной окажется в некотором интервале.
R
305. Правило трех сигм
Правило трех сигмДля нормально распределенной случайной величины, так называемое "правило трех сигм"
говорит о том, что вероятность получить значение случайной переменной в диапазоне
одного стандартного отклонения от ее средней величины равно 68,3%, в диапазоне
двух стандартных отклонений – 95,4%, трех стандартных отклонений – 99,7%. Остается
еще 0,3% вероятности того, что случайная величина примет любое другое значение,
выходящее за рамки отмеченных границ.
Пример 9.12.:
Применение правила трех сигм
Проиллюстрируем данное правило на основе премера 9.11. по расчету стандартного
отклонения (волатильности) акции.
Среднее значение, т.е. математическое ожидание доходности акции равнялось 9%, а
стандартное отклонение доходности в расчете на год – 8.38%.
Согласно правилу трех сигм, инвестор вправе ожидать, что с вероятностью 68,3%
доходность акции через год будет располагаться в интервале от 9% ±8.38%, т.е. от 0.62%
до 17,38%.
С вероятностью 95,4% этот интервал составит 9%±2(8.38%), т.е. от -7.76% до 25.76%.
С вероятностью 99,7% интервал возможной доходности будет равен 9% ±3(8.38%) или
от -16.14% до 34.14%.
Остаются еще 0,3% вероятности того, что акция принесет как гораздо более высокую так и
низкую доходность.
306. Оценка вероятности определенных исходов доходности
Оценка вероятности определенных исходов доходностиИспользуя среднеквадратичное отклонение, можно определить вероятность того, что
фактическая доходность будет больше или меньше определенной величины.
Пример 9.13.:
Используя данные примера 9.11., предположим, что вероятностное распределение
доходности является нормальным, ожидаемая (средняя) доходность составляет 9% и
стандартное отклонение равно 8.38%. Предположим, что необходимо найти
вероятность того, что фактическая будущая доходность будет меньше нуля.
Для начала необходимо найти количество стандартных отклолнений от средней величины
(9%). Для этой цели разницу между двумя величинами равную -9% (т.е. 0% – 9%)
необходимо разделить на стандартное отклонение. Таким образом, результат деления
– 0.09/0.0838 = – 1.07 стандартных отклонений. Также можно применить формулу:
Z
R R
0 0.09
1.07
0.0838
где:
Z = Z-оценка (Z- score)
R = гипотетическая велична доходности
Z-оценка
(стандартная
оценка)
позволяет
определить
меру
отклонения величины от среднего.
307. Стандартное нормальное (Z) распределение
Используем таблицу стандартного нормального (Z) распределения для оценки вероятности того, чтофактическая будущая доходность будет меньше нуля. Исходя из таблицы, P (z < – 1.07) = 0.1423, поэтому,
эта вероятность составляет приблизительно 14%.
Z
-2.4
-2.3
-2.2
-2.1
-2.0
-1.9
-1.8
-1.7
-1.6
-1.5
-1.4
-1.3
-1.2
-1.1
-1.0
-0.9
-0.8
-0.7
-0.6
-0.5
-0.4
-0.3
-0.2
-0.1
-0.0
0.00
0.0082
0.0107
0.0139
0.0179
0.0228
0.0287
0.0359
0.0446
0.0548
0.0668
0.0808
0.0968
0.1151
0.1357
0.1587
0.1841
0.2119
0.2420
0.2743
0.3085
0.3446
0.3821
0.4207
0.4602
0.5000
0.01
0.0080
0.0104
0.0136
0.0174
0.0222
0.0281
0.0351
0.0436
0.0537
0.0655
0.0793
0.0951
0.1131
0.1335
0.1562
0.1814
0.2090
0.2389
0.2709
0.3050
0.3409
0.3783
0.4168
0.4562
0.4960
0.02
0.0078
0.0102
0.0132
0.0170
0.0217
0.0274
0.0344
0.0427
0.0526
0.0643
0.0778
0.0934
0.1112
0.1314
0.1539
0.1788
0.2061
0.2358
0.2676
0.3015
0.3372
0.3745
0.4129
0.4522
0.4920
0.03
0.0075
0.0099
0.0129
0.0166
0.0212
0.0268
0.0336
0.0418
0.0516
0.0630
0.0764
0.0918
0.1093
0.1292
0.1515
0.1762
0.2033
0.2327
0.2643
0.2981
0.3336
0.3707
0.4090
0.4483
0.4880
0.04
0.0073
0.0096
0.0125
0.0162
0.0207
0.0262
0.0329
0.0409
0.0505
0.0618
0.0749
0.0901
0.1075
0.1271
0.1492
0.1736
0.2005
0.2296
0.2611
0.2946
0.3300
0.3669
0.4052
0.4443
0.4840
0.05
0.0071
0.0094
0.0122
0.0158
0.0202
0.0256
0.0322
0.0401
0.0495
0.0606
0.0735
0.0885
0.1056
0.1251
0.1469
0.1711
0.1977
0.2266
0.2578
0.2912
0.3264
0.3632
0.4013
0.4404
0.4801
0.06
0.0069
0.0091
0.0119
0.0154
0.0197
0.0250
0.0314
0.0392
0.0485
0.0594
0.0721
0.0869
0.1038
0.1230
0.1446
0.1685
0.1949
0.2236
0.2546
0.2877
0.3228
0.3594
0.3974
0.4364
0.4761
0.07
0.0068
0.0089
0.0116
0.0150
0.0192
0.0244
0.0307
0.0384
0.0475
0.0582
0.0708
0.0853
0.1020
0.1210
0.1423
0.1660
0.1922
0.2206
0.2514
0.2843
0.3192
0.3557
0.3936
0.4325
0.4721
0.08
0.0066
0.0087
0.0113
0.0146
0.0188
0.0239
0.0301
0.0375
0.0465
0.0571
0.0694
0.0838
0.1003
0.1190
0.1401
0.1635
0.1894
0.2177
0.2483
0.2810
0.3156
0.3520
0.3897
0.4286
0.4681
0.09
0.0064
0.0084
0.0110
0.0143
0.0183
0.0233
0.0294
0.0367
0.0455
0.0559
0.0681
0.0823
0.0985
0.1170
0.1379
0.1611
0.1867
0.2148
0.2451
0.2776
0.3121
0.3483
0.3859
0.4247
0.4641
308. Стандартное нормальное (Z) распределение
Z0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
2.1
2.2
2.3
2.4
0.00
0.5000
0.5398
0.5793
0.6179
0.6554
0.6915
0.7257
0.7580
0.7881
0.8159
0.8413
0.8643
0.8849
0.9032
0.9192
0.9332
0.9452
0.9554
0.9641
0.9713
0.9772
0.9821
0.9861
0.9893
0.9918
0.01
0.5040
0.5438
0.5832
0.6217
0.6591
0.6950
0.7291
0.7611
0.7910
0.8186
0.8438
0.8665
0.8869
0.9049
0.9207
0.9345
0.9463
0.9564
0.9649
0.9719
0.9778
0.9826
0.9864
0.9896
0.9920
0.02
0.5080
0.5478
0.5871
0.6255
0.6628
0.6985
0.7324
0.7642
0.7939
0.8212
0.8461
0.8686
0.8888
0.9066
0.9222
0.9357
0.9474
0.9573
0.9656
0.9726
0.9783
0.9830
0.9868
0.9898
0.9922
0.03
0.5120
0.5517
0.5910
0.6293
0.6664
0.7019
0.7357
0.7673
0.7967
0.8238
0.8485
0.8708
0.8907
0.9082
0.9236
0.9370
0.9484
0.9582
0.9664
0.9732
0.9788
0.9834
0.9871
0.9901
0.9925
0.04
0.5160
0.5557
0.5948
0.6331
0.6700
0.7054
0.7389
0.7704
0.7995
0.8264
0.8508
0.8729
0.8925
0.9099
0.9251
0.9382
0.9495
0.9591
0.9671
0.9738
0.9793
0.9838
0.9875
0.9904
0.9927
0.05
0.5199
0.5596
0.5987
0.6368
0.6736
0.7088
0.7422
0.7734
0.8023
0.8289
0.8531
0.8749
0.8944
0.9115
0.9265
0.9394
0.9505
0.9599
0.9678
0.9744
0.9798
0.9842
0.9878
0.9906
0.9929
0.06
0.5239
0.5636
0.6026
0.6406
0.6772
0.7123
0.7454
0.7764
0.8051
0.8315
0.8554
0.8770
0.8962
0.9131
0.9279
0.9406
0.9515
0.9608
0.9686
0.9750
0.9803
0.9846
0.9881
0.9909
0.9931
0.07
0.5279
0.5675
0.6064
0.6443
0.6808
0.7157
0.7486
0.7794
0.8078
0.8340
0.8577
0.8790
0.8980
0.9147
0.9292
0.9418
0.9525
0.9616
0.9693
0.9756
0.9808
0.9850
0.9884
0.9911
0.9932
0.08
0.5319
0.5714
0.6103
0.6480
0.6844
0.7190
0.7517
0.7823
0.8106
0.8365
0.8599
0.8810
0.8997
0.9162
0.9306
0.9429
0.9535
0.9625
0.9699
0.9761
0.9812
0.9854
0.9887
0.9913
0.9934
0.09
0.5359
0.5753
0.6141
0.6517
0.6879
0.7224
0.7549
0.7852
0.8133
0.8389
0.8621
0.8830
0.9015
0.9177
0.9319
0.9441
0.9545
0.9633
0.9706
0.9767
0.9817
0.9857
0.9890
0.9916
0.9936
309. Коэффициент вариации
Коэффициент вариацииКоэффициент вариации (coefficient of variation) является относительной мерой риска, в
отличие от дисперсии и среднеквадратического отклонения, поэтому позволяет
сопоставлять риск и доходность двух и более активов, которые могут существенно
отличаться. Другими словами, этот показатель увязывает среднеквадратическое
отклонение с ожидаемой доходностью актива, что дает возможность оценить
соотношение риск/доходность в относительном выражении, что позволяет обеспечить
сопоставимость полученных результатов.
Рассчитывается по формуле:
CV / R
где:
σ – среднеквадратическое отклонение случайной величины;
R – ожидаемое (среднее) значение случайной величины.
310. Коэффициент вариации
Пример 9.14.:Историческая доходность акций предприятий А и B за последние пять лет представлена в
таблице. Определить коэффициент вариации для каждой акции и определить какая из
них обладает лучшим соотношением риск/доходность.
Период
Доходность
акции А, %
Доходность
акции B, %
2012
14.75
20.33
2013
7.23
10.85
2014
15.66
5.22
2015
18.45
22.41
2016
12.14
19.23
Решение:
Определим среднюю доходность для каждой акции:
n
RA
R
i 1
n
i
14.75 7.23 15.66 18.45 12.14
13.646%
5
RB 15.608%
311. Коэффициент вариации
При этом среднеквадратическое отклонение доходности для акций Компании A составляет4.236%, а акций Компании B 7.284%:
n
sA
( Ri R) 2
i 1
n 1
(14.75 13.646) 2 (7.23 13.646) 2 (15.66 13.646) 2 (18.45 13.646) 2 (12.14 13.646) 2
5 1
71.79
17.94663 4.236%
5 1
s B 7.284%
Чтобы сопоставить эти ценные бумаги необходимо рассчитать коэффициент вариации
доходности, который для акций Компании А будет равен 0,31, а для акций Компании В
0,47.
CV A
4.236
0.31
13.646
CVB
7.284
0.47
15.608
Акции Компании А обладают лучшим соотношением риск/доходность.
312. Оценка доходности портфеля
Оценка доходности портфеляСпособы оценки доходности и риска инвестиционного портфеля значительно отличаются от
способов оценки доходности и риска отдельно взятого финансового актива.
Владея портфелем, инвестор (институциональный или индивидуальный) в большей степени
заинтересован в оценке риска и доходности портфеля, чем отклонений фактических
значений доходности отдельных ценных бумаг от ожидаемого значения.
Портфель представляет собой определенный набор активов, которые могут включать
акции, облигации, казначейские векселя и т.п.
Ожидаемая доходность портфеля зависит от ожидаемой доходности каждого из активов,
входящих в него.
Ожидаемая доходность портфеля
Ожидаемая доходность портфеля E(Rp) представляет собой суммарную ожидаемую
доходность входящих в него N ценных бумаг, взвешенную с учетом их доли в портфеле:
N
E ( R p ) wi E ( Ri ) w1 E ( R1 ) w2 E ( R2 ) ... wN E ( RN )
i 1
где:
N – количество активов (ценных бумаг), входящих в портфель
wi – удельный вес i-го актива в портфеле
E(Ri) – oжидаемая доходность i-го актива в портфеле
313. Ожидаемая доходность портфеля
Пример 9.15.:Инвестор приобретает актив А на €10,000, актив B на €6,000 и актив C на €4,000. Ожидаемая
доходность актива А равна 10%, В – 14% и C – 6%. Определить ожидаемую доходность
сформированного портфеля.
Решение:
Определим удельный вес каждого актива в портфеле:
10,000
0.5
20,000
6,000
wB
0.3
20,000
4,000
wC
0.2
20,000
wA
Ожидаемая доходность портфеля:
E ( R p ) 0.5(0.1) 0.3(0.14) 0.2(0.06) 0.104 10.4%
314. Риск портфеля
Оценка риска портфеляРиск портфеля ценных бумаг зависит от:
• риска отдельных ценных бумаг, включенных в него;
• корреляции ценных бумаг (синхронности изменения доходности);
• доли инвестирования в каждую ценную бумагу.
Для того чтобы определить риск портфеля ценных бумаг, в первую очередь необходимо
определить степень взаимосвязи и направления изменения доходностей двух активов.
Для оценки синхронности изменения доходности (тесноты связи) используются два
показателя:
• ковариация
• коэффициент корреляции
Коэффициент корреляции более удобен для сравнения различных активов. Его значения
находятся в интервале от —1 до +1.
315. Оценка взаимосвязи доходностей активов портфеля
КовариацияКовариация используется для определения зависимости между доходностью двух
финансовых активов. Используя исторические данные по доходности каждого из
активов, ковариация рассчитывается след. образом:
T
cov1, 2
(R
t 1
t ,1
R1 )( Rt , 2 R2 )
T 1
где:
Rt,1 = доходность актива 1 в t-ом периоде;
Rt,2 = доходность актива 2 в t-ом периоде;
R1 = ожидаемая (средняя) доходность актива 1;
R2 = ожидаемая (средняя) доходность актива 2;
T = количество наблюдений
Значение коэффициента ковариации может быть как отрицательным, так и
положительным. Его отрицательное значение говорит о том, что доходности
финансового актива 1 и финансового актива 2 демонстрируют разнонаправленное
движение. Другими словами, если доходность финансового актива 1 будет расти, то
доходность финансового актива 2 будет падать, и наоборот. Положительное значение
свидетельствует о том, что доходности финансовых активов изменяются в одном
направлении.
316. Оценка взаимосвязи доходностей активов портфеля
КорреляцияВ статистике коэффициент корреляции используется для проверки гипотезы о
существовании зависимости между двумя случайными величинами, а также позволяет
оценить ее силу.
Коэффициент корреляции более удобен для сравнения различных активов. Его значения
находятся в интервале от —1 до +1. Его отрицательное значение говорит о том, что
между переменными наблюдается обратная взаимосвязь. Положительное значение
свидетельствует о прямой взаимосвязи, то есть, если доходность актива 1 будет расти,
доходность актива 2 также будет расти, и наоборот.
Коэффициент корреляции является стандартизированной мерой зависимости между
доходностью двух финансовых активов:
r1, 2
cov1, 2
s1 s 2
где:
cov1,2 = ковариация между двумя активами
s1 = стандартное отклонение актива 1;
s2 = стандартное отклонение актива 2.
317. Оценка взаимосвязи доходностей активов портфеля
Пример 9.16.:Информация об исторической доходности двух активов представлена в таблице:
Год
Доходность актива 1
Доходность актива 2
2011
0.200
0.100
2012
0.100
0.150
2013
– 0.150
– 0.050
2014
– 0.200
0.100
2015
0.050
0.050
2016
0.100
0.200
Определить среднюю доходность, дисперсию, ковариацию и коэффициент корреляции для
каждого актива.
318. Оценка взаимосвязи доходностей активов портфеля
Решение:Год
Доходность
актива 1,
Rt ,1
Доходность
актива 2,
Rt , 2
Rt ,1 R1
Rt , 2 R2
( Rt ,1 R1 )( Rt , 2 R2 )
2011
0.200
0.100
0.183
0.008
0.002
2012
0.100
0.150
0.083
0.058
0.005
2013
– 0.150
– 0.050
– 0.167
– 0.142
0.024
2014
– 0.200
0.100
– 0.217
0.008
– 0.002
2015
0.050
0.050
0.033
– 0.042
– 0.001
2016
0.100
0.200
0.083
0.108
0.009
Сумма
0.100
0.550
Актив 1:
Определим среднюю доходность:
T
R1
R
t 1
T
t ,1
0 .1
1.67%
6
0.036
319. Оценка взаимосвязи доходностей активов портфеля
Определим дисперсию и стандартное отклонение доходности актива 1:T
s12
(R
t
t 1
R1 ) 2
T 1
[(0.183) 2 (0.083) 2 ( 0.167) 2 ( 0.217) 2 (0.033) 2 (0.083) 2 ]
s
0.0247
(6 1)
2
1
s1 0.0247 0.1572
Актив 2:
T
R2
R
t 1
T
t ,2
0.55
9.17%
6
[(0.008) 2 (0.058) 2 ( 0.142) 2 (0.008) 2 ( 0.042) 2 (0.108) 2 ]
s
0.0074
(6 1)
2
2
s2 0.0074 0.0860
320. Оценка взаимосвязи доходностей активов портфеля
Определим ковариацию и коэффицент корреляции доходности для активов 1 и 2:T
cov1, 2
r1, 2
(R
t 1
cov1, 2
s1 s2
t ,1
R1 )( Rt , 2 R2 )
T 1
0.036
0.0072
(6 1)
0.0072
0.5326
(0.1572)(0.0860)
Так как r1,2 > 0, доходности активов положительно коррелируют, т.е. им характерна прямая
взаимосвязь.
321. Оценка взаимосвязи доходностей активов портфеля
Пример 9.17.:Предположим, что даны три возможных прогноза экономического состояния — подъем,
нормальное состояние и рецессия. Доходности по акциям А и B в зависимости от
состояния экономики и вероятности вариантов прогноза представлены в таблице.
Стандартное отклонение доходности для акции А составляет 0.351, а для акции B —
0.57.
Определить ковариацию и коэффициент корреляции доходностей по акциям на основе
вероятностных данных.
Состояние
Вероятность состояния, P(S)
RA
RB
Подъем
0.25
0.04
0.02
Нормальное
0.36
0.08
0.01
Рецессия
0.39
0.01
0.04
Σ(P) = 1.0
322. Оценка взаимосвязи доходностей активов портфеля
Решение:Сначала oпределим ожидаемую доходность каждой акции:
E ( R A ) (0.25)(0.04) (0.36)(0.08) (0.39)(0.01) 0.0427
E ( RB ) (0.25)(0.02) (0.36)(0.01) (0.39)(0.04) 0.0242
Состояние
P(S)
RA
RB
P(S) [RA – E(RA)] [RB – E(RB)]
Подъем
0.25
0.04
0.02
(0.25)(0.04–0.0427)(0.02–0.0242) = 0.00000284
Нормальное
0.36
0.08
0.01
(0.36)(0.08–0.0427)(0.01–0.0242) = –0.000191
Рецессия
0.39
0.01
0.04
(0.39)(0.01–0.0427)(0.04–0.0242) = –0.000201
Определим ковариацию и коэффицент корреляции:
cov A, B 0.00000284 ( 0.000191) ( 0.000201) 0.000389
A, B
0.000389
0.00195
(0.351)(0.57)
Так как ρA,B ≈ 0, доходности акций А и В не коррелируют.
323. Оценка риска портфеля
Взаимосвязь между риском портфеля и риском входящих в него активов носит болеесложный характер и не описывается формулой средней арифметической.
Необходимо дополнительно оценить взаимосвязь доходностей активов портфеля с
помощью ковариации и коэффициента корреляции. Формула для оценки риска
портфеля, состоящего из n активов, имеет следующий общий вид:
P
2
P
n
w
i 1
2
i
n
2
i
n
wi w j covi , j
i j
i 1 j 1
Для портфеля состоящего из двух активов формула существенно упрощается и имеет
следующий вид:
P w12 12 w22 22 2w1 w2 cov1, 2
где:
w1 = доля актива 1 в портфеле
w2 = доля актива 2 в портфеле
σ1= среднеквадратическое отклонение актива 1
σ2= среднеквадратическое отклонение актива 2
cov1,2 = ковариация доходностей актива 1 и актива 2
ρ1,2 = корреляция доходностей актива 1 и актива 2
cov1, 2 1, 2 1 2
324. Оценка риска портфеля
Диверсификация портфеляДиверсификация инвестиционного портфеля — это способ снижения рискa портфеля с
помощью включения в портфель не связанных друг с другом активов. Если в портфеле
много различных активов, то даже сильное падение какого-то одного актива, например,
акции одной компании, не сильно отразится на общей стоимости портфеля и прибыли.
Наилучший результат (максимально возможное сокращение значения риска) дает
включение в портфель активов с наибольшей отрицательной корреляцией.
Влияние корреляции на риск портфеля
Из вышеуказанной формулы очевидно, что если доходности активов отрицательно
коррелируют (ρ1,2 < 0), стандартное отклонение (риск) портфеля ниже, при всех равных
условиях.
Если ρ1,2 = 0, риск портфеля выше, чем при отрицательной корреляции.
Если ρ1,2 > 0, риск портфеля выше, чем при отсутствии корреляции.
Если ρ1,2 = 1, диверсификация портфеля не обеспечивается.
Отсюда следует, что снижение риска при диверсификации портфеля тем больше, чем ниже
корреляция между активами входящими в портфель.
На практике наибольшее снижение риска достигается включением в портфель
инструментов с разных рынков – облигации, акции, товары, валюты.
325. Оценка риска портфеля
Пример 9.18.:Ожидаемая доходность, удельный вес в портфеле, дисперсия и среднеквадратическое
отклонение доходностей активов А и В представлены в таблице:
Актив
E(R)
Удельный вес
σ2
σ
A
0.10
0.5
0.0081
0.09
B
0.05
0.5
0.0049
0.07
При неизменном удельном весе активов, определим риск инвестиционного портфеля при
заданных коэффициентах корреляции от -1 до +1. Результаты представим в таблице:
Сценарий
ρA,B
σP
a
–1
0.01
b
– 0.5
0.0409
c
0
0.057
d
0.5
0.0695
e
1
0.08
Очевидно, что при увеличении коэффициента корреляции стандартное отклонение (риск)
портфеля увеличивается.
326. Оценка риска портфеля
Пример 9.19.:Продолжим пример 9.18. Теперь предположим, что коэффициент корреляции останется
неизменым и будет равным нулю (ρA,B = 0). Определим риск инвестиционного
портфеля, изменяя доли активов в портфеле.
Портфель
wA
wB
E(RP)
σP
f
0
1
0.05
0.07
g
0.25
0.75
0.0625
0.0571
h
0.5
0.5
0.075
0.057
i
0.75
0.25
0.0875
0.0697
j
1
0
0.1
0.09
Доходность, Е(Rp)
0,12
0,1
i
0,08
Используя активы, корреляция
доходностей которых ниже +1,
можно сформировать портфели,
риск которых ниже риска
отдельных
активов.
Такими
являются портфели g, h и i.
j
h
0,06
g
f
0
0,04
0,02
Риск, σp
0
0
0,02
0,04
0,06
0,08
0,1
327. Оценка риска портфеля
При корреляции доходностей активов равной -1, теоретически возможным являетсядальнейшее снижение риска портфеля до 0, варьируя удельные веса активов.
Доходность, Е(Rp)
0,12
0,1
0,08
0,06
1
0,04
0,02
Риск, σp
0
0
0,02
0,04
0,06
0,08
0,1
Однако при корреляции равной +1, возможные портфели из комбинаций двух активов
будут располагаться на отрезке прямой линии.
0,12
0,1
0,08
1
0,06
0,04
0,02
Риск, σp
0
0
0,02
0,04
0,06
0,08
0,1
328. Систематический риск
Систематический рискСистематический (рыночный) риск (systematic risk, market risk) — риск, связанный с
изменениями
конъюнктуры
всего
финансового
рынка
под
влиянием
макроэкономических факторов. Он возникает для всех участников этого рынка и не
может быть устранен путем диверсификации инвестиционного портфеля, т.к. в
процессе колебаний конъюнктуры всего финансового рынка уровень цен отдельных
финансовых инструментов изменяется аналогично рыночному индексу в целом.
Систематический риск означает, что выигрыши или убытки, происходящие от
потенциальных рисков, произойдут скорее одновременно для всего портфеля в целом,
а не для отдельного вида актива. Поэтому невозможно снизить систематический риск
посредством диверсификации портфеля. Потери, происходящие в связи с общими
экономическими условиями, представляют собой систематический риск, потому что
они воздействуют на все компании, находящиеся на рынке, одновременно.
329. Источники систематического риска
Источники систематического рискаСистематический риск возникает из внешних событий, которые влияют на рынок в целом, и
включает в себя следующие виды рисков:
риск изменения процентной ставки — риск, связанный с изменением процентной ставки
центральным банком страны. При снижении процентной ставки уменьшается стоимость
кредитов, которые получают компании, и увеличивается рост их прибыли, что является
благоприятным и перспективным для рынка ценных бумаг и деловой конъюнктуры в
целом. И наоборот, увеличение процентной ставки негативно влияет на рынок;
инфляционный риск — этот вид риска вызывается ростом инфляции. Он уменьшает
реальную прибыль компаний, что отрицательно влияет на рынок, а также вызывает
возникновение другого риска — риска изменения процентной ставки, т.к. уровень
процентной ставки должен как минимум компенсировать размер инфляции;
валютный риск — риск, возникающий в силу политических и экономических факторов,
происходящих в стране;
политический риск — это угроза отрицательного воздействия на рынок из-за
политических действий (смены правительства, войны и т.д.).
330. Несистематический риск
Несистематический рискНесистематический (диверсифицируемый) риск (unsystematic risk, diversifiable risk) — риск,
который может быть вызван событиями, специфическими для фирмы, например:
забастовки,
техногенная катастрофа,
провал нового продукта,
неумелые действия менеджмента,
успехи или неудача в реализации маркетинговых программ;
получение прибыли или убытков от основной деятельности;
открытие судебного процесса
Поскольку события, относящиеся к отдельной фирме (или отрасли), носят случайный
характер, их воздействие на инвестиционный портфель можно устранить с помощью
диверсификации (плохое положение дел в одной компании компенсируется хорошим
финансовым состоянием другой).
Систематический (недиверсифицируемый или рыночный) риск появляется под
воздействием таких событий общего характера, как экономический спад, увеличение
процентных ставок, инфляция, которые влияют на состояние дел любой фирмы и,
следовательно, не могут быть устранены через диверсификацию.
331. Общий риск в сравнении с систематическим риском
Общий рискОбщий риск представляет собой риск отдельно взятого актива. Общий риск актива
измеряется дисперсией возможных значений доходности относительно их средней
величины. Чем выше этот разброс, тем выше вероятность того, что фактическая
доходность окажется ниже ожидаемой, и, следовательно, тем выше риск этого актива.
Общий риск является релевантным измерителем рискa актива, рассматриваемого
изолированно. При обьединении активов в портфели релевантным является рыночный
(систематический) риск.
Понятие релевантного риска
Рациональные инвесторы предпочитают объединять ценные бумаги в портфель, так как это
приводит к снижению риска (эффект диверсификации), поэтому цена финансового
актива (напр., акции и облигации) рассматривается исходя из систематического, а не
общего риска.
Например, если инвестор владеет портфелем, состоящим из большого числа акций, на первый план выдвигается
проблема агрегированного риска портфеля акций, поскольку потери по одним акциям могут компенсироваться
получением дохода по другим. В данной ситуации релевантный риск акции - это ее систематический риск, на
который оказывает воздействие ее общий риск, а также корреляция между доходностью данной акции и
доходностью всего портфеля ценных бумаг.
332. Элементы общего риска
Ключевые компоненты общего рискаОбщий риск актива включает в себя специфический для компании (диверсифицируемый)
риск, который можно устранить с помощью диверсификации, и рыночный
(систематический) риск, который нельзя устранить диверсификацией:
Общий риск = диверсифицируемый риск + рыночный риск
Зависимость риска портфеля от степени диверсификации
Риск портфеля уменьшается по мере увеличения количества активов. Степень воздействия
добавления новых активов на снижение риска портфеля зависит от уровня корреляции
между отдельными активами: чем меньше значение коэффициента корреляции, тем
ниже риск крупного портфеля.
Теоретически при помощи диверсификации можно полностью устранить специфические
для компании риски путем включения в портфель множества активов разного вида. В
результате совокупный риск полностью диверсифицированного портфеля будет
определяться только величиной рыночного риска (см. рис.).
По этой причине только рыночный риск является релевантным для рационального
инвестора, так как не может быть устранен при помощи диверсификации.
333. Элементы общего риска
Риск, σДиверсифицируемый риск
Общий
риск
Рыночный риск
Число активов, n









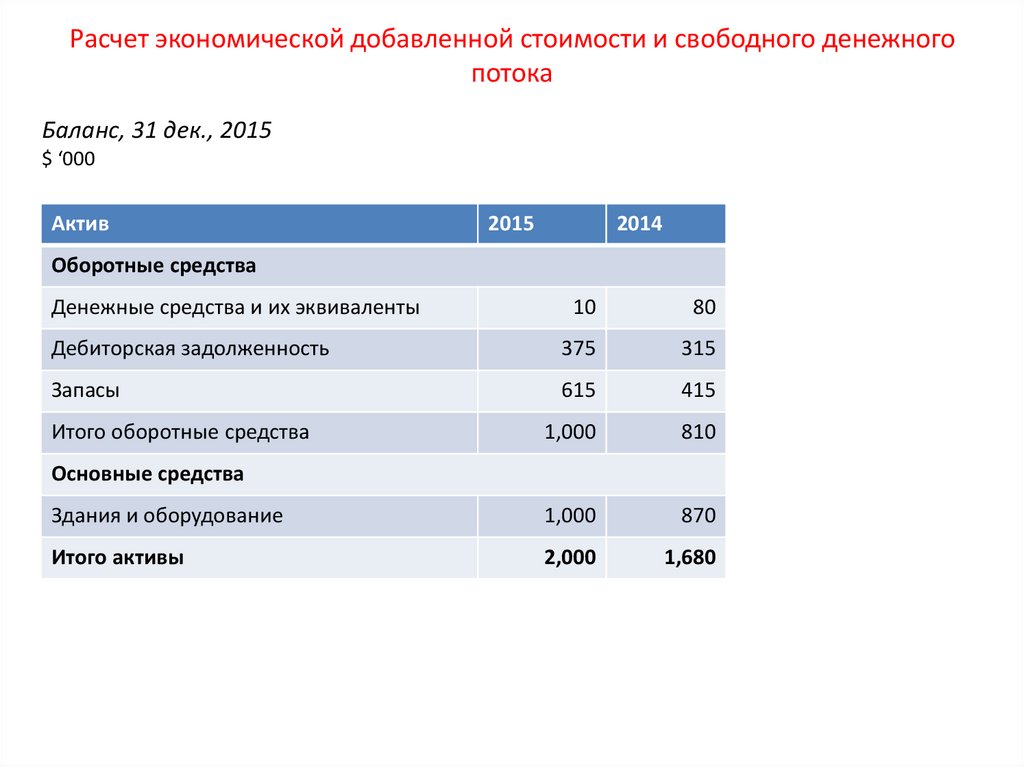
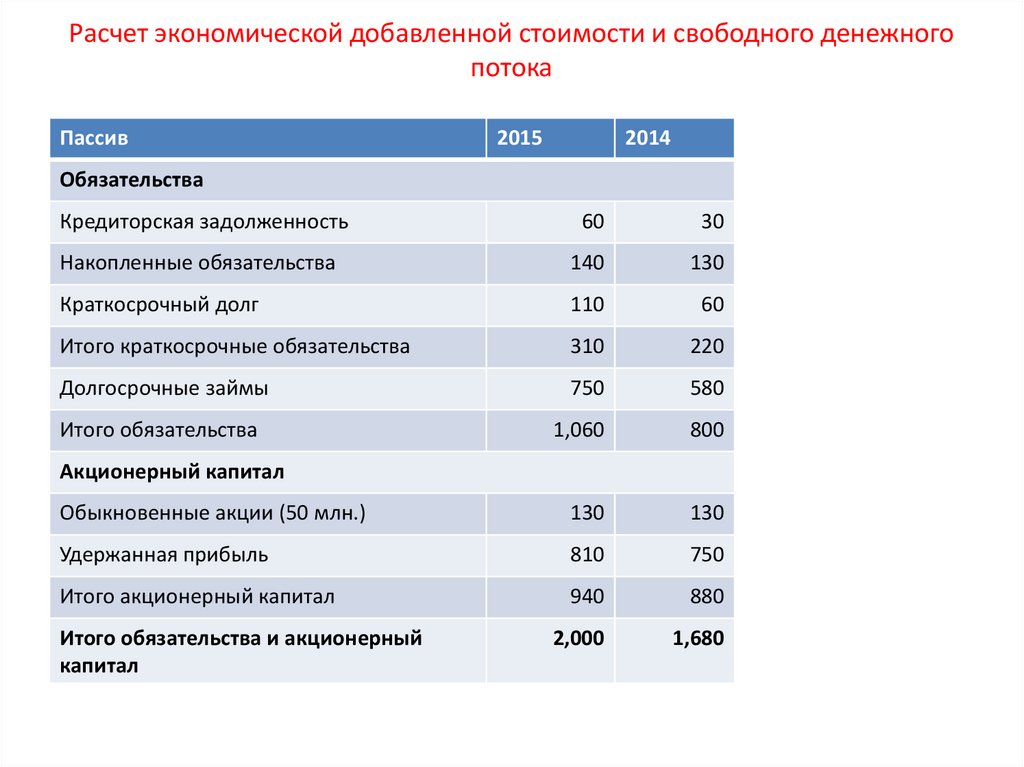
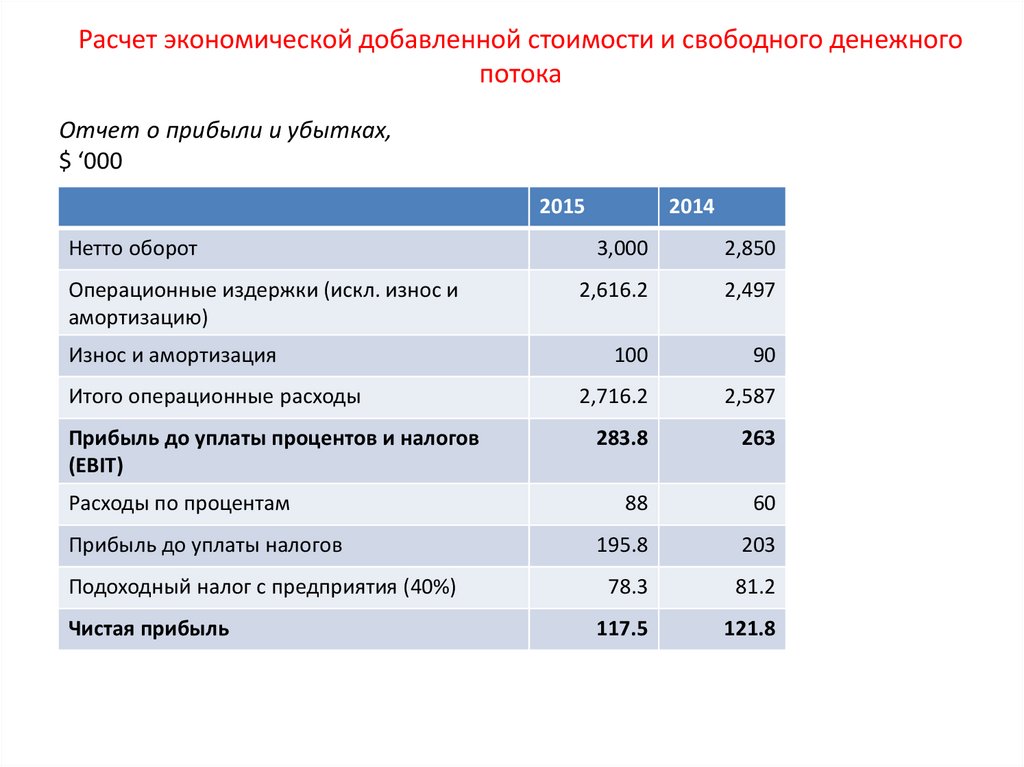

















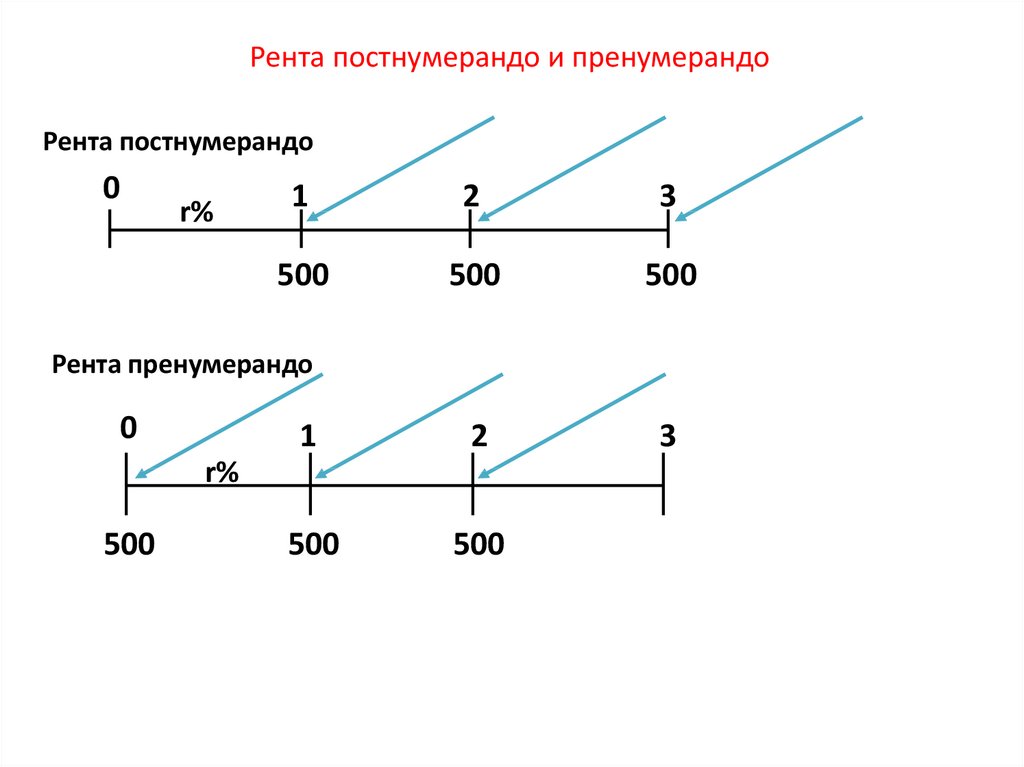
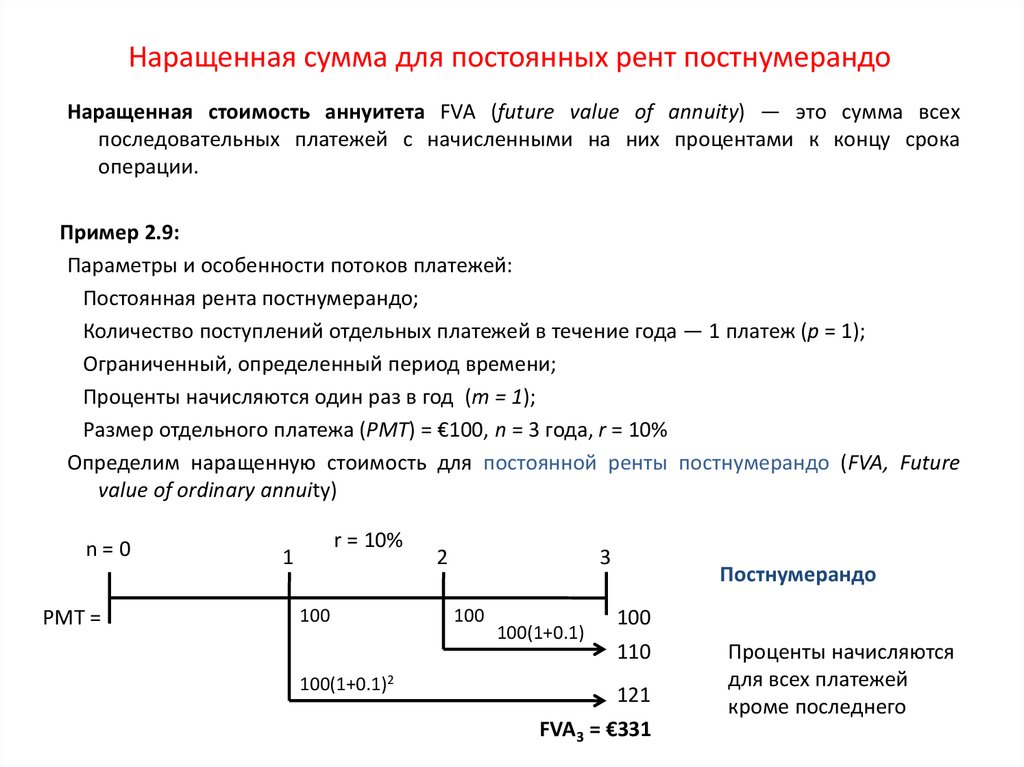













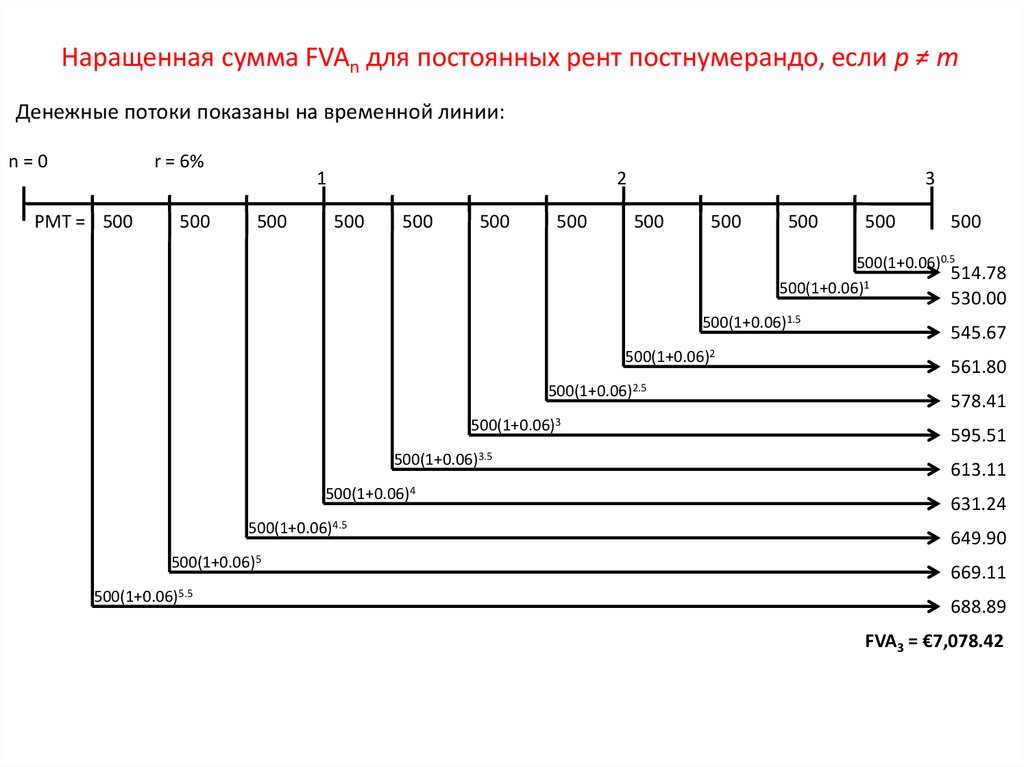




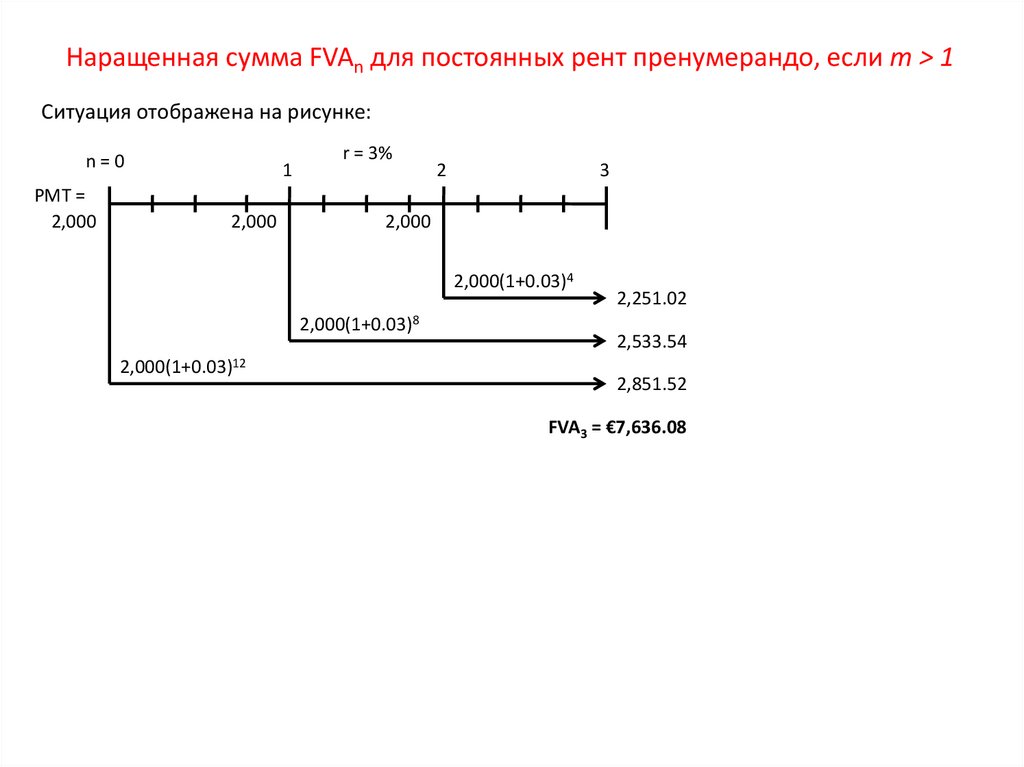


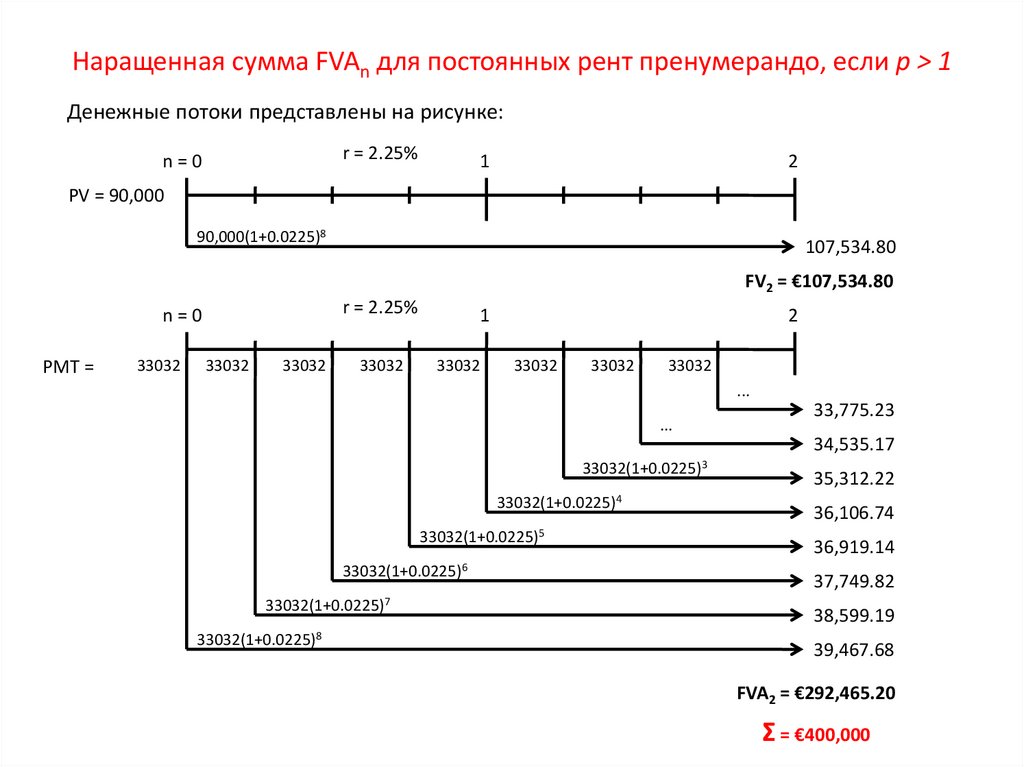





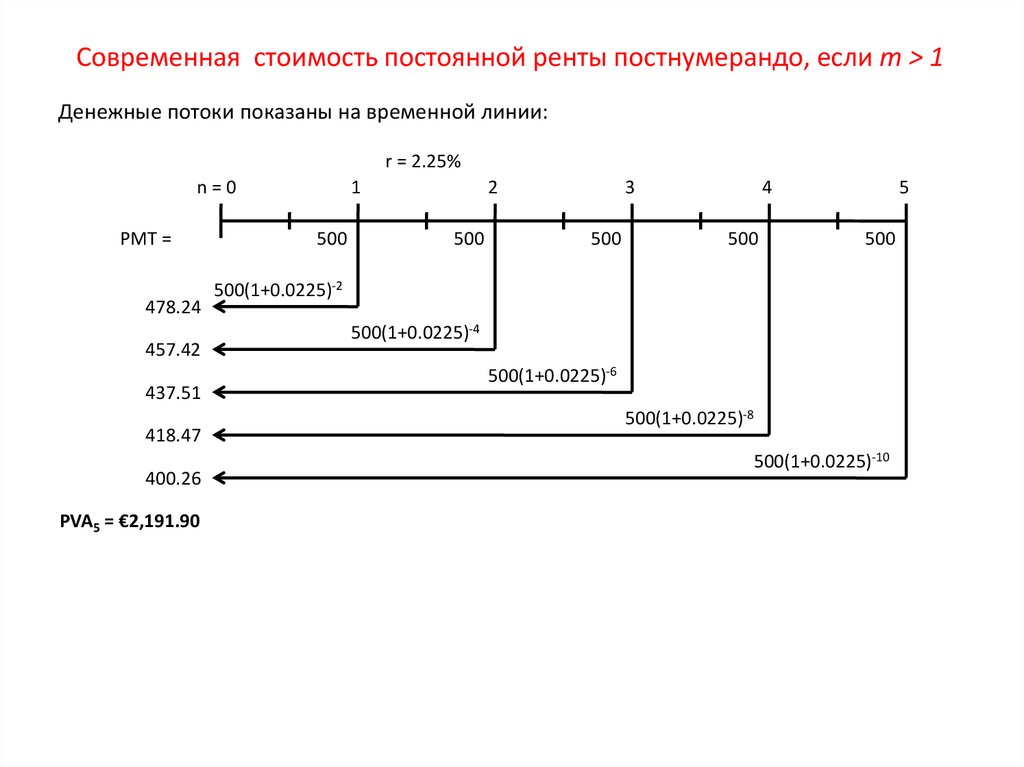

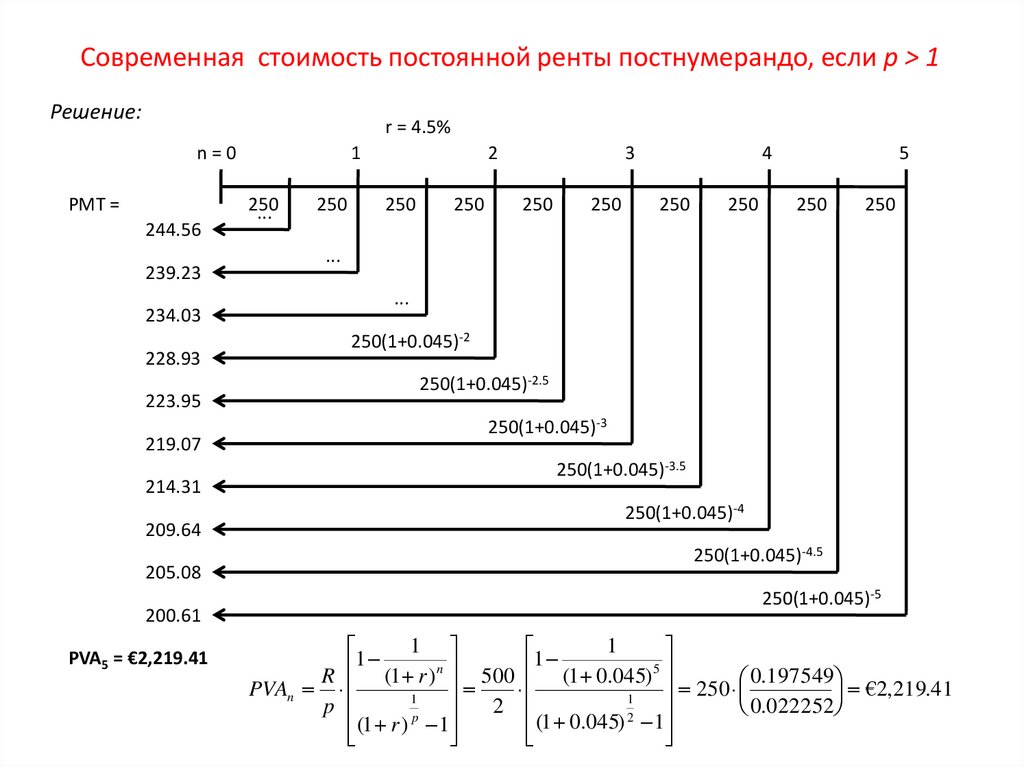





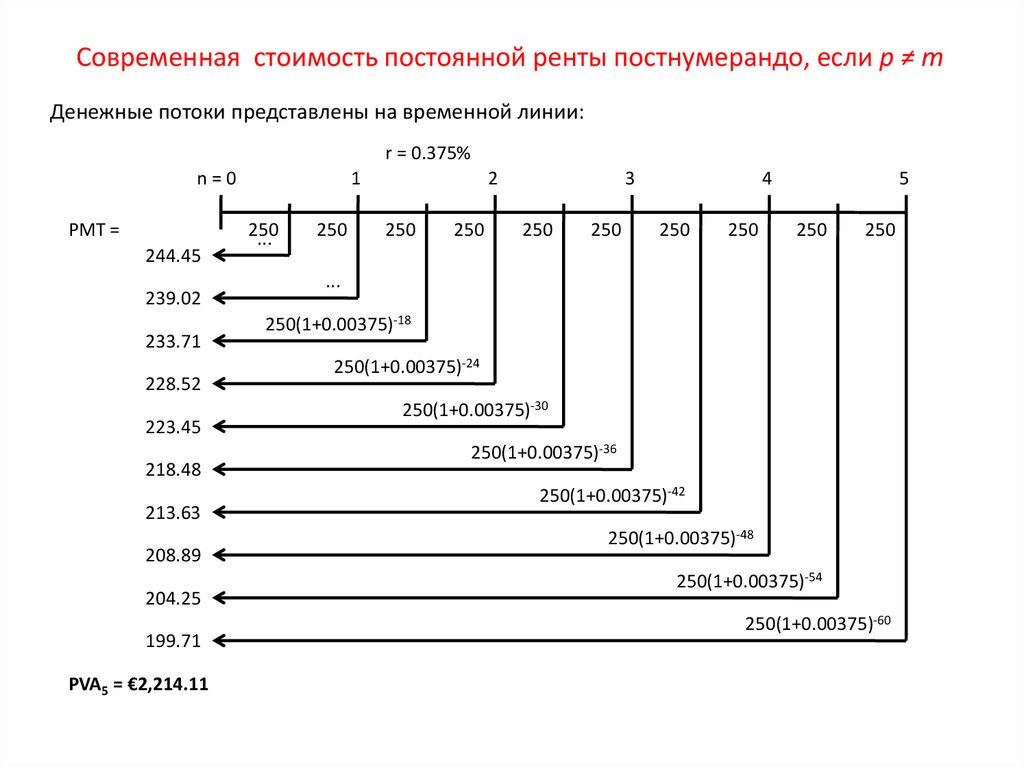



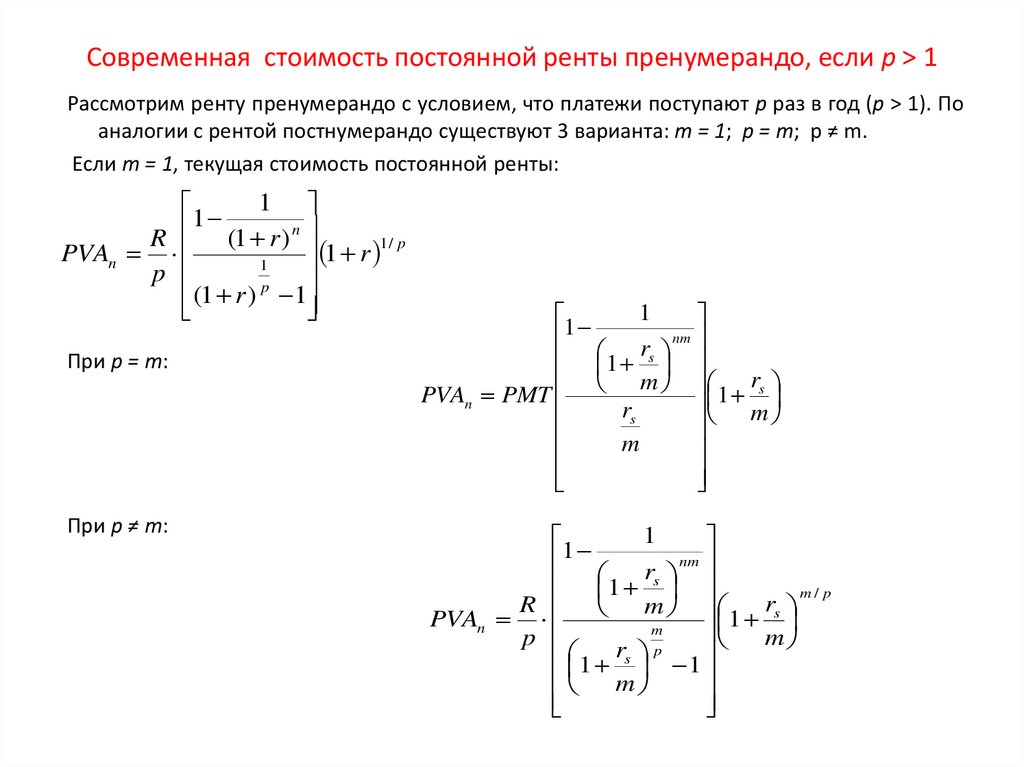


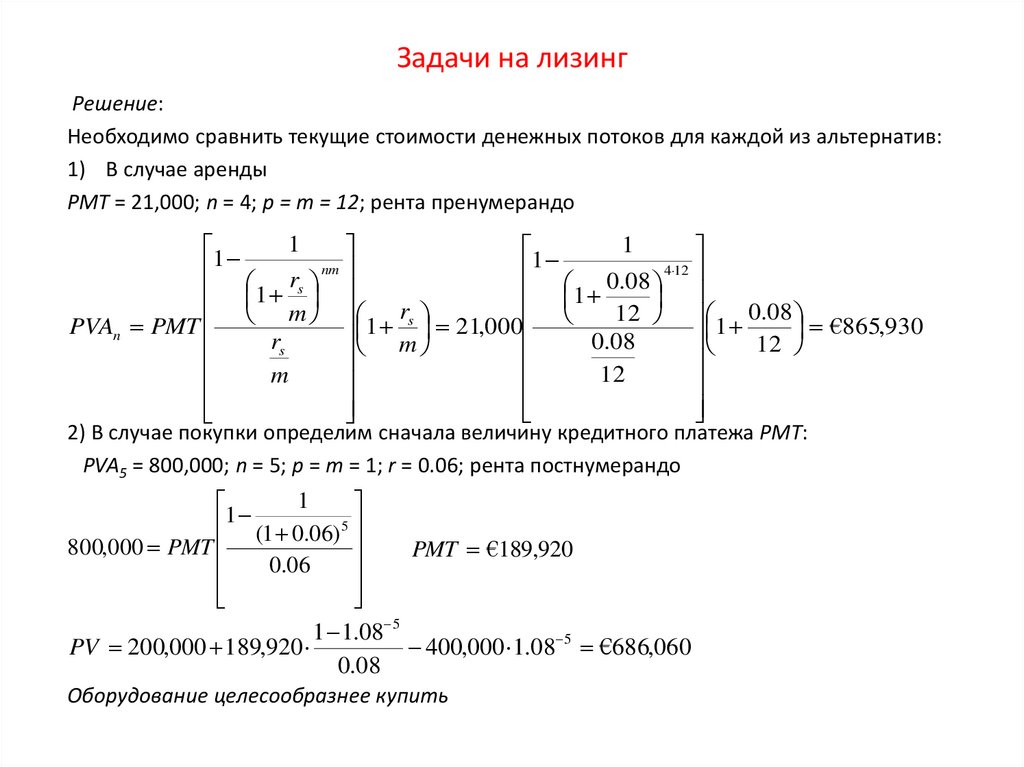





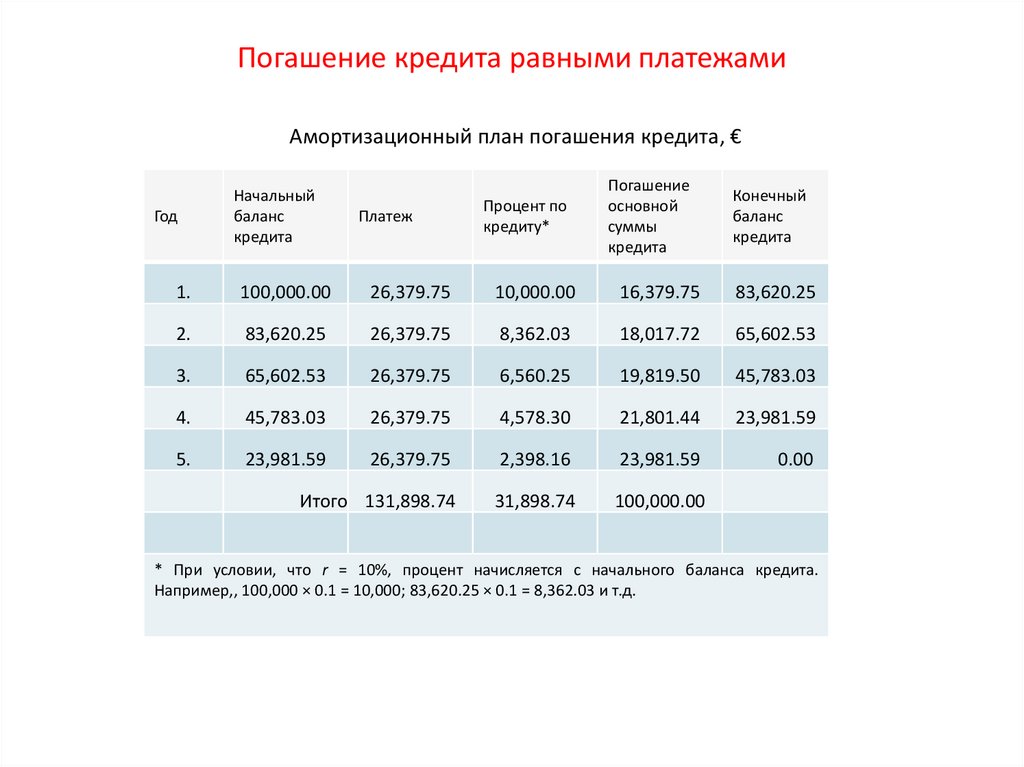

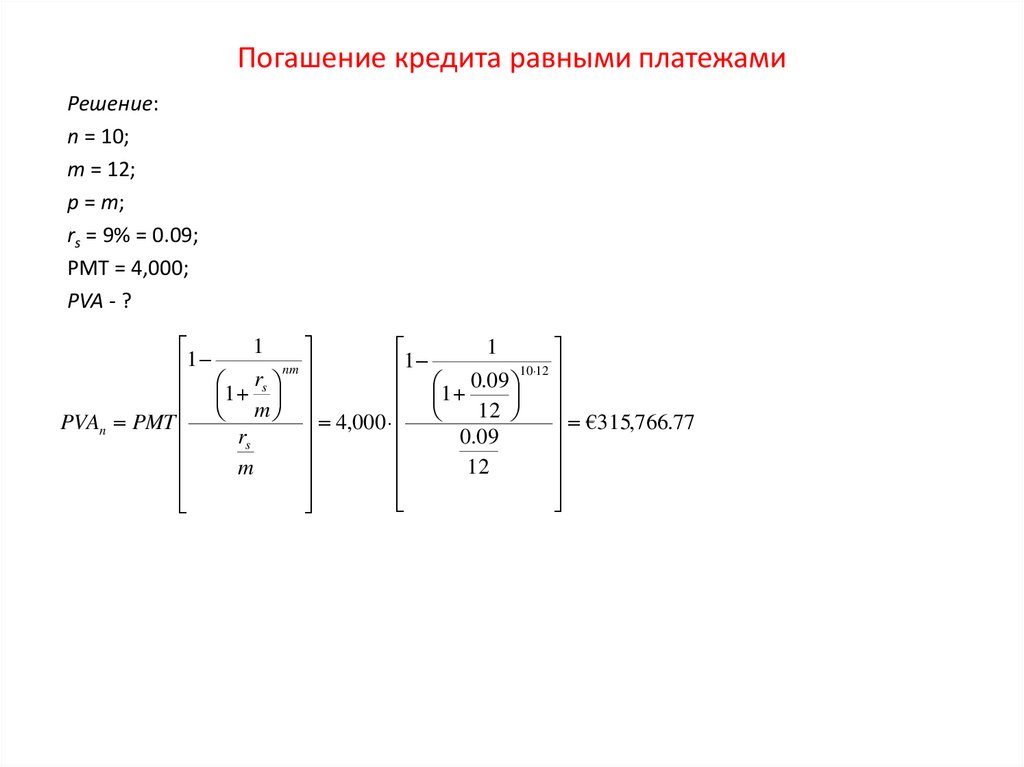



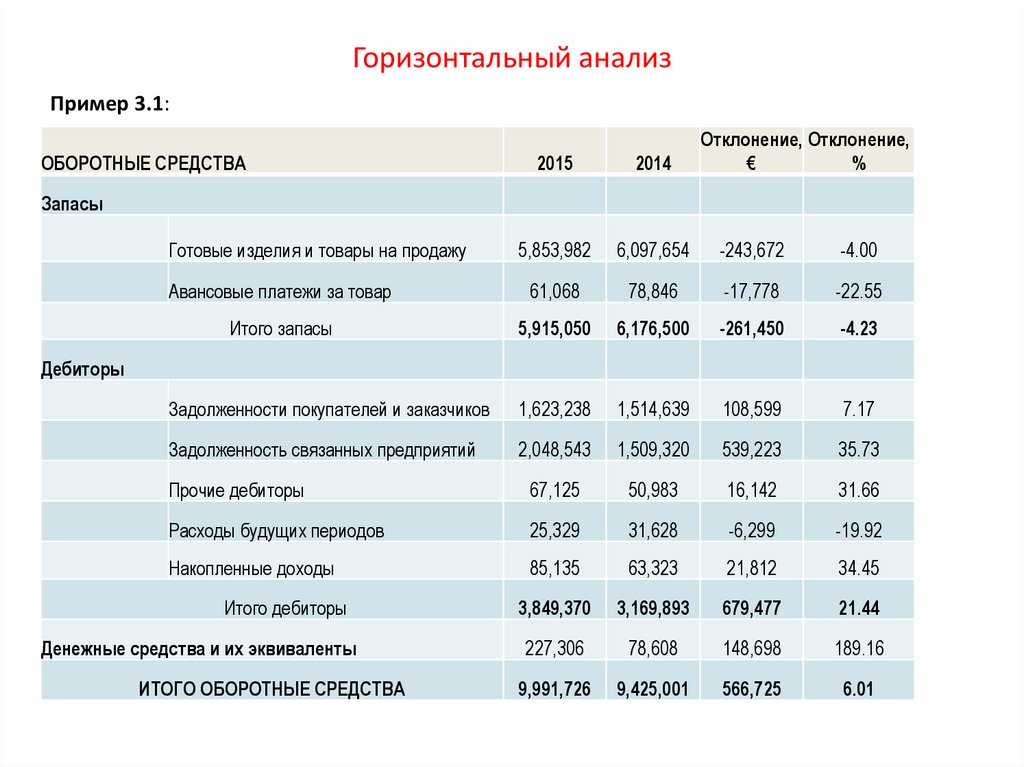
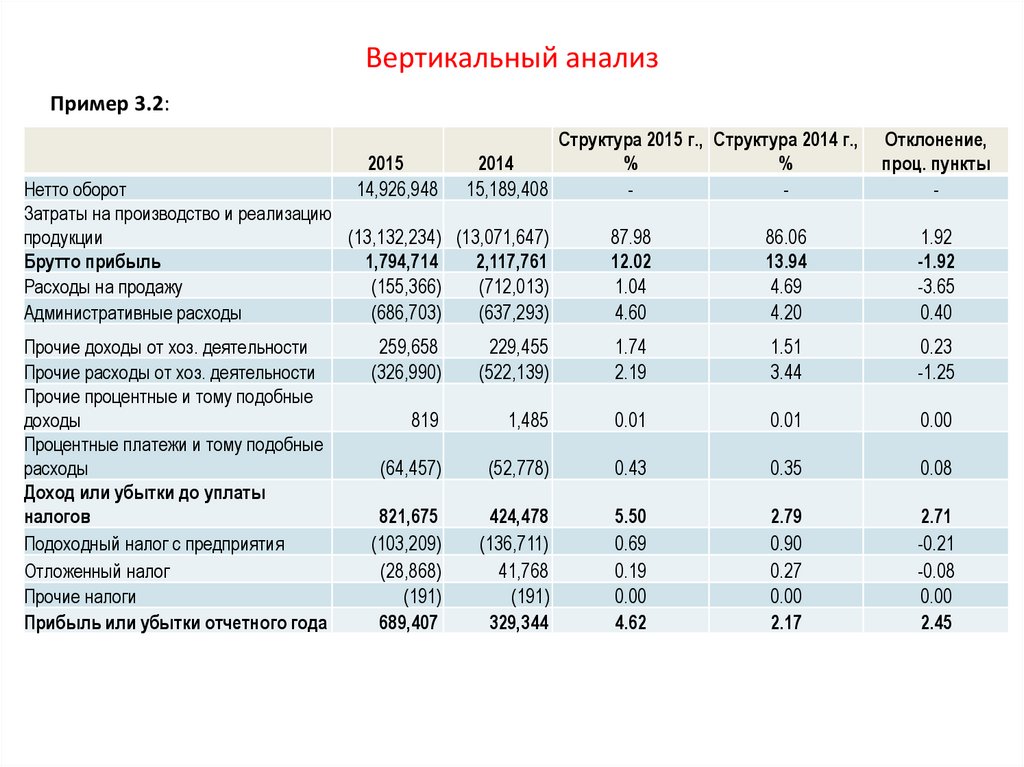


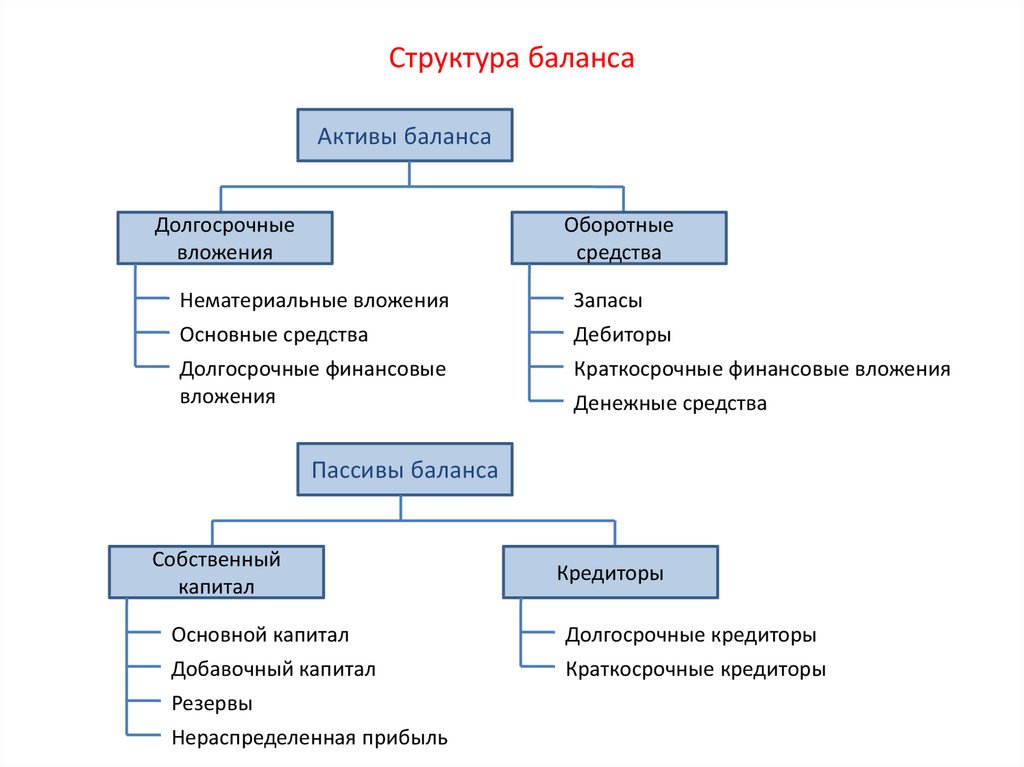




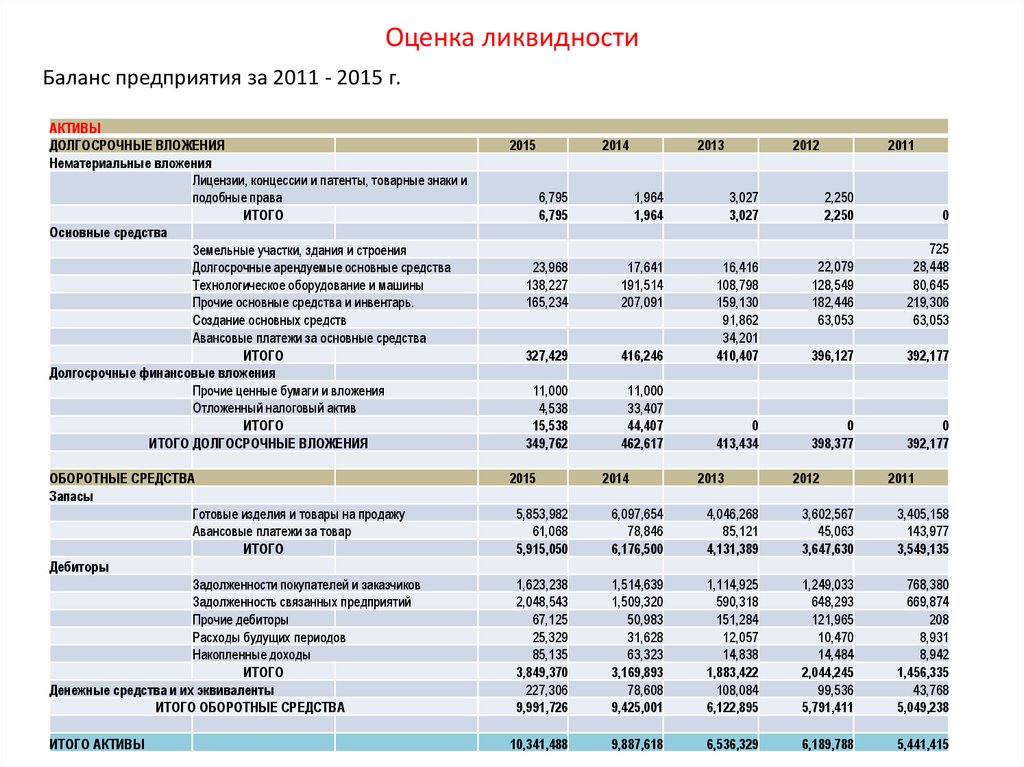
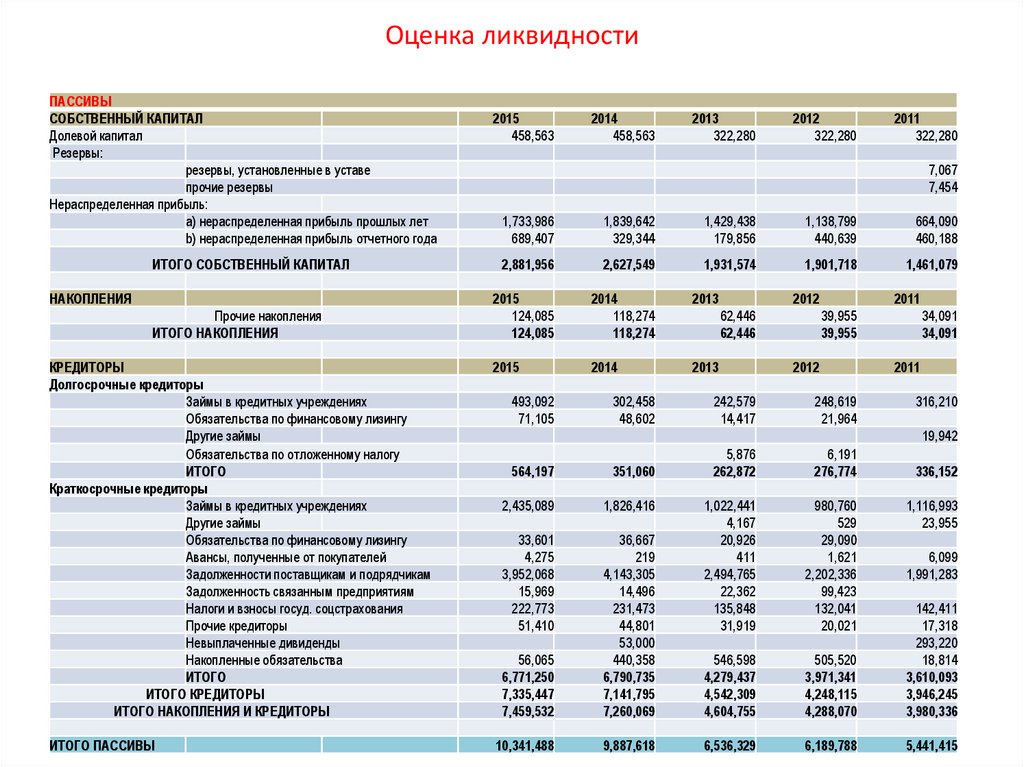
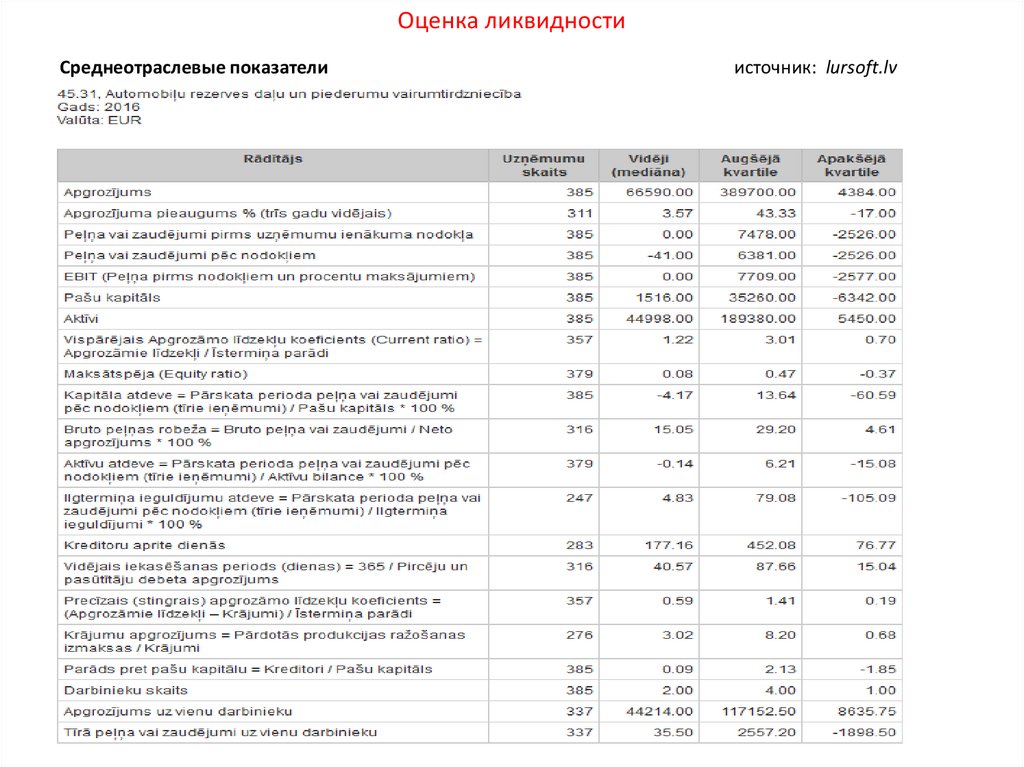
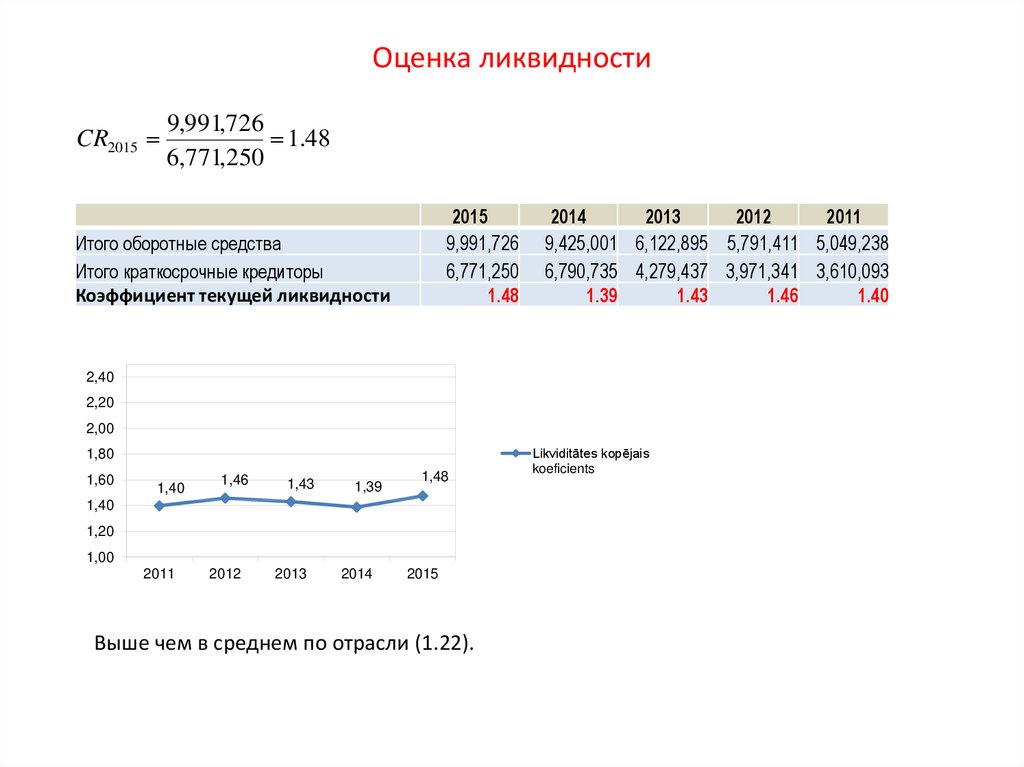
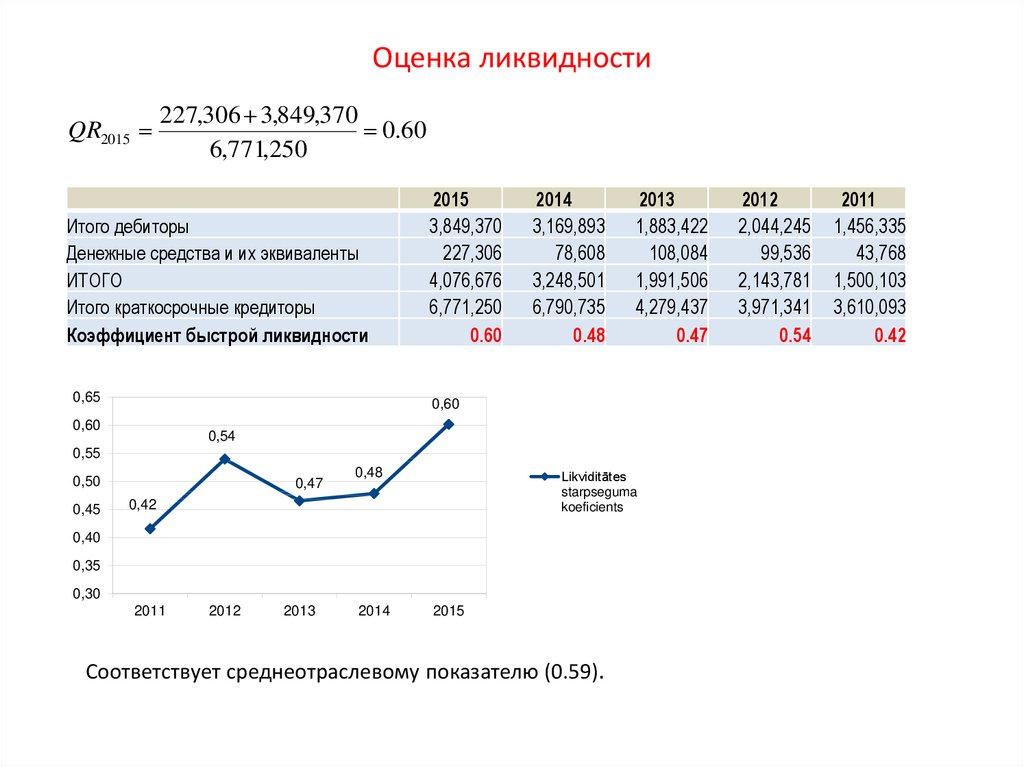
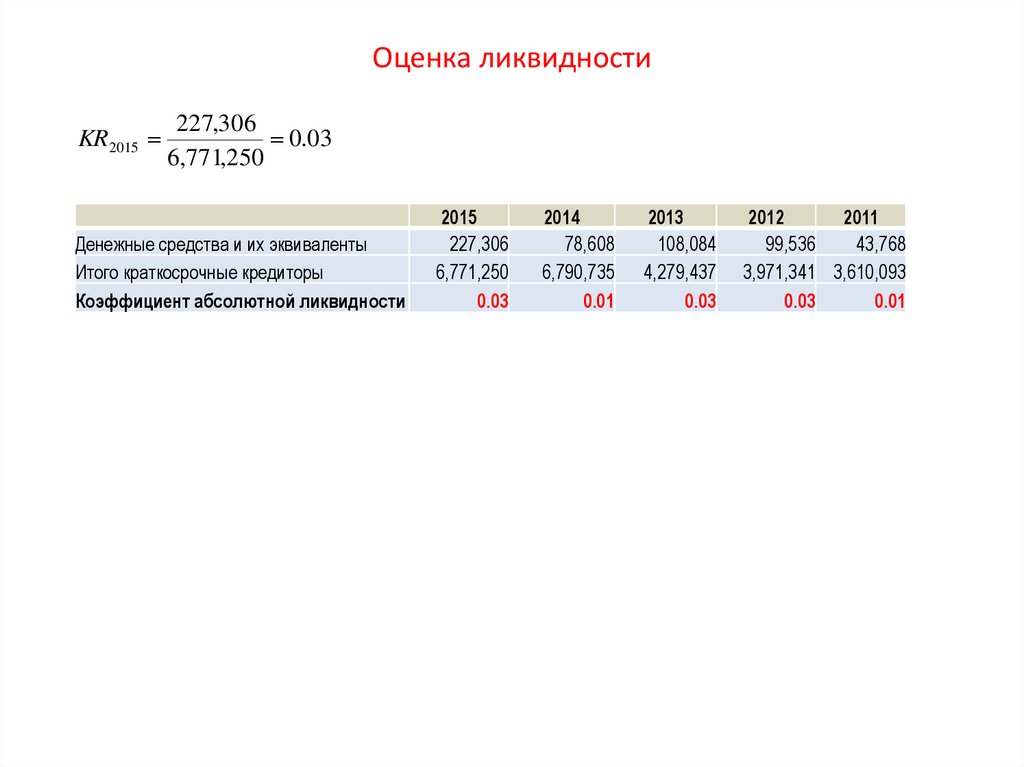





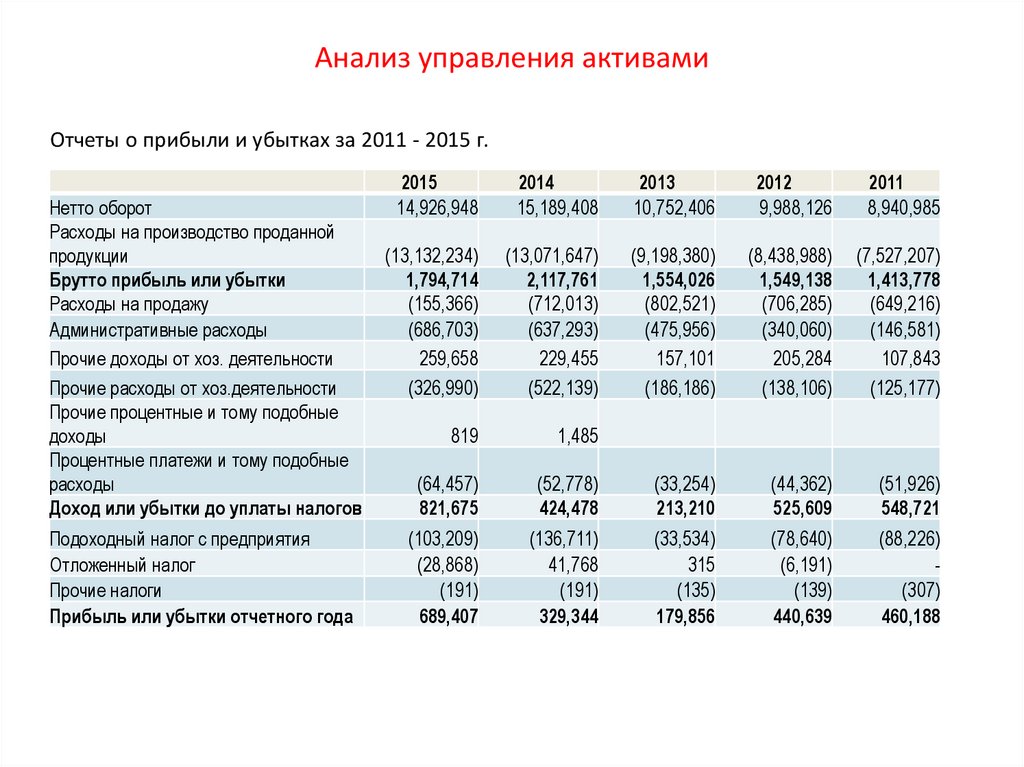
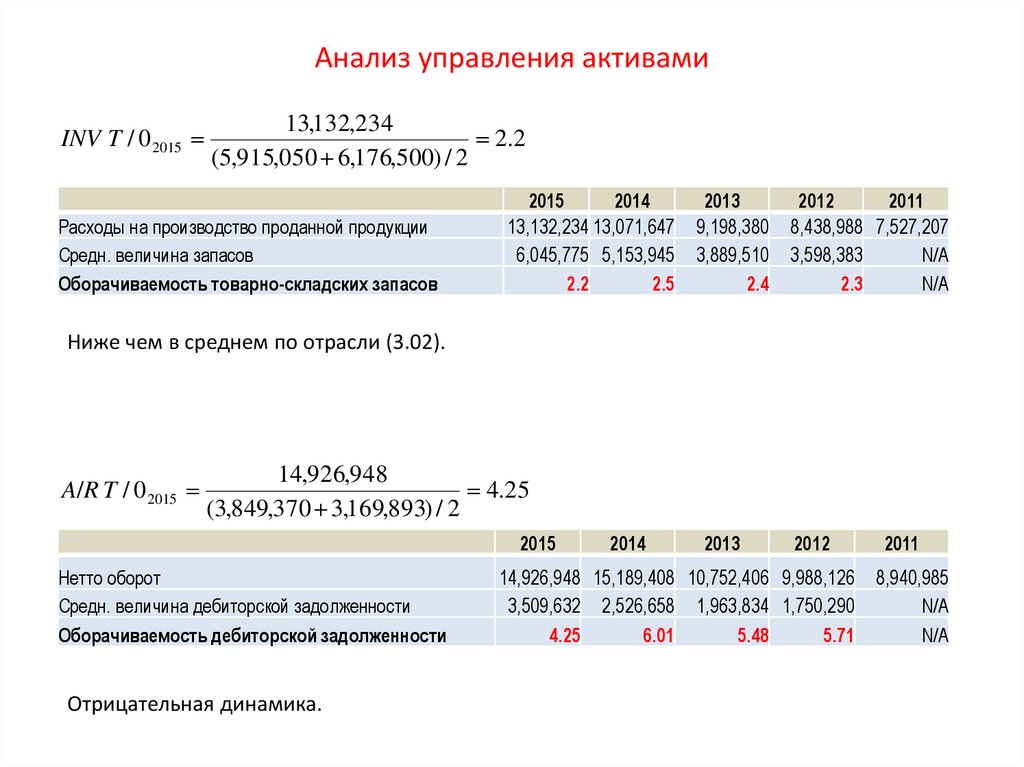
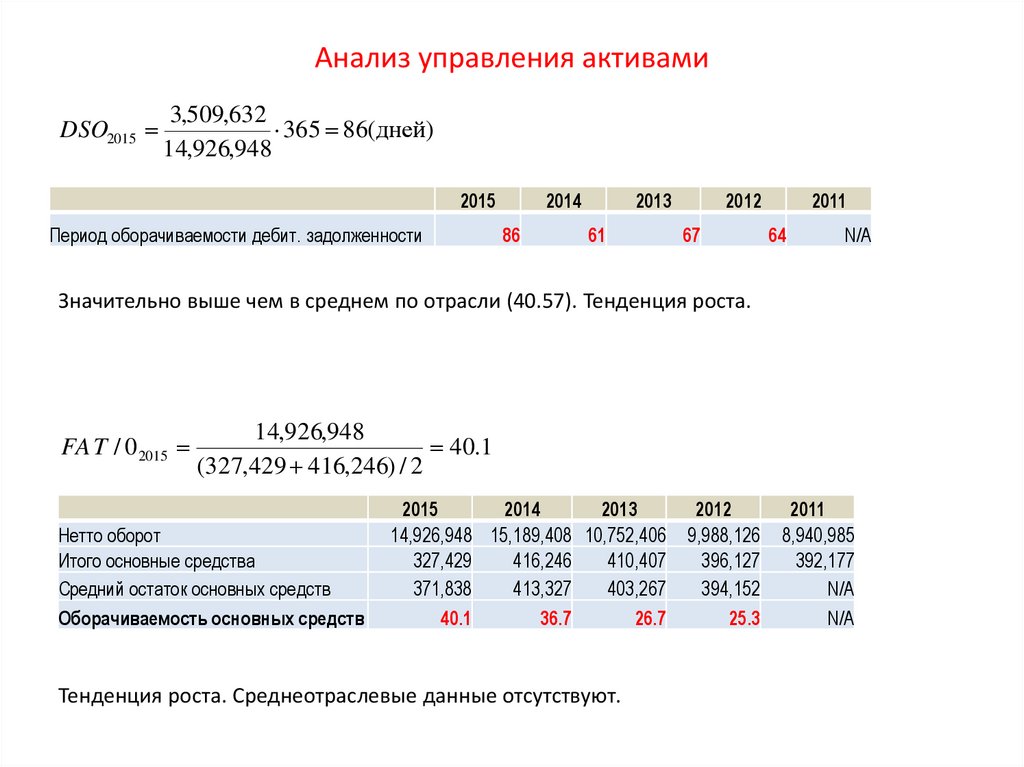





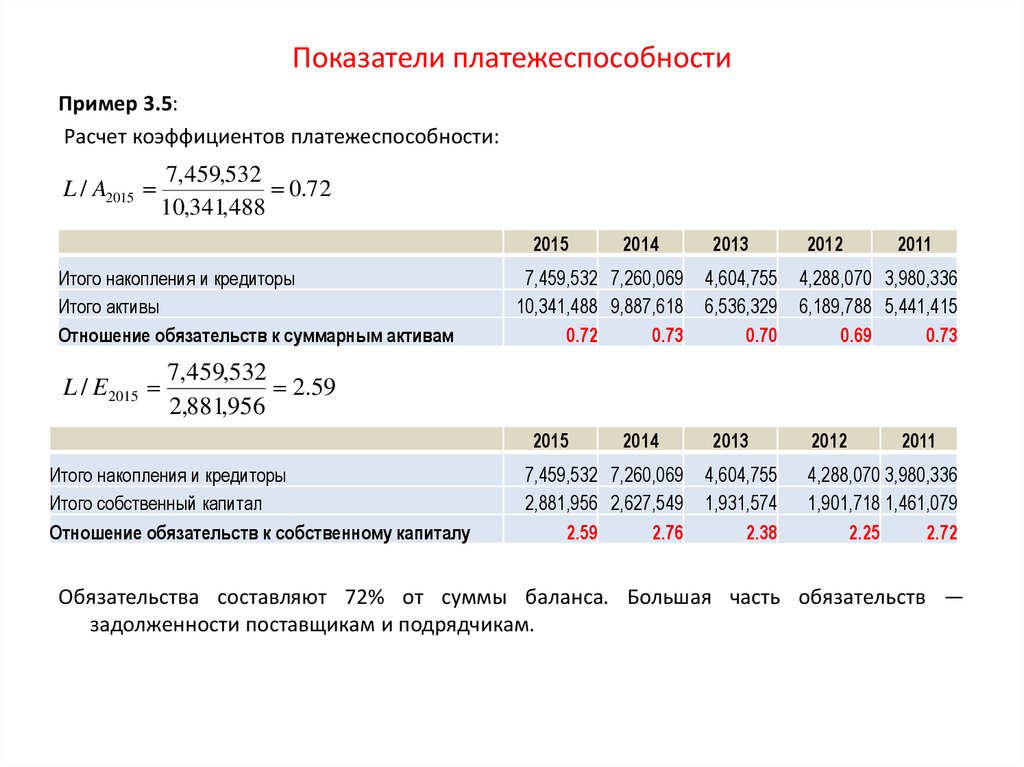
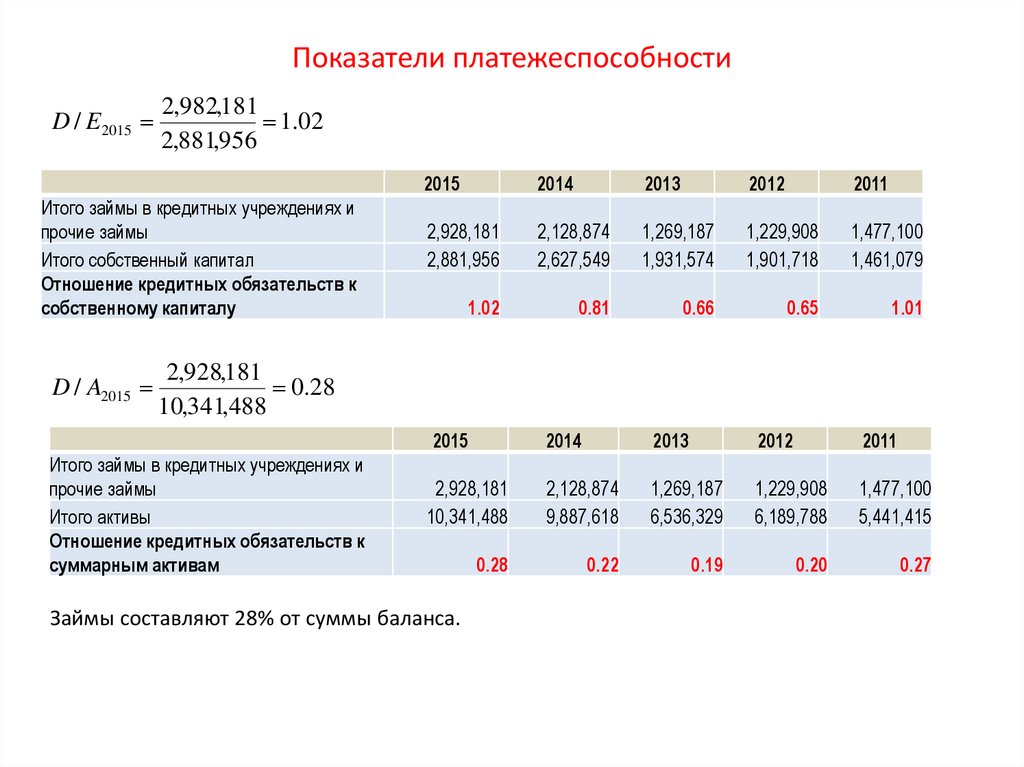
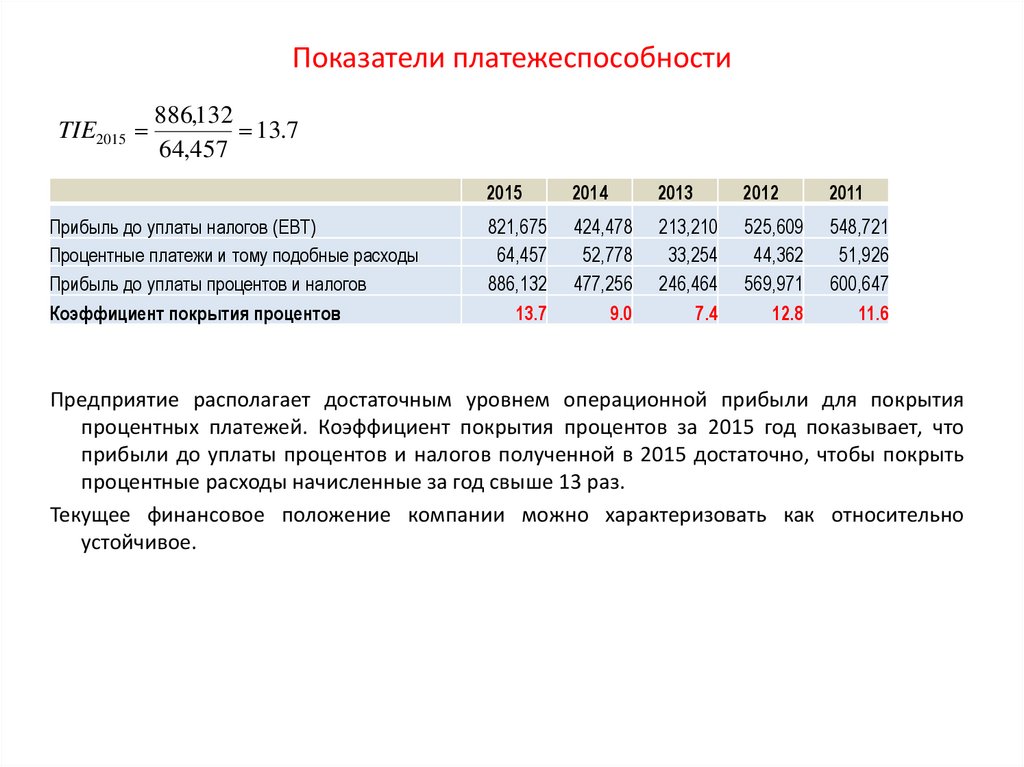



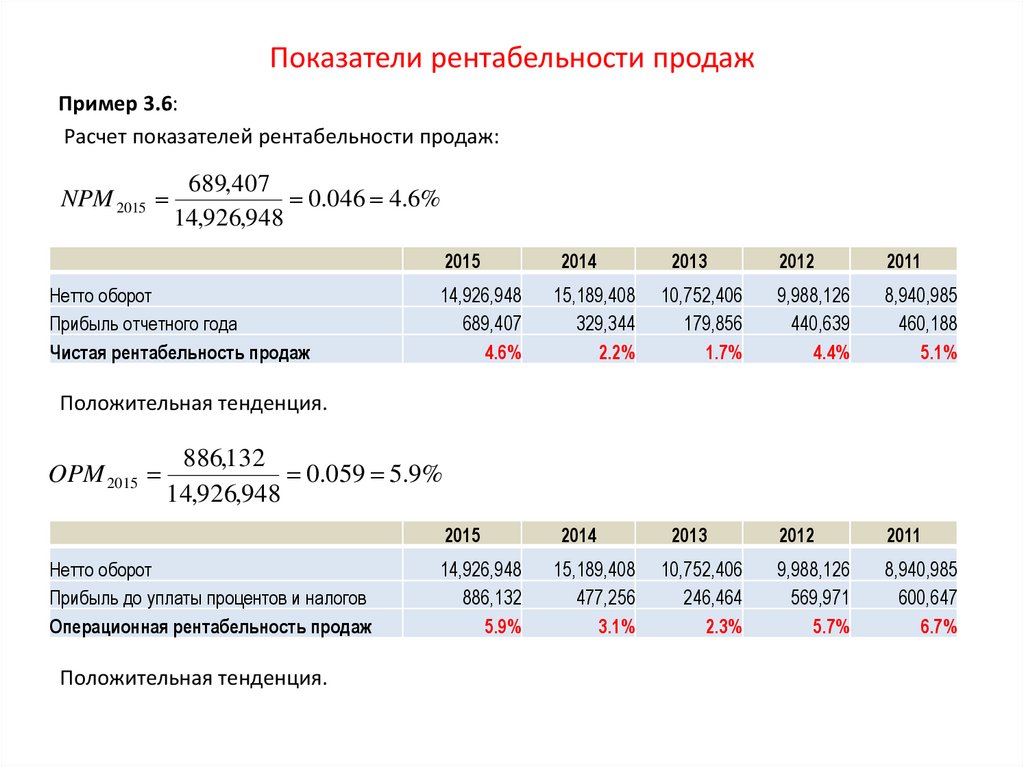
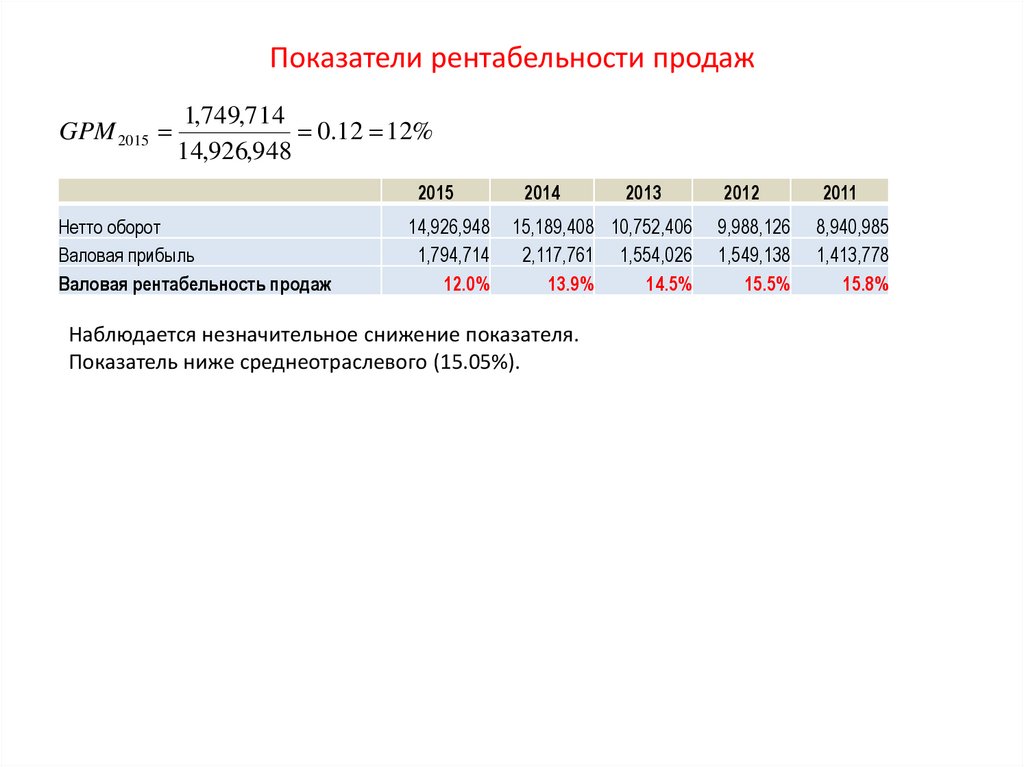



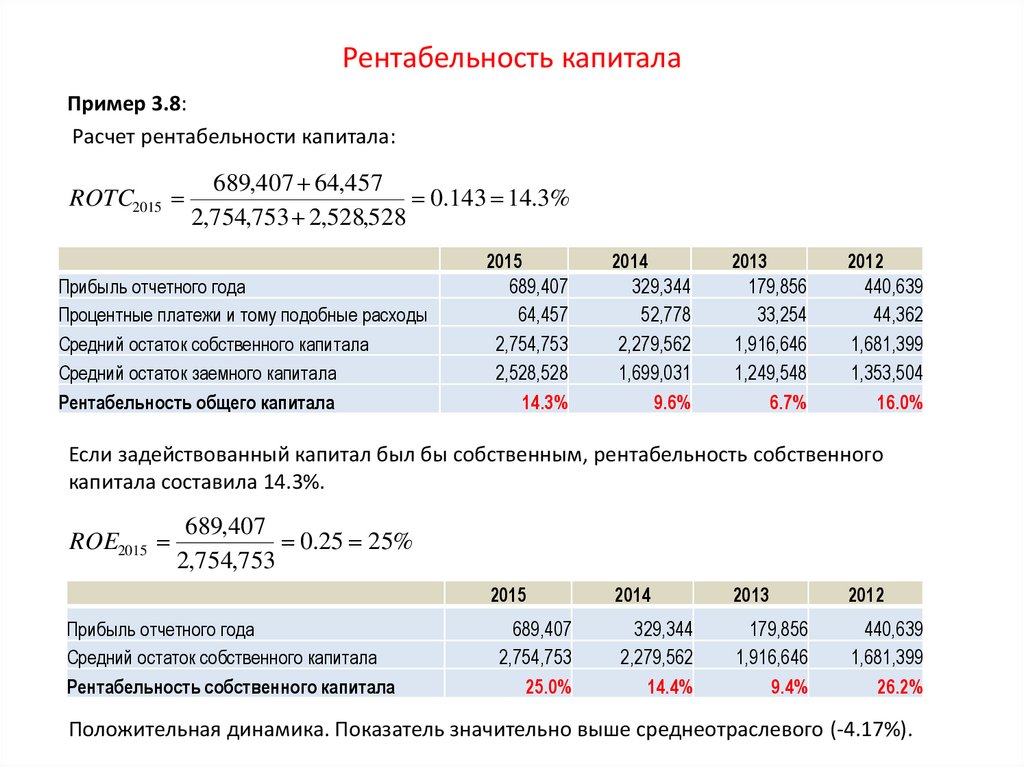




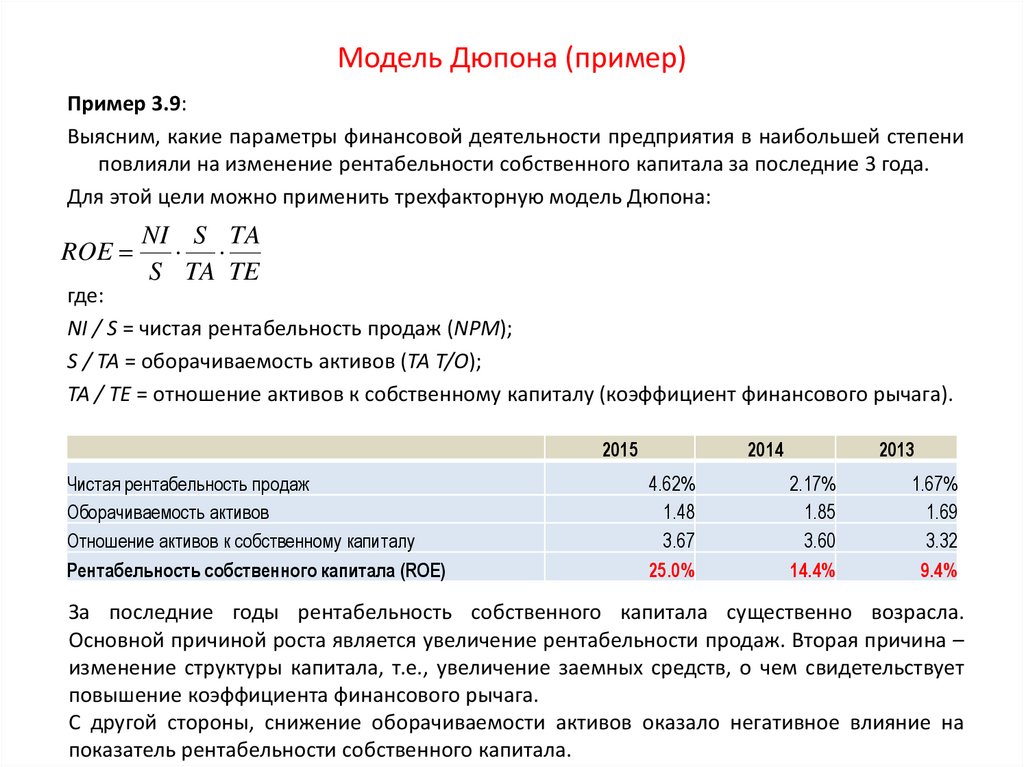

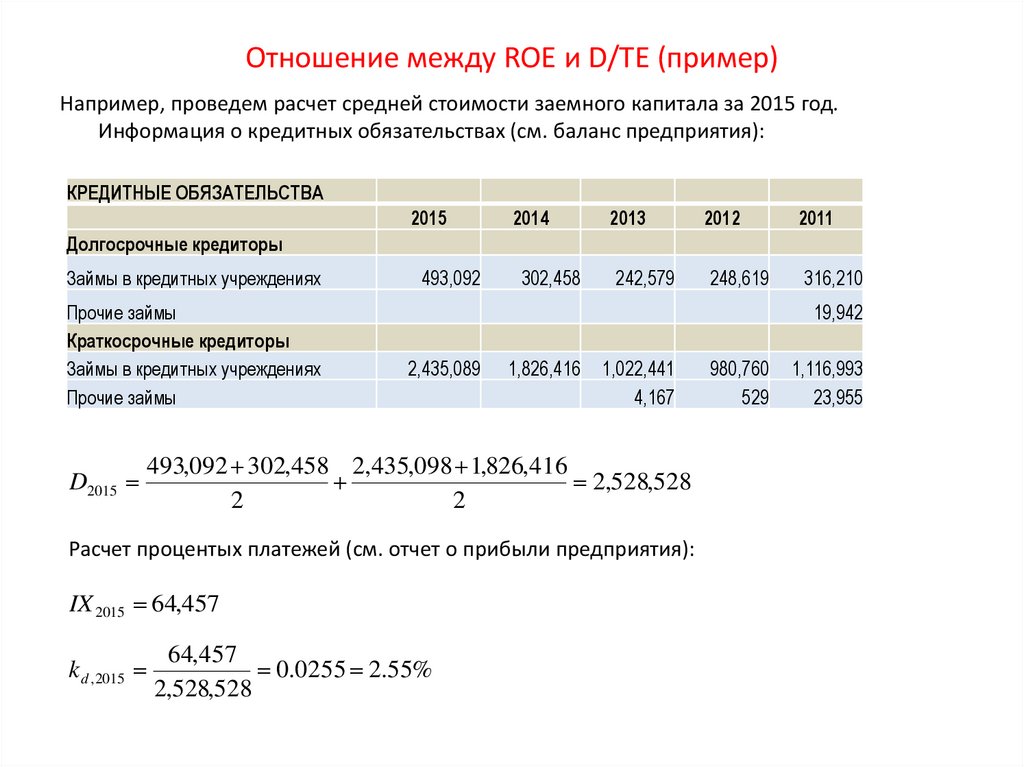







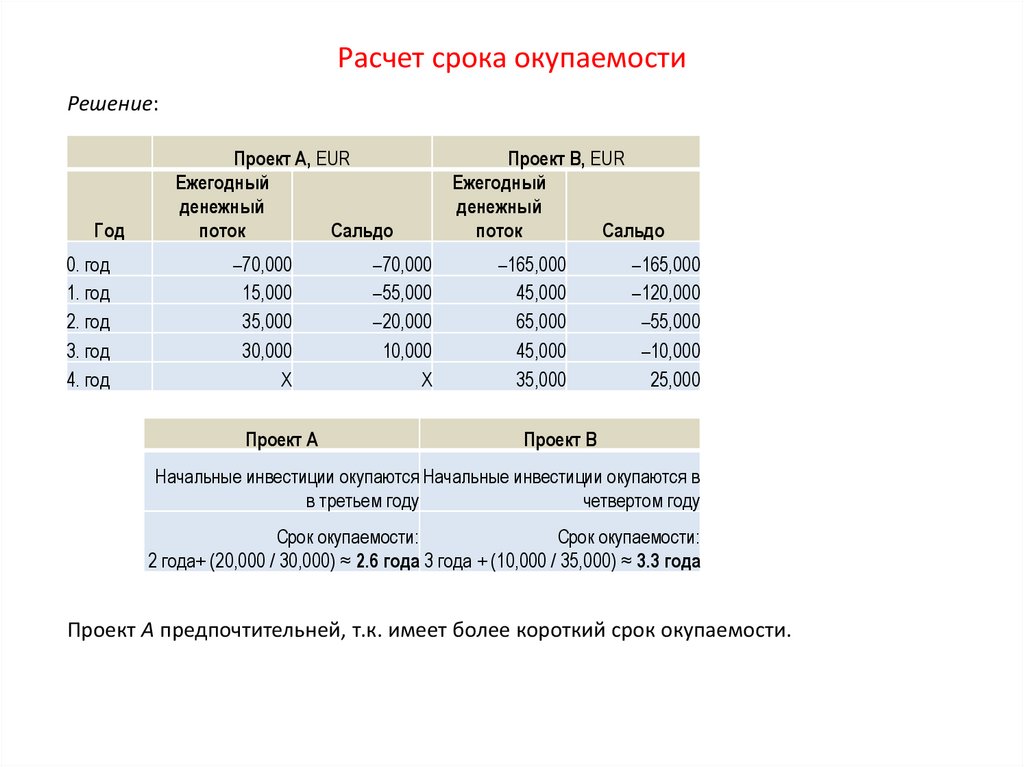
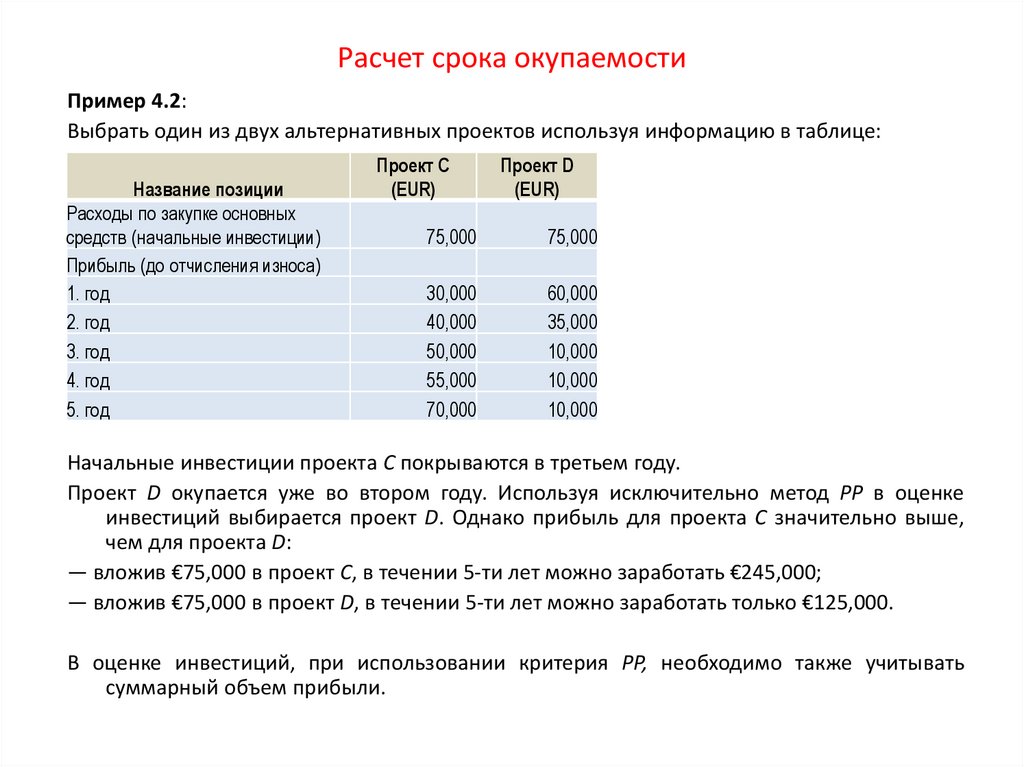




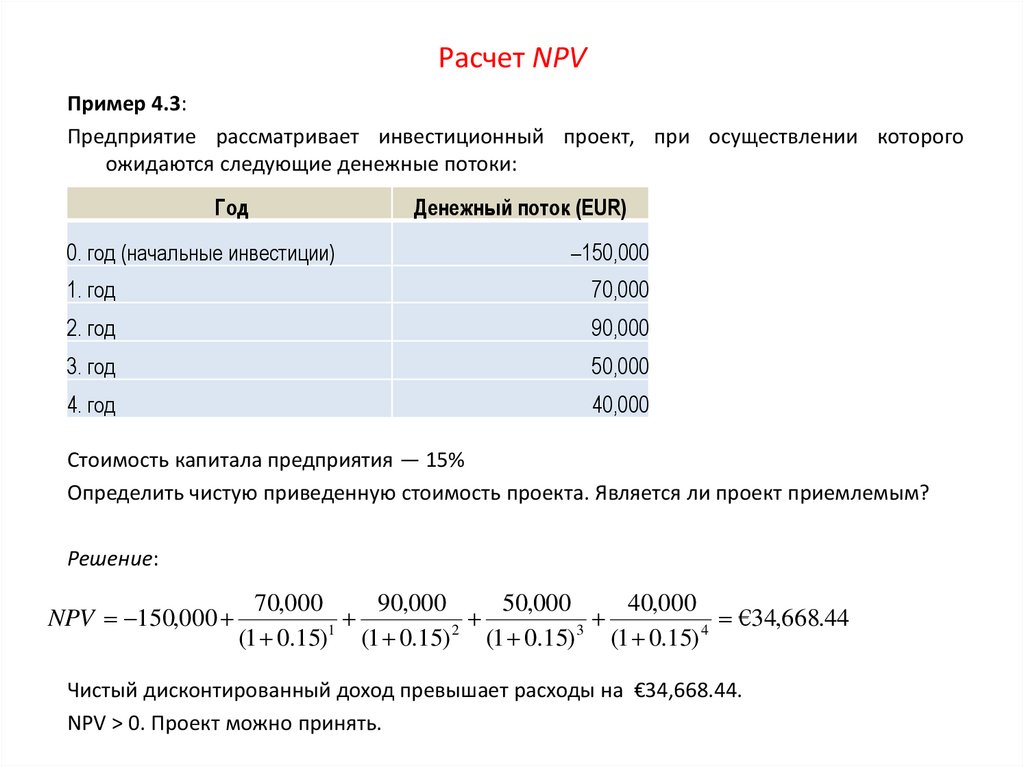



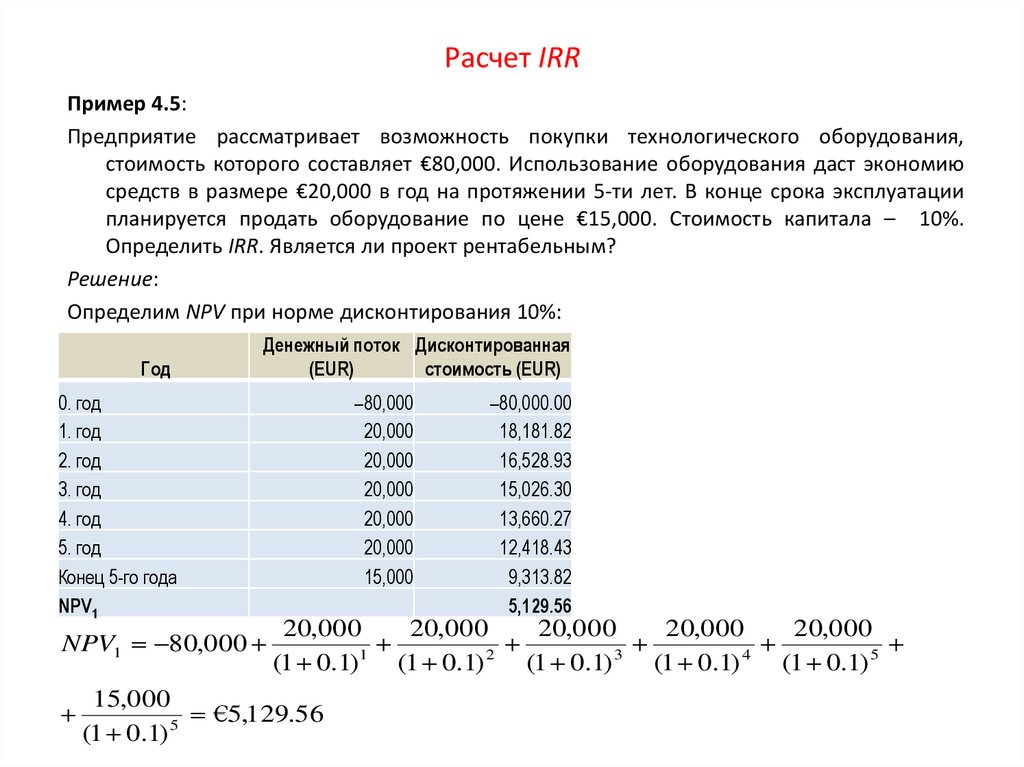
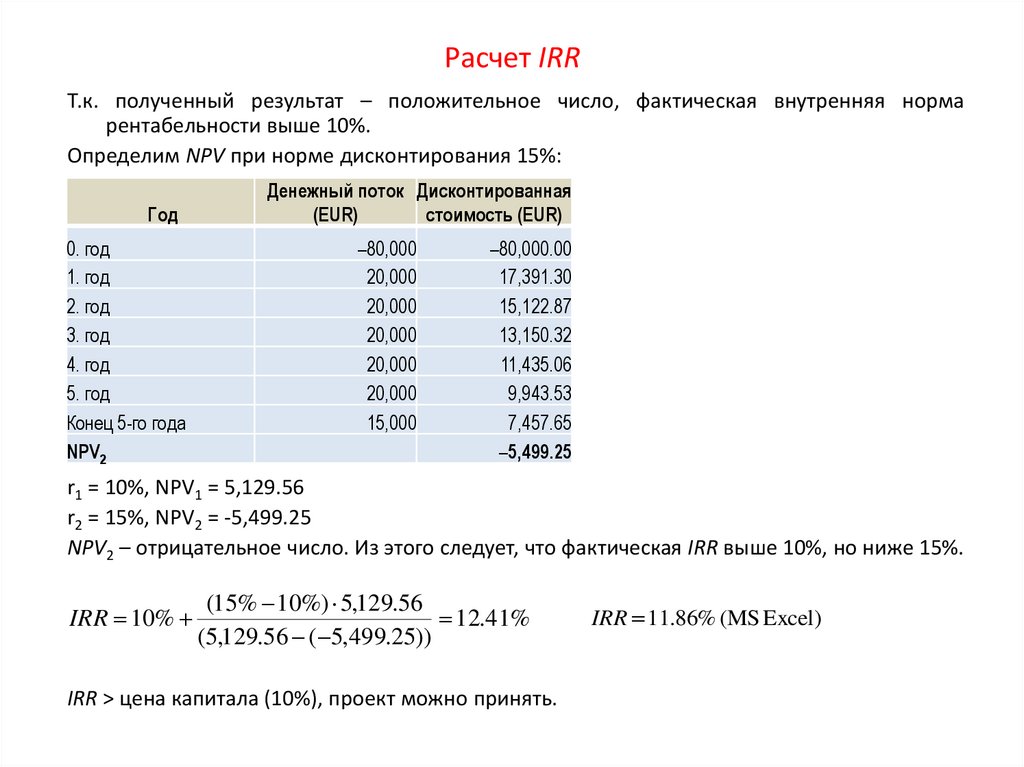





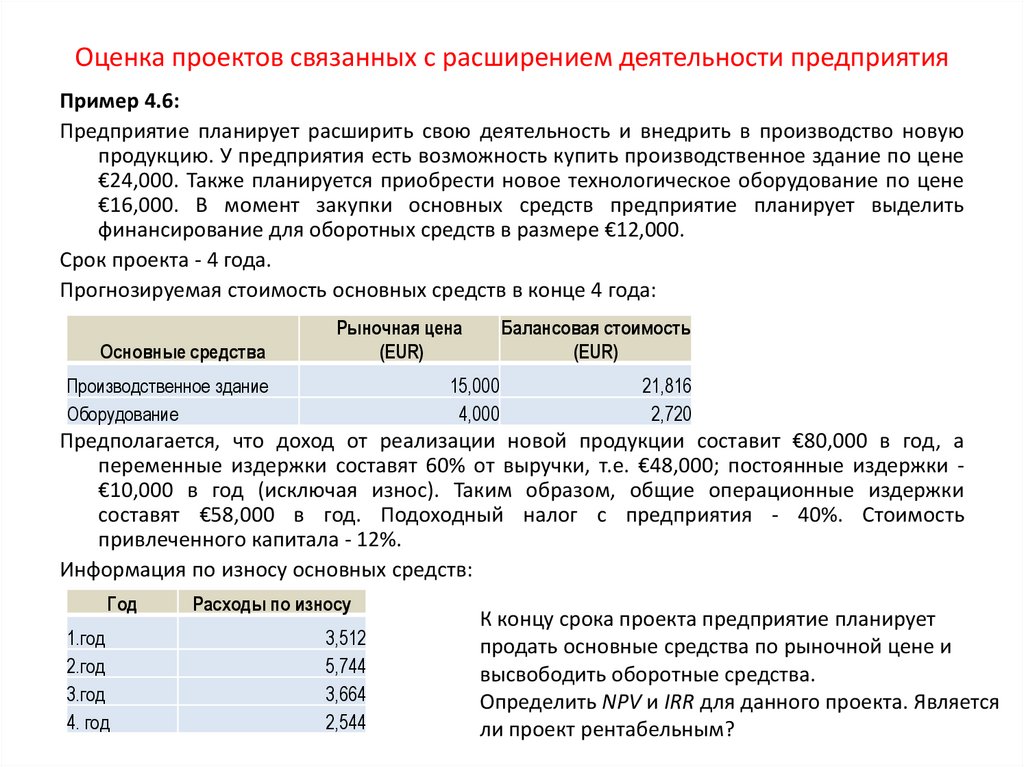


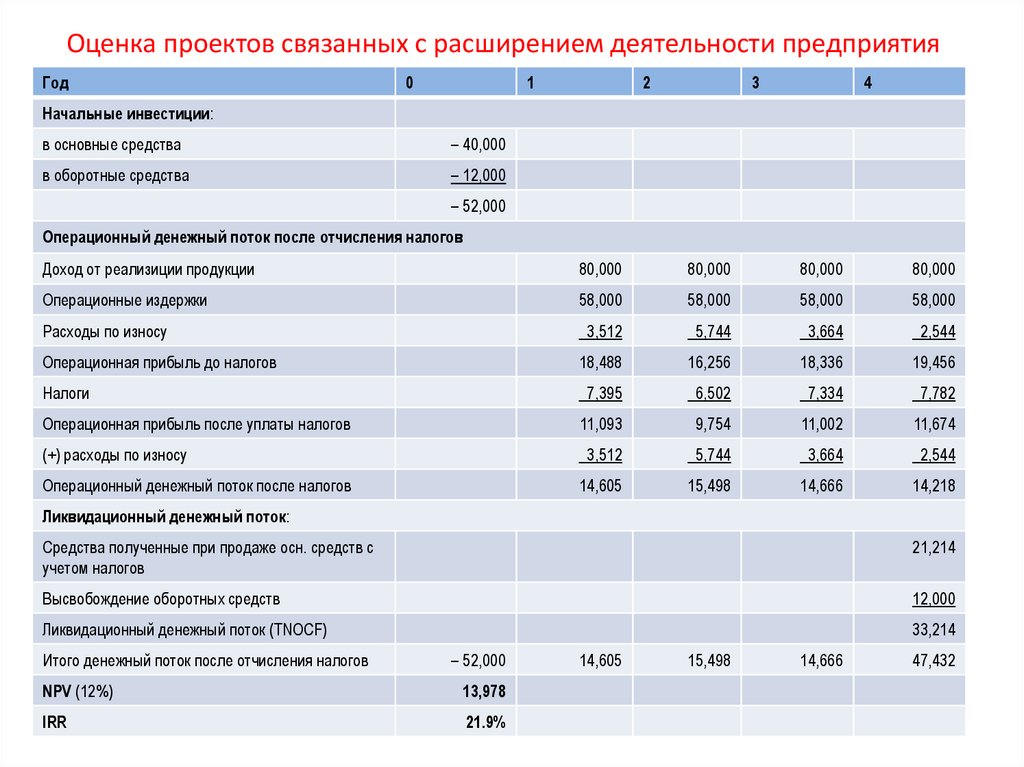








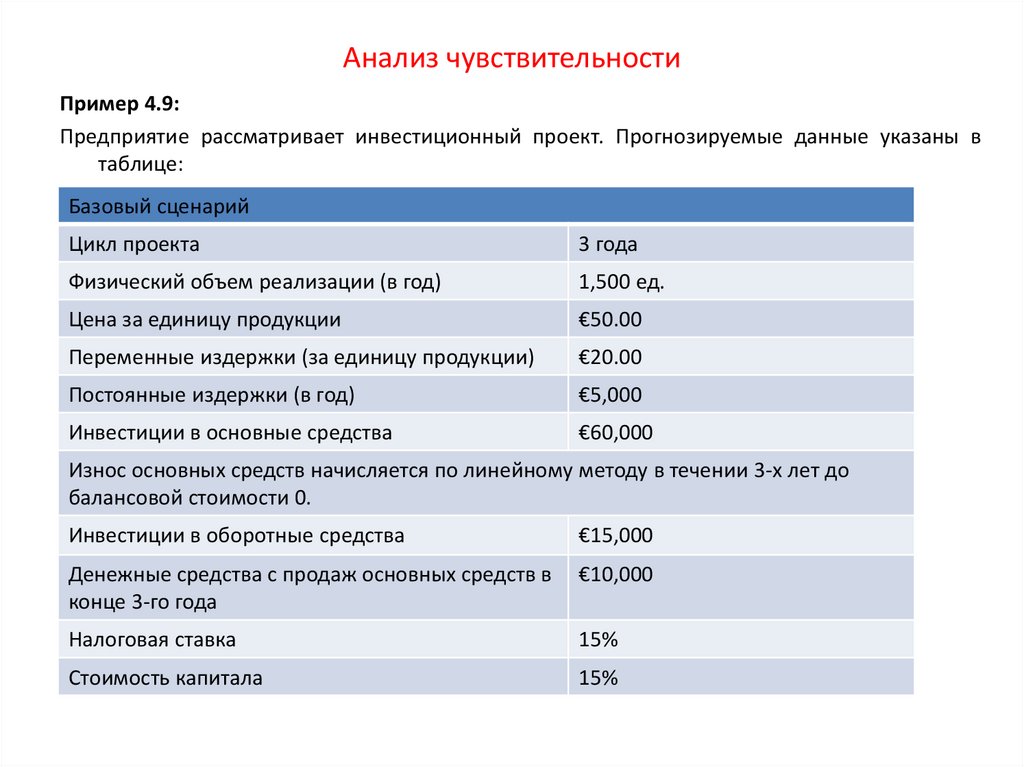


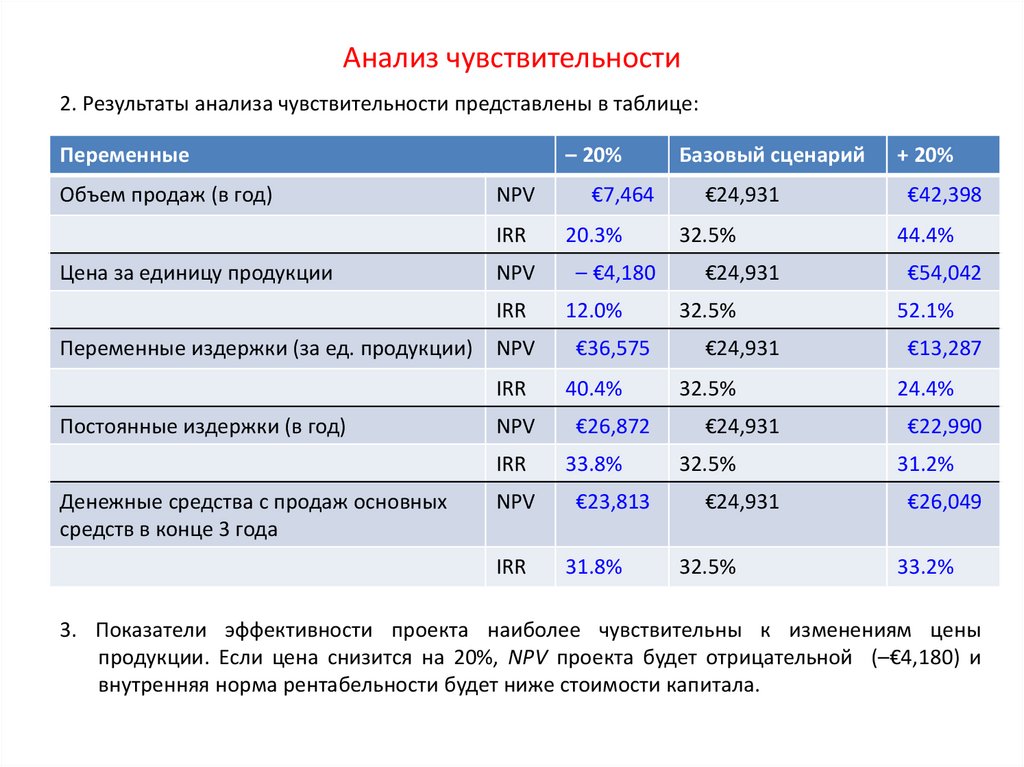

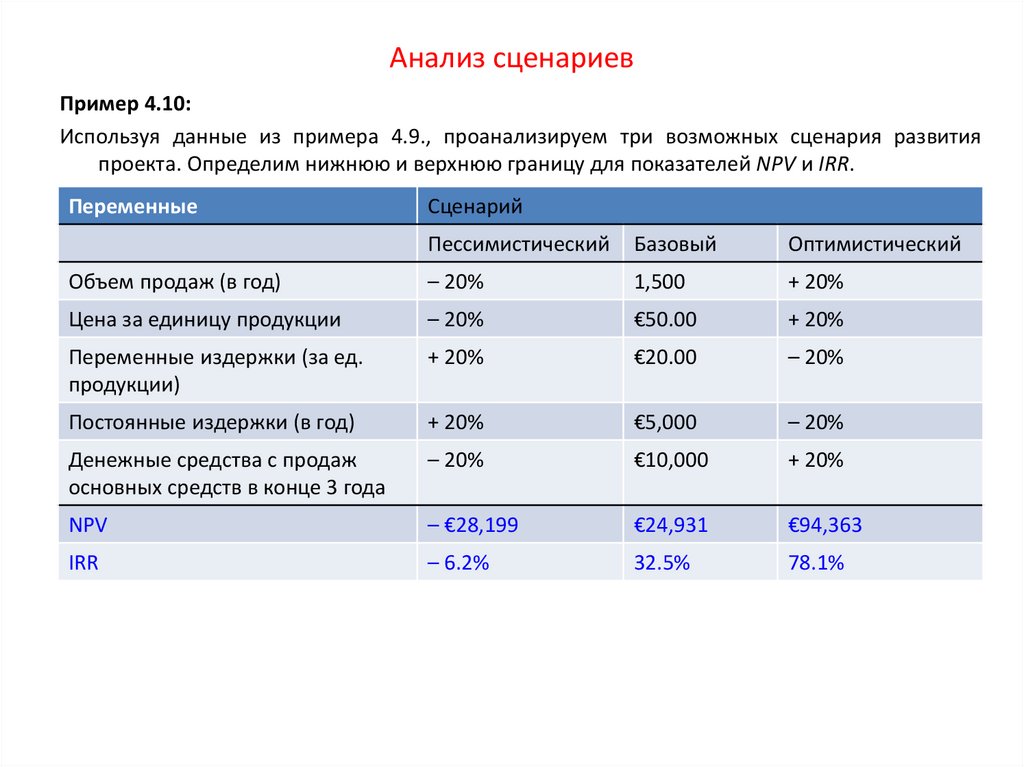





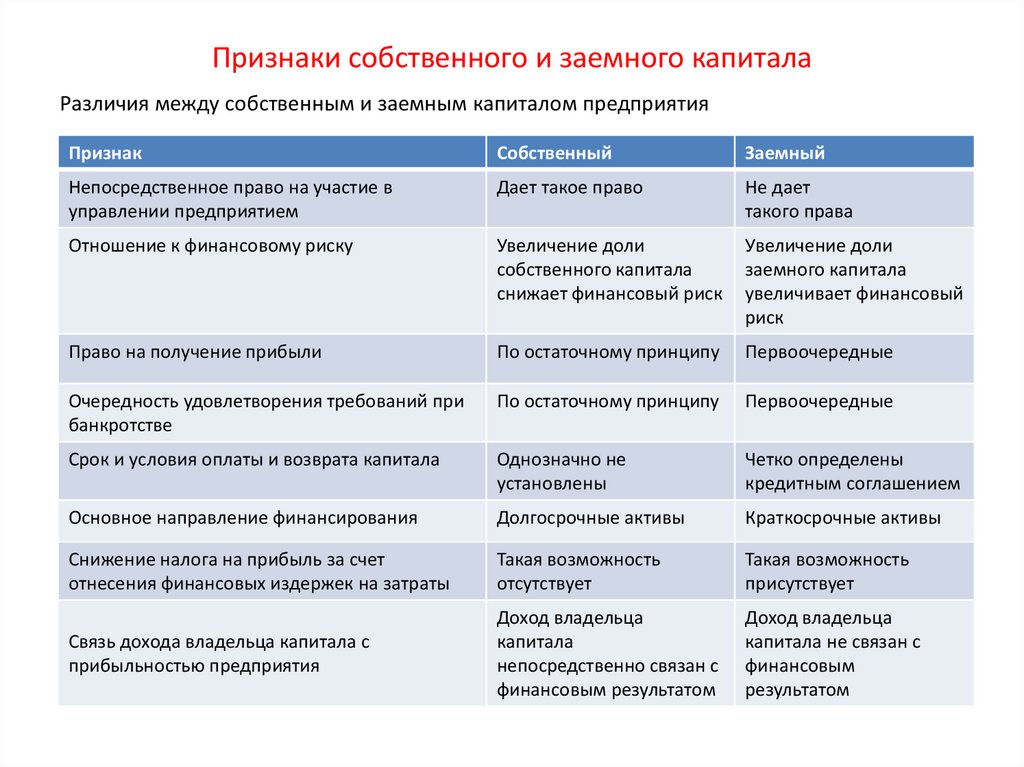
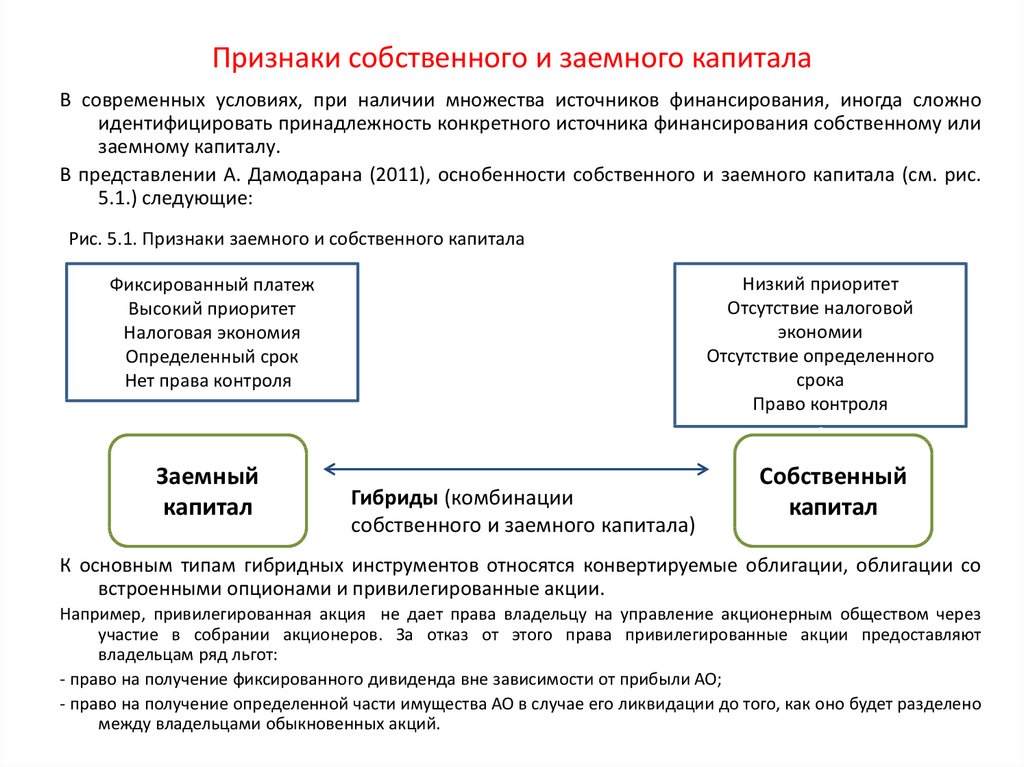








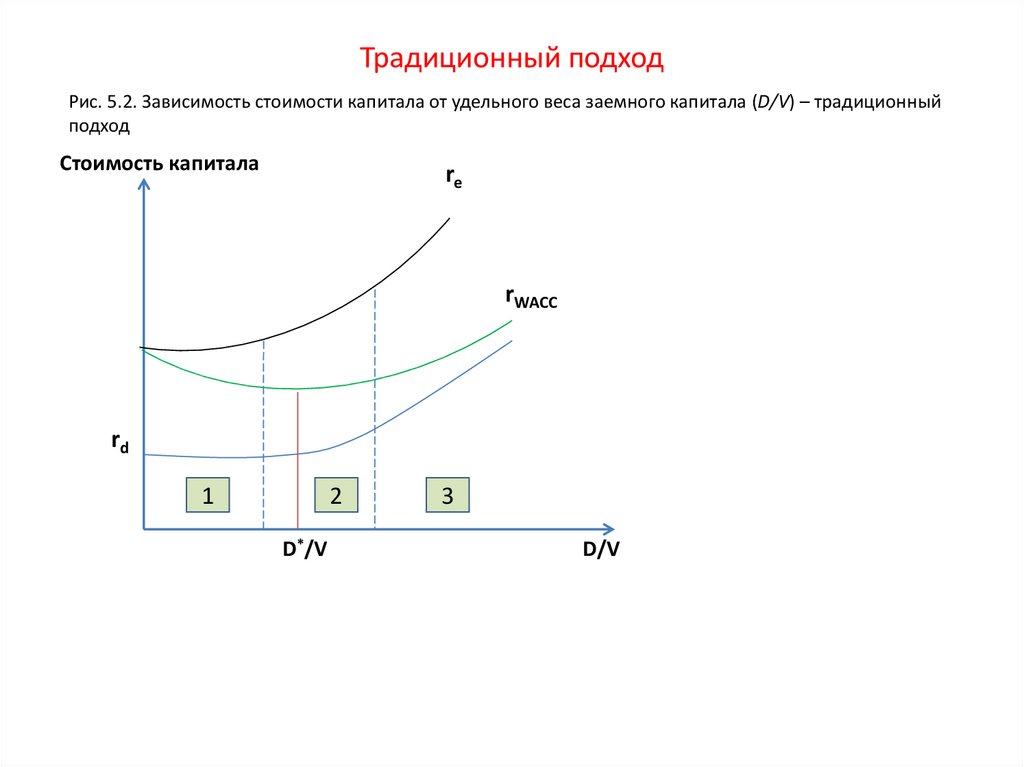
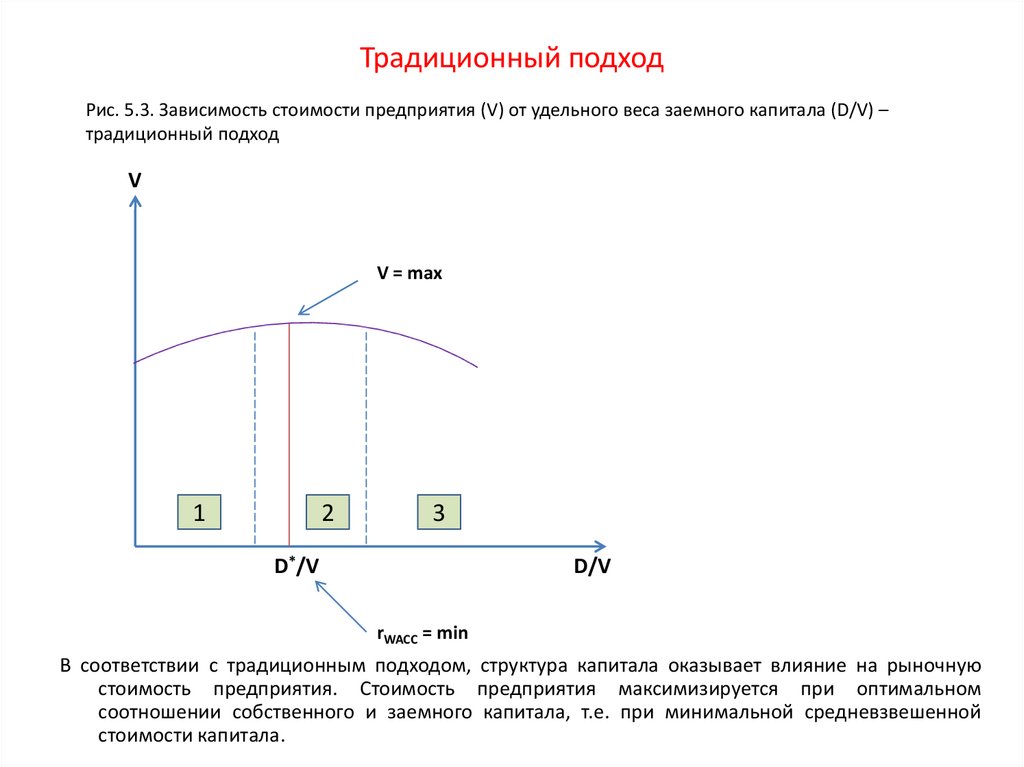







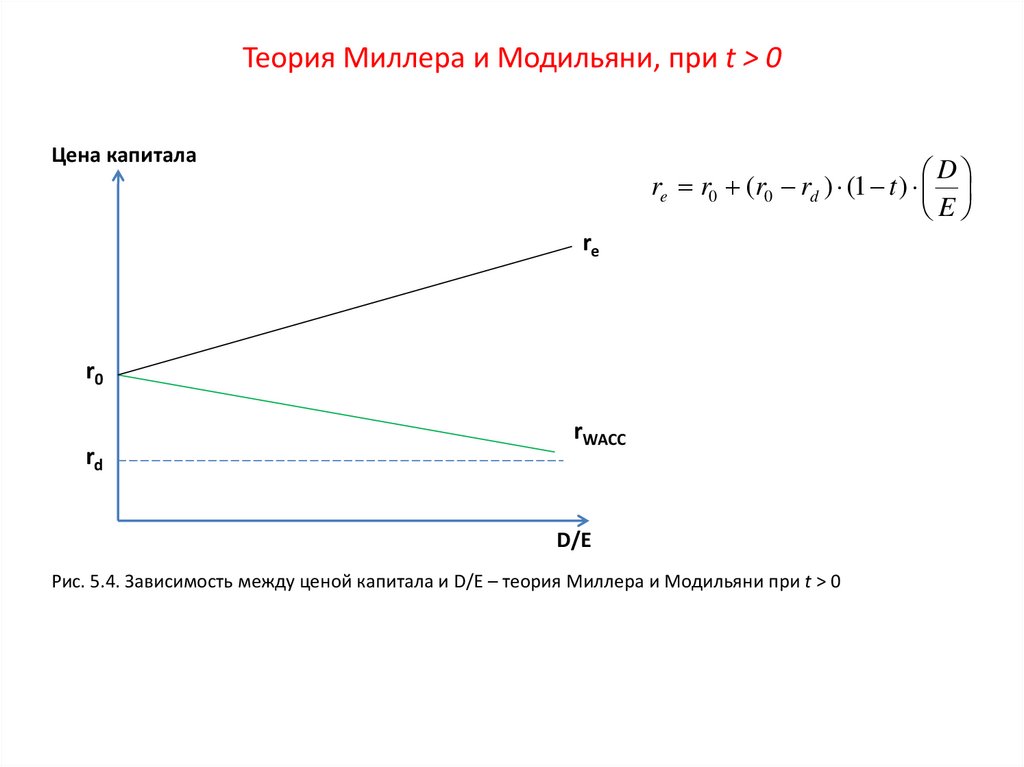






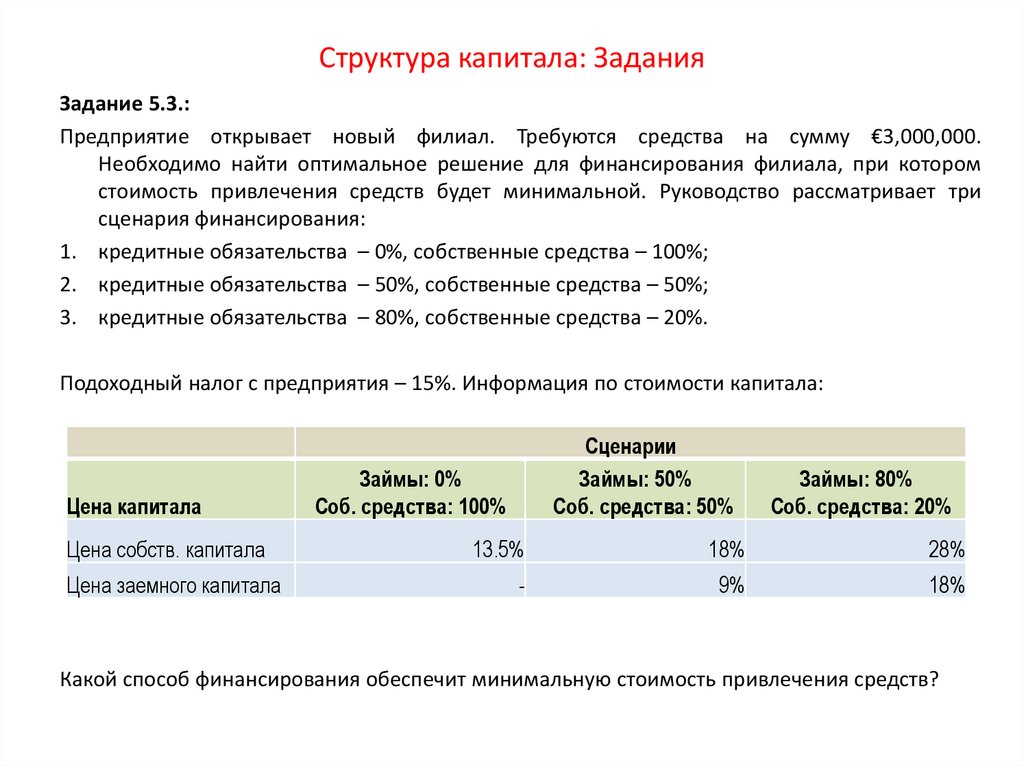




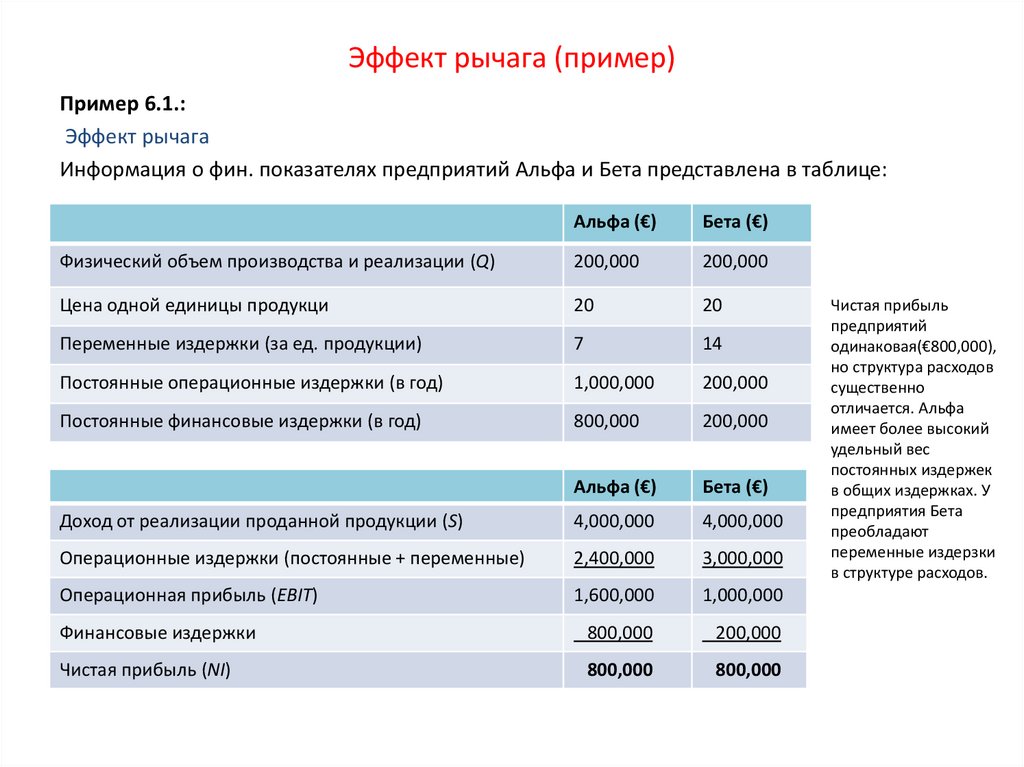
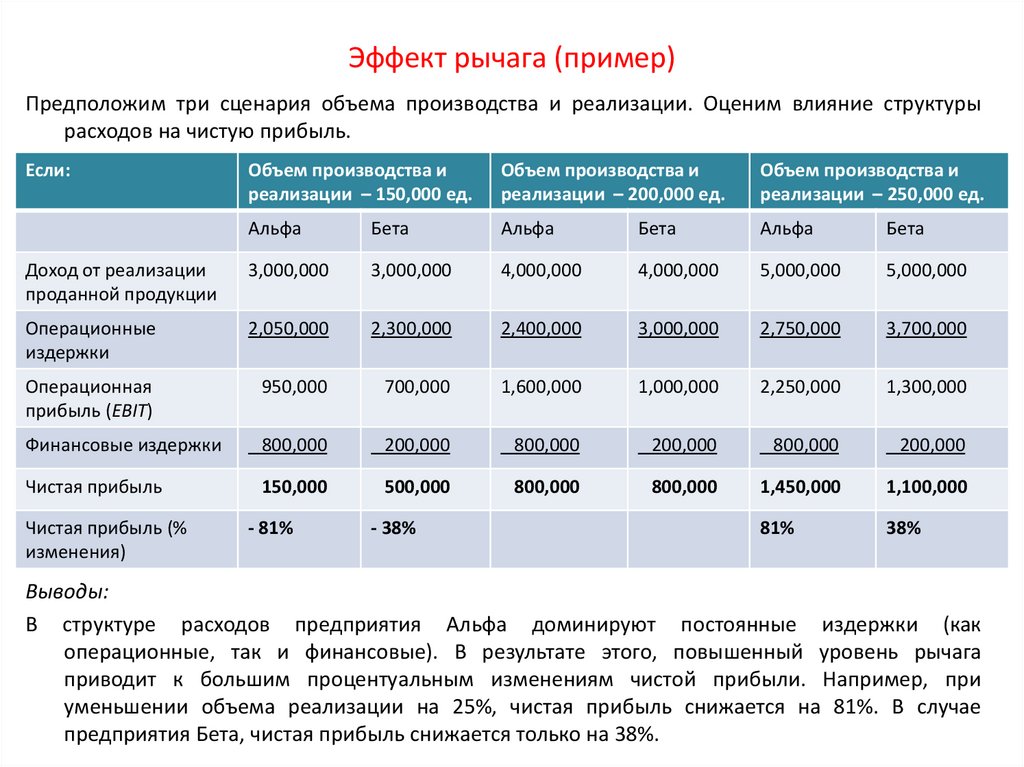

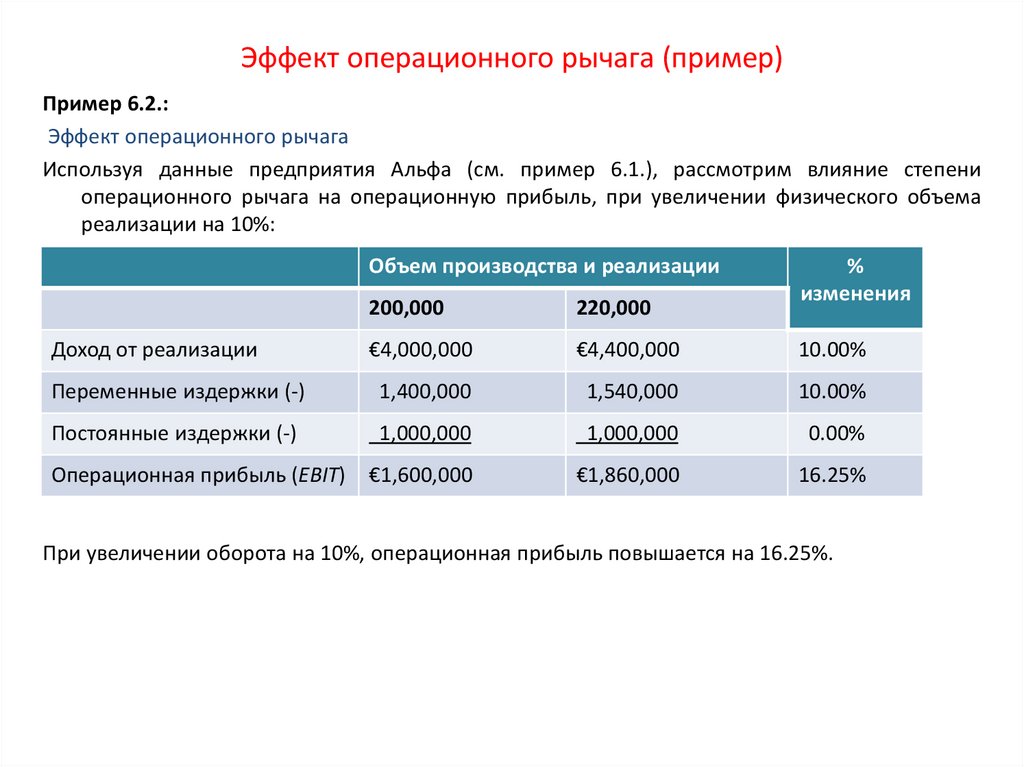




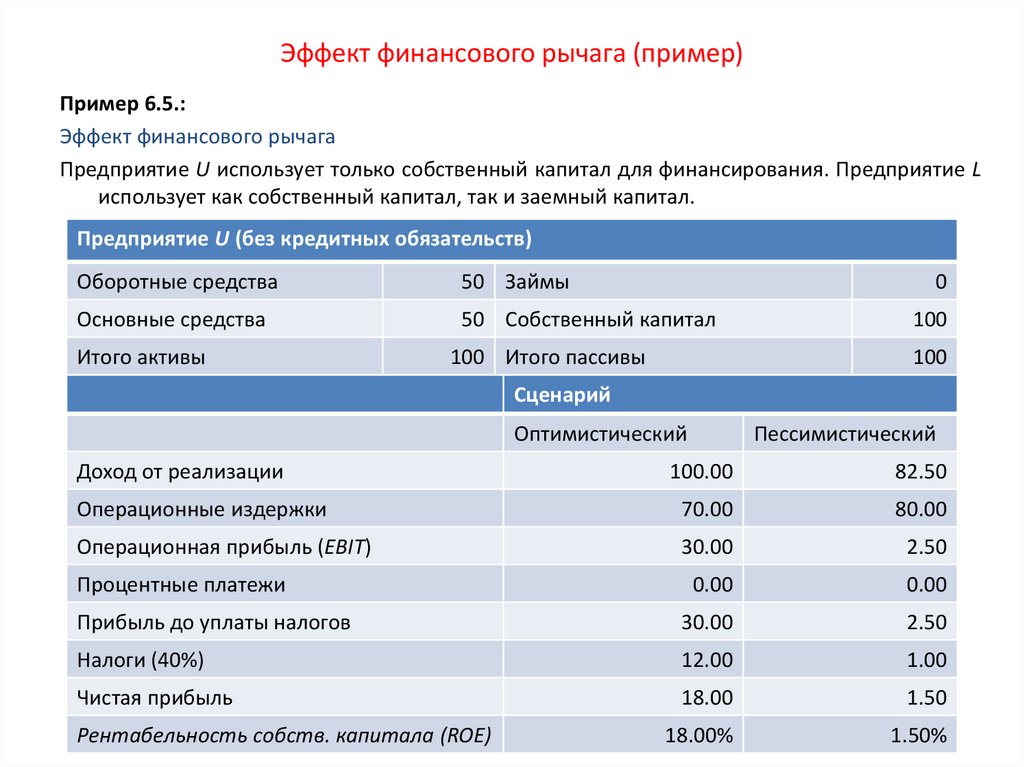
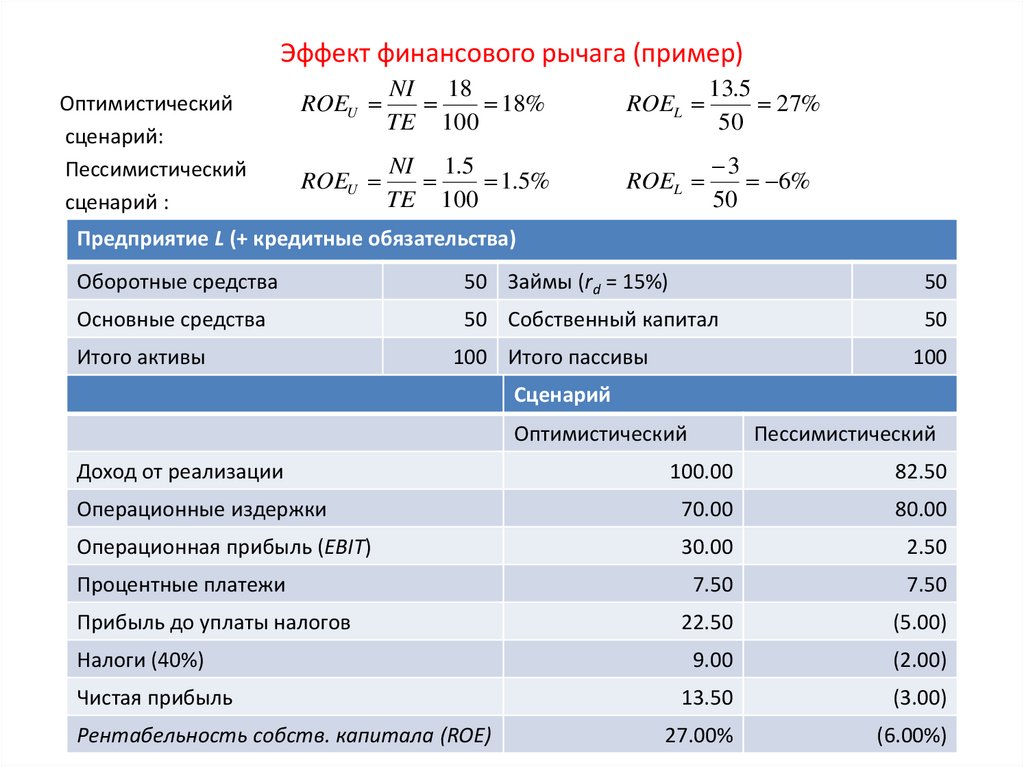


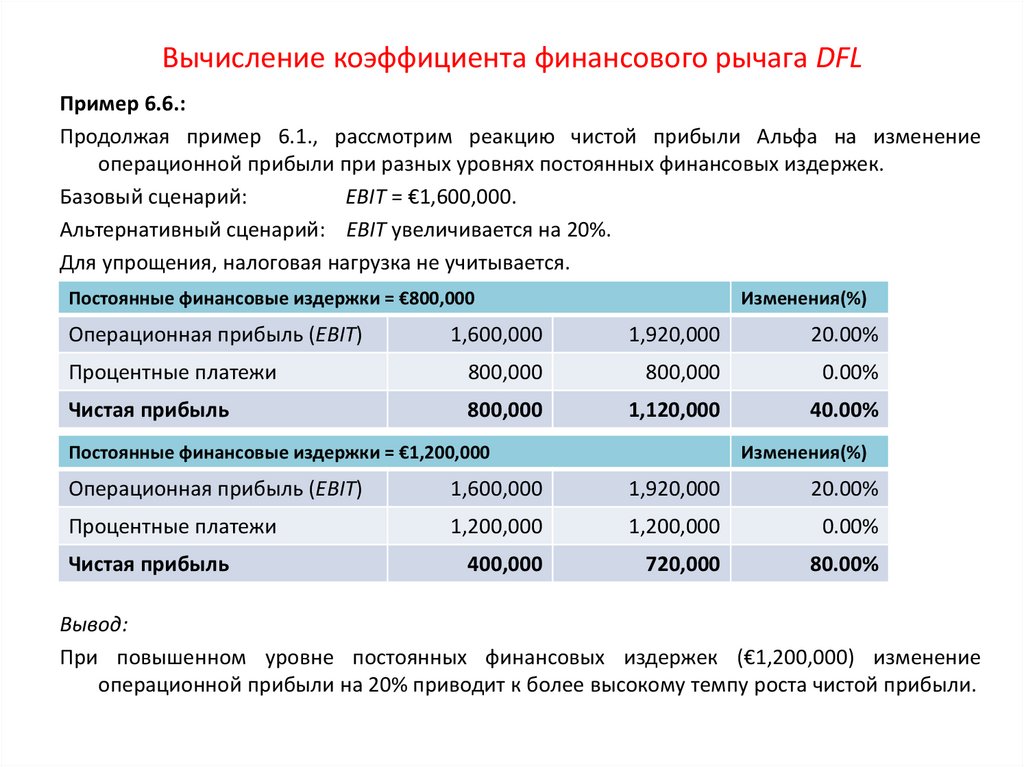


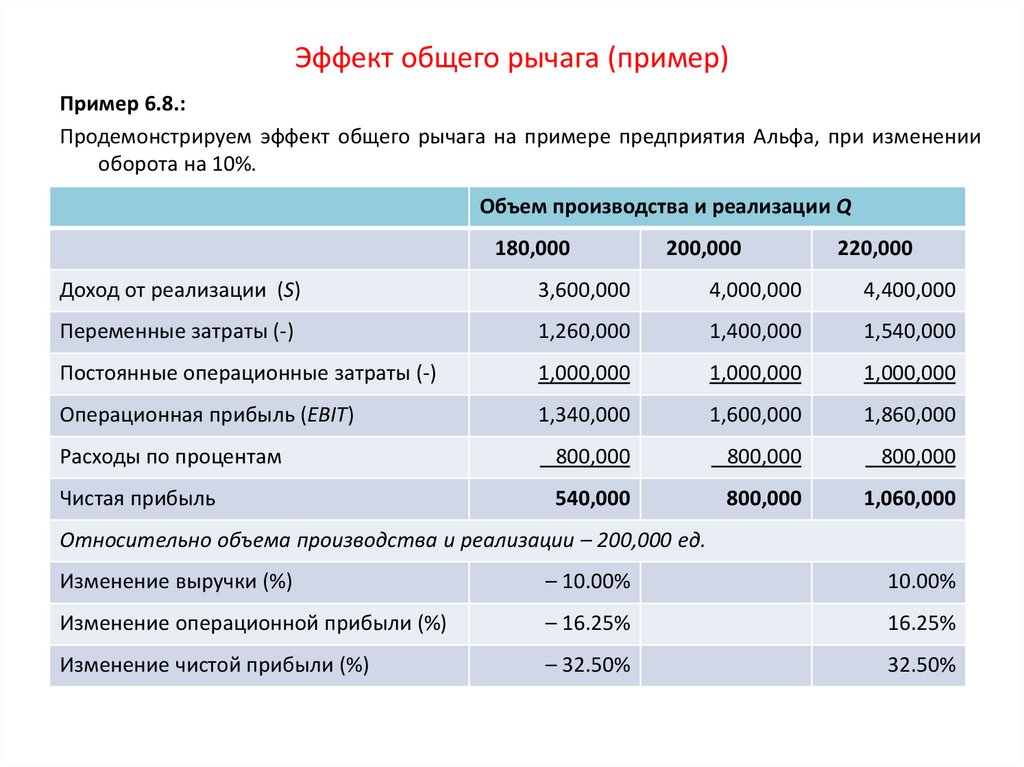

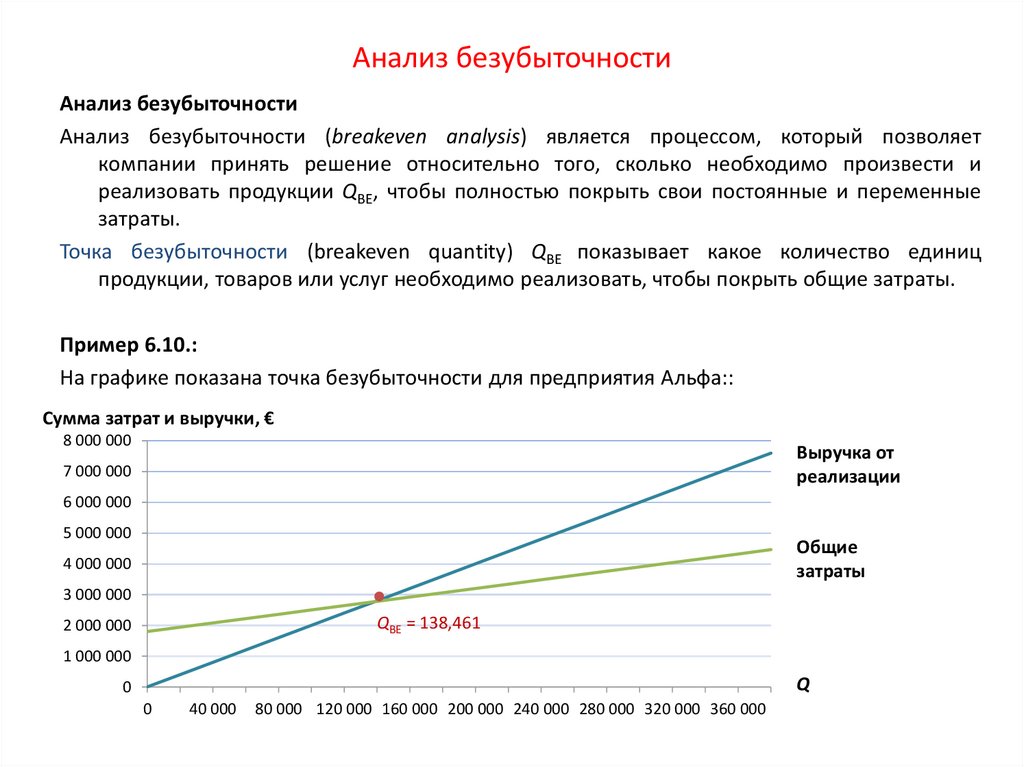

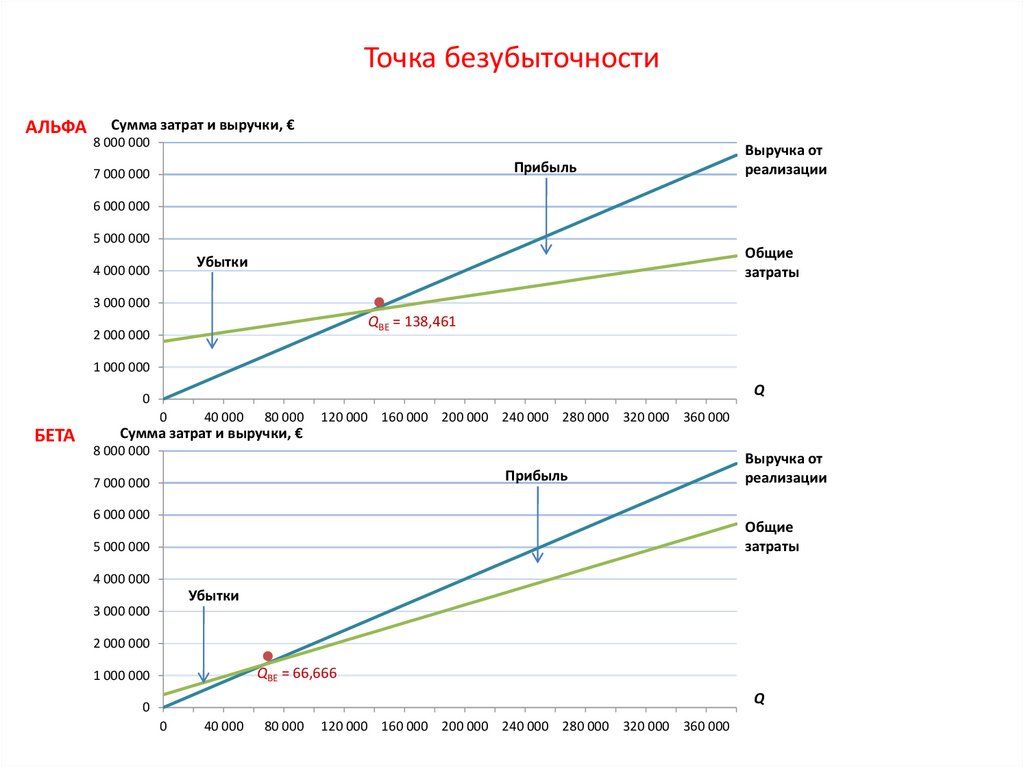












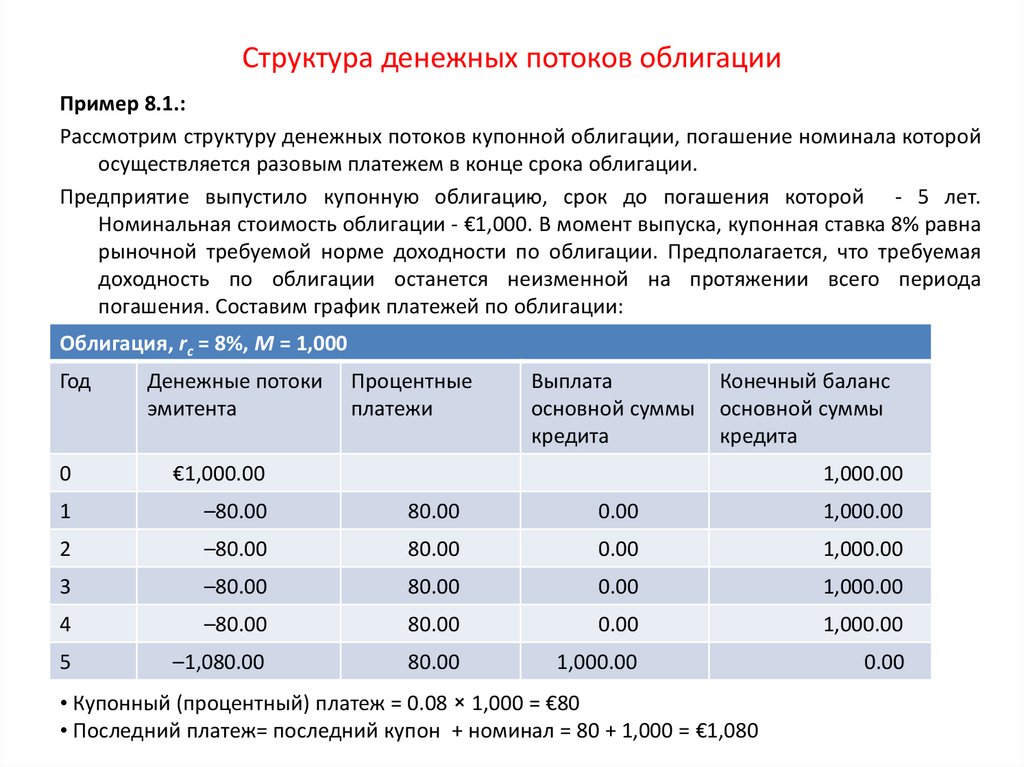
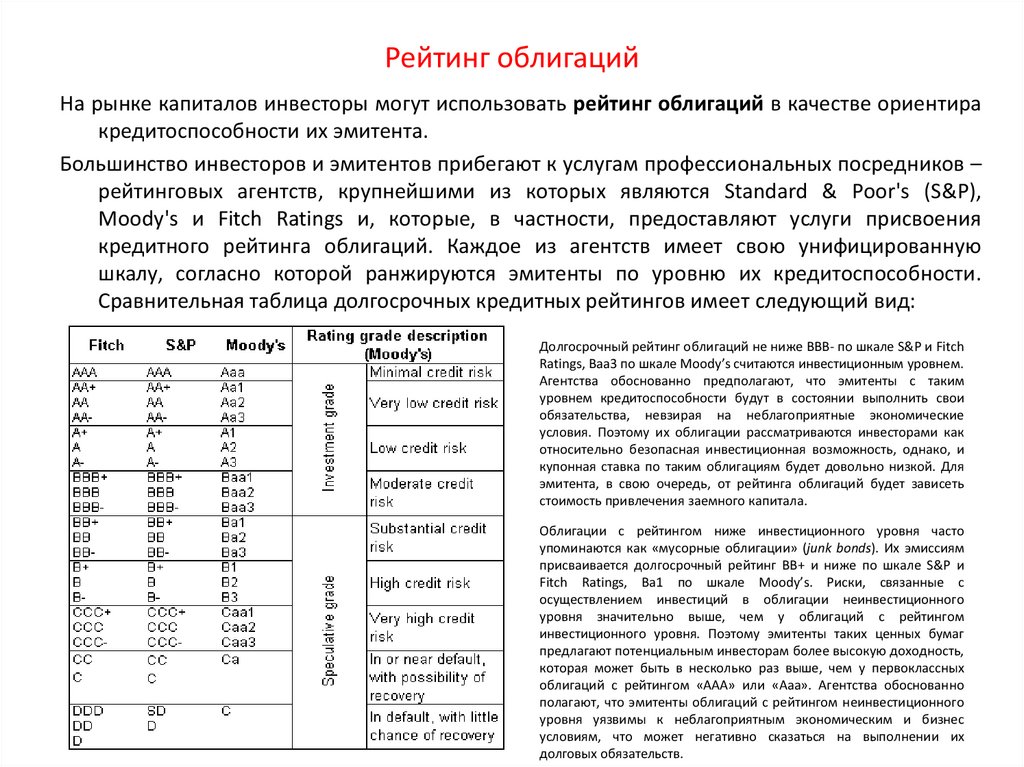







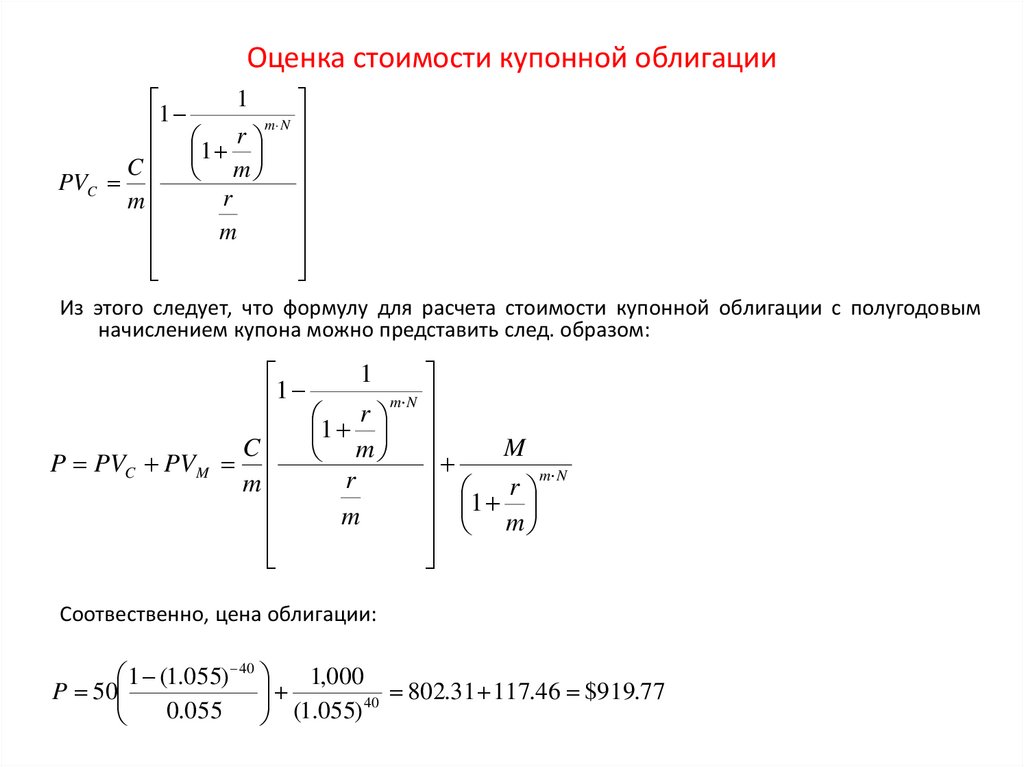









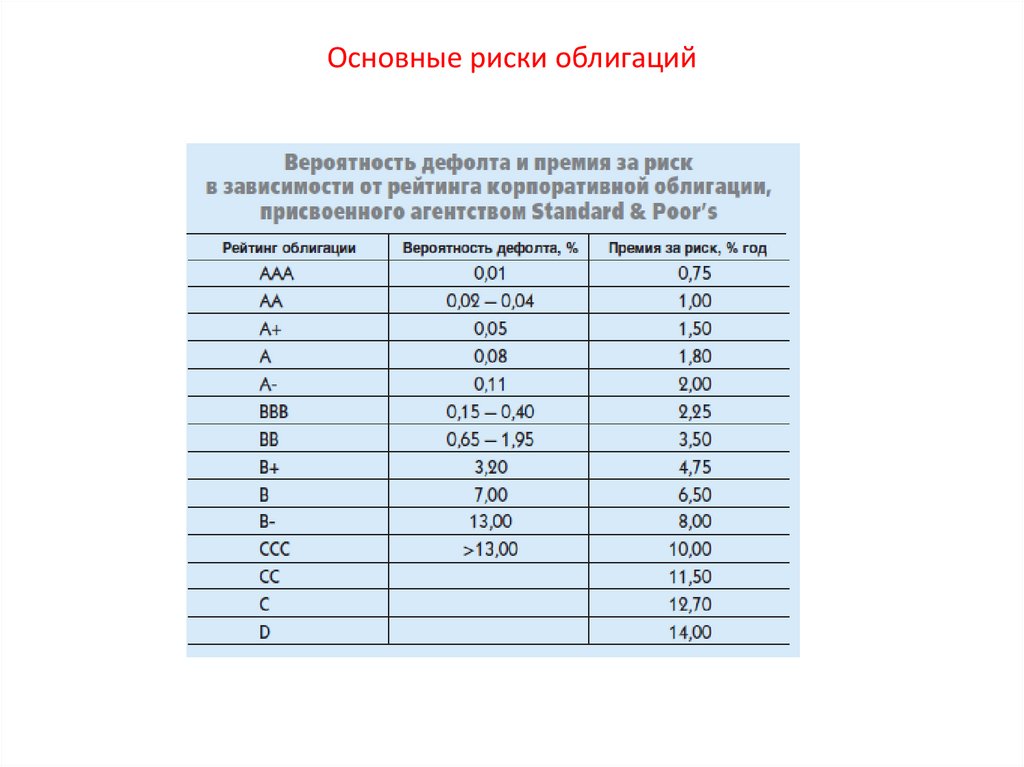

















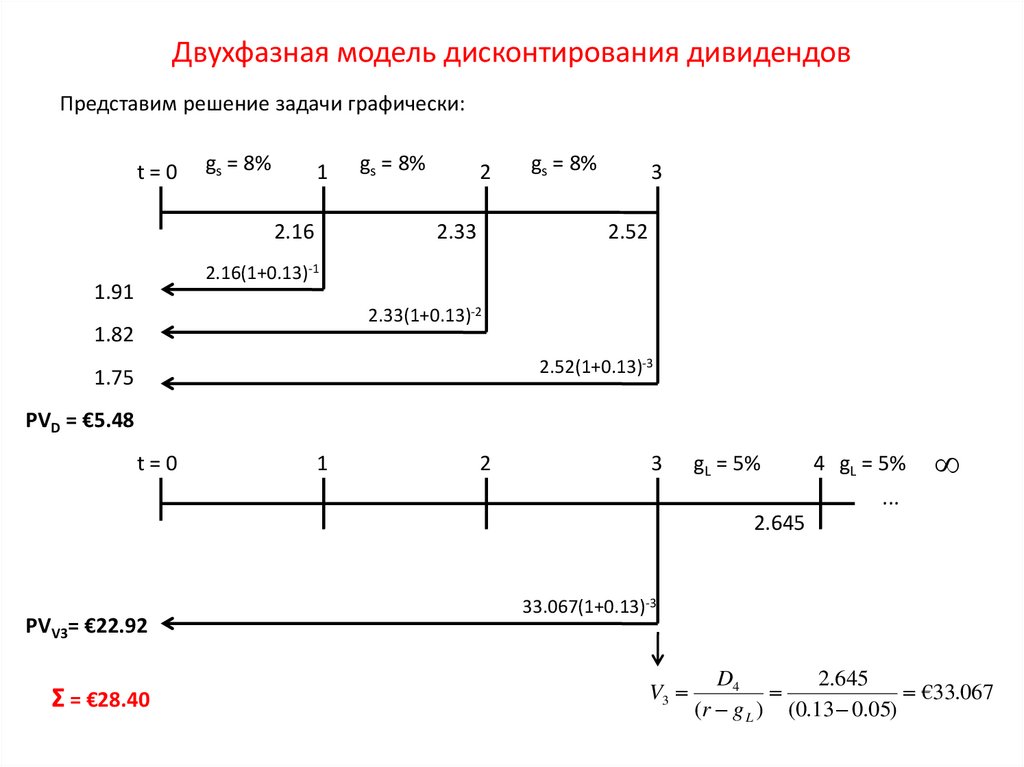



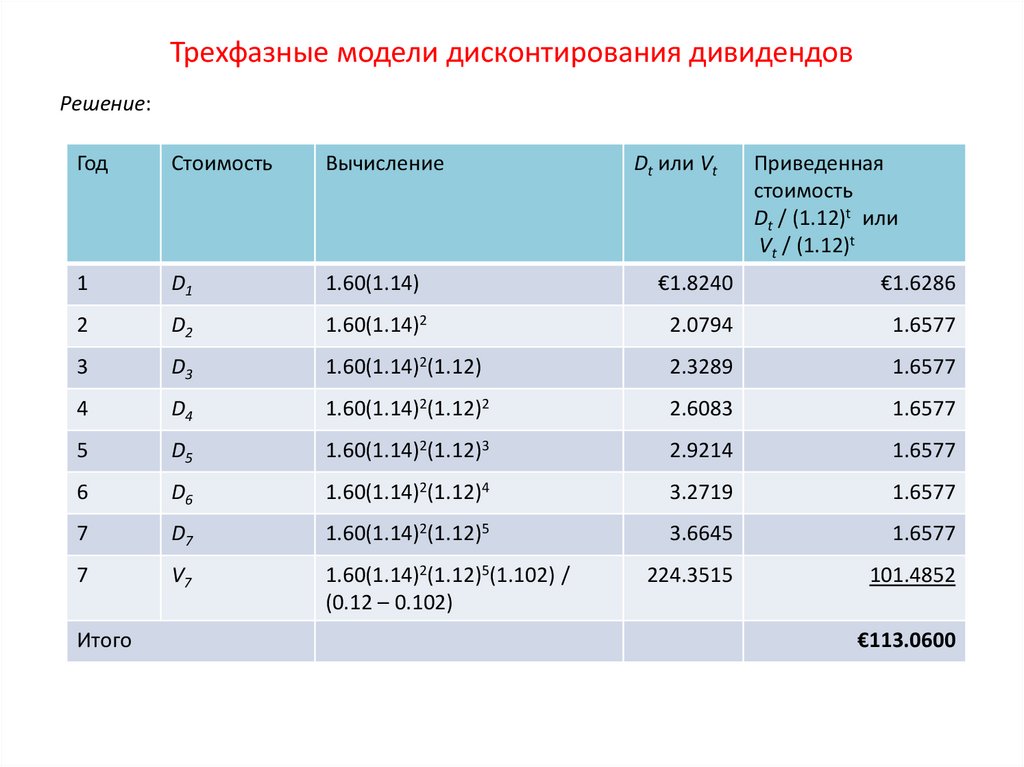




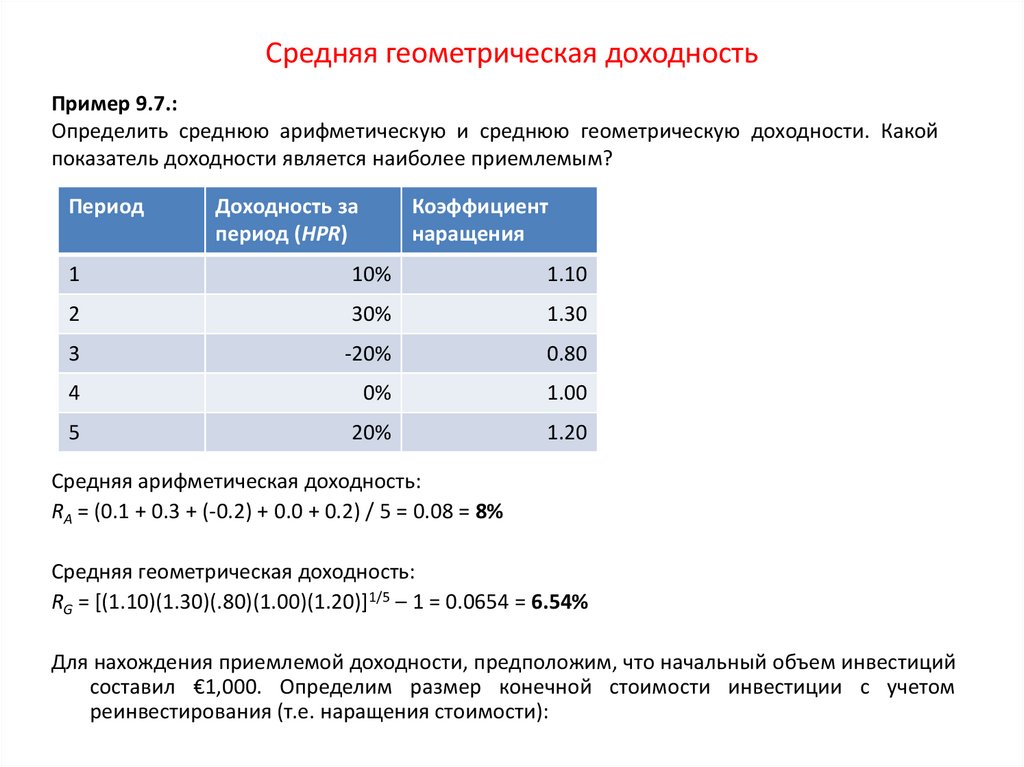
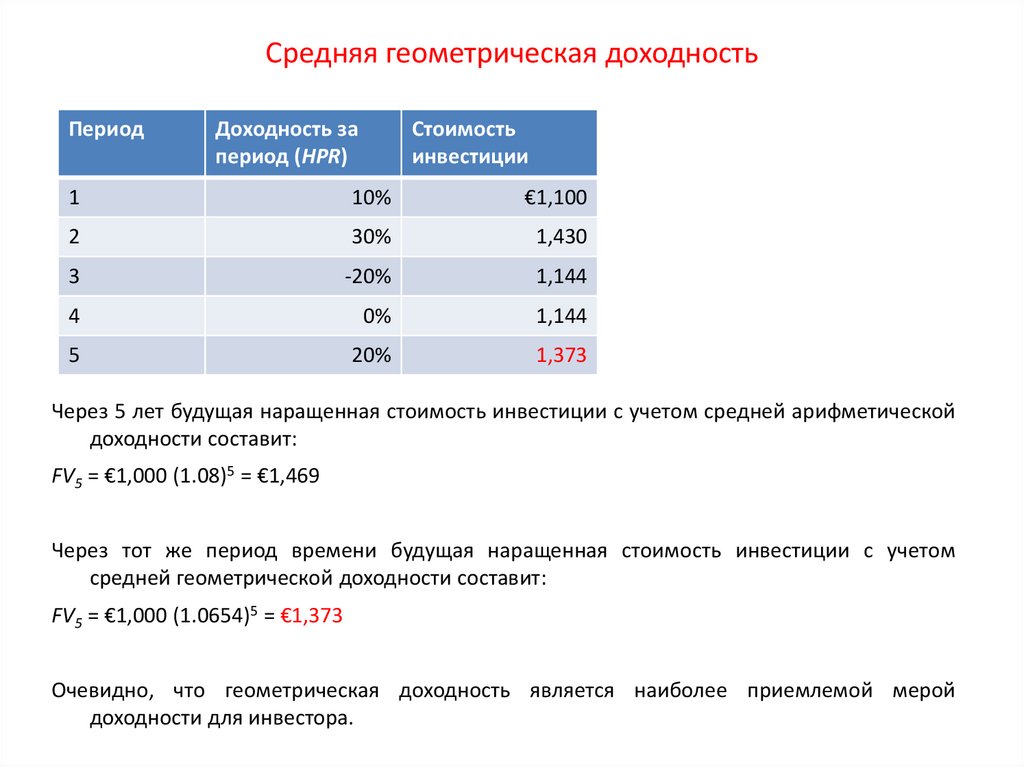










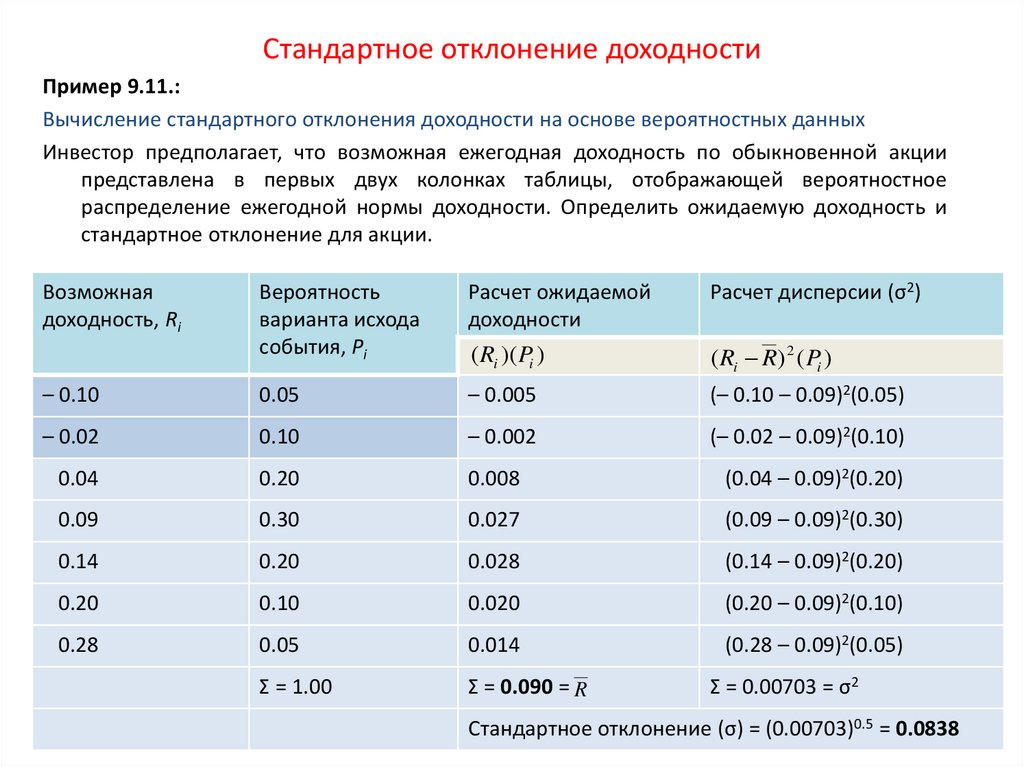

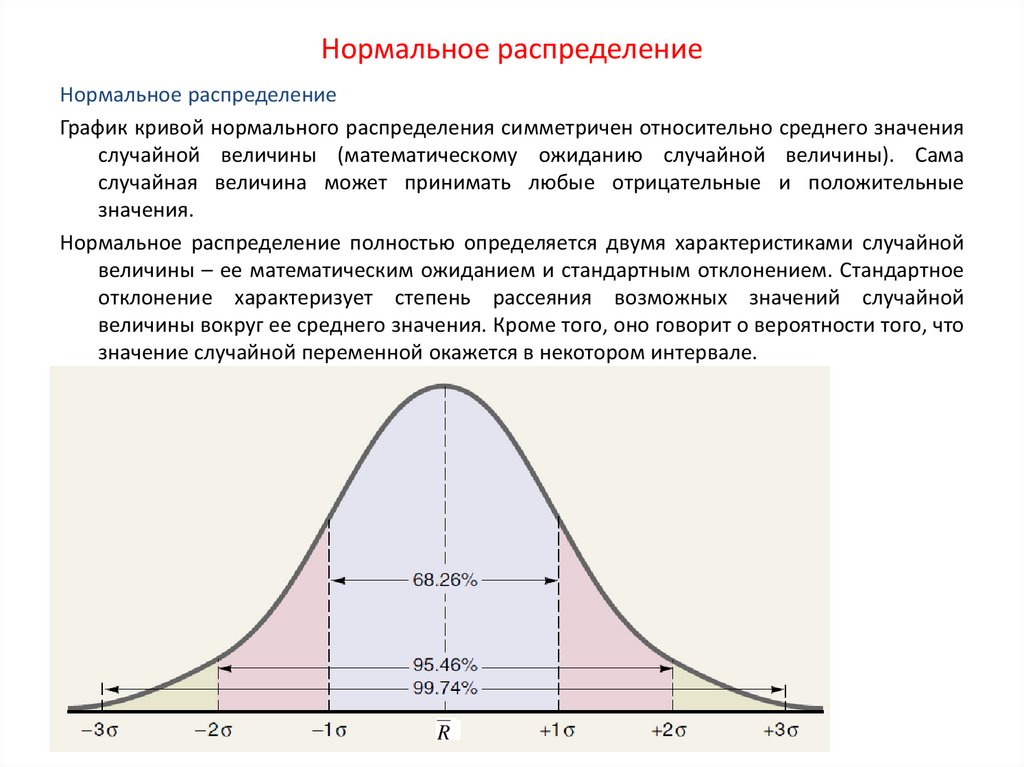


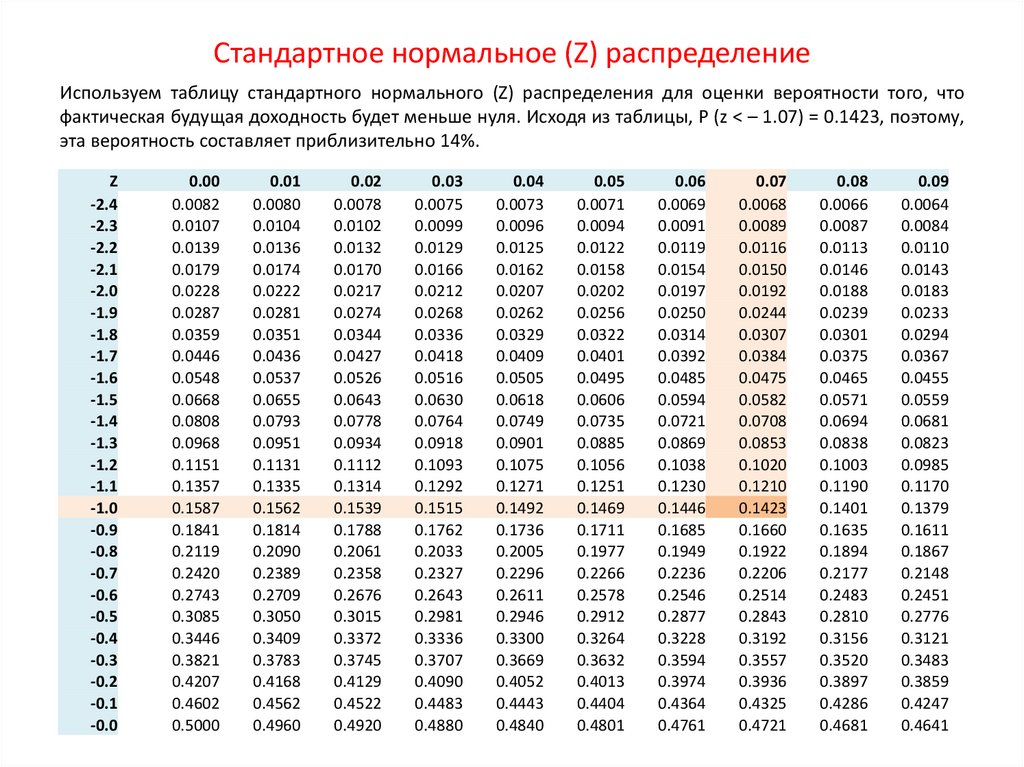


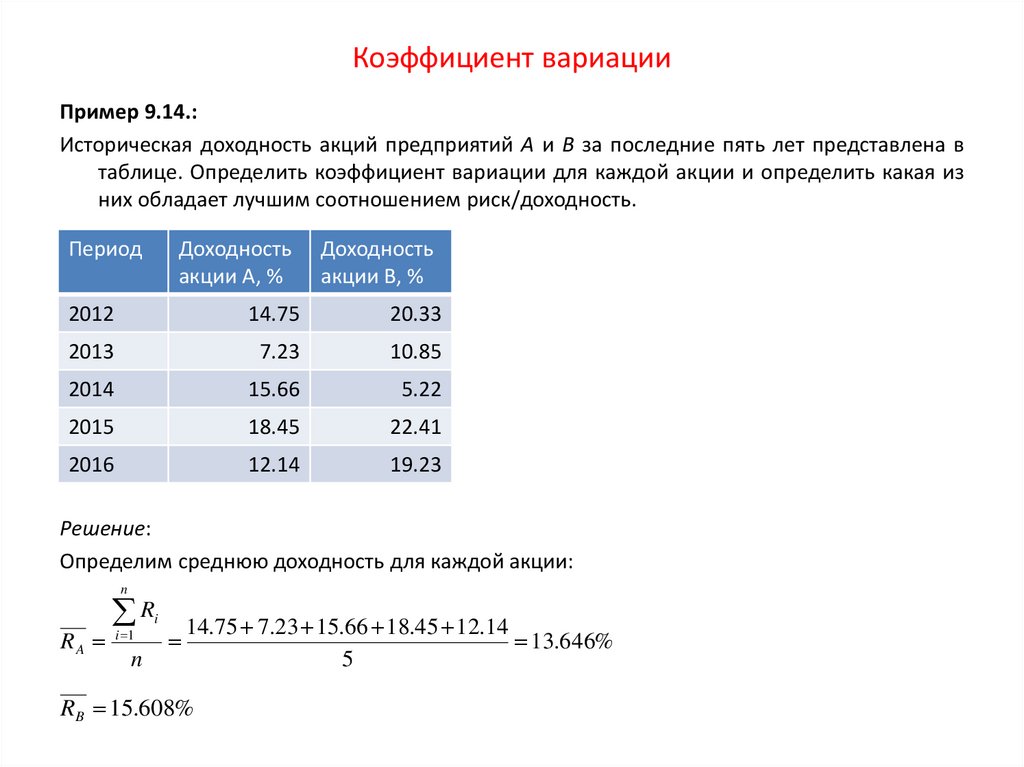






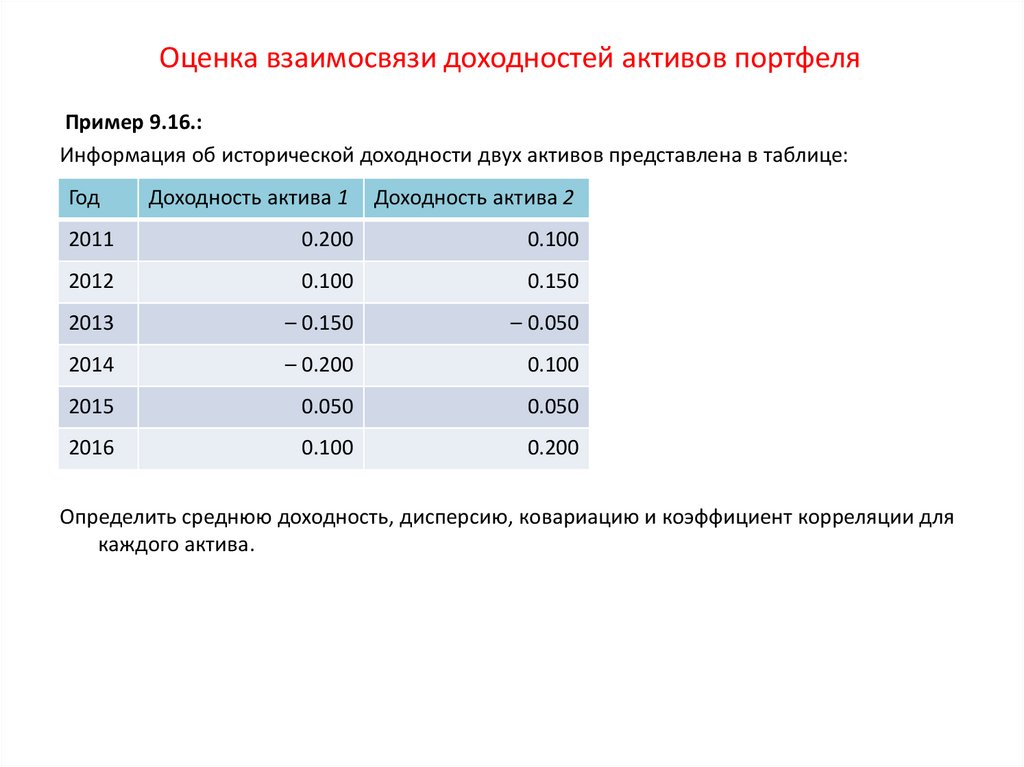
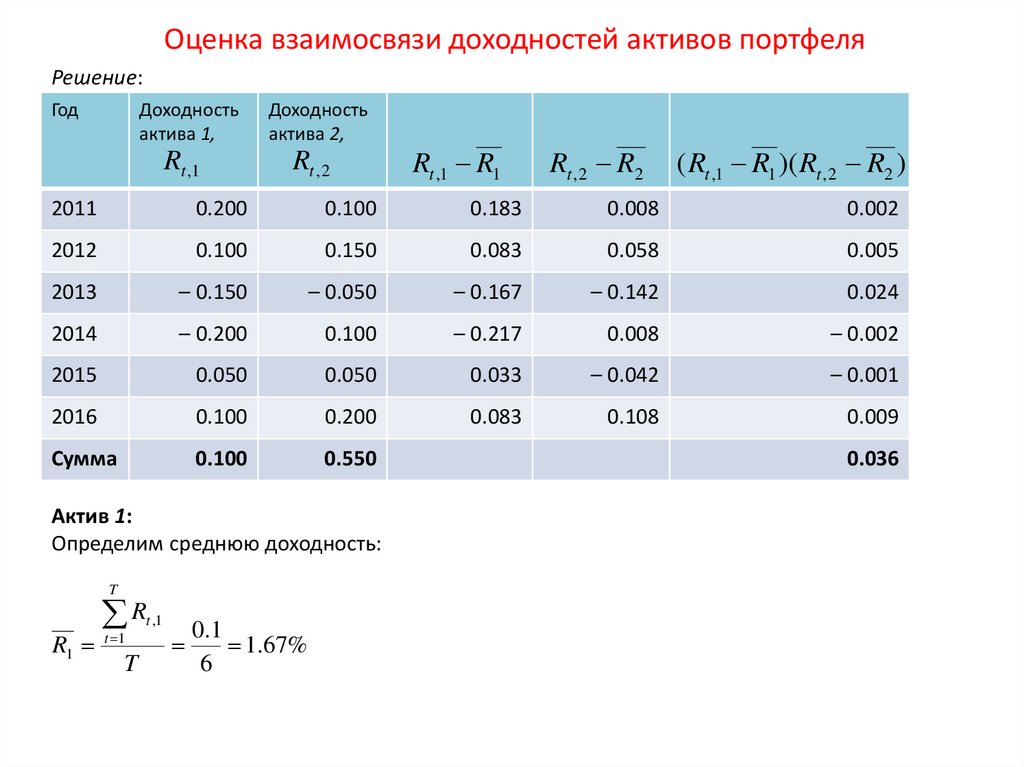


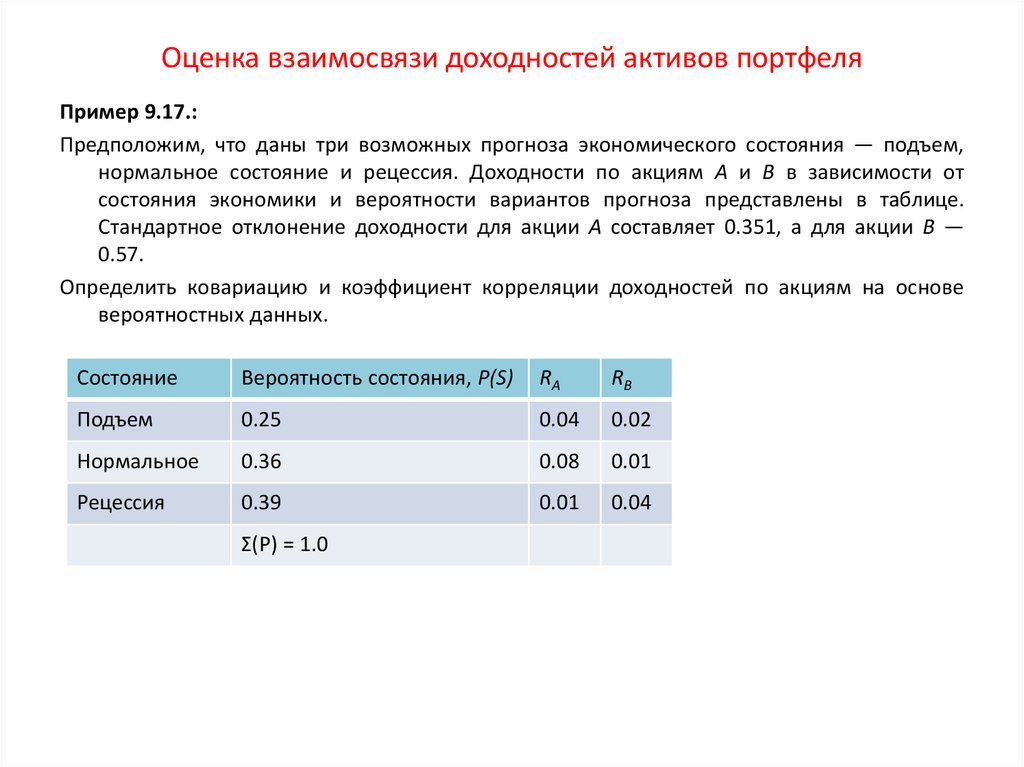



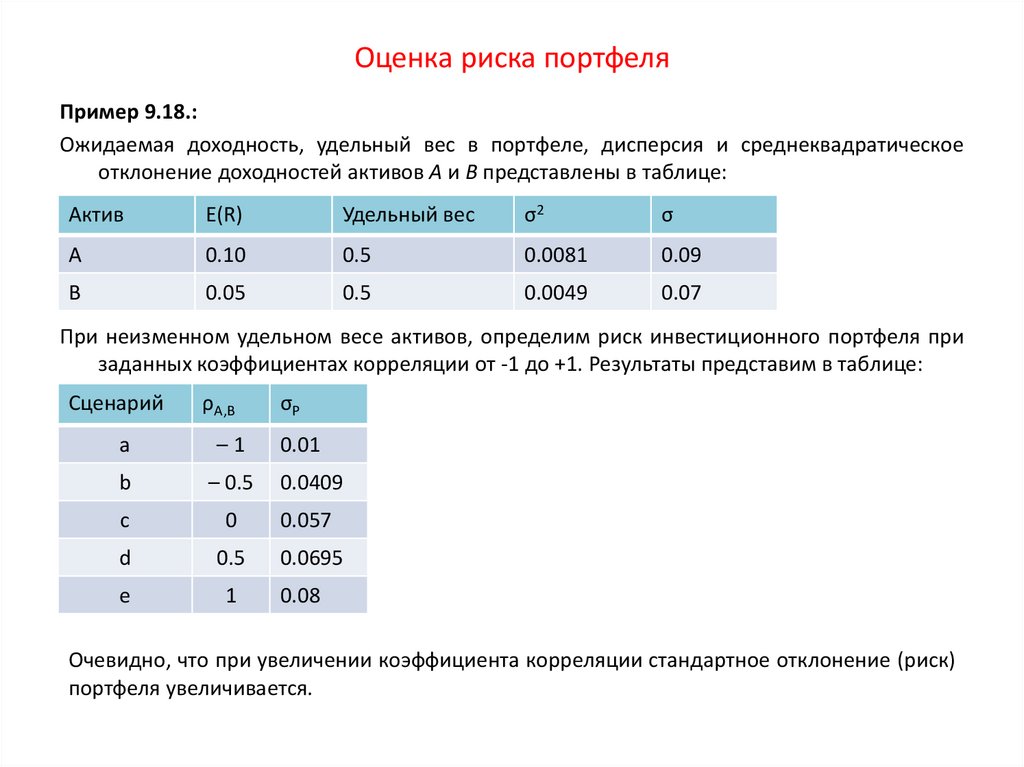
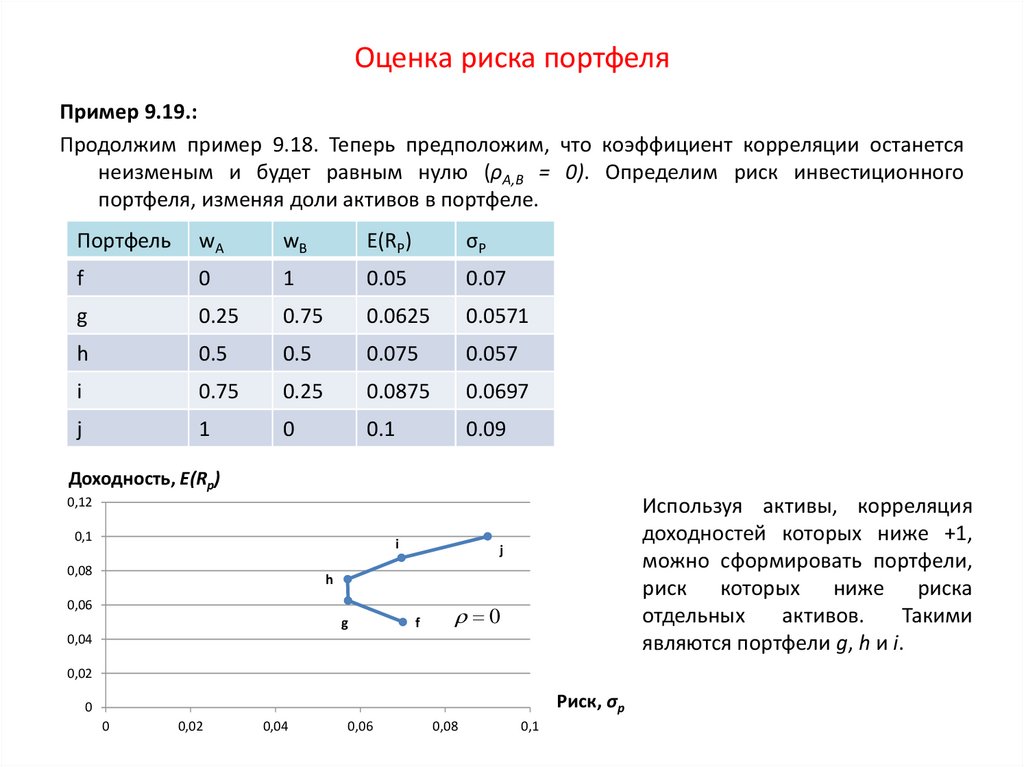
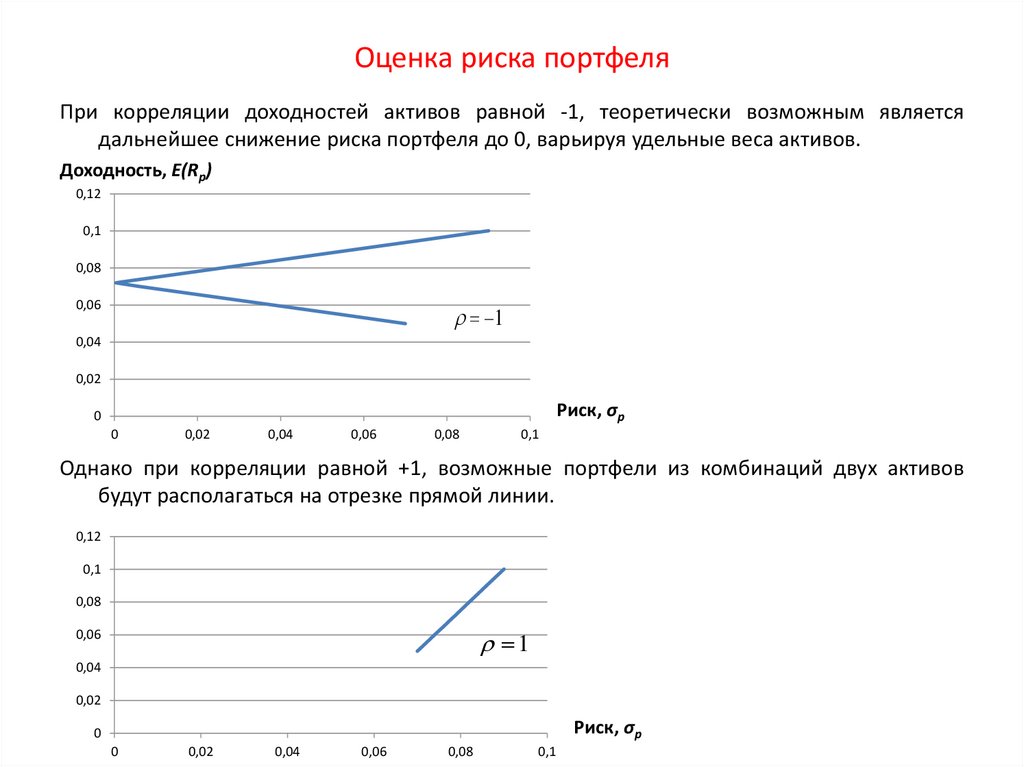





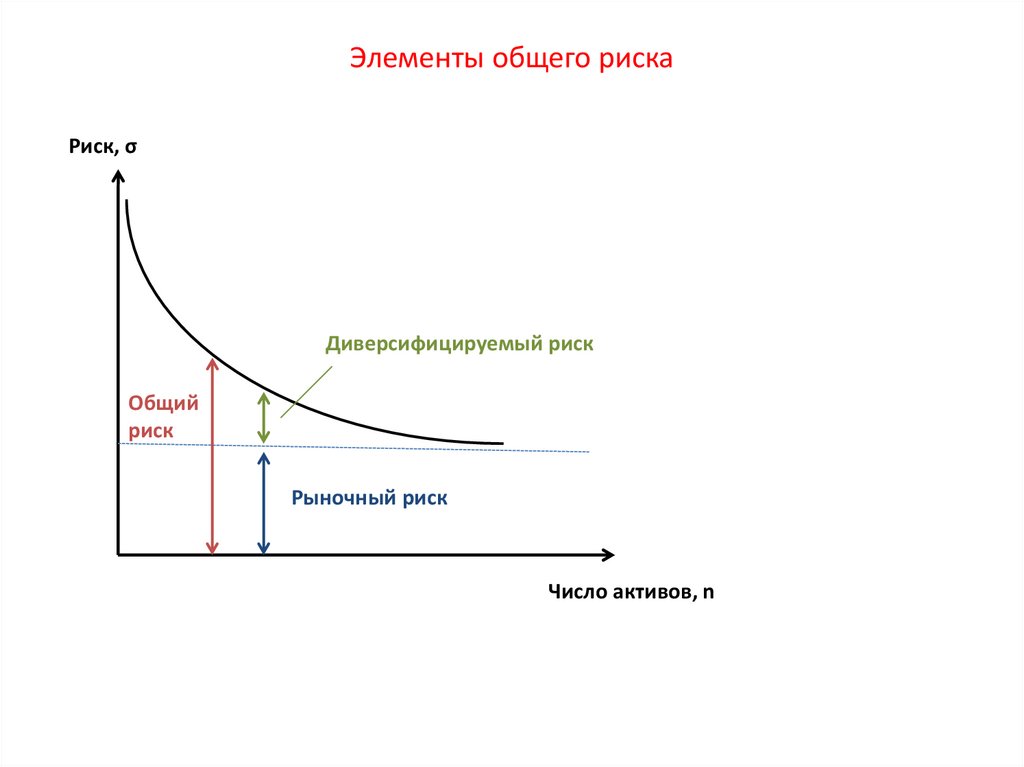
 Финансы
Финансы








