Похожие презентации:
Математическое обеспечение финансовых решений. Финансовые вычисления
1. Математическое обеспечение финансовых решений. Финансовые вычисления
1. Теория процентов2. Финансовые потоки, ренты
3. Облигации
1
2. Понятие процента
Величина b составляет долюот величины a , если
i
b ia
b
Величина
от величины
a
составляет
, если
p
b
a
100
p%
2
3. Наращение капитала по процентной ставке
Долю i величины капитала a называютпроцентной ставкой. Процентной ставкой.
Процент p связан с процентной ставкой
формулой p 100 i
За один период времени (например год)
капитал может увеличится на p% . Тогда
наращенный капитал вычисляется по
p
формуле
a
100
a a ia a (1 i )
3
4. Наращение капитала
Обозначим через S 0 первоначальнуюсумму капитала, через S1 сумму
капитала по истечении одного периода
(года), через i процентную ставку. Тогда
S
S
1
0
S1 S0 (1 i)
i
S0
Как вычислить наращение капитала за
несколько периодов ( n периодов).
4
5. Простые проценты
За первый период прирост капиталасоставляет величину iS0
В случае применения метода расчета по
формуле простых процентов считается,
что и в каждый последующий период
прирост капитала (например долга)
составляет величину iS0
Тогда за n периодов прирост
5
6. Простые проценты
Капитала составит величину niS0 .Таким образом сумма капитала Sn
образующегося через
периодов
вычисляется по формуле
Формула
Sn S0 niS0 S0 (1 ni)
n
Sn S0 (1 ni)
называется формулой простых процентов.
Множитель (1 ni ) называется
коэффициентом наращения.
6
7. Сложные проценты
Придлительных
сроках
кредитно
денежных
отношений
естественно
применять процентную ставку не к
первоначальному капиталу, а к капиталу
предыдущего периода. Т. е. полученные
проценты реинвестируются или другими
словами
происходит
капитализация
полученных процентов. В этом случае
Sn Sn 1 (1 i )
7
8. Сложные проценты
Т. О.S1 S0 (1 i) S2 S1 (1 i) S0 (1 i)(1 i) S0 (1 i)
S3 S2 (1 i) S0 (1 i) (1 i) S0 (1 i)
2
Sn S0 (1 i)
2
3
n
Последняя формула называется формулой
сложных процентов
n
(1 i )- множитель наращения за n периодов
8
9. Проценты за нецелое число периодов
Вформулы
простых
и
сложных
процентов можно подставить вместо
целого числа периодов n нецелое число.
В результате
t получим формулы
St S0 (1 ti)
St S0 (1 i )
t
Применяется также смешанный метод
вычисления
процентов t n, b за
периодов Sn S0 (1 i)n (1 bi) где n — целая
часть числа t , b — его дробная часть.
9
10. Учёт времени в днях.
tK
t
T
K
K 360
K 365(366)
10
11. Примеры
Пример 1. Ссуда 150000 руб. выдана на 4 годапод 20% годовых (простые проценты). Какова
величина накопленного долга?
20
S4 S0 (1 4i ) 150000 1 4
270000
100
Пример 2. Вклад в размере 3000 руб. положен
в банк на депозит 10 марта под 15% годовых по
схеме сложных процентов. Какую сумму
вкладчик получит 22 октября? (Считаем, что в
месяце 30 дней, а году 360 дней).
11
12. Примеры (продолжение)
1213. Решение примера 3
Подпроцентом
или
процентными
деньгами
подразумевается
разность
между наращенной суммой и величиной
вклада. В случае простых процентов эта
разность вычисляется по формуле
18
I tiS0 Отсюда
0,15S 10000
12
Следовательно
10000 12
0
S0
18 0,15
44444, 44
13
14. Кратное начисление процентов
St , mm 12
St , m
m 4
i
S0 1 mt S0 (1 it )
m
14
15. Кратное начисление процентов
В случае сложных процентовSt , m
i
S0 1
m
mt
Пример. В банк положен депозит в
размере 1000 руб. под 10% годовых по
схеме
сложных
процентов.
Найти
величину депозита через 3 года при
начислении процентов 1; 4; 6; 12 раз в
году.
15
16. Решение примера
Вычислим по приведённой формулеS3;1 1000(1 0,1)3 1331
S3;4
S3;6
s3;12
0,1
1000 1
4
3 4
0,1
100 1
6
0,1
s0 1
12
1344,9
3 6
1346,5
3 12
1348, 2
16
17. Непрерывное начисление процентов
Если частота начисления сложных процентовнеограниченно возрастает, то имеет место
непрерывное
начисление
процентов.
Наращенная величина вычисляется с помощью
второго замечательного предела
mt
i
St , lim St ,m lim S0 1 S0 eit
m
m
m
Процентную ставку называют силой роста и
обозначают через . Формула непрерывного
начисления процентов S (t ) S e t
0
17
18. Эквивалентность процентных ставок
Схемыначисления
процентов
называются
эквивалентными,
если
коэффициенты наращения по этим
схемам
одинаковы.
Исследуем
эквивалентность простой и сложной
формул начисления процентов, исходя из
условия Sn ,прост Sn ,сложн , т.е.
n
1 iсл 1
n
S0 (1 niпр ) S0 1 iсл Откуда iпр
n
18
19. Эффективная процентная ставка
Для каждой схемы начисления процентовможно найти такую годовую ставку сложных
процентов
iэфф , начисление по которой
эквивалентно начислению по первоначальной
схеме. Ставка iэфф называется эффективной
процентной ставкой.
Найдём эффективные процентные ставки для
кратного
и
непрерывного
начисления
процентов.
19
20. Эффективная процентная ставка
Обозначим через j номинальную процентнуюставку при p-кратном начислении процентов.
Тогда
S0 1 iэфф
t
j
S0 1
p
pt
p
iэфф
j
1 1
p
1
j p 1 iэфф p 1
В случае непрерывного начисления процентов
с силой роста
t
S0 1 iэфф S0e t iэфф e 1
20
21. Дисконтирование
S0St
S0
St
21
22. Математическое дисконтирование
St
В случае простых процентов S0
1 t i
St
В случае сложных процентов S0
t
(1 i )
В случае кратного начисления процентов
и непрерывного начисления процентов
St
формулы имеют вид
S
St
S0 t
e
0
i
1 p
pt
22
23. Банковский учёт
Банковский учёт ─ это покупка банкомденежных обязательств по цене меньшей
номинальной.
Примером может служить вексель ─ долговая
расписка,
содержащая
обязательство
выплатить определённую денежную сумму
(номинал) в определённый срок.
В случае покупки денежного обязательства из
номинальной стоимости удерживается
23
24. Банковский учёт
Дисконт I t так что S0 St ItДисконт вычисляется с помощью учётной
ставки d
Различают простую и сложную учётную
ставку.
В случае простой учётной ставки
S0 St (1 td )
It St d t
t
Для сложной учётной ставки S0 St (1 d )
24
25. Пример 1
Вексельстоимостью
100000
руб.
учитывается за 4 года до погашения по
сложной учётной ставке 15% годовых.
Найти
сумму,
получаемую
векселедержателем,
и
величину
дисконта.
Сумма получаемая векселедержателем
равна S4 100000(1 0,15)4 52200,6 Величина
дисконта равна I4 S4 S0 100000 52200,6 47799,3
25
26. Пример 2
Клиент имеет вексель на 16000 у.е.,который он хочет учесть 10.01.2014 в
банке по сложной учётной ставке 8%.
Какую сумму он получит, если срок
погашения 10.07.2014?
Продолжительность
финансовой
T0 30 6
t
0, 49
операции составит
K
365
Сумма, полученная клиентом, составит
S0,49 16000(1 0,08)
0,49
15359,46
26
27. Пример 3
S (0)7
d 1
1
0,099
S (1)
7,77
27
28. Эффективная учётная ставка
Пусть d эфф ─ годовая (эффективная)учётная ставка (ставка дисконтирования)
при кратности начисления m . Эквивалент.
эффективная ставка определяется
исходя из принципа эквивалентности:
d
n
S0 (1 d эфф ) S0 1
m
nm
d
d эфф 1 1
m
m
Обратно учётная ставка d выражается
через эффективную учётную ставку d эфф
d m 1 m 1 d эфф
28
29. Вычисление параметров финансового процесса
Формулы наращения и дисконтированияSn S0 (1 i ) n
S0 Sn (1 d ) n
позволяют вычислять процентную или учётную
ставку, а также срок платежа, если остальные
параметры известны.
Пример. На какой срок необходимо положить в
банк 12000 руб., чтобы накопить 15000 руб.,
если банк принимает вклады под простые
(сложные) 8% годовых?
29
30. Решение примера
Для простых процентов воспользуемсяформулой Sn S0 (1 ni) Откуда 15000 1
n 12000 3,125
15000 12000(1 0,08n)
0,08
Для сложных процентов воспользуемся
S0
n
n
формулой
Sn S0 (1 i ) (1 i) S
n log1 i
Sn
ln
Sn
S0
S0 ln(1 i )
n
15000
ln
ln1, 25
12000
n
2,9
ln(1 0,08) ln1,08
30
31. Удвоение капитала. Правило 70
n31
32. Учёт инфляции
Говорят, что инфляция составляет долюα в год. Если стоимость товара за год
увеличивается в (1+α) раз. Инфляция
уменьшает реальную ставку процента.
При инфляции деньги обесцениваются в
1+α раз, поэтому реальный эквивалент
наращенной
за
год
суммы
будет в (1+α) меньше S1 S0 (1 )
32
33. Влияние инфляции на ставку процента
S0 (1 i ) S0 (1 i )S1
S
1
1
1
S0 (1 (i ))
1 i
S0
S0 1 i
1
1 1
Через i обозначена процентная ставка с
учётом инфляции ( i по прежнему
номинальная ставка без учёта инфляции)
33
34. Формула Фишера
Таким образом получается формуластавки процента с учётом инфляции,
называемая формулой Фишера
i
i
1
При
малой
инфляции
реальная
процентная ставка меньше номинально
примерно на величину инфляции.
34
35. Формула Фишера
При достаточно высокой инфляцииреальная ставка
может стать
i
отрицательной.
В
такой
ситуации
кредитор будет работать себе в убыток, а
заемщик обогащаться. Чтобы этого не
произошло, необходимо скорректировать
номинальную процентную ставку i , по
которой происходит наращение.
Она
должна по крайней мере не быть ниже
ставки инфляции i .
35
36. Пример
Какую ставку должен установить банк, чтобыпри инфляции 8% годовых он мог иметь 10%-ю
доходность?
i
Решим уравнение Фишера i
1
относительно
i i (1 ) 0,1(1 0,08) 0,08 0,188
Итак ответ 18,8% превышает простой ответ
18%, получаемый сложением темпа инфляции
и номинальной процентной ставки.
36
37. Темп инфляции за несколько периодов
Пустьтемпы
инфляции
за
последовательные периоды времени
t1 , t2 ,..., tn равны 1 , 2 ,..., n соответственно.
Найдём темп инфляции за период
t . t1 t2 ... tn Ввиду того, что уровень цен
вычисляется исходя из цен предыдущего,
а не начального периода, темп инфляции
за период t t1 t2 ... tn равен
1 1 1 2 ... 1 n 1
37
38. Темп инфляции за несколько периодов
Как видим суммарный темп инфляции неравен сумме инфляций. Для равных
темпов инфляции 1 2 ... n общий
темп вычисляется по формуле
1 1 1
n
Зная суммарный темп инфляции
Можно вычислить темп инфляции 1
За малый период
1 n 1 1
38
39. Примеры
t1 , t2t1 t2
1 1 1 2 1 1 2 1 2 0,1 0,2 0,1 0,2 0,32
39
40. Примеры
1 1 1 (1 0,02) 1 26,8%12
12
40
41. Финансовые потоки
Платёж P , произведённый в моментвремени t
, называется финансовым
событием и обозначается упорядоченной
парой ( P, t ) или (t , P)
Конечная
или
бесконечная
последовательность
финансовых
событий ( P0 , t0 ),( P1 , t1, ),( P2 , t2 ),...,( Pn , tn )
Называется дискретным финансовым
потоком.
41
42. Приведённая величина финансового потока
Финансовыепотоки
символом CF (cash flow)
обозначатся
CF {( P0 , t0 ),( P1 , t1 ),...,( Pn , tn )
Напомним, что деньги имеют временную
ценность.
Это
не
позволяет
непосредственно суммировать платежи,
относящиеся к различным моментам
времени.
42
43. Приведённая величина финансового потока
Для того, чтобы вычислить величину потока вкакой то момент времени
t необходимо
каждый платёж привести к этому моменту
времени по некоторой процентной ставке i ,
которая
предполагается
известной
и
неизменной для всего потока, и затем
суммировать эти дисконтированные платежи.
Обычно дисконтирование происходит по схеме
сложных процентов.
i
43
44. Приведённая величина финансового потока
tt
PVt
P0
P1
PVt
...
t0 t
t1 t
(1 i )
(1 i )
44
45. Современная и будущая величина финансового потока
t0 0PV
P1
P2
PV P0
...
t1
t2
(1 i )
(1 i )
n
P P0 (1 i) P1 (1 i) ... Pn (1 i) Pk (1 i)
t t0
t t1
t t0
t t k
k 0
45
46. Будущее накопленное значение
FVt (CF , i)FVt
t tn tn tk
(1 i )
t
FVt FVtn (1 i)
t tn
tn
t tn
46
47. Средний срок финансового потока
4748. Средний срок потока платежей
PnP1 P2 ... Pn
P1
P2
...
(1 i )t1 (1 i )t2
(1 i )tn
(1 i )t
x
(1 i) 1 ix
Pt
1 1 ... Pn t n
t
P1 ... Pn
48
49. Дюрация потока платежей
Формула среднего срока потока платежейявляется приближенной так не учитывает
срока поступления каждого платежа.
Если все платежи привести к начальному
моменту
времени
(или
любому
одинаковому моменту времени), то по
аналогии со средним сроком потока
платежей получим точную среднюю
продолжительность потока, называемую
дюрацией (duration).
49
50. Дюрация
5051. Пример
Найти средний срок потокаCF {(0,100),(1,200),(2,400),(3,100)}
По предыдущей формуле
Pt
100 0 200 1 400 2 100 3 1300
1 1 ... Pn tn
t
1,025
P1 ... Pn
100 200 400 100
800
Если все платежи положительные, то t1 t tn
в общем же случае средний срок потока может
лежать вне временного интервала платежей.
51
52. Обыкновенные ренты
Поток положительных платежей, разделённыхравными
временными
интервалами,
называется финансовой рентой, или просто
рентой. Промежуток времени между двумя
последовательными платежами называется
периодом ренты (rent period, payment period).
Считается, что каждый платёж производится
либо в начале соответствующего периода,
либо в конце.
52
53. Обыкновенные ренты
В первом случае ренту называютавансовой или пренумерандо (annuity
due), во втором ─ постнумерандо
(ordinary annuity). Ренты с конечным
числом платежей называют конечными.
Промежуток времени между началом
первого
периода
и
окончанием
последнего называется сроком конечной
ренты.
53
54. Обыкновенные ренты
Ренты с бесконечным числом платежейназываются бесконечными, вечными или
перпетуететами (perpetuity). Если же платежи
равны меду собой, ренту называют постоянной.
В дальнейшем будем рассматривать именно
постоянные ренты.
Рента описывается следующими параметрами:
Размером отдельного
платежа (член ренты),
периодом и сроком ренты, числом платежей в
году p (p-срочные ренты). Существуют также
непрерывные ренты, p .
54
55. Коэффициенты приведения и наращения рент
Ренты характеризуются также числомначисления процентов (k-кратные ренты).
В случае когда период постоянной ренты
равен одному году рента называется
годовой рентой или аннуитетом (annuity).
Найдём
текущую
(приведённую)
стоимость A ренты постнумерандо
{(0,0),( R,1),( R,2),...,( R, n)}
55
56. Коэффициенты приведения и наращения рент
Вычислим приведённую величину поR
R
R
формуле
A
...
2
n
1 i (1 i )
(1 i )
Величина A является суммой n членов
геометрической прогрессии с первым
1
R
членом b1
и знаменателем q
1 i
1 i
Воспользуемся формулой суммы n
56
57. Коэффициенты приведения и наращения
членов геометрической прогрессииSn
b1 1 q n
1 q
R
1
1
1 i (1 i ) n
A
1
1
1 i
1
n
1
(1
i
)
1 (1 i) n
1 i
R
1 i 1
i
1 i
Таким образом
а величина an i
1 (1 i )
i
1 (1 i ) n
A R
i
n
57
58. Коэффициент наращения
коэффициентом приведения ренты.Наращенная сумма определяется
n 1
n 2
равенством S R(1 i) R(1 i) ... R
которая также является суммой
геометрической прогрессии с первым
членом b1 R и знаменателем (1 i )
n
n
1
(1
i
)
(1
i
)
1
Тогда S R
R
1 (1 i )
Величина
sn i
(1 i )
i
i
n
58
59. Рента пренумерандо
называется коэффициентом наращенияренты. Коэффициенты приведения и
наращения связаны формулой
sn i an i (1 i )
n
Найдём текущую (приведённую)
стоимость A ренты пренумерандо
{( R,0),( R,1),( R,2),...,( R, n 1),(0, n)}
Эта приведенная величина представляет
собой сумму
59
60. Рента пренумерандо
геометрической прогрессииA R
R
R
...
1 i
(1 i ) n 1
1
С первым членом R и знаменателем
1 i
1
Тогда
R 1
n
n
A
Множитель
(1 i )
1 (1 i )
R
(1 i )
1
i
1
1 i
n
an i
1 (1 i )
(1 i )
i
60
61. Рента пренумерандо
называется коэффициентом приведенияренты пренумерандо.
Наращенная сумма ренты пренумерандо
S R(1 i)n R(1 i) n 1 ... R(1 i)
Также
вычисляется
как
сумма
геометрической прогрессии и равна
(1 i ) n 1
S R
(1 i )
i
61
62. Связь между приведённой величиной и наращенной суммой аннуитета
Коэффициент при Rназывается
множителем
наращения
ренты
пренумерандо
n
(1 i) 1
sn i
(1 i )
и равен
i
Приведённая величина A и наращенная
сумма S ренты пренумерандо связаны
между собой простым соотношением
S A(1 i )
n
62
63. Расчет параметров ренты
Действительноn
1 (1 i)
(1 i) 1
n
A(1 i ) R
(1 i ) R
S
i
i
n
n
Рассмотрим параметры, характеризующие ренту: срок ренты n ,
размер
отдельного платежа R
, процентную
ставку i
, наращенную сумму A ,
приведённую величину S .
63
64. Расчёт параметров ренты
Эти величины являются зависимыми,поэтому одни из них можно выразить
через другие.
1. Если известны A, i, R , то n
1 (1 i ) n
вычисляется из уравнения A R
i
Ai
Ai
n
n
1 (1 i) (1 i) 1
Ai
ln 1
R
R
Ai R
n log1 i 1
R ln(1 i)
64
65. Расчёт параметров ренты
Ailn 1
R
n
ln(1 i )
2. аналогично предыдущему случаю, если
известны S , i, R то n находится из
уравнения S R (1 i)n 1
S
ln 1
i
3. Если известны n, i, A то
R
n
ln(1 i )
Ai
R
1 (1 i ) n
65
66. Расчёт параметров ренты
Si4. Если известны n, i, S ,то R
(1 i ) n 1
5. Если заданы n, R, A , то процентная
ставка i определяется из уравнения
n
1 (1 i)
A R
i
6. Если заданы n, R, S то процентная
ставка определяется из уравнения
66
67. Расчёт параметров ренты
(1 i ) 1S R
i
n
Последние два уравнения не решаются
аналитически, их можно решить только
приближённо с любой степенью точности.
Пример.
Найти
срок
ренты
постнумерандо, если известны S=2000,
i=15%, R=100.
67
68. Расчёт срока ренты (решение примера)
iSВоспользуемся формулой
2000 0,15
ln 1
Тогда
ln 4
100
n
ln(1 0,15)
ln1,15
ln 1
R
n
ln(1 i )
9,9
Таким образом годовая рента может
выплачиваться 10 лет. Но в конце
десятого года наращенная сумма
немного превысит величину S 2000
поэтому платёж R в конце десятого
года можно уменьшить.
68
69. Вечные ренты
Если рента выплачивается бесконечнодолго,n , то наращенная сумма не
существует, она тем более бесконечна,
( S ).
Однако приведённая
величина существует. Можно вычислить
сумму денег A , которую надо положить
на счёт, чтобы из этой суммы ежегодно
выплачивался платёж R
69
70. Вечные ренты
Рассмотрим бесконечную последовательностьплатежей
{(0;0),( R;1),( R;2),...}
Приведённая сумма платежей определяется
как бесконечная сумма
R
R
A
...
2
1 i (1 i )
Эта сумма представляет собой сумму
бесконечно убывающей геометрической
прогрессии
2
b1 b1q b1q ...
70
71. Вечные ренты
и вычисляется по формулеВ нашем случае
1
R
q
b1
1 i
1 i
b1
1 q
Поэтому приведённая сумма
R
1
R
R
A
1 i 1 i
1 i 1 1
(1 i )
1 i
1 i
Множитель приведения
a i
1
i
71
72. Примеры
Пример1.
Найти
размер
вклада,
обеспечивающего получение в конце каждого
года 2000 руб. бесконечно долго при сложной
ставке 14% годовых
Решение. По формуле получим
R 2000
A
14285,71
i
0,14
Пример 2. Для бессрочной ренты определить,
что больше увеличит приведённую стоимость
этой ренты: увеличение рентного платежа на
1% или уменьшение процентной ставки на 1%?
72
73. Решение примера 2
0,01RR
1,01R
1,01A
i
i
0,99i
R
1,0101A
0,99i
73
74. P-срочная рента
7475. P-срочная рента в случае однократного начисления процентов (k=1)
nnp
( p)
A
S ( p)
R
p(1 i )
R (1 i ) n 1
p (1 i ) 1 p 1
1
p
1 (1 i )
np
1 (1 i )
1
p
p
R 1 (1 i ) n
p (1 i ) 1 p 1
S ( p)
75
76. P-срочная рента с k-кратным начислением процентов
Если рентные платежи производятся p вгод, а проценты начисляются k раз в год,
то наращенная величина ренты
i kn
(1
) 1
вычисляется по формуле ( p ) R
k
S
p (1 i ) k p 1
k
А приведённая величина
kn
i
1 1
по формуле
R
k
A( p )
k
p
i p
1
1
k
76
77. P-срочная рента с непрерывным начислением процентов
k( p)
k
A
R 1 e
1
p e p 1
R e 1
1
p e p 1
ni
ni
S
( p)
k
77
78. Непрерывная рента
Переходя к пределу приp , получимнепрерывный
поток
платежей
с
постоянной плотностью
, называемую
R
непрерывной рентой. Находя предел при
n
R
1
(1
i
)
( p)
от
получим
A
p
p (1 i )
1
p
1
выражение для приведенной величины
непрерывной ренты ( )
1 (1 i ) n
A R
ln(1 i )
78
79. Непрерывная рента
Для наращенной суммы непрерывной рентыаналогичным образом
n
(1
i
)
1
( )
получаем формулу
S R
ln(1 i )
Найдём приведенную величину непрерывной
ренты с k-кратным начислением процентов как
предел
p-срочной
ренты
с
k-кратным
начислением процентов при
от
( )
( p ) получим
p
A lim A
k
p
k
nk
Ak( p )
i
1 1
R
k
1
p
i p
1 1
k
79
80. Непрерывная рента с k-кратным начислением процентов
Вычисляя предел находимnk
Ak( )
i
1 1
k
R
i
k ln 1
k
Аналогичным
образом
наращенную
величину
ренты
с
k-кратным
процентов
вычисляем
непрерывной
начислением
80
81. Непрерывная рента с непрерывным начислением процентов
nkS k( )
i
1 1
k
R
i
k ln 1
k
Переходя в последних формулах к
пределу при k
получаем формулы
для
вычисления
приведённой
и
наращенной
A , , S , величин
непрерывной ренты с непрерывным
начислением процентов
81
82. Непрерывная рента с непрерывным начислением процентов
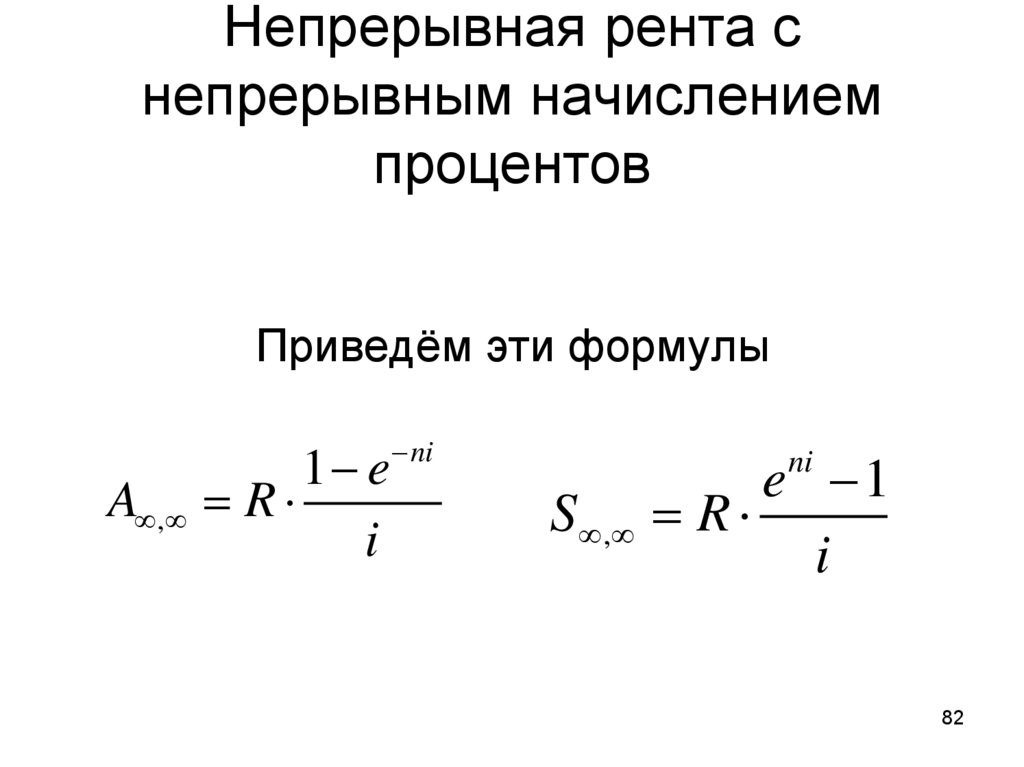
Приведём эти формулыA ,
1 e
R
i
ni
e 1
R
i
ni
S ,
82
83. Задача 1
Определитьпериод,
за
который
начальный капитал в размере 46000 руб.
вырастет до 75000 руб., если ставка
простых процентов равна 15% годовых.
Выразим период t из равенства
75000 46000 1 t 0,15
Откуда
75000
1
t 46000
4, 202
0,15
83
84. Задача 2
На счет в банке кладется сумма вразмере 20000 руб. на 4 года под 11%
годовых по схеме простых процентов с
дальнейшей
пролонгацией
на
последующие 2 года под 6% годовых по
той же схеме. Найти размер вклада через
6 лет. Определить наращенную сумму,
если вклад изымается через 4 года и
кладется на новый счет на 2 года по той
же схеме.
84
85. Задача 2
В первом случае проценты начисляются напервоначальную сумму 20000. Во втором
последние 2 года проценты начисляются на
наращенную за
первые 4 года сумму
20000(1+4∙0,11).
Поэтому в первом случае наращенная сумма
равна 20000(1+4∙0,11)+2000∙2∙0,06=31200
Во втором 20000(1+4∙0,11)(1+2∙0,06)=32256
85
86. Задача 3
В банк положена сумма 150000 руб.сроком на 6 лет по ставке 14% годовых.
Найти наращенную сумму, величину
полученного процента и эффективную
процентную ставку для следующих
вариантов начисления процентов: а)
полугодового; б) ежеквартального; в)
ежемесячного; г) непрерывного при силе
роста 14%.
86
87. Задача 3
Воспользуемся формуламиi
S n S0 1
k
а)
kn
k
iэфф
j
1 1
k
2 6
0,14
S6 150000 1
337828,74
2
2
iэфф
0,14
1
1 0,1449 14, 49%
2
87
88. Задача 3
б)0,14
S6 150000 1
4
4 6
342499, 27
4
iэфф
в)
0,14
1
1 0,1475 14,75%
4
12 6
0,14
S12 150000 1
12
345769,74
12
0,14
iэфф 1
1 0,1493 14,93%
12
88
89. Задача 3
г) наращенная сумма вычисляется поформуле S S e n а эффективная
n
0
процентная ставка по формуле iэфф e 1
S6 150000e
6 0,14
347455,04
iэфф e 1 0,1503 15,02%
0,14
89
90. Задача 4
Для создания премиального фонда один раз вгод производятся взносы в размере 15000 руб.
На вносимые средства начисляются проценты
под 12% годовых. Определить размер фонда
через 7 лет в следующих случаях: а)
поступление
средств
в
конце
года,
ежеквартальное
начисление
процентов;
б) поступление средств в конце квартала,
начисление процентов 6 раз в году;
в) ежемесячное поступление средств и
ежеквартальное начисление процентов.
90
91. Задача 4
Воспользуемся формулой вычислениянаращенной суммы p-кратной ренты при
k-кратном начислении процентов
kn
S n( ,pk)
а) p=1, k=4
i
1 1
R k
k
p
i p
1 1
k
б) p=4, k=6 в) p=12, k=4
91
92. Задача 4
4 7а)
0,12
1
1
4
S 15000
153424,77
4
0,12
1
1
4
6 7
б)
0,12
1
1
15000
6
S
161351, 47
6
4
0,12 4
1
1
6
4 7
в)
0,12
1
1
15000
4
S
162590, 29
4
12 0,12 12
1
1
4
92
93. Немедленные и отложенные ренты
tt
A
93
94. Пример 1
9495. Решение примера 1.
1 1 in
A R
Воспользуемся формулой
,
i
подставив A=1000000, R=100000, n=12.
Получим уравнение
относительно i
12
1000000 100000
1 1 i
i
10i 1 1 i
12
преобразуем это уравнение.
10 1 i 10 1 1 i 10 1 i 11 1 i 1 0
12
13
12
Обозначим x=1+i и запишем уравнение в
виде
f x 10x13 11x12 1 0
95
96. Решение примера 1.
Полученное уравнение можно решитьтолько приближённо. Решим его с
точностью до 0,01, найдя числа a и b,
такие что f(a) и f(b) имеют разные знаки, b
- a < 0,01 b и положив 0,5(b – a).
Вычислим последовательно f(1.02) =
-0,015<0, f(1,03) = 0,002>0, f(1,029) = 0,00056,
f(1,0294)
=
0,00043.
Следовательно
x=1,0292,
i=0,0292
(2,92%)
96
97. Пример 2
В течении 12 лет предполагается погасить долгв
размере
1000000
у.е.
платежами
постнумерандо по 100000 у.е. ежегодно.
Первые пять выплат были сделаны согласно
достигнутой договорённости. Затем было
решено на три года отложить погашение
задолженности и возобновить погашение
равными выплатами постнумерандо с конца
восьмого
года.
Каковы
должны
быть
погасительные платежи во втором периоде,
чтобы
выплатить
задолженность
в
установленный срок?
97
98. Решение примера 2
A1 R1 1 i
A2 R
5
100000
i
1 1 i
i
n
1 1 0,0292
0,025
1 i R
t
5
459018,69
1 1 0,0292
0,0292
4
1 0,0292 2,958276R
8
98
99. Решение примера 2
Приравниваясумму
величин двух выплат ко
долга, получим уравнение
погасительного платежа
периоде.
современных
всей сумме
относительно
во втором
A1 A2 1000000 459018,69 2,958266R 1000000
откуда
1000000 459018,69
R
182871,11
2.958266
99
100. Пример 3
Начало выплат годовой ренты со сроком12 лет, процентной ставкой 11%, рентным
платежом 16000 руб. отложено на 4,5
года. Найти современную величину
отсроченной ренты.
A R
1 1 i
i
n
1 i
t
16000
1 1 0,11
0,11
12
1 0,11
4,5
69948,47
100
101. Пример 4
В течение 7 лет предполагается погасить долгв размере 400000 у.е. равными выплатами в
конце каждого года. На остаток долга
начисляется 6% годовых. В каком случае
годовые расходы на обслуживание долга
возрастут больше и на сколько, если: а) будет
предоставлена годовая отсрочка, проценты за
этот период присоединяются к сумме долга, б)
ставка годовых процентов возрастёт на 0,25%?
101
102. Решение примера 4
102103. Решение примера 4
103104. Пример 5
Начало выплат квартальной ренты сосроком 7 лет, процентной ставкой 8,5%
годовых, рентным платежом 24000 руб.
отложено
на
три
года.
Найти
современную
величину
отсроченной
ренты.
Применив стандартную формулу,
n
получим
1 1 i
1 1,085 7
t
3
A R
i
1 i
24000
0,085
1,085 96175,82
104
105. Пример 6
Начало выплат квартальной ренты сосроком 7 лет, процентной ставкой 9,75%
годовых, рентным платежом 21500 руб.
отложено на 1,8 лет. Найти современную
величину А отсроченной ренты.
Применив стандартную формулу,
получим
n
7
1 1 i
1 1,0975
t
1,8
A R
1,0975 89265,03
1 i 21500
i
0,0975
105
106. Конверсия рент
Бываютситуации,
когда
возникает
необходимость изменить условия выплаты
ренты, заменив одну ренту другой или разовым
платежом, а также заменить несколько рент с
разными платежами одной или опять же
несколькими другими рентами. Во всех
вышеперечисленных случаях производится
конверсия рент, подчиняющаяся следующему
простому правилу.
106
107. Конверсия рент
Современные величины старой (старых)и новой (новых) рент должны быть равны.
Это следует из предположения о том, что
конверсия рент не должна менять
финансового положения сторон, т.е
должен
соблюдаться
принцип
финансовой
эквивалентности
(финансовой справедливости) Алгоритм
расчета
параметров
новой
ренты
следующий.
107
108. Конверсия рент
1. Определяется современная величина старой(старых) ренты.
2. В случае объединения рент это величины
складываются и дают современную величину
новой ренты.
3. Зная современную величину новой ренты,
рассчитываются параметры новой ренты, такие
как размер отдельного платежа R, срок ренты
n, процентная ставка i.
108
109. Пример 1.
Заменить обычную (годовую) ренту спараметрами R1 200, n 5, i 10%
срочной
(квартальной) рентой с параметрами
R2 100, i 10% .
Найдём
сначала
приведённую величину годовой ренты
A R
1 1 i
i
n
200
1 1 0,1
0,1
5
200 3,79 758
и приравняет её к приведённой величине
квартальной ренты с неизвестным
параметром n
R2 1 1 i
100 1 1 0,1
1 1,1 n
n
A
25
1036,
75
1
1,1
1
1
p
4
0,
024
1 i p 1
1 0,1 4 1
n
n
109
110. КОНВЕРСИЯ РЕНТ
110111. Решение примера 2
Найдём современные величины обеихR 1 1 i
1300 1 1,08
рент
A
6187,15
n
1
A2 R
1 1 i
i
n
p 1 i 1 p 1
1 i
t
6
4 1 0,08 0,25 1
1 1,08 5
1500
1,08 t 5989,07 1,08 t
0,08
Приравнивая эти величины, находим t.
ln
5989, 07 1, 08 t 6187,15 t
6187,15
5989, 07
0, 423
ln1, 08
111
112. Консолидация рент
При замене нескольких рент однойрентой
имеет
место
равенство
A Ai
современных величин
i
Пример1. консолидируйте три ренты
постнумерандо с параметрами R1 1000 ,
n1 3 , R2 1500, n2 5 , R3 2000 , n3 7 , i 10%
четырехлетней рентой постнумерандо с
i 15%
112
113. Решение примера 1
Вычислим современные величины трёхконсолидируемых
рент
и
консолидирующей ренты по формуле
3
1 1 i
1 1 0,1
A R
A 1000
2486,85
n
1
i
A3 2000
A R
1 1 0,1
1 1 0,15
0,1
0,1
7
9736,84
4
0,15
A A1 A2 A3
2,855R
A2 1500
1 1 0,1
0,1
5
5686,18
Найдём R из равенства
2,855R 2486,85 5686,18 9736,84 R 6273,16
113
114. Пример 2
Долг 100000 у.е. должен быть погашен втечение 10 лет равными платежами в конце
каждого года. На остаток долга начисляется 7%
годовых. После 5 лет выплат должник решил
гасить задолженность равными выплатами в
конце каждого полугодия. Явившись в банк в
конце девятого года должник решил погасить
задолженность разовым платежом. Какую
сумму он при этом заплатит.
114
115. Решение примера 2
1 1 in
Применяя формулу A R i приведённой
величины ренты, найдём регулярный
10
1 1 0,07
платёж R . Откуда 100000 R
0,07
. Далее найдём первую
100000 0,07
R
14237,75
10
1 1.07
часть долга (выплаченную
за первые
5
пять лет) A1 14237,75 1 1 0,07 58525,19 и остаток
0,07
A2 100000 58525,19 41474,81
115
116. Решение примера 2
AR 1 1 i
n
1 i
t
p 1 i 1 p 1
По формуле
найдём размер
регулярного платежа R при выплате второй
части долга, полагая А=41474,81; n=5; i=0,07;
p=2; t=5.
5
5
2 41474,8 1,07 1
1
1,07
1,07
R
R
13947,3
41474,81
5
5
1 1,07 1,07
2 1 0,07 12 1
Применим найденное
значение R для
вычисления оплаченной суммы долга пред
приходом в банк в конце девятого года, n=3,5.
116
117. Решение примера 2
Вычитая полученную величину из оставшеесяпосле пятилетней выплаты суммы долга,
получим приведённую к начальному моменту
времени оставшуюся сумму долга, которою
надо нарастить
к моменту времени n=9.
3,5
3,5
R 1 1 i
t 13947,8 1 1.07
5
A2
1 i
1 0,07 30470,6
1
2 1 i 2 1
2
1,07 1
Остаток долга к моменту прихода в банк (n=9)
равна 41474,81-30470,6=11004,21. Выплате
подлежит сумма
9
11004, 21 1,07 20230,79
117
118. Пример 3
Задолженность в сумме 100000 у.е. должнабыть погашена за 9 лет равными выплатами в
конце каждого месяца. На остаток долга
начисляется 6% годовых. После четырёх лет
выплат клиент попросил в банке отсрочку на 3
года погашению долга. За последние 2 года
долг
должен
быть
погашен
равными
поквартальными платежами. Чему равен
размер
поквартальных
платежей
выплачиваемых в конце каждого квартала,
если: а) в течение трёхлетнего льготного
периода выплачиваются только процентные
118
119. Пример 3
• Платежи в конце каждого года; б) втечение льготного периода процентные
платежи
не
выплачиваются,
а
присоединяются к сумме долга.
n
R 1 1 i
1
• Решение. Применяя формулу A p
1 i p 1
вычисления приведённой величины
ренты, найдём регулярный платёж R.
R 1 1 0,06
100000
12 1 0,06 112 1
9
R
100000 1 0,06 1 12
1
12
1 1.06
9
14668,64
119
120. Решение примера 3
Найдём часть долга, выплаченную за первыечетыре года, и его остаток
n
4
1
1
i
1
1
0,
06
R
14668, 64
A1
52211, 46
1
1
p 1 i p 1
12
1 0, 06 12 1
А = 100000 – 52211,46 = 47788,54.
б) наращенная сумма этой величины к концу 7го года составляет
7
A 47788,54 1 0,06 71856,29
и
является
современной величиной для последней
двухлетней квартальной ренты.
A 47788, 54 1 0, 06
7
71856, 29
120
121. Решение примера 3
Получаем уравнение относительно годовогоплатежа R этой
ренты.
n
2
R 1 1 i
1
1
0,
06
R
A
71856, 29
p 1 i 1 p 1
4 1 0, 06 1 4 1
1
R
38340,87
4 71856, 29 1,06 4 1
1 1,06 2
Квартальный платёж равен R/4 = 9585,22
а) так как за последние три года процентные
платежи выплачиваются, то наращенная
величина остатка долга к концу 7-го года
121
122. Решение примера 3
Равна наращенной величине к концу 4-го года и4
равна
A 47788,54 1 0,06 60331,96
Получаем уравнение относительно годового
платежа R этой ренты.
2
n
R 1 1 0, 06
60331,96
R 1 1 i
1
A
4
4
1
1
0,
06
1
p 1 i p 1
1
4
R
32191,75
4 60331,96 1,06 1
1 1,06 2
Квартальный платёж равен R/4
= 8047,94
122
123. Задача 1
Какую сумму нужно положить в банк под8% годовых женщине 42 лет, чтобы по
достижению пенсионного возраста 55 лет
в течение 25 лет в начале каждого
месяца снимать по 15000 руб., если
проценты капитализируются: а) в конце
каждого года, б) в конце каждого
полугодия, в) в конце каждого квартала, г)
в конце каждого месяца?
123
124. Решение задачи 1
124125. Решение задачи 1
125126. Задача 2
• Три фирмы A, B, C сливаются в одну фирмуD. Фирма A 3 года назад взяла в банке кредит
на сумму 100000 у.е. на 5 лет с погашением
задолженности равными уплатами в конце
каждого полугодия. Фирма B 2 года назад
взяла кредит на сумму 200000 у.е. на 6 лет с
погашением долга в конце каждого квартала
равными выплатами. Фирма C 4 года назад
получила кредит на сумму 400000 у.е. на 8
лет и погашала его платежами в конце года.
126
127. Задача 2 (продолжение)
• Процентная ставка для всех кредитовравна 12% годовых. Объединённая
фирма D должна погасить долги A, B, C
за 4 года равными платежами в конце
каждого года при условии, что на
остаток
долга
начисляется
11%
годовых. Какую сумму фирма D должна
возвращать ежегодно?
127
128. Решение задачи 2
Найдём современную величину долговфирм A, B. C, сумма которых даст
современную величину долга фирмы D.
Сначала найдём рентные платежи
уплаты долгов, исходя из формулы
R 1 1 i
A
p 1 i 1 p 1
n
Для фирмы А
5
200000 1,12 1
R 1 1 0,12
100000
R
26955,22
1
5
2 1 0,12 2 1
1 1,12
128
129. Продолжение решения задачи 2
Для фирмы В800000 1,12 4 1
1
1
0,12
R
200000
R
45597,74
1
6
4 1 0,12 4 1
1 1,12
6
1 1 0,12
8
1
48000
R
80521,14
8
1 1,12
400000 R
Для фирмы С
0,12
После этого из величин взятых кредитов
вычтем приведённые величины
выплаченной части долгов и приведём к
моменту слияния фирм, что
выражается следующей
формулой
n
1 1 i
R
A
1 i n
p 1 i 1 p 1
129
130. Продолжение решения задачи 2
Получим современные величиныдолгов, используя найденные значения
рентных платежей R и времени n от
момента взятия кредита до момента
слияния фирм.
26935, 22 1 1,12
1,12 46953,12
Для фирмы А 100000 2
3
3
Для фирмы В
Для фирмы С
1,12
1
2
1
45597, 74 1 1,12 2
2
200000
1,12
149965, 45
1
4
1,12 4 1
1 1,12
400000 80521,14
0,12
4
4
1,12 244570,81
130
131. Продолжение решения задачи 2
Таким образом долг фирмы D составит46953,12 + 149965,45 + 244570,81 =
441489,38. Для вычисления ежегодной
оплаты долга фирмой D воспользуемся
формулой A R 1 1 i . Откуда
n
i
1 1,11 4
441489.38 0,11
441489.38 R
R
142303, 61
4
0,11
1 1,11
131
132. Облигации
Помимо кредитов в качестве заёмныхсредств широко распространён выпуск
облигаций. Основное отличие от кредита
состоит в том, что заем производится ни
у одного банка, а у большого числа
физических и юридических лиц в виде
продажи облигаций эмитентом.
Облигация– это обязательство выплатить
в определённые моменты времени в
будущем
заранее
установленные
денежные суммы.
132
133. Облигации
Отдельная облигация рассматривается вусловиях определённости. Т.е.
–
эмитент
не
может
отозвать
облигацию до установленной даты
погашения;
– платежи по облигации задаются
фиксированными
значениями
в
определённые моменты времени;
– облигации не имеют кредитного
133
134. Облигации
134135. Облигации
135136. Облигации
136137. Основные характеристики облигаций
137138. Основные характеристики облигаций
138139. Основные характеристики облигаций
Если купонная ставка не выплачивается,то
такую
облигацию
называют
бескупонной. Доход по такой облигации
образуется за счёт курсовой разницы
стоимости облигации.
Перейдём к анализу потока платежей,
создаваемого облигацией, а также к
исследованию
портфеля
облигаций
(совокупности разных видов облигаций).
139
140. Текущая стоимость облигации
140141. Пример 1
141142. Решение примера 1
142143. Решение примера 1
143144. Сравнение текущей стоимости с номинальной
Мывидим,
что
при
ставке
рефинансирования
(10%)
меньшей
купонной ставки (12%) текущая стоимость
облигации
(1034,71руб.)
больше
номинальной стоимости (1000 руб.). При
ставке рефинансирования (14%) большей
купонной ставки (12%) текущая стоимость
(967,067 руб.) меньше номинальной
стоимости.
При
ставке
рефинансирования
(12%)
текущая
стоимость равна номинальной.
144
145. Сравнение текущей стоимости с номинальной
Пример 1 демонстрирует свойствотекущей стоимости.
При повышении купонной ставки текущая
стоимость растет, а при
повышении
процентной ставки текущая стоимость
падает. В случае, когда купонная ставка
равна процентной, текущая стоимость
равна номинальной стоимости облигации.
145
146. Пример 2
146147. Курс облигации
147148. Текущая доходность облигации
148149. Пример 1.
149150. Доходность к погашению
150151. Доходность к погашению
151152. Доходность к погашению
152153. Доходность к погашению
153154. Пример 1
154155. Решение примера 1
155156. Доходность к погашению
156157. Доходность к погашению
157158. Средний срок погашения облигации
Среднийсрок
потока
платежей
позволяет учитывать риск, связанный с
изменением процентной ставки и вообще
с изменением ситуации на рынке. Чем
меньше средний срок тем меньше риск.
Понятно, что нельзя взять просто
среднее арифметическое сроков всех
платежей, а необходимо учитывать
денежную величину каждого платежа.
Это применимо и к распределению
158










































































































































































 Финансы
Финансы








