Похожие презентации:
Динамика материальной точки. Лекция 2
1. Лекция 2 Динамика материальной точки
Лекция 2ДИНАМИКА МАТЕРИАЛЬНОЙ
ТОЧКИ
2. ДИНАМИКА, статика
ДИНАМИКА, СТАТИКА• Динамика материальной точки
• Динамика системы материальных точек
• Динамика абсолютно твердого тела
2
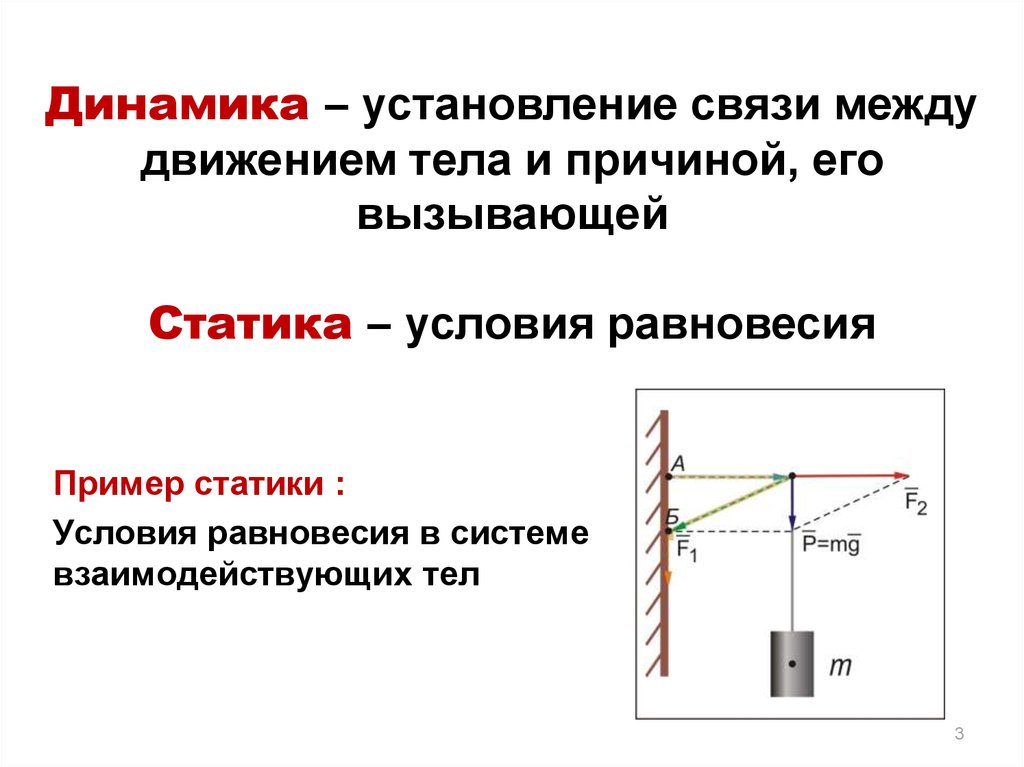
3. Динамика – установление связи между движением тела и причиной, его вызывающей Статика – условия равновесия
Пример статики :Условия равновесия в системе
взаимодействующих тел
3
4. Законы динамики (законы Ньютона)
I закон:Всякое тело находится в состоянии
покоя
или
равномерного
прямолинейного движения до тех пор,
пока воздействие со стороны других тел
не заставит изменить это состояние.
«Покой» и «равномерное прямолинейное движение» суть одно и то
же состояние! Это – естественное состояние тела, поскольку для этого
ничего не надо делать.
Свойство тел сохранять состояние покоя или скорость при
отсутствии воздействия каких-либо других тел называется инерцией.
Системы отсчета, где эти свойства сохраняются – называются
инерциальными системами отсчета(ИС)
Поэтому первый закон Ньютона называют Законом инерции.
4
5. (2-й закон Ньютона)
II закон:Мера воздействия – сила F :
гравитационная
трения
упругая
Если много сил – то равнодействующая сила
Ускорение, приобретаемое телом в
инерциальной системе отсчета, прямо
пропорционально равнодействующей
сил, приложенных к телу, и обратно
пропорционально массе тела.
a F m
(2.5)
Масса тела –
Мера инертности
Количество вещества
5
6.
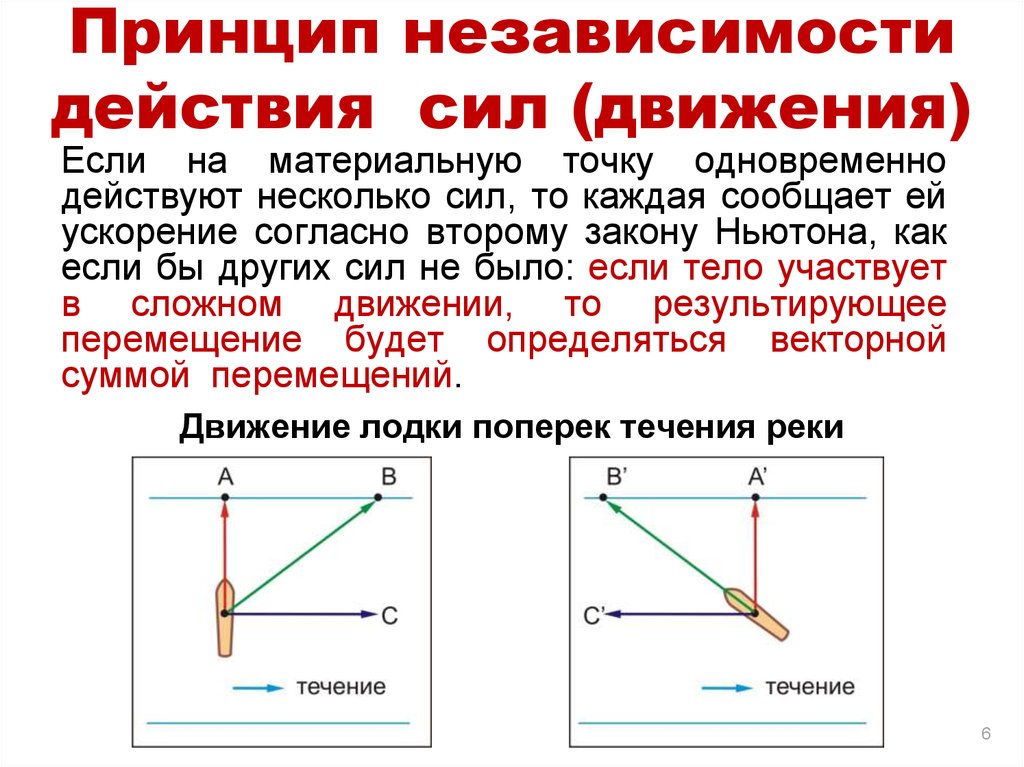
Принцип независимостидействия сил (движения)
Если на материальную точку одновременно
действуют несколько сил, то каждая сообщает ей
ускорение согласно второму закону Ньютона, как
если бы других сил не было: если тело участвует
в сложном движении, то результирующее
перемещение будет определяться векторной
суммой перемещений.
Движение лодки поперек течения реки
6
7. Система единиц Формула размерности
Единица измерения величины А – условно выбраннаявеличина, имеющая тот же смысл, что и величина А.
Система единиц – совокупность единиц измерения,
определенных установленным образом для всех величин
конкретной области знания.
Основные единицы – независимо установленные
единицы измерения произвольно выбранных величин.
Размерность, формула размерности – соотношение,
определяющее связь между единицами измерения
величины А и основными единицами измерения А1, А2, А3
….. Аi , называется формулой размерности(α,β,ϒ,τ-любые
числа):
А=[ А1] · [А2]β · [А3]ϒ……..· [Аi ]τ
8. Система единиц: СИ, СГС
Основные единицы :длина l, [L] :
м
см
время t, [T] :
с
с
масса m, [M] :
кг
г
Производные единицы:
скорости u:[u]= LT-1
м·с-1
см·с-1
ускорения a:[a] =LT-2
м·с-2
см·с-2
силы F (f):[F] = MLT-2
Н, кг·м·с-2
дн, г см·с-2
1Н(ньютон) = 105 дин
Техническая единица силы (МКГСС):
1 кгс = 9.81 Н
8
9. Импульс
du d mu d pF ma m
du
a
dt
dt
dt
dt
p mu Импульс материальной точки
(2.6)
(2.6а)
d p Fdt Импульс силы
(2.6б)
Закон сохранения импульса материальной точки:
F 0 dp 0
(2.7)
III закон Ньютона:
Сила действия равна силе противодействия
F12 F21
(2.8)
(силы приложены к разным телам 1 и 2)
9
10. Динамика системы материальных точек
pi mi u ip pi
координата центра инерции (масс) -
m1 r 1 ... mi r i
rC
m1 m2 ... mi
d rC
uc
dt
m
i
d ri
MC
m r
m M
i
i
i
C
(2.9)
dt 1
MC
1
pi M pC
C
(2.10)
скорость перемещения центра масс (инерции)
или
pC M C u c
(2.10а)
10
11.
Уравнение движения системыматериальных точек или твердого тела
mi ai fi ,внj fi вш
(2.11)
вн
f
i, j 0
вн
вш
m
a
f
f
i i i, j i
вш
m
a
f
i i i (2.11а)
rC
mr
=
m
i i
Ускорение элементарной массы mi
(2.11б)
d 2r
ai
i
2
dt
d 2 ri
m
d 2 rС i dt 2
aC 2
MaC mi ai f i вш
dt
mi
MaC fi вш (2.12)
i
Центр инерции (масс, тяжести) движется так, как двигалась
бы материальная точка с суммарной массой M под
действием всех приложенных сил (равнодействующей).
11
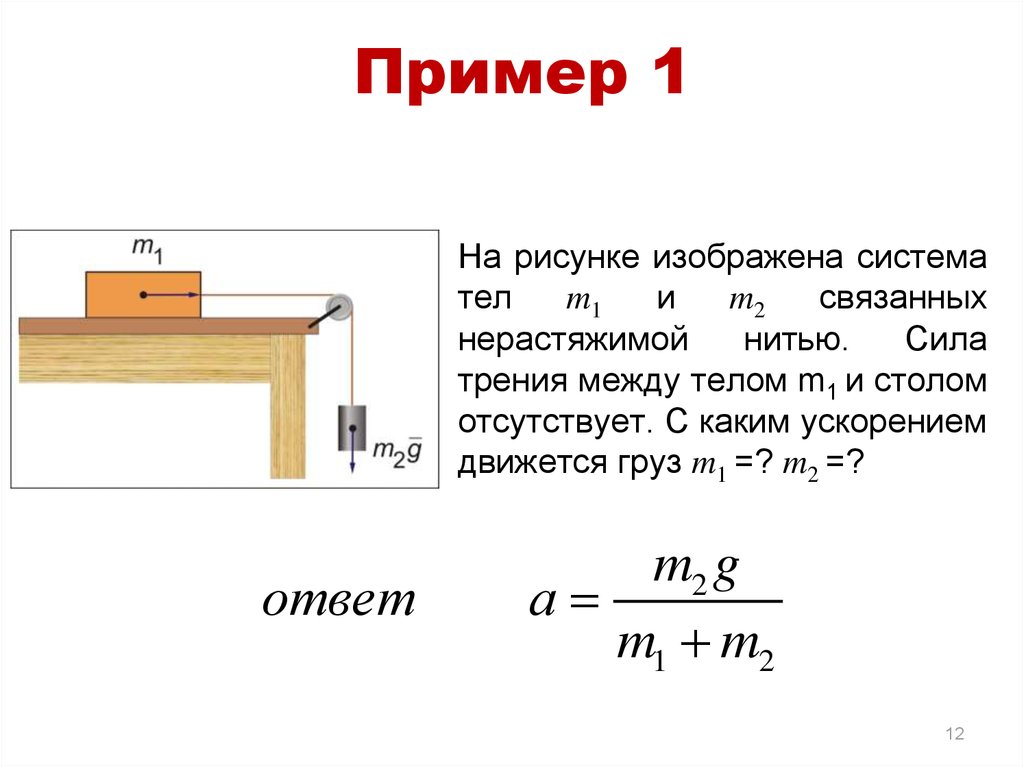
12. Пример 1
На рисунке изображена системател
m1
и
m2
связанных
нерастяжимой
нитью.
Сила
трения между телом m1 и столом
отсутствует. С каким ускорением
движется груз m1 =? m2 =?
ответ
m2 g
a
m1 m2
12
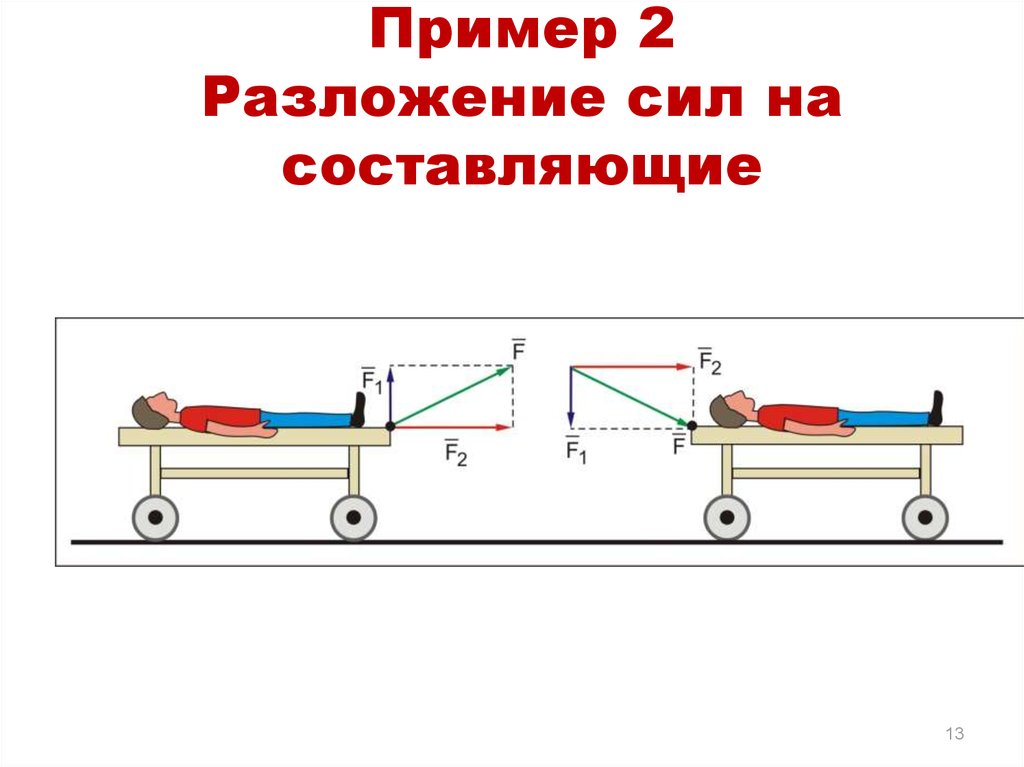
13. Пример 2 Разложение сил на составляющие
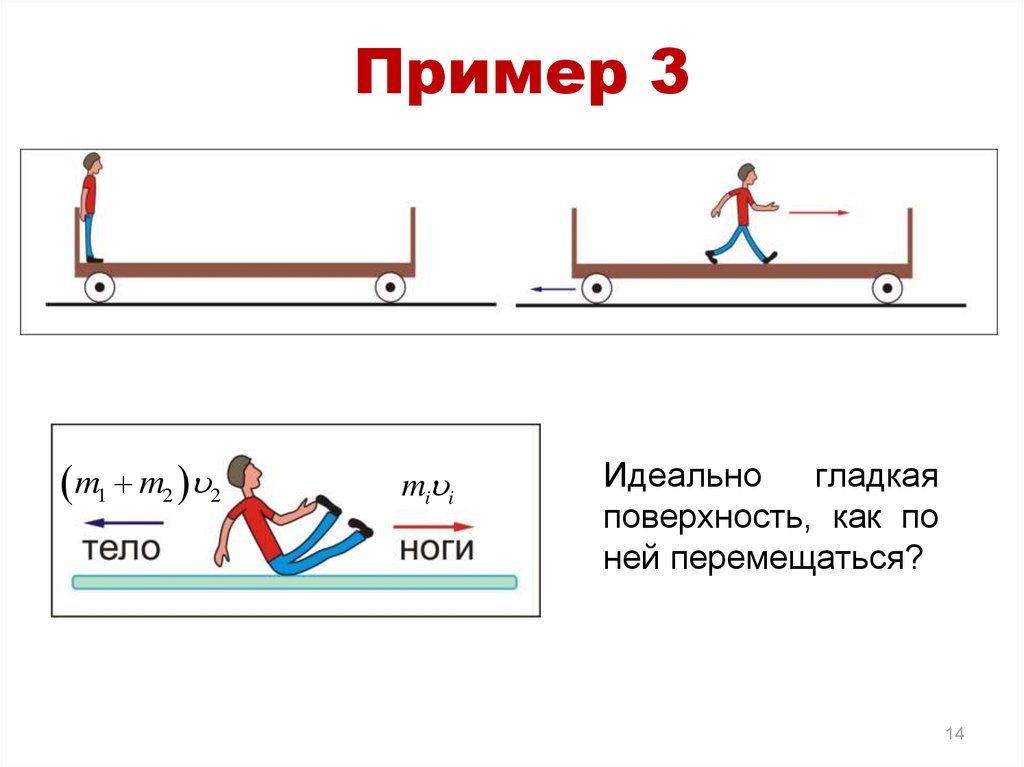
1314. Пример 3
m1 m2 u2miui
Идеально
гладкая
поверхность, как по
ней перемещаться?
14
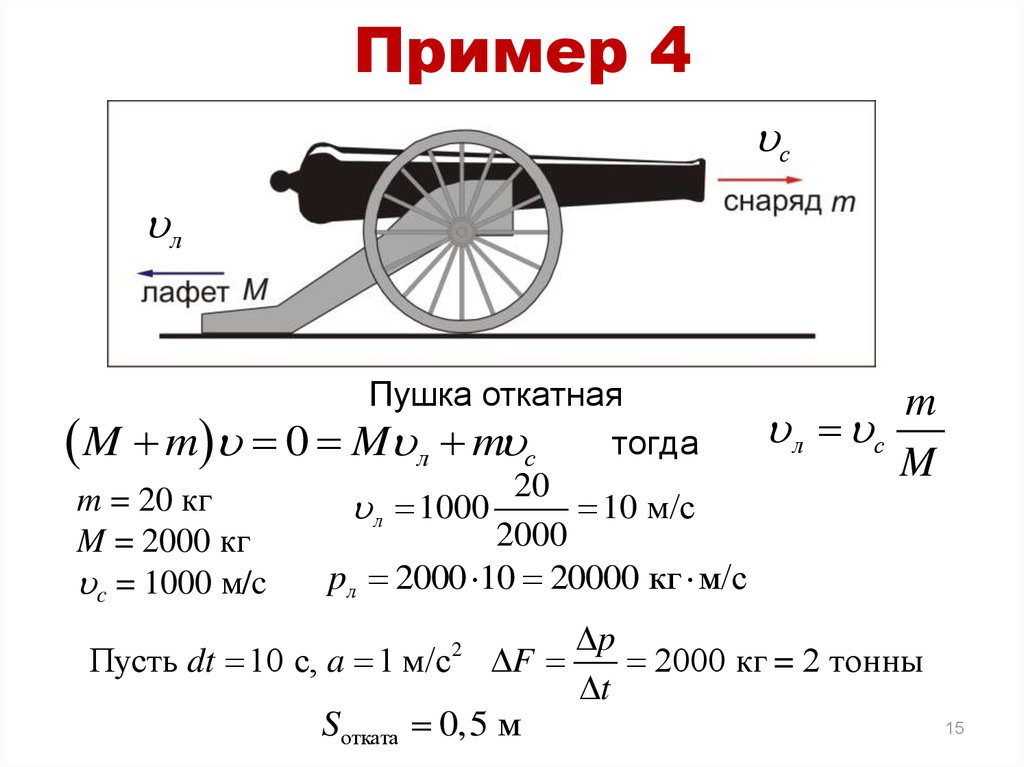
15. Пример 4
uсuл
Пушка откатная
тогда
M m u 0 Muл muс
20
m = 20 кг
u л 1000
10 м/с
2000
M = 2000 кг
pл 2000 10 20000 кг м/с
uc = 1000 м/c
Пусть dt 10 c, a 1 м/с 2 F
Sотката 0,5 м
m
u л uс
M
p
2000 кг = 2 тонны
t
15
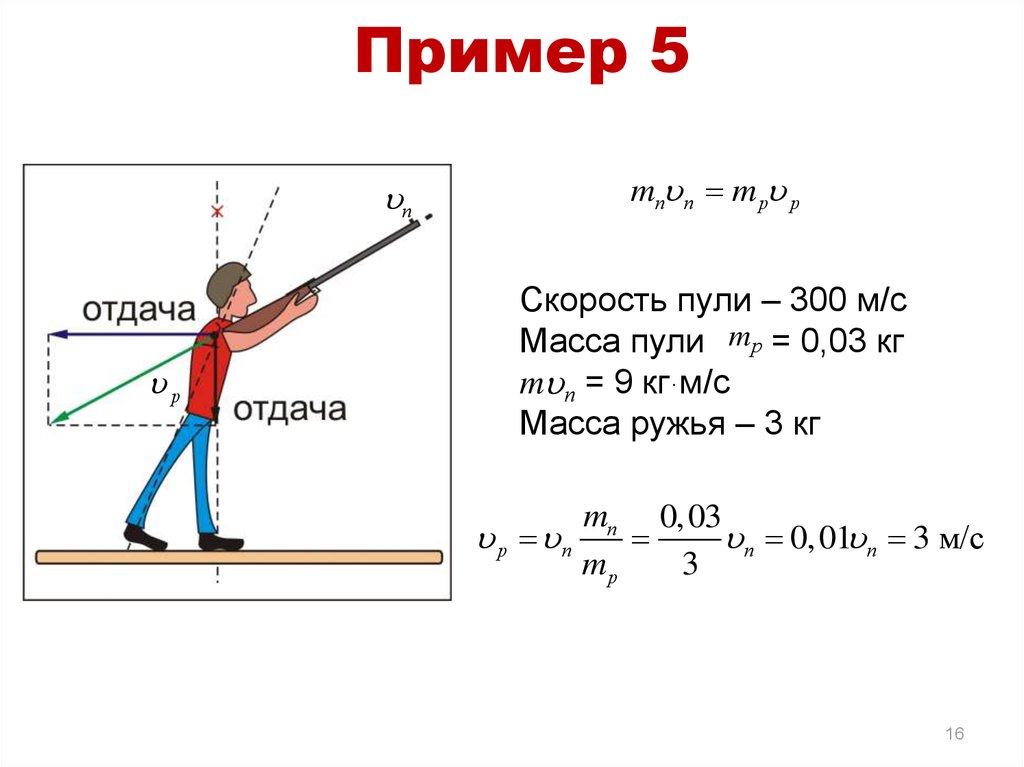
16. Пример 5
uпuр
mпuп m рu р
Скорость пули – 300 м/с
Масса пули mр = 0,03 кг
muп = 9 кг м/с
Масса ружья – 3 кг
mп 0,03
u р uп
uп 0,01uп 3 м/с
mр
3
16
17. Пример 5 (продолжение)
uрuп
mпuп m рu р
Контакт с телом (половиной) M = 80 кг/2 = 40 кг
Если ружье прижать плотно:
uтела
mп
0, 03
uп
300
0, 002 м/с
mр M
3 40
тело немного шелохнется, но если не прижимать плотно:
dp
dP m р u р 3 кг 3 м/с = 9 кг м/с
F
dt
Все зависит от dt: если dt = 0,1, то F = 90 кг м/с2 9 кг
17










 Физика
Физика








