Относительное положение прямой и плоскости, плоскостей

1. относительное положение прямой и плоскости, плоскостей

1
Лекция 5

2. Особые линии плоскости. Линии наибольшего наклона плоскости

Линии наибольшего наклона заданной плоскости к
плоскости проекций - линии принадлежащие плоскости и
перпендикулярные горизонтали и фронтали плоскости :
1.Линия наибольшего наклона плоскости к горизонтальной
плоскости проекций называется линией ската
2.Линия наибольшего наклона плоскости к фронтальной
или профильной плоскости проекций не имеет другого
названия
2

3. Особые линии плоскости. Линии наибольшего наклона плоскости

Линии наибольшего наклона заданной плоскости к плоскости
проекций – линии, принадлежащие плоскости и перпендикулярные
горизонтали и фронтали плоскости :
1. Линия наибольшего наклона плоскости к горизонтальной
плоскости проекций называется линией ската
2. Линия наибольшего наклона плоскости к фронтальной плоскости
проекций не имеет другого названия
3

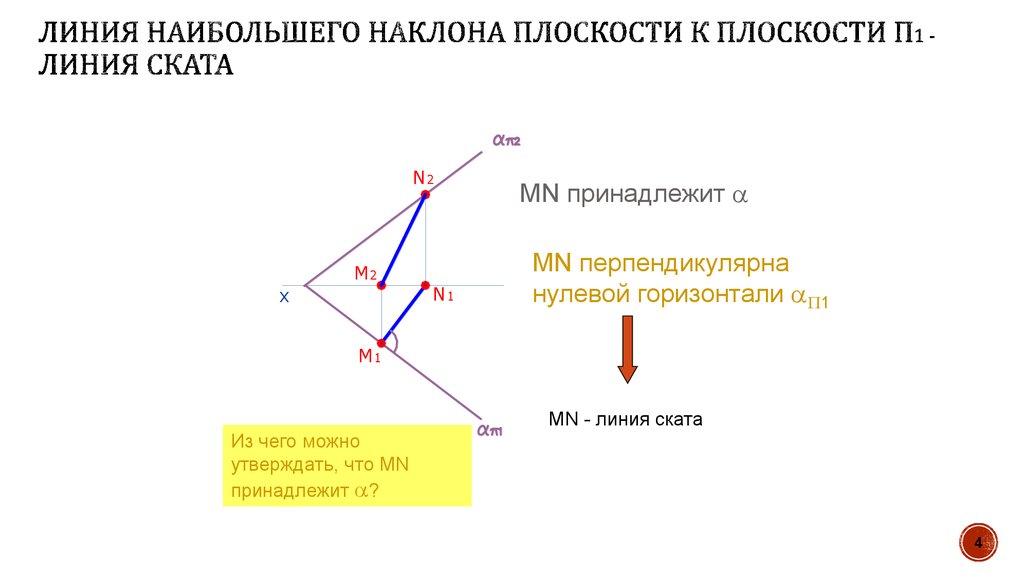
4. Линия наибольшего наклона плоскости к плоскости П1 -Линия ската

N2
M2
xx
NN11
MN принадлежит
MN перпендикулярна
нулевой горизонтали 1
MM11
MN - линия ската
Из чего можно
утверждать, что MN
принадлежит ?
4

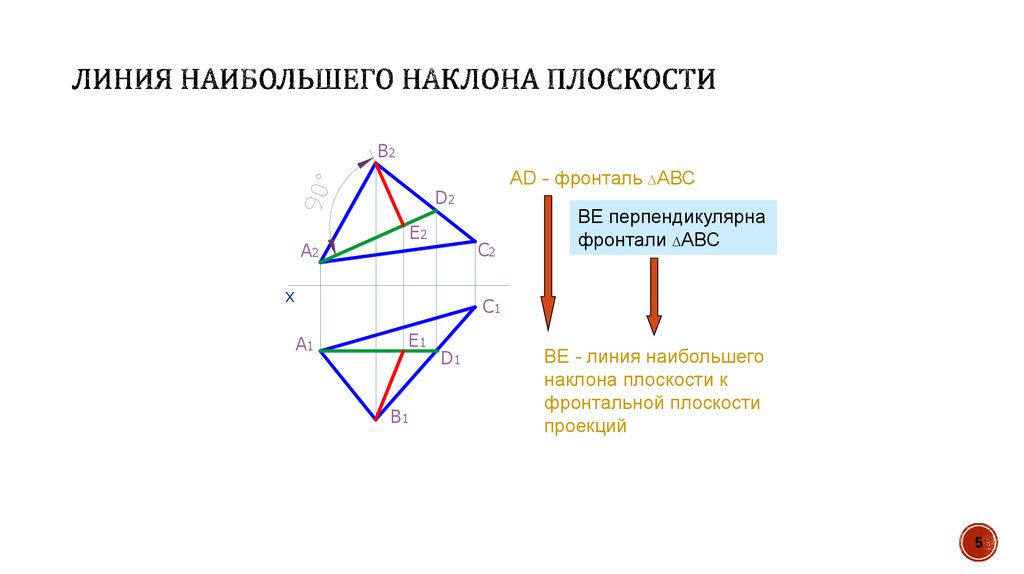
5. Линия наибольшего наклона плоскости

B2
AD - фронталь АВС
D2
E2
A2
C2
x
ВЕ перпендикулярна
фронтали АВС
C1
A1
E1
B1
D1
ВЕ - линия наибольшего
наклона плоскости к
фронтальной плоскости
проекций
5

6. Вопрос 1

ВОПРОС 1
Построение линии ската следует начинать с построения ...
6

7. Относительное положение прямой и плоскости

Прямая принадлежит плоскости, если она проходит
через две точки, принадлежащие этой плоскости
Если плоскость задана следами и прямая принадлежит
плоскости, то следы прямой лежат на соответствующих
следах плоскости
Прямая принадлежит плоскости, если:
она проходит через точку, лежащую в плоскости,
параллельна прямой, принадлежащей этой плоскости
7

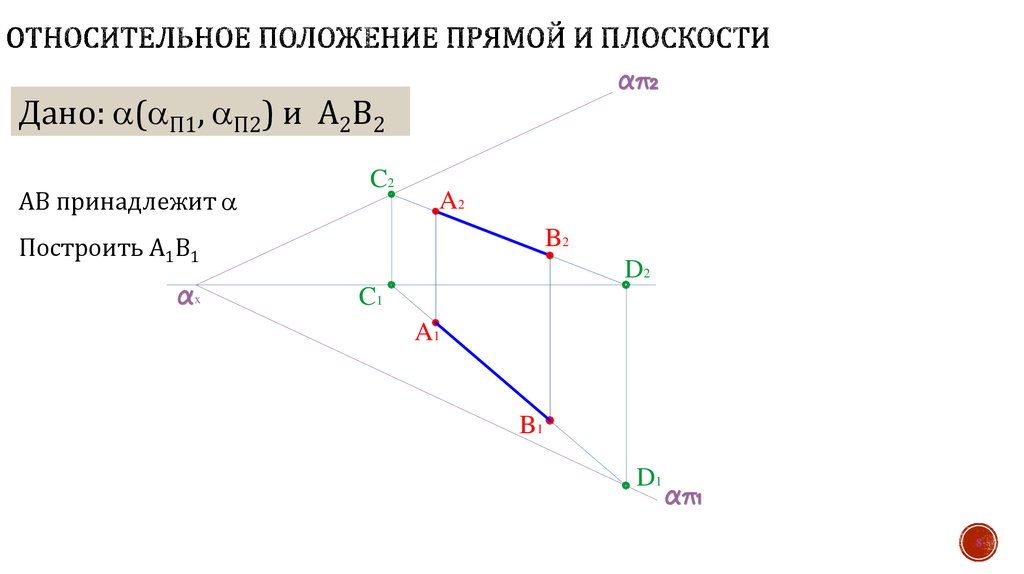
8. Относительное положение прямой и плоскости

Дано: ( П1, П2) и А2В2
АВ принадлежит
C2
A2
B2
Построить А1В1
x
D2
C1
A1
B1
D1
8

9. Относительное положение прямой и плоскости

BB22
AA22
12
m
m22
22
CC22
11
CC11
AA11
m
m11
BB11
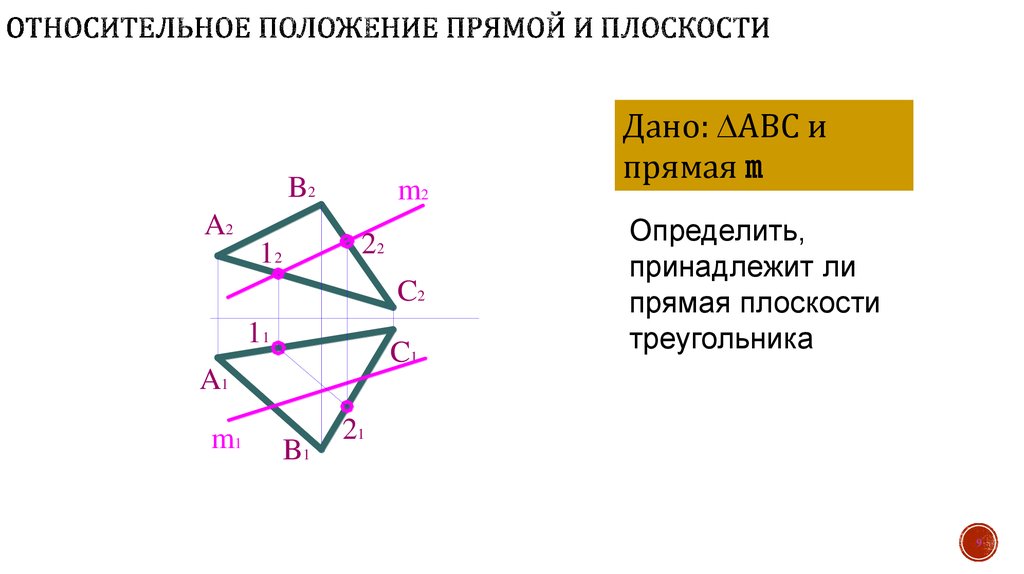
Дано: АВС и
прямая m
Определить,
принадлежит ли
прямая плоскости
треугольника
21
9

10. Относительное положение прямой и плоскости

n
n22
m
m22
2
222
1
122
3
C22
3 22 C
4
422
A
A22
x
x
21
2
211
11
1111
A
A11
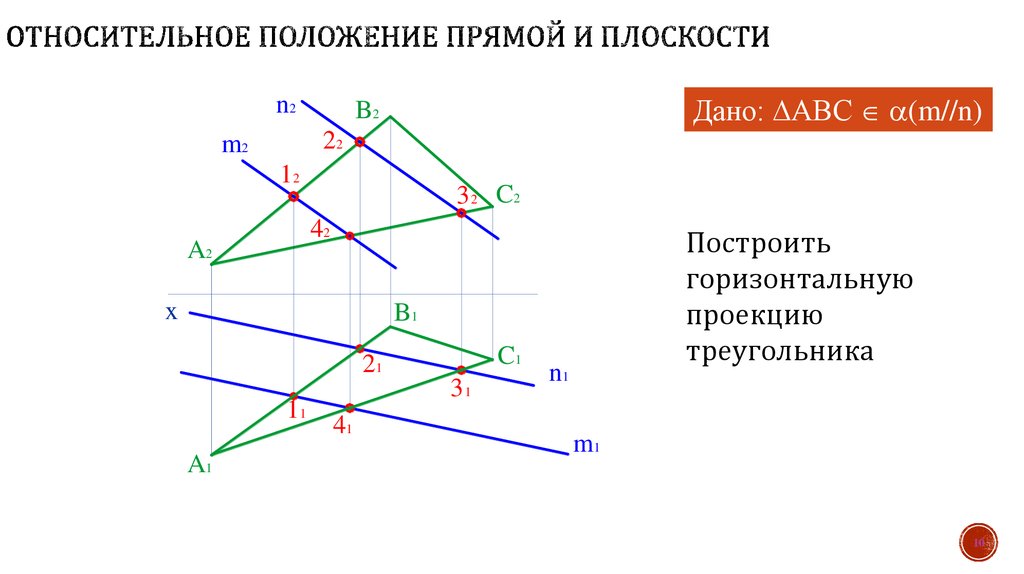
Дано: АВС (m//n)
B
B22
4
411
Построить
горизонтальную
проекцию
треугольника
B
B11
3 1 C1
3
3 11
n
n11
m
m11
10

11. Относительное положение точки и плоскости

Точка принадлежит плоскости, если она
принадлежит прямой, принадлежащей этой
плоскости
11

12. Относительное положение точки и плоскости

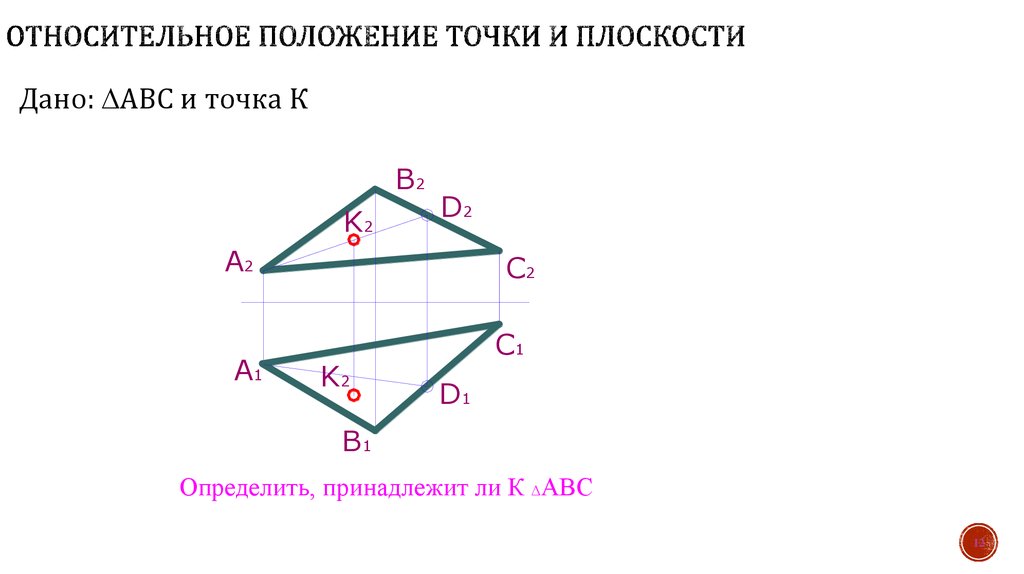
Дано: АВС и точка К
B2
K2
D2
A2
A1
C2
K2
C1
D1
B1
Определить, принадлежит ли К АВС
12

13. Вопрос 2

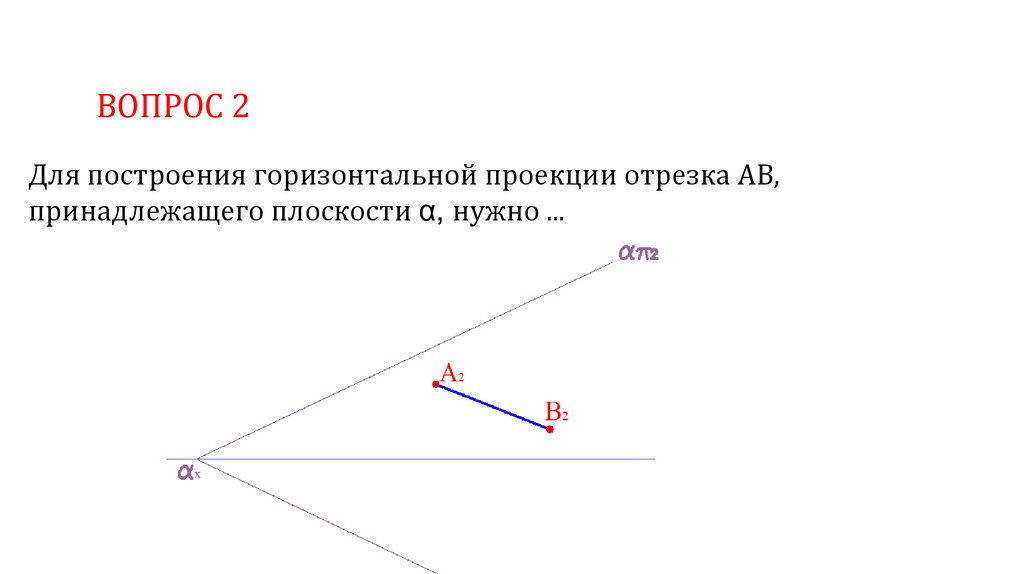
ВОПРОС 2
Для построения горизонтальной проекции отрезка АВ,
принадлежащего плоскости α, нужно ...
13

14. Взаимная параллельность плоскостей, прямой и плоскости

1. Прямая параллельна плоскости, если в этой плоскости
имеется прямая, параллельная ей
2. Две плоскости взаимно параллельны, если две
пересекающиеся прямые одной плоскости попарно
параллельны двум пересекающимся прямым другой
плоскости
3. Две плоскости параллельны, если они заданы следами и два
пересекающихся между собой следа одной плоскости
параллельны одноименным с ними следам другой плоскости
14

15. Параллельные плоскости

B2
n2
D2
A2
E2
m2
K2
C2
x
A1
C1
E1
K1
m1
D1
B1
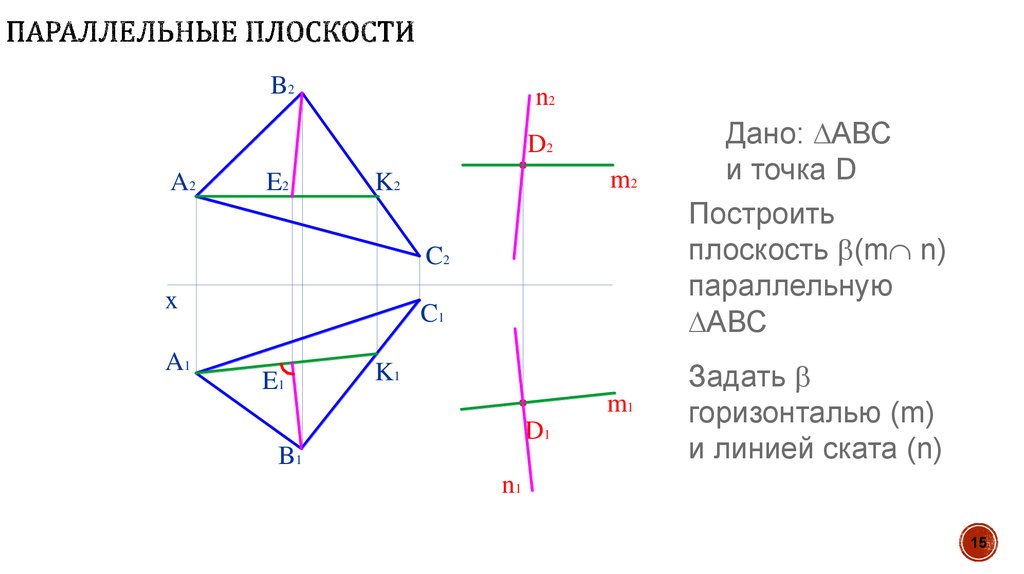
Дано: АВС
и точка D
Построить
плоскость (m n)
параллельную
АВС
Задать
горизонталью (m)
и линией ската (n)
n1
15

16. Вопрос 3

ВОПРОС 3
Дано: плоскость.
Построить линию, параллельную заданной плоскости
Решение:
...
16

17. Перпендикулярность прямых и плоскостей

Две плоскости перпендикулярны, если одна из них проходит через
прямую линию перпендикулярную другой плоскости
Нормаль - прямая перпендикулярная плоскости
(Не принадлежит плоскости, имеет с ней одну общую точку)
Прямая перпендикулярна плоскости, если она перпендикулярна
двум пересекающимся прямым этой плоскости
За эти две прямые, лежащие в одной плоскости, принимают
горизонталь и фронталь плоскости, т.к. к ним можно провести
линии под прямым углом
17

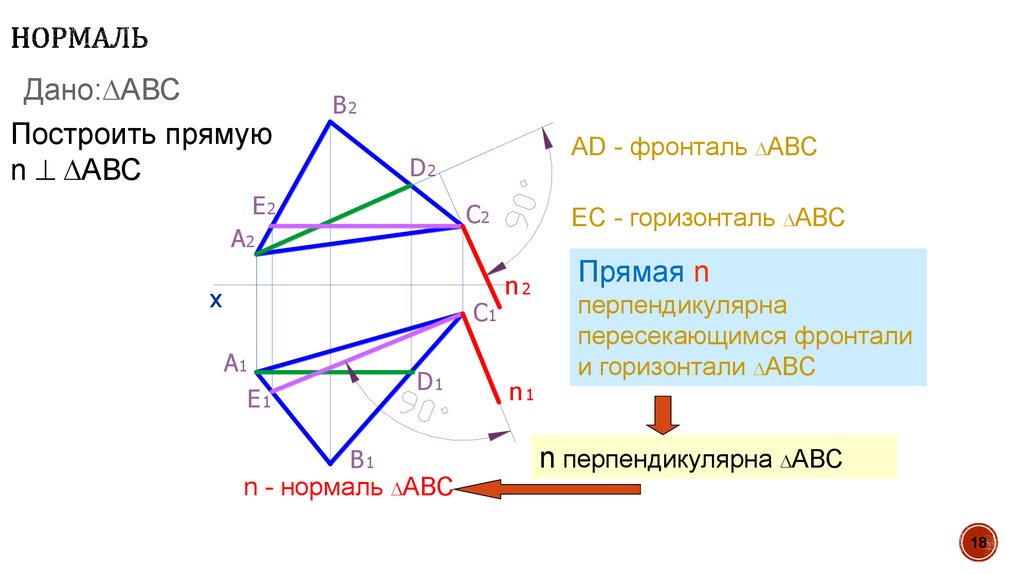
18. Нормаль

Дано: АВС
Построить прямую
n АВС
B2
B2
AD - фронталь АВС
D2
E2
C2
C 2 C2
AA2 2
xx
C1 C1
AA1 1
E1
D1
B1
B1
n - нормаль АВС
ЕС - горизонталь АВС
n2
n1
Прямая n
перпендикулярна
пересекающимся фронтали
и горизонтали АВС
n перпендикулярна АВС
18

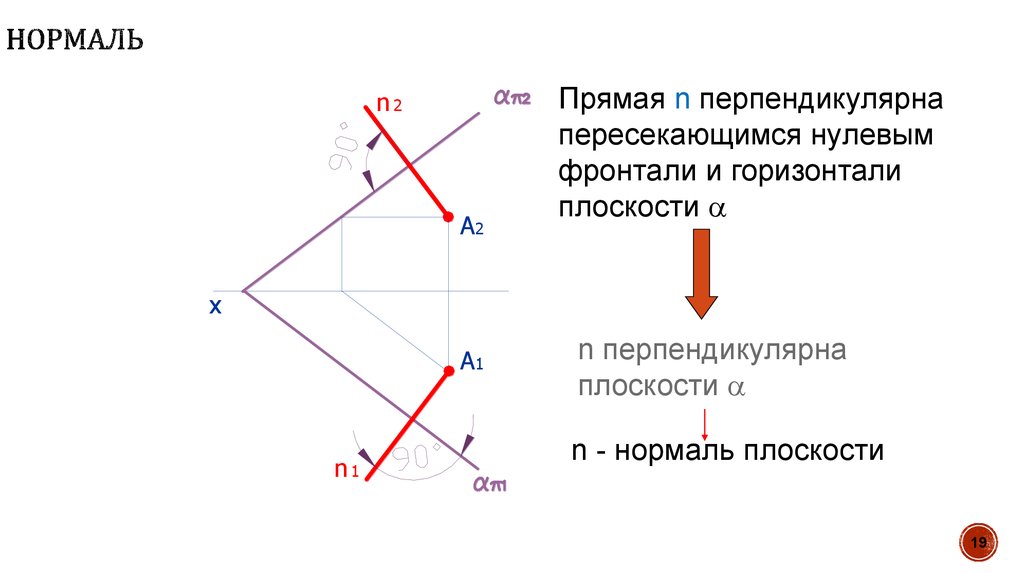
19. Нормаль

n2
A
A22
Прямая n перпендикулярна
пересекающимся нулевым
фронтали и горизонтали
плоскости
xx
A
A11
n1
n перпендикулярна
плоскости
n - нормаль плоскости
19

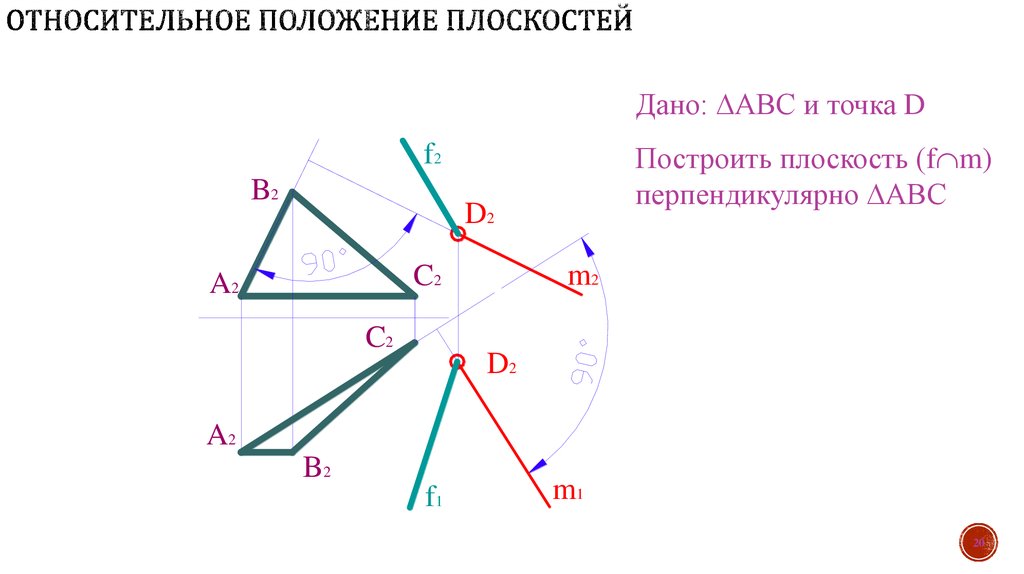
20. Относительное положение плоскостей

Дано: АВС и точка D
B
2
B2
D
D22
C
2
C2
A
A22
C
C22
A
2
A2
Построить плоскость (f m)
перпендикулярно АВС
f2
m2
D
D22
B
B22
f1
m1
20

21. Вопрос 4

ВОПРОС 4
Дано: Прямая и плоскость. Прямая перпендикулярна
плоскости.
Построить плоскость, перпендикулярную заданной
плоскости
Решение:
...
21

22. Пересечение прямой с проецирующей плоскостью

Любая фигура, принадлежащая проецирующей
плоскости, имеет одну из своих проекций на
соответствующем следе этой плоскости
Эта особенность используется при решении
задач на определение точек пересечения
прямых линий с проецирующими плоскостями
и линий пересечения с ними плоскостей
произвольного положения
22

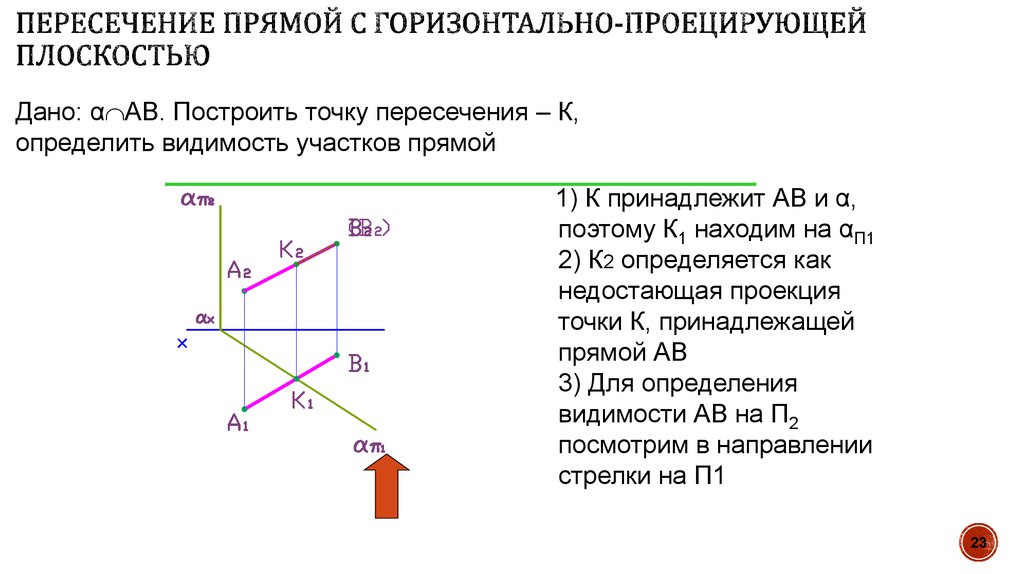
23. Пересечение прямой с горизонтально-проецирующей плоскостью

Дано: α АВ. Построить точку пересечения – К,
определить видимость участков прямой
1) К принадлежит АВ и α,
поэтому К1 находим на αП1
2) К2 определяется как
недостающая проекция
точки К, принадлежащей
прямой АВ
3) Для определения
видимости АВ на П2
посмотрим в направлении
стрелки на П1
23

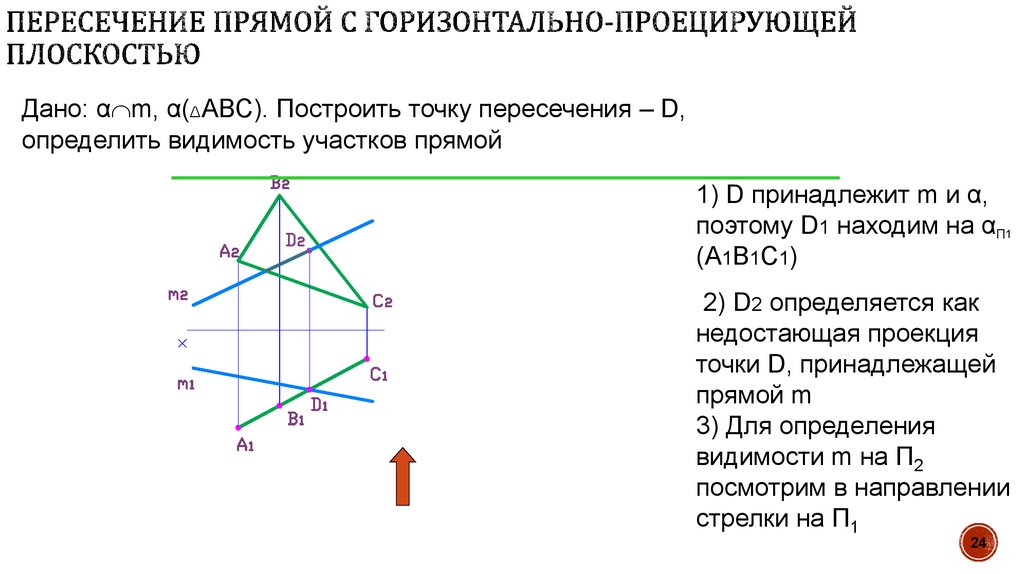
24. Пересечение прямой с горизонтально-проецирующей плоскостью

Дано: α m, α(∆АВС). Построить точку пересечения – D,
определить видимость участков прямой
1) D принадлежит m и α,
поэтому D1 находим на αП1
(А1В1С1)
2) D2 определяется как
недостающая проекция
точки D, принадлежащей
прямой m
3) Для определения
видимости m на П2
посмотрим в направлении
стрелки на П1
24

25. Схема решения задачи на определение точки пересечения прямой линии с плоскостью

1.
Через проекцию исходной прямой проводим вспомогательную
плоскость
2.
Определяем линию пересечения заданной плоскости с
вспомогательной плоскостью
3.
Определяем точку пересечения данной прямой с построенной линией
пересечения – эта точка, общая для заданных прямой и плоскости,
является искомой точкой пересечения
4.
Определяем видимые и невидимые (относительно плоскостей
проекций) отрезки прямой линии, применяя способ «конкурирующих
точек»
25

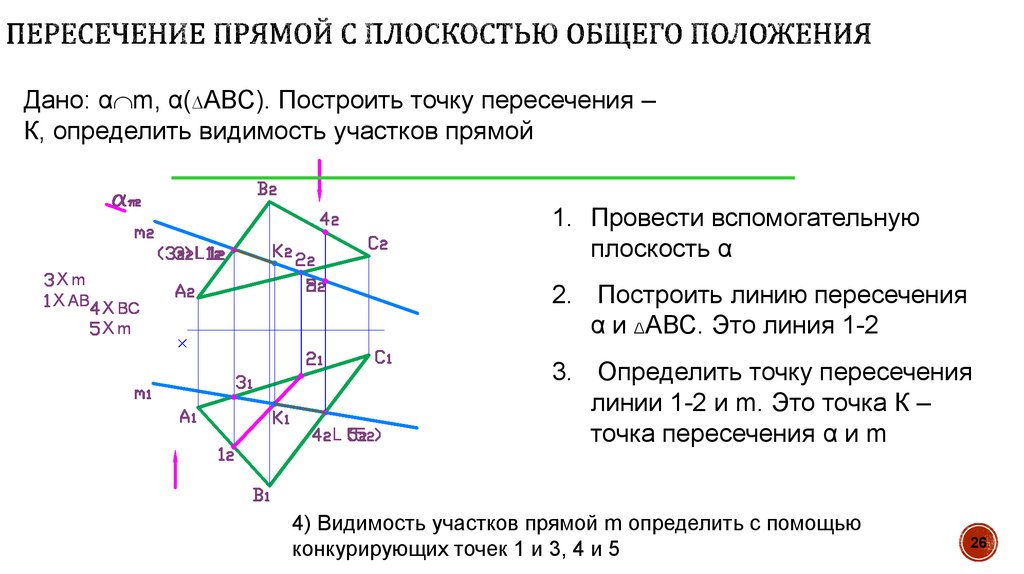
26. Пересечение прямой с плоскостью общего положения

Дано: α m, α(∆АВС). Построить точку пересечения –
К, определить видимость участков прямой
1. Провести вспомогательную
плоскость α
L
Xm
X АВ X ВС
Xm
2. Построить линию пересечения
α и ∆АВС. Это линия 1-2
L
3. Определить точку пересечения
линии 1-2 и m. Это точка К –
точка пересечения α и m
4) Видимость участков прямой m определить с помощью
конкурирующих точек 1 и 3, 4 и 5
26

27. Вопрос 5

ВОПРОС 5
Дано: прямая пересекает плоскость
Построить точку пересечения
Решение:
...
27

28. Пересечение плоскостей

Если две плоскости пересекаются, то линия их
пересечения – прямая линия и она принадлежит
обеим плоскостям
Если одна из плоскостей – проецирующая, то одна
из проекций линии пересечения располагается на
соответствующем следе этой плоскости
28

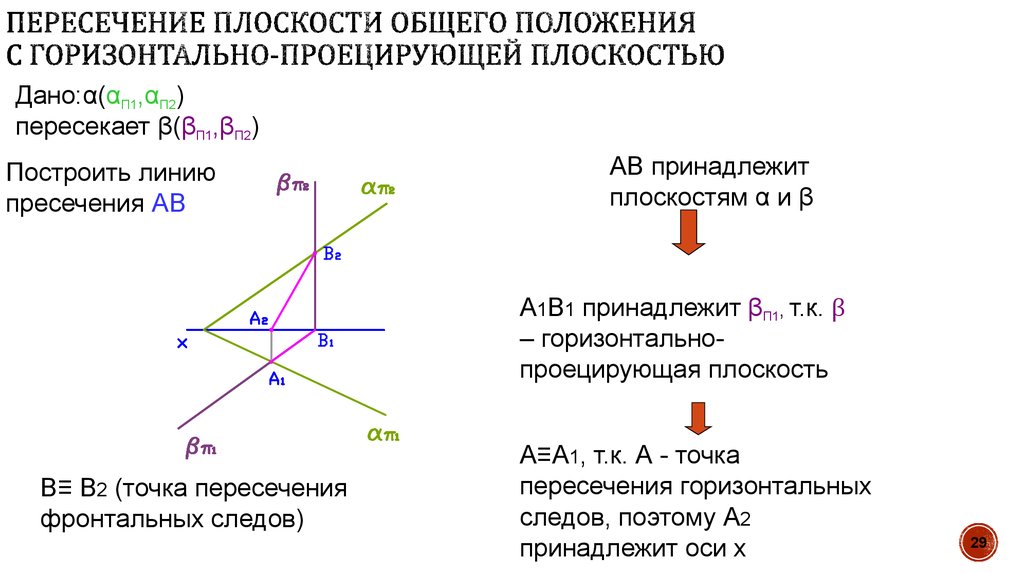
29. Пересечение плоскости общего положения с горизонтально-проецирующей плоскостью

Дано:α(αП1,αП2)
пересекает β(βП1,βП2)
Построить линию
пресечения АВ
АВ принадлежит
плоскостям α и β
А1В1 принадлежит βП1, т.к. β
– горизонтальнопроецирующая плоскость
В≡ В2 (точка пересечения
фронтальных следов)
А≡А1, т.к. А - точка
пересечения горизонтальных
следов, поэтому А2
принадлежит оси x
29

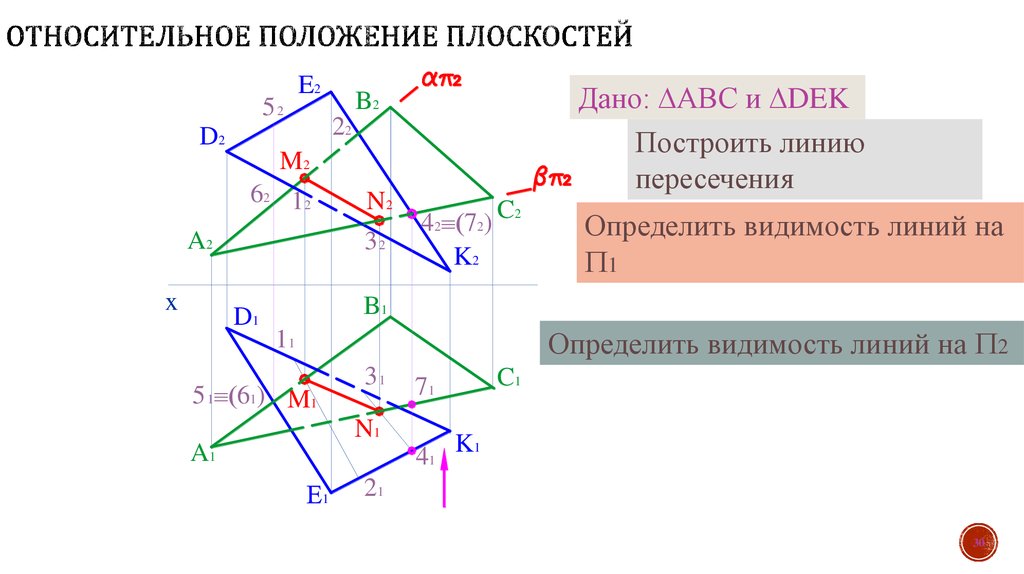
30. Относительное положение плоскостей

52
E2
B2
22
D2
M2
612 2 12
N2
A2
x
32
D1
C2
42
72 2) C2
42 7
K2
Дано: АВС и DEK
Построить линию
пересечения
Определить видимость линий на
1
B1
Определить видимость линий на 2
11
31
1 6
5 15 6
1)1 M1
N1
A1
1
71
C1
K
1
41
21 1
30

31. ВЫВОДЫ

1.
Точка принадлежит плоскости, если она принадлежит
прямой этой плоскости
2.
Прямая принадлежит плоскости, если она проходит
через две точки этой плоскости
3.
Прямая принадлежит плоскости, если она имеет общую
точку с этой плоскостью и параллельна прямой этой
плоскости
4.
Прямая перпендикулярна плоскости, если она
перпендикулярна двум пересекающимся прямым этой
плоскости. За эти пересекающиеся прямые плоскости
принимают обычно фронталь и горизонталь, т. к. к ним
можно провести линию под прямым углом
5.
Две плоскости перпендикулярны, если одна из них
проходит через прямую перпендикулярную другой
плоскости
31

32. ВЫВОДЫ

6.
Прямая параллельна плоскости, если она
параллельна прямой этой плоскости
7.
Две плоскости параллельны, если две
пересекающиеся прямые одной плоскости
параллельны двум пересекающимся прямым
другой
32

33. Контрольные вопросы

1.
Условие принадлежности точки плоскости
2.
Условие принадлежности прямой плоскости
3.
Условие перпендикулярности прямой и
плоскости
4.
Условие перпендикулярности двух
плоскостей
5.
Условие параллельности прямой и плоскости
6.
Условие параллельности двух плоскостей
7.
Если плоскость задана следами, как
определить, принадлежит ли отрезок прямой
этой плоскости?
33