Прямая. Плоскость

1. Прямая. Плоскость

Лекция 2
1

2. ПРЯМАЯ

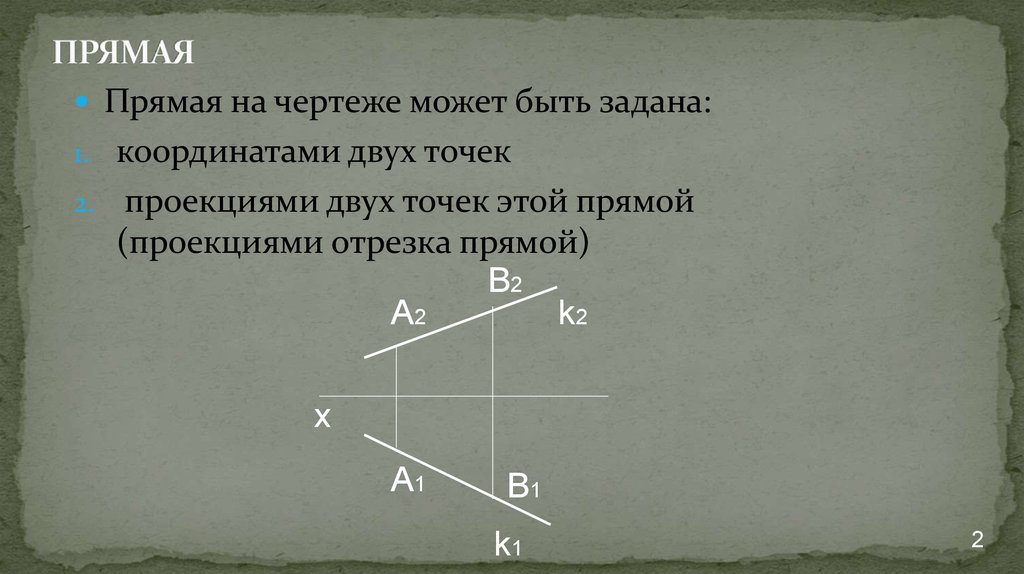
Прямая на чертеже может быть задана:
1. координатами двух точек
2.
проекциями двух точек этой прямой
(проекциями отрезка прямой)
В2
A2
k2
x
A1
В1
k1
2

3. ПРЯМЫЕ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯ

Прямая общего положения не имеет проекций,
параллельных или перпендикулярных осям
координат
Прямые частного положения
1. Прямая параллельна одной плоскости
проекций*
2. Прямая параллельна двум плоскостям
проекций*
*В первом случае одна проекция отрезка прямой
равна самому отрезку. Во втором случае две
проекции отрезка равны ему
3

4. ПРИМЕР ПОСТРОЕНИЯ ПРОЕКЦИЙ ПРЯМОЙ

zz
B2
B3
A3
y = 40
y = 20
z = 30
z = 40
A2
xx
y
B1
A1
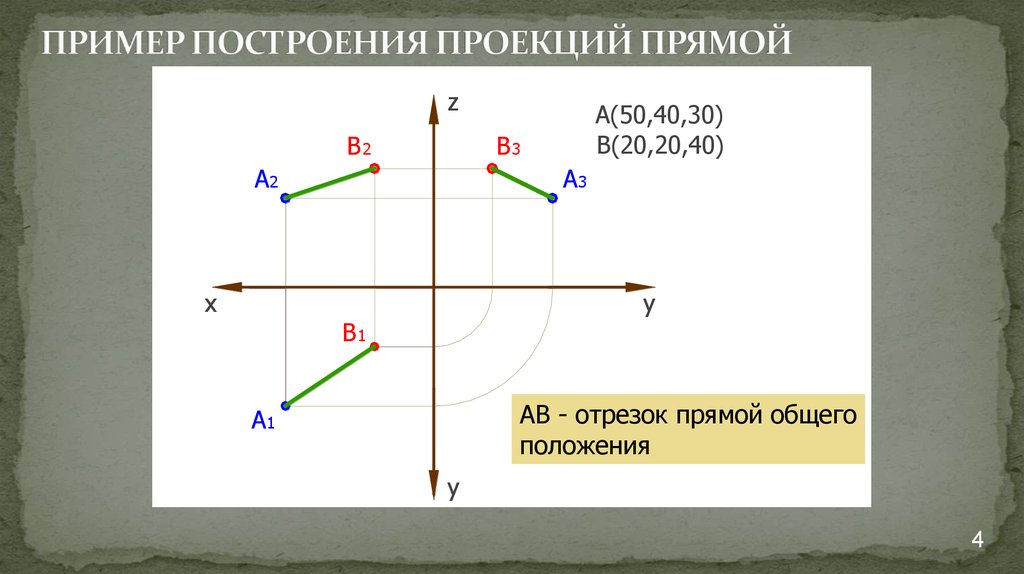
A(50,40,30)
B(20,20,40)
АВ - отрезок прямой общего
положения
x=
x=
2050
y
4

5. ПРЯМАЯ ПАРАЛЛЕЛЬНА ОДНОЙ ПЛОСКОСТИ ПРОЕКЦИЙ

Горизонтальная прямая – параллельна
горизонтальной плоскости проекций
Фронтальная прямая – параллельна
фронтальной плоскости проекций
Профильная прямая – параллельна профильной
плоскости проекций
Перечисленные прямые также называют
прямыми уровня
5

6. ГОРИЗОНТАЛЬНАЯ ПРЯМАЯ

z
A2
B2
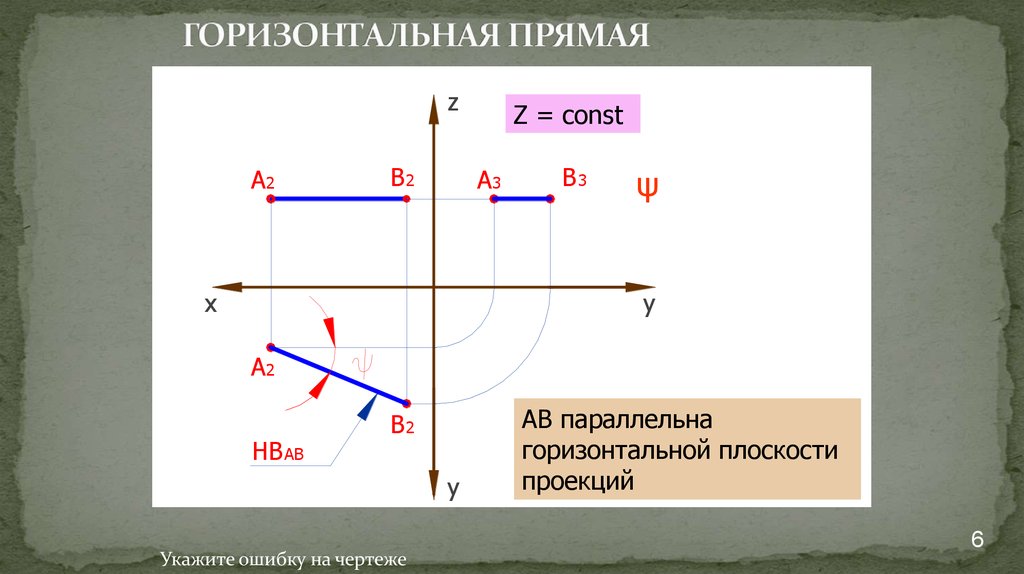
Z = const
A3
x
B3
ψ- угол между
АВ и П2
y
A2
HB AB
B2
y
Укажите ошибку на чертеже
АВ параллельна
горизонтальной плоскости
проекций
6

7. ФРОНТАЛЬНАЯ ПРЯМАЯ

A2
z
HB AB
A3
B2
B3
x
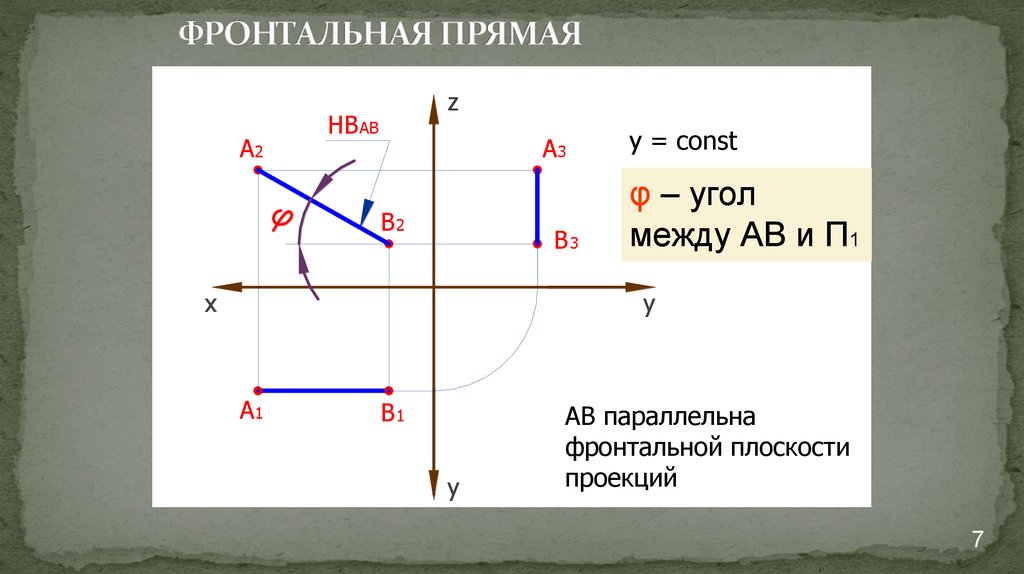
y = const
φ – угол
между АВ и П1
y
A1
B1
y
АВ параллельна
фронтальной плоскости
проекций
7

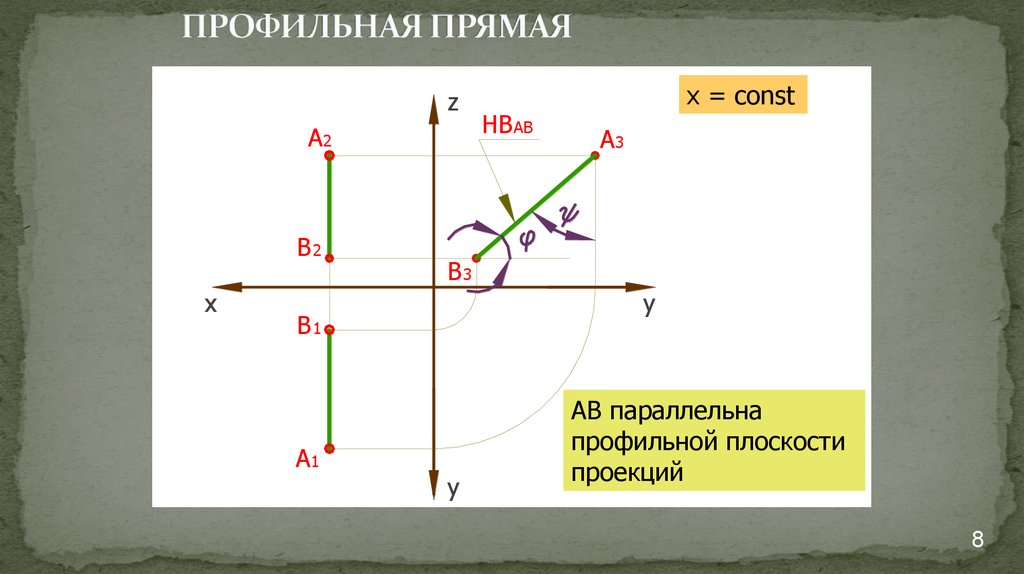
8. ПРОФИЛЬНАЯ ПРЯМАЯ

z
A2
B2
x
A3
B3
y
B1
A1
HB AB
x = const
y
АВ параллельна
профильной плоскости
проекций
8

9. ПРЯМАЯ ПАРАЛЛЕЛЬНА ДВУМ ПЛОСКОСТЯМ

1. Прямая параллельна плоскостям П1и П2 , т.е.
перпендикулярна плоскости П3 – профильнопроецирующая прямая
2. Прямая параллельна плоскостям П1 и П3 , т.е.
перпендикулярна плоскости П2 – фронтальнопроецирующая прямая
3. Прямая параллельна плоскостям П2 и П3 , т.е.
перпендикулярна плоскости П1 –
горизонтально-проецирующая прямая
9

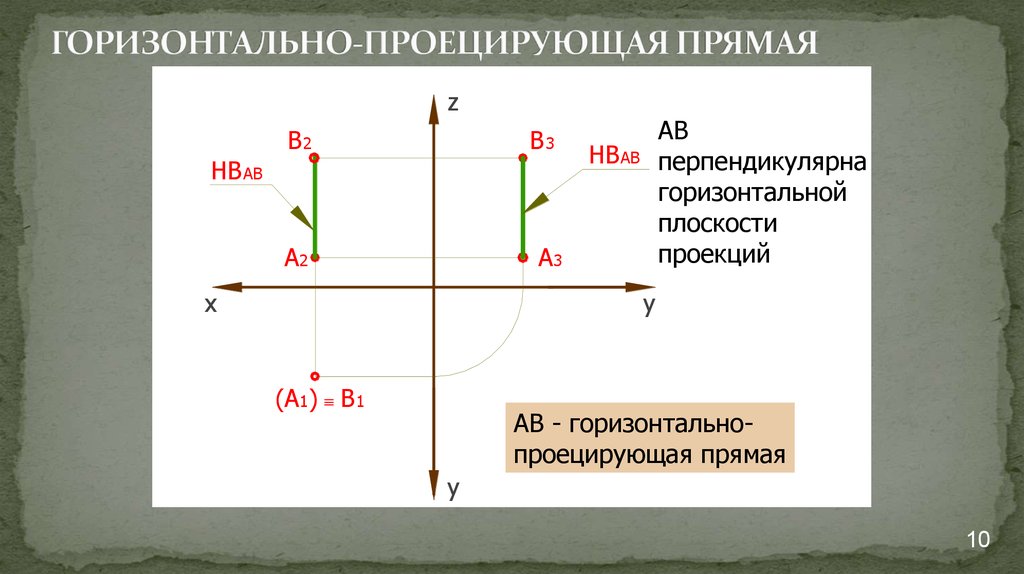
10. ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПРЯМАЯ

z
B2
HB AB
B3
z
A2
АВ
перпендикулярна
горизонтальной
плоскости
проекций
HB AB
A3
x
y
x
y
A11 ) B 1B 1
(A
АВ - горизонтальнопроецирующая прямая
y y
10

11. ФРОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПРЯМАЯ

z
A22 ) B 2B 2
(A
HB AB
A
3
z
x
B3
АВ
перпендикулярна
фронтальной
плоскости
проекций
y
xA1
HB AB
B1
y
АВ - фронтальнопроецирующая прямая
y y
11

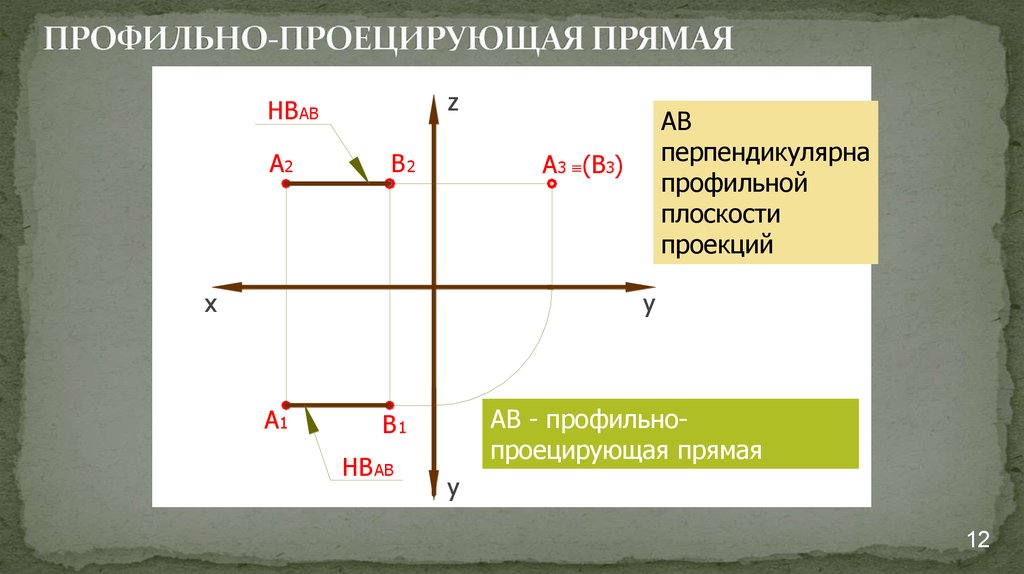
12. ПРОФИЛЬНО-ПРОЕЦИРУЮЩАЯ ПРЯМАЯ

z
HB AB
A2
B2
z
x
АВ
перпендикулярна
профильной
плоскости
проекций
B 33)
A3 (B
y
x
A1
y
АВ - профильнопроецирующая прямая
B1
HB AB
y y
12

13. СЛЕДЫ ПРЯМОЙ

Точки пересечения прямой линии с
плоскостями проекции называются следами
прямой
Точка пересечения прямой с горизонтальной
плоскостью проекций называется
горизонтальным следом прямой
Точка пересечения прямой с фронтальной
плоскостью проекций называется
фронтальным следом прямой
13

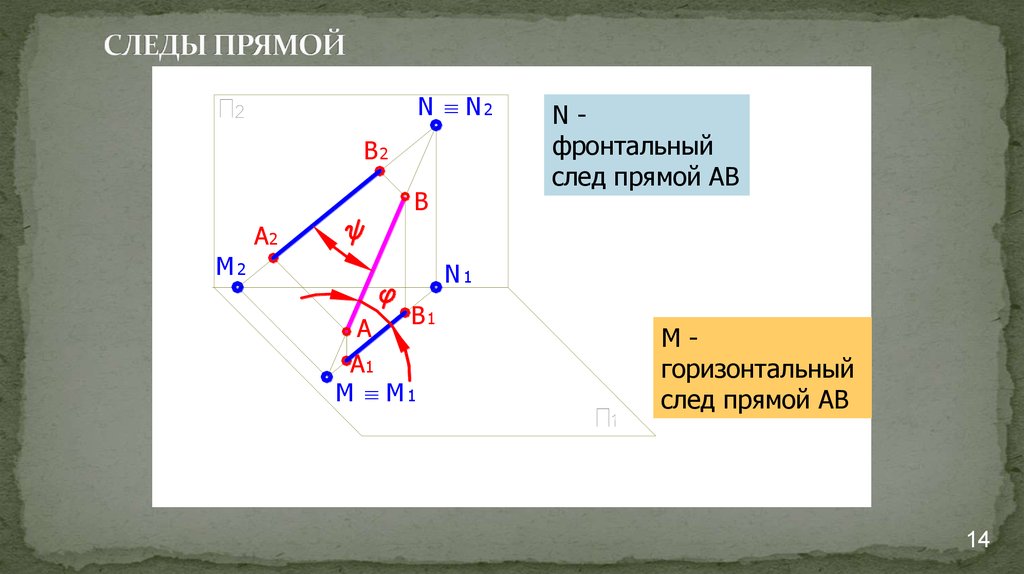
14. СЛЕДЫ ПРЯМОЙ

N N 2
B2
B
M 2
Nфронтальный
след прямой АВ
A2
N 12
B1
A
A1
M M 1
Мгоризонтальный
след прямой АВ
14

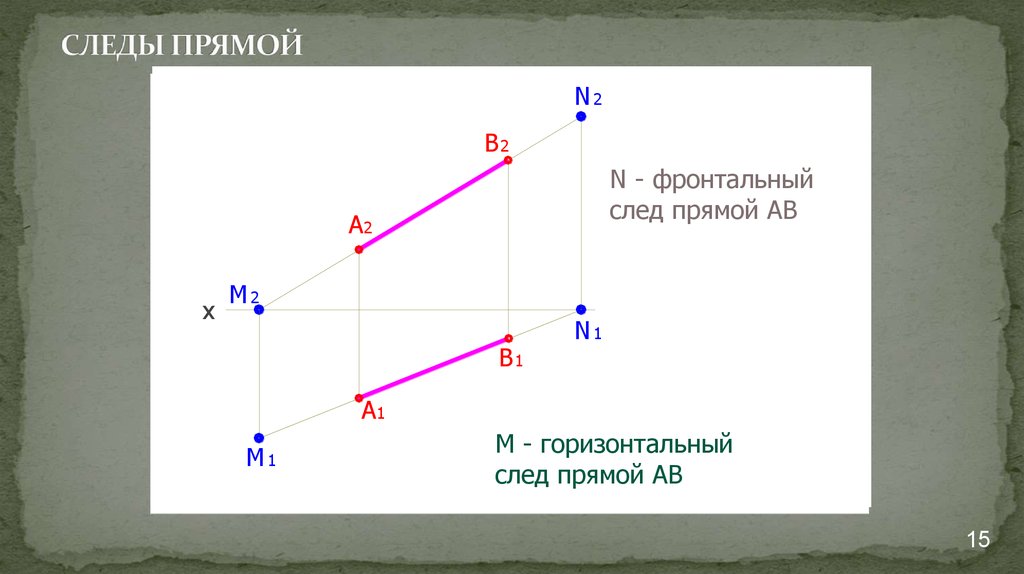
15. СЛЕДЫ ПРЯМОЙ

N2
B22
B
N - фронтальный
след прямой АВ
A22
A
M22
M
xx
B11
B
N11
N
A11
A
M11
M
М - горизонтальный
след прямой АВ
15

16. СПОСОБЫ ЗАДАНИЯ ПРЯМОЙ

1. По координатам точек концов отрезка прямой
(проекциям отрезка прямой)
2. Параметрами отрезка прямой линии:
- натуральной величиной отрезка (НВ)
- углами наклона к плоскостям проекций - (П₁) и (П₂)
- угол между линией отрезка и горизонтальной
плоскостью (П₁)
- угол между линией отрезка и фронтальной
плоскостью (П₂)
16

17. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ

По расположению относительно друг друга
прямые могут:
быть параллельными
пересекаться
скрещиваться
У скрещивающихся прямых одноименные
проекции прямых пересекаются, но точки
пересечения не лежат на одной линии связи
17

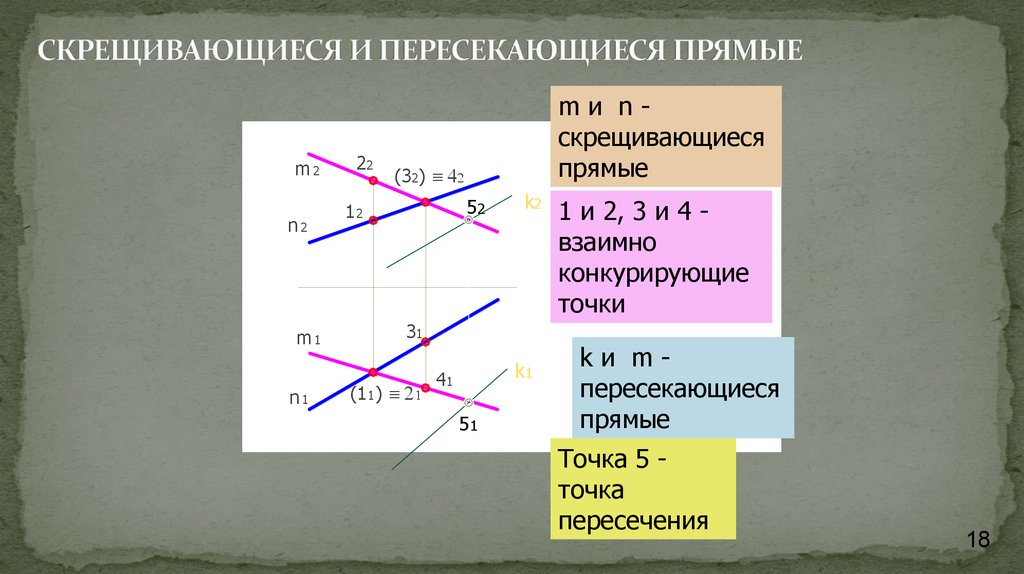
18. СКРЕЩИВАЮЩИЕСЯ И ПЕРЕСЕКАЮЩИЕСЯ ПРЯМЫЕ

m2
n2
m1
n1
22
mи nскрещивающиеся
прямые
(32)
52
12
k2
31
1 11 )
(1
k1
41
51
1 и 2, 3 и 4 взаимно
конкурирующие
точки
kи mпересекающиеся
прямые
Точка 5 точка
пересечения
18

19. ВЫВОДЫ

По положению относительно плоскостей
проекций различают:
прямые общего положения (непараллельные
и неперпендикулярные плоскостям
проекций)
прямые частного положения: параллельные
или перпендикулярные плоскостям
проекций
Прямые частного положения и их отрезки на
соответствующих проекциях дают натуральные
величины и углы расположения относительно
плоскостей проекций
19

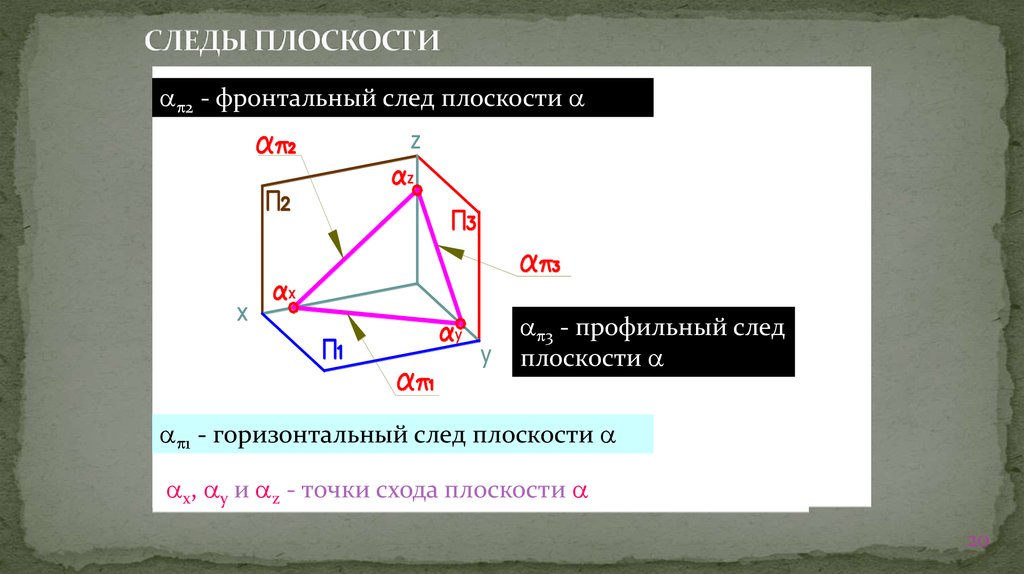
20. СЛЕДЫ ПЛОСКОСТИ

2 - фронтальный след плоскости
z z
z
xx
z
xx
y
3 - профильный след
y yплоскости
y
1 - горизонтальный след плоскости
x, y и z - точки схода плоскости
20

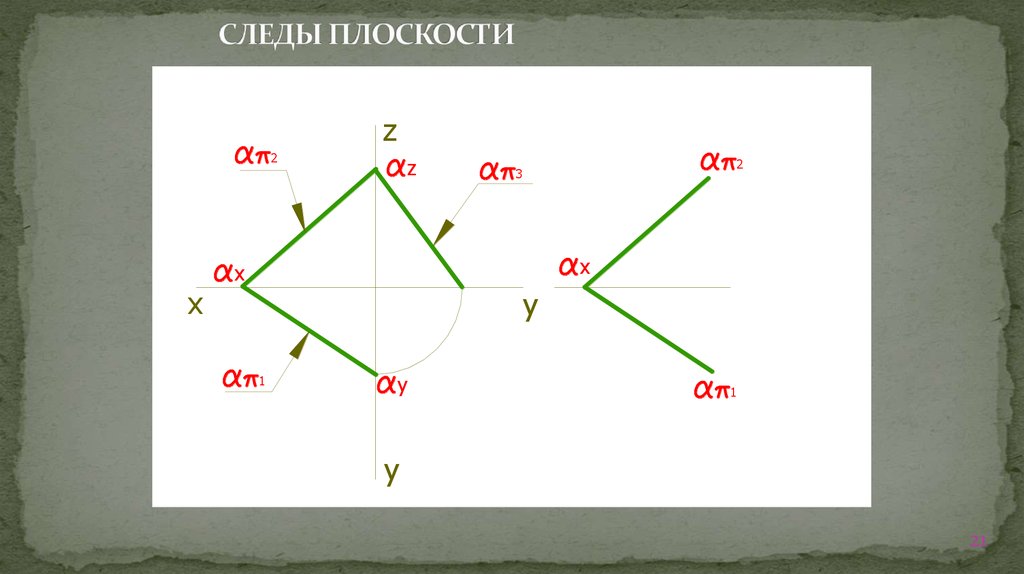
21. СЛЕДЫ ПЛОСКОСТИ

z
2
x
z
2
3
x
x
y
1
y
1
y
21

22. ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ

Плоскости общего положения - это
плоскости, неперпендикулярные и
непараллельные плоскостям проекций
Плоскости общего положения не
проецируются в натуральную величину
22

23. ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ

Плоскости, параллельные плоскостям проекций
Плоскости, перпендикулярные плоскостям
проекций (ПРОЕЦИРУЮЩИЕ)
23

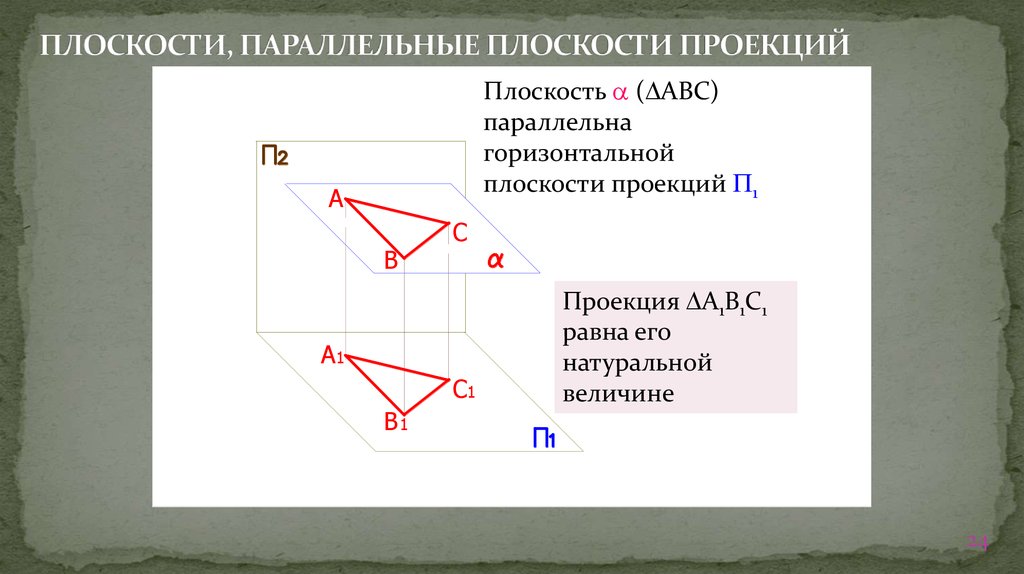
24. ПЛОСКОСТИ, ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ ПРОЕКЦИЙ

Плоскость ( АВС)
параллельна
горизонтальной
плоскости проекций 1
A
B
C
A1
C1
B1
Проекция А1В1С1
равна его
натуральной
величине
24

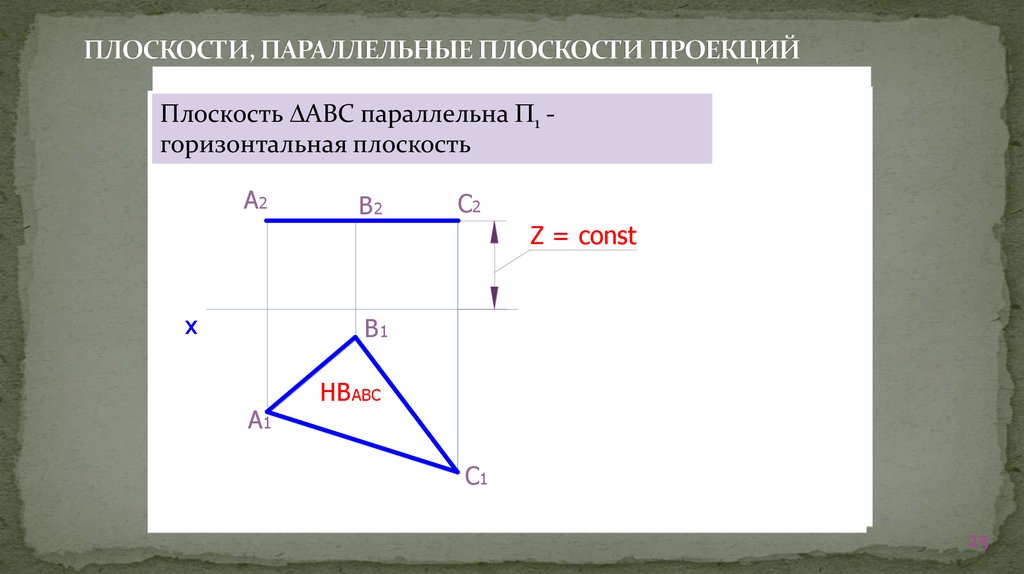
25. ПЛОСКОСТИ, ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ ПРОЕКЦИЙ

Плоскость АВС параллельна 1 горизонтальная плоскость
АА22 А2
ВВ22 В 2
СС22С2
Z = соnst
x
xx
x
В1
ВВ11
АА11
НВ ABC
А1 НВ ABC
С1
СС11
25

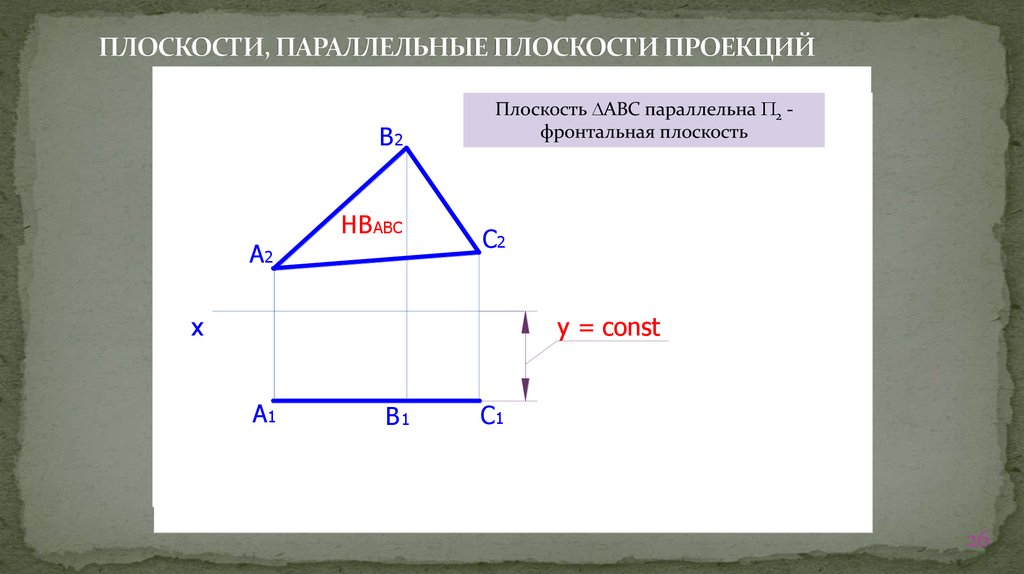
26. ПЛОСКОСТИ, ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ ПРОЕКЦИЙ

B2
B2
A2
A2
HB ABC
Плоскость АВС параллельна 2 фронтальная плоскость
C2
C2
x
x
y = const
A1
A1
B1
B1
C1
C1
26

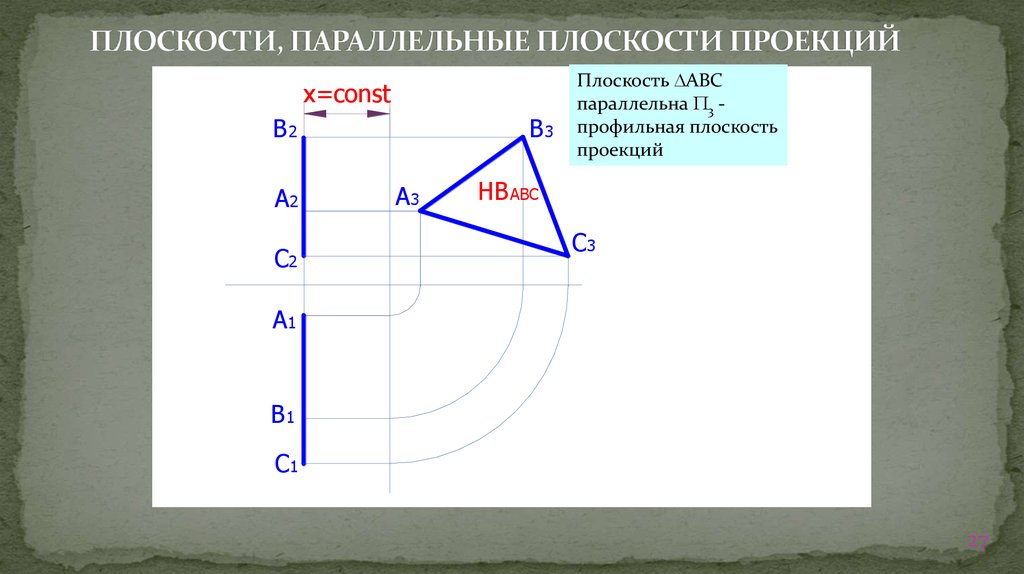
27. ПЛОСКОСТИ, ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ ПРОЕКЦИЙ

x=const
B2
A2
C2
B3
AA33
Плоскость АВС
параллельна 3 профильная плоскость
проекций
HB ABC
C3
A1
B1
C1
27

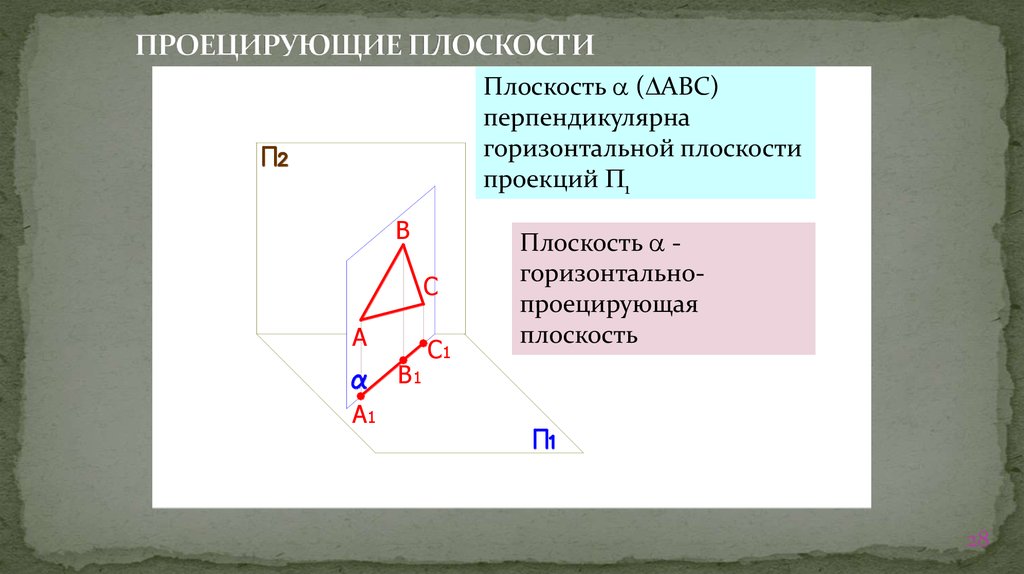
28. ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ

Плоскость ( АВС)
перпендикулярна
горизонтальной плоскости
проекций 1
B
C
A
B1
C1
Плоскость горизонтальнопроецирующая
плоскость
A1
28

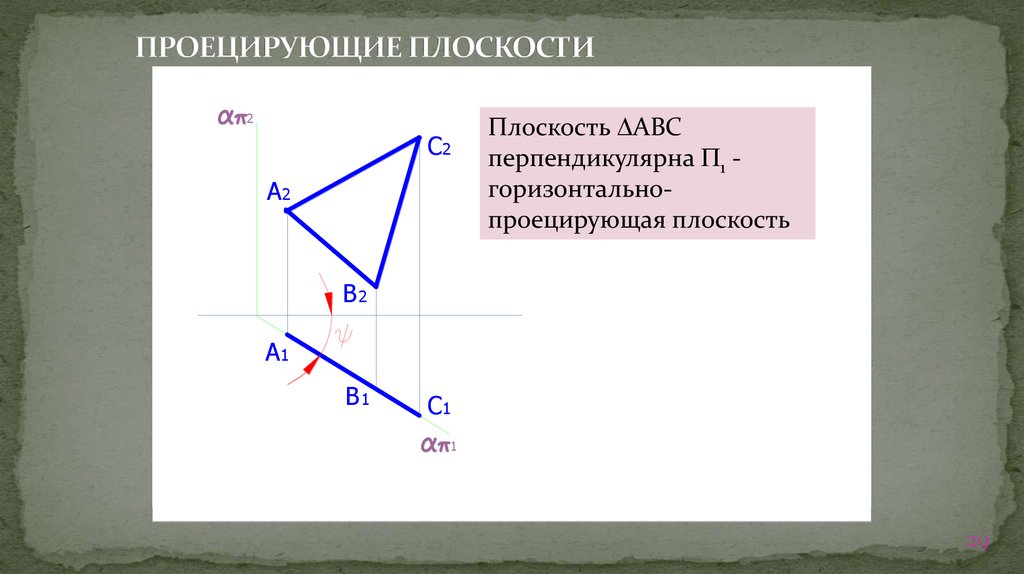
29. ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ

2
2
C2
C2
A2
A2
Плоскость АВС
перпендикулярна 1 горизонтальнопроецирующая плоскость
B2
B2
A1
A1
B1
B1
C1
C1
1
1
29

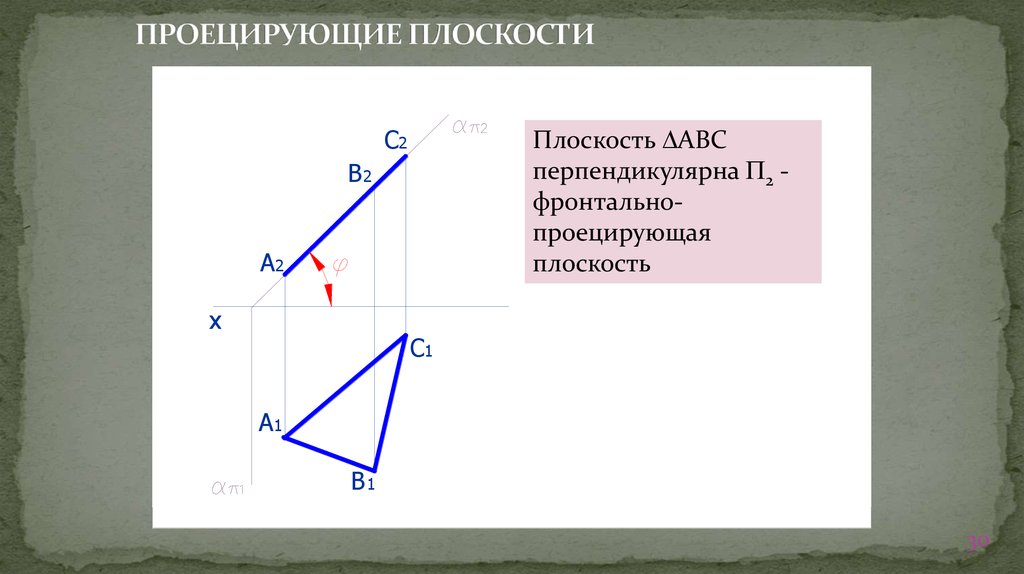
30. ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ

C2
B 2 C2
B2
Плоскость АВС
перпендикулярна 2 фронтальнопроецирующая
плоскость
A2
A2
x
x
C1
C1
A1
A1
B1
B1
30

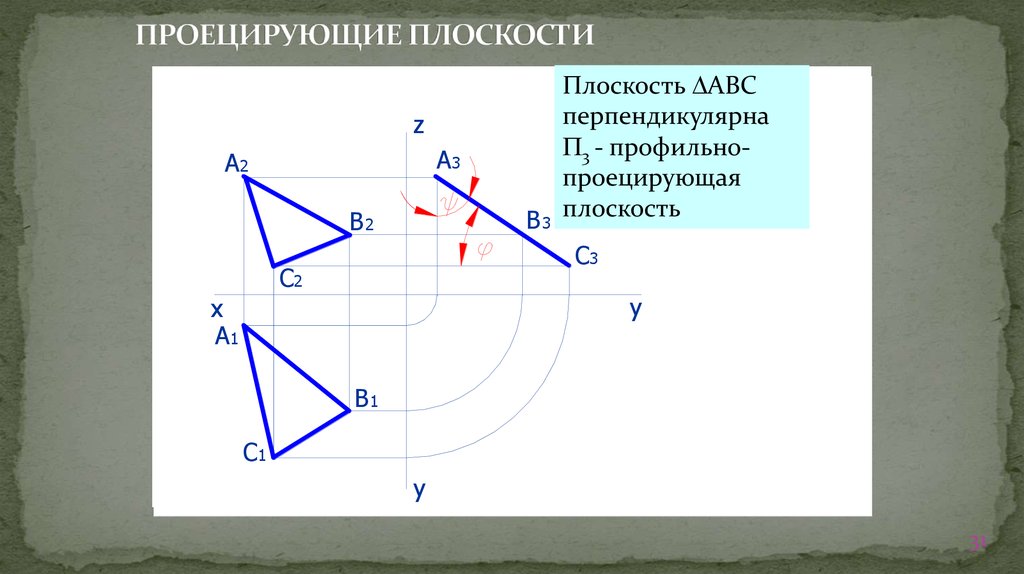
31. ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ

zz
A
A22
B
B22
C
C22
xx
A
A11
A
A33
Плоскость АВС
перпендикулярна
3 - профильнопроецирующая
B
B33 плоскость
C
C33
yy
B
B11
C
C11
yy
31

32. ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ. ГОРИЗОНТАЛЬ ПЛОСКОСТИ

Горизонталь плоскости - прямая принадлежащая
заданной плоскости и параллельная плоскости
проекций
Если плоскость задана следами, то горизонтальный
след плоскости - нулевая горизонталь этой
плоскости
32

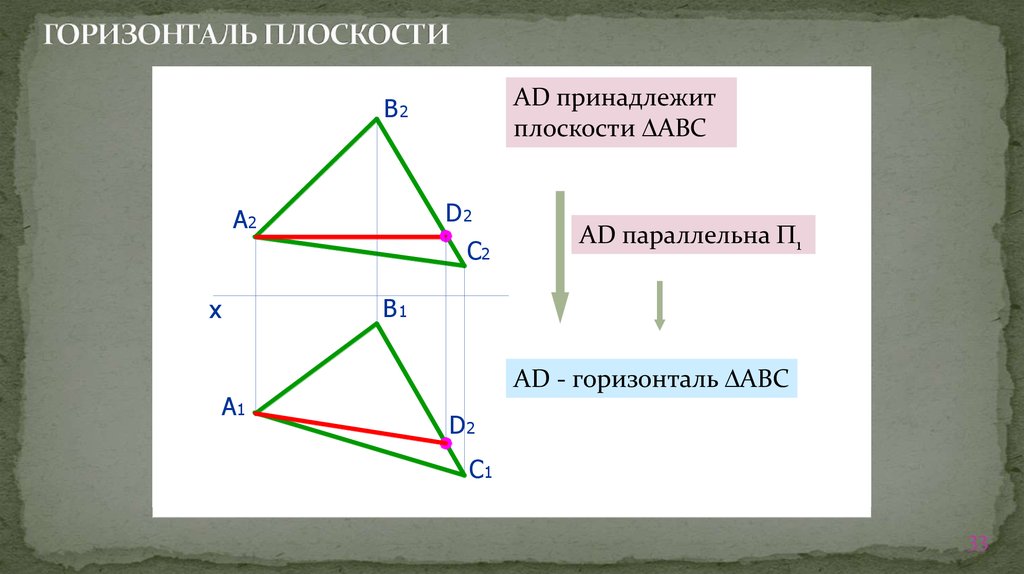
33. ГОРИЗОНТАЛЬ ПЛОСКОСТИ

B
B 22
AD принадлежит
плоскости АВС
D
D 22
C
C22
A
A22
AD параллельна 1
B
B 11
xx
A
A11
AD - горизонталь АВС
D2
C
C11
33

34. ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ. ФРОНТАЛЬ ПЛОСКОСТИ

Фронталь плоскости - прямая принадлежащая
плоскости и параллельная плоскости проекций
Если плоскость задана следами, то фронтальный
след плоскости - нулевая фронталь этой плоскости
34

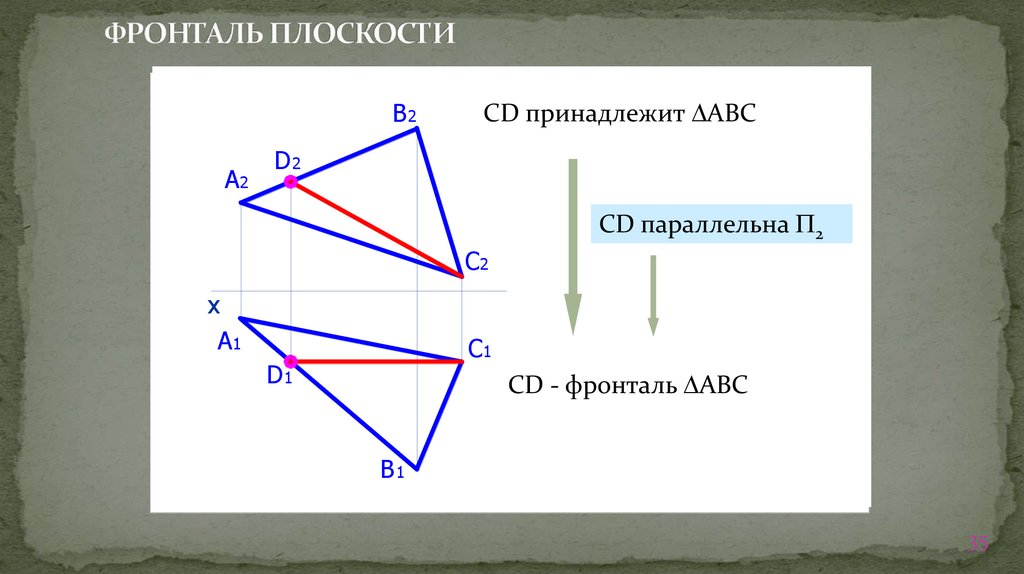
35. ФРОНТАЛЬ ПЛОСКОСТИ

B22
B
A22
A
CD принадлежит АВС
D2
C22
C
xx
A11
A
CD параллельна 2
C11
C
D1
CD - фронталь АВС
B11
B
35

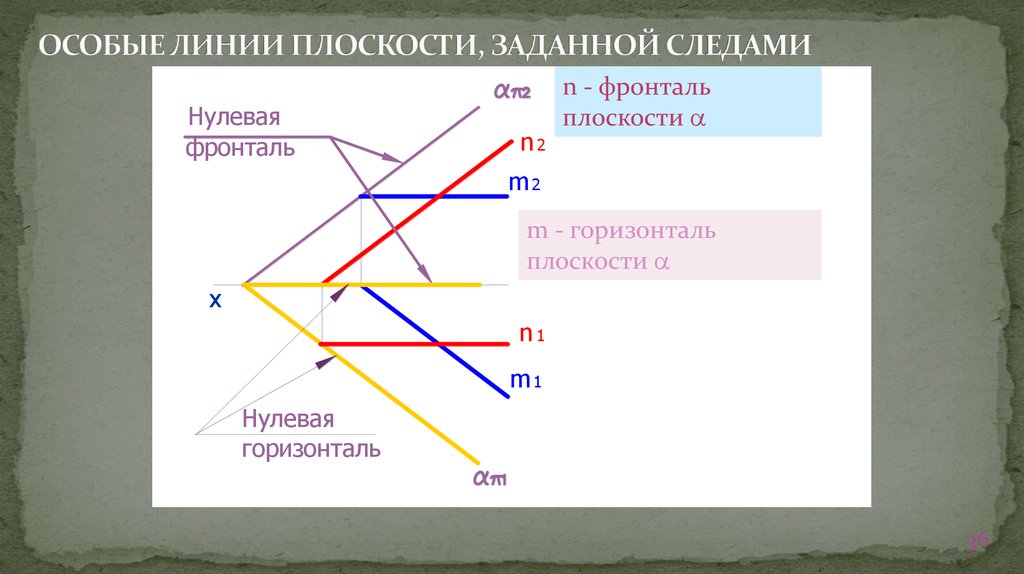
36. ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ, ЗАДАННОЙ СЛЕДАМИ

Нулевая
фронталь
n2
n - фронталь
плоскости
m2
m - горизонталь
плоскости
x
n1
m1
Нулевая
горизонталь
36

37. ВЫВОДЫ

Различают плоскости общего и частного
положения
Плоскости частного положения:
Параллельные плоскостям проекций
Перпендикулярные плоскостям проекций
Особые линии плоскости:
Горизонталь
Фронталь