Похожие презентации:
Электростатическое поле и его характеристики. Часть 2
1.
Часть 2ЭЛЕКТРОДИНАМИКА
Электростатическое
поле и его
характеристики
2.
Характеристики электрона и протонае =1,602.10-19 Кл
qe =-е
элементарный заряд
у электрона
me = 9,1 10-31 кг
qp =е
mp =
1,672 10-27
mp 1836me
кг
у протона
3.
1. Электрический заряд не являетсязнакоопределенной величиной
2. Электрический заряд величина инвариантная
3. Электрический заряд величина аддитивная
4. Электрический заряд обладает
свойством квантованности
Q = N e
5. Выполняется закон сохранения электрического
заряда
q1 + q2 + q3 + ... +qn = const.
6. Взаимодействие в соответствии с законом Кулона
4.
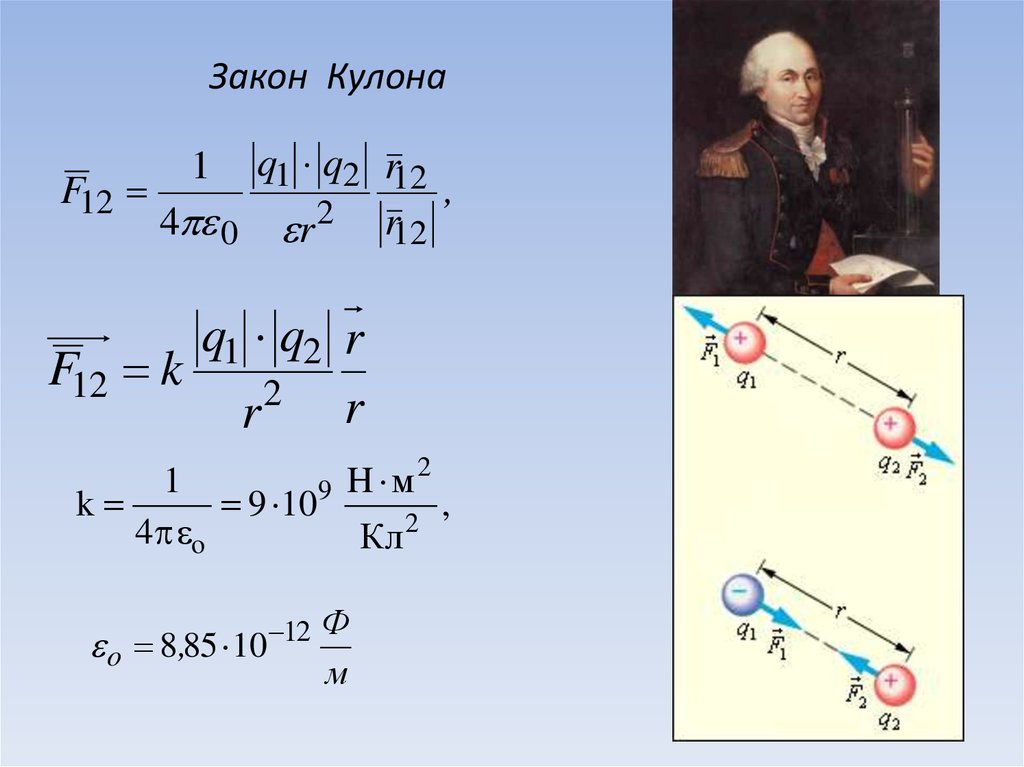
Закон Кулонаq1 q2 r12
F12
,
4 0 r 2 r12
1
q1 q2 r
F12 k
2
r
r
2
1
H
м
k
9 10 9
,
2
4 o
Кл
o 8,85 10
12 Ф
м
5.
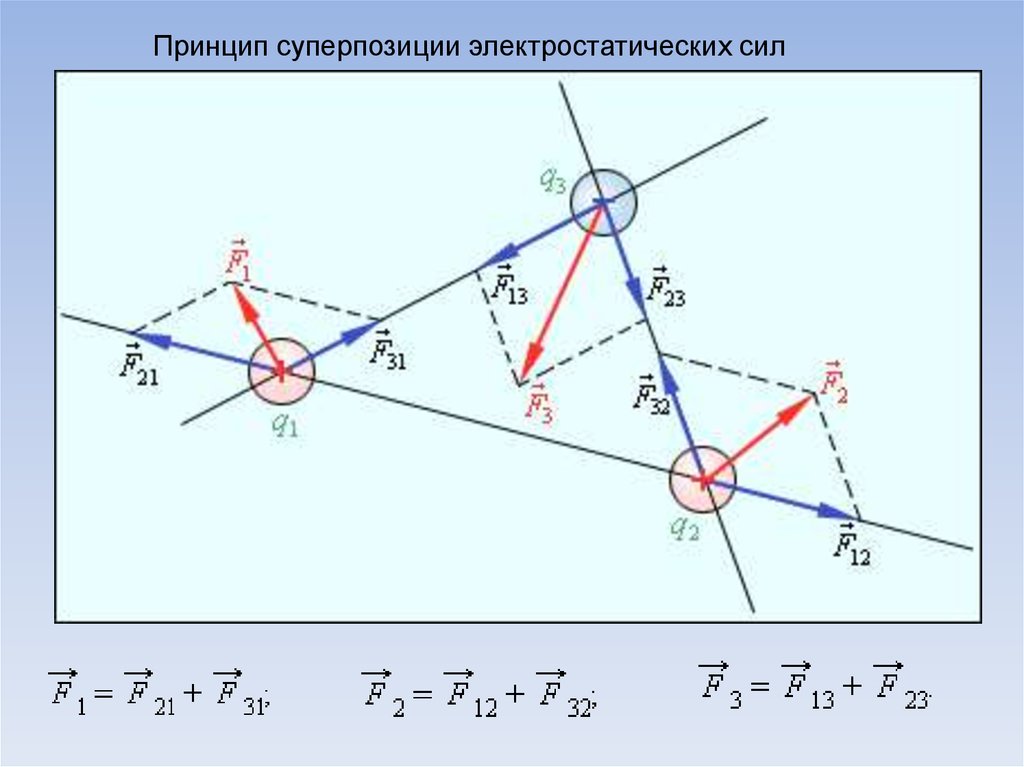
Принцип суперпозиции электростатических сил6.
Напряженность электрического поляq q пр
F k 2
r
r
.
r
Е
q r
E k
2
r r
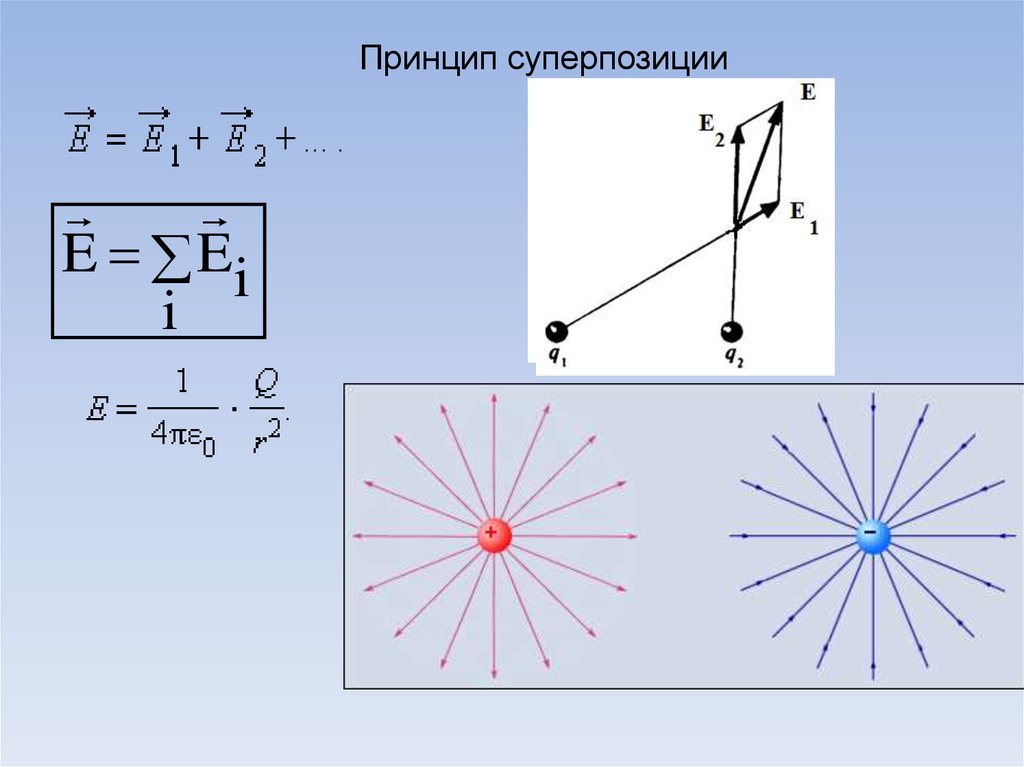
7.
Принцип суперпозицииE Ei
i
8.
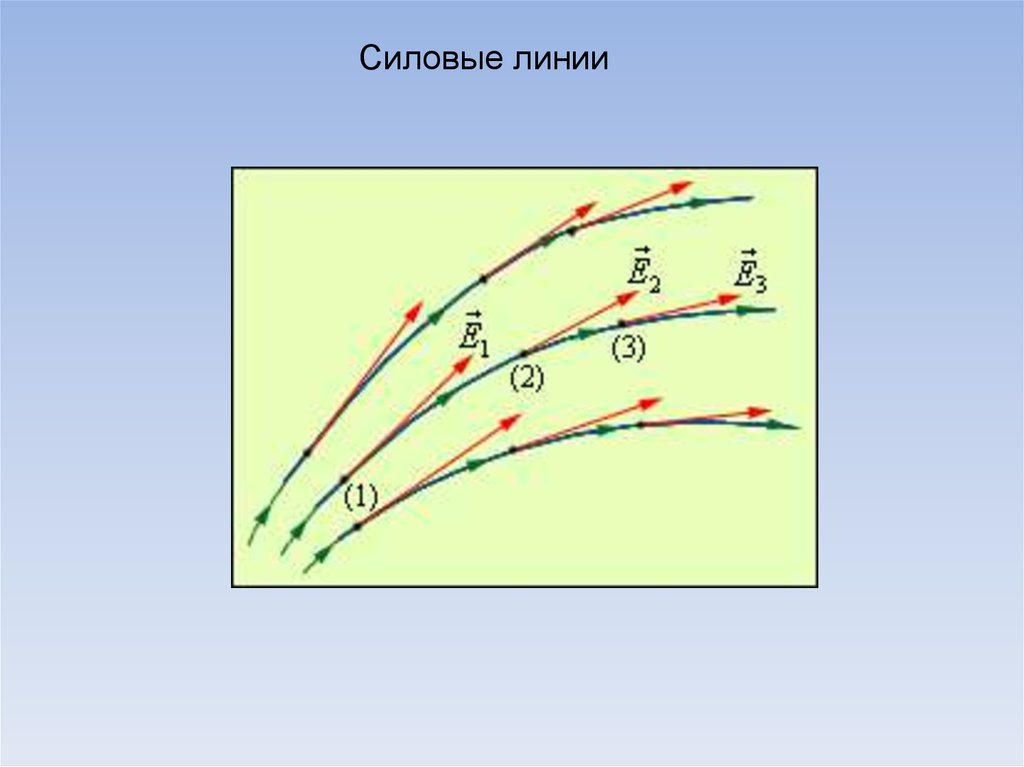
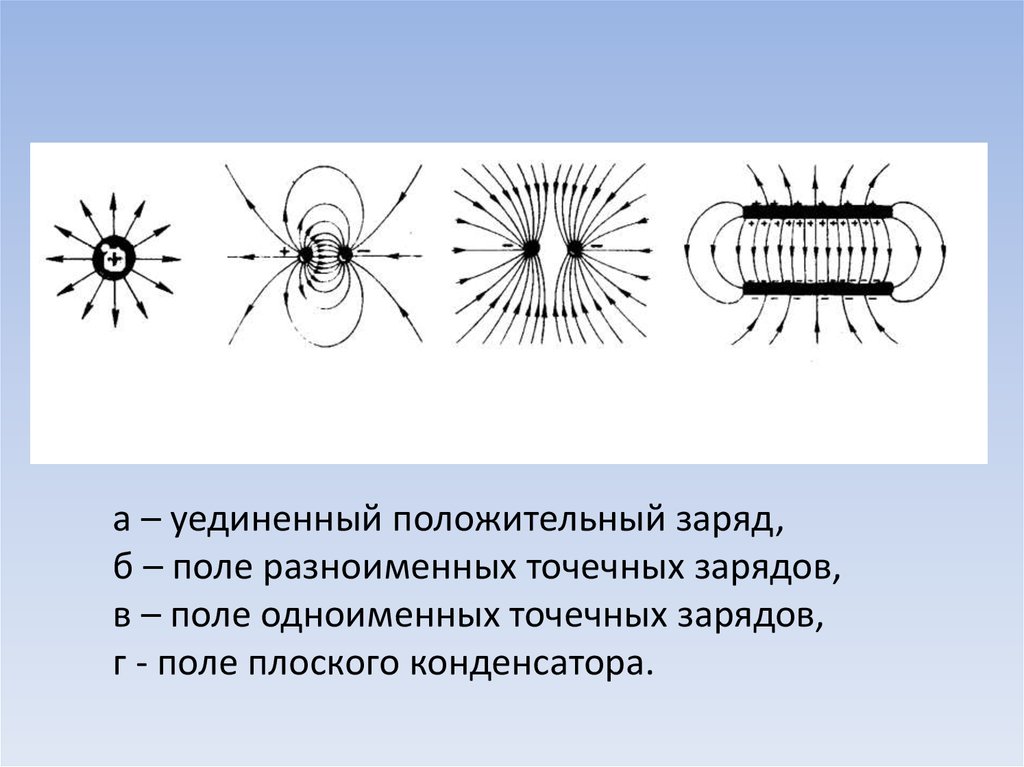
Силовые линии9.
а – уединенный положительный заряд,б – поле разноименных точечных зарядов,
в – поле одноименных точечных зарядов,
г - поле плоского конденсатора.
10.
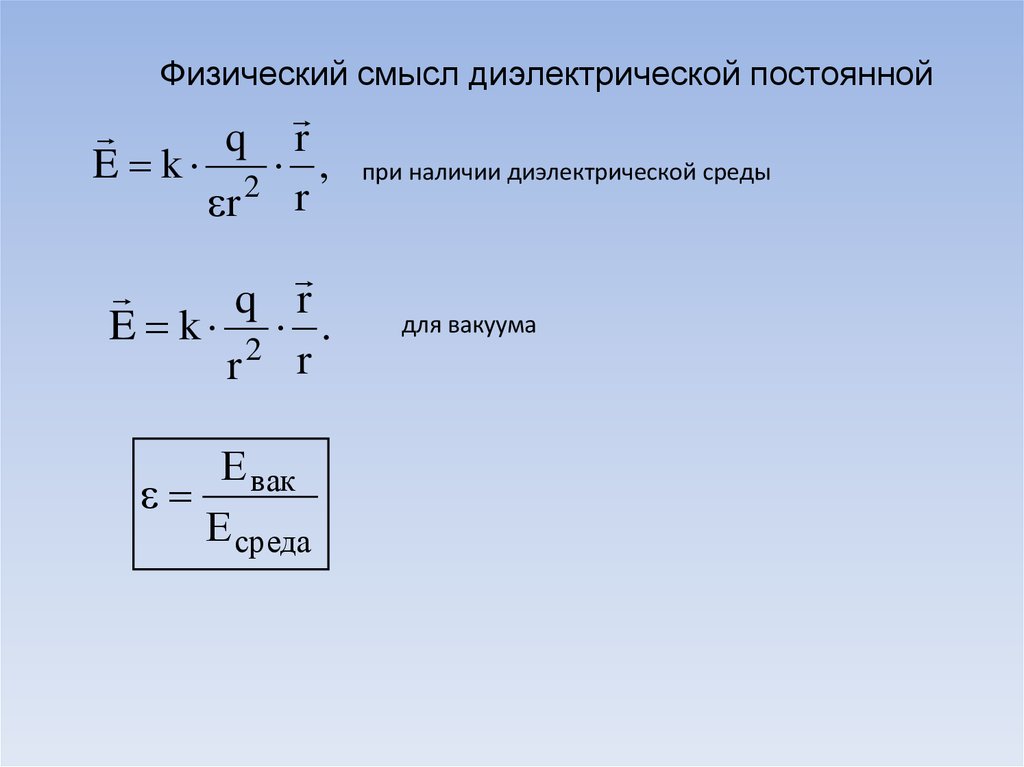
Физический смысл диэлектрической постояннойq r
E k 2 ,
r r
q r
E k 2 .
r r
Е вак
Е среда
при наличии диэлектрической среды
для вакуума
11.
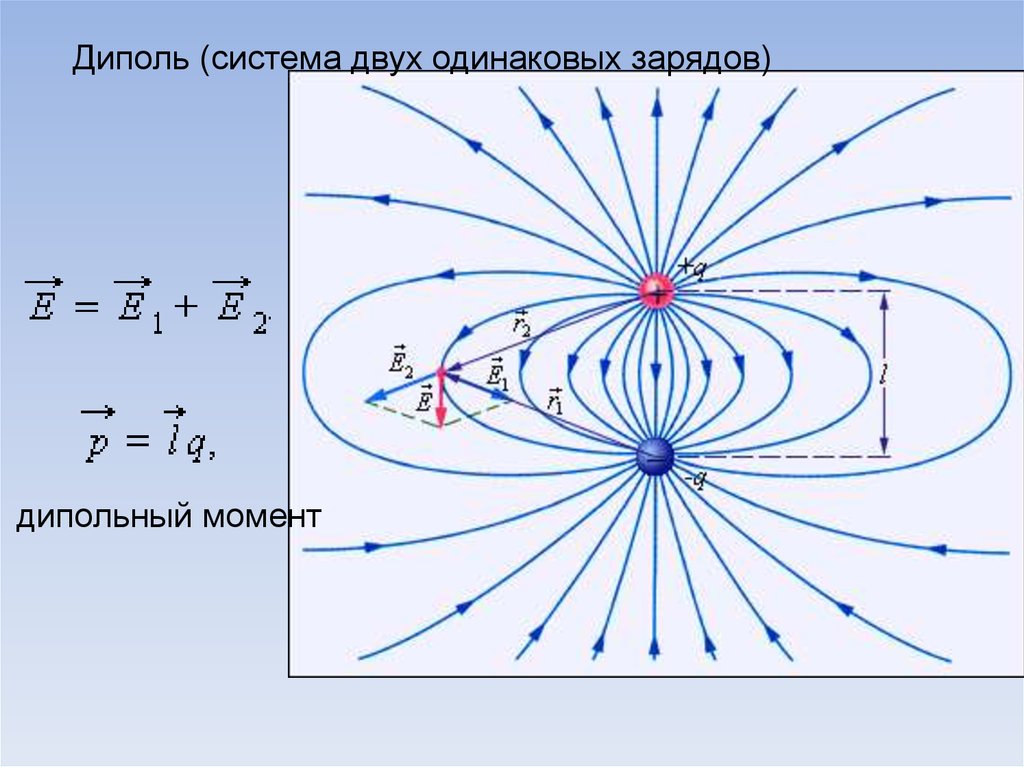
Диполь (система двух одинаковых зарядов)дипольный момент
12.
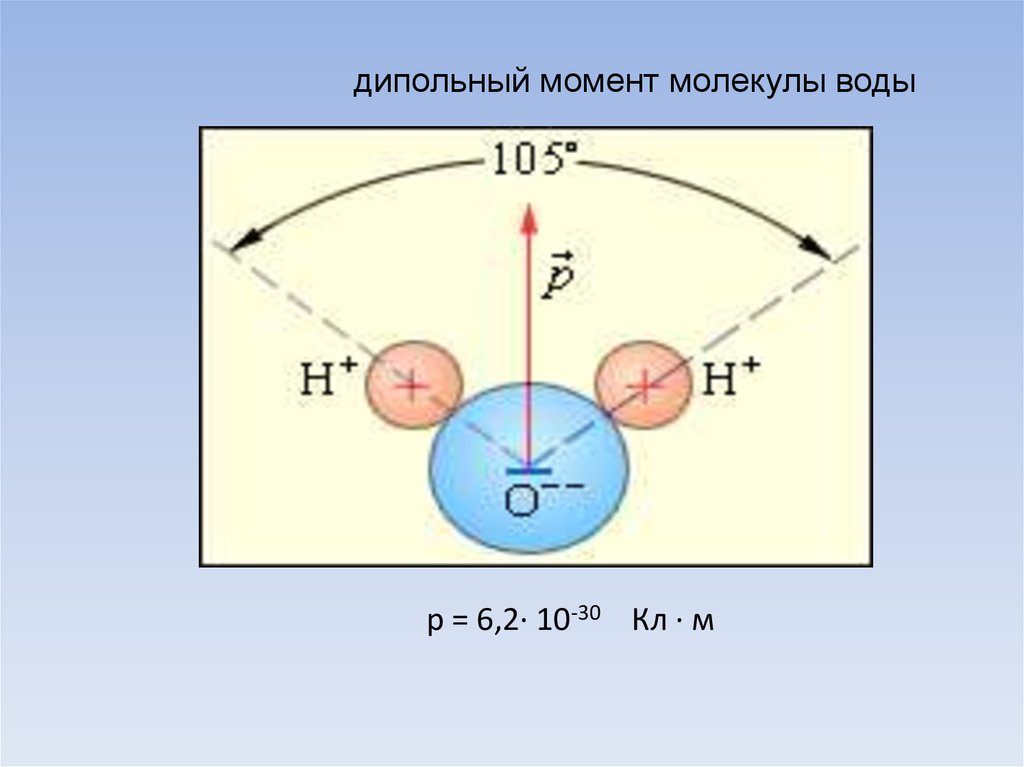
дипольный момент молекулы водыp = 6,2· 10-30 Кл · м
13.
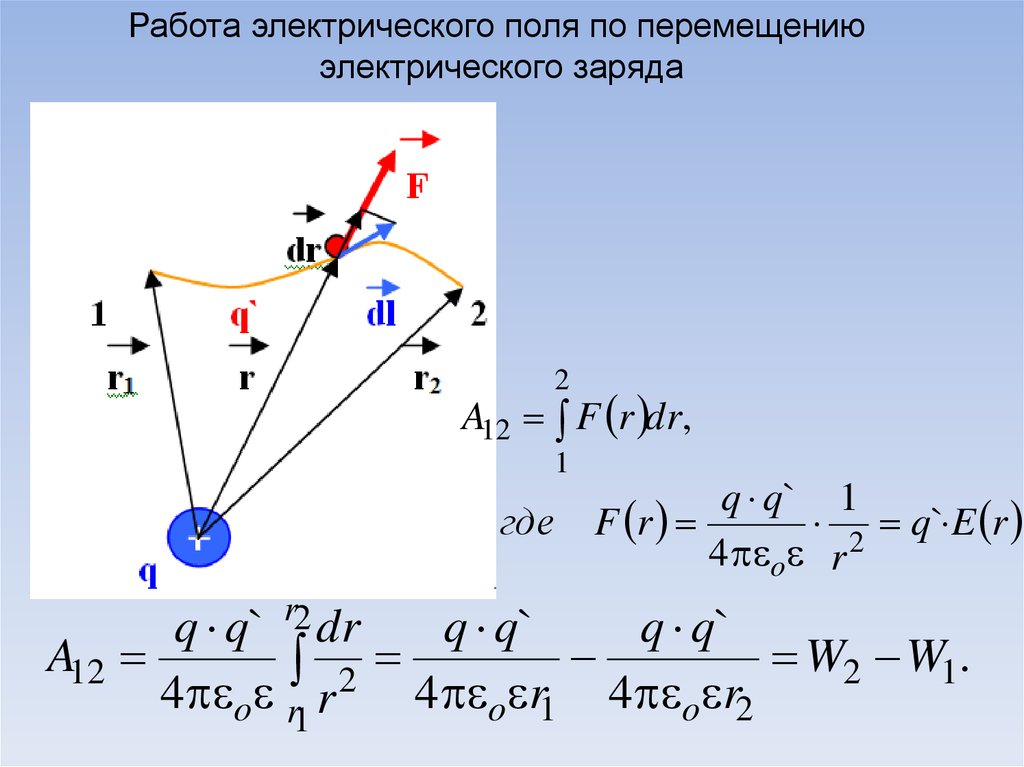
Работа электрического поля по перемещениюэлектрического заряда
2
A12 F r dr,
1
где
q q` 1
F r
2 q` E r
4 o r
q q`
q q`
q q`
A12
W2 W1.
2
4 o r1 r
4 o r1 4 o r2
r2
dr
14.
A F d q E d q E d 0Циркуляция вектора напряженности
по замкнутому контуру
E d
0
15.
Ротор электрического поляЕсли замкнутый контур стягивать в точку,
то циркуляция вектора напряженности
по замкнутому контуру
E d
rot E lim
s 0
s
0
В электростатическом поле
rot E 0
16.
Потенциальная энергия и потенциал электрического поля.Энергия взаимодействия
двух зарядов
q qпр
Wp
const
4 o r
Введем параметр поля
Wp
1
q
qпр 4 o r
Тогда энергия и работа
потенциал
W p q , A12 q 2 1 qU
A1 = q
17.
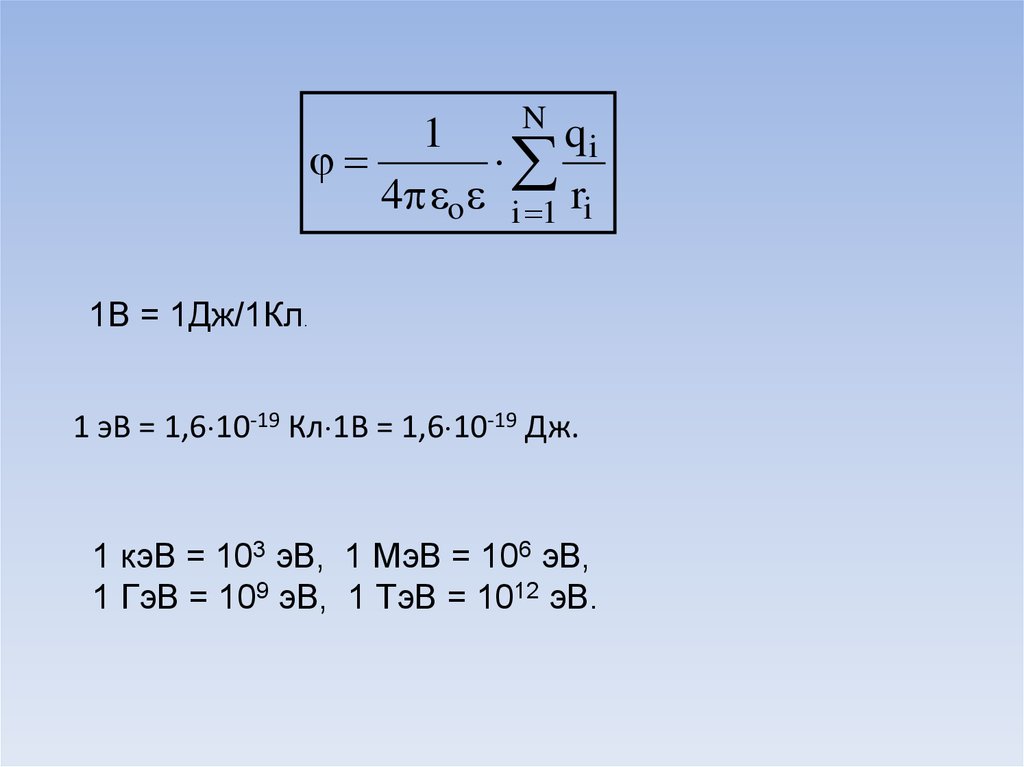
Nqi
1
4 o i 1 ri
1В = 1Дж/1Кл.
1 эВ = 1,6 10-19 Кл 1В = 1,6 10-19 Дж.
1 кэВ = 103 эВ, 1 МэВ = 106 эВ,
1 ГэВ = 109 эВ, 1 ТэВ = 1012 эВ.
18.
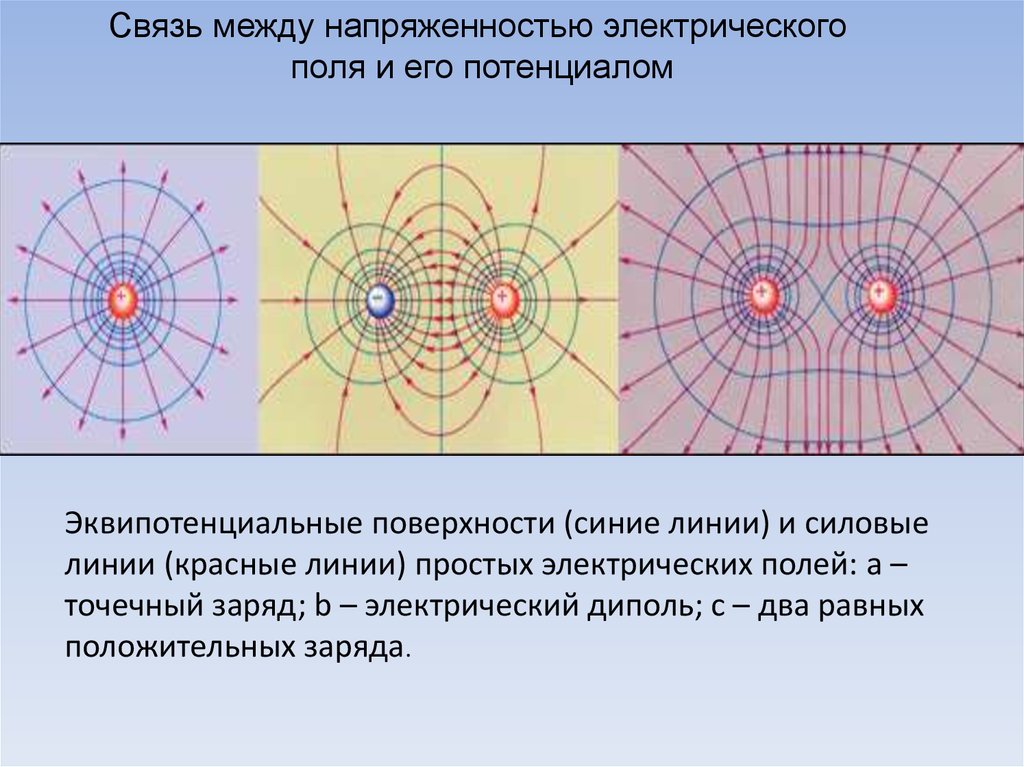
Связь между напряженностью электрическогополя и его потенциалом
Эквипотенциальные поверхности (синие линии) и силовые
линии (красные линии) простых электрических полей: a –
точечный заряд; b – электрический диполь; c – два равных
положительных заряда.
19.
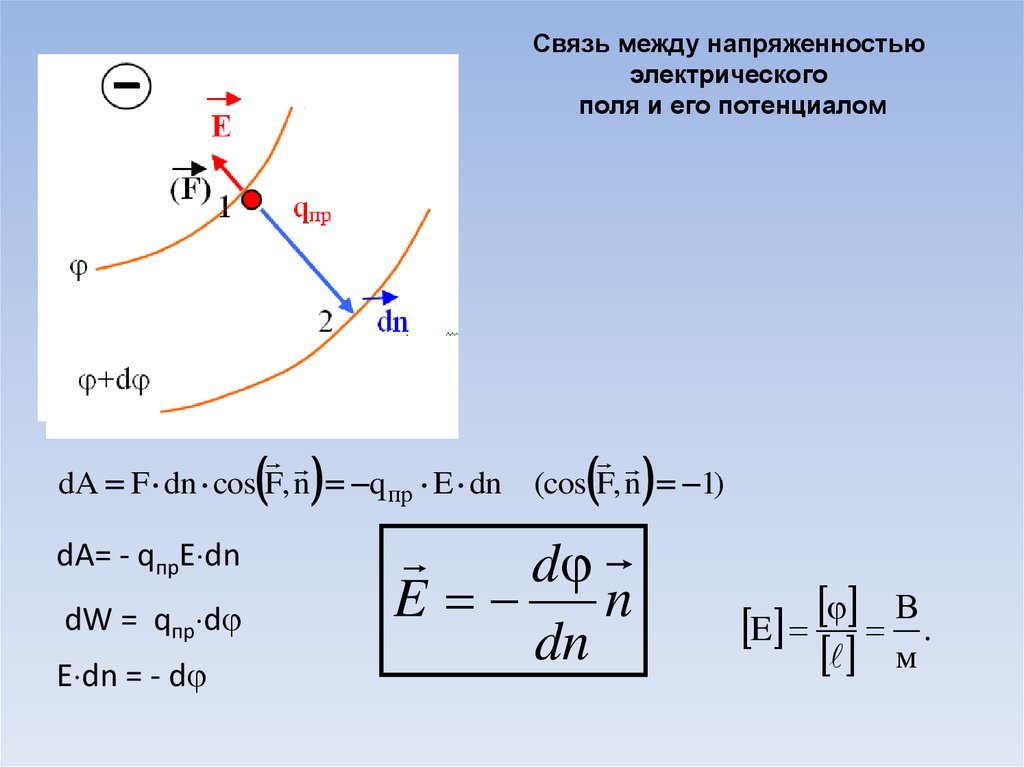
Связь между напряженностьюэлектрического
поля и его потенциалом
dA F dn cos F, n q пр E dn (cos F, n 1)
dA= - qпрE dn
dW = qпр d
E dn = - d
d
E
n
dn
В
E .
м
20.
Exx
Ey
y
Ez
z
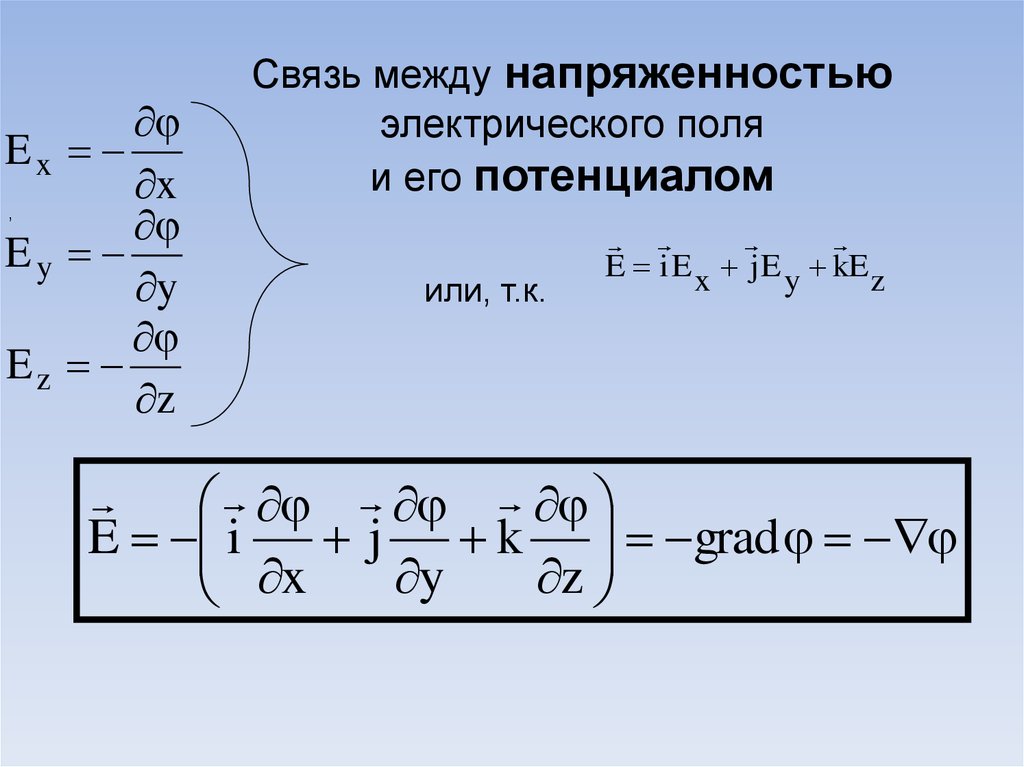
Связь между напряженностью
электрического поля
и его потенциалом
,
или, т.к.
E i E x j E y kE z
E i
j
k grad
y
z
x
21.
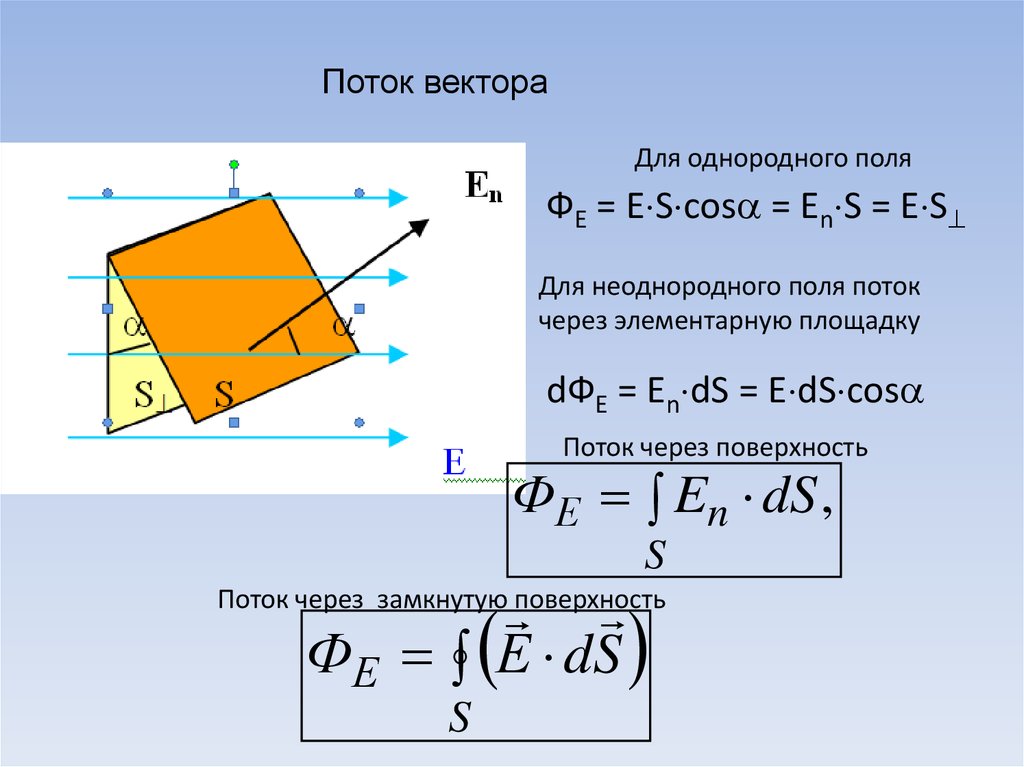
Поток вектораДля однородного поля
ФЕ = Е S cos = En S = E S
Для неоднородного поля поток
через элементарную площадку
dФЕ = En dS = E dS cos
Поток через поверхность
ФЕ En dS ,
S
ФЕ Е dS
Поток через замкнутую поверхность
S
22.
Иога́нн Карл Фри́дрих Га́уссD o E
а = о
1 q r
D o E
2
4 r r
Кл
2
м
23.
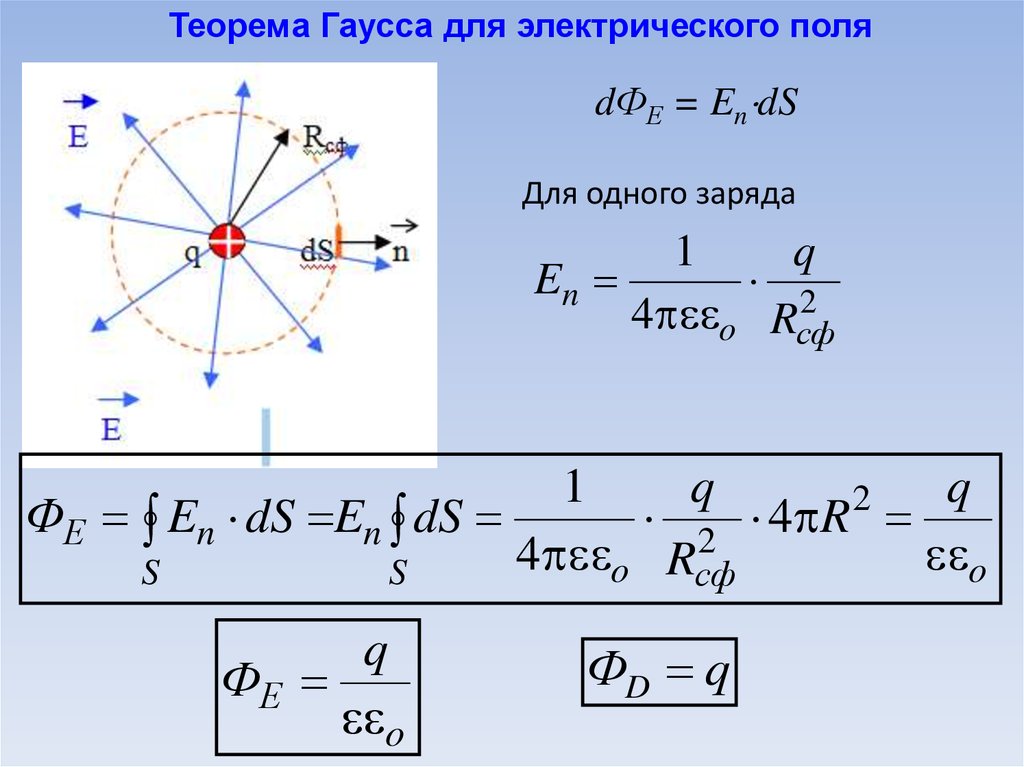
Теорема Гаусса для электрического поляdФЕ = En dS
Для одного заряда
1
q
En
2
4 o Rсф
1
q
q
2
ФЕ En dS En dS
2 4 R
4 o Rсф
o
S
S
q
ФЕ
o
ФD q
24.
Для дискретной системы зарядов1 N
ФЕ En dS E dS
qi
о i 1
S
S
1 N
qi .
E dS
о i 1
S
N
ФD qi
i 1
25.
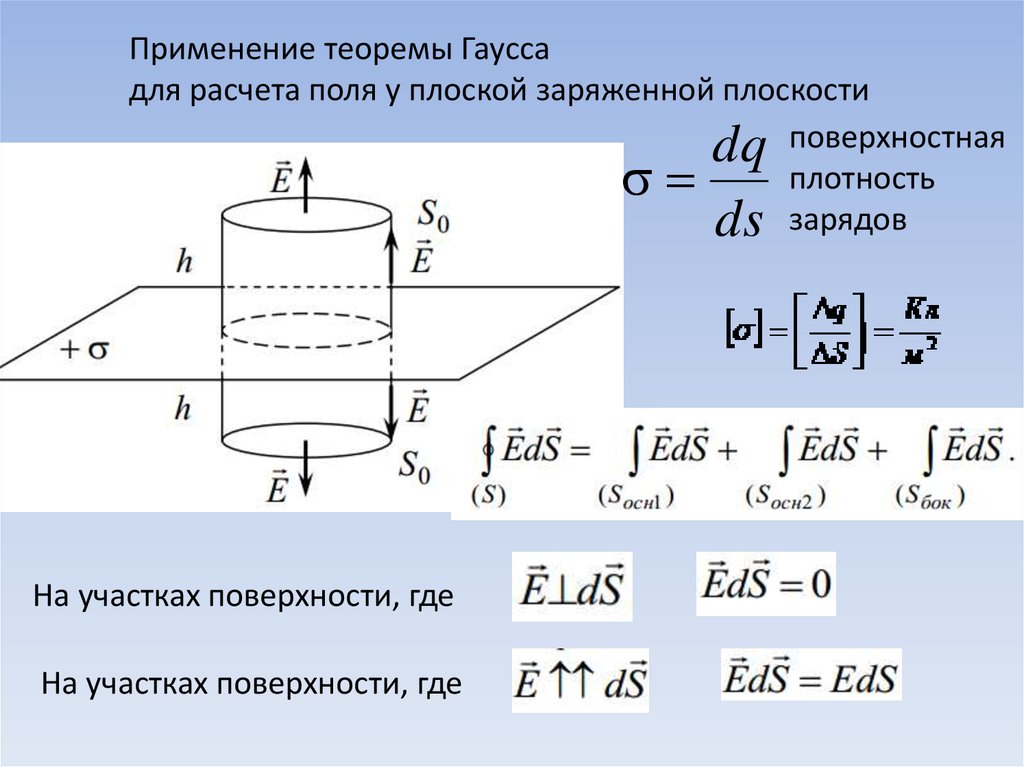
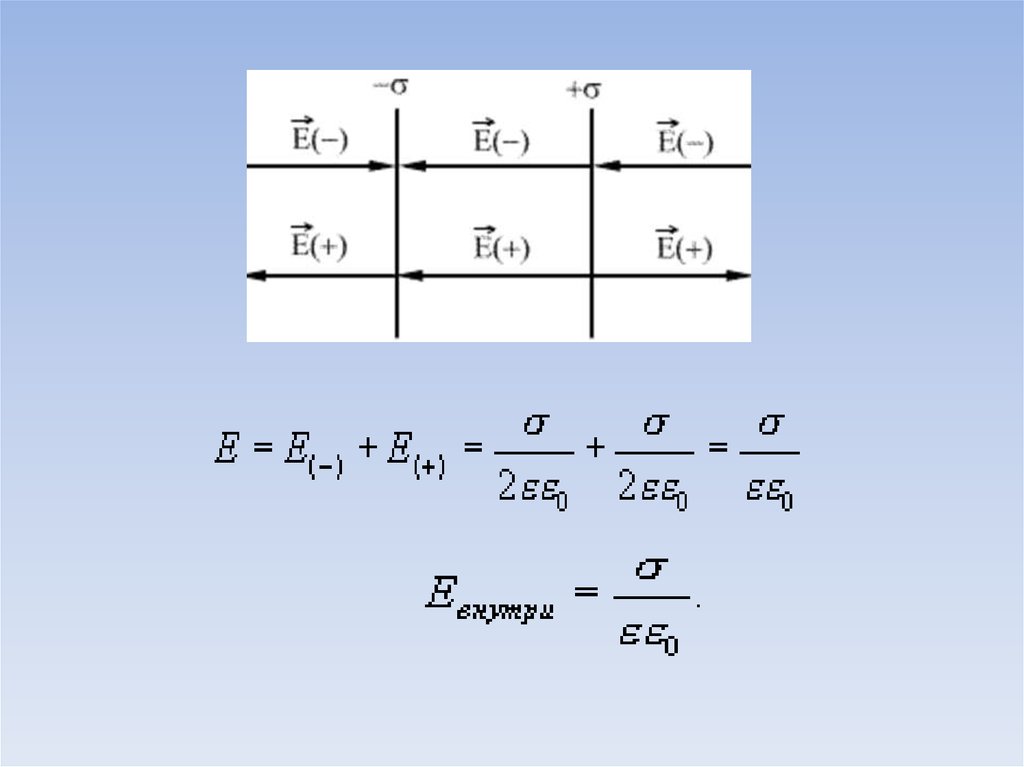
Для распределенного заряда26.
Применение теоремы Гауссадля расчета поля у плоской заряженной плоскости
dq поверхностная
плотность
ds зарядов
На участках поверхности, где
На участках поверхности, где
27.
28.
29.
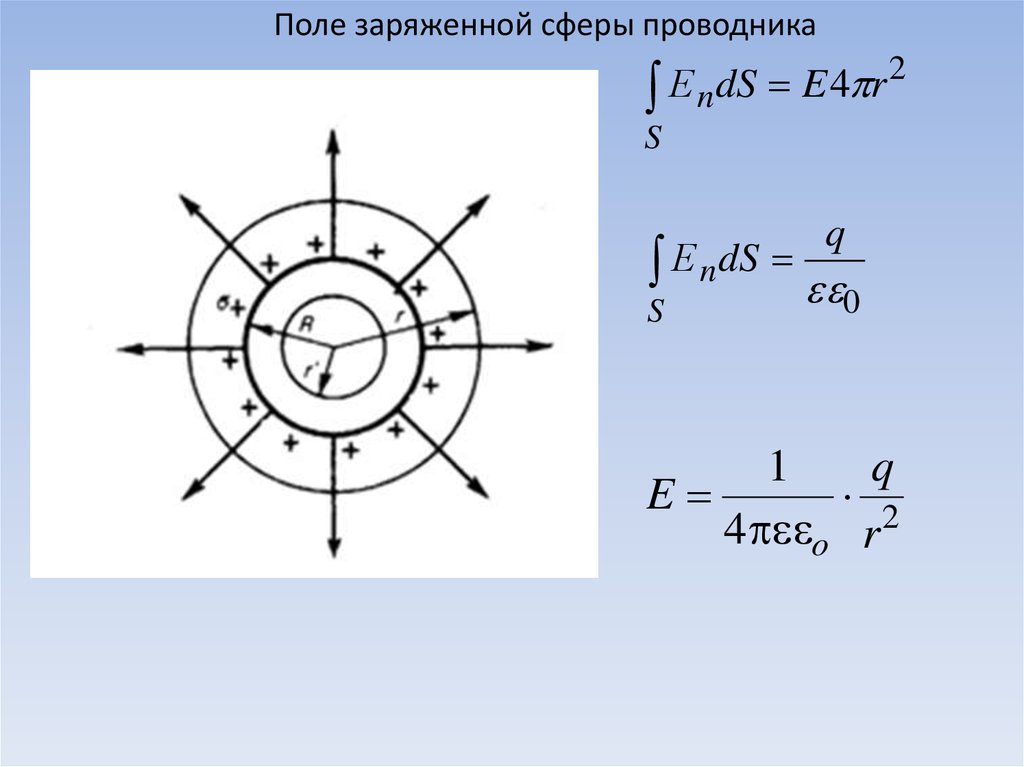
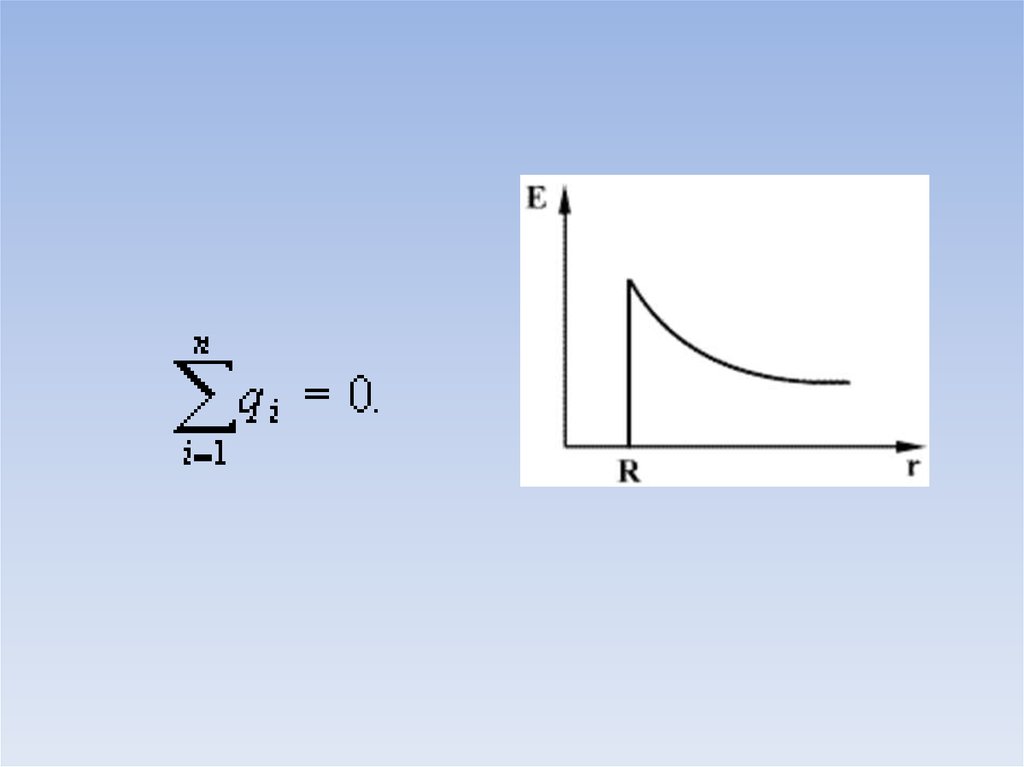
Поле заряженной сферы проводника2
Е
dS
E
4
r
n
S
q
Е n dS
S
0
1
q
E
2
4 o r
30.
31.
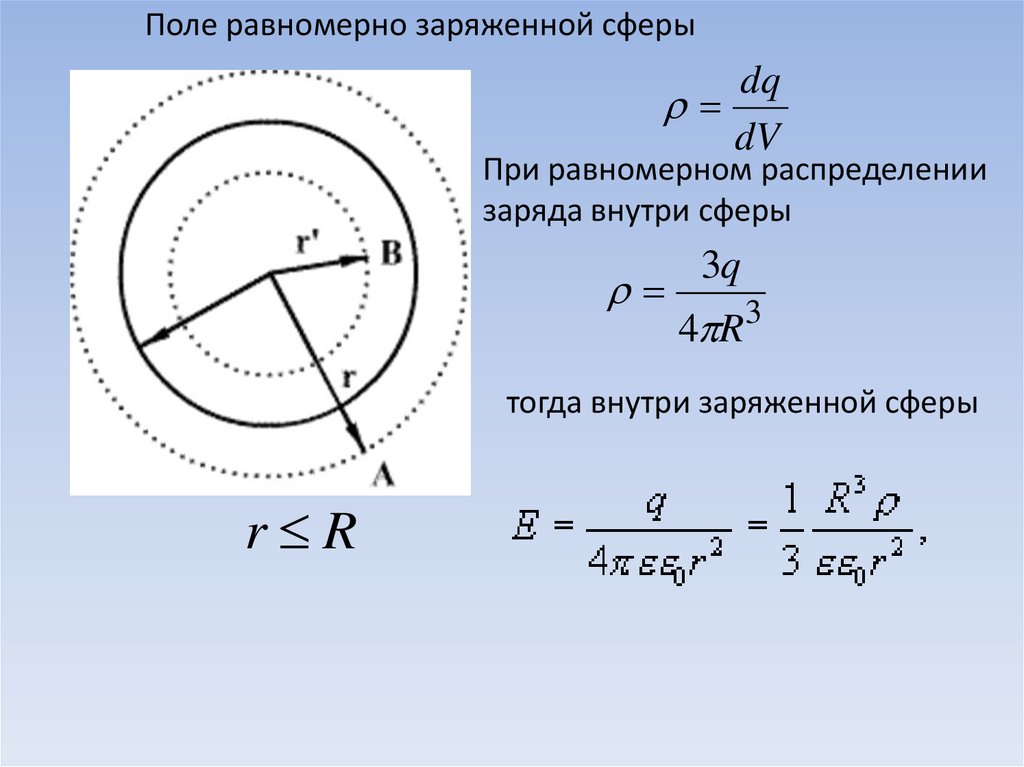
Поле равномерно заряженной сферыdq
dV
При равномерном распределении
заряда внутри сферы
3q
4 R
3
тогда внутри заряженной сферы
r R
32.
33.
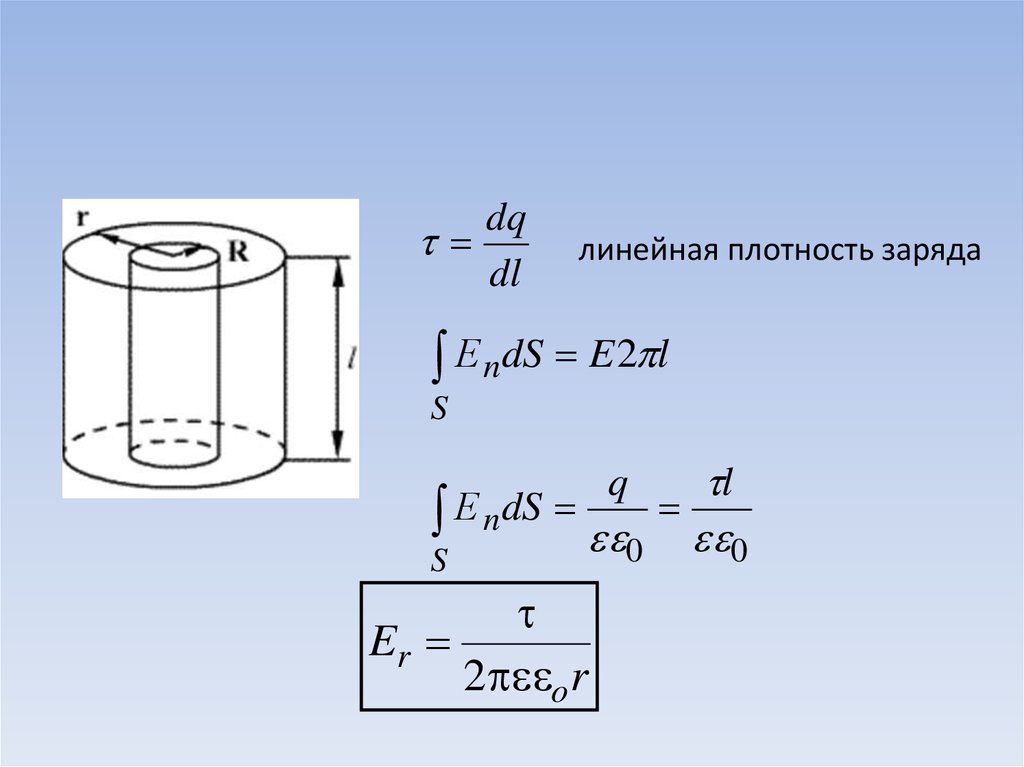
dqdl
линейная плотность заряда
Е ndS E 2 l
S
l
Е ndS
0
0
S
q
Er
2 o r
34.
Дивергенция электрического поляЕсли замкнутую поверхность стягивать в точку,
то поток вектора напряженности
через замкнутую поверхность
div E lim
V 0
q
div E
0
Es ds
s
V
q
0
div D q
35.
Интегральная и дифференциальная формызаписи теоремы Гаусса и
теоремы о циркуляции вектора напряженности
электрического поля
1 N
qi .
E dS
о i 1
S
E d
0
q
div E
0
rot E 0














 Физика
Физика








