Похожие презентации:
Электростатика Электростатическое поле и его характеристики
1. Лекция 20 Электростатика Электростатическое поле и его характеристики
Продолжим рассмотрение примеров вывода формулдля расчета характеристик электростатического поля,
созданного зарядами, распределенными по объектам
различной формы.
2. Пример 4 Напряженность поля, созданного зарядом, равномерно распределенным с объемной плотностью заряда ρ по объему шара из
диэлектрика радиусом R.Проводящий металлический шар (и проводник любой
формы) невозможно зарядить с распределением заряда по
объему.
Сообщенный проводнику избыточный заряд из-за
взаимного отталкивания одноименных заряженных
частиц и проводимости распределяется по поверхности.
Диэлектрики – материалы, не проводящие электричество,
и сообщенный заряд может быть распределен по объему.
3.
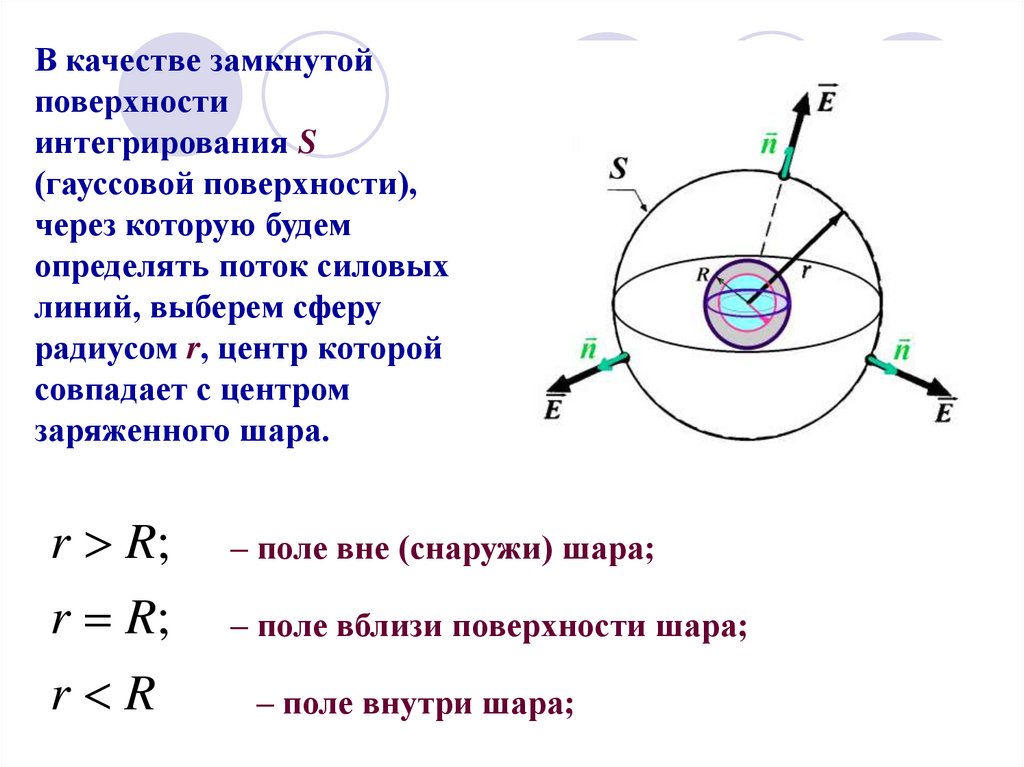
В качестве замкнутойповерхности
интегрирования S
(гауссовой поверхности),
через которую будем
определять поток силовых
линий, выберем сферу
радиусом r, центр которой
совпадает с центром
заряженного шара.
r R;
– поле вне (снаружи) шара;
r R;
– поле вблизи поверхности шара;
r R
– поле внутри шара;
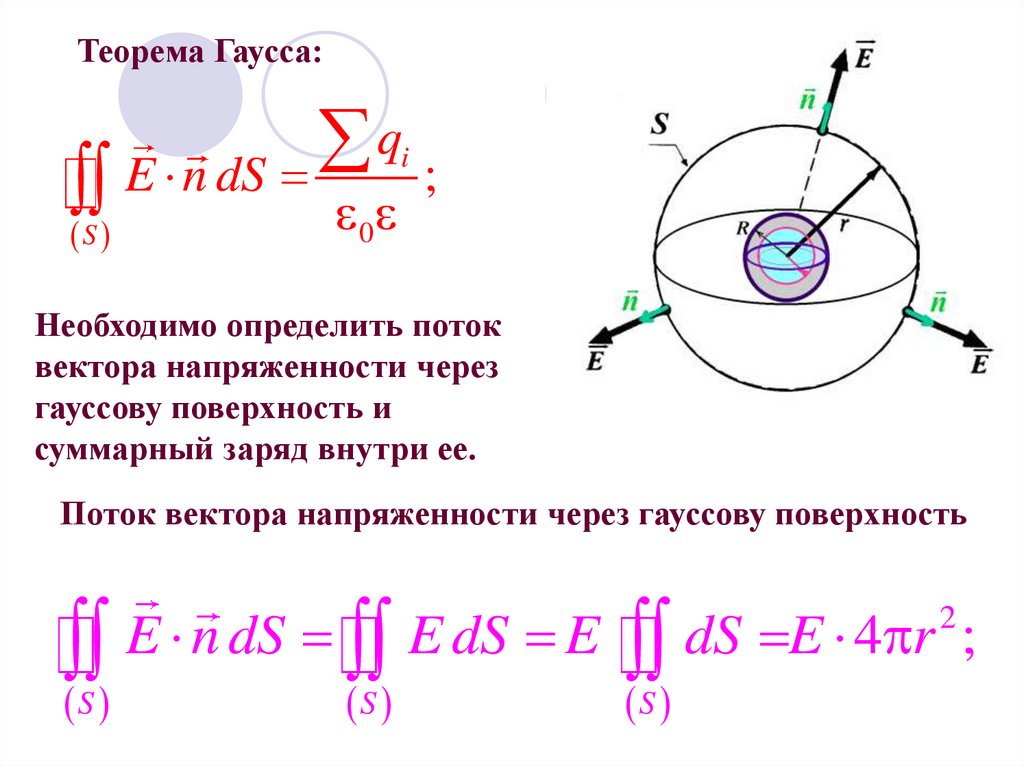
4.
Теорема Гаусса:S
q
E n dS
;
i
0
r R;
Необходимо определить поток
вектора напряженности через
гауссову поверхность и
суммарный заряд внутри ее.
q
i
0
q
q
; E
;
0
4 0 r 2
Поток вектора напряженности через гауссову поверхность
E
n
dS
E
dS
E
S
S
dS
E
4
r
;
2
S
5.
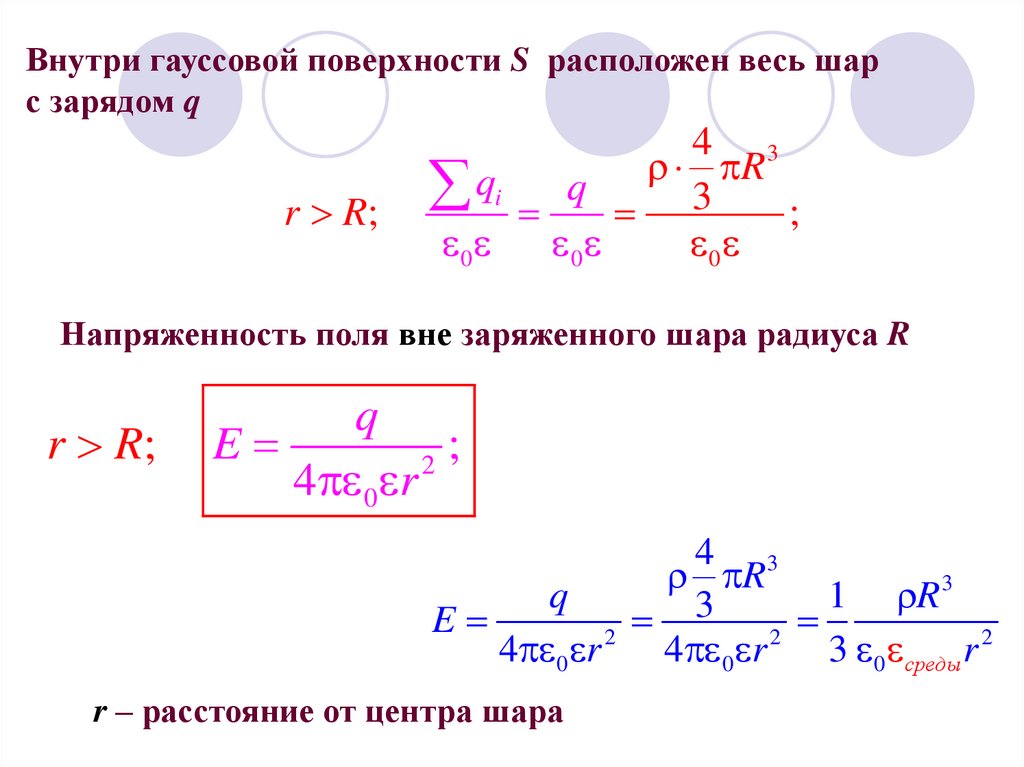
Внутри гауссовой поверхности S расположен весь шарс зарядом q
r R;
4 3
R
q
i q 3 ;
0
0
0
Напряженность поля вне заряженного шара радиуса R
r R;
q
E
;
2
4 0 r
4 3
R
3
q
1
R
3
E
2
2
4 0 r
4 0 r
3 0 среды r 2
r – расстояние от центра шара
6.
Напряженность поля внутриоднородно заряженного шара
радиуса R из диэлектрика
E n dS E 4 r
2
;
S
Заряд части шара внутри
гауссовой поверхности
4 3
r R; q dV dV r ;
3
V
V
1
4 3
1
E 4 r
r ; E
r
0 3
3 0
2
7.
r R;q
E
;
2
4 0 r
1
r R; E
r
3 0 диэл.
Напряженность поля вблизи поверхности
однородно заряженного шара радиуса R из
диэлектрика
Если приближаться к поверхности
изнутри
извне
r R;
1
E
R;
3 0 диэл.
4 3
R
q
1
3
E
R
2
2
4 0 R
4 0 R
3 0 среды
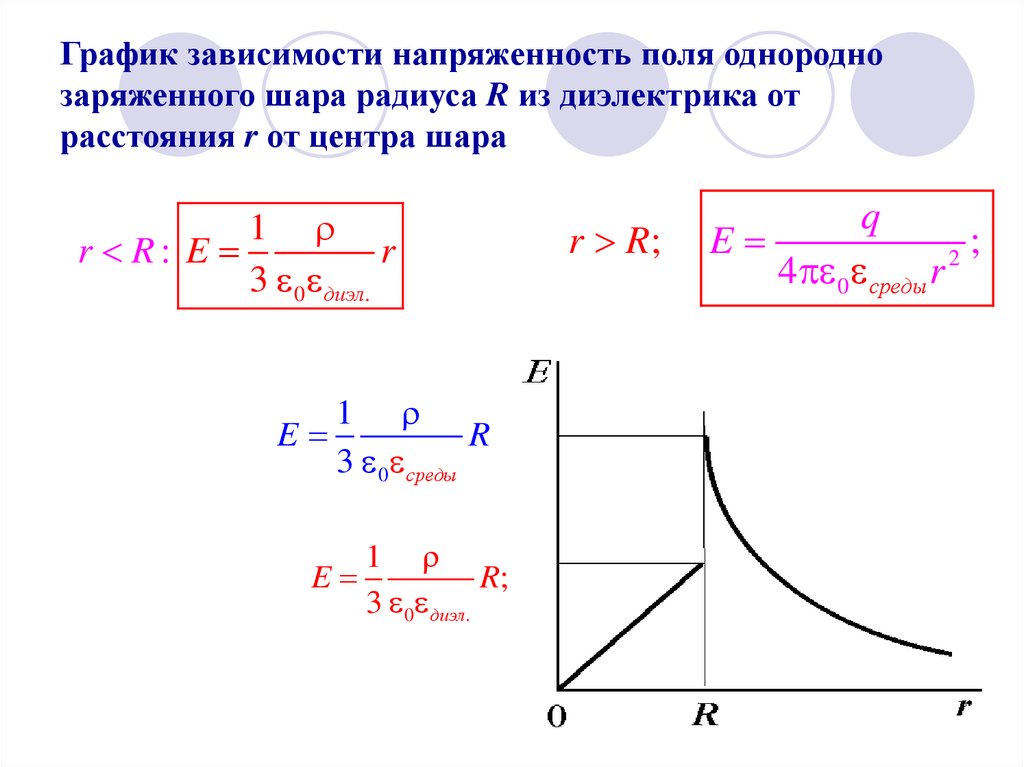
8. График зависимости напряженность поля однородно заряженного шара радиуса R из диэлектрика от расстояния r от центра шара
1r R: E
r
3 0 диэл.
1
E
R
3 0 среды
1
E
R;
3 0 диэл.
r R;
q
E
;
2
4 0 среды r
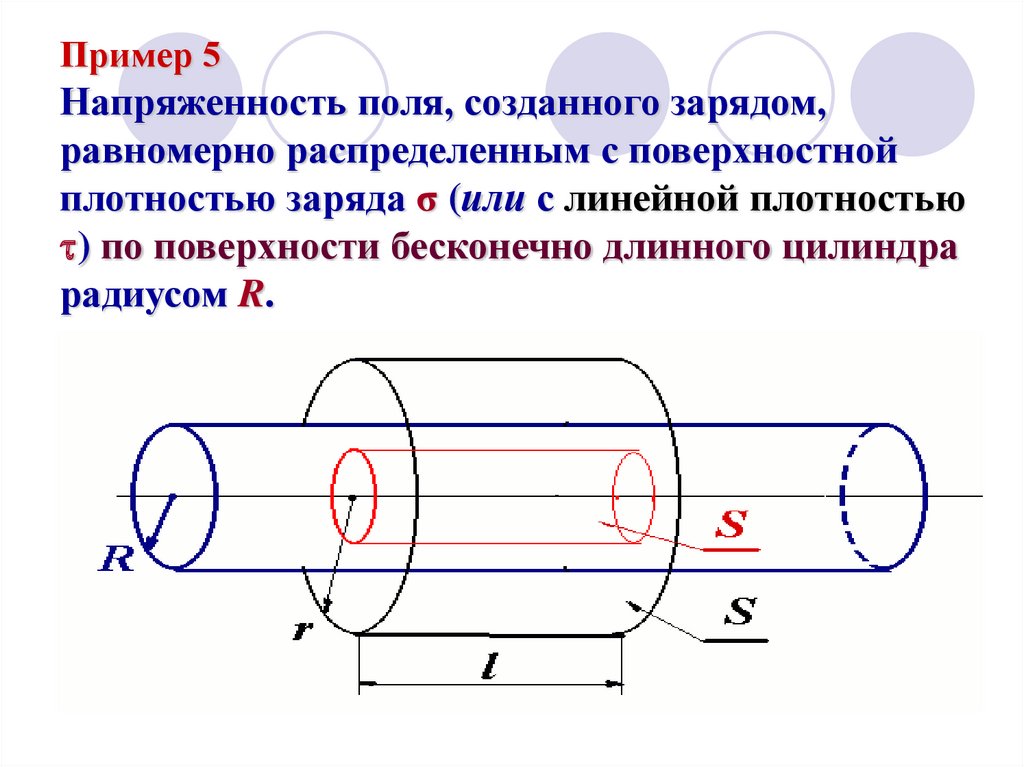
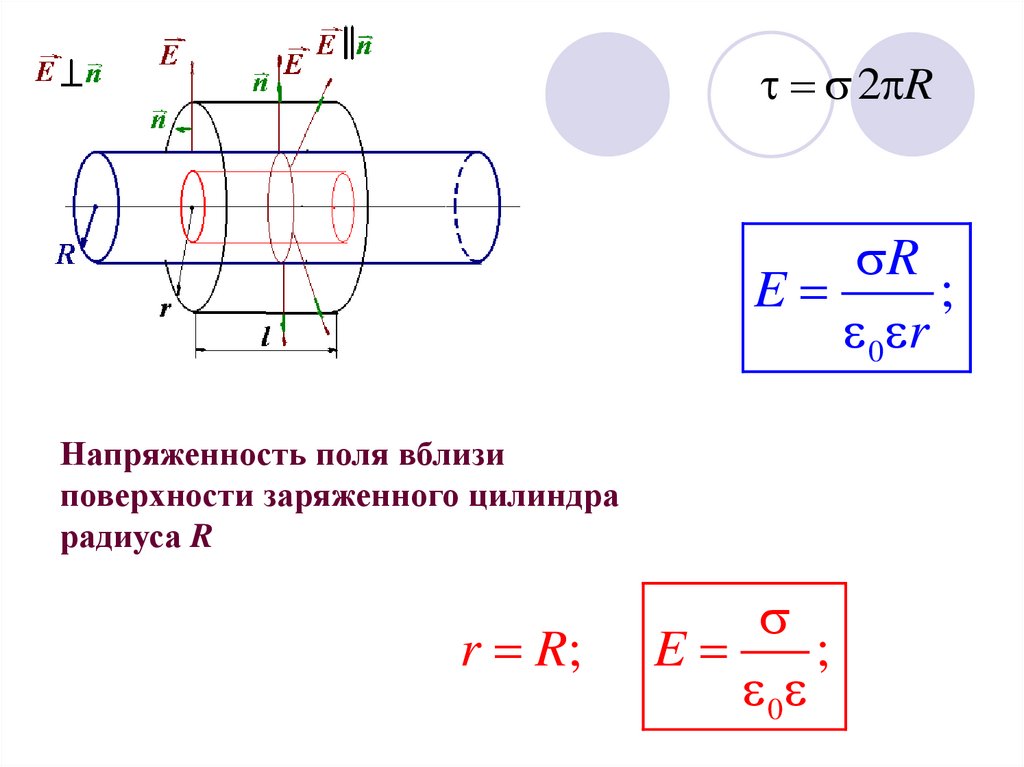
9. Пример 5 Напряженность поля, созданного зарядом, равномерно распределенным с поверхностной плотностью заряда σ (или с линейной
плотностью) по поверхности бесконечно длинного цилиндра
радиусом R.
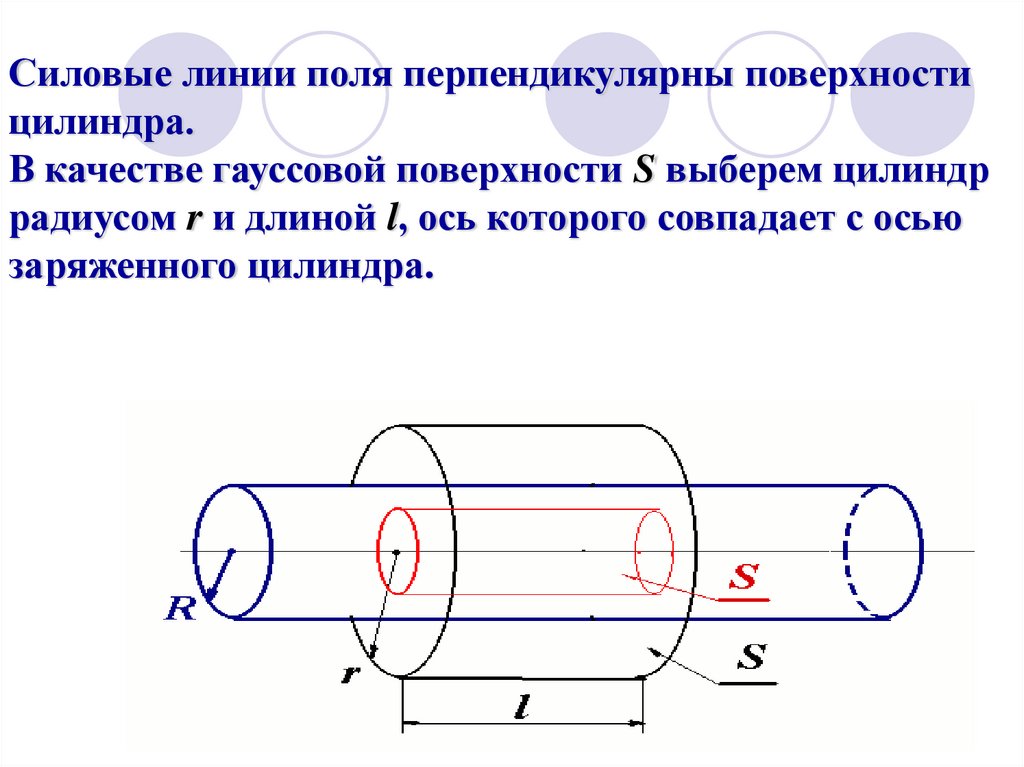
10. Силовые линии поля перпендикулярны поверхности цилиндра. В качестве гауссовой поверхности S выберем цилиндр радиусом r и длиной
l, ось которого совпадает с осьюзаряженного цилиндра.
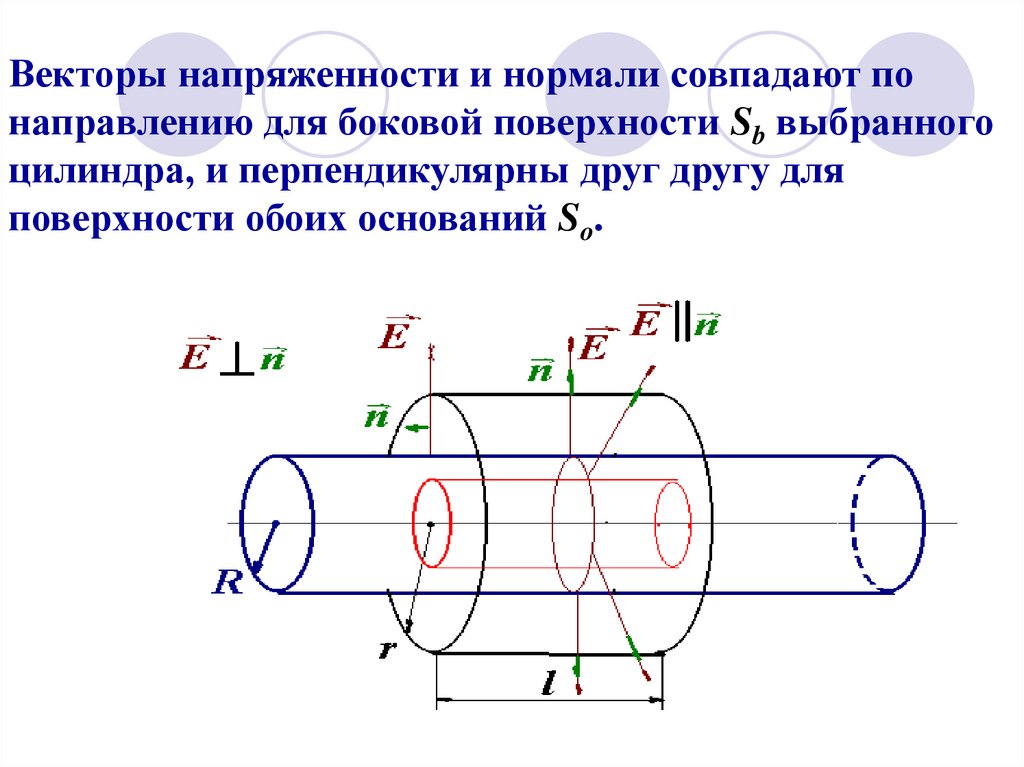
11. Векторы напряженности и нормали совпадают по направлению для боковой поверхности Sb выбранного цилиндра, и перпендикулярны друг
другу дляповерхности обоих оснований So.
12.
qE n dS
;
S
i
0
Поток вектора напряженности Е через гауссову поверхность
E n dS E n dS 2 E n dS
S
Sb
E dS 0 E 2 rl;
Sb
So
13.
2 RE n dS
S
E 2 rl ;
Напряженность поля вне заряженного цилиндра радиуса R
q
r R;
l
2 Rl
;
0
0
0
i
R
E
;
0 r
14.
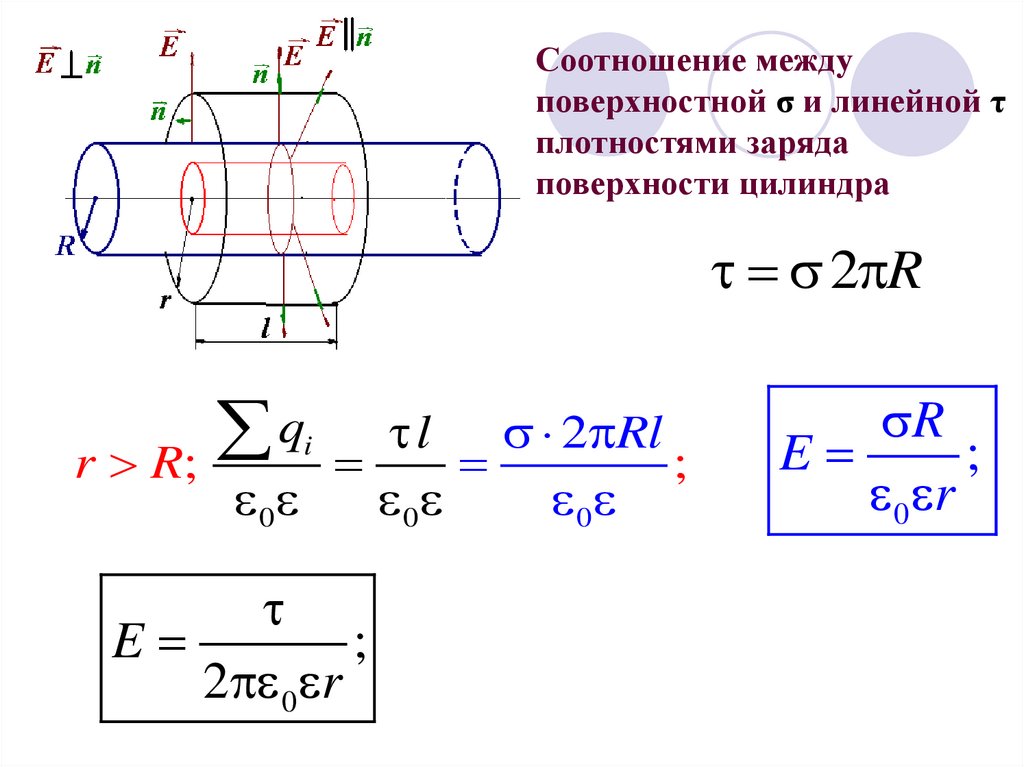
Соотношение междуповерхностной σ и линейной τ
плотностями заряда
поверхности цилиндра
2 R
q
r R;
l
2 Rl
;
0
0
0
i
E
;
2 0 r
R
E
;
0 r
15.
2 RR
E
;
0 r
Напряженность поля вблизи
поверхности заряженного цилиндра
радиуса R
r R;
E
;
0
16.
qE n dS
;
i
0
S
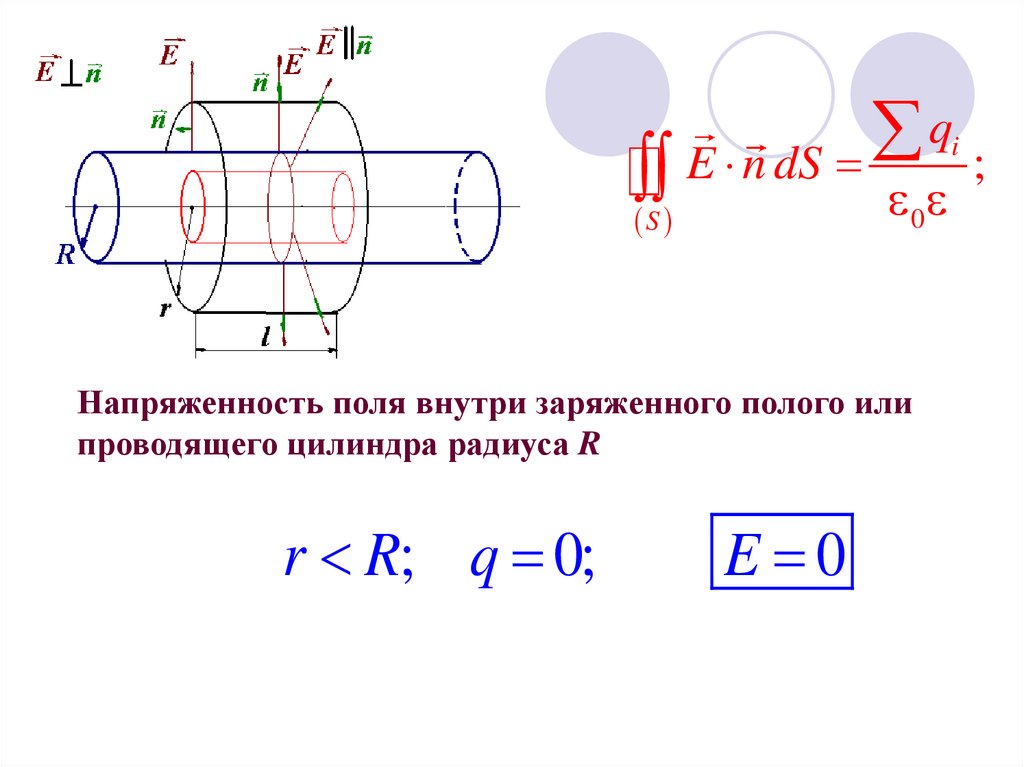
Напряженность поля внутри заряженного полого или
проводящего цилиндра радиуса R
r R; q 0;
E 0
17.
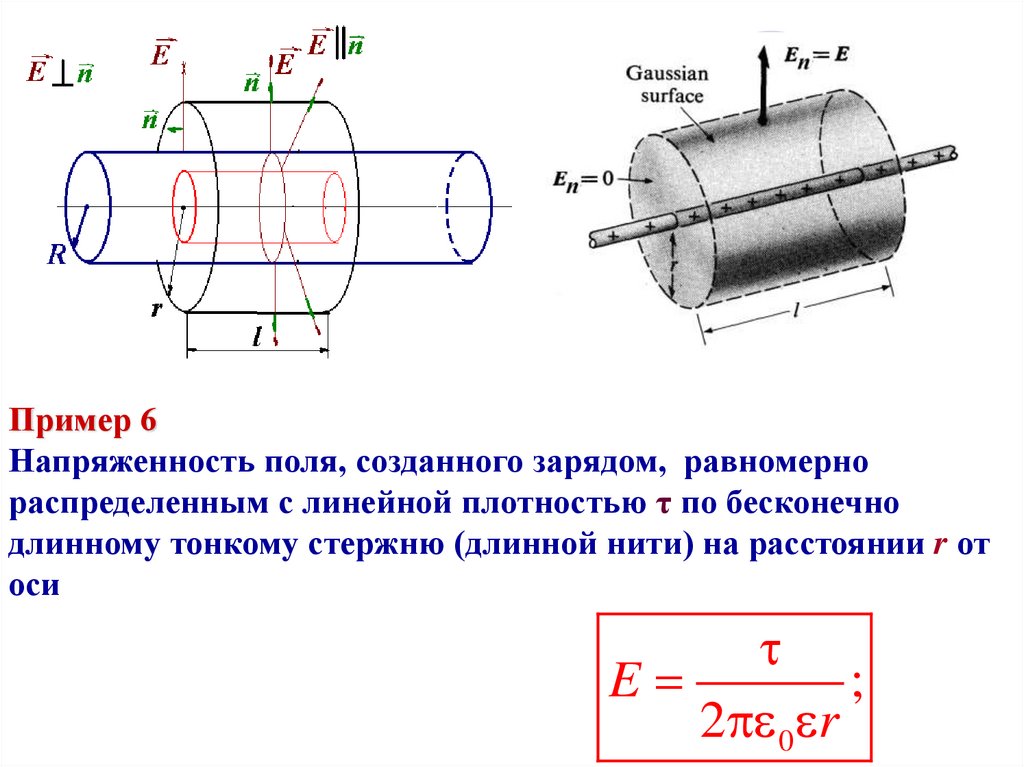
Пример 6Напряженность поля, созданного зарядом, равномерно
распределенным с линейной плотностью τ по бесконечно
длинному тонкому стержню (длинной нити) на расстоянии r от
оси
E
;
2 0 r
18. Пример 7 Разность потенциалов двух точек поля, созданного зарядом, равномерно распределенным с линейной плотностью τ по
бесконечно длинному тонкомустержню
E
;
2 0 r
E grad ;
Поле осевой симметрии (связь между напряженностью и
потенциалом):
d
E
;
dr
d E dr;
r2
E dr;
r1
19.
r1dr
E dr
ln ;
2 0 r1 r
2 0 r2
r1
r2
r2
r1
ln ;
2 0 r2
Напряжение между двумя точками поля
U ;
r2
U
ln ;
2 0 r1
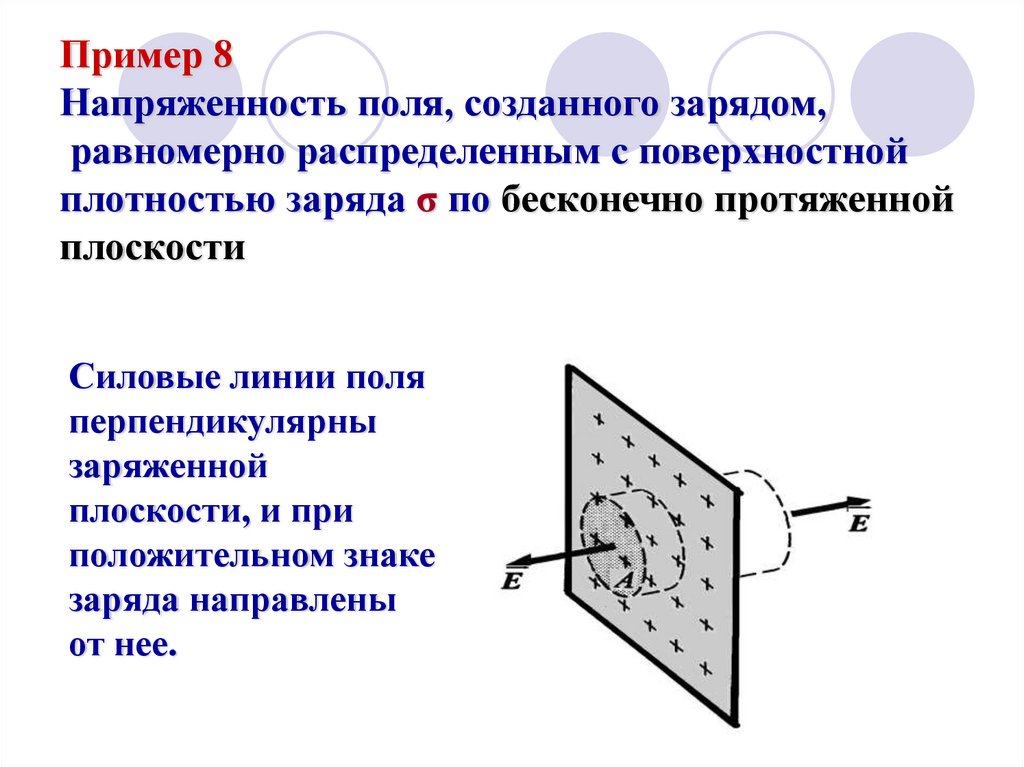
20. Силовые линии поля перпендикулярны заряженной плоскости, и при положительном знаке заряда направлены от нее.
Пример 8Напряженность поля, созданного зарядом,
равномерно распределенным с поверхностной
плотностью заряда σ по бесконечно протяженной
плоскости
Силовые линии поля
перпендикулярны
заряженной
плоскости, и при
положительном знаке
заряда направлены
от нее.
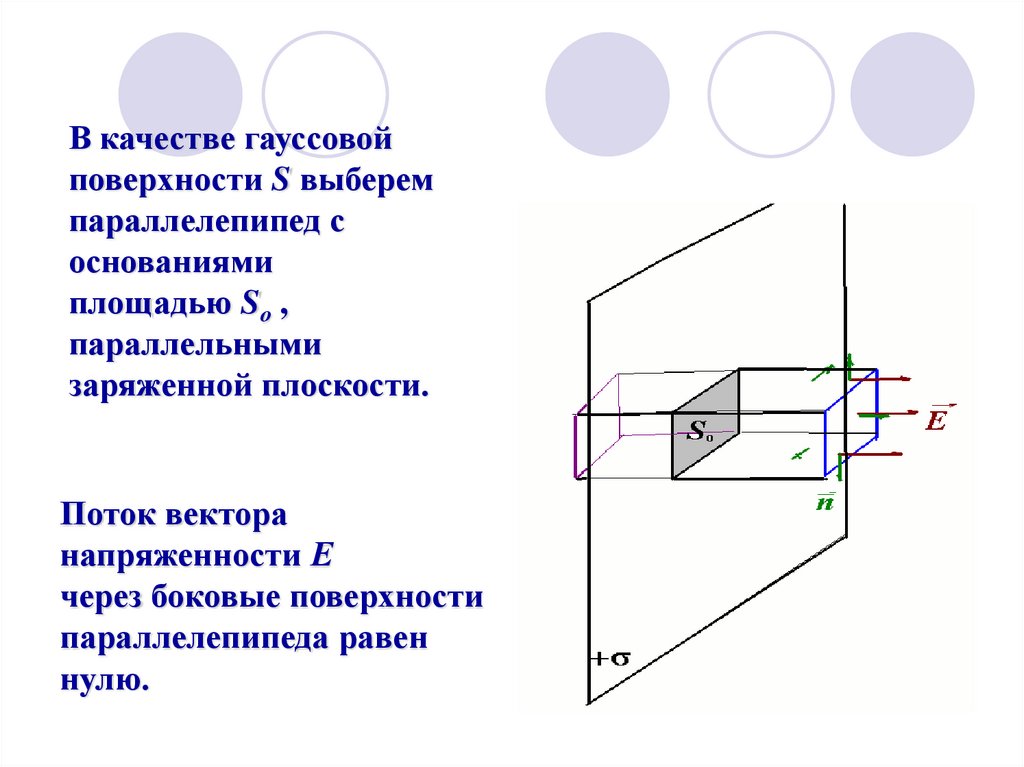
21. В качестве гауссовой поверхности S выберем параллелепипед с основаниями площадью Sо , параллельными заряженной плоскости.
Поток векторанапряженности Е
через боковые поверхности
параллелепипеда равен
нулю.
22.
qE n dS
;
i
0
S
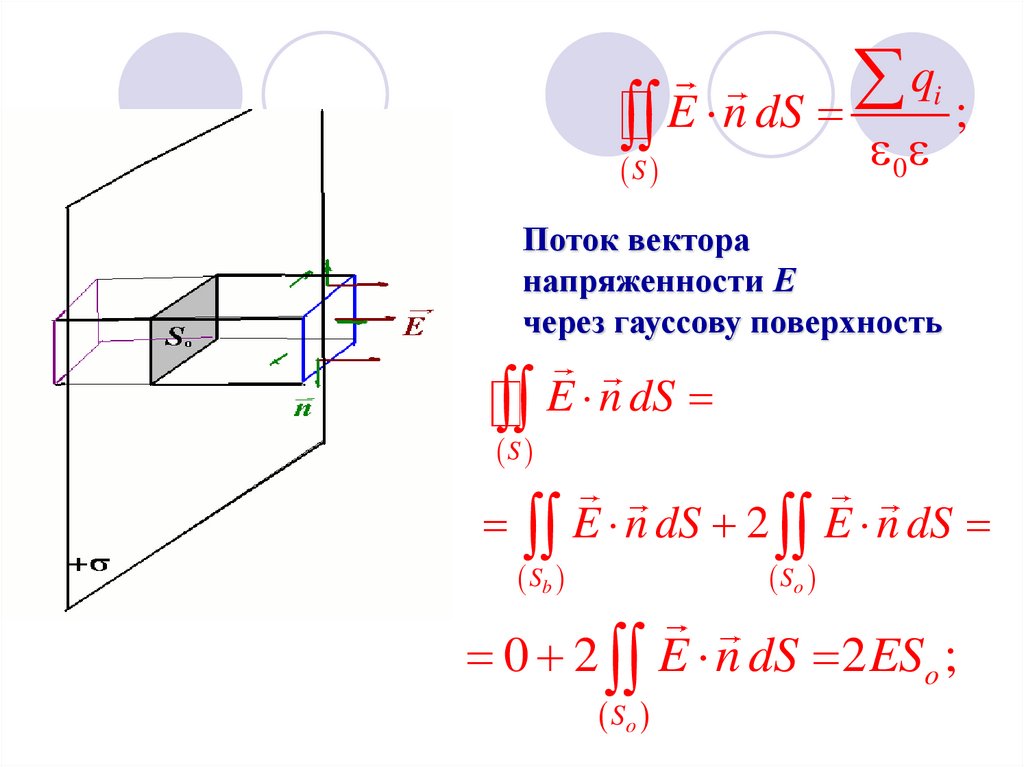
Поток вектора
напряженности Е
через гауссову поверхность
E n dS
S
E n dS 2 E n dS
Sb
So
0 2 E n dS 2 ESo ;
So
23.
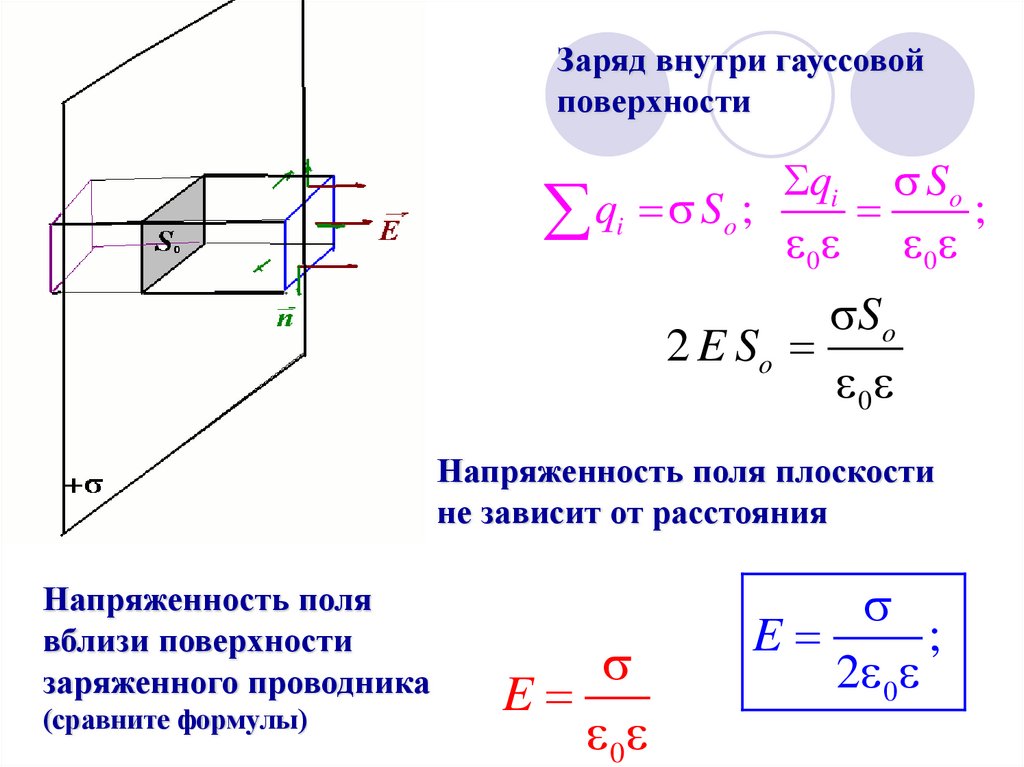
Заряд внутри гауссовойповерхности
qi So
qi So ; ;
0
0
So
2 E So
0
Напряженность поля плоскости
не зависит от расстояния
Напряженность поля
вблизи поверхности
заряженного проводника
(сравните формулы)
E
0
E
;
2 0
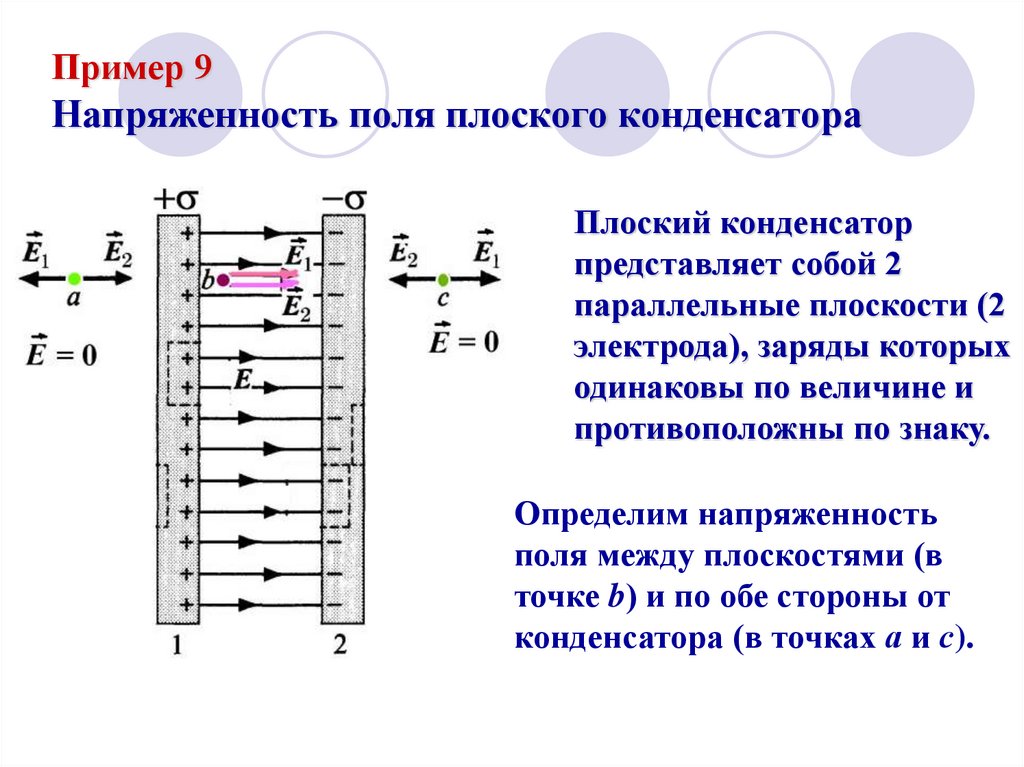
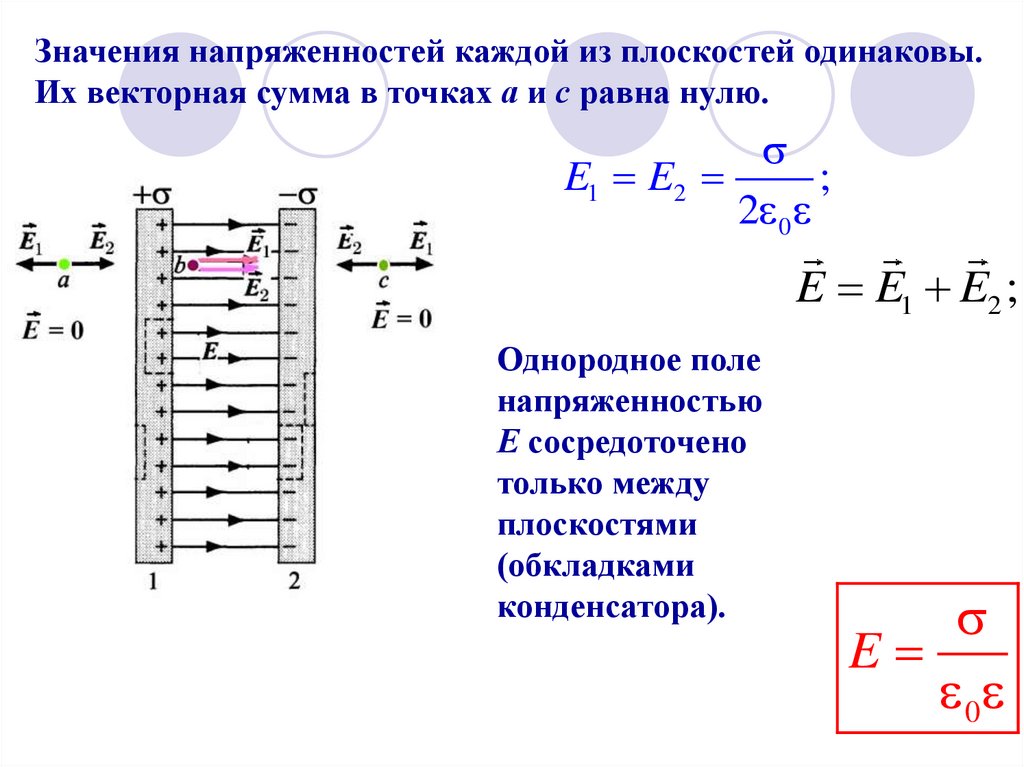
24. Пример 9 Напряженность поля плоского конденсатора
E1 E2;
2 0
Плоский конденсатор
представляет собой 2
параллельные плоскости (2
электрода), заряды которых
одинаковы по величине и
противоположны по знаку.
Определим напряженность
поля между плоскостями (в
точке b) и по обе стороны от
конденсатора (в точках а и с).
25.
В соответствии с определением напряженности поместим вкаждую из точек пробный положительный заряд и
определим направления векторов напряженности в них.
F
E
q0
E1 E2
;
2 0
В точках а и с векторы
напряженности поля
направлены в
противоположные
стороны, а между
плоскостями (в точке b) оба
вправо.
26.
Значения напряженностей каждой из плоскостей одинаковы.Их векторная сумма в точках а и с равна нулю.
E1 E2
;
2 0
E E1 E2 ;
E1 E2
;
2 0
Однородное поле
напряженностью
Е сосредоточено
только между
плоскостями
(обкладками
конденсатора).
E
0
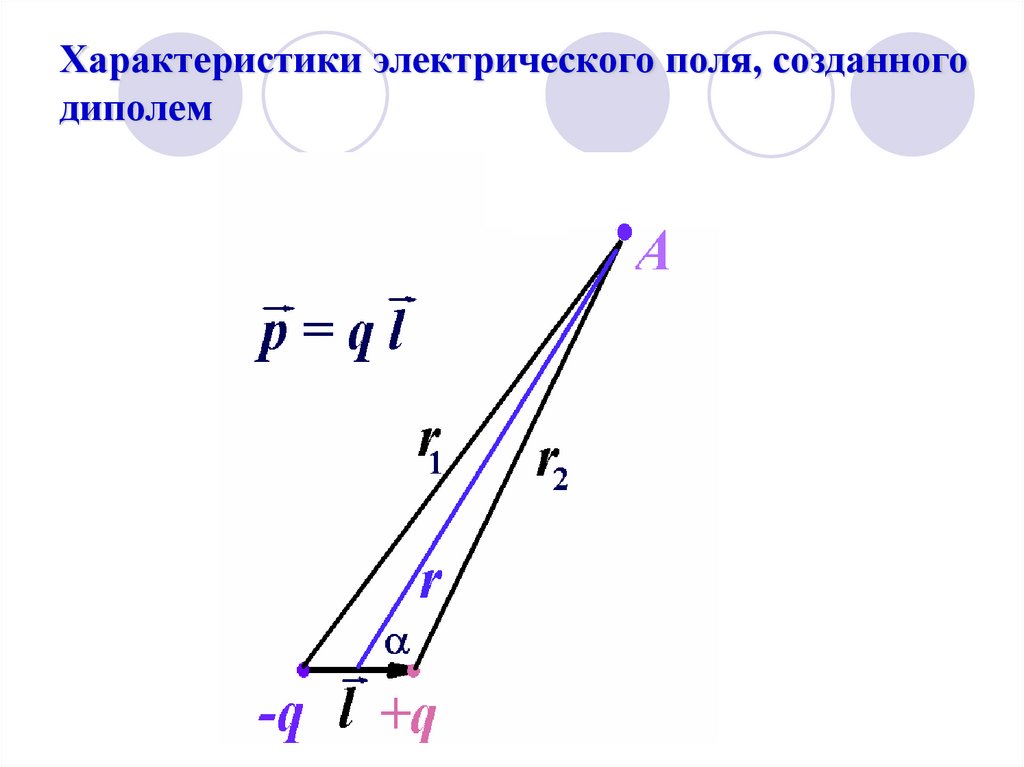
27. Электрический диполь
p ql41 ;
Электрический диполь – система двух
взаимосвязанных точечных зарядов одинаковой
величины и противоположных знаков,
расположенных на малом расстоянии друг от
друга.
Дипольный электрический момент
Диполем моделируются молекулы веществ при
описании их поведения в электрическом поле.
28. Характеристики электрического поля, созданного диполем
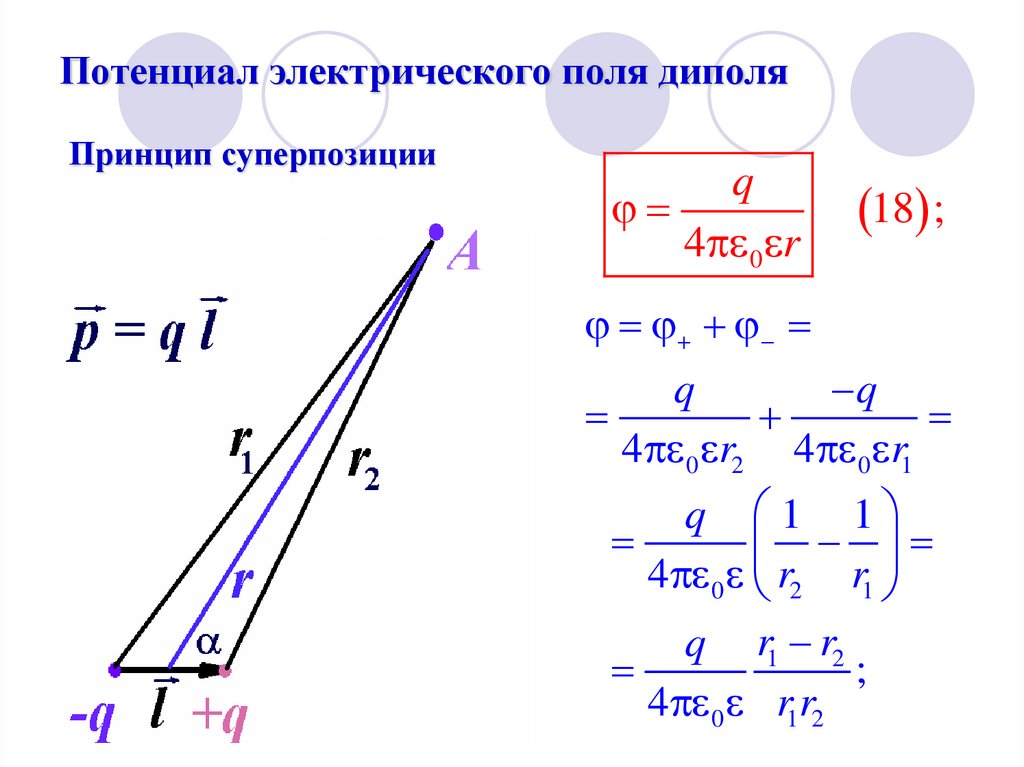
29. Потенциал электрического поля диполя
Принцип суперпозицииq
4 0 r
18 ;
q
q
4 0 r2 4 0 r1
q 1 1
4 0 r2 r1
q r1 r2
;
4 0 r1r2
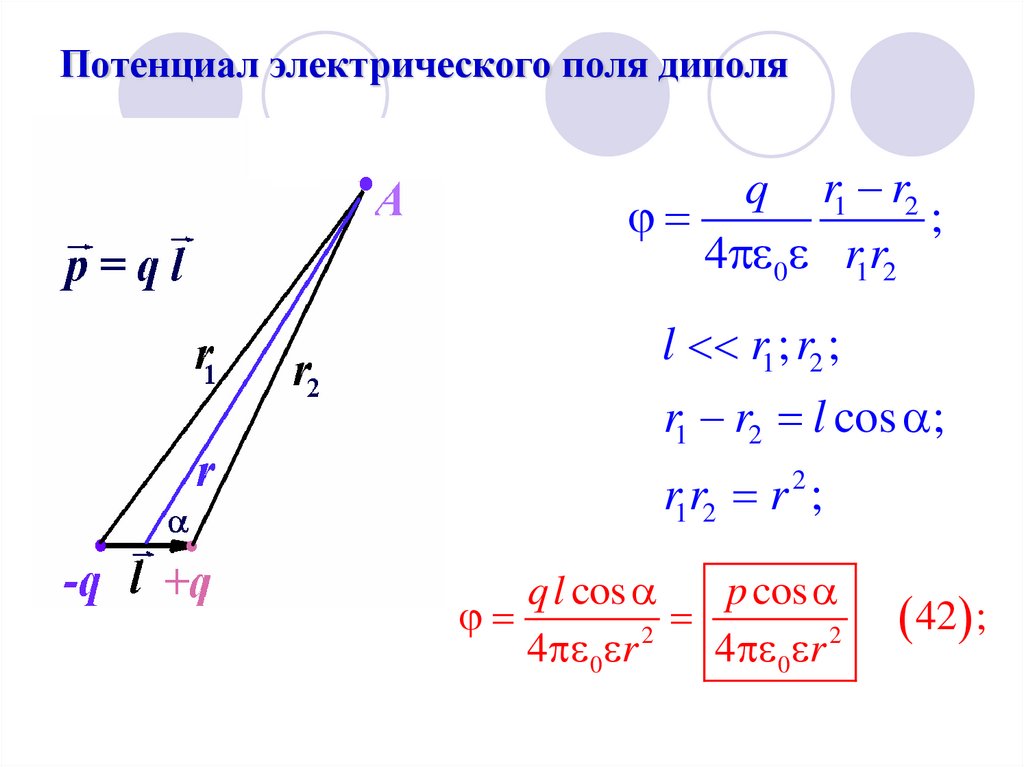
30. Потенциал электрического поля диполя
q r1 r2;
4 0 r1r2
l r1 ; r2 ;
r1 r2 l cos ;
r1r2 r ;
2
q l cos
p cos
2
2
4 0 r
4 0 r
42 ;
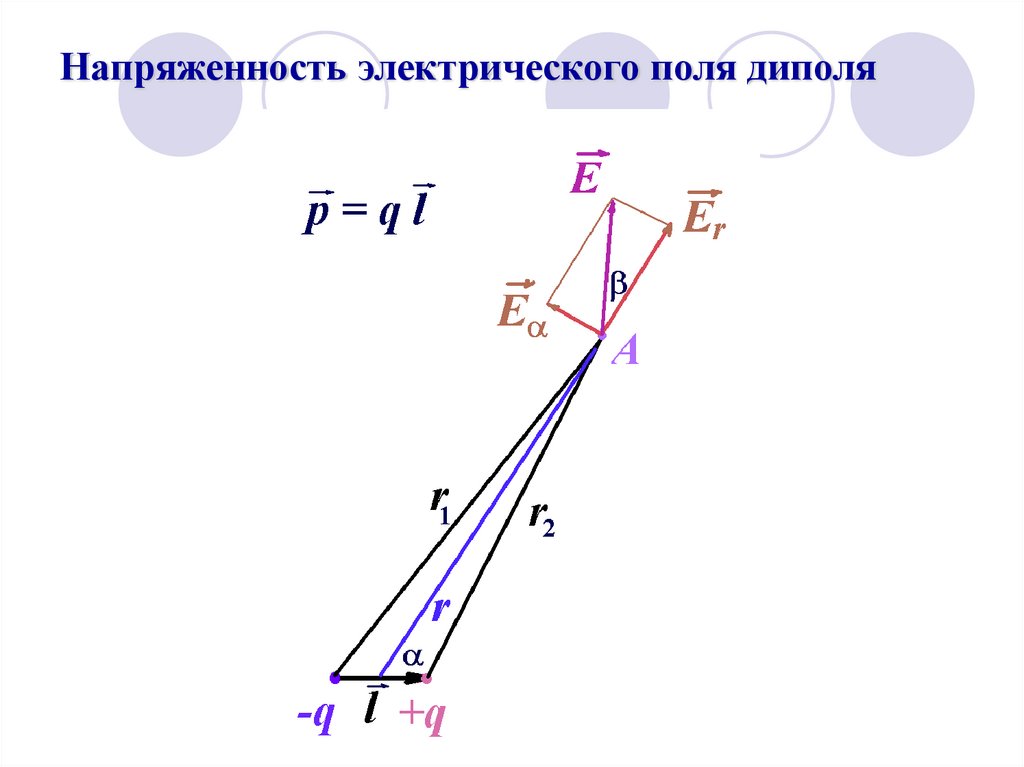
31. Напряженность электрического поля диполя
p cos2
4 0 r
42 ;
E grad
28 ;
f r, E f r, ;
d p cos
Er
3
r 2 0 r
1 d p sin
E
3
r 4 0 r
43 ;
44 ;
E Er E ;
32. Напряженность электрического поля диполя
33. Напряженность электрического поля диполя
E E E2
r
2
p
2
2
4cos
sin
3
4 0 r
p
2
3cos 1
3
4 0 r
E 1
tg
tg
Er 2
44 ;
45 ;
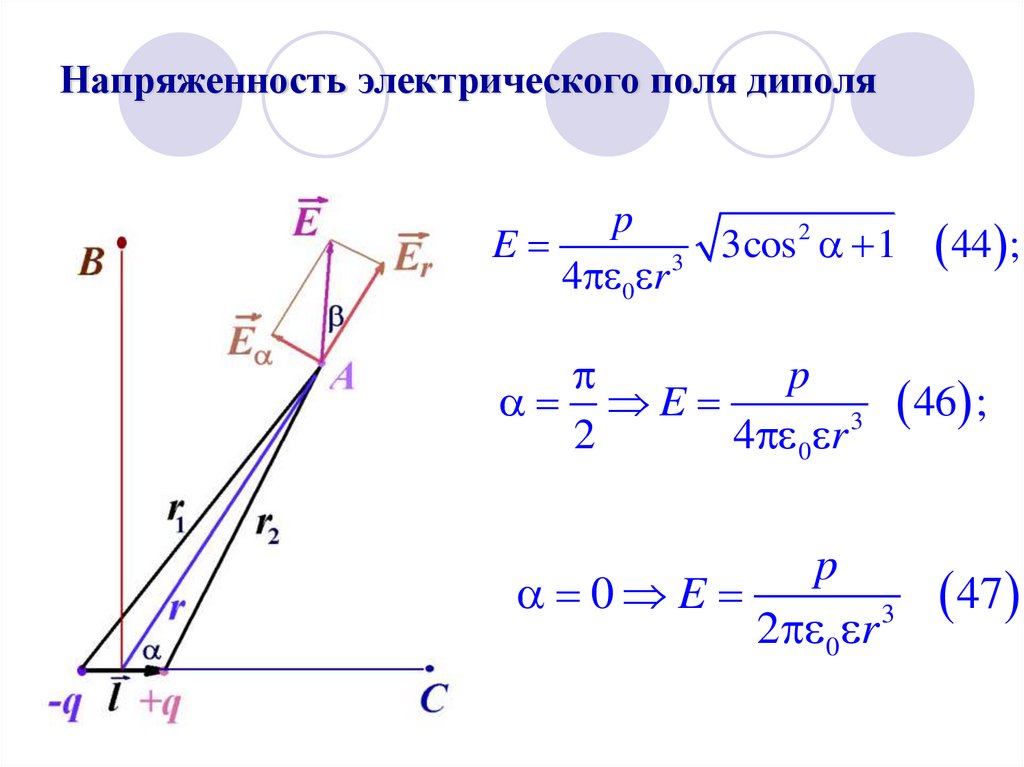
34. Напряженность электрического поля диполя
p2
E
3cos
1
3
4 0 r
p
E
2
4 0 r 3
p
0 E
2 0 r 3
44 ;
46 ;
47
35. Диполь во внешнем электрическом поле
Однородное полеE const;
F1 F2 ;
Силы, действующие на
заряды диполя, создают
момент пары сил,
поворачивающих диполь.
M F l sin
qE l sin
p E sin
48 ;
M p E
49 ;
36. Диполь во внешнем электрическом поле
Неоднородное поле,(убывающее в
направлении х)
F2 F1 ; F F ;
F F F
dE
qE q E
l
dx
dE
dE
q
l p
;
dx
dx
F p gradE
50
37. Диполь во внешнем электрическом поле
В электрическом поледиполь поворачивается
под действием момента
пары сил,
а в случае неоднородного
поля втягивается в
область более сильного
поля с силой
M p E
49 ;
F p gradE
50















 Физика
Физика








