Похожие презентации:
Integraal
1. Integraal
Heldena Tapersonwww.welovemath.ee
2.
muudujagatise
funktsiooni diferentserimiseks
3.
0a x ln a
1
1
x 1
1
x2
cos x
sin x
1
cos 2 x
x ln a
1
2 x
nx n 1
ex
korrutisega
u v
u v
cu
u v uv
uv
4.
Tuletise leidmise pöördoperatsiooniks on algfunktsioonileidmine.
funktsioon
f ( x) 5 x 2 2 x 3
funktsioon
f ( x) ?
tuletis
f ( x) 10 x 2
tuletis
f ( x) 3x
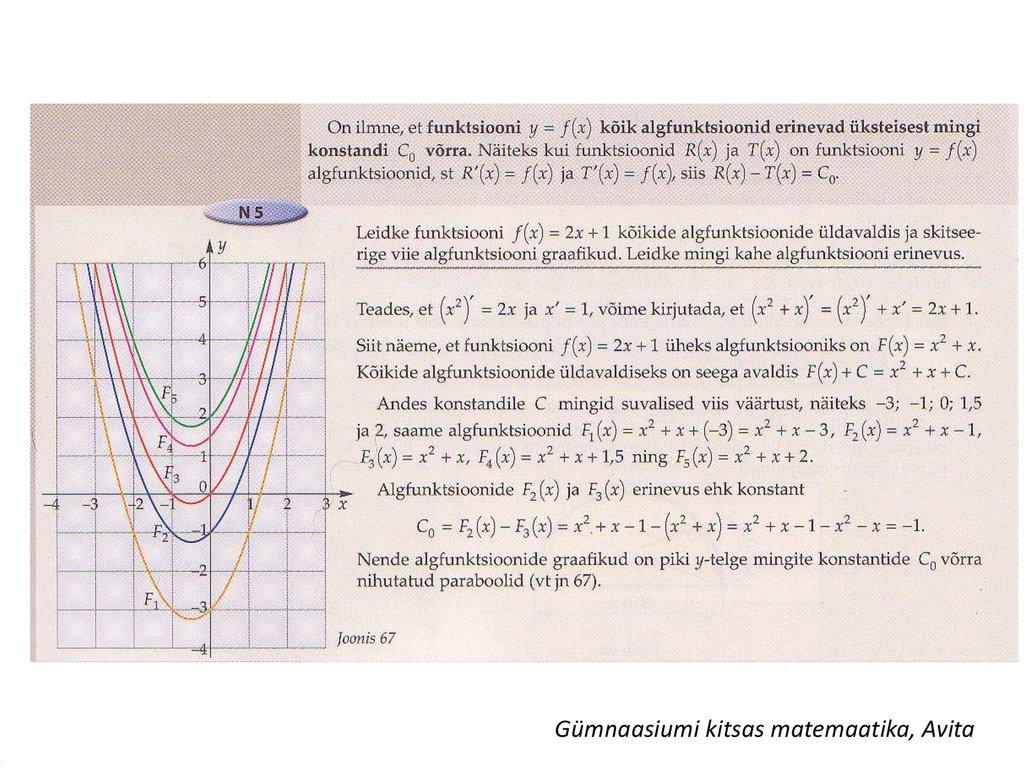
5.
1. Funktsiooni y F (x) nimetatakse funktsiooniPiirkonnas X, kui selles piirkonnas F ( x) f ( x) .
algfunktsiooniks
y f (x) ....................................
2. Funktsiooni
5
4
x
3
a) y 5x algfunktsiooniks on näiteks ...........................
cos x 10
b) y sin1x algfunktsiooniks on näiteks ...........................
ln x 4
c) y
algfunktsiooniks on näiteks ...........................
x
3.Funktsiooni algfunktsiooni leidmist nimetatakse integreerimiseks ja see on
pöördtehe
tuletise leidmise ...........................................
6.
Gümnaasiumi kitsas matemaatika, Avita7.
G ( x) F ( x) Ckonstant
f ( x)dx F ( x) C
f (x)
f ( x)dx
x
C
Integreerimine on algfunktsioonide üldavaldise ehk
määramata integraali leidmine.
8.
Cx
2
x+C
n+1
x
ex C
ax
cos x
sin x
9.
summagacos xdx cos x C1 sin x C2
sin x cos x C
märgi ette
x5
3
x dx 3 C x 5 C
5
5
4
10.
1 5 3 x2
C
3
1,5
9
1, 5
1
6
2 6x
5 3x 3 C
1
cos 2 x 5 C
2
C
4 x2
C
1 x 3
C
x 3
C
11.
22
5
5
ln 6 x
6
ln 6 x
C
18
C
12.
9 x 5 C4
4
t4
11x 2
C
C
44
44
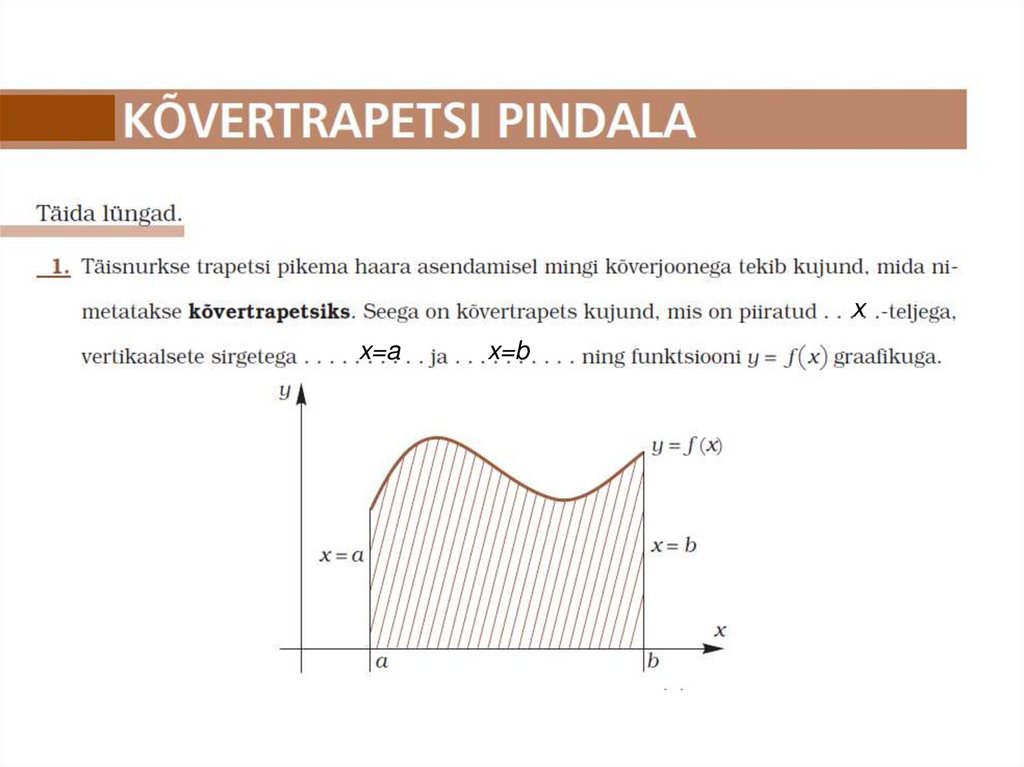
13.
t 2x
x=a
x=b
t C
1
ln x 2 2 C
2
14.
Gümnaasiumi kitsas matemaatika, Avita15.
Gümnaasiumi kitsas matemaatika, Avita16.
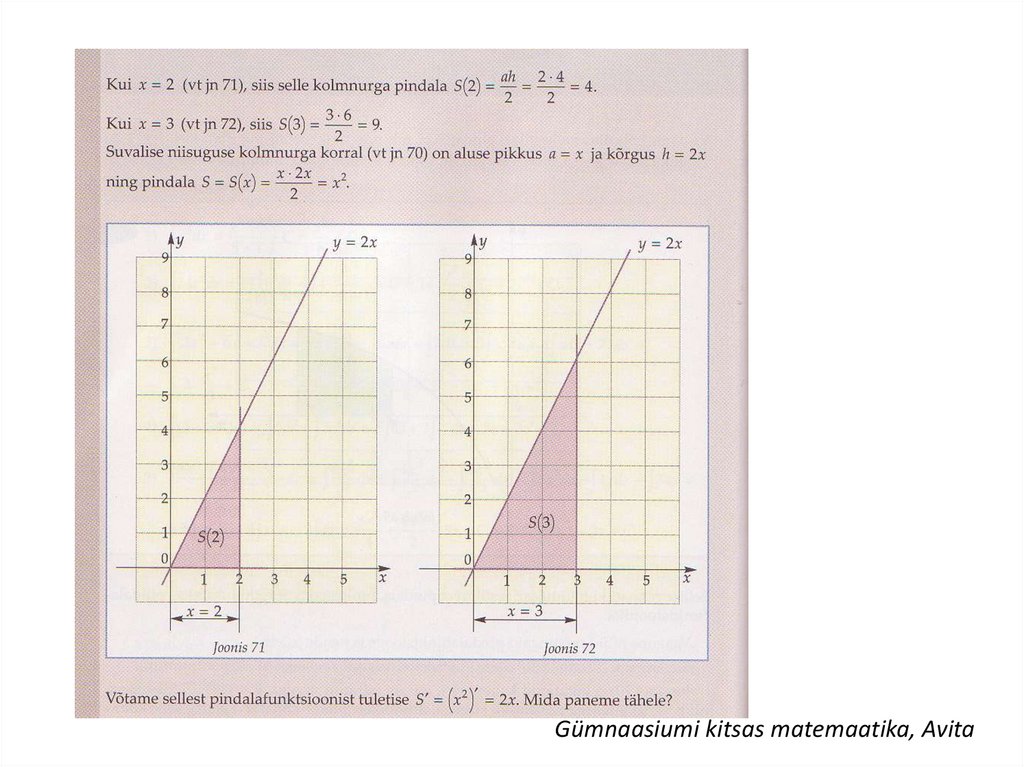
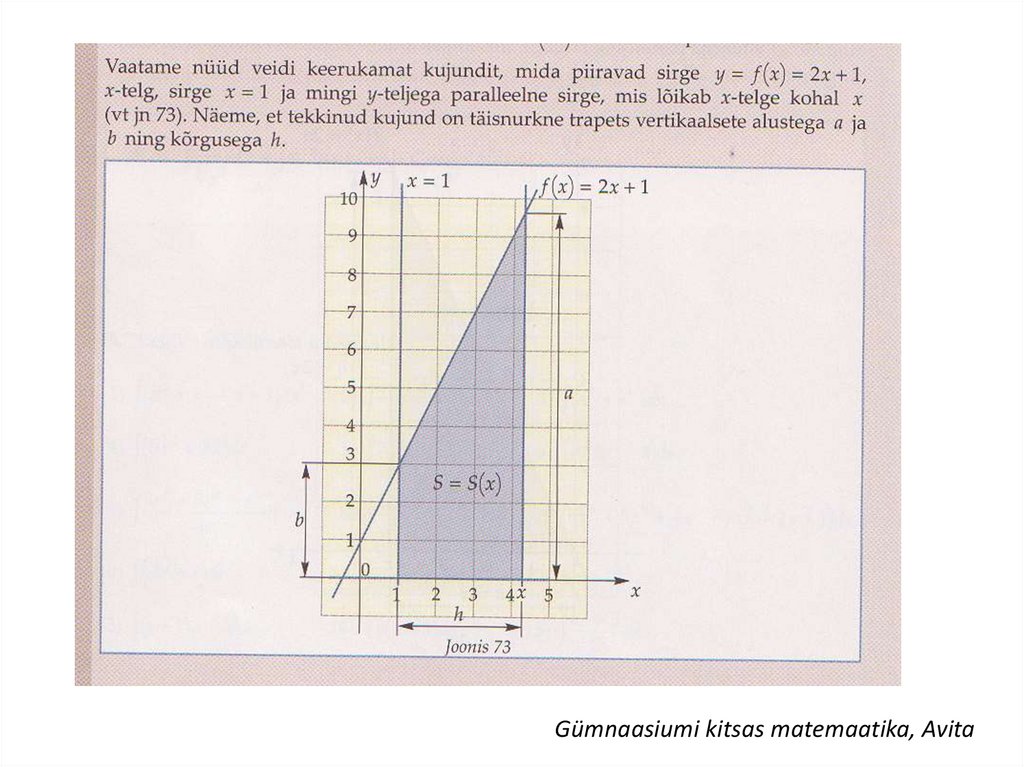
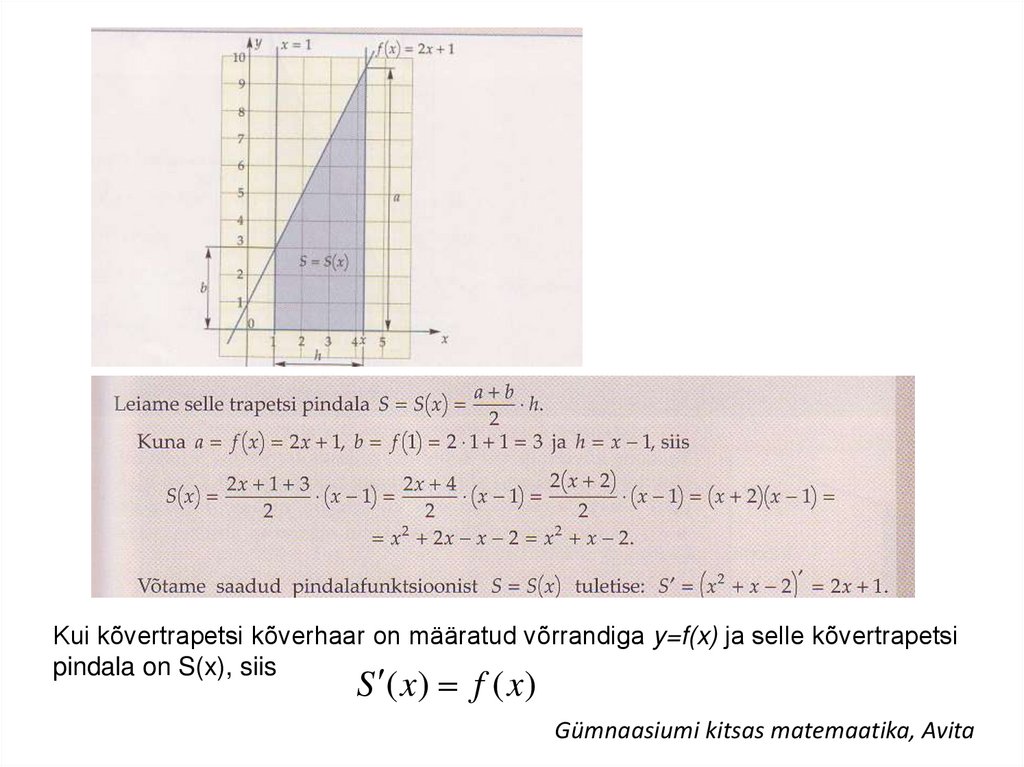
Kui kõvertrapetsi kõverhaar on määratud võrrandiga y=f(x) ja selle kõvertrapetsipindala on S(x), siis
S ( x) f ( x)
Gümnaasiumi kitsas matemaatika, Avita
17.
määratud integraaliksülemiseks rajaks
a-st b-ni
alumiseks rajaks
18.
algfunktsioonülemise
ülemise
alumise
alumise
19.
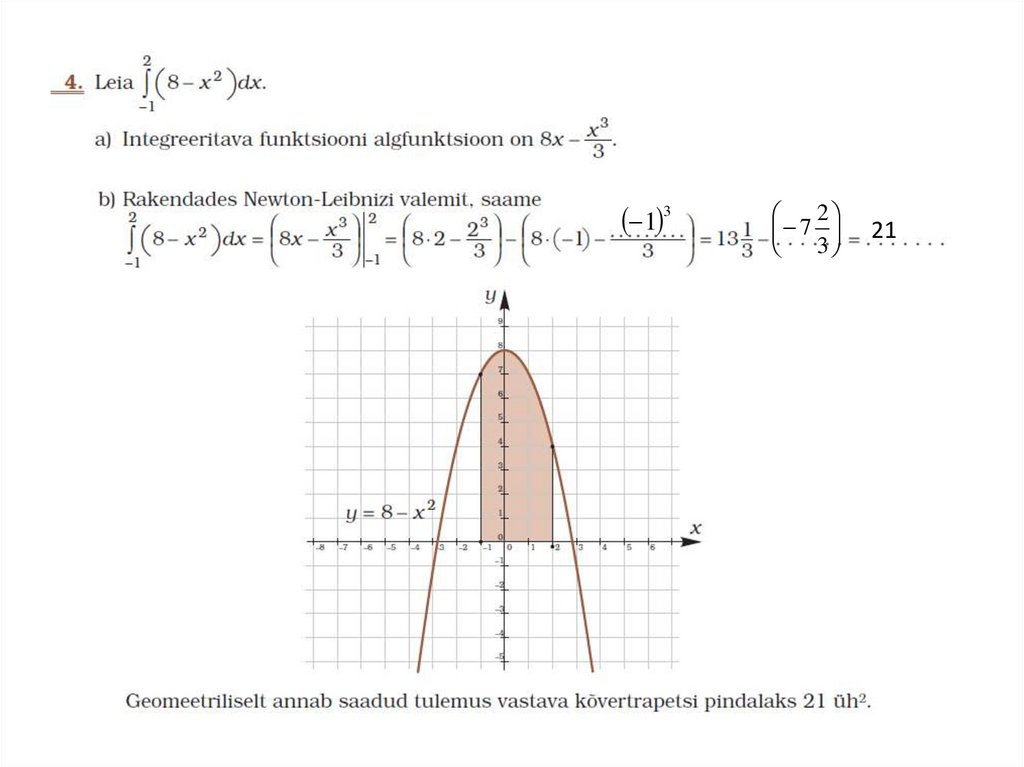
1 32
7
3
21
20.
x22
x
6
2 2 5 2
3
1
2
1
x1,5
9
x 1,5
1 x 1,5
x
2 2
4 1
2 1
4 1 1 2 5 3 2
Matemaatika lisamaterjal 12.kl, Avita
21.
2x 22x 2
2x
2 x 21
2 2
ln 2
2
1
2
2
4
1
7
7 4 ln 2
2 2
2 ( 1)
4
2
2
2 ln 2
2 ln 2
2 ln 2
ln 2
ln 2
ln 2
x
1 sin x 1 sin x
1 sin x
1 sin x
1 sin x
x cos x
3
6
1
3 1 3
3 2 6 2
2
22.
2 x 1 dx 2dx dx dt2
2 x 1
5 1
4
10
1 4
t5
2 x 1 dx 2 t dt 10 C
4
0
2 1 1 0 1 1 1 1
10
10 10 10 5
23.
summagamärgi ette
24.
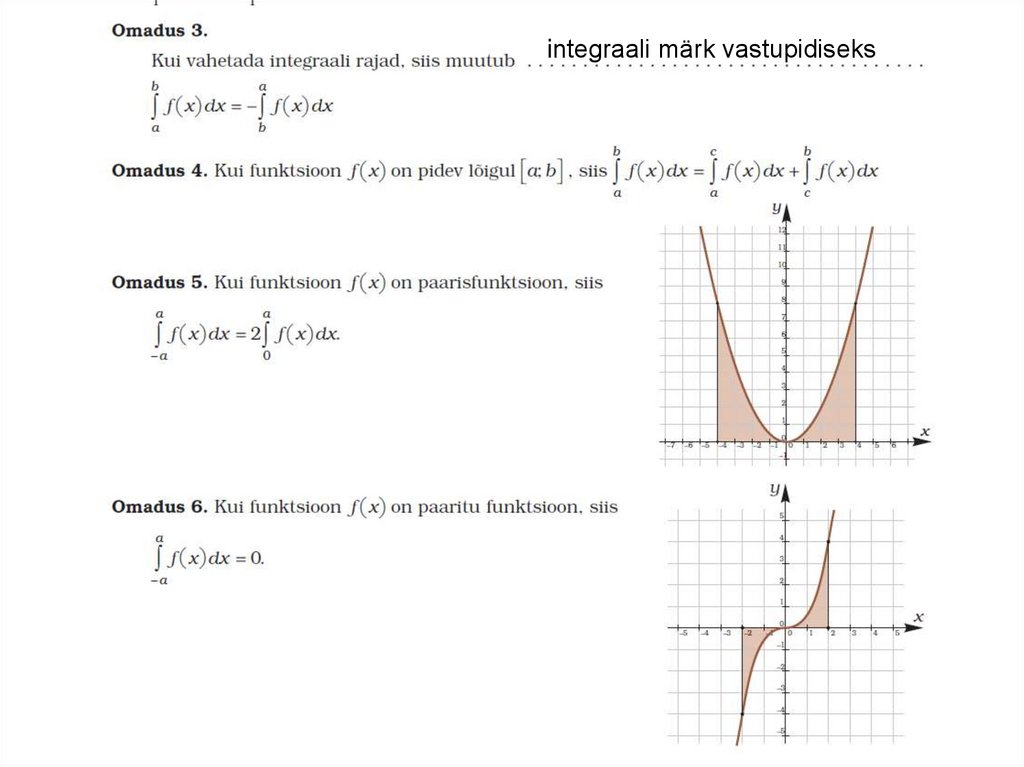
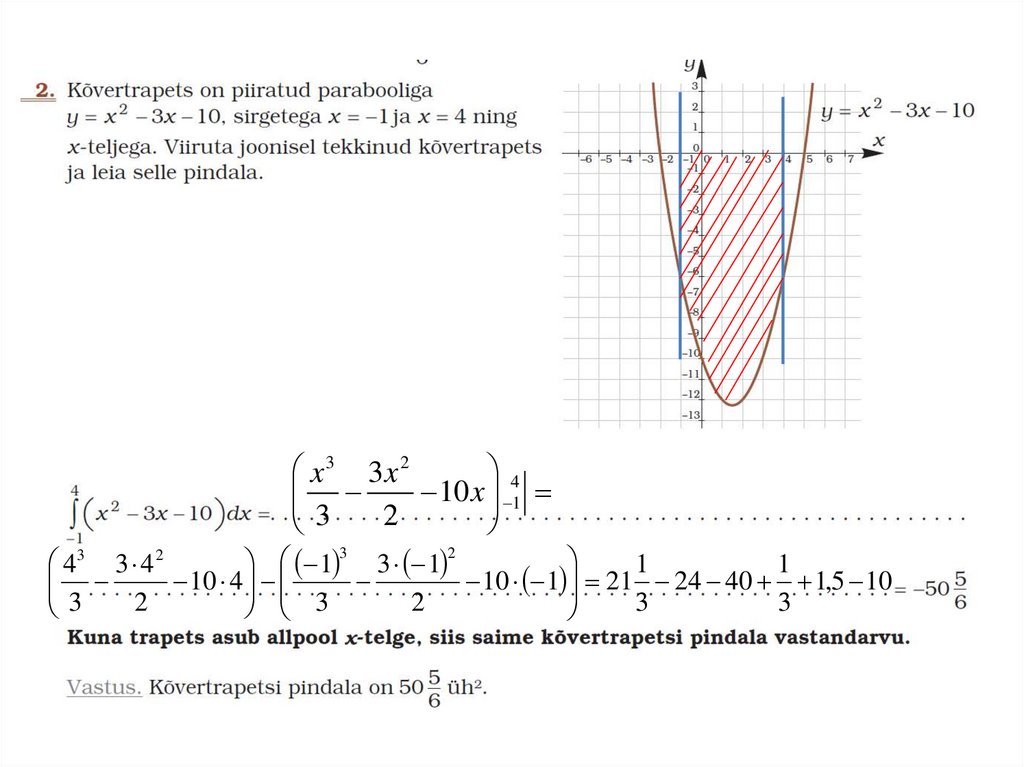
integraali märk vastupidiseks25.
x 3 3x 24
10 x 1
2
3
43 3 4 2
1 3 3 1 2
1
1
10 4
10 1 21 24 40 1,5 10
2
2
3
3
3
3
26.
x=aa; b
x=b
r 2
S (x)
ristlõike
ruumalade
27.
06
6
0,5 x 4
0
0
x3
x2
4 16 x
12
2
6
0
6
0
2 6 2 16 6 2 0 2 16 0
12
12
3
6
3
x2
4 x 16
4
28.
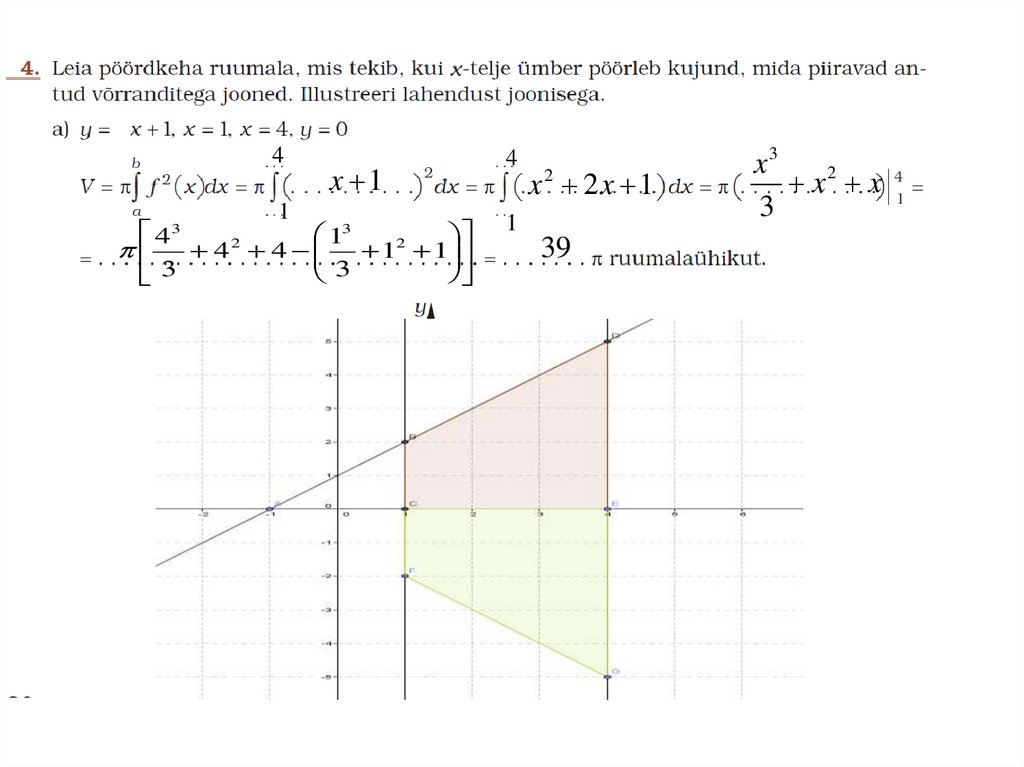
41
x 1
4
13
2
2
4 4
1
1
3
3
3
4
x 2x 1
2
1
39
x3
x2 x
3
29.
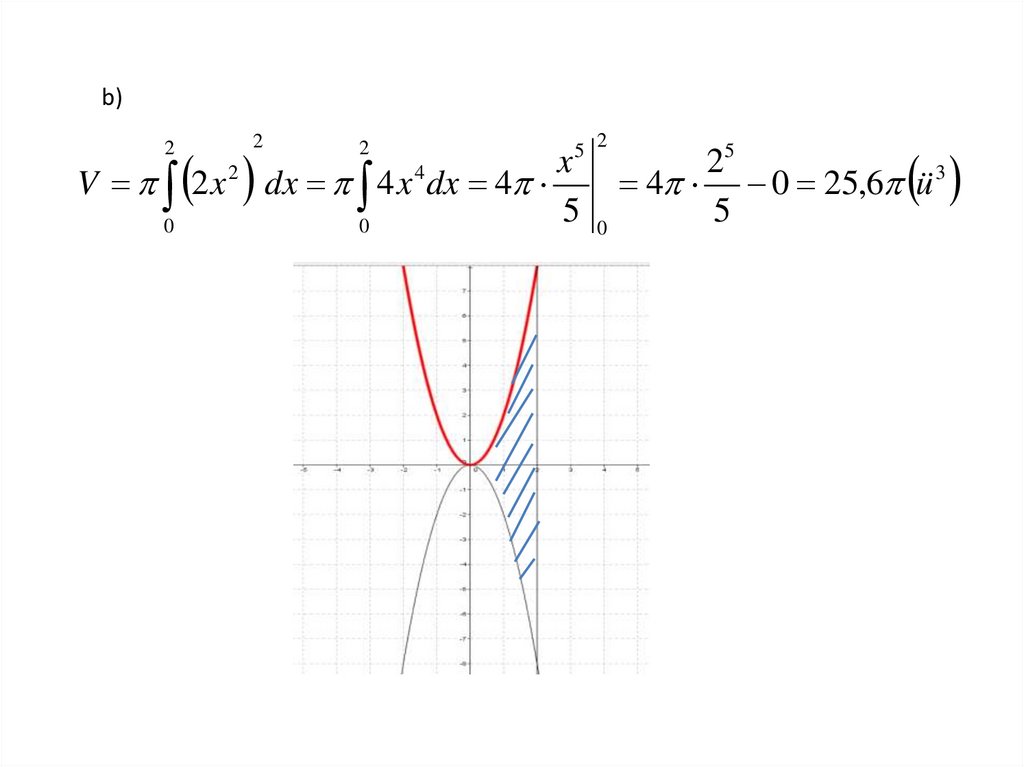
b)2
V 2x2
0
2
2
5 2
x
4
dx 4 x dx 4
5
0
0
25
4 0 25,6 ü 3
5
30.
c)NB! sin 2 x
1 cos 2 x
2
1 cos 2 x
V sin 2 xdx
dx 1 cos 2 x dx
2
20
0
0
1
1
1
x sin 2 x sin 2 0 sin 0 0,5 2 ü 3
2
2
2
2
0 2
2
31. Integraali seos füüsikaga
Kui keha liigub mööda sirget kohast a kohani b muutuvajõu P mõjul, mis mõjub piki sirget ja sõltub läbitud tee
pikkusest s, st P=f(s), kui a ˂b, siis avaldub tehtud töö
n 1
b
n i 0
a
A lim f si s f s ds
32.
Näide. Venimata olekus vedru on 20 cm pikk. Jõud suurusega100 N suudab hoida selle vedru 5 cm pikemana. Kui palju tööd
minimaalselt on vaja teha, et venitada vedru pikkuselt 25 cm
pikkuseni 35 cm?
Hooke’i seaduse põhjal venitusjõud P on vedru tasakaaluasendis
võrdeline vedru algpikkuse muuduga x s st P=ks.
Et 100 N suurune jõud hoiab vedru 5 cm = 0,05 m pikemana
100=k·0,05, st k=2000 ja P=2000s. Meid huvitab töö pärast
seda, kui vedru on juba venitatud 0,05 m võrra ja seda jätkatakse
Kuni vedru on pikenenud 15 cm = 0,15 m võrra.
0 ,15
2000 s 2
A 2000 s ds
2
0 , 05
0 ,15
0 , 05
1000 0,152 0,052 20 J
O. Prinits Matemaatika 11. klassile, Valgus 1988
33.
Harjutusülesanne 5, lk. 77.(0;0,4)
y ax 2 0,4
0,16a 0,4 0
0,16a 0,4
a 2,5
0,4;0
y 2,5 x 2 0,4
0.4
S 2 2,5 x 2 0,4 dx
0
2,5 x 3
0, 4
2,5 0,43
2
0,4 x 0 2
0,4 0,4 0 0,2 m 2
3
3
Vastus. Kaarhalli otsa pindala on ligikaudu 0,2 m².









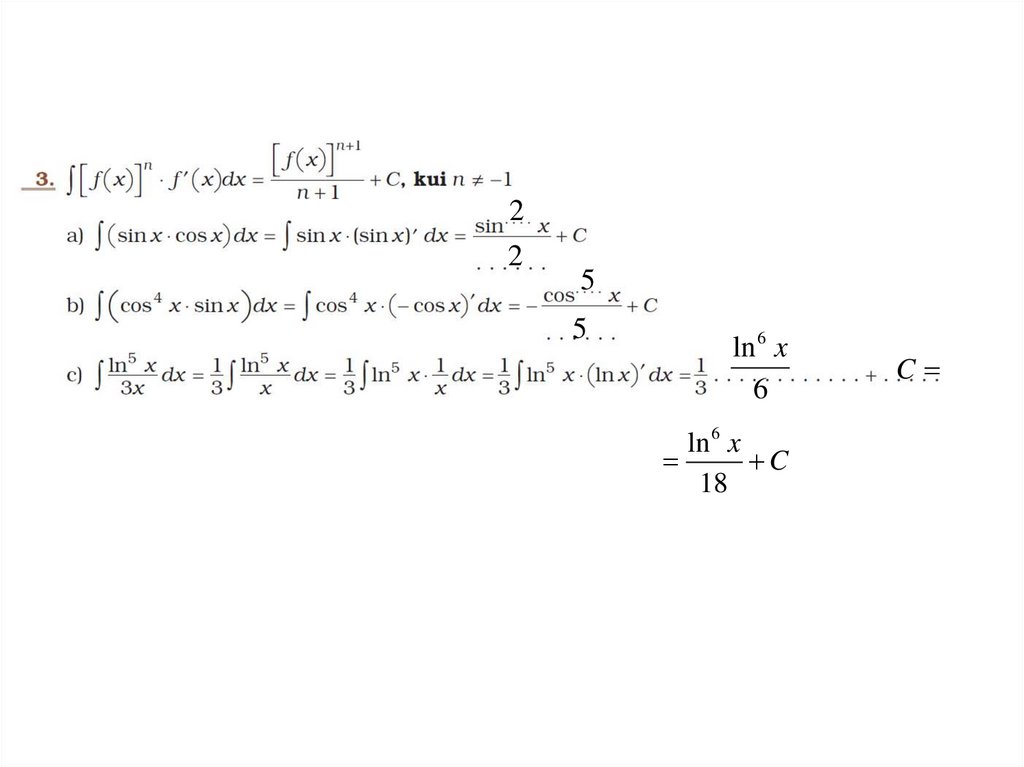









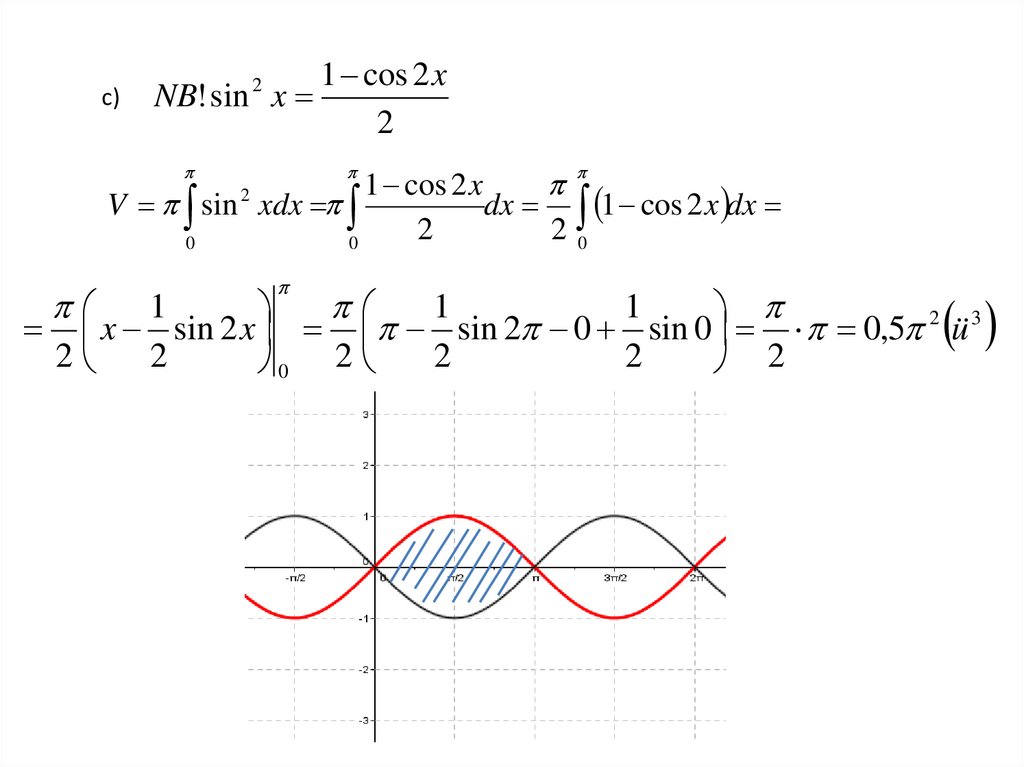



 Математика
Математика








