ეკონომიკისა და ბიზნესის სტატისტიკა. მონაცემთა გაბნევის (გაფანტულობის) მახასიათებლები. თემა 3

1.

ეკონომიკისა და ბიზნესის
სტატისტიკა
თემა 3
მონაცემთა გაბნევის (გაფანტულობის)
მახასიათებლები

2. გაფანტულობის საზომები

გაფანტულობა
გაბნევის
დიაპაზონი
კვარტილური
დიაპაზონი
სტანდარტ.
გადახრა
ვარიაციის
კოეფიციენტი
გაფანტულობის საზომები გვაწვდის ინფორმაციას
მონაცემთა მნიშვნელობების განსხვავებებზე ან
ცვალებადობაზე

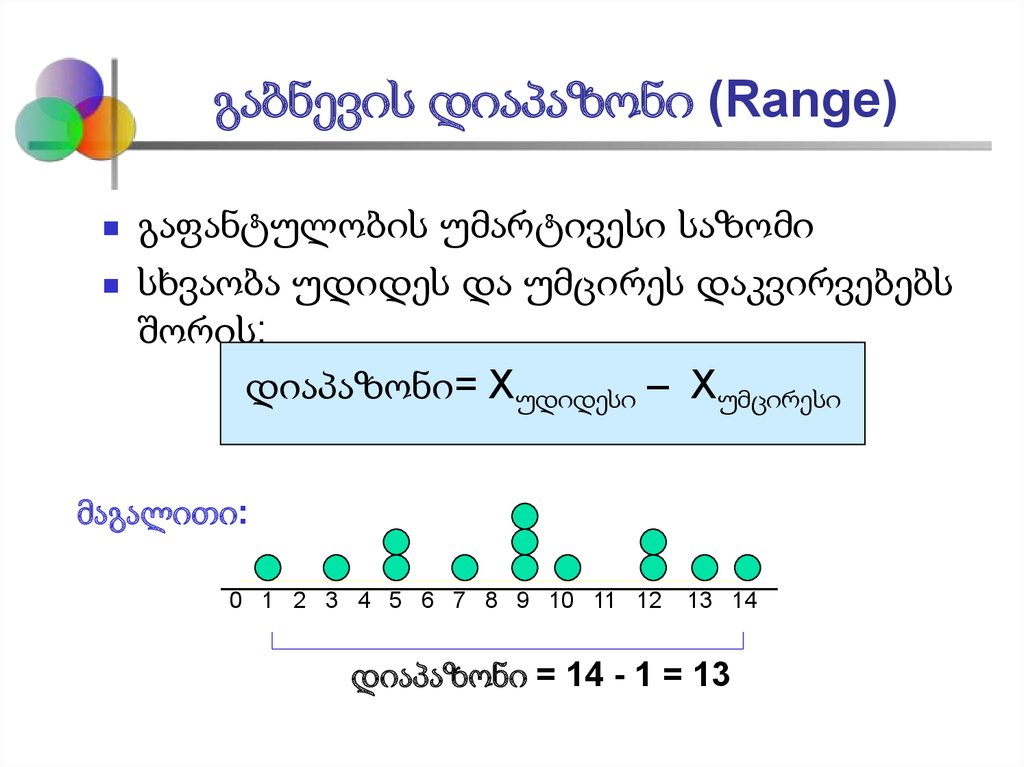
3. გაბნევის დიაპაზონი (Range)

გაფანტულობის უმარტივესი საზომი
სხვაობა უდიდეს და უმცირეს დაკვირვებებს
შორის:
დიაპაზონი= Xუდიდესი – Xუმცირესი
მაგალითი:
0 1 2 3 4 5 6 7 8 9 10 11 12
13 14
დიაპაზონი = 14 - 1 = 13

4. გაბნევის დიაპაზონის ნაკლი

უგულებელყოფს მონაცემთა განაწილებას
7
8
9
10
11
12
დიაპაზონი = 12 - 7 = 5
7
8
9
10
11
12
დიაპაზონი = 12 - 7 = 5
მგრძნობიარე ამოვარდნილი მნიშვნელობების მიმართ
1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,3,3,3,3,4,5
დიაპაზონი = 5 - 1 = 4
1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,3,3,3,3,4,120
დიაპაზონი = 120 - 1 = 119

5. კვარტილური დიაპაზონი

ამოვარდნილი მნიშვნელობების პრობლემის
დაძლევა გარკვეულწილად შესაძლებელია
კვარტილური დიაპაზონის (interquartile range)
მეშვეობით
ხდება მაღალი და დაბალი მნიშვნელობების
ამოყრა და გაბნევის დიაპაზონის გამოთვლა
მონაცემთა შუა 50%–ისათვის
კვ. დიაპაზონი = მე-3 კვარტილი – 1-ელი კვარტილი
IQR = Q3 – Q1

6. კვარტილური დიაპაზონი

მაგალითი:
X
Q1
min
25%
12
მედიანა
Q3
(Q2)
25%
30
25%
45
კვარტალური
დიაპაზონი
= 57 – 30 = 27
X
max
25%
57
70

7. პოპულაციის ვარიაცია (დისპერსია)

პოპულაციის საშუალოდან მნიშვნელობათა
კვადრატული გადახრების საშუალო:
N
პოპულაციის ვარიაცია:
σ
2
სადაც
(x
i 1
i
μ)
N
μ = პოპულაციის საშუალო
N = პოპულაციის ზომა
xi = x ცვლადის i–ური მნიშნელობა
2

8. შერჩევის ვარიაცია (დისპერსია)

საშუალოდან მნიშვნელობათა კვადრატული
გადახრების (მიახლოებითი) საშუალო
n
შერჩევის ვარიაცია:
s
2
სადაც
(x x)
i
i 1
n -1
X = არითმეტიკული საშუალო
n = შერჩევის ზომა
xi = x ცვლადის i–ური მნიშნელობა
2

9. პოპულაციის სტანდარტული გადახრა

გაფანტულობის გაზომვის ყველაზე ხშირად
გამოყენებადი საზომი
გვიჩვენებს ვარიაციას საშუალოს მიმართ
პოპულაციის სტანდარტული გადახრა:
N
σ
(x
i 1
i
μ)
N
2

10. შერჩევის სტანდარტული გადახრა

გაფანტულობის გაზომვის ყველაზე ხშირად
გამოყენებადი საზომი
გვიჩვენებს ვარიაციას საშუალოს მიმართ
შერჩევის სტანდარტული გადახრა :
n
S
(x x)
i 1
i
n -1
2

11. მაგალითი: შერჩევის სტანდარტული გადახრა

შერჩევის
მონაცემები(xi) 10
12
14
n=8
s
15
17
18
18
24
საშუალო = x = 16
(10 X )2 (12 x)2 (14 x)2 (24 x)2
n 1
(10 16)2 (12 16)2 (14 16)2 (24 16)2
8 1
126
7
4.2426
საშუალო მნიშვნელობიდან
“საშუალო” გადახრა

12. სტანდარტული გადახრების შედარება

A მონაცემები
11
12
13
14
15
16
17
18
19
20 21
B მონაცემები
11
12
13
14
15
16
17
18
19
20 21
საშუალო= 15.5
s = 3.338
საშუალო = 15.5
s = 0.926
C მონაცემები
11
12
13
14
15
16
17
18
19
20 21
საშუალო = 15.5
s = 4.570

13. დისპერსიის და სტანდარტული გადახრის უპირატესობები

მონაცემთა სიმრავლის თითოეული
მნიშვნელობა მონაწილეობს გათვლებში
საშუალოდან შედარებით უფრო
დაშორებულ მნიშვნელობებს მეტი წონა
აქვთ
(რადგან საშუალოდან გადახრები კვადრატში
აიყვანება)

14. ვარიაციის კოეფიციენტი

ზომავს ფარდობით განფენილობას
ყოველთვის აისახება პროცენტულად (%)
გვიჩვენებს გაფანტულობას საშუალოსთან
მიმართებაში
შესაძლებელია მისი გამოყენება მონაცემთა
ორი ან მეტი სიმრავლის შემთხვევაში (რომლებიც
ასახულია ზომის განსხვევებულ ერთულებში)
s
C V 100%
x

15. ვარიაციის კოეფიციენტის შედარება

A დასახელების აქცია:
საშუალო ფასი გასულ წელს = $50
სტანდარტული გადახრა = $5
s
$5
CVA 100%
100% 10%
$50
x
B დასახელების აქცია :
საშუალო ფასი გასულ წელს = $100
სტანდარტული გადახრა = $5
s
$5
CVB 100%
100% 5%
$100
x
ორივე აქციას
აქვს თანაბარი
სტანდარტული
გადახრა,
მაგრამ B აქცია
ნაკლებად
ცვალებადია

16. კოვარიაცია

კოვარიაცია ზომავს ორ ცვლადს შორის წრფივი
დამოკიდებულების მიმართულებას
პოპულაციის კოვარიაცია:
N
Cov (x , y) xy
(x
i
i 1
x
)(y i y )
N
შერჩევის კოვარიაცია:
n
Cov (x , y) s xy
(x x)(y y)
i 1
i
i
n 1
ზომავს მხოლოდ დამოკიდებულების მიმართულებას
არ გულისხმობს მიზეზ–შედეგობრივ კავშირებს

17. კოვარიაციის ინტერპრეტაცია

კოვარიაცია ორ ცვლადს შორის:
Cov(x,y) > 0
x და y მოძრაობენ ერთსა და იმავე
მიმართულებით
Cov(x,y) < 0
x და y მოძრაობენ სხვადასხვა
მიმართულებით
Cov(x,y) = 0
x და y დამოუკიდებლები არიან

18. კორელაციის კოეფიციენტი

ზომავს ორ ცვლადს შორის წრფივი
დამოკიდებულების ფარდობით სიძლიერეს
პოპულაციის კორელაციის კოეფიციენტი:
Cov (x , y)
ρ
σXσY
შერჩევის კორელაციის კოეფიციენტი:
Cov (x , y)
r
sX sY

19. r კორელაციის კოეფიციენტის თვისებები

არ არის გამოსახული აბსოლუტურ ერთეულებში
იცვლება –1-სა და1-ს შორის
რაც უფრო ახლოსაა –1-თან, მით უფრო ძლიერია
უარყოფითი წრფივი დამოკიდებულება
რაც უფრო ახლოსაა 1-თან, მით უფრო ძლიერია
დადებითი წრფივი დამოკიდებულება
0-თან სიახლოვეში, ზოგადად წრფივი
დამოკიდებულება სუსტდება

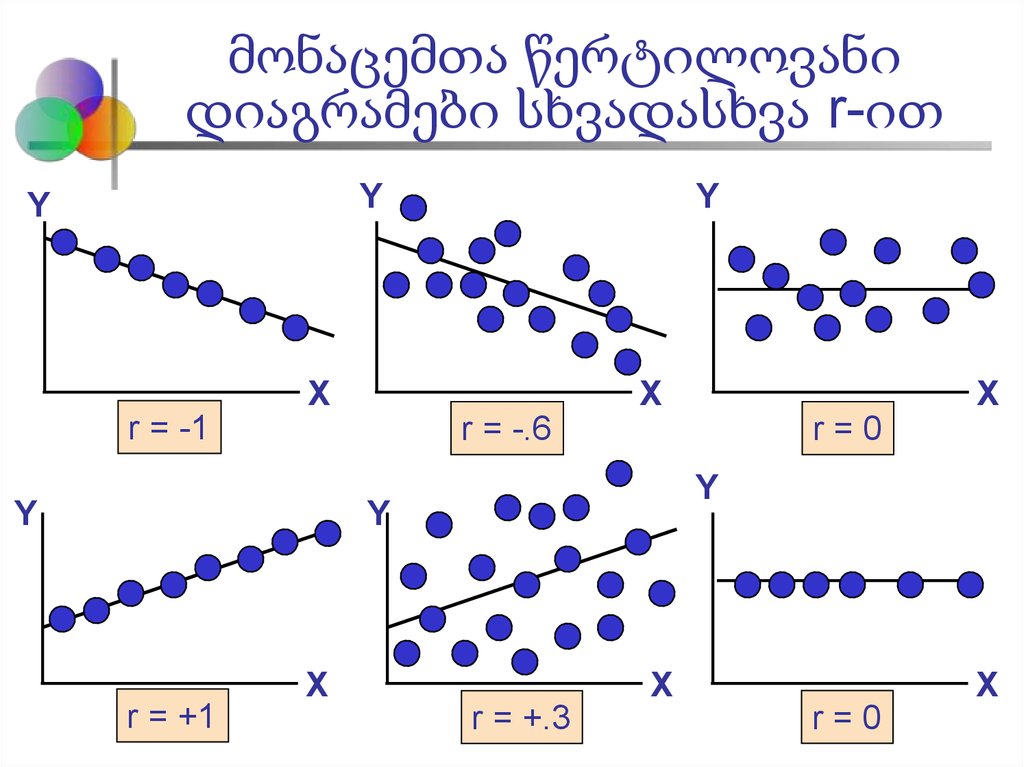
20. მონაცემთა წერტილოვანი დიაგრამები სხვადასხვა r-ით

Y
Y
Y
X
X
r = -1
r = -.6
Y
r=0
Y
Y
r = +1
X
X
X
r = +.3
X
r=0

21. წრფივი კავშირის ძიება

Chap 3-21