მენეჯერული სტატისტიკა. შერჩევა და შერჩევის განაწილება. თავი 7

1.

მენეჯერული სტატისტიკა
თავი 7
შერჩევა და შერჩევის
განაწილება
Chap 7-1

2. თავის მიზნები

თავის შესწავლის შემდეგ თქვენ შეძლებთ:
აღწეროთ მარტივი შემთხვევითი შერჩევა და ახსნათ
რატომაა შერჩევა მნიშვნელოვანი
ახსნათ განსხვავება აღწერით და დასკვნით სტატისტიკებს
შორის
ახსნათ შერჩევითი განაწილების ცნება
განსაზღვროთ საშუალო და სტანდარტული გადახრა
შერჩევის საშუალოს X შერჩევითი განაწილებისთვის
ახსნათ ცენტრალური ზღვრის თეორემა და მისი
მნიშვნელოვნება
განსაზღვროთ საშუალო და სტანდარტული გადახრა
ˆ შერჩევითი განაწილებისთვის
შერჩევითი პროპორციის p
ახსნათ შერჩევის ვარიაციის შერჩევითი განაწილება
Chap 7-2

3. ბიზნეს სტატისტიკის ინსტრუმენტები

აღწერითი სტატისტიკა
მონაცემების შეგროვება, წარდგენა და
აღწერა
დასკვნითი სტატისტიკა
დასკვნების გაკეთება და/ან შერჩევის
მონაცემებზე დაყრდნობით პოპულაციის
შესახებ გადაწყვეტილების მიღება
Chap 7-3

4. შერჩევა და პოპულაცია

პოპულაცია (Population) არის შესასწავლი ობიექტების
(ერთეულების) ყველა შესაძლო მნიშვნელობათა
ერთობლიობა
მაგალითები: ყველა შესაძლო ამომრჩეველი, რომელიც მივა
არჩევნებზე, ყველა წარმოებული ნაწილი, ნოემბრის თვის
მთლიანი გაყიდვები.
შერჩევა (Sample) არის პოპულაციის გარკვეული ნაწილი
(ქვესიმრავლე)
მაგალითები: შემთხვევით შერჩეული 1000 ამომრჩეველი,
ტესტირებისთვის შერჩეული რამოდენიმე ნაწილი,
აუდიტისთვის შერჩეული რამოდენიმე ქვითარი.
Chap 7-4

5. პოპულაცია vs. შერჩევა

პოპულაცია
a b
შერჩევა
cd
b
ef gh i jk l m n
o p q rs t u v w
x y
z
c
gi
o
n
r
u
y
Chap 7-5

6. რატომ შერჩევა?

საჭიროებს ნაკლებ დროს ვიდრე
პოპულაციის აღწერა
საჭიროებს ნაკლებ ხარჯებს ვიდრე
პოპულაციის აღწერა
შესაძლებელია მიღებულ იქნას მაღალი
სიზუსტის სტატისტიკური შედეგები
შერჩევაზე დაყრდნობით
Chap 7-6

7. მარტივი შემთხვევითი შერჩევა

პოპულაციის ყველა ობიექტს აქვს შერჩევაში
მოხვედრის თანაბარი შანსი
ობიექტების შერჩევა ხდება ერთმანეთისგან
დამოუკიდებლად
შერჩევს განხორციელება შეიძლება შემთხვევითი
ცხრილების ან კომპიუტერული პროგრამის
გამოყენებით
მარტივი შემთხვევითი შერჩევა საუკეთესოა სხვა
შერჩევის მეთოდებთან შედარებით
Chap 7-7

8. დასკვნითი სტატისტიკა

შერჩევის შედეგებზე დაყრდნობით,
აკეთებს განაცხადს პოპულაციის შესახებ
შერჩევის სტატისტიკა
პოპულაციის პარამეტრი
(ცნობილი)
დასკვნა
(უცნობი, მაგრამ
შესაძლოა შეფასებულ იქნას შერჩევაზე დაყრდნობით)
Sample
Population
Chap 7-8

9. დასკვნითი სტატისტიკა

დასკვნის გაკეთება და/ან შერჩევის მონაცემებზე
დაყრდნობით პოპულაციის შესახებ
გადაწყვეტილების მიღება
შეფასება
მაგ, შერჩევის საშუალო წონაზე
დაყრდნობით, პოპულაციის
საშუალო წონის განსაზღვრა.
ჰიპოთეზის შემოწმება
მაგ, მტკიცების შემოწმება, რომ
მოსახლეობის საშუალო სიმაღლე
არის 170 სმ.
Chap 7-9

10. შერჩევის განაწილება

შერჩევის განაწილება არის
პოპულაციიდან მიღებული გარკვეული
ზომის შერჩევის სტატისტიკის ყველა
შესაძლო მნიშვნელობის განაწილება.
Chap 7-10

11. თავის მიმოხილვა

შერჩევითი
განაწილება
შერჩევის
საშუალოს
შერჩევითი
განაწილება
შერჩევის
პროპორციის
შერჩევითი
განაწილება
შერჩევის
ვარიაციის
შერჩევითი
განაწილება
Chap 7-11

12. შერჩევის საშუალოს შერჩევითი განაწილება

შერჩევითი
განაწილება
შერჩევის
საშუალოს
შერჩევითი
განაწილება
შერჩევის
პროპორციის
შერჩევითი
განაწილება
შერჩევის
ვარიაციის
შერჩევითი
განაწილება
Chap 7-12

13. შერჩევითი განაწილების განვითარება

დავუშვათ მოცემული გვაქვს პოპულაცია…
პოპულაციის ზომა N=4
A
B
C
D
შემთხვევითი ცვლადი, X,
არის ინდივიდების ასაკი
X-ის მნიშვნელობები:
18, 20, 22, 24 (წელი)
Chap 7-13

14. შერჩევითი განაწილების განვითარება

(გაგრძელება)
პოპულაციის განაწილების შემაჯამებელი მაჩვენებლები:
X
μ
P(x)
i
N
18 20 22 24
21
4
σ
(X μ)
i
N
.25
0
2
2.236
18
20
22
24
A
B
C
D
x
თანაბარი განაწილება
Chap 7-14

15. ახლა განვიხილოთ შერჩევა, რომლის ზომაა n = 2

შერჩევითი განაწილების
განვითარება
(გაგრძელება)
ახლა განვიხილოთ შერჩევა, რომლის ზომაა n = 2
1st
Obs
2nd Observation
18
20
22
24
18 18,18 18,20 18,22 18,24
16 შერჩევის
საშუალო
20 20,18 20,20 20,22 20,24
1st 2nd Observation
Obs 18 20 22 24
22 22,18 22,20 22,22 22,24
18 18 19 20 21
24 24,18 24,20 24,22 24,24
20 19 20 21 22
16 შესაძლო შერჩევა
(შერჩევა
ჩანაცვლებით)
22 20 21 22 23
24 21 22 23 24
Chap 7-15

16. შერჩევითი საშუალოს შერჩევითი განაწილება

შერჩევითი განაწილების
განვითარება
(გაგრძელება)
შერჩევითი საშუალოს შერჩევითი განაწილება
შერჩევითი
საშულოს
განაწილება
16 შერჩევითი საშუალო
1st 2nd Observation
Obs 18 20 22 24
_
18 18 19 20 21
P(X)
.3
20 19 20 21 22
.2
22 20 21 22 23
.1
24 21 22 23 24
0
18 19
20 21 22 23
24
_
X
(არა ერთგვაროვანი)
Chap 7-16

17. შერჩევითი განაწილების შემაჯამებელი საზომები:

შერჩევითი განაწილების
განვითარება
(გაგრძელება)
შერჩევითი განაწილების შემაჯამებელი საზომები:
X
E(X)
18 19 21 24
21 μ
N
16
i
σX
2
(
X
μ)
i
N
(18 - 21)2 (19 - 21)2 (24 - 21)2
1.58
16
Chap 7-17

18. პოპულაციის შედარება თავის შერჩევის განაწილებასთან

შერჩევის საშუალოს
განაწილება
n=2
პოპულაცია N = 4
μ 21
σ 2.236
μX 21
_
P(X)
.3
P(X)
.3
.2
.2
.1
.1
0
18
20
22
24
A
B
C
D
X
0
18 19
σ X 1.58
20 21 22 23
24
_
X
Chap 7-18

19. შერჩევის საშუალოს მოსალოდნელი მნიშვნელობა

დავუშვათ X1, X2, . . . Xn არის პოპულაციიდან
მიღებული შემთხვევითი შერჩევა
შერჩევის საშუალო განისაზღვრება, როგორც:
1 n
X Xi
n i 1
Chap 7-19

20. შერჩევის სტანდარტული შეცდომა

ერთიდაიგივე პოპულაციის, ერთი და იგივე ზომის
სხვადასხვა შერჩევა მოგვცემს სხვადასხვა შედეგებს:
საშუალოს ცვალებადობის საზომი შერჩევიდან
შერჩევამდე განსაზღვრულია შერჩევის
სტანდარტული შეცდომით:
σ
σX
n
ყურადღება მიაქციეთ, რომ სტანდარტული შეცდომა
მცირდება, როდესაც შერჩევის ზომა იზრდება
Chap 7-20

21. თუ პოპულაცია ნორმალურია

თუ მოპულაცია ნორმალურია საშუალო μ-თი
და სტანდარტული გადახრა σ-ით, შერჩევითი
განაწილება იქნება ასევე ნორმაულრად
განაწილებული X
μX μ
და
σ
σX
n
Chap 7-21

22. Z-მნიშვნელობა საშუალოს შერჩევითი განაწილებისათვის

Z-მნიშვნელობა X-ის შერჩევითი
განაწილებისათვის არის:
( X μ) ( X μ)
Z
σ
σX
n
სადაც:
X = შერჩევის საშუალო
μ = პოპულაციის საშუალო
σ = პოპულაციის სტანდარტული გადახრა
n = შერჩევის ზომა
Chap 7-22

23. პოპულაციის სასრული კორელაცია

შერჩევითი განაწილების
თვისებები
μx μ
x
(ანუ
არის
მიუკერძოებელი)
პოპულაციის
ნორმალური
განაწილება
μ
x
μx
x
შერჩევის ნორმალური
განაწილება
(აქვთ ერთი და იგივე საშუალო)
Chap 7-25

24. პოპულაციის სასრული კორელაცია

შერჩევითი განაწილების თვისებები
(გაგრძელება)
შერჩევისთვის გადანაცვლებადობის შემთხვევაში:
როდესაც n იზრდება,
შერჩევის
დიდი ზომა
σ x მცირდება
შერჩევის
პატარა ზომა
μ
x
Chap 7-26

25. შერჩევითი განაწილების თვისებები

თუ პოპულაცია არაა
ნორმალურად განაწილებულია
ჩვენ შეგვიძლია გამოვიყენოთ ცენტრალური
ზღვრის თეორემა:
მაშინაც კი თუ პოპულაცია არაა ნორმალური,
…პოპულაციიდნ მიღებული შერჩევის საშუალო
იქნება მიახლოებით ნორმალური, თუ შერჩევის
ზომა იქნება საკმარისად დიდი.
შერჩევითი განაწილების თვისებები:
μx μ
და
σ
σx
n
Chap 7-27

26. შერჩევითი განაწილების თვისებები

ცენტრალური ზღვრის თეორემა
როდესაც
შერჩევის
ზომა
ხდება
საკმარისად
დიდი…
n↑
შერჩევითი
განაწილება
ხდება
თითქმის
ნორმალური,
მიუხედავად
პოპულაციის
განაწილების
ფორმისა
x
Chap 7-28

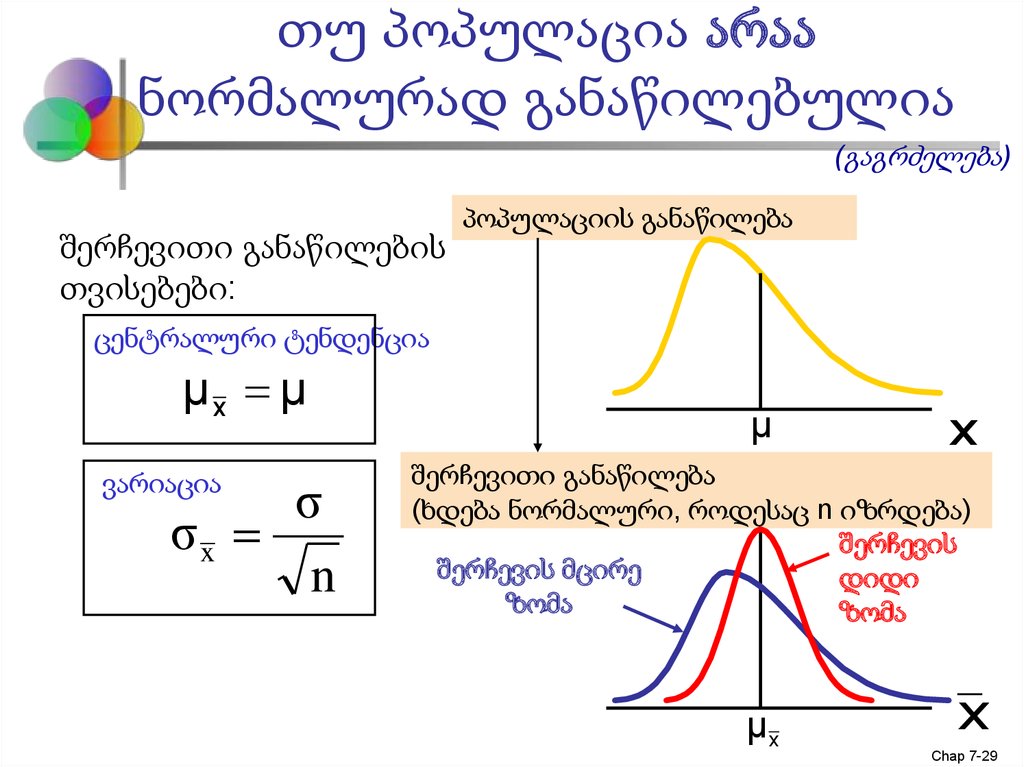
27. თუ პოპულაცია არაა ნორმალურად განაწილებულია

(გაგრძელება)
შერჩევითი განაწილების
თვისებები:
პოპულაციის განაწილება
ცენტრალური ტენდენცია
μx μ
ვარიაცია
σ
σx
n
μ
x
შერჩევითი განაწილება
(ხდება ნორმალური, როდესაც n იზრდება)
შერჩევის
შერჩევის მცირე
დიდი
ზომა
ზომა
μx
x
Chap 7-29

28. ცენტრალური ზღვრის თეორემა

რამდენია საკმაოდ დიდი?
უმრავლესობა განაწილებისათვის, n > 25
მოგვცემს შეეჩევით განაწილებას, რომელიც
ახლოსაა ნორმალურთან
ნორმალურად განაწილებული
პოპულაციისათვის, შერჩევითი
განაწილების საშუალო ყოველთვის
ნორმალურია.
Chap 7-30

29. თუ პოპულაცია არაა ნორმალურად განაწილებულია

მაგალითი
დავუშვათ პოპულაციის საშუალოა μ = 8 და
სტანდარტული გადახრაა σ = 3. დავუშვათ
შემთხვევითი შერჩევის ზომაა n = 36.
რა არის ალბათობა იმისა, რომ შერჩევის
საშუალო მოთავსებული იქნება 7.8-სა და 8.2ს შორის?
Chap 7-31

30. რამდენია საკმაოდ დიდი?

მაგალითი
(გაგრძელება)
ამოხსნა:
მაშინაც კი თუ პოპულაცია ნომრალურად არაა
განაწილებული, ცენტრალური ზღვრის
თეორეა შეიძლება იქნას გამოყენებული(n >
25)
… ანუ x -ის შერჩევითი განაწილება იქნება
მიახლოებით ნორმალური
… საშუალო μx = 8
σ
3
σx
0.5
…და სტანდარტული გადახრა
n
36
Chap 7-32

31. მაგალითი

(გაგრძელება)
ამოხსნა (გაგრძელება):
μX -μ
7.8 - 8
8.2 - 8
P(7.8 μ X 8.2) P
3
σ
3
36
n
36
P(-0.5 Z 0.5) 0.3830
პოპულაციის
განაწილება
?
???
შერჩევის
განაწილება
??
?
??
μ 8
?
?
სტანდარტული
ნორმალური
განაწილება
შერჩევა
?
X
.1915
+.1915
ნორმალიზაცია
7.8
μX 8
8.2
x
-0.5
μz 0
0.5
Z
Chap 7-33