Тепловое равновесное излучение. Лекция 1

1.

Тепловое равновесное
излучение
ЛВВ
1,05 10
34
Дж с
Свойства, основные законы
Тепловое излучение – электромагнитное
излучение, испускаемое веществом и
возникающее за счет его внутренней тепловой
энергии

2.

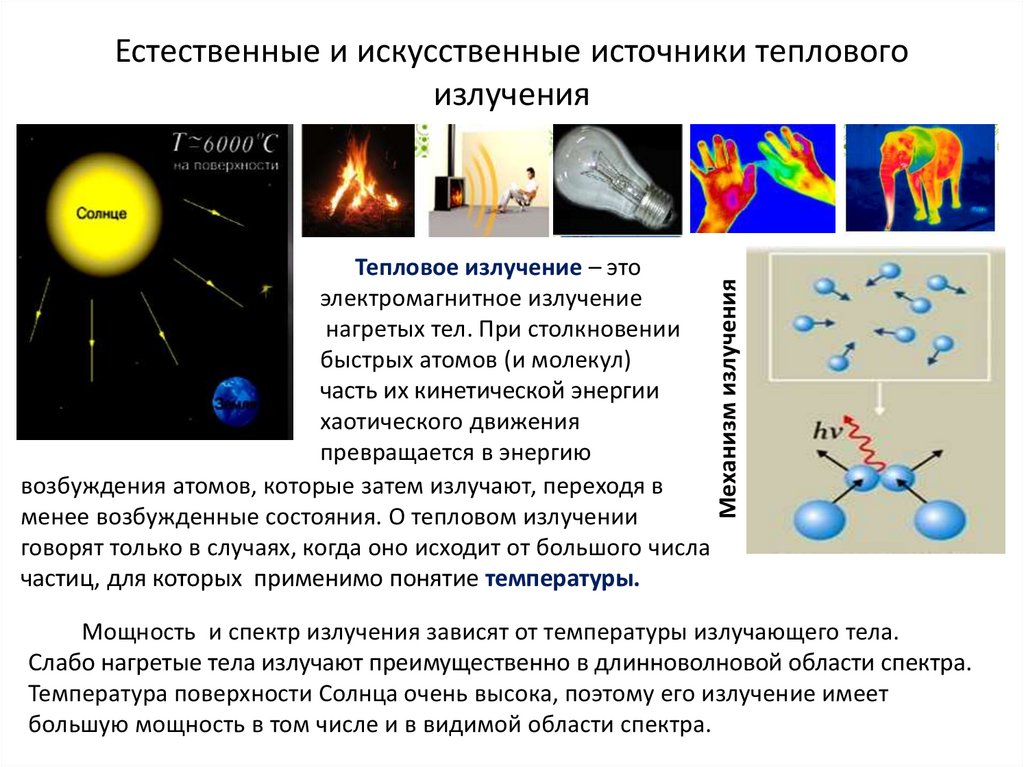
Содержание лекции

3. Естественные и искусственные источники теплового излучения

Тепловое излучение – это
электромагнитное излучение
нагретых тел. При столкновении
быстрых атомов (и молекул)
часть их кинетической энергии
хаотического движения
превращается в энергию
возбуждения атомов, которые затем излучают, переходя в
менее возбужденные состояния. О тепловом излучении
говорят только в случаях, когда оно исходит от большого числа
частиц, для которых применимо понятие температуры.
Механизм излучения
Естественные и искусственные источники теплового
излучения
Мощность и спектр излучения зависят от температуры излучающего тела.
Слабо нагретые тела излучают преимущественно в длинноволновой области спектра.
Температура поверхности Солнца очень высока, поэтому его излучение имеет
большую мощность в том числе и в видимой области спектра.

4.

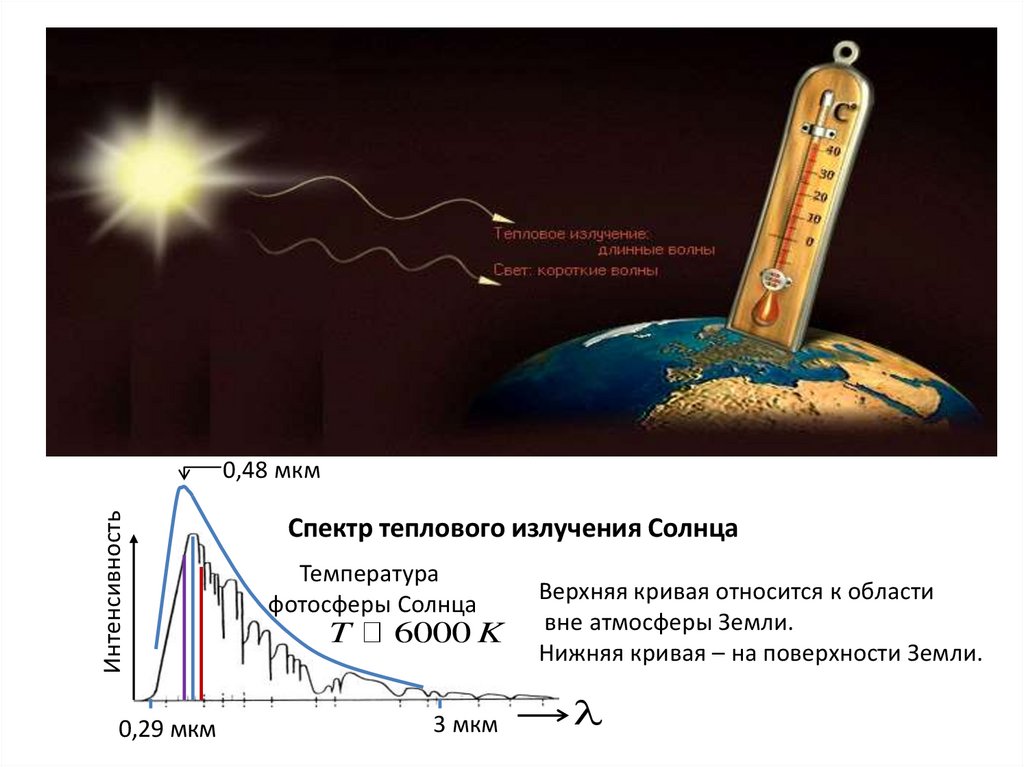
Интенсивность
0,48 мкм
0,29 мкм
Спектр теплового излучения Солнца
Температура
фотосферы Солнца
T
6000 K
3 мкм
Верхняя кривая относится к области
вне атмосферы Земли.
Нижняя кривая – на поверхности Земли.

5.

1. Термодинамическое равновесие теплового
излучения с веществом
Поглощение
потока Фпогл
Т
Излучение
потока Ф
изл
Тепловое излучение в изолированной системе
«вещество + излучение» - равновесное, если Фпогл Физл :
1) Все тела, входящие в систему, имеют одинаковую
температуру T, и эта же температура характеризует
тепловое излучение;
2) Каждое тело, независимо от его свойств, излучает в
единицу времени столько же энергии, сколько поглощает
обратно.

6.

2. Свойства и
спектральные
характеристики
теплового
равновесного
излучения.
Равновесное тепловое
излучение : однородное
(плотность энергии
одинакова во всех точках
области, где оно заключено),
изотропное и не
поляризовано (содержит все
возможные направления
распространения и
направления колебаний
векторов E и H ,
имеет непрерывный
спектр, не ограниченный
по частоте: 0 < <
Объемная плотность энергии
излучения (энергия в единице объема)
в интервале частот d :
dW w T d
w T w( , T ) - спектральная
плотность
энергии
w T
W w T d
dW
0
m
Распределение энергии
равновесного излучения
по частоте.

7.

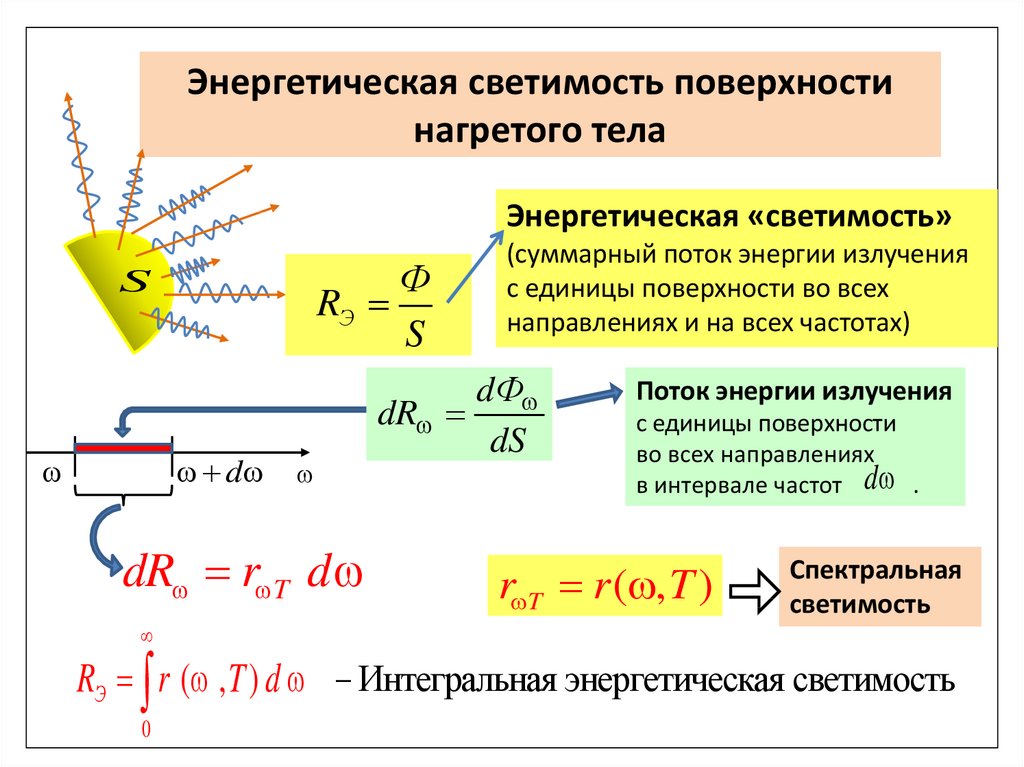
Энергетическая светимость поверхности
нагретого тела
Энергетическая «светимость»
Ф
RЭ
S
S
d
dR r T d
(суммарный поток энергии излучения
с единицы поверхности во всех
направлениях и на всех частотах)
dФ
dR
dS
Поток энергии излучения
с единицы поверхности
во всех направлениях
в интервале частот d .
r T r ( , T )
Спектральная
светимость
RЭ r ( , T ) d Интегральная энергетическая светимость
0

8.

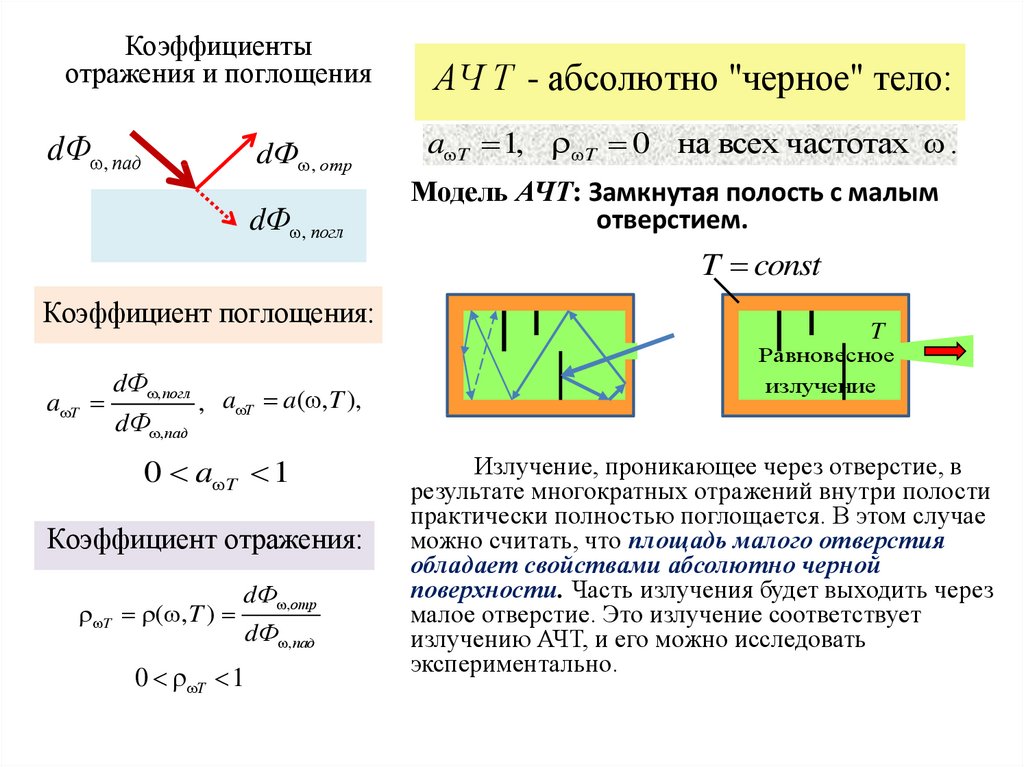
Коэффициенты
отражения и поглощения
dФ , пад
dФ , отр
dФ , погл
АЧ Т - абсолютно "черное" тело:
a T 1, T 0 на всех частотах .
Модель АЧТ: Замкнутая полость с малым
отверстием.
T const
Коэффициент поглощения:
T
Равновесное
a T
dФ , погл
dФ , пад
, a T a( , T ),
0 a T 1
Коэффициент отражения:
T ( , T )
dФ ,отр
dФ ,пад
0 T 1
излучение
Излучение, проникающее через отверстие, в
результате многократных отражений внутри полости
практически полностью поглощается. В этом случае
можно считать, что площадь малого отверстия
обладает свойствами абсолютно черной
поверхности. Часть излучения будет выходить через
малое отверстие. Это излучение соответствует
излучению АЧТ, и его можно исследовать
экспериментально.

9.

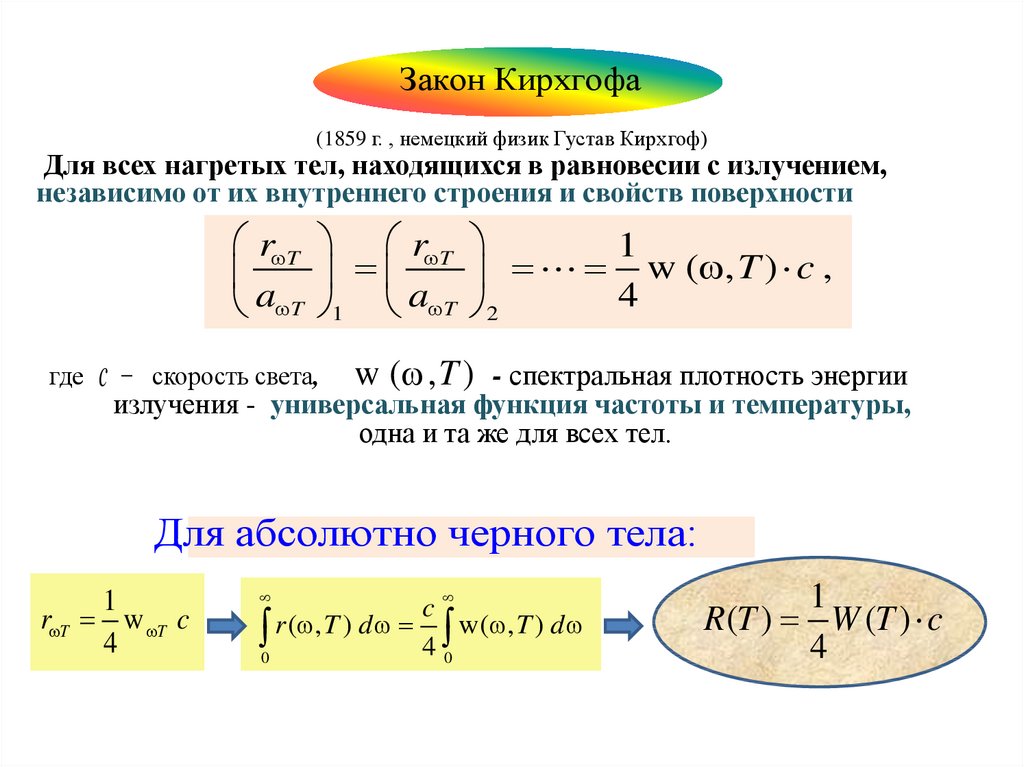
Закон Кирхгофа
(1859 г. , немецкий физик Густав Кирхгоф)
Для всех нагретых тел, находящихся в равновесии с излучением,
независимо от их внутреннего строения и свойств поверхности
r T r T
1
w ( , T ) c ,
4
a T 1 a T 2
где
c
w ( , T )
- спектральная плотность энергии
излучения - универсальная функция частоты и температуры,
одна и та же для всех тел.
скорость света,
Для абсолютно черного тела:
1
r T w T c
4
c
r
(
,
T
)
d
w( , T ) d
0
40
1
R(T ) W (T ) c
4

10.

Следствия из закона Кирхгофа
Тела интенсивнее излучают на тех частотах, на которых они
сильнее поглощают.
Спектральная светимость АЧТ не зависит от устройства тела,
от свойств вещества, его поверхности, а зависит только от частоты
и температуры.
Все реальные тела, для которых a T 1 ,
при любой температуре всегда излучают меньше энергии, чем АЧТ.
Пример 1. Красное стекло выглядит красным потому, что оно сильно
поглощает излучение из зеленой части видимого нами спектра. Сильно
нагретое стекло становится зеленоватым, так как оно испускает излучение
из зеленой части спектра, которое оно раньше поглощало.
Пример 2. Черное пятно на полированном металлическом шаре при
нормальной температуре выглядит темнее, чем остальная отражающая
поверхность шара. При достаточно высокой температуре, когда шар
начинает испускать видимый свет, то пятно, которое сначала поглощало
сильнее металла, теперь больше излучает и выглядит ярче, чем
окружающая поверхность.

11.

Классическая теория. Формула Рэлея - Джинса
Классическая физика исходит из следующих положений:
1) Равновесное излучение в полости с нагретыми
стенками существует в виде дискретного набора
электромагнитных стоячих волн, когда от стенки
до стенки укладывается целое число полуволн 2 .
2) Закон равномерного распределения энергии
теплового излучения по степеням свободы.
На каждую стоячую электромагнитную
волну в среднем приходится kБT тепловой энергии.
2 d
dN V 2 3
c
L n
n
2
n 1, 2,3,
число стоячих волн в полости объема V с частотами
из узкого интервала частот d .
Исходя из этих положений английские физики Джон Стретт (лорд Рэлей) в
1900 г. и Джеймс Джинс в 1905 г. получили:
Спектральная плотность
энергии в единичном объеме:
w T
2
2 3 kБT
c
(Формула Рэлея-Джинса)

12.

Следствия из формулы Рэлея - Джинса
w T
Формула Рэлея – Джинса достаточно
хорошо согласуется с экспериментом только в
области малых частот и резко расходится
Формула
Рэлея-Джинса
Опыт
с опытом при больших частотах.
Классическая физика привела к парадоксу, которому позднее дали название
« ультрафиолетовая катастрофа»:
С увеличением частоты уменьшается , растет число возможностей (вплоть
до бесконечности) выполнения условия образования стоячих волн.
Если бы на каждую стоячую волну действительно приходилась
одинаковая энергия , то сделав в полости отверстие, мы получили бы источник ни с
чем несравнимой яркости. Излучение забрало бы на себя всю энергию стенок
полости, сколько бы тепла к ним не подводилось. Равновесие между веществом и
излучением при высоких частотах становится теоретически невозможным.

13.

Рождение квантовой теории
Немецкий физик - теоретик
Макс Планк
(1858 – 1947)
Вывел закон спектрального
распределения энергии
излучения абсолютно черного
тела (1900 г.).
Ввел фундаментальную
постоянную
.
Нобелевская премия
1918 г

14.

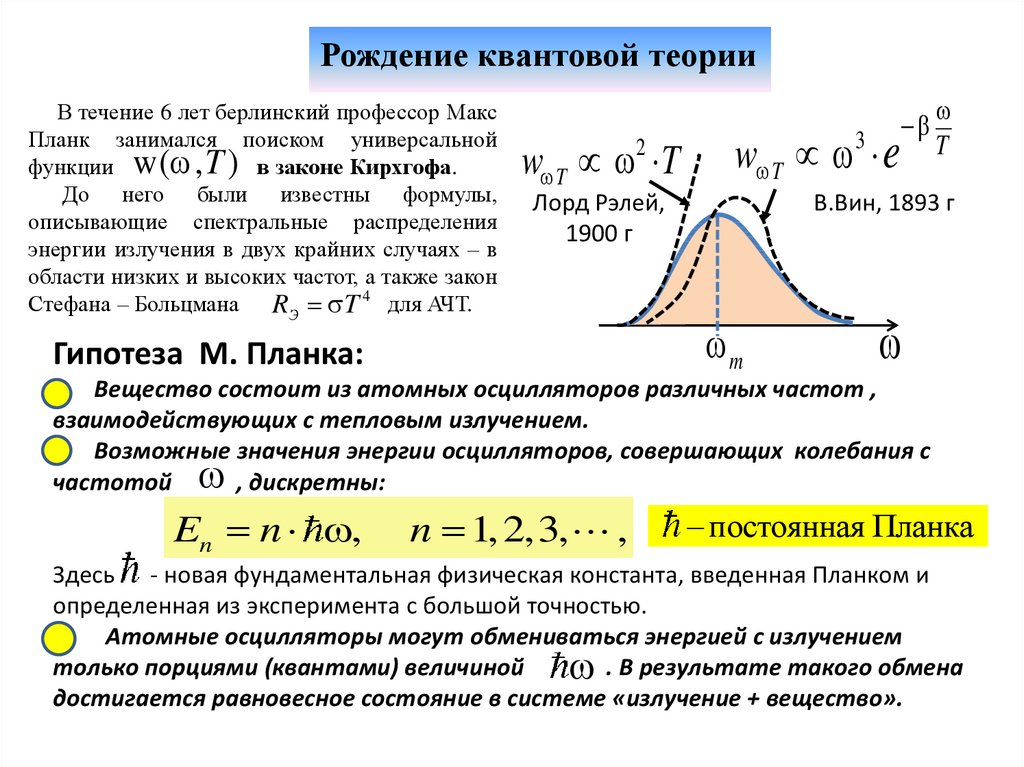
Рождение квантовой теории
В течение 6 лет берлинский профессор Макс
Планк занимался поиском универсальной
функции w( , T ) в законе Кирхгофа.
До него были известны формулы,
описывающие спектральные распределения
энергии излучения в двух крайних случаях – в
области низких и высоких частот, а также закон
Стефана – Больцмана RЭ T 4 для АЧТ.
w T T
2
w T 3 e
Лорд Рэлей,
1900 г
Гипотеза М. Планка:
T
В.Вин, 1893 г
m
Вещество состоит из атомных осцилляторов различных частот ,
взаимодействующих с тепловым излучением.
Возможные значения энергии осцилляторов, совершающих колебания с
частотой , дискретны:
En n ,
n 1, 2,3, ,
постоянная Планка
Здесь - новая фундаментальная физическая константа, введенная Планком и
определенная из эксперимента с большой точностью.
Атомные осцилляторы могут обмениваться энергией с излучением
только порциями (квантами) величиной
. В результате такого обмена
достигается равновесное состояние в системе «излучение + вещество».

15.

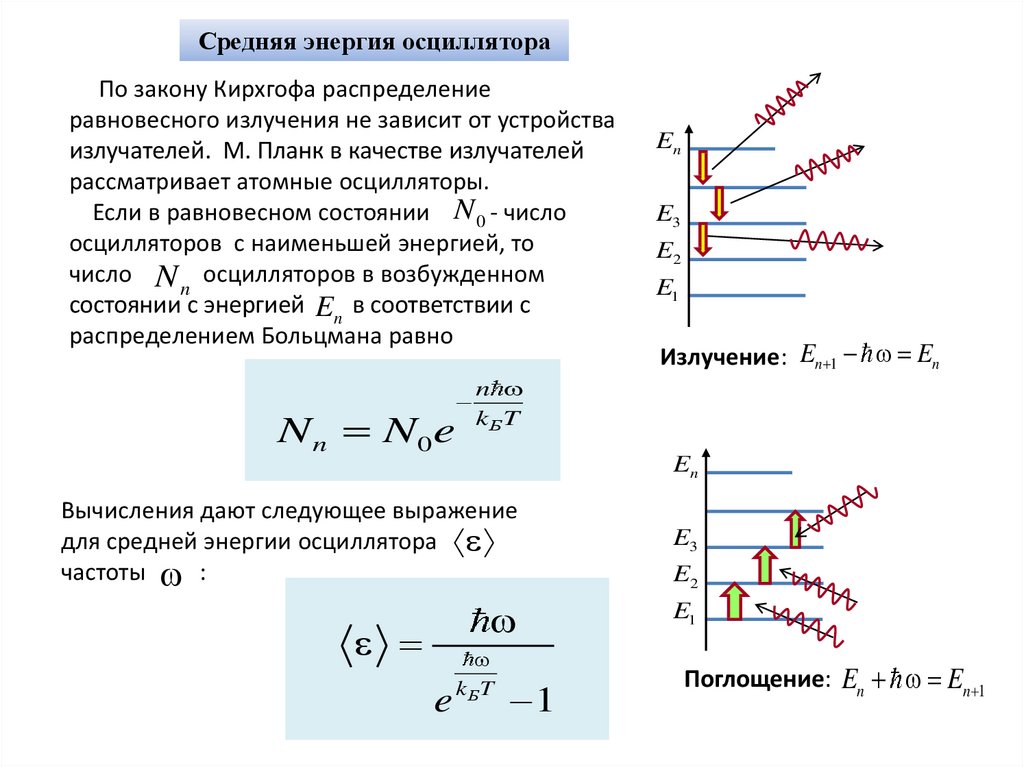
Средняя энергия осциллятора
По закону Кирхгофа распределение
равновесного излучения не зависит от устройства
излучателей. М. Планк в качестве излучателей
рассматривает атомные осцилляторы.
Если в равновесном состоянии N 0 - число
осцилляторов с наименьшей энергией, то
число N n осцилляторов в возбужденном
состоянии с энергией En в соответствии с
распределением Больцмана равно
N n N0e
En
E3
E2
E1
Излучение: En 1 En
n
kБ T
En
Вычисления дают следующее выражение
для средней энергии осциллятора
частоты :
E3
E1
e
kБ T
1
E2
Поглощение: En En 1

16.

Распределение Планка по частоте для равновесного теплового
излучения.
Стоячие волны в полости можно рассматривать как электромагнитные
осцилляторы со средней энергией изл . Средняя энергия осциллятора не
должна зависеть от его устройства. Если вещество стенок полости
поддерживается при температуре T и находится в равновесии с тепловым
излучением в этой полости, то . Тогда
изл
dN
w( , T )
Vd
изл
2
2 3
c e
kБ T
1
Формула М.Планка
Формула М.Планка согласуется с экспериментом во
всем диапазоне частот и при всех температурах.

17.

Закон Стефана – Больцмана для излучения АЧТ.
Как следует из закона Кирхгофа, спектральная светимость абсолютно черного тела
1
(АЧТ), для которого a T a 1 на всех частотах, равна
r T
4
w T c
Для вычисления полной энергетической светимости воспользуемся
формулой Планка, в которой введем переменную x k Б T . Тогда
(k Б T ) 4
c
RЭ w( , T ) d
40
4 2 c 3 3
x 3 dx
0 e x 1
Вычисление интеграла дает константу, равную 15 . В результате получим:
4
RЭ T 4
(Закон Стефана – Больцмана),
где - постоянная Стефана – Больцмана, которая выражается через универсальные
константы и равна
kБ4
4
8 Вт
4 c
2 3 3
15
5,67 10
м2 K 4
Австрийские физики: Й. Стефан получил этот закон в 1879 г. при анализе
экспериментов; затем его ученик Л.Больцман через 5 лет вывел его, применяя
методы термодинамики.

18.

Распределение энергии излучения по длинам волн
В теории в качестве переменной удобна частота , а в экспериментах
преимущественно используется длина волны . Эти величины связаны
соотношением 2 с . На рисунке показана схема перехода от
частот в распределении Планка к распределению по длинам волн.
w ,T d w ,T d
Из равенства плотностей энергии излучения
dW w T d
следует
w T
d
dW w T d
d
d
2 c
2 c
w ( , T ) 2 w (
,T )
d
После преобразования
получим распределение
Планка по длинам волн
16 c
1
w( , T )
5 e2 c kБT 1
2

19.

Законы смещения максимума спектральной
кривой распределения энергии излучения при
изменении температуры АЧТ.
w T
w T
0
m
T T1
T1
Закон смещения
m 2,82 kБT
m,1 m
w T
w T
0
m
T T1
T1
m
1m
3 3 e
kБT
m kБT
k Б 1,38 10 23 Дж К
Закон смещения В.Вина
mT b
2 c
b
2,9 103 мкм K
4,96 k Б

20.

Фотосфера Солнца как модель АЧТ
Огромная масса Солнца М 2 1030 кг вследствие собственной гравитации
создает в его центральной части (ядре ) давление в 250 миллиардов атмосфер.
Плотность вещества достигает величины 1,6 105 кг м3 , что во много раз
превышает плотности металлов. Температура в центре – 150 млн. град.
При таких условиях вещество в ядре находится в состоянии плазмы, и внем
протекают термоядерные реакции с выделением энергии. Основная реакция –
превращение ядер водорода (протонов) в ядра гелия, побочным продуктом которых
является излучение.
p
p
d
e
e
Энергия, выделяющаяся в ходе термоядерных
p d 3He
реакций идет на поддержание температуры
3
Ядро
внутри Солнца и на солнечное излучение.
He 3He 4 He 2 p
R
Фотосфера
300 км
Возникающее в недрах Солнца гамма – излучение не может выйти
наружу из-за большой плотности вещества. На пути из недр оно
многократно поглощаются и вновь переизлучается. В каждом таком
акте частота излучения уменьшается. Таким образом, почти все
коротковолновое излучение, идущее изнутри, поглощается на пути
до поверхности Солнца, и она становится видимой. Поэтому
поверхностный сферический слой (фотосфера) дает излучение,
близкое к излучению АЧТ. Вне атмосферы Земли спектр излучения
близок с спектру излучения по формуле Планка.

21.

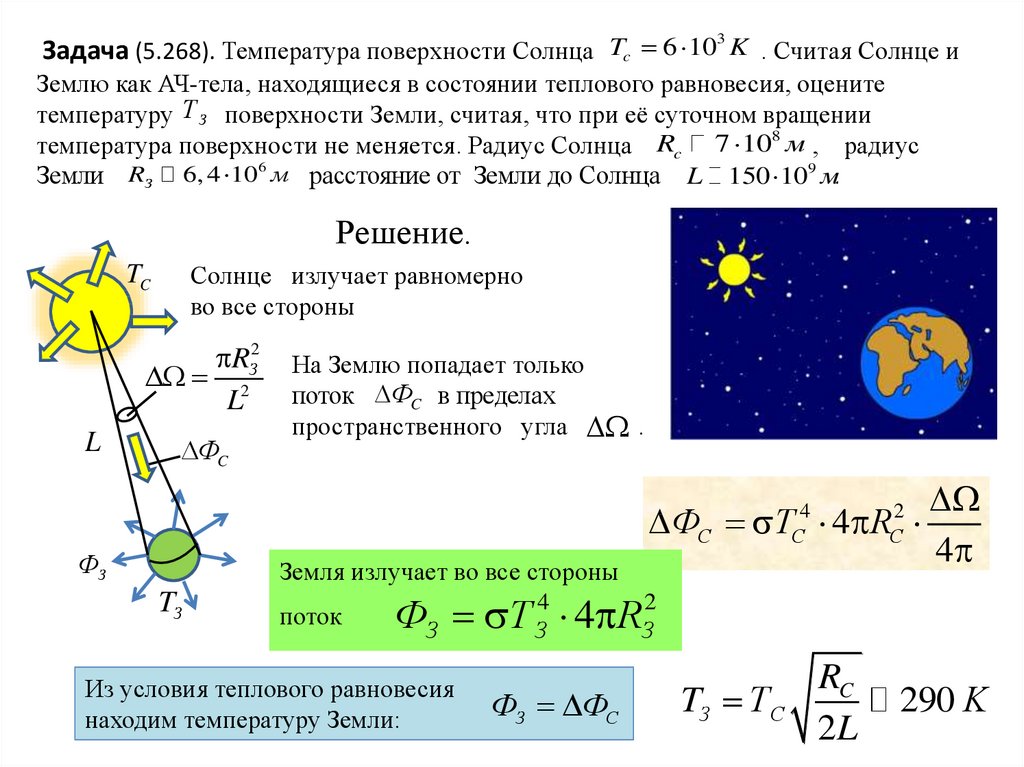
3
Задача (5.268). Температура поверхности Солнца Tc 6 10 K . Считая Солнце и
Землю как АЧ-тела, находящиеся в состоянии теплового равновесия, оцените
температуру Т З поверхности Земли, считая, что при её суточном вращении
температура поверхности не меняется. Радиус Солнца Rc 7 108 м , радиус
Земли RЗ 6, 4 106 м расстояние от Земли до Солнца L 150 109 м.
Решение.
Солнце излучает равномерно
во все стороны
TC
RЗ2
2
L
L
ФC
На Землю попадает только
поток ФC в пределах
пространственного угла .
ФС T 4 R
4
4
C
ФЗ
Земля излучает во все стороны
TЗ
поток
2
C
ФЗ Т З4 4 RЗ2
Из условия теплового равновесия
находим температуру Земли:
ФЗ ФС
TЗ Т С
RC
2L
290 K

22.

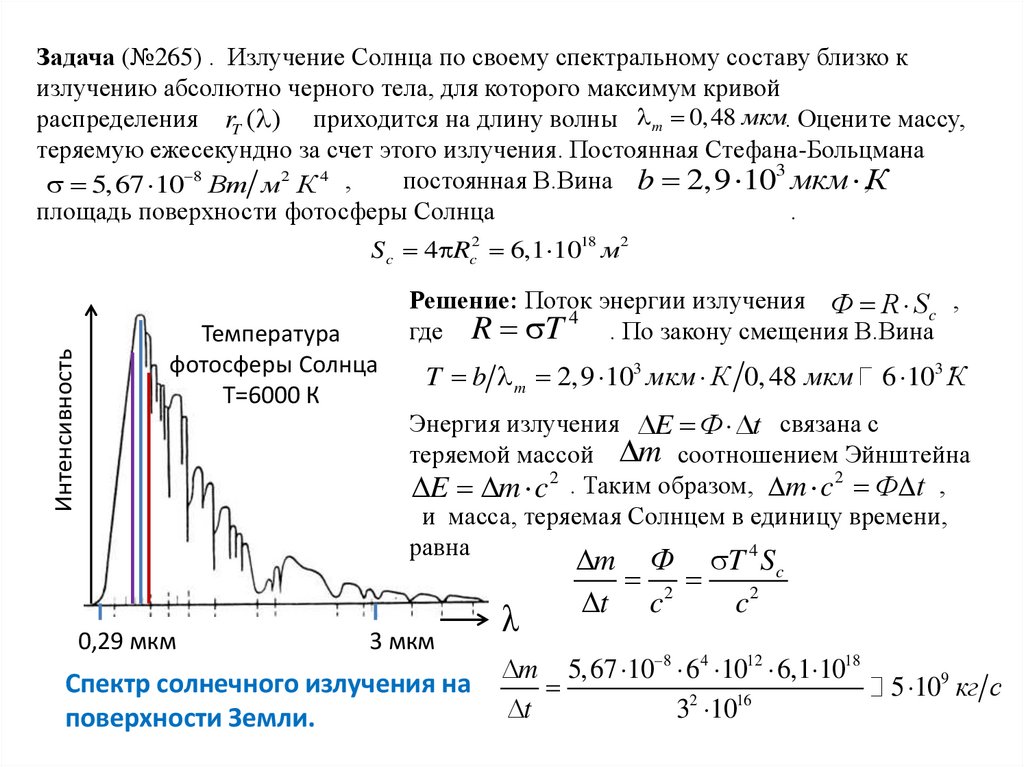
Интенсивность
Задача (№265) . Излучение Солнца по своему спектральному составу близко к
излучению абсолютно черного тела, для которого максимум кривой
распределения rT ( ) приходится на длину волны m 0, 48 мкм. Оцените массу,
теряемую ежесекундно за счет этого излучения. Постоянная Стефана-Больцмана
3
постоянная В.Вина b 2,9 10 мкм ,К
5, 67 10 8 Вт м2 К 4 ,
площадь поверхности фотосферы Солнца
.
Sc 4 Rc2 6,1 1018 м 2
Температура
фотосферы Солнца
Т=6000 К
0,29 мкм
Решение: Поток энергии излучения Ф R Sc ,
4
где R T
. По закону смещения В.Вина
3
3.
T b m 2,9 10 мкм К 0, 48 мкм
6 10 К
Энергия излучения E Ф t связана с
теряемой массой m соотношением Эйнштейна
E m c 2 . Таким образом, m c 2 Ф t ,
и масса, теряемая Солнцем в единицу времени,
равна
4
3 мкм
Спектр солнечного излучения на
поверхности Земли.
m Ф T Sc
2
t c
c2
m 5,67 10 8 64 1012 6,1 1018
t
32 1016
5 109 кг с

23.

Приложение 1. Вывод формулы
Рэлея – Джинса.
w( , T ) 2 3 kБT
c
Пусть полость в веществе («ящик») имеет форму куба с
ребром l и идеально отражающие стенки . Стенки полости
поддерживаются при температуре T.
В результате многократных испусканий и поглощений
электромагнитных волн в полости устанавливается
равновесное излучение. Это и есть излучение абсолютно
черного тела (АЧТ).
Для волны, распространяющейся вдоль оси x
с волновым вектором k k e , условие
x x
образования стоячей волны имеет вид:
l n1
, n1 1, 2,3, , или для волнового числа:
2
2
kx
k x n1
l
2
z
k
x
y
l
Кубическая полость с
равновесным излучением
kx l
kx
На одну стоячую волну , образованной вдоль оси x , на оси волновых чисел
приходится отрезок, равный k l .
x
kx

24.

Для волны, распространяющейся в направлении вектора k k x ex k y ey k z ez ,
для каждого из трёх направлений вдоль ребер кубической полости должно
укладываться целое число полуволн. Тогда волновой вектор k имеет компоненты
и k z n3
k x n1 , k y n2
l
l
l
kz
Здесь n1 , n2 , n3 целые числа, принимающие независимо
значения 1, 2, 3, … .
Рассмотрим пространство волновых чисел ( k x , k y , k z ).
В этом пространстве разрешенные колебательные состояния
располагаются в виде точек, находящихся в узлах решетки
с шагом l вдоль трех осей.
На каждое разрешенное состояние ( на каждый узел в
решетке ) приходится объем
V 3 l 3 3 V ,
k
где V объем кубической полости с излучением
в координатном пространстве (x, y, z ).
Vk
k
kx
ky
Пространство
волновых чисел
Поделив объем положительного октанта шара с радиусом Rk k на элементарный
объём Vk , получим количество разрешенных колебательных состояний N k ,
когда волновое число не превышает заданного значения k .

25.

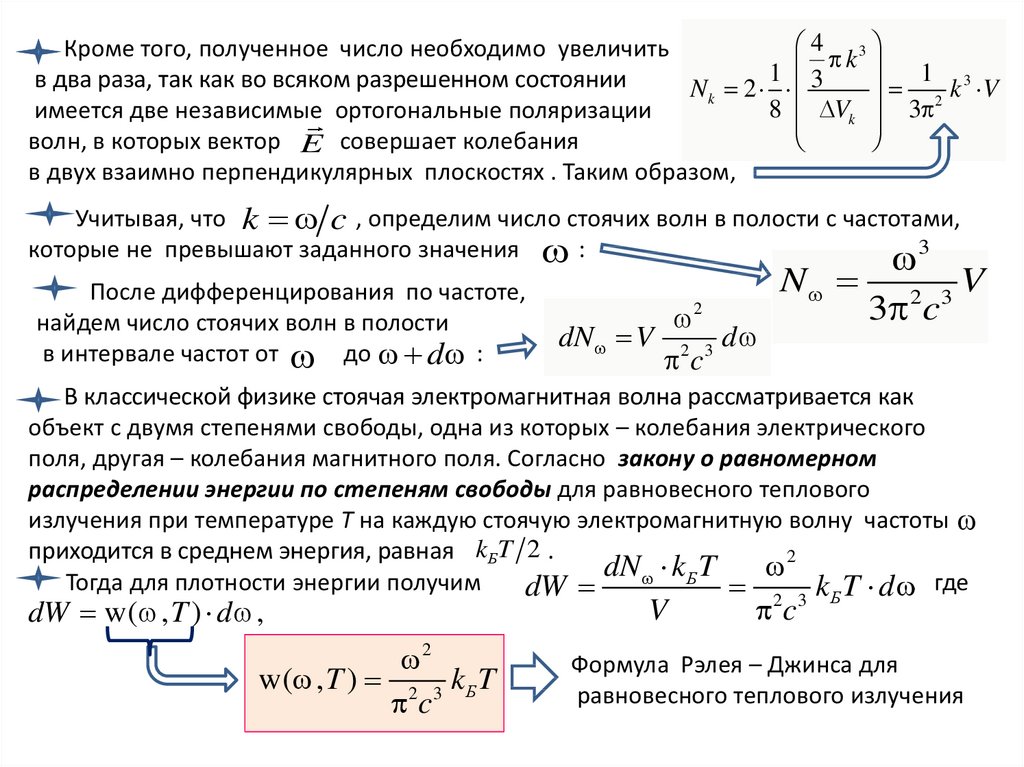
4 3
Кроме того, полученное число необходимо увеличить
k
1 3
1 3
в два раза, так как во всяком разрешенном состоянии
Nk 2
k V
2
8
V
3
имеется две независимые ортогональные поляризации
k
волн, в которых вектор E совершает колебания
в двух взаимно перпендикулярных плоскостях . Таким образом,
Учитывая, что k c , определим число стоячих волн в полости с частотами,
которые не превышают заданного значения :
3
После дифференцирования по частоте,
найдем число стоячих волн в полости
в интервале частот от до d :
2
dN V 2 3 d
c
N
3 c
2 3
V
В классической физике стоячая электромагнитная волна рассматривается как
объект с двумя степенями свободы, одна из которых – колебания электрического
поля, другая – колебания магнитного поля. Согласно закону о равномерном
распределении энергии по степеням свободы для равновесного теплового
излучения при температуре T на каждую стоячую электромагнитную волну частоты
приходится в среднем энергия, равная kБT 2 .
2
dN
k
T
Б
Тогда для плотности энергии получим
dW
k T d , где
dW w( , T ) d ,
2
w( , T ) 2 3 k БT
c
V
2 c 3
Б
Формула Рэлея – Джинса для
равновесного теплового излучения

26.

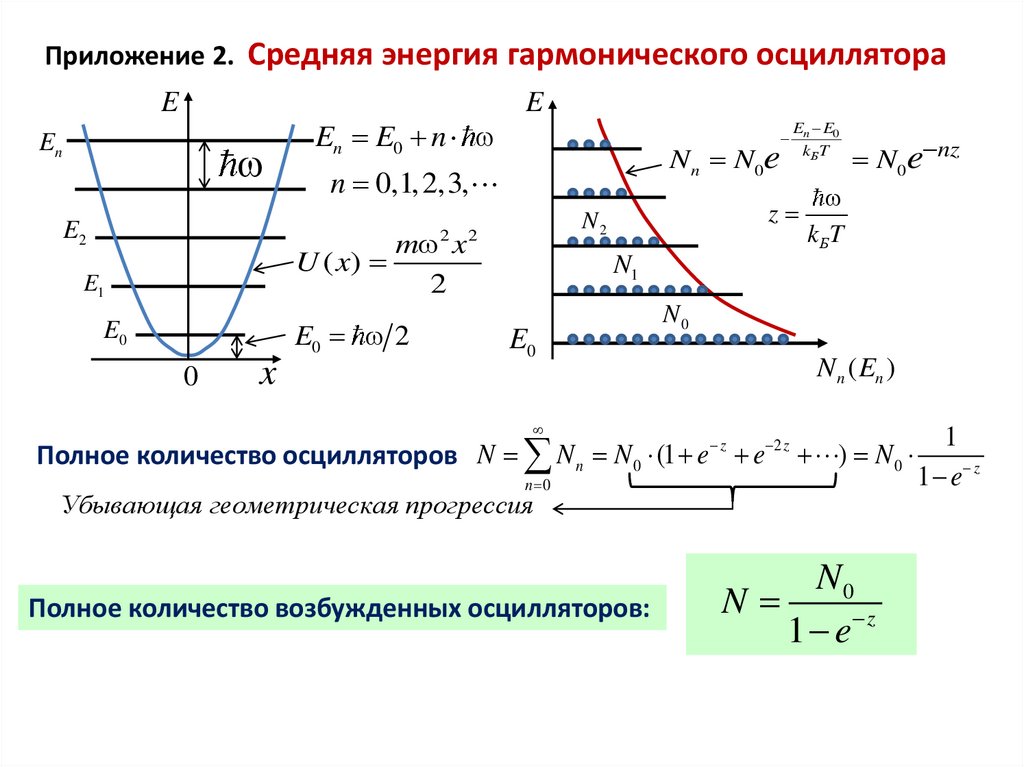
Приложение 2. Средняя энергия гармонического осциллятора
E
En
E2
En E0 n
m x
2
E0 2
E0
0
x
N n N0e
n 0,1, 2,3,
U ( x)
E1
E
2
En E0
kБ T
z
N2
2
N0e nz
kБT
N1
E0
N0
N n ( En )
Полное количество осцилляторов N N n N 0 (1 e z e 2 z ) N 0
n 0
Убывающая геометрическая прогрессия
Полное количество возбужденных осцилляторов:
N0
N
1 e z
1
1 e z

27.

Полная энергия возбужденных осцилляторов
Только возбужденные осцилляторы дают вклад в энергию излучения частоты
Найдем их полную энергию.
.
Eвозб E NE0 N1 N2 Nn
N0
N0e nz N 0e nz N
z
z
1
e
z
n 0
z n
После дифференцирования получаем Eвозб
N0e z
1 e
z 2
N
ez 1
В среднем на один осциллятор приходится энергия возбуждения, равная
Eвозб N .
Таким образом,
e
kБ T
1
z
kБT z
e 1
2
w( , T ) 2 3
и формула М.Планка
c
e
kT
1

28.

Приложение 3. Вклад низкочастотных и высокочастотных осцилляторов
в энергию теплового излучения (предельные случаи).
1. Высокочастотные осцилляторы: kБT .
На рисунке показано распределение Больцмана для осцилляторов
по энергетическим состояниям(красная кривая) . Число осцилляторов
условно указано точками на каждом уровне энергии. E
Полное число
осцилляторов
N
N0
1 e
Число возбужденных
осцилляторов
N
возб
N0 (1 e
kБ T
N N0
N0e
kБ T
kБ T
)
E1
Распределение
Больцмана
N n N0e
N0
En E0
kБ T
Почти все осцилляторы находятся в
kБT
E
0
невозбужденном (основном) состоянии E0 .
Для перехода осцилляторов даже в первое
возбужденное состояние E1 требуется большая энергия , поэтому такие
переходы маловероятны и происходят весьма редко. Доля возбужденных
осцилляторов с ростом частоты резко падает, их вклад в тепловое излучение
становится незначительным.
e
kБ T
1
e
kБT
w( , T )
3 kБT (Распределение В. Вина
e
2 3
c
1893 г.)

29.

2. Низкочастотные осцилляторы:
kБT , z k БT
1 , ez
1 z
2
Из формулы М.Планка следует формула Рэлея – Джинса: w( , T ) 2 3 k Б T .
c
Эта формула получена в рамках классической физики
с использованием закона равномерного распределения
энергии по степеням свободы.
В предельном случае, когда
осцилляторов
N0
N
1 e z
kБT
, полное число
kБT
N0
kБT
N0
В этих условиях почти все осцилляторы возбуждены и примерно равномерно
распределены по возбужденным состояниям ( см. рисунок). Дискретность энергии
и квантовые свойства заметно не проявляются.

30.

Приложение 4. Вывод формулы Планка для теплового излучения АЧТ,
используя три процесса взаимодействия фотонов с атомами.
Исходные положения
Макс Планк, убежденный сторонник классической физики, считал что природа
не терпит скачков, но пришел к выводу, что единственная возможность объяснить
свойства теплового излучения – это предположить, что частицы вещества,
излучающие электромагнитные волны с частотой , могут изменять свою
энергию только скачкообразно, дискретными порциями .
В 1905 г А. Эйнштейн исследует флуктуации энергии излучения.
Он обнаружил, что флуктуации энергии точно такие же, как если бы излучение
частоты представляло газ частиц с энергией .
Эйнштейн формулирует гипотезу:
Свет (излучение) испускается, поглощается квантами
H
и распространяется пространстве в виде потока квантов
энергии (световых частиц- фотонов).
Энергия электронов в атомах может принимать
только ряд, дискретных значений (квантуется).
He
О квантовании энергии свидетельствуют , например,
линейчатые спектры излучения атомов.
При самопроизвольном (спонтанном )переходе атома из состояния с энергией
En в состояние с энергией Em с излучением фотона соблюдается закон
сохранения энергии : En Em , где энергия фотона.

31.

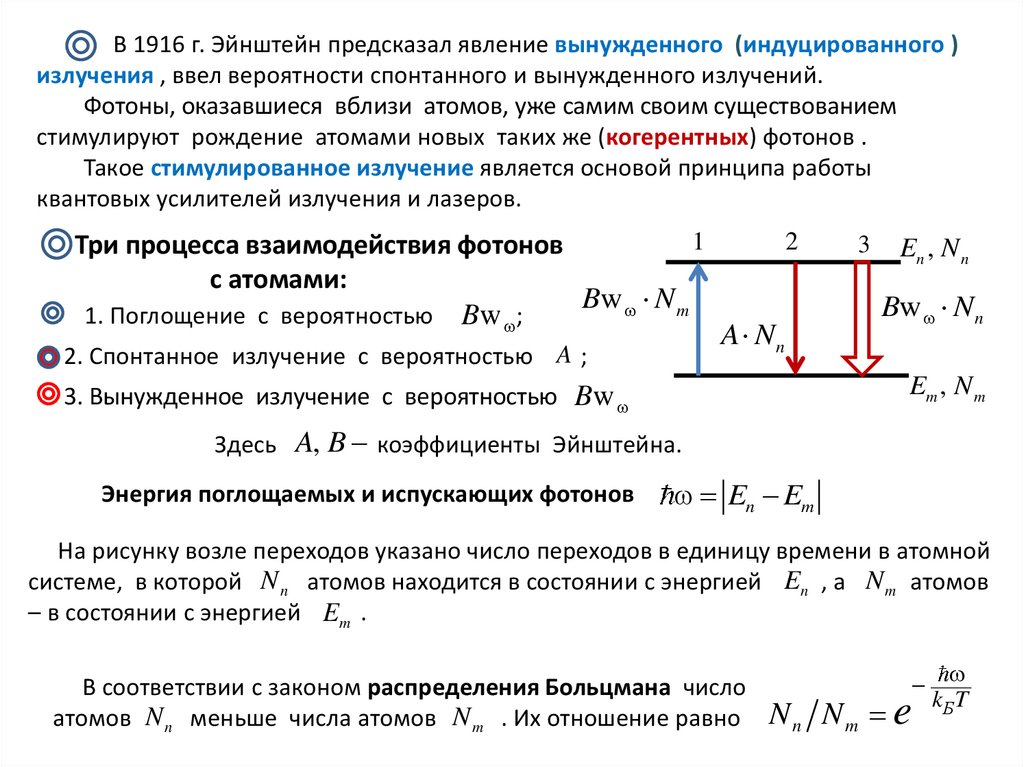
В 1916 г. Эйнштейн предсказал явление вынужденного (индуцированного )
излучения , ввел вероятности спонтанного и вынужденного излучений.
Фотоны, оказавшиеся вблизи атомов, уже самим своим существованием
стимулируют рождение атомами новых таких же (когерентных) фотонов .
Такое стимулированное излучение является основой принципа работы
квантовых усилителей излучения и лазеров.
1
Три процесса взаимодействия фотонов
с атомами:
Bw N m
1. Поглощение с вероятностью Bw ;
2. Спонтанное излучение с вероятностью A ;
2
A Nn
3
En , N n
Bw Nn
Em , N m
3. Вынужденное излучение с вероятностью Bw
Здесь A, B коэффициенты Эйнштейна.
Энергия поглощаемых и испускающих фотонов
En Em
На рисунку возле переходов указано число переходов в единицу времени в атомной
системе, в которой N n атомов находится в состоянии с энергией En , а N m атомов
– в состоянии с энергией Em .
В соответствии с законом распределения Больцмана число
атомов N n меньше числа атомов N m . Их отношение равно
Nn Nm e
kБ T

32.

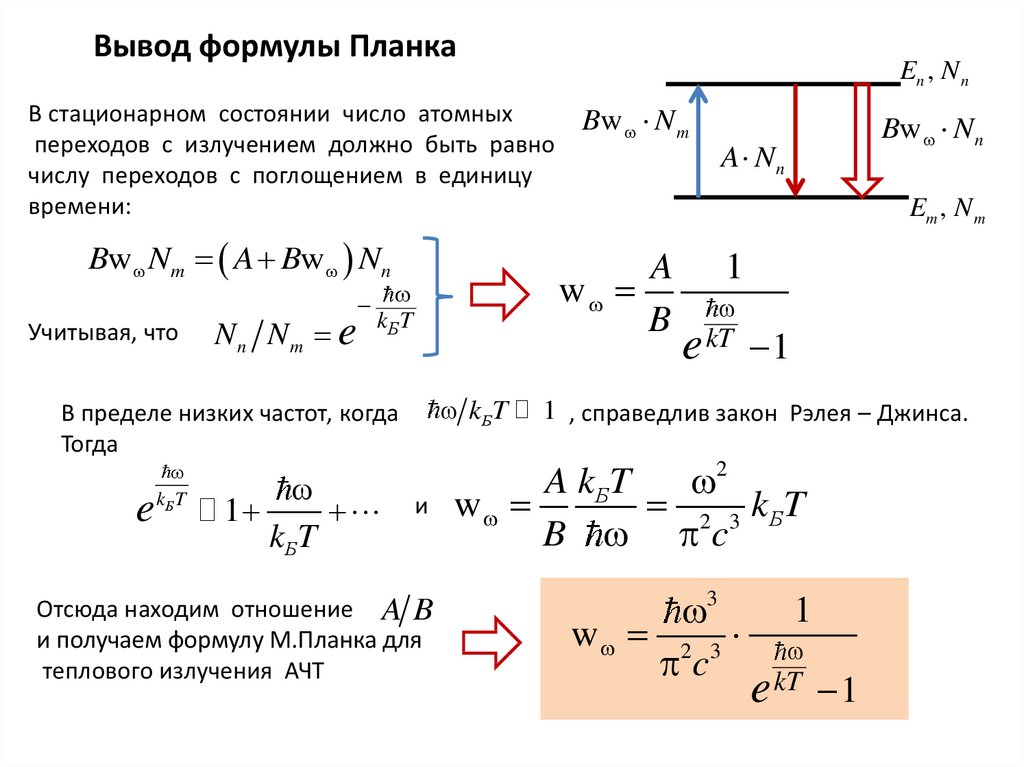
Вывод формулы Планка
En , N n
В стационарном состоянии число атомных
переходов с излучением должно быть равно
числу переходов с поглощением в единицу
времени:
Bw Nm A Bw Nn
Учитывая, что
Nn Nm e
kБ T
kБT
e
1
kБT
и
Отсюда находим отношение A B
и получаем формулу М.Планка для
теплового излучения АЧТ
Bw Nn
A Nn
Em , N m
A
w
B
В пределе низких частот, когда
Тогда
kБ T
Bw N m
1
e
kT
1
1 , справедлив закон Рэлея – Джинса.
A kБT
2
w
2 3 kБT
B c
3
w 2 3
c
1
e
kT
1