Похожие презентации:
Тепловое излучение. Равновесное излучение
1.
2.
Тепловоеизлучение
–
это
излучение,
осуществляемое за счет внутренней энергии тела.
Тепловое излучение – особый вид излучения,
которое обладает следующими свойствами:
Тепловое излучение равновесное.
Понятие равновесия предполагает равновесие
между излучением и излучающим телом.
Все хорошо поглощающие тела излучают в
одинаковом спектральном интервале при данной
температуре, то есть спектр излучения таких тел
одинаковый.
Равновесие носит динамический характер. То
есть процесс излучения и поглощения идет
непрерывно.
3. Равновесное излучение
Рассмотрим полость, температурастенок которой поддерживается
постоянной.
В начальный период времени полость
будет заполнена излучением с
характерным для материала полости
спектром.
За счет частичного поглощения, за счет
хаотического теплового движения, атомы полости переходят в
возбужденное состояние и излучают. При этом происходит изменение
интенсивности, спектрального состава, состояния поляризации света.
Система постепенно переходит в состояние равновесия, которому
соответствует наибольшая вероятность. Это излучение
называется равновесным
4.
Спектральный состав и другие характеристики независят от свойств материала стенок полости (и тел
внутри нее), а определяются только температурой
стенок
Излучение также можно характеризовать этой
температурой и считать ее свойством самого
излучения, которое также называется тепловым.
Только тепловое излучение может быть равновесным.
5.
Интенсивность теплового излучениявозрастает при повышении температуры.
При нарушении равновесия между телом и
излучением, тело либо поглощает больше,
чем излучает (т.е. нагревается),
либо излучает, за счет убыли внутренней
энергии (охлаждается).
05
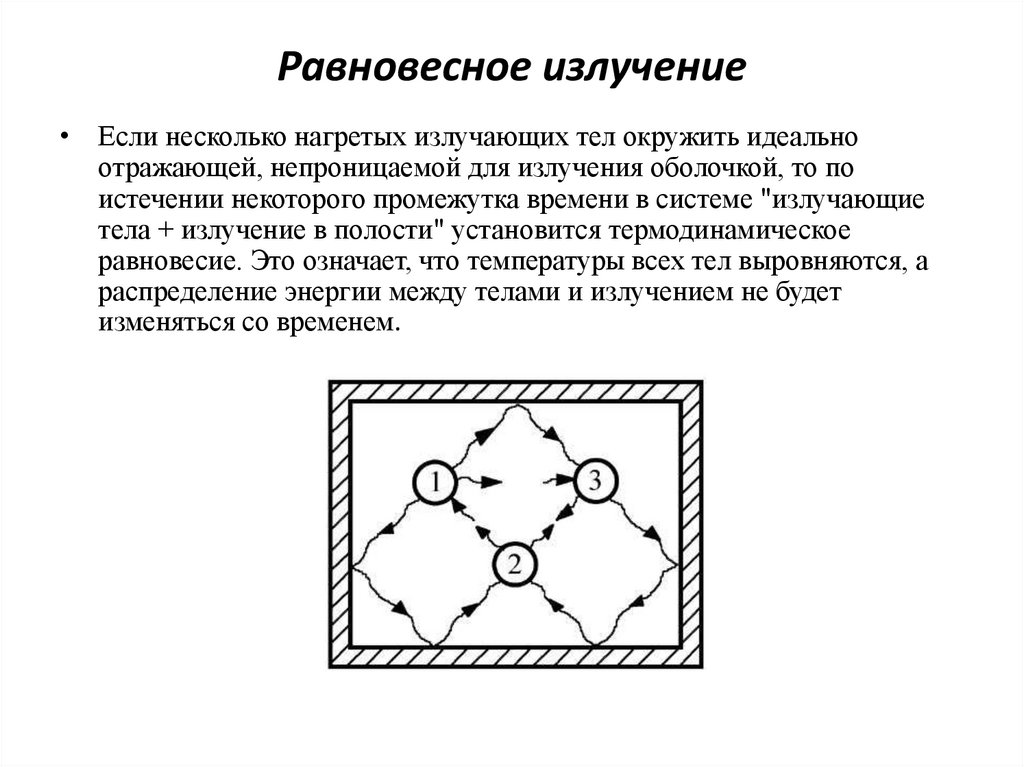
6. Равновесное излучение
• Если несколько нагретых излучающих тел окружить идеальноотражающей, непроницаемой для излучения оболочкой, то по
истечении некоторого промежутка времени в системе "излучающие
тела + излучение в полости" установится термодинамическое
равновесие. Это означает, что температуры всех тел выровняются, а
распределение энергии между телами и излучением не будет
изменяться со временем.
7.
Количественные характеристикитеплового излучения:
Световой поток Ф – энергия, излучаемая всей
поверхностью нагретого тела в единицу времени.
Энергетическая светимость R определяется потоком
излучаемой энергии, отнесенным к поверхности
излучающего тела, то есть энергией, излучаемой
единицей поверхности тела в единицу времени по
всем направлениям.
8.
• Энергетическая светимость тела для различныхинтервалов различна и пропорциональна этим
интервалам.
dR r , d
r , - испускательная способность тела.
9.
Энергетическая светимость зависит толькоот
температуры.
Испускательная
способность зависит не только от
температуры, но и от частоты.
R r , d - полная энергетическая
0
светимость тела.
Перейдем от частотного интервала к
интервалу длин волн:
10.
11.
d d2 2 c
2 c
d 2 d
Так как d и d относятся к одному и
тому же интервалу, то энергетическая
светимость остается величиной постоянной.
12.
r , d r , dr ,
r ,
2 c
2 c
r , 2 d r , d
2
f ( , )
( , )
2 c
2
13.
Помимоиспускательной
способности
тело
характеризуется поглощательной способностью.
d
a ,
, где
d
d - поток, поглощенный телом,
d - поток, падающий на тело.
Существуют тела, которые поглощают все
падающее на них излучение. Такие тела были
названы абсолютно черными.
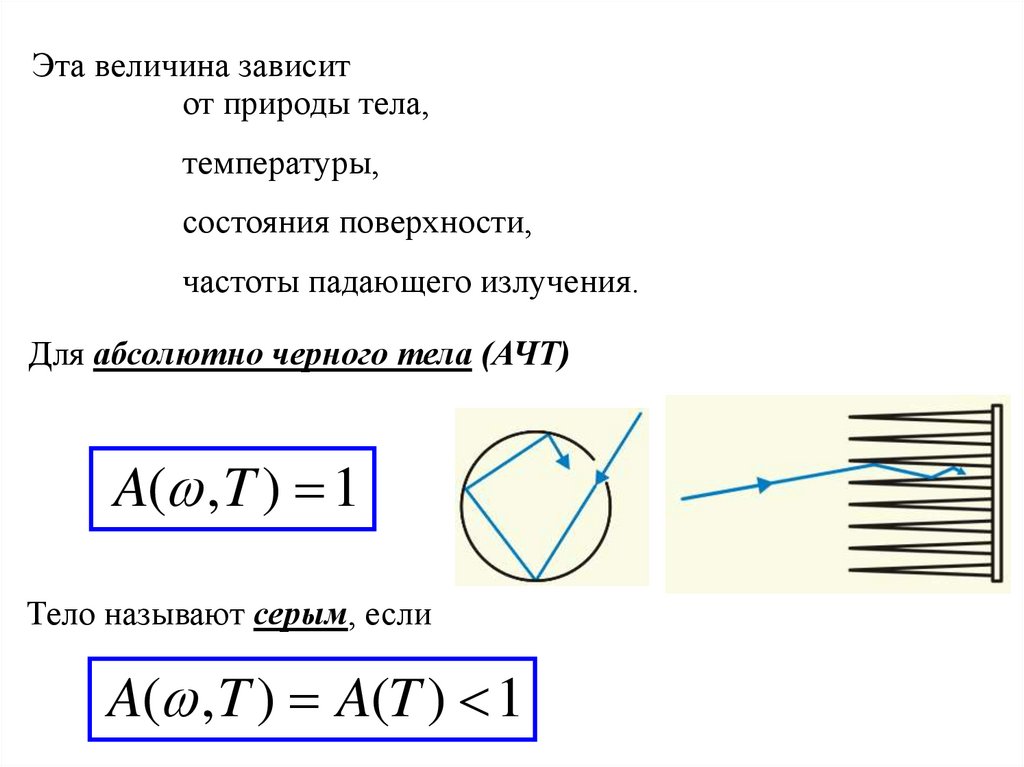
14.
Эта величина зависитот природы тела,
температуры,
состояния поверхности,
частоты падающего излучения.
Для абсолютно черного тела (АЧТ)
A( , T ) 1
Тело называют серым, если
A( , T ) A(T ) 1
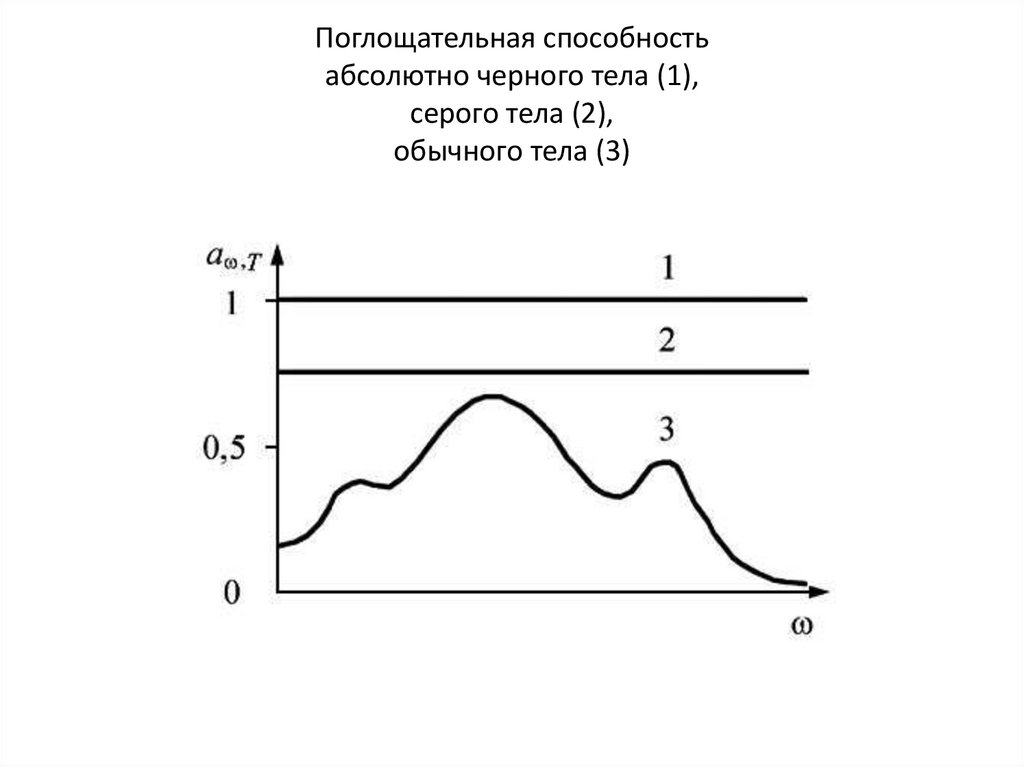
15. Поглощательная способность абсолютно черного тела (1), серого тела (2), обычного тела (3)
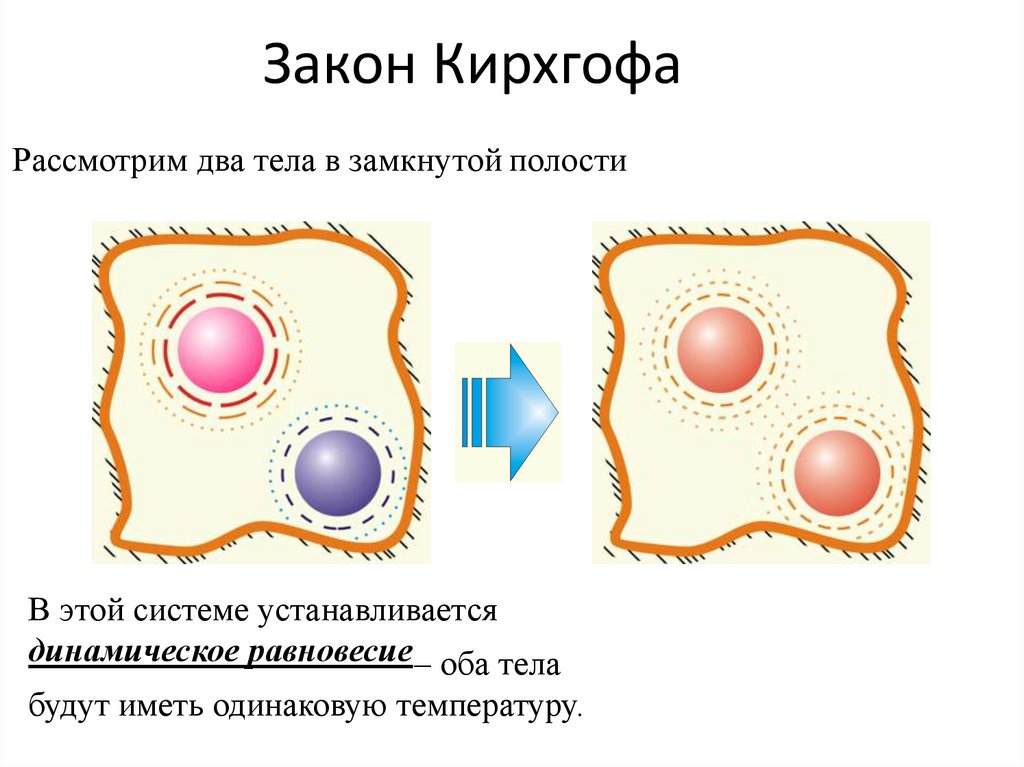
16. Закон Кирхгофа
Рассмотрим два тела в замкнутой полостиВ этой системе устанавливается
динамическое равновесие – оба тела
будут иметь одинаковую температуру.
17.
Если тело обладает большей излучательной способностью, тооно теряет на излучение больше энергии и, для поддержания
температуры, такое тело должно больше поглощать.
r ( , T )
f ( , T )
A( , T )
r ,
r ,
(
)1тела (
)2 тела
a ,
a ,
Кирхгоф, 1859
r ,
(
) f ( , )
a ,
f ( , T ) – универсальная функция Кирхгофа или
испускательная способность абсолютно черного тела.
18.
Закон Стефана-Больцмана:R r , d
4
0
• Энергетическая светимость абсолютно черного
тела пропорциональна четвертой степени
абсолютной температуры.
• 5,7 10 8 Вт - постоянная Больцмана
м2 К 4
Позволяет вычислить энергию излучения по известной
температуре.
Недостаток- не дает информации о спектральном составе
излучения.
19.
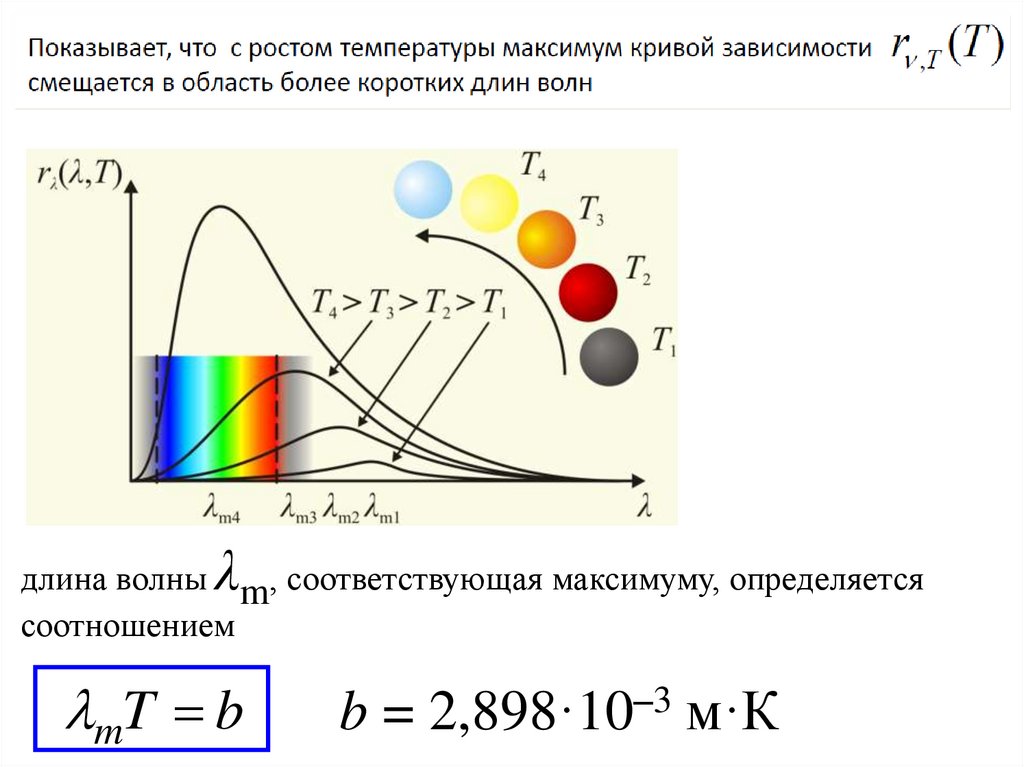
Закон смещения ВинаИсследуя излучение абсолютно черного тела,
Вин показал, что универсальная функция
Кирхгофа, выраженная через длину волны
должна иметь вид
c5
( , ) 5 ( )
Исследуя функцию ( , ) на экстремум, Вин
пришел к следующему закону:
max b
0
b 2,90 10 A K - постоянная Вина.
7
20.
λдлина волны m, соответствующая максимуму, определяется
соотношением
mT b
b = 2,898·10–3 м·К
21.
Объяснить особенности теплового излучения наоснове классической физики пытались Рэлей и
Джинс. Они в качестве модели абсолютно черного
тела использовали полость. В результате
многократного отражения от стенок полости,
внутри нее образуются стоячие волны. Их число,
возникающее в единице объема:
2 d
dn
2 3
2 c
2
22.
• Согласно закону равнораспределения энергии накаждую стоячую волну приходится энергия,
равная kT .
1
1
k ( k ) электрическая ( k ) магнитная
2
2
составляющая
составляющая
23.
Энергетическая светимость определяется энергией,испущенной единицей поверхности в единицу
времени. Если эту энергию отнести к единице объема,
то получим новую функцию, которая называется
плотностью энергии излучения. Между этими
величинами существует простая связь
c
RT U T
4
24.
• Подобно тому, как энергетическая светимостьразлична для разных частотных интервалов,
различна и энергетическая плотность. Для
частотного интервала :
dRT r ,T d ;
dU T u ,T d ;
c
r ,T u ,T
4
25.
Соответствующаяплотность
абсолютно черного тела:
энергии
d
u , d dn kT 2 3
c
2
2k
2
u ,
T ;
2 3
2 c
c
kT
2
r , u ,T
2 2
4
4 c
Формула Рэлея – Джинса
f ( , T )
kT
2 2
4 c
2
26.
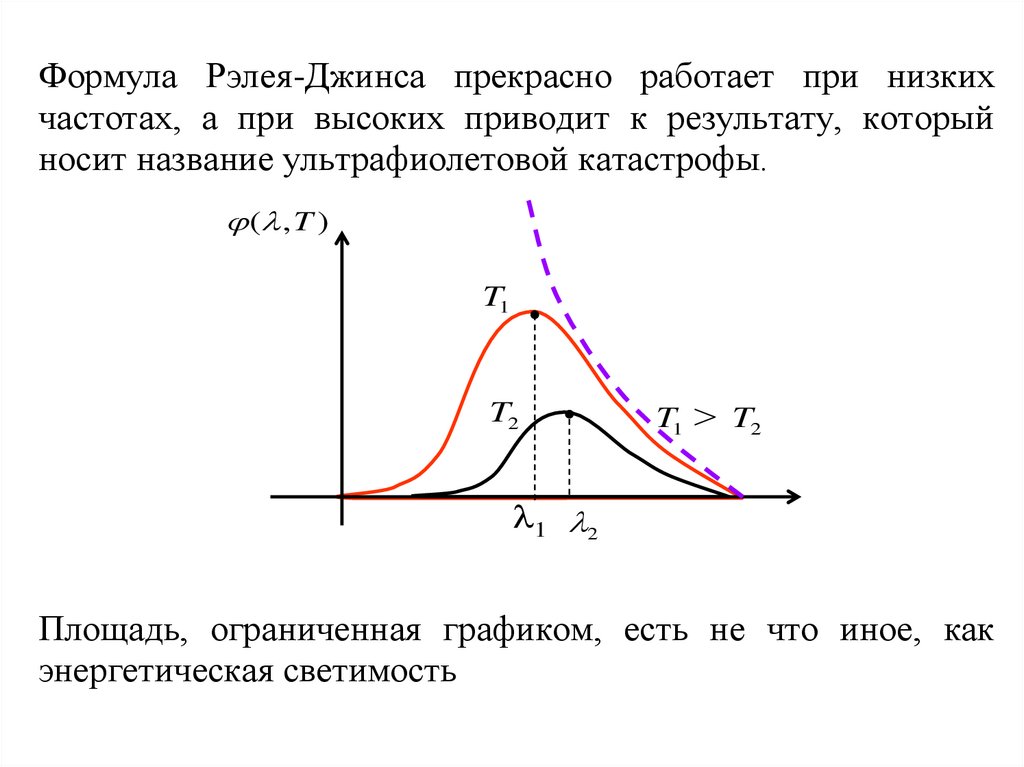
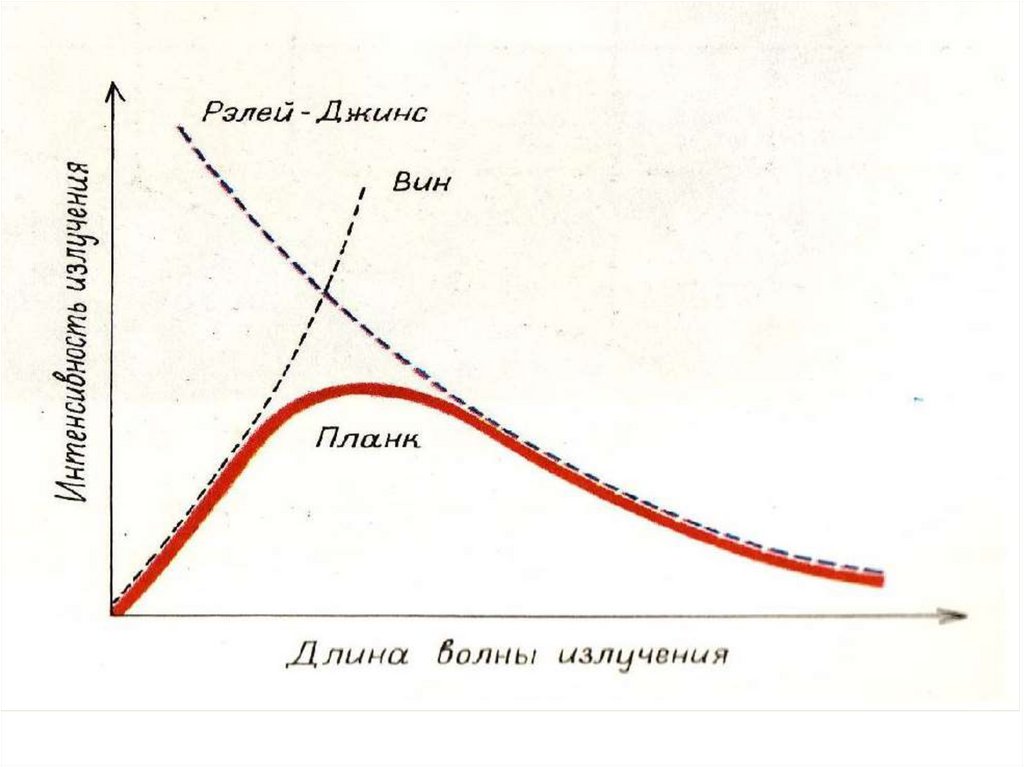
Формула Рэлея-Джинса прекрасно работает при низкихчастотах, а при высоких приводит к результату, который
носит название ультрафиолетовой катастрофы.
( , T )
T1
T2
T1 T2
1 2
Площадь, ограниченная графиком, есть не что иное, как
энергетическая светимость
27.
Однако,f
(
,
T
)
d
, а не к
0
и полученное выражение не описывает
1) равновесие между
телом и излучением
2) уменьшение спектральной
плотности для высоких частот
T
4
28.
29.
Теория ПланкаРассматриваем вещество стенок полости как набор
осцилляторов, которые могут занимать лишь дискретный ряд
уровней
–
Em – m-й уровень
E1 – возбужденное состояние
– E0 – основное состояние
–
30.
• Рассматривая систему стоячих волн, Планк предположил,что энергия, излучаемая телом, должна быть
пропорциональна минимальной порции, то есть
n nh
Вероятность того, что будет испущена порция света с
энергией
, определяется
выражением:
nh n
Nn
Pn
N
Nn
- число
случаев,
результату.
N
- общее число случаев.
приводящих
к
данному
31.
• В состоянии равновесия распределение колебанийпо энергиям подчиняется закону Больцмана:
Nn
n
~ e kT
Для вероятности получим:
Pn
n
e kT
n
n
e kT
32.
Среднее значение энергии, приходящееся наодно нормальное колебание, то есть на одну
стоячую волну, определяется:
n Pn
n
n e
n
e
n
n
kT
n
kT
33.
Вводится замена:nx
x
e
n
n
n
kT
x
x(1 x)
x
2
1 x
(1 x)
n
e
x
n
n nx (1 x)2
1
n x 1 x
n
kT
1 e
kT
1
e
kT
1
34.
2 ddn
2 3
2 c
2
u ,T d dn
u ,T d
e kT 1
u ,T
d
2 3
c
2
3
2 c 3 (e kT 1)
3
r ,T f ( , T )
2 2
4 c
1
e
kT
1
35.
• Формула Планкаr ,T f ( , T )
2 2
4 c
3
1
e
kT
1
36.
В случаеДжинса:
kT
формула Планка переходит в формулу Рэлея-
3
1
kT
f ( , T ) 2 2
2 2 2
4 c 1 1 4 c
kT
Проверка закона Стефана-Больцмана:
3
d
RT r , d 2 2
4
4 c
0
0
e kT 1
Проверка закона Вина:
f ( , T ) перейдем к функции ( , T ) .
2
f ( , T )
( , T )
2 c
От функции
( , T )
2 c
2
(
2 c 3
)
1
2 c
4 2 c 2
kT
e
37.
Исследуем на максимум:d
0
d
Поучим трансцендентное уравнение
2 c
x
.
kT
Уравнение имеет решение при
xex 5(e x 1) 0 ,
2 c
4, 965,
kT m
max T b
Вывод:
Согласно гипотезе Планка, свет излучается порциями. Частица,
несущая порцию энергии, равную h , получила название фотона.
Постоянная Планка-это важнейшая универсальная константа,
играющая в квантовой физике такую же фундаментальную роль , как и
скорость света в теории относительности.










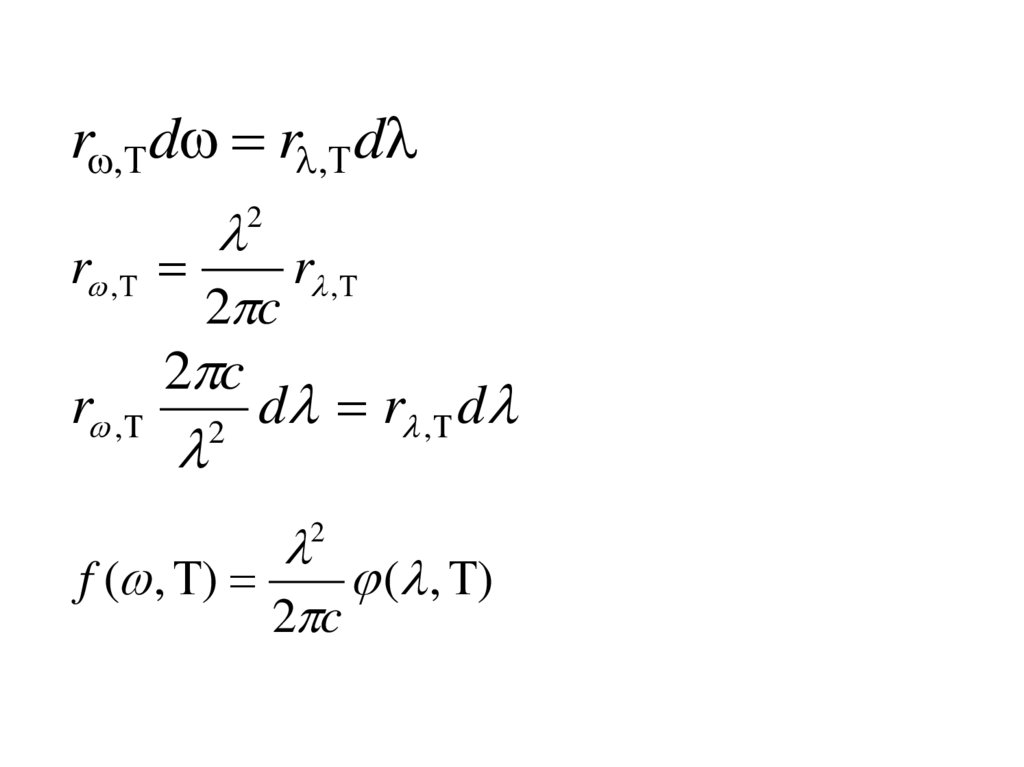















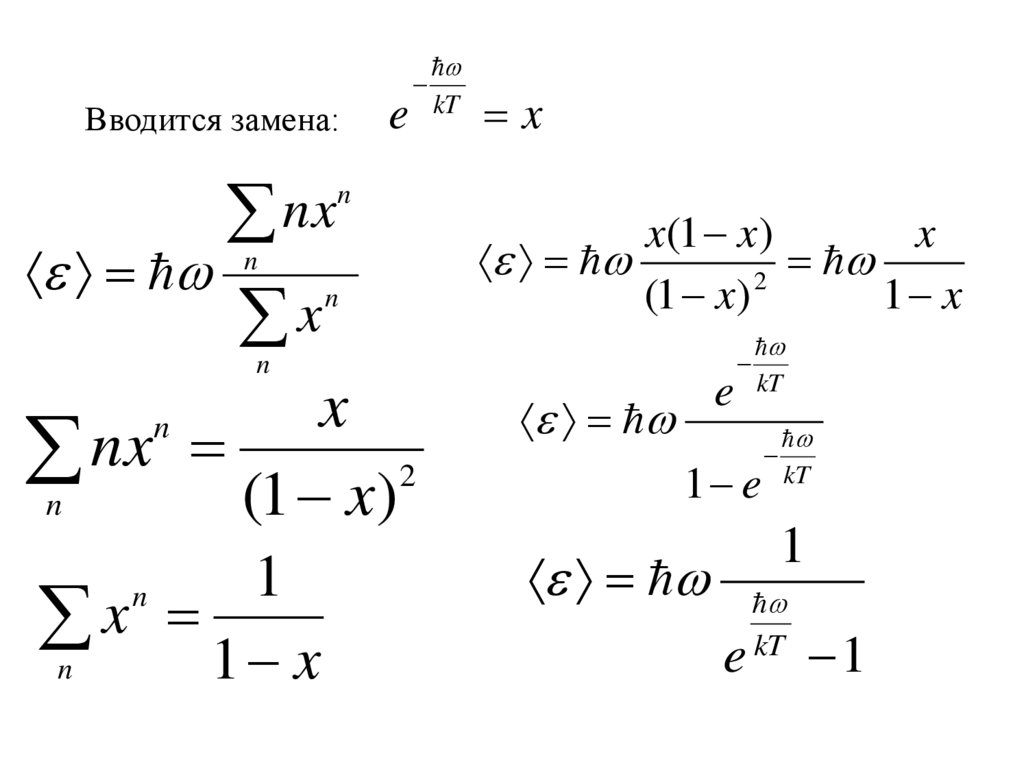
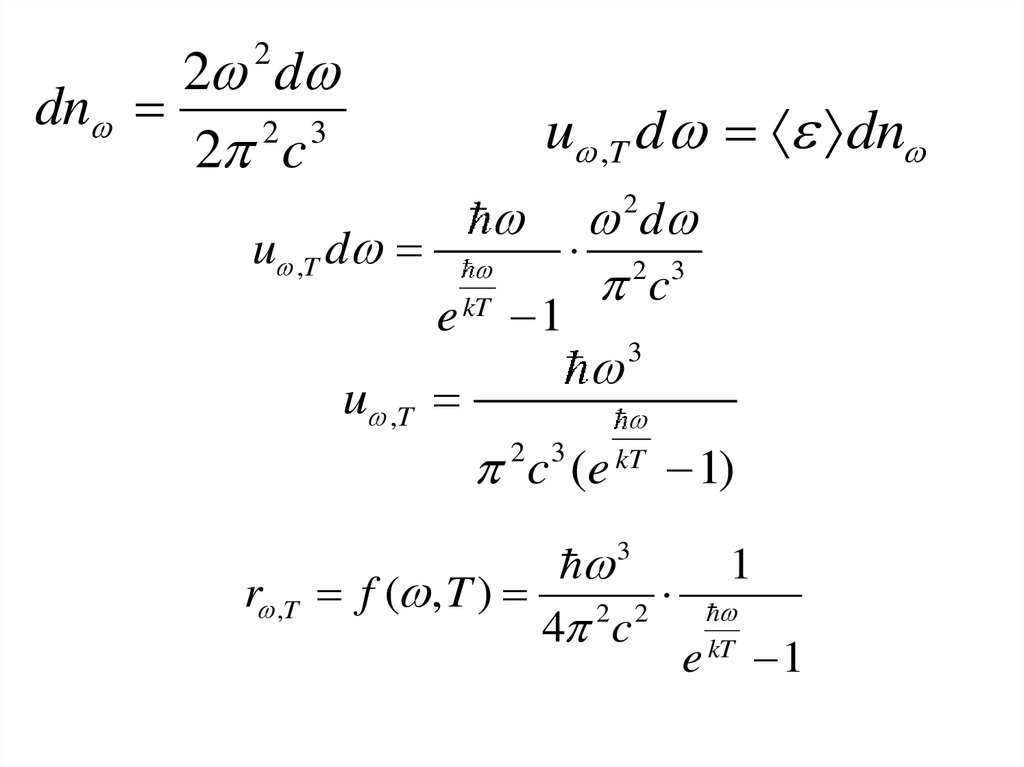



 Физика
Физика








