Похожие презентации:
Тепловое излучение
1. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
лекция 52. §§ Равновесное излучение
Рассмотрим полость,температура стенок
которой поддерживается
постоянной.
В начальный период
времени полость будет
заполнена излучением
с характерным для материала
полости спектром
02
3.
За счет частичного поглощения, за счетхаотического теплового движения,
атомы полости переходят в
возбужденное состояние и излучают.
При этом происходит изменение
интенсивности, спектрального состава,
состояния поляризации света.
Система постепенно переходит в
состояние равновесия, которому
соответствует наибольшая
вероятность.
Это излучение называется равновесным.
03
4.
Оно однородно, изотропно идеполяризовано.
Спектральный состав и другие характеристики не зависят от свойств материала
стенок полости (и тел внутри нее), а
определяются только температурой стенок
Излучение также можно характеризовать
этой температурой и считать ее свойством
самого излучения, которое также
называется тепловым.
Только тепловое излучение может быть
равновесным.
04
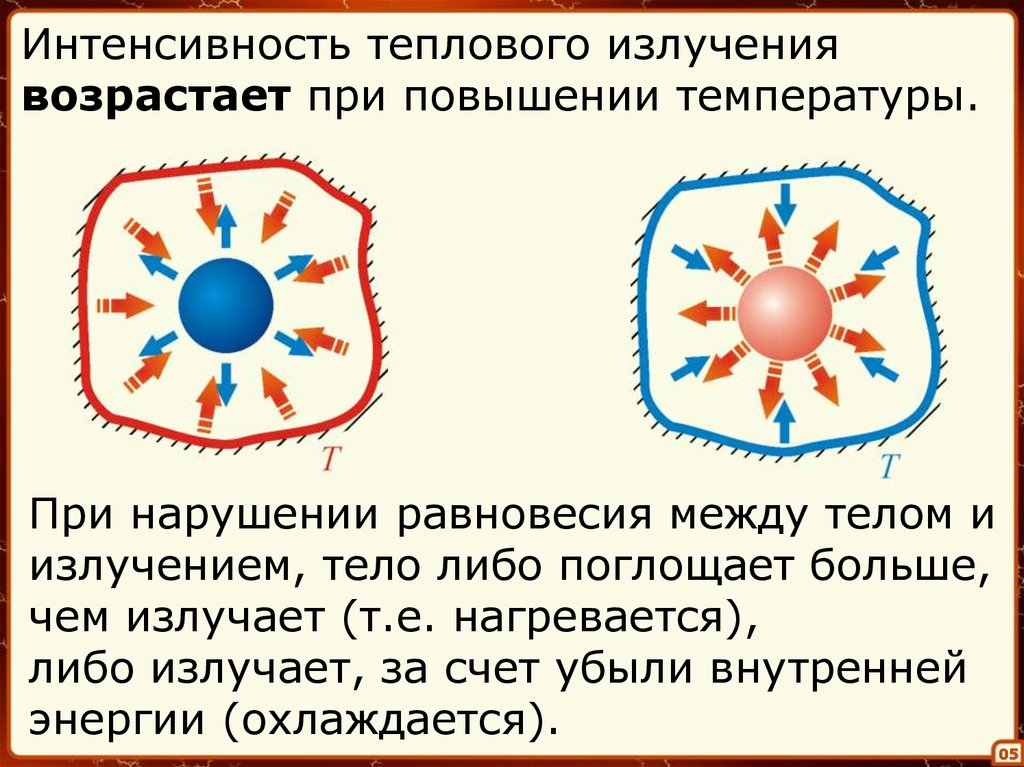
5.
Интенсивность теплового излучениявозрастает при повышении температуры.
При нарушении равновесия между телом и
излучением, тело либо поглощает больше,
чем излучает (т.е. нагревается),
либо излучает, за счет убыли внутренней
энергии (охлаждается).
05
6. §§ Характеристики излучения
Потоком (мощностью) излученияназывается количество энергии,
переносимой ЭМ волнами,
за единицу времени со всей
площади тела
W
t
Дж
[ ] 1
1 Вт
с
Это, например, та мощность, которую
указывают на лампе или нагревателе
06
7.
Энергетической светимостьюназывается величина, равная
мощности теплового излучения
с единицы площади тела.
R
S
[R] = 1 Вт/м2
Эти величины – интегральные,
т.е. учитывают энергию, переносимую
волнами всех частот (длин волн)
Рассмотрим спектры – распределение
энергии по частотам (по длинам волн)
07
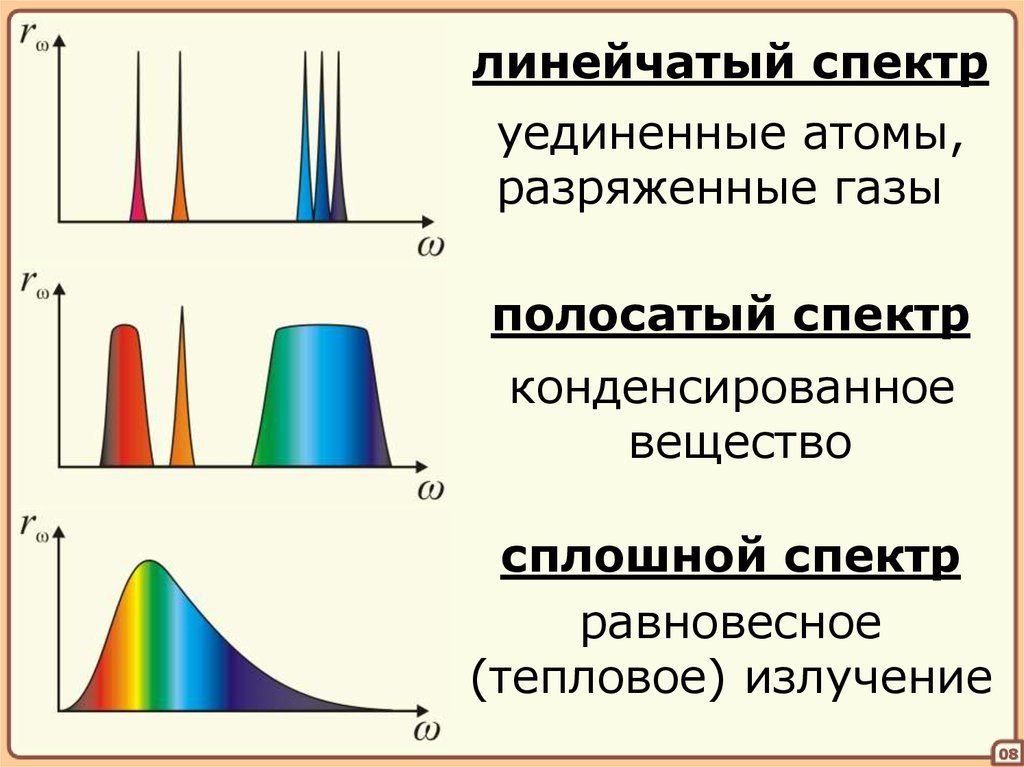
8.
линейчатый спектруединенные атомы,
разряженные газы
полосатый спектр
конденсированное
вещество
сплошной спектр
равновесное
(тепловое) излучение
08
9.
Испускательная способность –величина, равная спектральной
плотности энергетической светимости
Это энергия, излучаемая телом в
единицу времени с единицы площади
в единичном интервале длин волн
(частот)
dR r d
dR
r ( , T )
d
R (T ) r ( , T )d
0
d
09
10. §§ Поглощательная способность
Рассмотрим элементарную площадку иинтервал частот излучения [ω, ω + dω]
Пусть
d – падающий поток
d – поглощаемая мощность
тогда безразмерная величина
называется
d
A( , T )
1 поглощательной
d
способностью
10
11.
Эта величина зависитот природы тела,
температуры,
состояния поверхности,
частоты падающего излучения.
Для абсолютно черного тела (АЧТ)
A( , T ) 1
Тело называют серым, если
A( ,T ) A(T ) 1
11
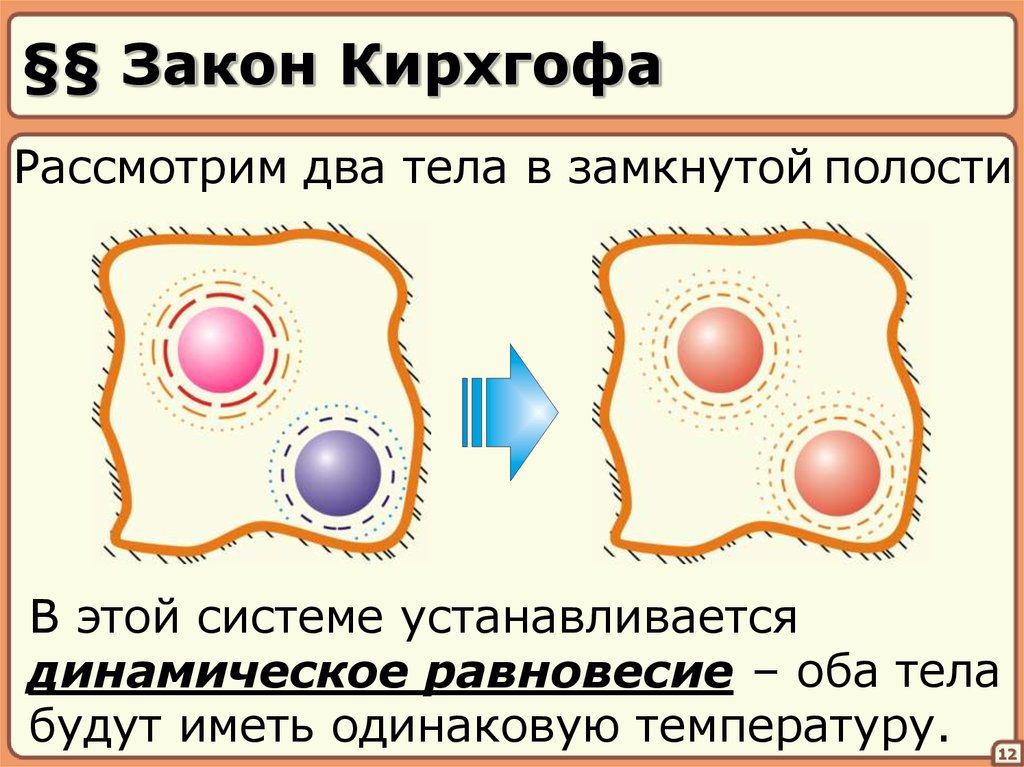
12. §§ Закон Кирхгофа
Рассмотрим два тела в замкнутой полостиВ этой системе устанавливается
динамическое равновесие – оба тела
будут иметь одинаковую температуру.
12
13.
Если тело обладает большейизлучательной способностью,
то оно теряет на излучение больше
энергии и, для поддержания
температуры, такое тело должно
больше поглощать.
r ( , T )
f ( , T )
A( , T )
Кирхгоф, 1859
f ( , T ) – универсальная функция
Кирхгофа или испускательная
способность абсолютно черного тела.
13
14. §§ Закон Стефана-Больцмана
Стефан, 1879, опытные данныеR const T – для любого тела
4
Больцман, 1884, теоретический расчет
R r ( , T )d T
0
4
– только для
АЧТ
8 Вт – постоянная
5,67 10 2 4
м К
Стефана–Больцмана
14
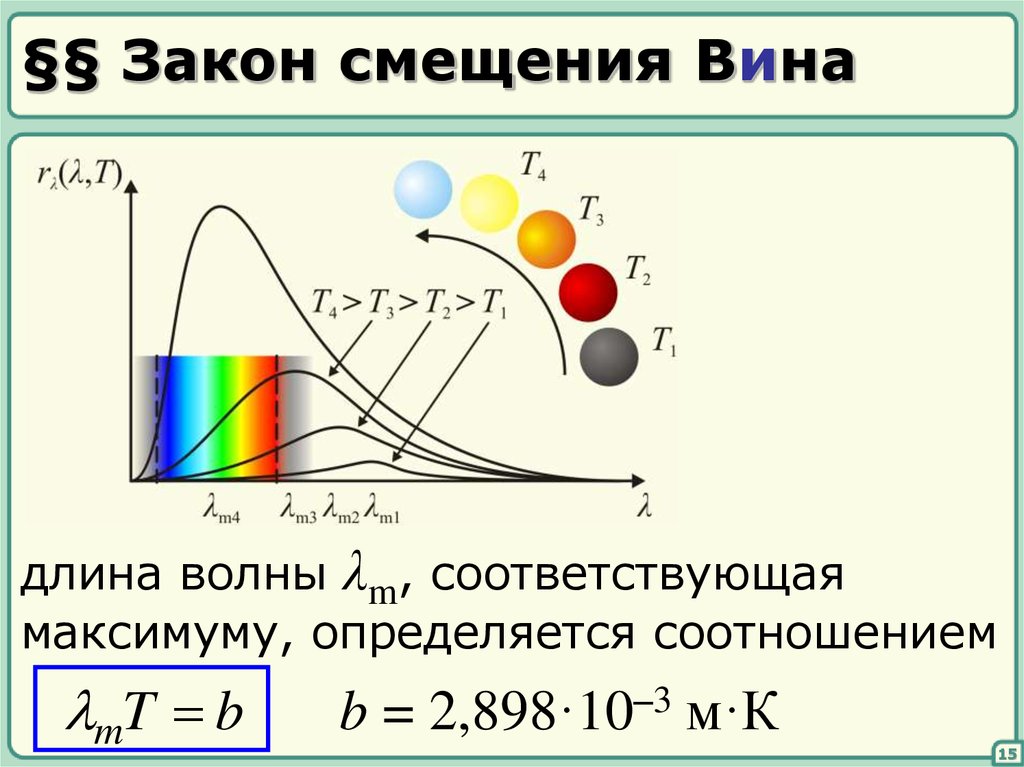
15. §§ Закон смещения Вина
длина волны λm, соответствующаямаксимуму, определяется соотношением
mT b
b = 2,898·10–3 м·К
15
16. §§ Формула Рэлея–Джинса
Рассмотрим, следуя Рэлею (1900) иДжинсу (1905), вывод выражения для
спектральной плотности излучения в
полости.
Пусть T const
Полная энергия теплового
(равновесного) излучения:
W W (T )
W
объемная плотность
U
U
(
T
)
энергии ЭМВ
V
16
17.
Энергия ЭМВ распределена почастотам неравномерно
U (T ) u ( , T )d
u ( , T )d
0
– энергия, приходящаяся на
интервал частот [ω, ω + dω]
Предположим, что равновесное
излучение в полости представляет собой
систему стоячих волн.
Пусть поверхность стенок – зеркальная,
а форма полости – параллелепипед
со сторонами a, b и c.
17
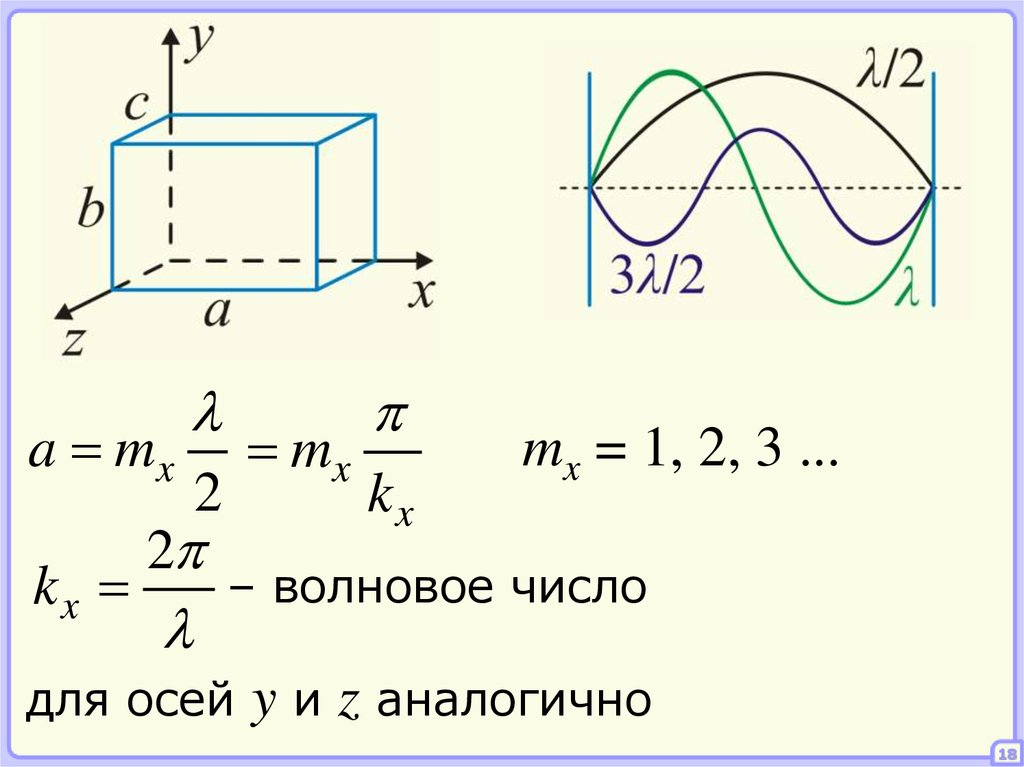
18.
a mxkx
2
2
mx
kx
mx = 1, 2, 3 ...
– волновое число
для осей
y и z аналогично
18
19.
k {k x , k y , k z } – волновой вектордля встречных волн: k , k
Модуль волнового вектора:
k
2
kx
2
ky
2
kz
2
c
mx m y mz
a
b
c
Каждой тройке mx , m y , mz соответствует
2
2
2
своя стоячая волна.
19
20.
Вычислим приблизительное число такихволн N в зависимости от k.
1 4 3
V0 k
8 3
– объем, занимаемый
всеми состояниями
в k-пространстве
V1
3
a b c
– объем одного состояния
20
21.
Число состоянийV0 a b c
V
N
2
3
2 3
V1
6
c
6 c
3
3
следовательно, число волн в интервале
[ω, ω + dω] равно
V
dN
dN
d 2 3 d
d
2 c
2
Учтем независимость двух состояний
поляризации (умножим на 2):
V
dN 2 3 d
c
2
21
22.
энергия, приходящаяся на интервалчастот [ω, ω + dω]
dN
u ( , T )d
,
V
– средняя энергия одного колебания
Из закона Больцмана следует, что на
каждую степень свободы приходится
одинаковая энергия ½kBT,
а на колебательную степень свободы –
энергия kBT.
22
23.
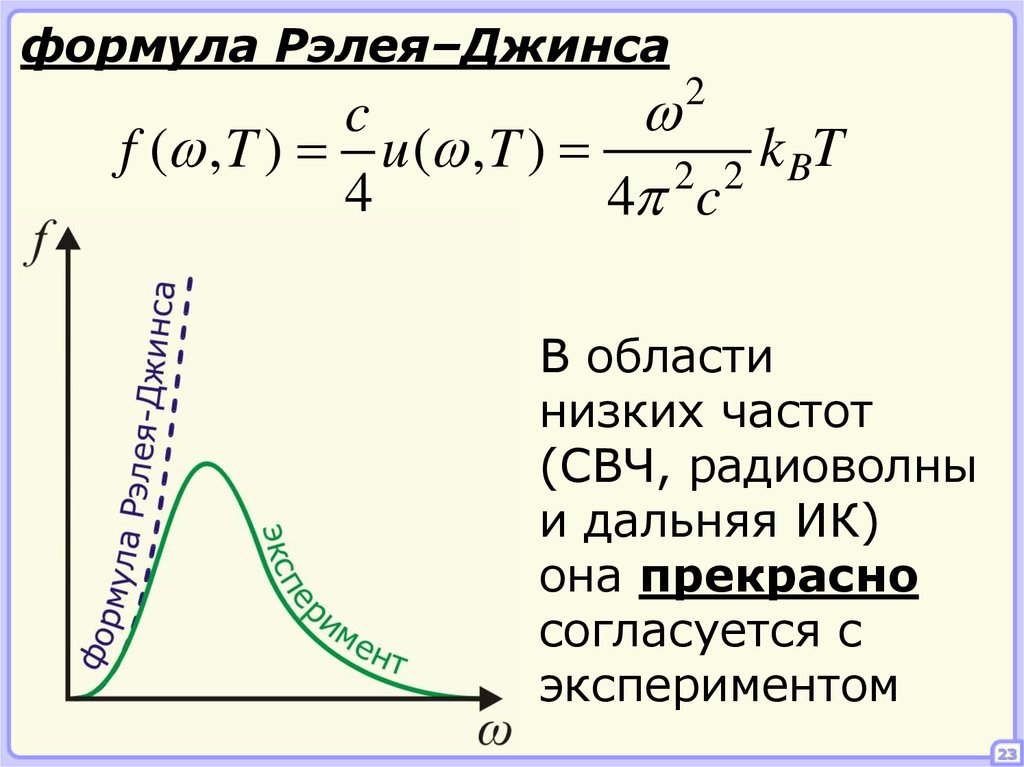
формула Рэлея–Джинсаc
f ( , T ) u ( , T ) 2 2 k BT
4
4 c
2
В области
низких частот
(СВЧ, радиоволны
и дальняя ИК)
она прекрасно
согласуется с
экспериментом
23
24.
Однако,f ( , T )d , а не к T
4
0
и полученное выражение не описывает
1) равновесие между
телом и излучением
2) уменьшение спектральной
плотности для высоких частот
24
25. §§ Формула Планка
Спектральная плотность энергетическойсветимости
f ( , T ) 2 2
4 c
2
где – средняя энергия на одну
степень свободы системы
(в данном случае – на одно колебание)
(закон Больцмана дает k BT и мы
приходим к формуле Рэлея–Джинса)
25
26.
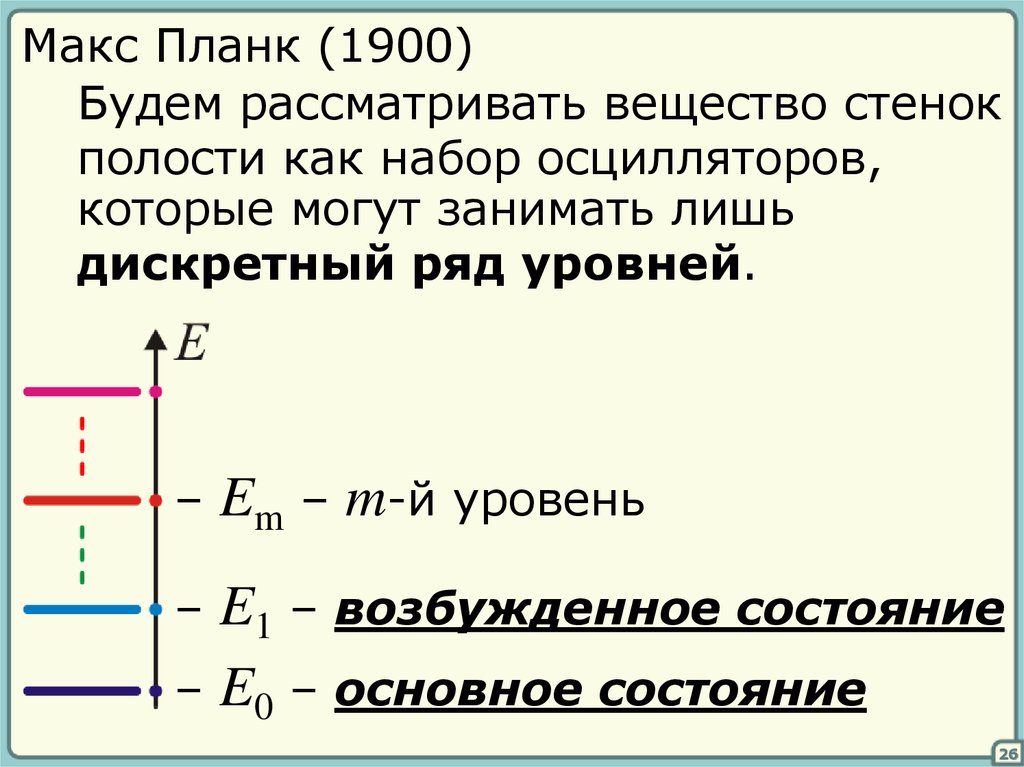
Макс Планк (1900)Будем рассматривать вещество стенок
полости как набор осцилляторов,
которые могут занимать лишь
дискретный ряд уровней.
–
Em – m-й уровень
–
E1 – возбужденное состояние
– E0 – основное состояние
26
27.
Пусть P(E) – вероятность того, чтосистема займет положение с энергией
(убывающая функция)
E
Обычно P ( E ) const exp
k BT
E
27
28.
Постоянную определяют из условияP( Em ) 1
m 0
получаем
1
const
Em
exp k T
B
m 0
Средняя энергия:
Em P( Em )
28
29.
Пусть уровни – «равноотстоящие», т.е.Em mE0
тогда
m exp(m )
,
E0
exp(m )
E0
k BT
Вычислим сумму
S ( )
2
exp(
m
)
1 q q ...
m 0
1 q (1 q q ...) 1 qS ( )
2
3
29
30.
11
S ( )
1 q 1 exp( )
dS
exp( )
m exp(m )
2
d
1 exp( )
Следовательно
exp( )
E0
1 exp( )
E0
E0
exp
k BT
1
30
31.
классический предельный случай E0k BT
0
Планк предположил, что E0 ≠ 0 и
определяется только свойствами
излучения
Пусть энергия поглощается/излучается
квантами (порциями) с энергией
E0 h
h 6,62 10
h
2
34
Дж·с – постоянная Планка
1,05 10
34
Дж·с (Поль Дирак)
31
32.
тогдаexp
1
k BT
f ( , T ) 2 2
4 c
2
формула Планка
3
4 c exp
k BT
2 2
1
32
33.
Формула Планка дает исчерпывающееописание свойств теплового излучения:
1) закон Стефана–Больцмана
f ( , T )d T
0
4
5,67 10
8
2) закон смещения Вина
max T b
b 2,9 10
3
3) описание спектра теплового
излучения во всем диапазоне
Дж
2
4
м ×К
м×К
λ
33
34. §§ Источники света
1) Солнцевне атмосферы
на земной
поверхности
i
Спектр излучения Солнца близок к
спектру АЧТ с T ≈ 6000 K (λm ≈ 0.47μ)
34
35.
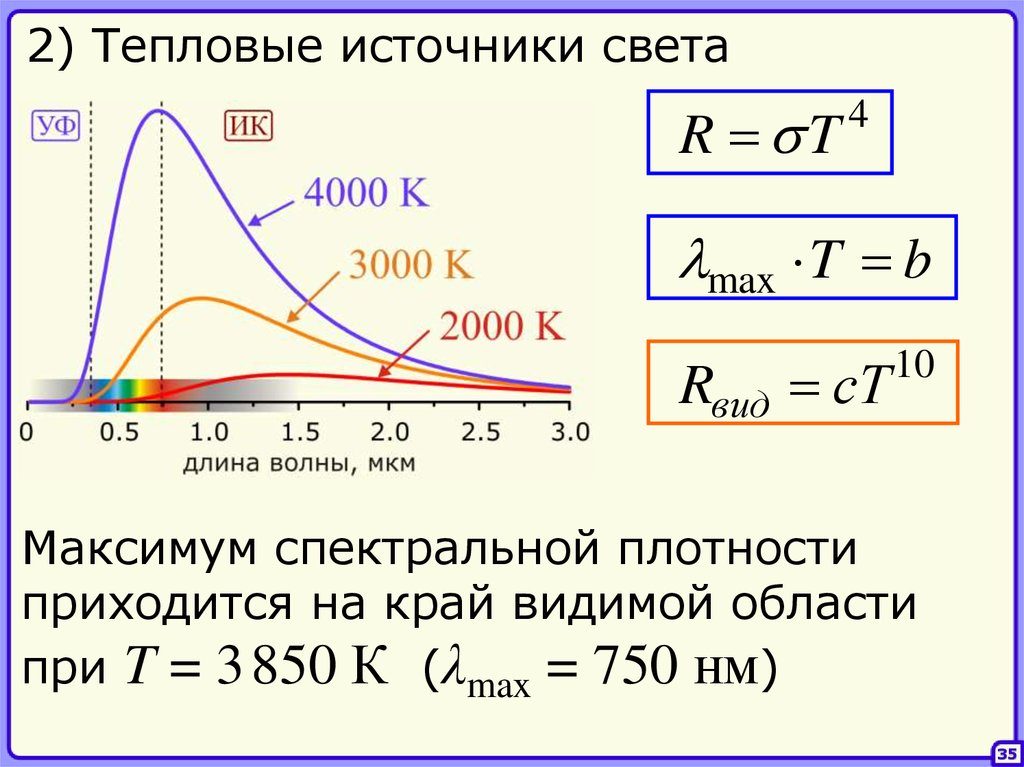
2) Тепловые источники светаR T
4
max T b
Rвид сT
10
Максимум спектральной плотности
приходится на край видимой области
при T = 3 850 К (λmax = 750 нм)
35
36.
Дейви (Davy, 1778-1829)в начале 19 в. изобрел
дуговую лампу
Лодыгин, 1872
T ~ 2200 К
η ~ 0.5 %
t ~ 500–1000 ч.
Гейссер в 1856 г. изобрел
флуоресцентную лампу
36
37.
1973 г., люминисцентныелампы
Пары ртути в инертном газе
(аргон, неон) испускают
ультрафиолет, который
вызывает свечение люминофора
Такие лампы потребляют в 5 раз меньше
энергии. Срок службы достигает 15000 ч.
37
38.
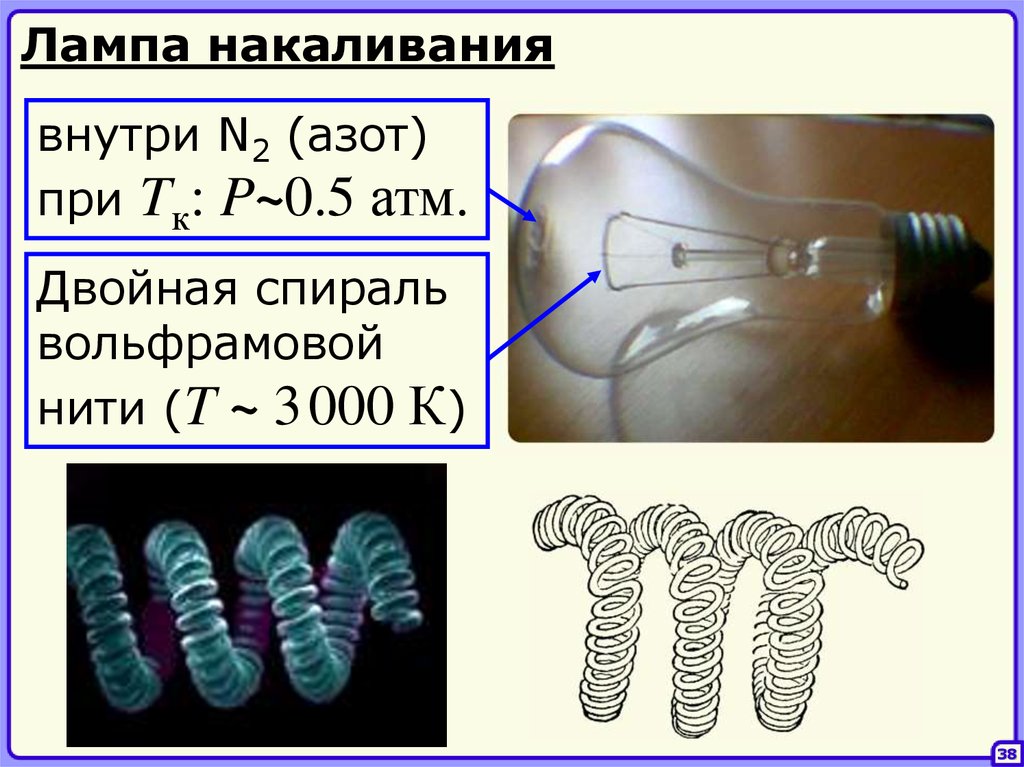
Лампа накаливаниявнутри N2 (азот)
при Tк: P~0.5 атм.
Двойная спираль
вольфрамовой
нити (T ~ 3 000 К)
38
39.
Излучение вольфрама не соответствуетизлучению АЧТ, что приводит к большей
светоотдаче.
срок службы:
500–1500 ч.
КПД не превышает 5 %
(у лучших источников не более
20 %)
Галогеновые лампы имеют
кварцевую колбу, а внутри –
инертный газ с добавками
галогенов , чтобы испаряющийся
вольфрам вновь осаждался на спирали
39
40.
«Ксеноновые» лампы – газоразрядныеисточники света
мощность:
75 Вт – 50 кВт
англ.:
HID
(High Intensity Discharge)
источником света является
электрическая дуга в газоразрядной
камере с инертными газами
Для их розжига нужен мощный разряд
— порядка 25 киловольт.
40
41. §§ Применение законов ТИ
1) ИК-сушка,нагрев
2) освещение
(при T ~ 6700
K
ηmax ~ 14 %
с учетом
спектральной
чувствительности
глаз)
41
42.
3) оптическая пирометрияа) закон Стефана–Больцмана
(радиационная пирометрия)
б) закон смещения Вина
(пирометр с исчезающей нитью)
в) цветовые пирометры
42





















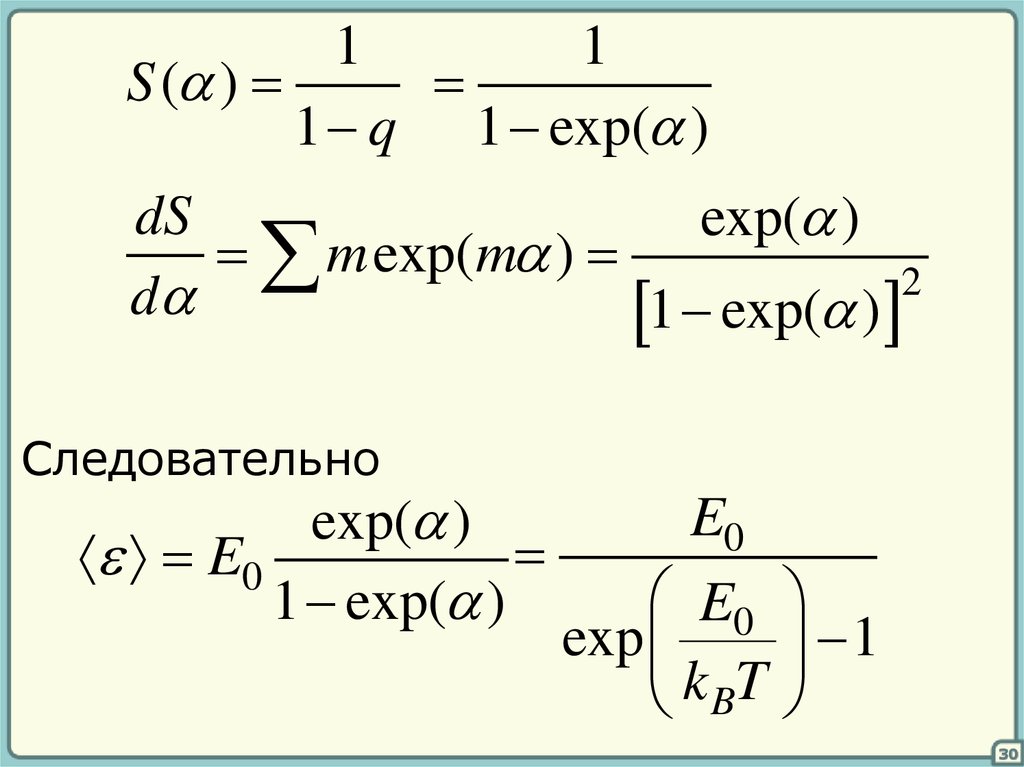









 Физика
Физика








