Похожие презентации:
Неразветвленные цепи однофазного тока. Лекция №3
1.
ЛЕКЦИЯ №3НЕРАЗВЕТВЛЕННЫЕ ЦЕПИ
ОДНОФАЗНОГО ТОКА
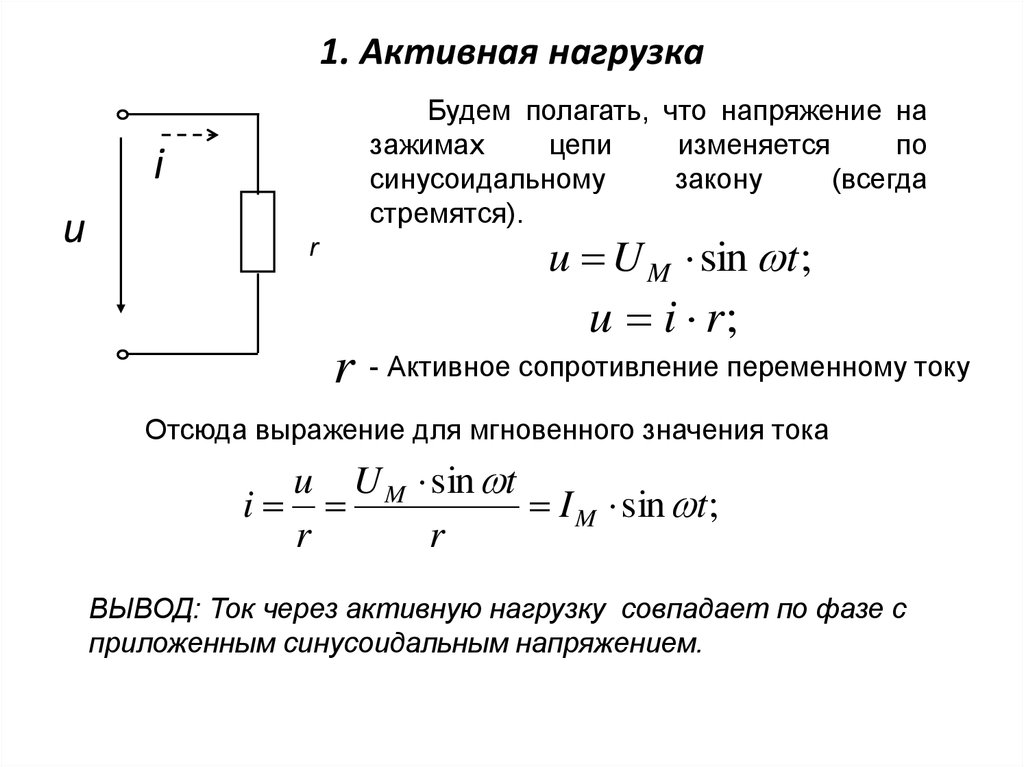
2. 1. Активная нагрузка
Будем полагать, что напряжение назажимах
цепи
изменяется
по
синусоидальному
закону
(всегда
стремятся).
i
u
r
u U M sin t ;
u i r;
r - Активное сопротивление переменному току
Отсюда выражение для мгновенного значения тока
u U M sin t
i
I M sin t;
r
r
ВЫВОД: Ток через активную нагрузку совпадает по фазе с
приложенным синусоидальным напряжением.
3.
IMUM
r
- амплитуда тока
Обычно левую и правую части делят на
2
и переходят к действующим значениям
U
I ;
r
– Закон Ома для цепи с активной нагрузкой
4. Мгновенная мощность
p u i U M sin t I M sin t U I (1 cos 2 t );1
sin sin cos( ) cos( )
2
1
1
cos( t t ) cos( t t ) 1 cos 2 t ;
2
2
ВЫВОД:
1) В цепи с активным сопротивлением мощность изменяется
по периодическому закону с двойной частотой относительно
приложенного напряжения.
2) Мощность всегда положительна. Это означает, что
поступающая от сети электроэнергия необратимо
преобразуется в другой вид энергии (в данном случае –в тепло)
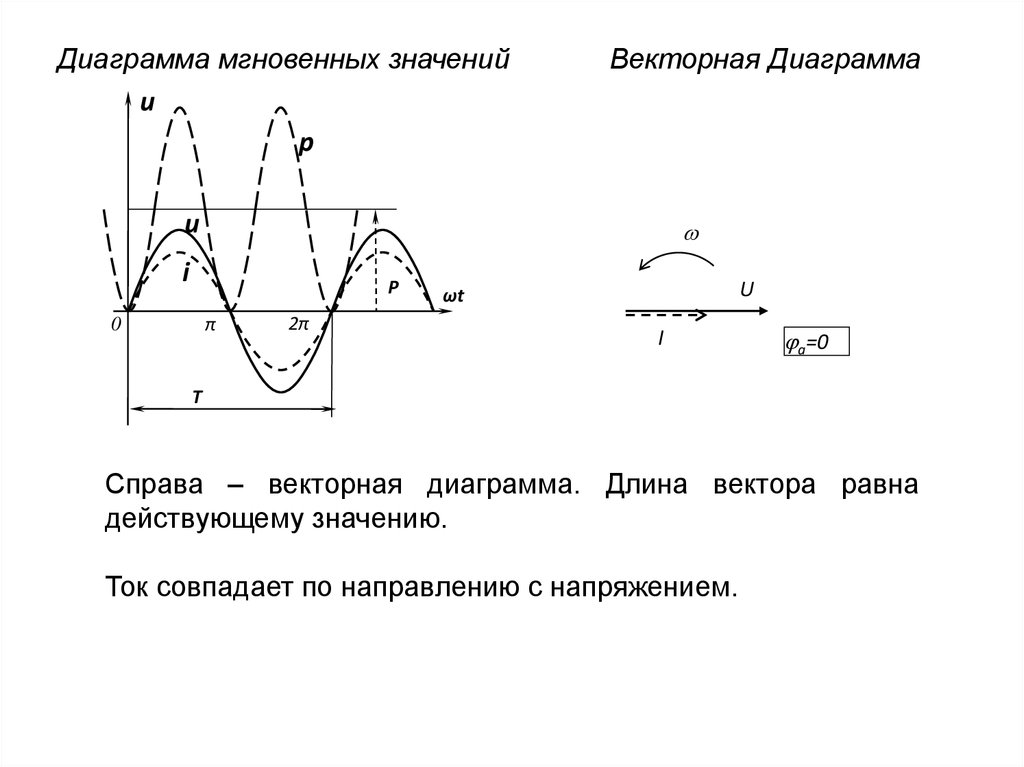
5. Диаграмма мгновенных значений
up
Векторная Диаграмма
u
i
P
π
0
2π
U
ωt
I
a=0
Т
Справа – векторная диаграмма. Длина вектора равна
действующему значению.
Ток совпадает по направлению с напряжением.
6. АКТИВНАЯ МОЩНОСТЬ Мощность в цепи переменного тока принято оценивать по среднему значению за период. Такая мощность называется
активной.1T
1T
P p dt U M I M sin 2 t dt U I ; ( Вт);
T0
T0
(Произведение действующих значений.)
7. 2. Индуктивная нагрузка
u U M sin t ;i
u
По закону ЭМИ
e
L
d
e
;
dt
L i -потокосцепление
L - индуктивность, Гн
По закону ЭМИ в катушке будет индуктироваться ЭДС, которая
называется ЭДС самоиндукции. При отсутствии ферромагнитных
материалов потокосцепление пропорционально току, а
коэффициентом пропорциональности является индуктивность.
e L
По II-му закону Кирхгофа
di
;
dt
e u;
u e;
8.
UMdi
sin t L
dt
UM
di
sin t dt
L
- разделим переменные
- Дифференциальное уравнение
Интегрируя левую и правую части дифференциального
уравнения получим
UM
UM
i
cos t
sin( t ) I M sin( t );
L
L
2
2
ВЫВОД:
Ток через индуктивную нагрузку отстает по фазе от
приложенного синусоидального напряжения на угол ;
2
9.
UML
IM
- амплитуда тока
L X L – индуктивное сопротивление, Ом;
разделим левую и правую части делят на
2
и перейдем к действующим значениям
U
I
XL
– Закон Ома для цепи с индуктивной нагрузкой
10. Мгновенная мощность
p u i U M sin t I M sin( t )2
U M I M sin t (cos
cos(2 t ))
2
2
U M I M cos(2 t ) U I cos(2 t );
2
2
ВЫВОД:
1) В цепи с индуктивным сопротивлением мощность
изменяется по периодическому закону с двойной частотой
относительно приложенного напряжения.
2)Анализ показывает:
– когда ток и напряжение совпадают по направлению –
мощность положительна;
– когда ток и напряжение не совпадают по направлению –
мощность отрицательна;
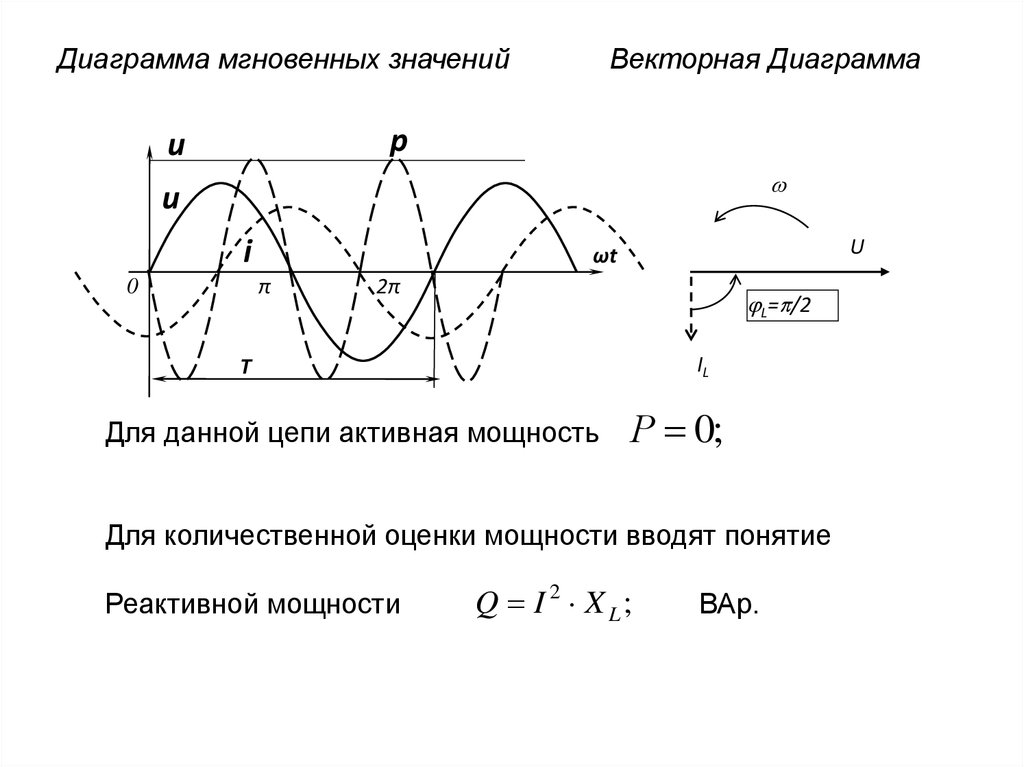
11. Диаграмма мгновенных значений
Векторная Диаграммаp
u
u
i
π
0
U
ωt
2π
L= /2
IL
Т
Для данной цепи активная мощность
Р 0;
Для количественной оценки мощности вводят понятие
Реактивной мощности
Q I 2 X L;
ВАр.
12. 3. Ёмкостная нагрузка
iu
С
uС
u U M sin t ;
u uC ;
q C uC - электрический заряд, Кл
С
- емкость, Ф
ток равен изменению заряда
duC
dq
d
i
C
C (U M sin t )
dt
dt
dt
C U M cos t
UM
sin( t ) I M sin( t );
1
2
2
C
13.
ВЫВОД:Ток через ёмкостную нагрузку опережает по фазе
приложенное синусоидальное напряжение на угол
IM
2
UM
1
С
;
- амплитуда тока
1
XС
С
– ёмкостное сопротивление, Ом;
разделим левую и правую части на
2
и перейдем к действующим значениям
U
I
XС
– Закон Ома для цепи с емкостной нагрузкой
14. Мгновенная мощность
p U I cos(2 t );2
ВЫВОД:
В цепи с ёмкостным сопротивлением мощность изменяется
по периодическому закону с двойной частотой относительно
приложенного напряжения.
15. Диаграмма мгновенных значений
pu
Векторная Диаграмма
u
С=- /2
i
π
0
IС
U
2π
Т
Для данной цепи активная мощность
Р 0;
Для количественной оценки мощности вводят понятие
Реактивной мощности
ЗАМЕЧАНИЕ:X L
и
Q I 2 XС ;
ВАр.
X С назыв-ся реактивные сопротивления
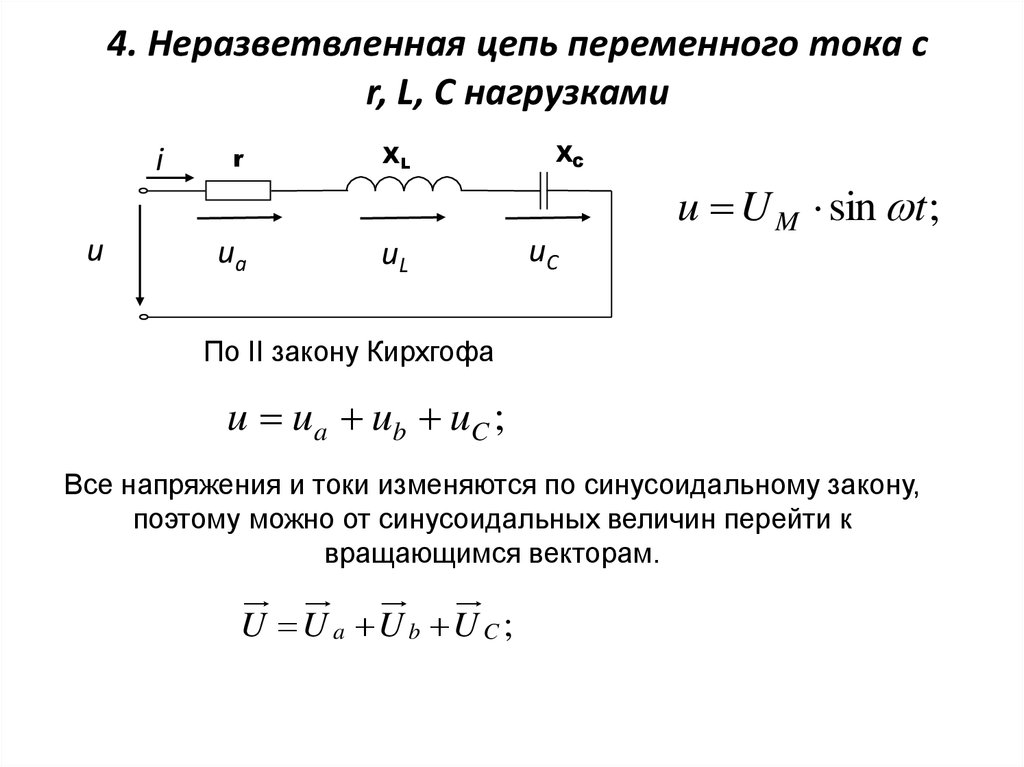
16. 4. Неразветвленная цепь переменного тока с r, L, C нагрузками
iu
r
uа
XL
uL
XC
uC
u U M sin t ;
По II закону Кирхгофа
u ua ub uC ;
Все напряжения и токи изменяются по синусоидальному закону,
поэтому можно от синусоидальных величин перейти к
вращающимся векторам.
U U a U b U C;
17.
U a I r– вектор активного напряжения;
U L I X L – вектор индуктивного напряжения;
U C I X C – вектор ёмкостного напряжения;
Дальше для анализа этой цепи переходим к трем частным случаям.
а)
X L XC; U L U C;
– в цепи преобладает индуктивное сопротивление.
Построим Векторную Диаграмму напряжений и тока.
За исходный вектор выбираем ТОК
18.
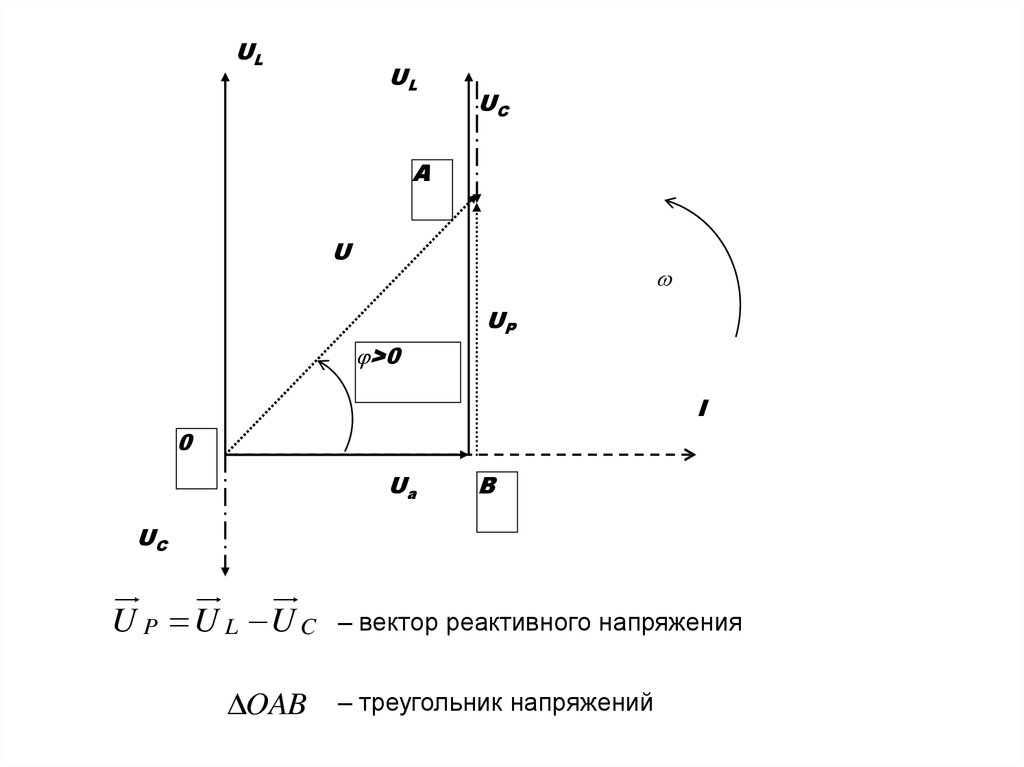
ULUL
UC
A
U
UP
>0
I
0
Ua
B
UC
U P U L U C
– вектор реактивного напряжения
OAB – треугольник напряжений
19.
По теореме ПифагораU U a2 U P2
U a2 (U L U C ) 2
I 2 r 2 (I X L I X C )2
I Z;
I
U
Z
Закон Ома для цепи переменного тока
Z r (X L XC )
2
2
– полное сопротивление последовательной цепи
20.
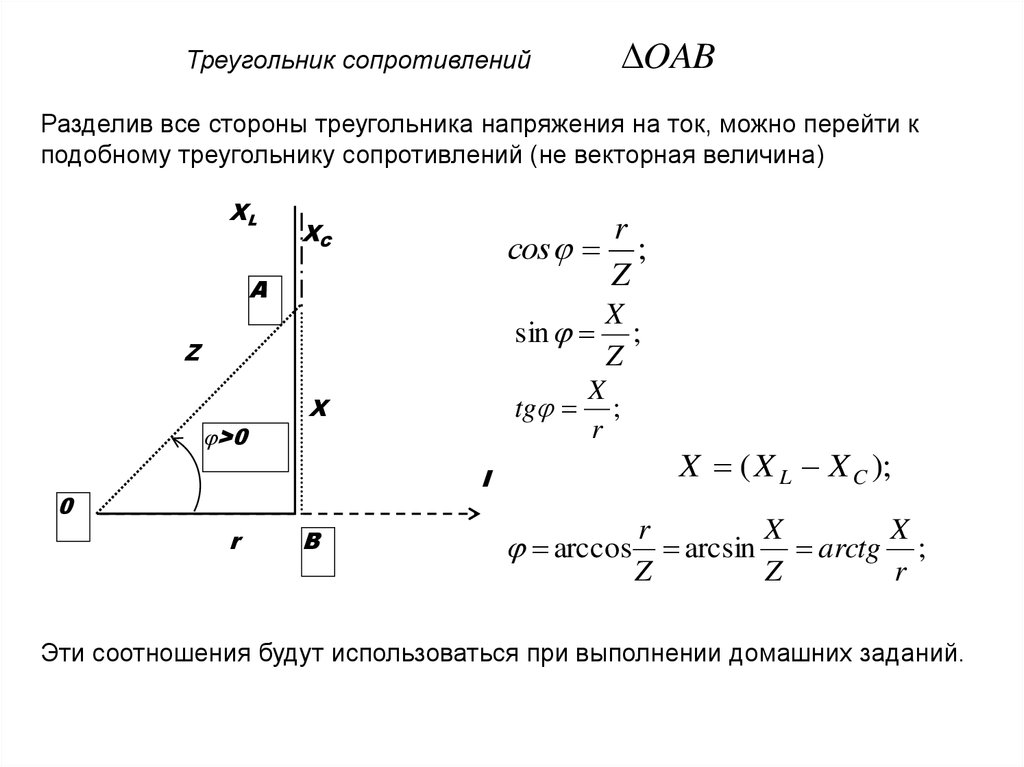
OABТреугольник сопротивлений
Разделив все стороны треугольника напряжения на ток, можно перейти к
подобному треугольнику сопротивлений (не векторная величина)
XL
XC
сos
r
;
Z
sin
X
;
Z
A
Z
>0
tg
X
X
;
r
X ( X L X C );
I
0
r
B
r
Z
arccos arcsin
X
X
arctg ;
Z
r
Эти соотношения будут использоваться при выполнении домашних заданий.
21. 5. Резонанс напряжений
X L XC;– условие резонанса напряжений
U L U C ;
UL
UC
=0
U
I
Ua
22.
Особенности резонанса напряжений:1) Полное сопротивление цепи равно активному сопротивлению
Z r 2 ( X L X C ) 2 r 2 02 r;
2) Приложенное напряжение и ток в цепи совпадают по фазе
сos
r r
1; 0;
Z r
3) Ток в цепи достигает максимальное значение
U U
I I МАКС ;
Z r
4) Напряжение на зажимах цепи равно напряжению на активном
сопротивлении
U I Z I r Ua;
5) Напряжения на индуктивности и емкости равны по величине и
противоположны по направлению:
U L U C ;
при этом если X L X C r ,
то
U L U C U ;
В цепи могут иметь место перенапряжения, что недопустимо.
















 Физика
Физика








