Строительная механика. Теория определения перемещений деформируемых систем. (Часть 1. Лекция 2)

1.

СТРОИТЕЛЬНАЯ МЕХАНИКА.
Часть I
ТЕОРИЯ ОПРЕДЕЛЕНИЯ
ПЕРЕМЕЩЕНИЙ
ДЕФОРМИРУЕМЫХ
СИСТЕМ
2

2.

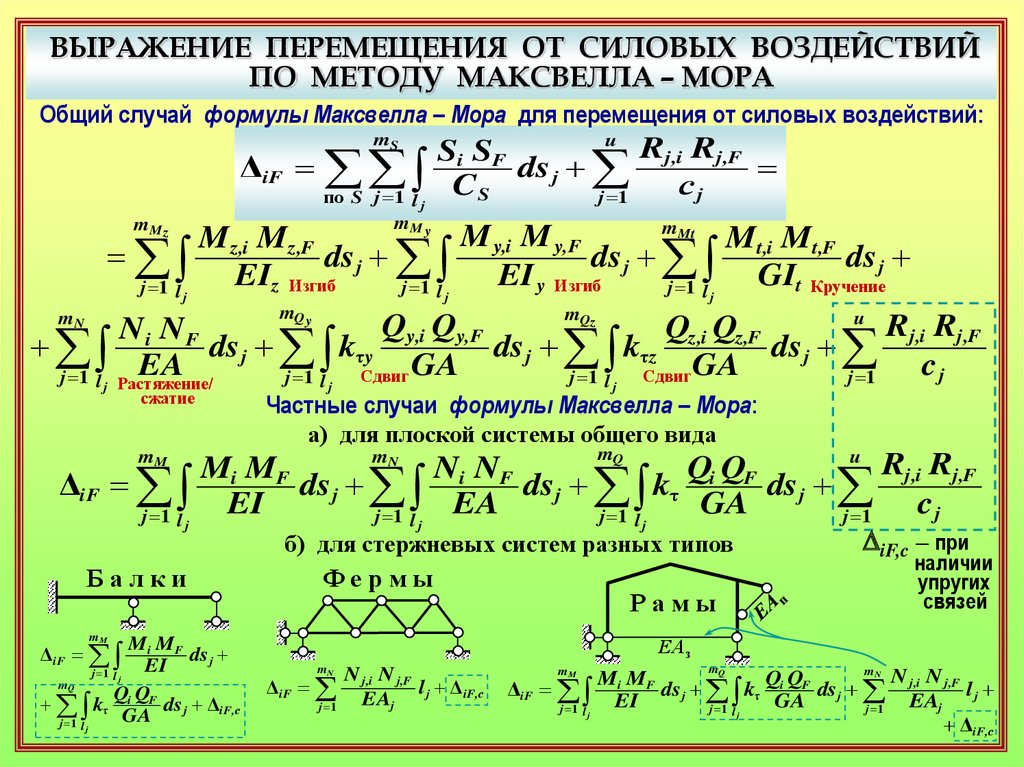
ВЫРАЖЕНИЕ ПЕРЕМЕЩЕНИЯ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ
ПО МЕТОДУ МАКСВЕЛЛА – МОРА
Общий случай формулы Максвелла – Мора для перемещения от силовых воздействий:
ΔiF
mM z
j 1 l j
mS
по S j 1 l j
mM y
u
Rj,i Rj,F
Si SF
ds j
CS
с
j
j 1
mMt
M y,i M y,F
Mz,i M z,F
Mt,i Mt,F
ds
ds j
ds j
EIz Изгиб j
EI
GI
y Изгиб
t Кручение
j 1 l
j 1 l
j
mQ y
mN
j
mQz
u
Qy,i Qy,F
R R
Qz,i Qz,F
Ni NF
ds j kτy
ds j kτz
ds j j,i j,F
EA
cj
Сдвиг GA
Сдвиг GA
j 1 l Растяжение/
j 1 l
j 1 l
j 1
j
сжатие
j
j
Частные случаи формулы Максвелла – Мора:
а) для плоской системы общего вида
mQ
mN
u
Rj,i Rj,F
Mi MF
Ni N F
Qi QF
ΔiF
ds j
ds j kτ
ds j
EI
EA
GA
cj
j 1 l
j 1 l
j 1 l
j 1
mM
j
Балки
j
j
б) для стержневых систем разных типов
Фермы
Рамы
mM
ΔiF
Mi MF
ds j
EI
j 1 l j
mQ
QQ
kτ i F ds j ΔiF,с
GA
j 1 l
j
DiF,c – при
наличии
упругих
связей
ЕАз
mN
ΔiF
j 1
N j,i N j,F
l j ΔiF,с
EAj
mQ
mN
N N
Mi M F
Qi QF
ΔiF
ds j kτ
ds j j,i j,F l j
EI
GA
EAj
j 1 l j
j 1 l j
j 1
ΔiF,с
mM

3.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ
МЕТОДОМ МАКСВЕЛЛА – МОРА
Алгоритм вычисления перемещения по формуле Максвелла – Мора
1. Исходя из типа и особенностей рассматриваемой системы определяется,
какие виды деформаций элементов должны быть учтены при вычислении
перемещения; выбирается нужный вариант записи формулы Максвелла –
Мора ( общий или частный случай ).
2. Рассматривается действительное состояние системы с определением
входящих в выбранный вариант формулы М – М внутренних силовых
факторов SF и реакций Rj,F упругих связей ( при их наличии ) от заданных
нагрузок.
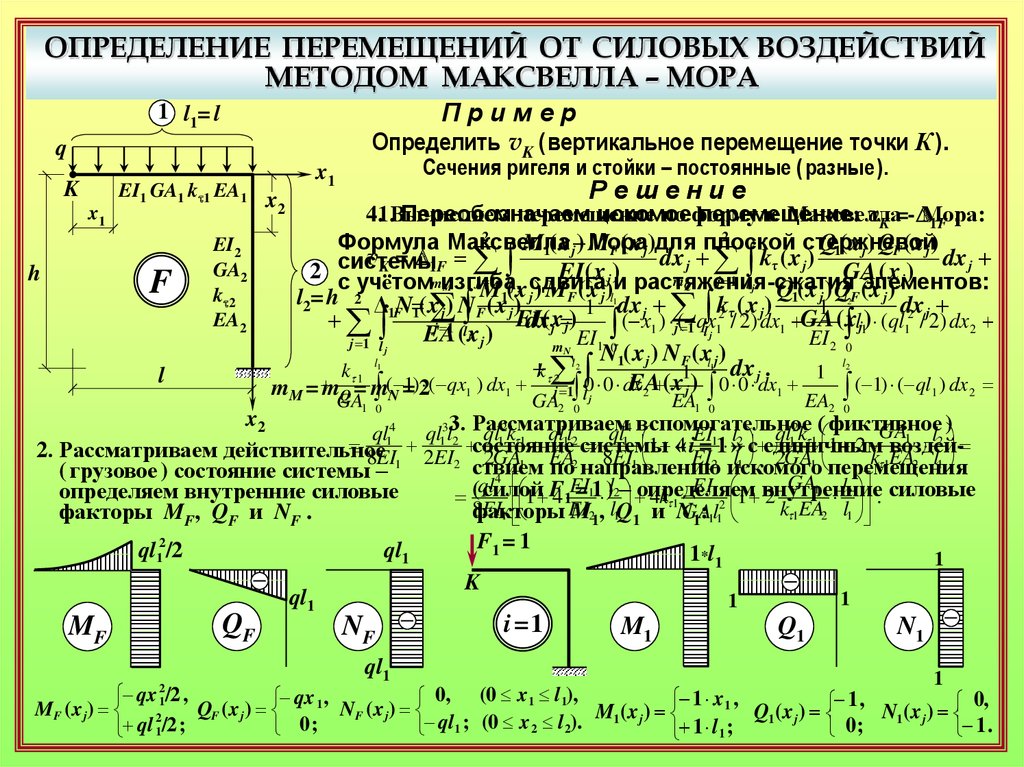
3. Рассматривается вспомогательное ( фиктивное ) состояние системы
с единичным воздействием соответствующего типа по направлению
искомого перемещения; определяются внутренние силовые факторы Si
и реакции Rj,i упругих связей от единичного воздействия.
4. Найденные силовые факторы действительного и единичного состояний,
представленные аналитически ( функциональными выражениями внутренних усилий ) или графически ( в форме эпюр ) используются в соответствующих членах формулы М – М; аналитически или численными способами
выполняется вычисление интегралов.
Примечания: 1). Если результат вычисления по формуле М – М имеет знак «плюс»,
то искомое перемещение направлено в ту же сторону, что и назначенное единичное
воздействие, в случае знака «минус» – в противоположную сторону.
2). Вычисление интеграла в формуле М – М называется «перемножением эпюр».

4.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ
МЕТОДОМ МАКСВЕЛЛА – МОРА
Пример
Определить vK ( вертикальное перемещение точки К ).
1 l1 = l
q
K
EI1 GA1 kt1 EA1
x1
h
F
EI2
GA2
kt2
EA2
Сечения ригеля и стойки – постоянные ( разные ).
x1
x2
Решение
4.1.Вычисляем
Переобозначаем
перемещение
искомое
по формуле
перемещение:
Максвелла
vK =-DМора:
1F .
2
2
Формула Максвелла
Мора
M ( x –) M
Q (x ) Q (x )
F ( x j )для плоской стержневой
vK = D1F 1 j
dx j kτ ( x j) 1 j F j dx j
системы
2 с учётомmизгиба,
EI( x j)и растяжения-сжатия
GA
( x j)
j 1 l j сдвига
j 1 l j
mQ
элементов:
M
M
(
x
)
M
(
x
)
Q
(
x
)
Q
(
x
F
jl
1
j lF
j)
l2= h 2 Δ N ( x ) N ( x1 ) j
(
x
)
dx
1 dx j k
1
1F 1
τ
j
j F
j
2
2 j
EI
GA
(
x
)
/
2
)
dx
l
(
ql
/ 2) dx2
dx( xj j) ( x1 ) j( 1 qx
j
j 1 l j
1
1
1
1
lj
EA
(
x
)
EI
EI
j
j 1 l j
1 0
2 0
mN
1
2
N1( x j) N F ( xl j)
kt 2 2
kt 1 1
1 1 dx j .
1 2
EA
(
x
)
(
1
)
(
qx
)
dx
0
0
dx
0
0
dx
( 1) ( ql1 ) dx 2
j
mM = mQ = m
=2
1
1
2
1
j 1
GA1 0 N
GA2 0 l j
EA1 0
EA2 0
l
l
l
l
x2
Рассматриваем
GA1 l2 )
ql14 ql13l3.
ql12kt1 ql1l2 ql14 вспомогательное
EI1 l2 ql12kt1 ( фиктивное
2
состояние
1 2 воздей
системы
1 «4 i = 1 » с единичным
2. Рассматриваем действительное
8EI1 2EI2 2GA1 EA2 8EI1
EI2 l1 2GA1
kt1EA2 l1
ствием
по направлению искомого перемещения
( грузовое ) состояние системы –
4
GA1 l2 силовые
ql
EI l
EI1 внутренние
1 F
1
определяем внутренние силовые
( силой
4 1 =11 )2– определяем
4kt1
.
2 1 2
8EI1
EI
k
EA
l1
l
факторы
M21, l1Q 1 и NGA
:
факторы MF, QF и NF .
t
1
2
1
1
1
F1 = 1
ql1
ql 12/2
1 * l1
1
K
ql1
1
1
QF
MF
NF
ql1
i =1
M1
Q1
N1
1
qx /2 ,
qx 1 ,
0, (0 x1 l 1),
1
x
,
1
,
0,
1
MF ( x j )
QF ( x j)
NF ( x j)
M
(
x
)
Q
(
x
)
N
(
x
)
1 .
1
j
1
j
1
j
ql1 ; (0 x 2 l 2).
0;
0;
ql /2 ;
1 l 1 ;
2
1
2
1

5.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ
МЕТОДОМ МАКСВЕЛЛА – МОРА
Пример
Определить vK ( вертикальное перемещение точки К ).
1 l1 = l
q
K
EI1 GA1 kt1 EA1
x1
h
F
EI2
GA2
kt2
EA2
Сечения ригеля и стойки – постоянные ( разные ).
x1
x2
Решение
4. Вычисляем перемещение по формуле Максвелла - Мора:
2
2
M1( x j) MF ( x j)
Q (x ) Q (x )
vK = D1F
dx j kτ ( x j) 1 j F j dx j
2
EI( x j)
GA ( x j)
j 1 l j
j 1 l j
l
l
l2= h 2 N ( x ) N ( x )
1
1
1
j
F
j
2
l1 (ql12 / 2) dx2
dx j ( x1 ) ( qx1 / 2) dx1
EA ( x j)
EI1 0
EI 2 0
j 1 l
1
2
j
l1
l
x2
l
l
l
k
k 2
1 1
1 2
t 1 ( 1) ( qx1 ) dx1 t 2 0 0 dx 2
0
0
dx
( 1) ( ql1 ) dx 2
1
GA1 0
GA2 0
EA1 0
EA2 0
GA1 l2
ql14 ql13l2 ql12kt1 ql1l2 ql14
EI1 l2 ql12kt1
1 2
1 4
8EI1 2EI2 2GA1 EA2 8EI1
EI2 l1 2GA1
kt1EA2 l1
GA1 l2
ql14
EI l
EI1
.
1 4 1 2 4kt1
2 1 2
8EI1
EI2 l1
kt1EA2 l1
GA1l1
Учитывая, что E1/G1 = 2(1+n1) ( n1 – коэффициент Пуассона ), I1 = r12 A1 (η1h1)2 A1
( здесь r1 – радиус инерции сечения, h1 – высота сечения на участке 1 ), получаем:
2
ql14
GA1 l2
EI1 l2
h1
vk
1
4
8(1
ν
)
k
η
1
2
.
1
τ1
8EI1
EI2 l1
kτ1EA2 l1
1 l1
От изгиба
От сдвига
От укорочения
стойки

6.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ СИЛОВЫХ ВОЗДЕЙСТВИЙ
МЕТОДОМ МАКСВЕЛЛА – МОРА
Пример
Определить vK ( вертикальное перемещение точки К ).
1 l1 = l
q
K
EI1 GA1 kt1 EA1
x1
h
F
EI2
GA2
kt2
EA2
l
x2
Сечения ригеля и стойки – постоянные ( разные ).
x1
x2
Решение
2
ql
GA1 l2
EI1 l2
h
1
vk
1 4 EI2 l1 8(1 ν1) kτ1 η1 l1 1 2 kτ1EA2 l1 .
8
EI
1
2
4
1
l2= h
От изгиба
От сдвига
От
укорочения
Для количественной оценки вклада каждого вида
стойки
деформации
в определяемое перемещение рассмотрим случай, когда
ригель
и стойка4 изготовлены из одного материала
( E1 = E2 , G1 =
2
G2 ): ql 1
I1 l2
A1 l2
h1
1
vk
.
1 4 8(1 ν1)k τ1 η1 1
8EI1
I2 l1
l1 k τ1(1 ν1) A2 l1
Для большинства изотропных материалов n1 = 0,15 … 0,3; для сечений от прямоугольных
до двутавровых h1 = 0,3…0,45; kt1 = 1,2…3, тогда
2
ql 14
I1 l2
h1
A l
vk
1 4 (0,99...6,32) 1 (0,256...0,725) 1 2 .
8EI1
I2 l1
A2 l1
l1
Если ригель и рама имеют одинаковые сечения ( А1 = А2 , I1 = I2 ) и длины ( l1 =
l2 ),
2
4
5 ql1 1 (0,25 ... 2,2) h1 ,
v
k
то
8 EI1
l1
где второе слагаемое в скобках оценивает суммарный вклад в перемещение vK деформации сдвига
( в ригеле ) и сжатия стойки. При обычных пропорциях колонн и ригелей рамных строительных
конструкций h1 / l1 = 1/8 … 1/15, и тогда доля перемещения за счёт сдвига и сжатия в сумме составляет
0,25 … 3,4 % от перемещения, возникающего от деформации изгиба элементов. При этом вклад сдвига
в 1,4 … 4 раза превышает вклад сжатия.

7.

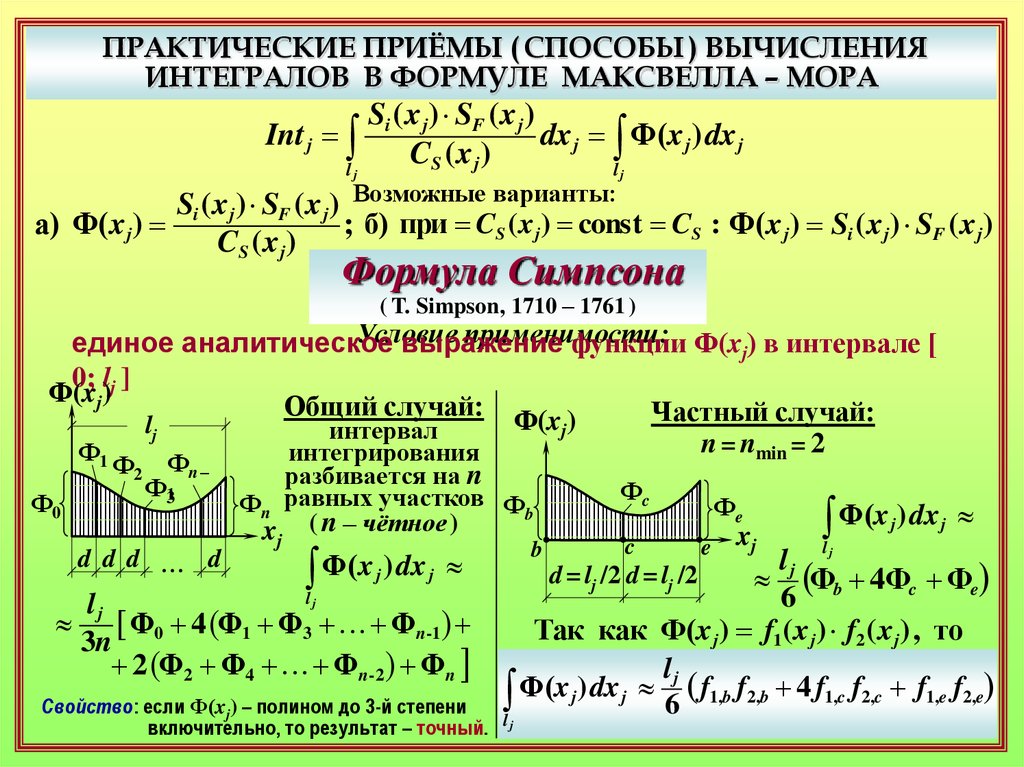
ПРАКТИЧЕСКИЕ ПРИЁМЫ ( СПОСОБЫ ) ВЫЧИСЛЕНИЯ
ИНТЕГРАЛОВ В ФОРМУЛЕ МАКСВЕЛЛА – МОРА
Int j
lj
Si ( x j) SF ( x j)
dx j Φ(x j) dx j , где Φ(x j) f1 ( x j) f2 ( x j)
CS ( x j )
l
j
Возможные варианты:
SF ( x j)
Si ( x j)
;
а) f1( x j)
, f2 ( x j) SF ( x j); б) f1( x j) Si ( x j) , f2 ( x j)
CS ( x j)
CS ( x j )
в) при CS ( x j) const CS : Int j 1 Si ( x j) SF ( x j) dx j
CS l
j
f1(xj) f2(xj)
Правило Верещагина
или
( А.К. Верещагин, 1925 )
f2(xj) f1(xj)
Условие применимости:
одна из функций ( f1 ) – линейная
( при этом f2 может быть любой – сложной или линейной )
y
a
lj
xj dxj y1(C2)
a
f1
f1(xj )
f2(xj )
bC2
C2
f2 ( x j ) dx j (a x j ) tg α f2 ( x j ) dx j
l j f1( x j )«перемножения
Результат
эпюр» f1 и f2 , из которых
lj
одна ( f1 ) линейная, равен произведению
площади
( f2 )
«сложной»
tg α (a эпюры
x j ) f2 ((x fj ) dx
j tg α S y tg α ω f2 bC2
)
на
ординату линейной эпюры
2
lj
в месте расположения
тяжести
«сложной»:
ω f ( bC центра
tg α) ω
f y1(C )
2
f2
2
f ( x ) f ( x ) dx
1
lj
j
2
j
2
j
2
ω f2 y1(C2)

8.

ПРАКТИЧЕСКИЕ ПРИЁМЫ ( СПОСОБЫ ) ВЫЧИСЛЕНИЯ
ИНТЕГРАЛОВ В ФОРМУЛЕ МАКСВЕЛЛА – МОРА
Int j
lj
Si ( x j) SF ( x j)
dx j Φ(x j) dx j
CS ( x j )
l
j
Si ( x j) SF ( x j) Возможные варианты:
а) Ф(x j)
; б) при CS ( x j) const CS : Ф(x j) Si ( x j) SF ( x j)
CS ( x j )
Формула Симпсона
( T. Simpson, 1710 – 1761 )
Условие
применимости:
единое аналитическое
выражение
функции Ф(xj) в интервале [
0; l ]
Ф(xj)j
Общий случай:
Частный случай:
Ф(xj)
lj
интервал
n = nmin = 2
интегрирования
Ф1 Ф Ф
n–
2
разбивается на n
Ф31
Фc
равных
участков Ф
Ф0
Фn
Фe
b
Φ(x j) dx j
(
n
–
чётное
)
xj
x
j
lj
c
e
b
d d d … d
l
d = lj /2 d = lj /2
l j Φ(x j ) dx j
j Φb 4Φc Φe
6
lj
Φ0 4 Φ1 Φ3 Φn-1
Так как Ф(x j) f1( x j) f2 ( x j) , то
3n
2 Φ2 Φ4 Φn-2 Φn
lj
l Φ(x j) dx j 6 f1,b f2,b 4 f1,c f2,c f1,e f2,e
Свойство: если Ф(xj) – полином до 3-й степени
включительно, то результат – точный.
j

9.

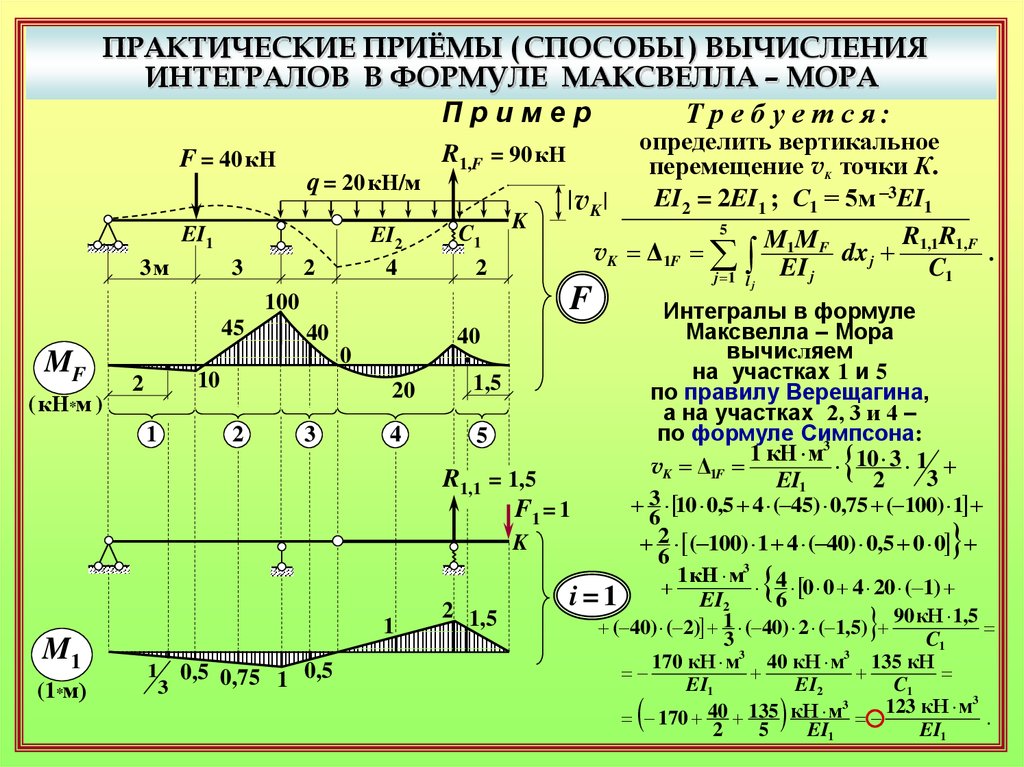
ПРАКТИЧЕСКИЕ ПРИЁМЫ ( СПОСОБЫ ) ВЫЧИСЛЕНИЯ
ИНТЕГРАЛОВ В ФОРМУЛЕ МАКСВЕЛЛА – МОРА
Пример
Т р е б у е т с я:
F = 40 кН
q = 20 кН/м
EI1
3м
3
EI2
4
2
R1,F = 90 кН
C1
2
K
MF
( кН*м )
40
10
1
2
3
Интегралы в формуле
Максвелла – Мора
вычисляем
на участках 1 и 5
по правилу Верещагина,
а на участках 2, 3 и 4 –
по формуле Симпсона:
1 кН м3 10 3 1
vK Δ1F
3
EI1
2
40
0
2
j
F
100
45
определить вертикальное
перемещение vK точки К.
EI2 = 2EI1 ; С1 = 5м –3EI1
|vK|
5
R R
MM
vK Δ 1F 1 F dx j 1,1 1,F .
EI j
C1
j 1 l
20
1,5
4
5
R1,1 = 1,5
F1 = 1
K
M1
(1*м)
1
1 0,5 0,75 1 0,5
3
2 1,5
i=1
3 10 0,5 4 ( 45) 0,75 ( 100) 1
6
2 ( 100) 1 4 ( 40) 0,5 0 0
6
1 кН м3 4
0 0 4 20 ( 1)
EI2
6
90 кН 1,5
( 40) ( 2) 1 ( 40) 2 ( 1,5)
3
C1
170 кН м3 40 кН м3 135 кН
EI1
EI2
C1
3
123 кН м3
40
135
кН
м
170
.
2
5
EI1
EI1

10.

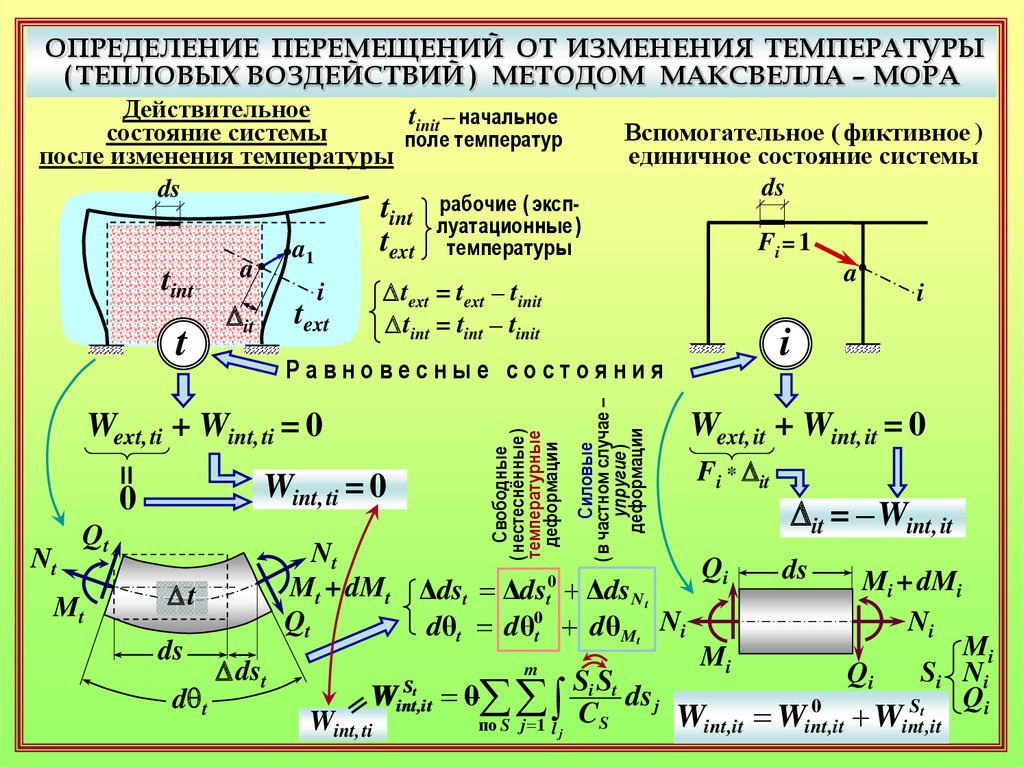
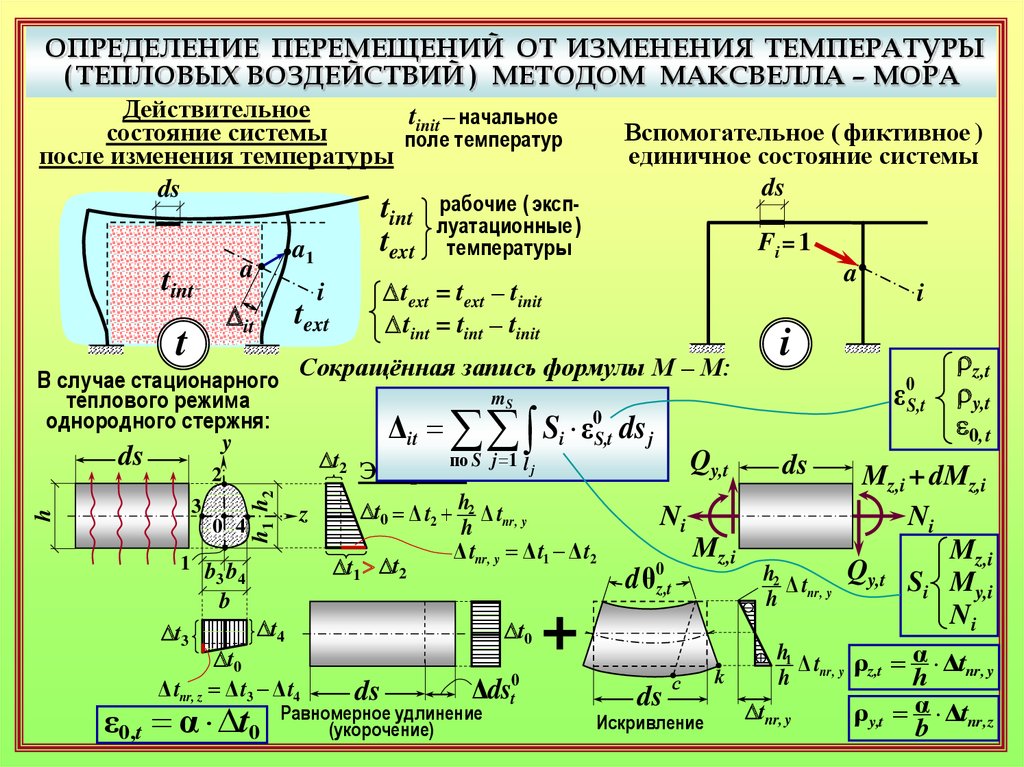
ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
( ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ ) МЕТОДОМ МАКСВЕЛЛА – МОРА
Действительное
Начальное
( условно
tinit – начальное
состояние системы )
недеформированное
поле температур
после состояние
изменениясистемы
температуры
ds
tint
init
t
a
Dit
tint
text
a1
i
text
рабочие ( эксплуатационные )
температуры
Вспомогательное ( фиктивное )
единичное состояние системы
ds
Fi = 1
a
D text = text – tinit
D tint = tint – tinit
Wext, it + Wint, it = 0
=
Nt
Mt
Fi * Dit
Wint, ti = 0
Qt
Dt
ds
ds
i
Равновесные состояния
Wext, ti + Wint, ti = 0
0
Nt
Mt + dMt
Qt
i
Qi
Ni
Mi
Dit = – Wint, it
ds
Mi + dMi
Ni
Qi

11.

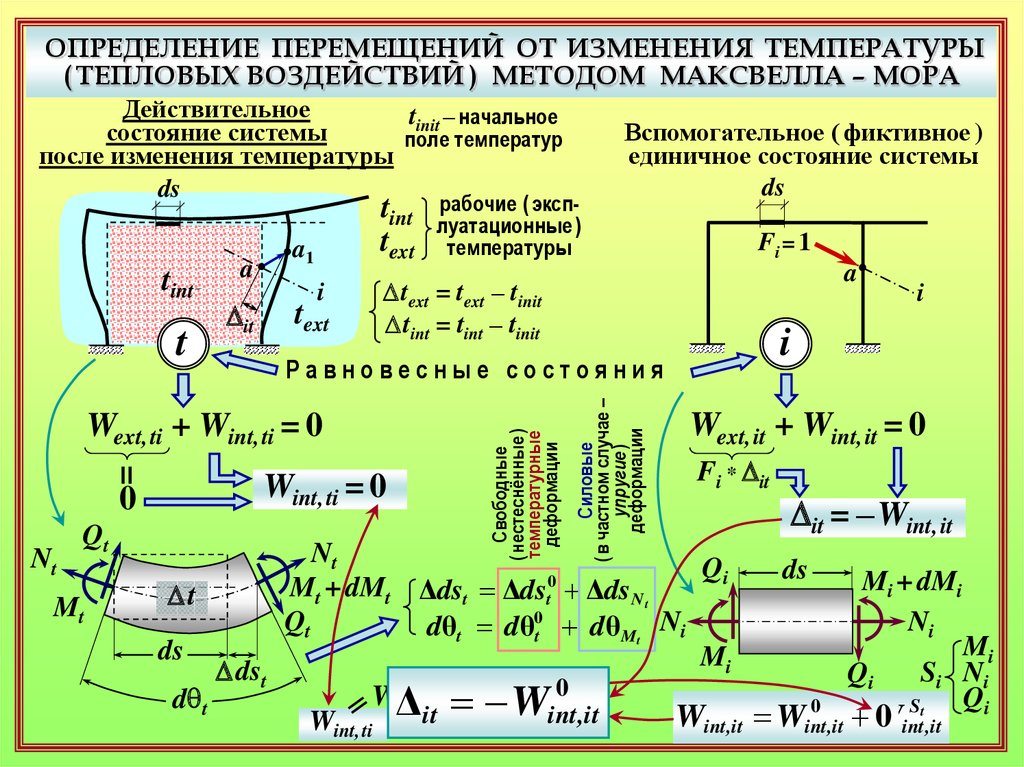
ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
( ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ ) МЕТОДОМ МАКСВЕЛЛА – МОРА
Действительное
tinit – начальное
состояние системы
поле температур
после изменения температуры
ds
Dit
i
text
=
Nt
Qt
Mt
a
Wint, ti = 0
i
i
Равновесные состояния
Wext, ti + Wint, ti = 0
0
Fi = 1
D text = text – tinit
D tint = tint – tinit
Силовые
( в частном случае –
упругие )
деформации
t
a
a1
рабочие ( эксплуатационные )
температуры
Свободные
( нестеснённые )
температурные
деформации
tint
init
tint
text
Вспомогательное ( фиктивное )
единичное состояние системы
ds
Wext, it + Wint, it = 0
Fi * Dit
Dit = – Wint, it
Nt
Qi
ds
0
Mi + dMi
M
+
dM
t
t Δdst Δdst Δds N t
Dt
Qt
Ni
dθt dθ0t dθMt Ni
Mi
ds
Mi
m
D dst
Si N i
Qi
Si St
St
Wint,it 0 St ds j
Qi
dqt
0
St
C
W
W
W
dWint,it dWint,поit S jdW
S
1 l j int,it
int,it
int,it
int,it

12.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
( ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ ) МЕТОДОМ МАКСВЕЛЛА – МОРА
Действительное
tinit – начальное
состояние системы
поле температур
после изменения температуры
ds
Dit
i
text
=
Nt
Qt
Mt
a
Wint, ti = 0
i
i
Равновесные состояния
Wext, ti + Wint, ti = 0
0
Fi = 1
D text = text – tinit
D tint = tint – tinit
Силовые
( в частном случае –
упругие )
деформации
t
a
a1
рабочие ( эксплуатационные )
температуры
Свободные
( нестеснённые )
температурные
деформации
tint
init
tint
text
Вспомогательное ( фиктивное )
единичное состояние системы
ds
Wext, it + Wint, it = 0
Fi * Dit
Dit = – Wint, it
Nt
Qi
ds
0
Mi + dMi
M
+
dM
t
t Δdst Δdst Δds N t
Dt
Qt
Ni
dθt dθ0t dθMt Ni
Mi
ds
Mi
m
D dst
Si N i
Qi
Si St
St
Wint,it
ds j
0
Qi
dqt
0
St
C
W
W
W
S
Wint, ti
по S j 1 l j
int,it
int,it
int,it

13.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
( ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ ) МЕТОДОМ МАКСВЕЛЛА – МОРА
Действительное
tinit – начальное
состояние системы
поле температур
после изменения температуры
ds
Dit
i
text
=
Nt
Qt
Mt
a
Wint, ti = 0
i
i
Равновесные состояния
Wext, ti + Wint, ti = 0
0
Fi = 1
D text = text – tinit
D tint = tint – tinit
Силовые
( в частном случае –
упругие )
деформации
t
a
a1
рабочие ( эксплуатационные )
температуры
Свободные
( нестеснённые )
температурные
деформации
tint
init
tint
text
Вспомогательное ( фиктивное )
единичное состояние системы
ds
Wext, it + Wint, it = 0
Fi * Dit
Dit = – Wint, it
Nt
Qi
ds
0
Mi + dMi
M
+
dM
t
t Δdst Δdst Δds N t
Dt
Qt
Ni
dθt dθ0t dθMt Ni
Mi
ds
Mi
D dst
Si N i
Qi
St
0
WΔ
0 W
Qi
dqt
int,it
0
St
it
int,
it
W
W
W
0
Wint, ti
int,it
int,it
int,it

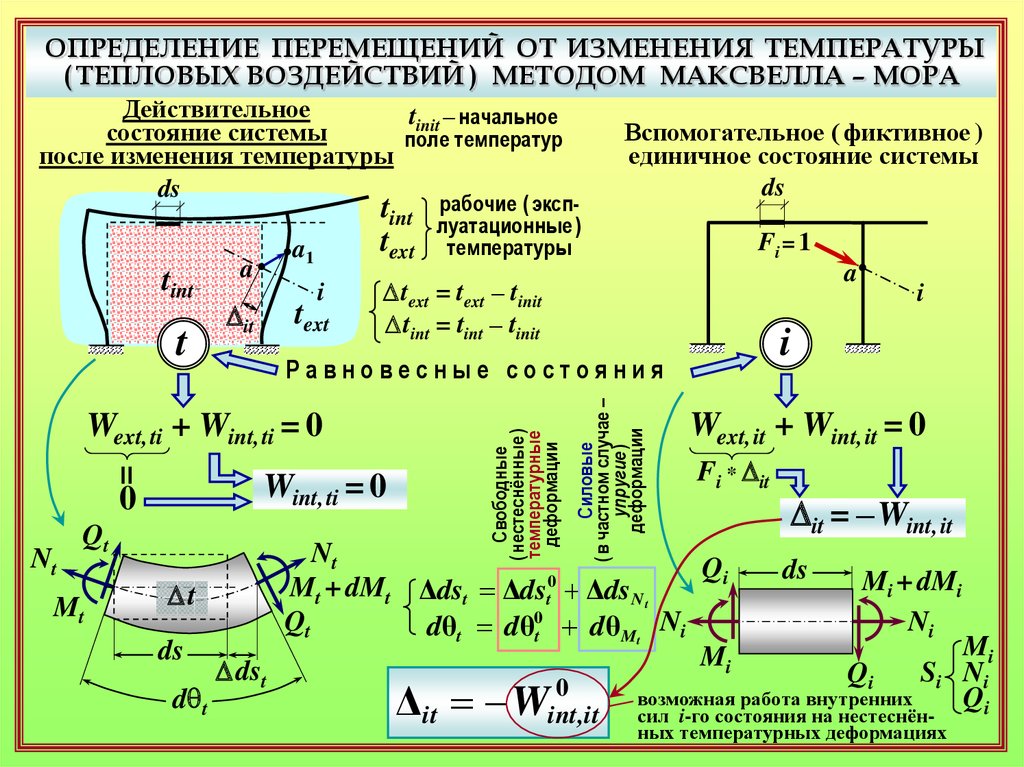
14.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
( ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ ) МЕТОДОМ МАКСВЕЛЛА – МОРА
Действительное
tinit – начальное
состояние системы
поле температур
после изменения температуры
ds
a
i
Dit
text
=
Nt
Wint, ti = 0
Dt
ds
dqt
D dst
Wext, it + Wint, it = 0
Fi * Dit
Nt
Qi
Mt + dMt Δdst Δdst0 ΔdsN t
Qt
dθt dθ0t dθMt Ni
Mi
0
Δit Wint,
it
i
i
Равновесные состояния
Qt
Mt
a
D text = text – tinit
D tint = tint – tinit
Wext, ti + Wint, ti = 0
0
Fi = 1
Силовые
( в частном случае –
упругие )
деформации
t
a1
рабочие ( эксплуатационные )
температуры
Свободные
( нестеснённые )
температурные
деформации
tint
init
tint
text
Вспомогательное ( фиктивное )
единичное состояние системы
ds
Dit = – Wint, it
ds
Mi + dMi
Ni
Mi
Si N i
Qi
возможная работа внутренних
Qi
сил i-го состояния на нестеснённых температурных деформациях

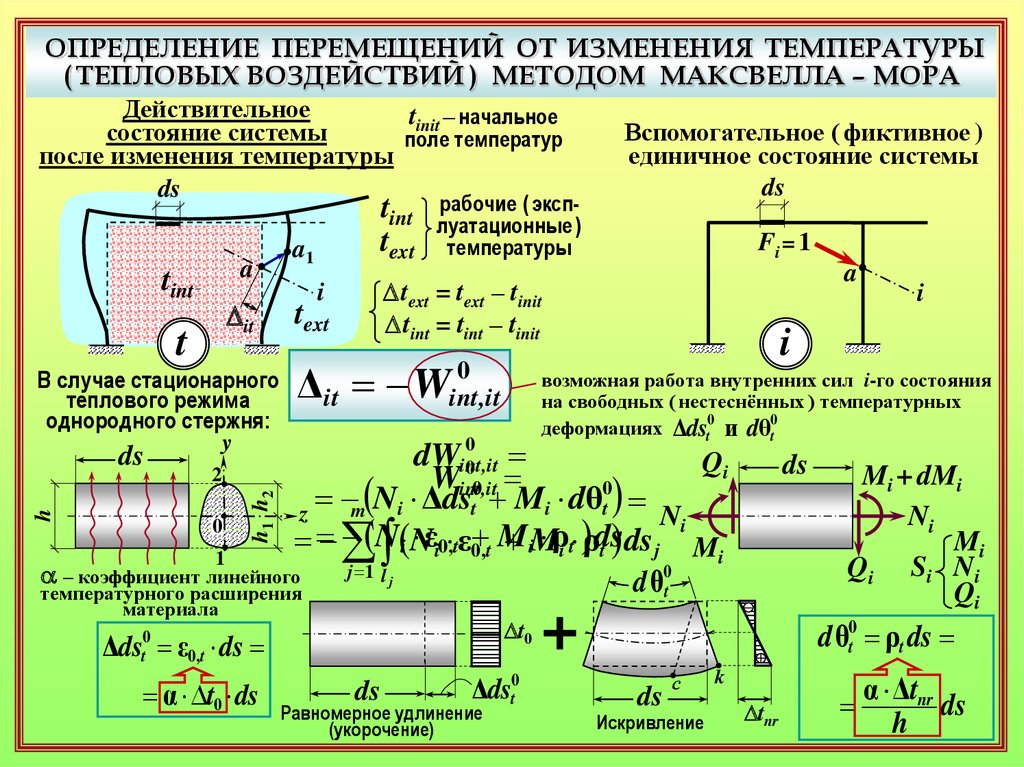
15.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
( ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ ) МЕТОДОМ МАКСВЕЛЛА – МОРА
Действительное
tinit – начальное
состояние системы
поле температур
после изменения температуры
ds
a
tint
init
Dit
t
В случае стационарного
теплового режима
однородного стержня:
a1
text
0
Δit Wint,
it
Dt2
2
0
z
1
a – коэффициент линейного
температурного расширения
материала
Dt
Δds ε0,t ds
0
Δ
ds
t
α Dt ds
рабочие ( эксплуатационные )
температуры
0
a
возможная работа внутренних сил i-го состояния
на свободных ( нестеснённых ) температурных
0
0
деформациях Δdst и dθt
Qi
Dt0 Δ t2 h2 Δ tnr
h
Δ tnr Δ t1 Δ t2
Dt1 > Dt2
Dt0
ds
Δdst0
Равномерное удлинение
(укорочение)
i
i
Эпюра Dt
0
t
d θ0t
Fi = 1
D text = text – tinit
D tint = tint – tinit
i
y
h1 h2
h
ds
tint
text
Вспомогательное ( фиктивное )
единичное состояние системы
ds
ds
Ni
d θ0t
Mi
h2
Δt
h nr
Mi + dMi
Ni
Mi
Q i Si N i
Qi
Деформация
сдвига не учитыh1
( в случае
Δ tnr вается
постоянного
h
k
с
сечения
ds
0 фактически
ck
d
θ
ρ
ds
Dt
t
t
nr
Искривление
отсутствует
h)

16.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
( ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ ) МЕТОДОМ МАКСВЕЛЛА – МОРА
Действительное
tinit – начальное
состояние системы
поле температур
после изменения температуры
ds
a
tint
init
Dit
t
В случае стационарного
теплового режима
однородного стержня:
a1
text
0
Δit Wint,
it
Dt2
2
0
рабочие ( эксплуатационные )
температуры
z
1
a – коэффициент линейного
температурного расширения
материала
a
возможная работа внутренних сил i-го состояния
на свободных ( нестеснённых ) температурных
0
0
деформациях Δdst и dθt
Qi
Dt0 Δ t2 h2 Δ tnr
h
Δ tnr Δ t1 Δ t2
Dt1 > Dt2
ds
Δdst0
Равномерное удлинение
(укорочение)
ds
Ni
Mi
d θ0t
h2
Δt
h nr
Mi + dMi
Ni
Mi
Q i Si N i
Qi
0
ds
ck
t
ds
d θ 0t α
dsρt0Δ
ds
(1)
t (2)
t nr
Dt0
Δds ε0,t ds
i
i
Эпюра Dt
0
t
α Dt0 ds
Fi = 1
D text = text – tinit
D tint = tint – tinit
i
y
h1 h2
h
ds
tint
text
Вспомогательное ( фиктивное )
единичное состояние системы
ds
ds
с
Искривление
k
h1
Δt
h nr
Dtnr
0 α Δtnr ck
d θt ρht ds ds
h

17.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
( ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ ) МЕТОДОМ МАКСВЕЛЛА – МОРА
Действительное
tinit – начальное
состояние системы
поле температур
после изменения температуры
ds
a
tint
init
Dit
t
В случае стационарного
теплового режима
однородного стержня:
y
2
0
h1 h2
h
ds
1
tint
text
a1
рабочие ( эксплуатационные )
температуры
Fi = 1
a
D text = text – tinit
D tint = tint – tinit
i
text
0
Δit Wint,
it
температурного расширения
материала
возможная работа внутренних сил i-го состояния
на свободных ( нестеснённых ) температурных
0
0
деформациях Δdst и dθt
j 1 l j
ds
i
dθ
0
t
Dt0
Δds ε0,t ds
0
t
ds
Δdst0
Равномерное удлинение
(укорочение)
i
i
0
dWint,
Qi
0 it
Wint,0 it
0
N
Δ
ds
M
d
θ
i
t
i
t
m
z
Ni
N
i N εi0, tε0, t M iM ρi t ρdst ds j M
a – коэффициент линейного
α Dt0 ds
Вспомогательное ( фиктивное )
единичное состояние системы
ds
Mi + dMi
Ni
Mi
Q i Si N i
Qi
d θ0t ρt ds
ds
с
Искривление
k
Dtnr
α Δtnr
ds
h

18.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
( ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ ) МЕТОДОМ МАКСВЕЛЛА – МОРА
Действительное
tinit – начальное
состояние системы
поле температур
после изменения температуры
ds
a
tint
init
Dit
t
В случае стационарного
теплового режима
однородного стержня:
a1
text
a
i
i
0
возможная работа внутренних сил i-го состояния
Δ
W
ds j ) температурных
Δitit N
Mi ρ(tнестеснённых
int,i it ε0,tна
свободных
j 1 l j
деформациях
Δdst0 и dθ0t
Qi
0
Wint,
it
z
m
ds
Ni
N i ε0,t Mi ρt ds j
1
a – коэффициент линейного
температурного расширения
материала
j 1 l j
Mi
d θ0t
Dt0
Δds ε0,t ds
0
t
α Dt0 ds
Fi = 1
m
2
0
рабочие ( эксплуатационные )
температуры
D text = text – tinit
D tint = tint – tinit
i
y
h1 h2
h
ds
tint
text
Вспомогательное ( фиктивное )
единичное состояние системы
ds
ds
Δdst0
Равномерное удлинение
(укорочение)
Mi + dMi
Ni
Mi
Q i Si N i
Qi
d θ0t ρt ds
ds
с
Искривление
k
Dtnr
α Δtnr
ds
h

19.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
( ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ ) МЕТОДОМ МАКСВЕЛЛА – МОРА
Действительное
tinit – начальное
состояние системы
поле температур
после изменения температуры
ds
a
tint
init
Dit
t
tint
text
a1
рабочие ( эксплуатационные )
температуры
Вспомогательное ( фиктивное )
единичное состояние системы
ds
Fi = 1
a
D text = text – tinit
D tint = tint – tinit
i
text
m
В случае стационарного Вариант записи формулы М – М:
Δit
N i ε0,t Mi ρt
теплового режима
однородного стержня:
j 1
z
ρt α Δtnr
h
1
a – коэффициент линейного
температурного расширения
материала
ds
Ni
Mi
d θ0t
Dt0
Δds ε0,t ds
0
t
α Dt0 ds
Qi
ε0,t α Dt0
2
0
i
lj
y
h1 h2
h
ds
ds j
i
ds
Δdst0
Равномерное удлинение
(укорочение)
Mi + dMi
Ni
Mi
Q i Si N i
Qi
d θ0t ρt ds
ds
с
Искривление
k
Dtnr
α Δtnr
ds
h

20.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
( ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ ) МЕТОДОМ МАКСВЕЛЛА – МОРА
Действительное
tinit – начальное
состояние системы
поле температур
после изменения температуры
ds
a1
a
tint
init
рабочие ( эксплуатационные )
температуры
Fi = 1
a
D text = text – tinit
D tint = tint – tinit
i
Dit
t
tint
text
Вспомогательное ( фиктивное )
единичное состояние системы
ds
text
i
В случае стационарного Вариант записи формулы М – М:
m0
теплового режима
однородного стержня:
Δit N i ε0,t ds j
y
ds
0
h1 h2
h
2
z
1
j 1 l j
mискрε0,t
ρ M
αi ρΔt tds j
t
j 1 l j
h
ε00, t
D t0
Δds
ε α ds
t
Qi
α Dt0
nr
ds
Ni
Mi
d θ0t
0,t
α Dt0 ds
Δdst0
Равномерное удлинение
(укорочение)
ds
Mi + dMi
Ni
Mi
Q i Si N i
Qi
α0 Δ
ρt
d θh
ρt tds
nr
t
Dt0
ds
i
с
Искривление
k
Dtnr
α Δtnr
ds
h

21.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
( ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ ) МЕТОДОМ МАКСВЕЛЛА – МОРА
Действительное
tinit – начальное
состояние системы
поле температур
после изменения температуры
ds
a1
a
tint
init
text
mMОбобщение
z
y
Dt2
h
0 4
h1 h2
2
3
z
1 b b
3 4
lj
mM y
Dt0
Δ tnr, z Δ t3 Δ t4
Qy,t
Эпюра Dt
Dt0 Δ t2 h2 Δ tnr, y
h
Δ tnr, y Δ t1 Δ t2
Dt1 > Dt2
Dt4
ε0,t α Dt0
a
lj
b
Dt3
Fi = 1
на случай
Δit пространственной
Mz,i ρz,t ds j
M y,i ρ y,t
температурной
деформации:
j 1
j 1
В случае стационарного
теплового режима
однородного стержня:
ds
рабочие ( эксплуатационные )
температуры
D text = text – tinit
D tint = tint – tinit
i
Dit
t
tint
text
Вспомогательное ( фиктивное )
единичное состояние системы
ds
Δdst0
Равномерное удлинение
(укорочение)
m0
ds j Ni ε0,t ds j
j 1 l j
ds
Ni
Mz,i
dθ
0
z,t
Dt0
ds
i
ds
с
Искривление
k
i
h2
Δt
h nr, y
Mz,i + dMz,i
Ni
M
Qy,t S Mz,i
i
y,i
Ni
h1
Δ tnr, y ρz,t α Δtnr, y
h
h
Dtnr, y
ρ y,t α Δtnr,z
b

22.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
( ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ ) МЕТОДОМ МАКСВЕЛЛА – МОРА
Действительное
tinit – начальное
состояние системы
поле температур
после изменения температуры
ds
a1
a
tint
init
text
mS
y
Dt2
h
0 4
h1 h2
2
3
z
1 b b
3 4
по S j 1 l j
Dt0
Δ tnr, z Δ t3 Δ t4
Qy,t
Dt0 Δ t2 h2 Δ tnr, y
h
Δ tnr, y Δ t1 Δ t2
Dt1 > Dt2
Mz,i
dθ
Dt0
ds
Δdst0
Равномерное удлинение
(укорочение)
ε
ds
Ni
0
z,t
ds
с
Искривление
k
i
i
0
S,t
Эпюра Dt
Dt4
ε0,t α Dt0
a
Δit Si ε ds j
b
Dt3
Fi = 1
Сокращённая запись формулы М – М:
В случае стационарного
теплового режима
однородного стержня:
ds
рабочие ( эксплуатационные )
температуры
D text = text – tinit
D tint = tint – tinit
i
Dit
t
tint
text
Вспомогательное ( фиктивное )
единичное состояние системы
ds
h2
Δt
h nr, y
0
S,t
rz,t
ry,t
e0, t
Mz,i + dMz,i
Ni
M
Qy,t S Mz,i
i
y,i
Ni
h1
Δ tnr, y ρz,t α Δtnr, y
h
h
Dtnr, y
ρ y,t α Δtnr,z
b

23.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
( ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ ) МЕТОДОМ МАКСВЕЛЛА – МОРА
Пример
o
text = – 30 C
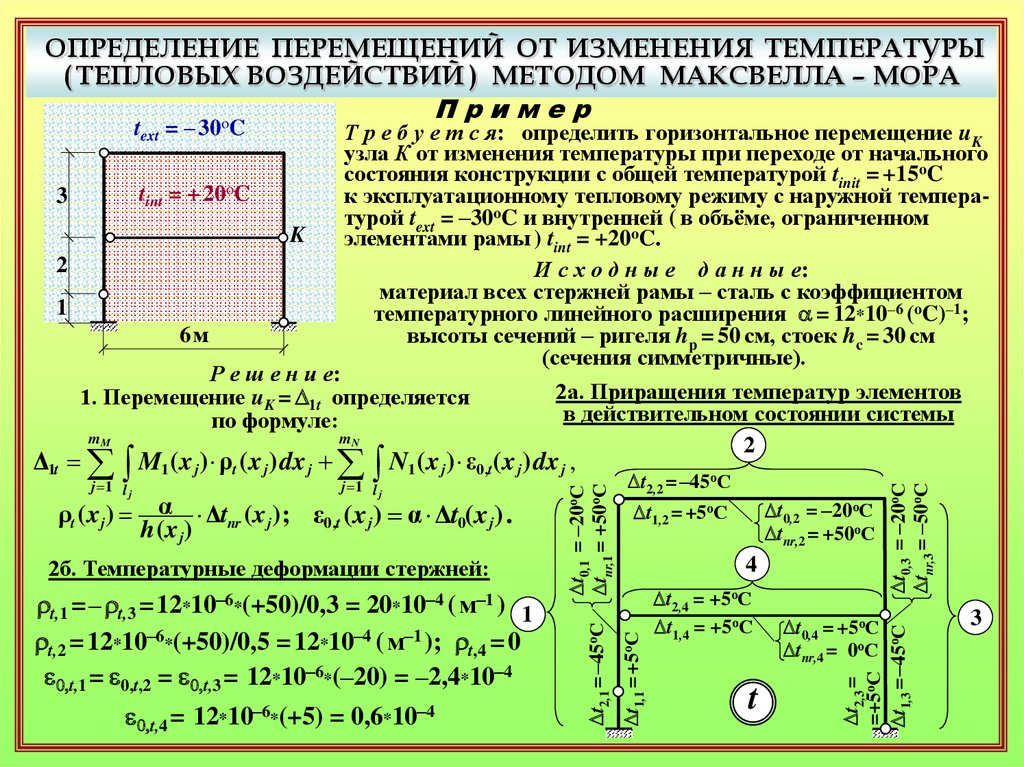
rt,1 = – rt,3 = 12*10–6*(+50)/0,3 = 20*10–4 ( м–1 ) 1
rt,2 = 12*10–6*(+50)/0,5 = 12*10–4 ( м–1 ); rt,4 = 0
e0,t,1 = e0,t,2 = e0,t,3 = 12*10–6*(–20) = –2,4*10–4
e0,t,4 = 12*10–6*(+5) = 0,6*10–4
Dt0,2 = –20оС
Dtnr,2 = +50оС
Dt1,2 = +5оС
4
Dt2,4 = +5оС
Dt1,4 = +5оС
t
Dt0,4 = +5оС
Dtnr,4 = 0оС
Dt2,3 =
=+5оС
Dt1,3 = –45оС
2б. Температурные деформации стержней:
Dt2,2 = –45оС
Dt1,1 = +5оС
α Δt ( x ) ; ε ( x ) α Δt ( x ) .
0,t
j
0
j
h ( x j) nr j
Dt2,1
ρt ( x j)
j 1 l j
= –45оС
j 1 l j
Dt0,1 = –20оС
Dtnr,1 = +50оС
Δ1t M1 ( x j) ρt ( x j) dx j N1 ( x j) ε0,t( x j) dx j ,
Dt0,3 = –20оС
Dtnr,3 = –50оС
Т р е б у е т с я: определить горизонтальное перемещение uK
узла К от изменения температуры при переходе от начального
состояния конструкции с общей температурой tinit = +15oC
tint = + 20oC
3
к эксплуатационному тепловому режиму с наружной температурой text = –30oC и внутренней ( в объёме, ограниченном
K
элементами рамы ) tint = +20oC.
2
И с х о д н ы е д а н н ы е:
материал всех стержней рамы – сталь с коэффициентом
1
температурного линейного расширения a = 12*10–6 (oC)–1;
6м
высоты сечений – ригеля hp = 50 см, стоек hc = 30 см
(сечения симметричные).
Р е ш е н и е:
2а. Приращения температур элементов
1. Перемещение uK = D1t определяется
в действительном состоянии системы
по формуле:
mM
mN
2
3

24.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
( ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ ) МЕТОДОМ МАКСВЕЛЛА – МОРА
Пример
o
text = – 30 C
Т р е б у е т с я: определить горизонтальное перемещение uK
узла К от изменения температуры при переходе от начального
состояния конструкции с общей температурой tinit = +15oC
tint = + 20oC
3
к эксплуатационному тепловому режиму с наружной температурой text = –30oC и внутренней ( в объёме, ограниченном
K
элементами рамы ) tint = +20oC.
2
И с х о д н ы е д а н н ы е:
материал всех стержней рамы – сталь с коэффициентом
1
температурного линейного расширения a = 12*10–6 (oC)–1;
6м
высоты сечений – ригеля hp = 50 см, стоек hc = 30 см
(сечения симметричные).
Р е ш е н и е:
2в. Эпюры температурных деформаций
1. Перемещение uK = D1t определяется
в действительном состоянии системы
по формуле:
mM
mN
j 1 l j
j 1 l j
Δ1t M1 ( x j) ρt ( x j) dx j N1 ( x j) ε0,t( x j) dx j ,
ρt ( x j)
α Δt ( x ) ; ε ( x ) α Δt ( x ) .
0,t
j
0
j
h ( x j) nr j
2б. Температурные деформации стержней:
rt,1 = – rt,3 = 12*10–6*(+50)/0,3 = 20*10–4 ( м–1 )
rt,2 = 12*10–6*(+50)/0,5 = 12*10–4 ( м–1 ); rt,4 = 0
e0,t,1 = e0,t,2 = e0,t,3 = 12*10–6*(–20) = –2,4*10–4
e0,t,4 = 12*10–6*(+5) = 0,6*10–4
20
12
2,4
0
0,6
rt
20
( 10–4 м–1 )
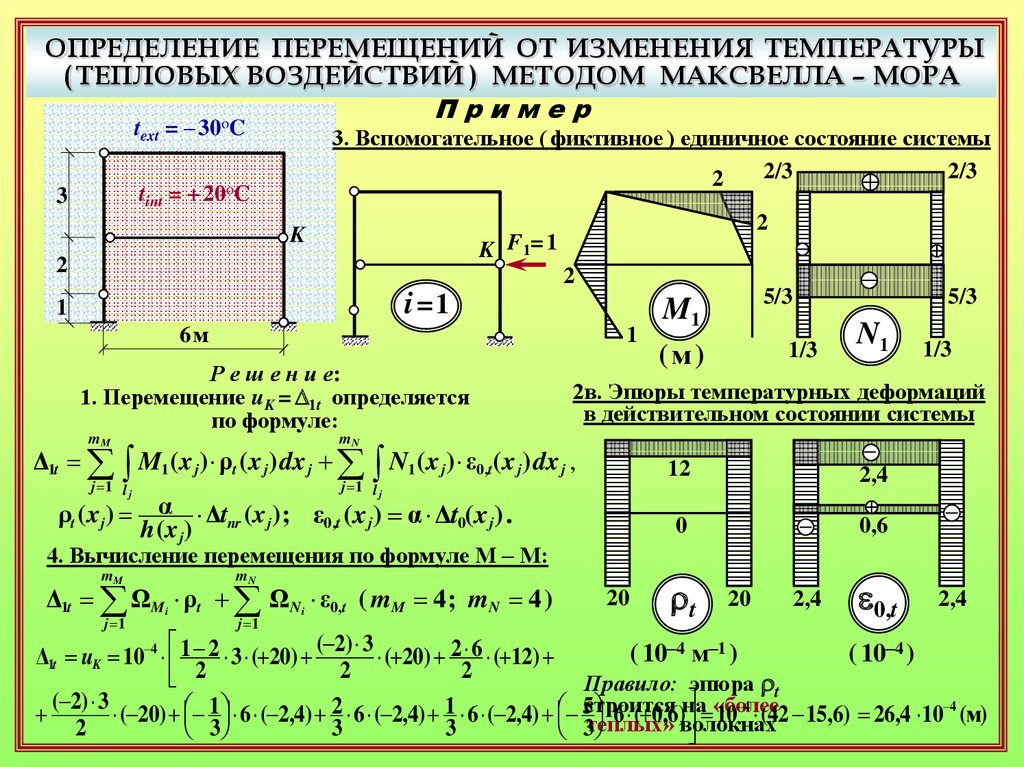
Правило: эпюра rt
cтроится на «более
теплых» волокнах
2,4
e0,t
( 10–4 )
2,4

25.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
( ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ ) МЕТОДОМ МАКСВЕЛЛА – МОРА
Пример
o
text = – 30 C
3. Вспомогательное ( фиктивное ) единичное состояние системы
2/3
2/3
2
tint = + 20oC
3
K
2
K F1 = 1
2
2
i =1
1
6м
1
Р е ш е н и е:
1. Перемещение uK = D1t определяется
по формуле:
mM
mN
j 1 l j
j 1 l j
α Δt ( x ) ; ε ( x ) α Δt ( x ) .
0,t
j
0
j
h ( x j) nr j
4. Вычисление перемещения по формуле М – М:
2б. Температурные
mM
mNдеформации стержней:
ρt –6
ΩN i ε0,t=(20
mM*10
–44 ;( мm–1N) 4 )
rΔt,11t= –
rt,3Ω=M12
*(+50)/0,3
i *10
j 1
j 1
–6
rt,2 = 12*10 *(+50)/0,5 = 12*10–4 ( м–1 ); rt,4 = 0
e0,t,1 = e0,t,2 = e0,t,3 = 12*10–6*(–20) = –2,4*10–4
e0,t,4 = 12*10–6*(+5) = 0,6*10–4
(м)
5/3
1/3
N1
1/3
2в. Эпюры температурных деформаций
в действительном состоянии системы
Δ1t M1 ( x j) ρt ( x j) dx j N1 ( x j) ε0,t( x j) dx j ,
ρt ( x j)
5/3
M1
20
12
2,4
0
0,6
rt
20
( 10–4 м–1 )
Правило: эпюра rt
cтроится на «более
теплых» волокнах
2,4
e0,t
( 10–4 )
2,4

26.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ
( ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ ) МЕТОДОМ МАКСВЕЛЛА – МОРА
Пример
o
text = – 30 C
3. Вспомогательное ( фиктивное ) единичное состояние системы
2/3
2/3
2
tint = + 20oC
3
K
2
K F1 = 1
2
2
i =1
1
6м
1
Р е ш е н и е:
1. Перемещение uK = D1t определяется
по формуле:
mM
mN
j 1 l j
j 1 l j
(м)
5/3
1/3
N1
1/3
2в. Эпюры температурных деформаций
в действительном состоянии системы
Δ1t M1 ( x j) ρt ( x j) dx j N1 ( x j) ε0,t( x j) dx j ,
ρt ( x j)
5/3
M1
α Δt ( x ) ; ε ( x ) α Δt ( x ) .
0,t
j
0
j
h ( x j) nr j
12
2,4
0
0,6
4. Вычисление перемещения по формуле М – М:
mM
mN
Δ1t ΩMi ρt ΩN i ε0,t ( mM 4 ; mN 4 )
j 1
j 1
20
rt
20
2,4
e0,t
2,4
( 2) 3
( 10–4 м–1 )
( 10–4 )
Δ1t uK 10 4 1 2 3 ( 20)
( 20) 2 6 ( 12)
2
2
2
Правило: эпюра rt
( 2) 3
«более
4
4
cтроится
6 ( 0,6)на
( 20) 1 6 ( 2,4) 2 6 ( 2,4) 1 6 ( 2,4) 5теплых»
10
(42
15,6)
26,4
10
(м)
волокнах
2
3
3
3
3

27.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ СМЕЩЕНИЙ СВЯЗЕЙ
МЕТОДОМ МАКСВЕЛЛА – МОРА
Действительное состояние системы
с кинематическими возмущениями
( смещениями связей )
Dic
a
с
D(2)
D(1)
a1
Равновесные
состояния
i
=
Wint,ic
по S j 1 l j
Si Sc
ds j = – Wint, ci
CS
i
i
D( j ) r – число компонентов
заданных смещений
D( r ) связей
Wint, ci = 0
m
Fi = 1
a
Wext, ci + Wint, ci = 0
0
Вспомогательное ( фиктивное )
единичное состояние системы
R( 1 ), i
R( 2 ), i
R( r ), i
R( j ), i
Правило знаков для единичных
реакций смещаемых связей:
W R ic +положительная,
Wint, ic = 0
реакцияext,
( j ), i
если её возможная работа
Fi Δic D положительная
на перемещении
( j)
r
R
и D( j )
( иначе:
R(векторы
j), i Δ( j) ( j ), i
направлены
в одну и ту же сторону )
j 1
r r
Δ
W
Δicic R(Rj),(i j ),Δi ( jΔ
)
( j) int,ic
j j1 1

28.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ СМЕЩЕНИЙ СВЯЗЕЙ
МЕТОДОМ МАКСВЕЛЛА – МОРА
Пример
2. Действительное состояние системы
с заданными смещениями связей
6м
Т р е б у е т с я:
определить горизонтальное перемещение uK
узла К от углового и линейных смещений
опор А и В.
Р е ш е н и е:
1. Перемещение uK = D1c определяется
по формуле:
3
r
Δ1c R( j), i Δ( j) , где r 4
K
2
А
1
А*
D0,002
(1) =0,002
с
j 1
В
D
1,2
(3) =1,2 см
см
Нумерация компонентов смещений связей
D(4)см
=1,5 см
В* 1,5
3. Вспомогательное ( фиктивное )
единичное состояние системы
1D
см
(2) =1 см
4. Вычисление перемещения по формуле М – М:
K F1 = 1
4
uK Δ1c R( j), i Δ( j)
j 1
R( 2 ), 1 = –1 А
i =1
В
1
( 1 м ) 0,002 ( 1) 0,01 м 0,012 м
3
R( 1 ), 1 = 1м
R( 3 ), 1 = –1/3 R( 4 ), 1 = 1/3
1 0,015 м 0,007 м
3

29.

УНИВЕРСАЛЬНАЯ ФОРМУЛА МАКСВЕЛЛА – МОРА
ДЛЯ ПЕРЕМЕЩЕНИЙ ЛИНЕЙНО ДЕФОРМИРУЕМЫХ СИСТЕМ
ΔiΣ ΔiF Δit Δic
m
mM z
mN
My
mMt
M y,i M y,F
M z,i M z,F
M M
ds j
ds j t,i t,F ds j
EIz Изгиб
EI y Изгиб
GIt Кручение
j 1 l j
j 1 l j
j 1 l j
mQ y
mQz
u
Qy,i Qy,F
Rj,i Rj,F
Qz,i Qz,F
Ni NF
ds j kτy
ds j kτz
ds j
EA
GA
GA
c
j
j 1 l
j 1 l
j 1
Сдвиг
Сдвиг
j 1 l j Растяжение/
сжатие
mM z
j
j
mM y
m0
Mz,i ρz,t ds j M y,i ρ y,t ds j Ni ε0,t ds j
j 1 l j Температурные
искривления
j 1 l j Температурные
j 1 l j
искривления
r
R( j ), i Δ( j )
Деформации
упругих связей
Продольные
температурные
деформации
j 1 Смещения связей
Сокращённая форма записи:
ΔiΣ ΔiF Δit Δic
mS
по S j 1 l j
r
u
mS
Rj,i Rj,F
Si SF
0
ds j
Si εS,t ds j R( j), i Δ( j)
CS
с
j
j 1
по S j 1 l От изменения
j 1 От смещений
От силовых воздействий ( нагрузок )
j
температуры
связей

30.

Контрольные
вопросы
( в скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 30» )
1. Частные случаи формулы Максвелла – Мора ( ФМ – М ) для перемещений от силовых
воздействий: а) в случае плоской стержневой системы; ( 2 )
б) для стержневых систем разных типов. ( 2 )
2. Алгоритм вычисления перемещения по ФМ – М. ( 3 )
3. Как истолковываются знаки « + » или « – » в результате вычисления перемещения
по ФМ – М? ( 3 )
4. Что означает термин «перемножение эпюр»? ( 3 )
5. Формулировка правила Верещагина для «перемножения эпюр». Каково необходимое
условие применимости правила Верещагина? ( 7 )
6. Как используется правило Верещагина для «перемножения эпюр» в случае, когда «грузовая» эпюра – параболическая общего вида? ( разложение на простые составляющие –
самостоятельно )
7. Формула Симпсона, условие её применимости для «перемножения эпюр». ( 8 )
8. В каких случаях вычисление интегралов в ФМ – М по формуле Симпсона даёт точный
результат? ( 8 )
9. Формула Максвелла – Мора для перемещения от изменения температуры,
варианты её записи. ( 18 – 22 )
10. От каких характеристик температурного режима и параметров системы зависит
температурное перемещение? ( 15 )
_11. Как вычисляются нестеснённые температурные деформации ( кривизна
и относительная продольная деформация ) в ФМ – М для перемещения
от изменения температуры? ( 19 )
___________________________________________________
*)
Только в режиме «Показ слайдов»

31.

Контрольные
вопросы
( в скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 31» )
12. Почему в ФМ – М для температурного перемещения отсутствуют характеристики
жёсткости элементов системы? ( 12 )
13. Правила знаков для температурных деформаций. Как стоится эпюра кривизн? ( 24 )
14. Формула Максвелла – Мора для перемещения от кинематических воздействий
( смещений связей ). ( 27 )
15. Правило знаков для единичных реакций смещаемых связей. ( 27 )
16. Универсальная формула Максвелла – Мора для перемещений линейно деформируемых
пространственных стержневых систем ( полная развернутая запись ). ( 29 )
17. Сокращённая запись универсальной формулы Максвелла – Мора,
смысл её составляющих. ( 29 )
_____________________________________________________
*)
Только в режиме «Показ слайдов»