Похожие презентации:
Общая постановка задачи оптимизации
1.
Литература1. Аттетков А.В., Галкин С.В., Зарубин B.C. Методы
оптимизации: учеб. для вузов. ‑ М.: Изд-во МГТУ им. Н.Э.
Баумана, 2003.
2. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов
оптимизации: учеб. пособие. ‑ 2-е изд. ‑ М.: ФИЗМАТЛИТ,
2005.
3. Пантелеев А.В., Летова Т.А. Методы оптимизации в
примерах и задачах: учеб. пособие. ‑ 2-е изд., исправл.
– М.: Высшая школа, 2005.
2.
Общая постановка задачи оптимизацииТребуется найти вектор x* x1* , x2* , , xn* ,
соответствующий экстремальному (минимальному или
максимальному) значению функции f (x) и принадлежащий
Для существования решения задачи оптимизации целеваяn функция
области n-мерного эвклидова пространства R
и допустимое множество должны обладать
определенными
n
(x) extr,случае
x Rсуществование
свойствами.
В fобщем
решения
устанавливается следующей теоремой Вейерштрасса:
extr f (x) : x
Всякая функция, непрерывная
на непустом замкнутом и
ограниченном множестве,extr
обладает
наибольшим и наименьшим
f (x)
значениями,
которые достигаются
либо внутри множества, либо
x
Целевая функция
Допустимая область
на его границе.
*
x
Для определения глобального экстремума необходимо выявить и
Точка экстремума
исследовать все точки, подозреваемые на экстремум. Эти точки
называют также экстремальными
или критическими.
n
min f (x) max( f (x))
f (x) min, x R
x
x
3.
Математические основы безусловнойоптимизации
Необходимые математические сведения
Точка x * называется точкой глобального (абсолютного)
минимума функции f (x) на множестве , если функция
достигает в этой точке своего наименьшего значения,
т.е.
f (x* ) f (x), x
Точка x * называется точкой локального (относительного)
минимума функции f (x) на множестве , если существует ,
такое, что для любых x , удовлетворяющих условию x x * ,
справедливо неравенство f (x* ) f (x) . Т.е.
f (x* ) f (x), x : x x x *
4.
Необходимые математическиесведения
Градиент непрерывно дифференцируемой функции
f f
f
f ( x )
,
, ,
xn
x1 x2
T
Градиент функции в точке х направлен в сторону наибольшего возрастания
функции в данной точке.
Матрица Гессе дважды дифференцируемой функции
2 f
2
x
1
2
f
H(x) x x
2 1
2 f
x x
n 1
2 f
x1 x2
2 f
x22
2 f
xn x2
2 f
x1 xn
2 f
x2 xn
2 f
xn2
2 f ( x) f (x)
hij
, i, j 1, , n
xi x j xi x j
5.
Необходимые математическиесведения
Угловые миноры матрицы
a11 a12
a21 a22
i det
ai1 ai 2
1 a11
2
a11
a1i
a2i
aii
a12
a21 a22
a11 a12
3 a21 a22
a13
a23
a31
a33
a32
6.
Задание 1. Вычислить градиент и матрицу Гессе функции1
1
f x , x x3 x 2 в точке (0; 1).
1
2
3
1
2
2
7.
Необходимые математическиесведения
Критерий Сильвестра
Матрица H положительно определена H>0 тогда и только
тогда, когда все ее угловые миноры положительны.
Матрица H отрицательно определена H<0 тогда и только
тогда, когда все ее угловые миноры чередуют знак, начиная с
отрицательного.
Матрица H положительно полуопределена H ≥ 0 тогда и только
тогда, когда все ее угловые миноры неотрицательны.
8.
Необходимые математическиесведения
Множество X R n называется выпуклым, если оно содержит
всякий отрезок, которой целиком принадлежит X .
0 1
x (1) , x ( 2 ) X
x (1) (1 ) x ( 2 ) X
Примеры
выпуклого
и
невыпуклого
множеств
9.
Необходимые математическиесведения
Свойства выпуклых функций
Дважды дифференцируемая на интервале [a, b] функция f (x)
выпукла, если на этом интервале ее вторая производная
неотрицательная:
2
d f ( x)
0
2
dx
Выпуклость функции f (x) можно определить также по
матрице Гессе:
- если H 0 , то f (x) - выпуклая функция;
- если H 0 , то f (x) - строго выпуклая функция.
Если f (x) выпуклая функция на выпуклом множестве Х, то
всякая точка локального минимума является точкой ее
глобального минимума на Х.
10.
Условия экстремальностиНеобходимые условия экстремума 1-го порядка
f (x*)
0, i 1, , n
f (x*) 0 или
xi
x *- стационарные точки.
Необходимые условия экстремума 2-го порядка
Вычисляем собственные числа матрицы Гессе det( H(x*) E) 0
i 0 локальный минимум
i 0 локальный максимум
i 0 возможен локальный максимум
i 0 возможен локальный минимум
Если собственные числа разных знаков, экстремума нет!
11.
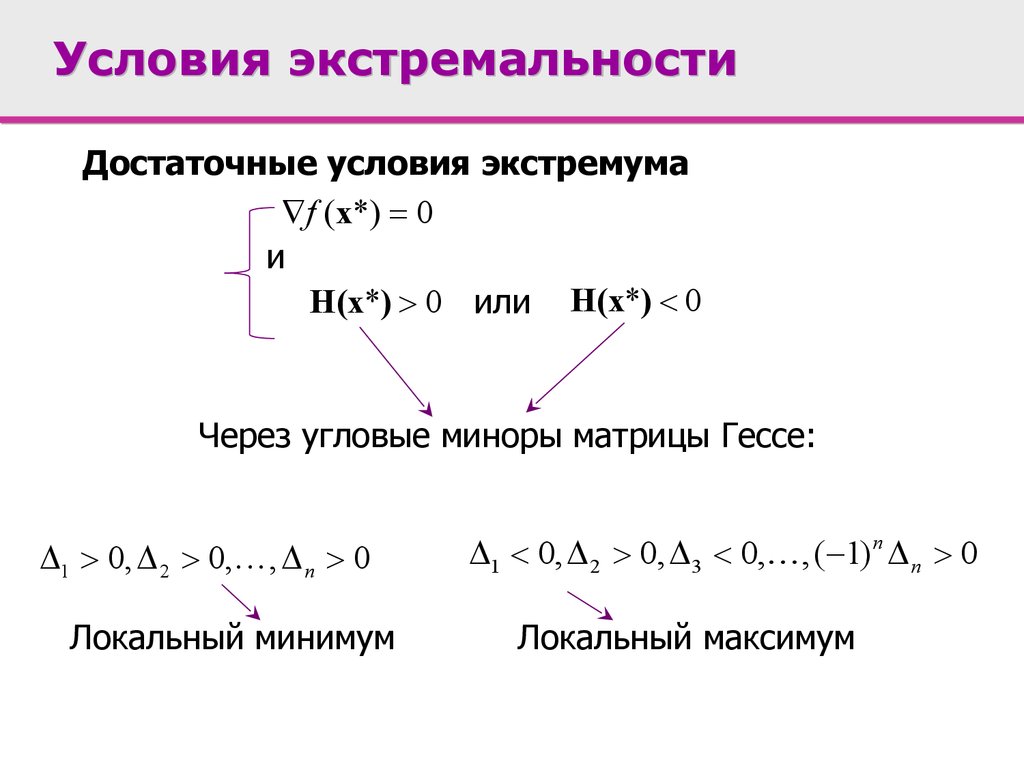
Условия экстремальностиДостаточные условия экстремума
f (x*) 0
и
H(x*) 0 или H(x*) 0
Через угловые миноры матрицы Гессе:
1 0, 2 0, , n 0
Локальный минимум
1 0, 2 0, 3 0, , ( 1) n n 0
Локальный максимум
12.
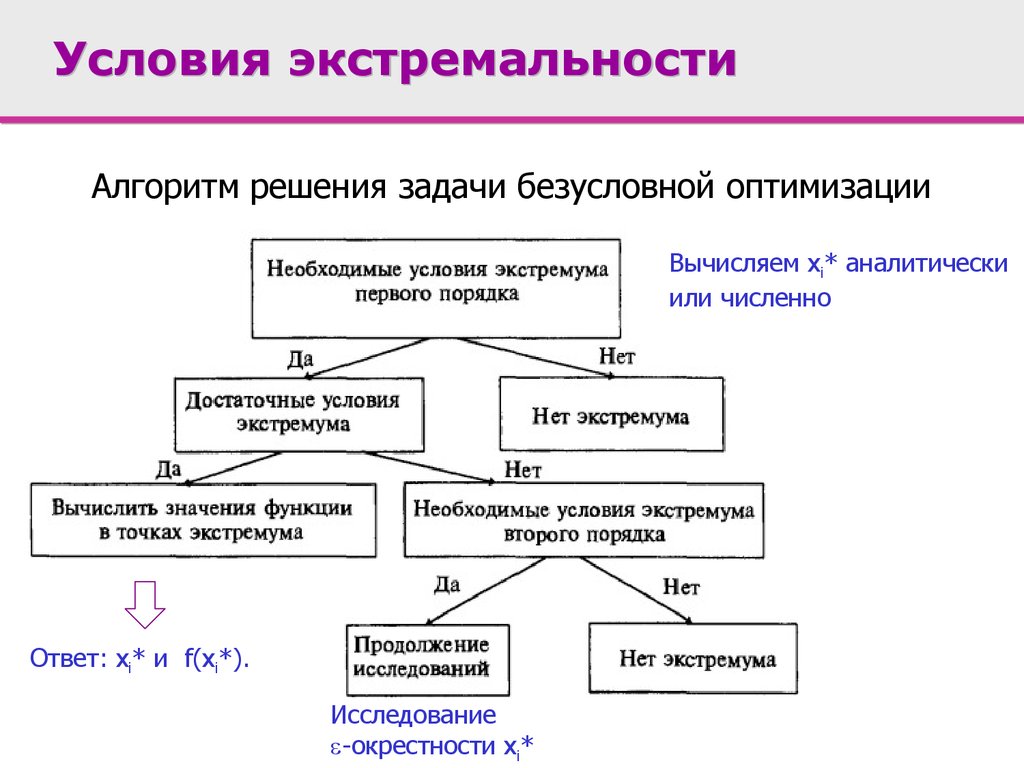
Условия экстремальностиАлгоритм решения задачи безусловной оптимизации
Вычисляем xi* аналитически
или численно
Ответ: xi* и f(xi*).
Исследование
-окрестности xi*
13.
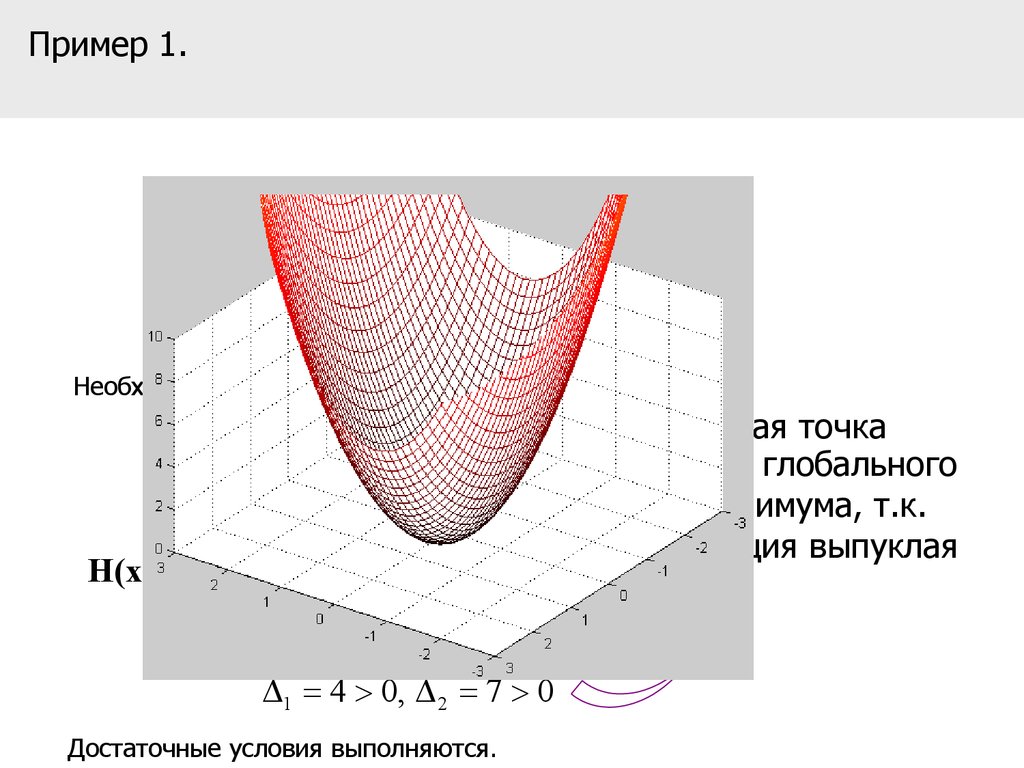
Пример 1.f (x) 2 x12 x1 x2 x22
f (x)
f (x)
4 x1 x2 0,
2 x2 x1 0.
x1
x2
Необходимые условия 1-го порядка выполняются.
стационарная точка
точка глобального
2 f
2 f
минимума, т.к.
функция выпуклая
x12
x1 x2 4 1
H(x)
2
2 f
f
1 2
2
x
x
x
2
2 1
1 4 0, 2 7 0
x* (0,0)
Достаточные условия выполняются.
14.
Пример 2.f (x) 2 x13 4 x1 x22 10 x1 x2 x22
f (x)
6 x12 4 x22 10 x2 0,
x1
x* (0,0)
x* (1,1)
f (x)
8 x1 x2 10 x1 2 x2 0.
x2
стационарные точки
Необходимые условия 1-го порядка выполняются.
8 x2 10
12 x1
H(x)
8 x2 10 8 x1 2
15.
8 x2 1012 x1
H(x)
8 x2 10 8 x1 2
H ( 0, 0)
10
0
10 2
1 0, 2 100
- достаточные условия не выполняются.
Проверяем необходимые условия 2-го порядка:
1
det(H (x* ) E) 0 2 2 100 0
1
2 1 101
x* (0,0) - экстремума нет, т.к. собственные числа разного знака
12 2
H (1,1)
2 10
1 12, 2 116
x* (1,1)
- достаточные условия выполняются.
- точка локального минимума
101
16.
Пример 3.f ( x)
2
x1
4
x2
f (x)
2 x1 0,
x1
x* (0,0)
f (x)
4 x23 0.
x2
Необходимые условия 1-го порядка выполняются.
0
2
H(x)
2
0
12
x
2
1 2 0, 2 0
*
2 0
H(x )
0 0
*
- достаточные условия не выполняются.
det(H (x ) E) 0 (2 ) 0
1 0
1 2
x* (0,0) - возможно, локальный минимум. Необходимо доп. исследование.
17.
f (x) x12 x24x* (0,0)
По определению, если локальный минимум, то
f (x* ) f (x), x : x x x *
0 0 2 0 4 ,
x* (0,0)
- глобальный минимум
18.
Задания для закрепления материала19.
Задания для самостоятельного решенияВ качестве д/з – по 0,4 балла за задачу.
1. Найти экстремум функции:
а)
f (x) x 1 6
б)
f ( x) x 3 2 x 2 x 1
в)
f (x) 1 x1 10 x2
г)
f (x) x12 x22 x32 x1 x1x2 2 x3
д)f
2
2 2
x1
(x) x1 x3 2 4 x22 x32
















 Математика
Математика








