Оптимизация химико-технологических процессов. Одномерная и многомерная задачи оптимизации

1.

1
Оптимизация химикотехнологических процессов.
Лекция 2. Одномерная и
многомерная задачи
оптимизации

2.

2
Математическая формулировка задачи оптимизации
Необходимо найти такие значения вектора переменных х, при
которых критерий оптимальности (или оптимизации) R(х) принимает
минимальное значение и при этом выполняются ограничения типа
равенства, неравенства и двухстороннее ограничение на поисковые
переменные:
min R(x),
(1)
x X
1. Ограничения типа равенства
φi(х )= 0, i = 1, … m
(2)
соответствуют условиям выполнения материального и теплового
балансов.
2. Ограничения типа неравенства
ψj(x) ≤ 0, j = 1, … p
(3)
определяют область значений параметров, внутри которой должна
находиться оценка.
3. Двухстороннее ограничение на поисковые переменные по
минимальному и максимальному значениям:
xmin ≤ x ≤ xmax ,
(4)
где R(x) – критерий оптимальности (оптимизации) (скаляр);
X = (х1, х2, …,хn) – вектор поисковых переменных; хmin и хmax –
минимальная (нижняя) и максимальная (верхняя) границы параметров.

3.

3
Отметим, что задача минимизации связана с задачей
максимизации равенством
maxR(x) = – min[–R(x)]
(5)
Поэтому все методики решения, алгоритмы и т.п.,
связанные с задачей минимизации могут быть применены к
задаче максимизации.
Задачей оптимизации является задача поиска минимума
или максимума критерия оптимизации (целевой функции),
другими словами – это задача поиска экстремума.
Ограничения (1) –(3) определяют допустимую область
решения задачи оптимизации.
Допустимое решение – это такое решение, которое
удовлетворяет ограничениям равенства и неравенства,
верхним и нижним границам изменения поисковых
переменных

4.

Существование решения поставленной задачи вытекает из
теоремы Вейерштрасса.
Всякая функция f(x), непрерывная на отрезке
a,b
принимает на этом отрезке наименьшее и наибольшее
значения, т. е. на отрезке
a,b
существуют такие точки
x1
и
что для любого
x2
x a ,b
имеют место неравенства
f x1 f x f x2
4

5.

5
Основные классы задач оптимизации
Два типа задач оптимизации по условиям оптимизации
1. Задача условной оптимизации (или задачи с
ограничениями) - это такие, при формулировке
которых на значения аргументов налагаются
ограничения в виде равенств или неравенств, т.е.
в задаче имеются ограничения (2) – (4).
2. Безусловная задача состоит в нахождении
минимума или максимума функции в отсутствие
каких-либо ограничений.

6.

Геометрическая интерпретация задачи оптимизации
6
Значения критерия оптимальности можно рассмотреть как
функцию, определенную в n-мерном пространстве переменных
xi (j=1, … , n), т.е.
R(X),
min
X
(5)
x X
Поскольку наглядное графическое изображение n-мерного
пространства отсутствует, то используем приём представления
функции R(X) на плоском чертеже

7.

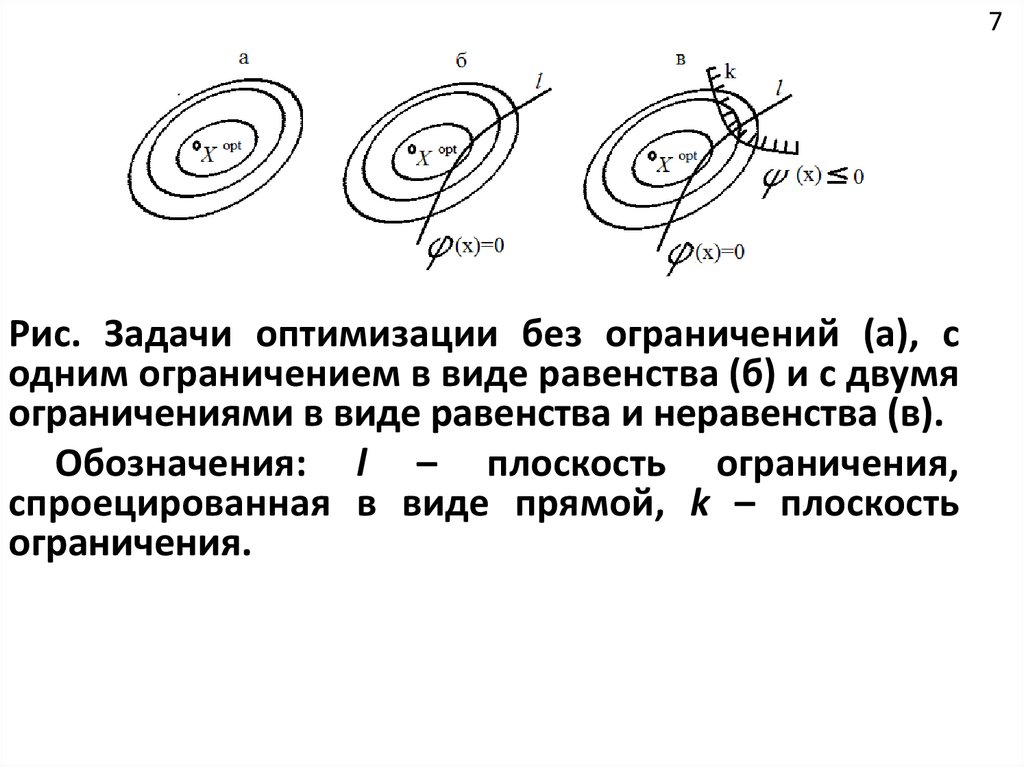
7
Рис. Задачи оптимизации без ограничений (а), с
одним ограничением в виде равенства (б) и с двумя
ограничениями в виде равенства и неравенства (в).
Обозначения: l – плоскость ограничения,
спроецированная в виде прямой, k – плоскость
ограничения.

8.

Классификация по количеству точек
минимума
1. Если целевая функция R(x) имеет в области
допустимых значений один минимум
(максимум), то задача называется
одноэкстремальной задачей оптимизации.
2. Если целевая функция R(x) имеет в области
допустимых значений более одного минимума
(максимума), то задача называется
многоэкстремальной задачей оптимизации.
8

9.

Виды экстремумов (максимумов, минимумов)
1. Строгий экстремум
При оптимальном
параметре х* функция
f(x)* принимает
экстремальное
значение
2. Нестрогий
экстремум

10.

Классификация по характеру искомого решения.
Локальный и глобальный экстремумы
Пусть функция R(x) имеет несколько экстремумов
Точка х1* - строгий локальный минимум; точка х3*
- строгий глобальный минимум.
1. Если отыскивается любой локальный минимум
функции R(x), то задача называется задачей
локальной оптимизации.
2. Если отыскивается глобальный минимум
функции R(x), то задача называется задачей
глобальной оптимизации.
9

11.

Линейная и нелинейная оптимизация
10
1. Если функция F (x) и ограничения равенства φi(х )= 0 и
неравенства ψj(x) ≤ 0 линейны,n т.е.
f(x1, x2, …,xn) =i 1ci xi ,
(6)
то ставится задача линейной оптимизации (линейного
программирования).
2. Если функция F (x) или ограничения равенства φi(х )= 0
и неравенства ψj(x) ≤ 0, либо все месте нелинейны, то
ставится
задача
нелинейной
оптимизации
(нелинейного математического программирования).

12.

11
Различают задачи нелинейной оптимизации:
а) указанные функции относятся к классу выпуклых
(вогнутых), то ставится задача выпуклой (вогнутой)
оптимизации;
б) если критерий R(x) имеет вид квадратичной
зависимости, т.е.
n
n n
f(x1, x2, …,xn) = i 1ci xi i 1 j 1d ij xi x j ,
(7)
то ставится задача квадратичного программирования;
в) если критерий и ограничения относятся к классу
мультипликативных функций (функции
перемножаются), то ставится задача геометрического
программирования:
f(x1, x2, …,xn) = сх1ах2b… xnn.
(8)

13.

Непрерывная, дискретная, целочисленная
оптимизация
12
Если в задачах оптимизации функция R (x),
ограничения равенства φi(х) = 0 и неравенства ψj(x) ≤ 0
непрерывны на множестве допустимых значений, то
можно говорить о непрерывной задаче
оптимизации.
Если же какая-либо из функций не задана как
непрерывная, или множество оптимизации является
дискретным, то говорят о дискретной задаче
оптимизации.
Целочисленная оптимизация - это задача, в которой
функция F (x) и ограничения должны быть целыми
числами.

14.

Выпуклый критерий оптимизации
13
Непрерывный критерий оптимизации R(x)
называется выпуклым (строго выпуклым), если
для любых х1, х2 (х1≠ х2) и любого α [0,1 ]
выполняется равенство
R[(1-α)x1+αx2] ≤ (1-α)R(x1)+αR(x2)
(10)
R[(1-α)x1+αx2] < (1-α)R(x1)+αR(x2)
(11)
Аналогично, с заменой знака неравенства на
противоположный, можно определить вогнутый
(строго вогнутый) критерий оптимизации.

15.

14
Геометрический смысл выпуклости: все точки
кривой на интервале [х1, х2] лежат под хордой AB

16.

15
Условия существования минимума в безусловных
задачах оптимизации
Рассмотри одномерную задачу оптимизации
min R(х),
x [ a ,b ]
т.е. необходимо найти такие значения переменой х,
принадлежащей отрезку [a,b], при котором функция
R(x) принимает минимальное значение.
Необходимое условие минимума
R
(12)
R ( x )
0
x
Решениями уравнения (12) являются стационарные
точки – минимума, максимума и перегиба функции
R(x)

17.

Первое достаточное условие существования
экстремуму
Исследуют поведение функции R(х) в окрестности ε
«подозрительной» точки (точка локального экстремума) x0,
для чего вычисляют
R(x0-δ) и R(x0+δ)
где δ ≤ ε.
• Если R(x0-δ) < R(x0) и R(x0+δ) < R(x0), то х0 есть точка
максимума.
• Если R(x0+δ) < R(x0) и R(x0+δ) < R(x0), то х0 есть точка
максимума.
• Если R(x0-δ) > R(x0) и R(x0+δ) < R(x0), то х0 есть точка
минимума.
• Если R(x0+δ) > R(x0) и R(x0+δ) < R(x0), то х0 есть точка
минимума.
16

18.

17
Второе достаточное условие существования
экстремуму
Исследуют поведение первой производной
функции dR/dх в окрестности ε
«подозрительной» точки x0
• Если R'(x0-δ) ≠ R(x0+δ), то имеется экстремум
в точке х0.
• При этом, если R''(x0) -δ) > 0 и R'(x0+δ)<0, то
в точке х0 максимум;
если R'(x0-δ) > 0 и R'(x0+δ) >0, то в
точке х0 минимум.

19.

Третье достаточное условие существования
экстремуму
• Если R''(x0) > 0, то в точке х0 минимум
• Если R''(x0) < 0, то в точке х0 максимум
• Если R''(x0) = 0, то необходимо исследовать
знаки высших порядков.
18

20.

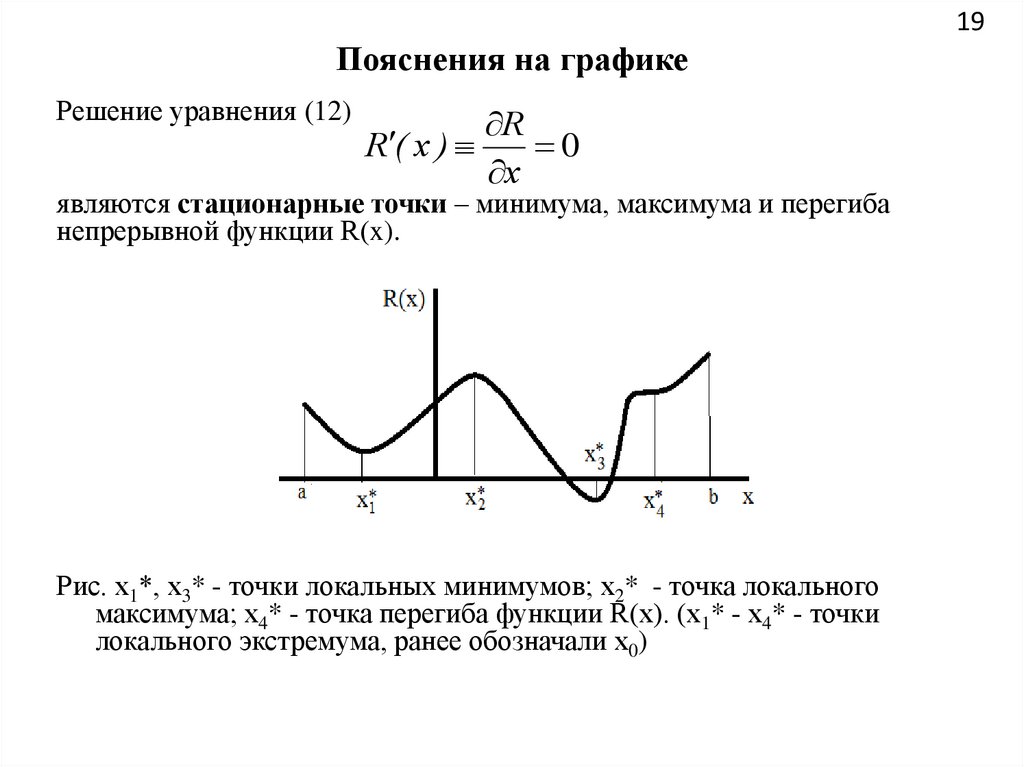
19
Пояснения на графике
Решение уравнения (12)
R
R ( x )
0
x
являются стационарные точки – минимума, максимума и перегиба
непрерывной функции R(x).
Рис. х1*, х3* - точки локальных минимумов; х2* - точка локального
максимума; х4* - точка перегиба функции R(х). (х1* - х4* - точки
локального экстремума, ранее обозначали х0)

21.

20
Для того чтобы определить, какая из точек
является точкой минимуму, или максимума,
то необходимо найти вторую производную
функции R(х).
Повторим еще раз:
Если R''(x0) > 0, то в точке х0 минимум.
Если R''(x0) < 0, то в точке х0 максимум.

22.

Многомерная задача безусловной оптимизации 21
В зависимости от числа управляемых параметров х
различают методы одномерной и многомерной
оптимизации.
До сих пор мы рассматривали один управляемый
параметр х – одномерную оптимизацию. В
многомерных задачах – размер вектора х не менее
двух.
Критерий оптимизации (целевая функция) имеет вид:
R = f (x1, x2, … , xn),
(13)
где x1, x2, … , xn – некоторые параметры объекта
оптимизации.
Рассмотрим поиска максимума для случая с двумя
факторами. Имеем приближенную функцию с двумя
переменными f(х1, х2):
Пример: R = c1x1 + c2x2.

23.

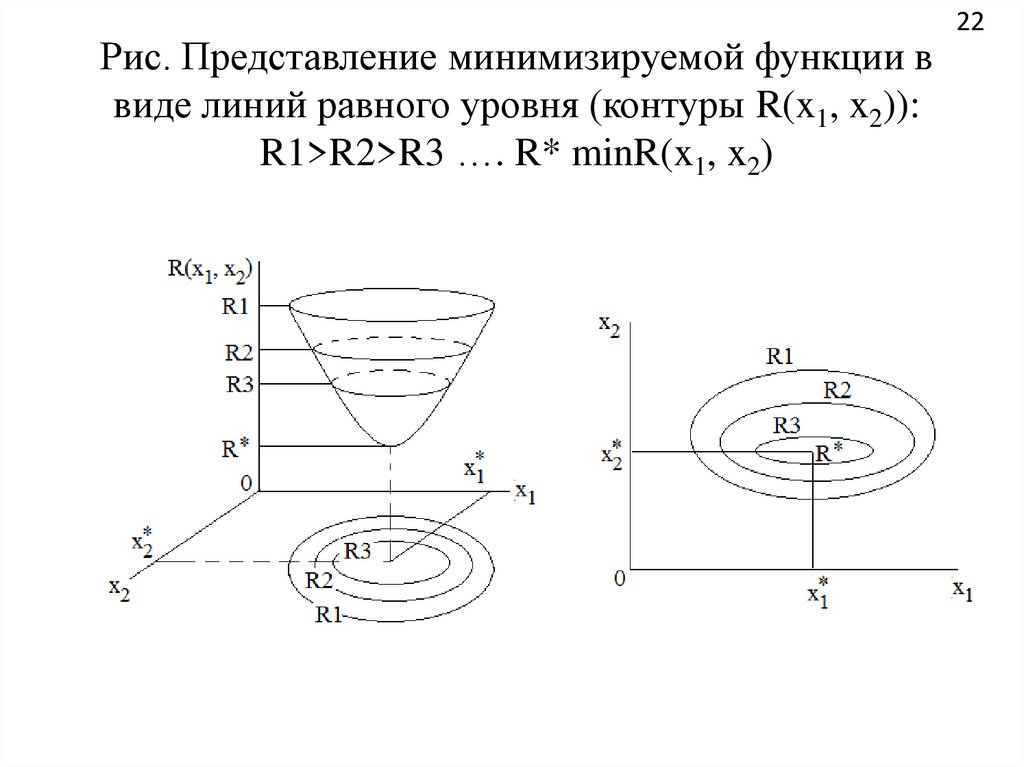
Рис. Представление минимизируемой функции в
виде линий равного уровня (контуры R(x1, x2)):
R1>R2>R3 …. R* minR(x1, x2)
22

24.

23
Многомерную задачу оптимизации удобно
представлять в виде линей равного уровня. На
рисунке представлена наша функция в виде
некоторого параболоида. Функция выпуклая.
Имеются координаты оптимальной точки (х1*, х2*).
Им соответствует функция R*. Задачу можно
представить в виде линий равного уровня. Задаемся
значениями критерия оптимальности R1, при
которых
рассекаем
параболоид
плоскость,
параллельной плоскости, на которой расположены
координаты x1,x2. Получаем замкнутую линию,
которую проецируем на плоскость координат.
Аналогично поступаем с остальными значениями
функций R2, R3 и т.д. Число таких линей может
быть бесконечно. Получаем правый рисунок.

25.

Формулировка многомерной
задачи оптимизации:
min R X
(13)
24
x E n
Необходимо определить такой вектор х, принадлежащий
евклидовому пространству размерности n, при которых
целевая функция принимает минимальное значение.
Другое определение
Необходимо определить максимум или минимум
действительной функции
R = f(x1, x2, … , xn)
(14)
от n действительных переменных и определить
соответствующие значения аргументов.

26.

25
Необходимое
условие
существования
экстремума функции многих переменных
является равенство нулю частных производных
первого порядка по всем переменным
(15)
R
R
R
0;
0; ...,
0
x1 x x*
x2 x x*
xn x x*
где
x * - безусловный локальный экстремум.

27.

26
Это утверждение равносильно утверждению о
равенстве
нулю
полного
дифференциала
дифференцируемой функции R:
dR(x1, x2, …, xn)=0
(17)
n R
R
R
R
dR( x1 , x2 ,...,xn )
dx1
dx2 ...
dxn
dxi 0
x1
x2
xn
i 1 xi
Решением
уравнения
стационарные точки.
(16)
являются

28.

27
Второе необходимое и достаточное условие
минимума дважды непрерывно дифференцируемой
функции R(x1, x2, …, xn) в окрестности точки (x1*,
x2*, …, xn*), исследуемой на экстремум: [Гордеев
Оптимизация ХТП с 34; Моисеев Методы
оптимизации с. 23; Казань 4 Оптимизация ХТП
слайд 14]. Воспользуемся разложением функции
R(x) в ряд Тейлора, предполагая её дважды
непрерывно
дифференцируемой
по
всем
переменным x1, x2, …, xn. Без вывода запишем
R x * 0,
Н(х*) > 0,
где Н(х) – n x n – матрица Гессе (вторых
производных) функции R(x).

29.

28
Если матрица Н(х*) < 0, то то х* — точка
локального максимума функции R(x).
Матрицей Гессе называется квадратная
матрица, составленная из вторых частных
производных функции f (X) по всем
переменным. Матрица имеет размерность
(n∙n), где n – количество переменных
функции.

30.

29
Пример
Дано R(x)=х3;
первая производная R'(x3) =3х2 . Имеем
точку х0 – подозрительная (по
необходимому условию).
R''(x3) =6х. При х=0 имеем R''=0;
R'''(x3)=6, т.е. R'''≠0, следовательно экстремум
нет.
В точке х0 максимум.