Задачи оптимизации

1.

2.

1. Наличие объекта оптимизации и цели оптимизации. При
этом формулировка каждой задачи оптимизации должна
требовать экстремального значения лишь одной величины.
2. Наличие ресурсов оптимизации - возможность выбора
значений некоторых параметров оптимизируемого объекта.
Объект должен обладать определенными степенями свободы управляющими воздействиями.
3. Возможность количественной оценки оптимизируемой
величины, поскольку только в этом случае можно сравнивать
эффекты от выбора тех или иных управляющих воздействий.
4. Учет ограничений.
Оптимизируемый вариант работы объекта должен оцениваться
какой-то количественной мерой-критерием оптимальности.

3.

Типичный пример неправильной
постановки задачи оптимизации:
"Получить максимальную
производительность при минимальной
себестоимости".
Ошибка заключается в том, что ставится
задача поиска оптимума 2-х величин,
противоречащих друг другу по своей сути.

4.

Правильная постановка задачи
могла быть следующая:
а) получить максимальную
производительность при заданной
себестоимости;
б) получить минимальную
себестоимость при заданной
производительности;
В первом случае критерий оптимизации производительность а во втором себестоимость.

5.

Поиск решения – инструмент для решения самых
разных задач оптимизации
При стандартной установке этот модуль скорее всего не будет подключен
Если не подключен, меню:
файл Параметры Надстройки
В окне «Надстройки»;
Установить «галочку»
Нажать «ОК»

6.

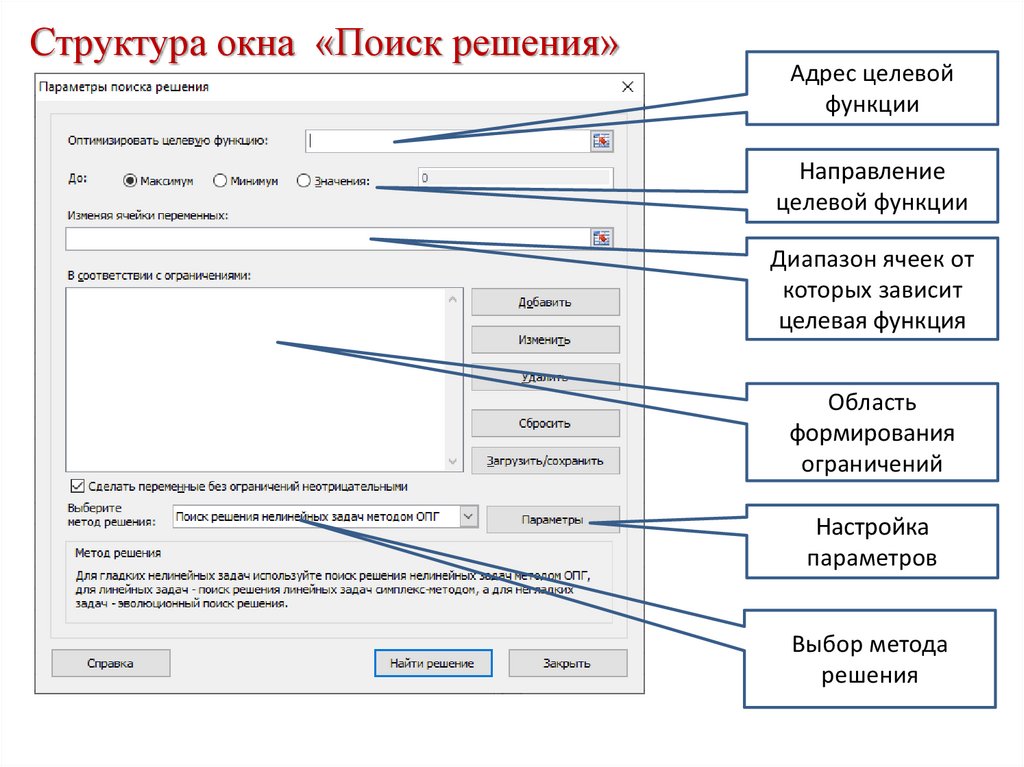
Структура окна «Поиск решения»
Адрес целевой
функции
Направление
целевой функции
Диапазон ячеек от
которых зависит
целевая функция
Область
формирования
ограничений
Настройка
параметров
Выбор метода
решения

7.

Для начала знакомая задача Решение нелинейного уравнения
1. Это тоже задача оптимизации.
2. Очень важный элемент - целевая функция.
Когда мы уточняли корни уравнения по одному
(Подбор параметра), целевой функцией являлась
левая часть уравнения F(x) и стремилась она к нулю:
F(x) => 0
Более мощная программа Поиск решения позволяет
найти несколько корней уравнения одновременно.
Но целевая функция одна !!!
Попробуем разобраться в решении этой проблемы.

8.

Решение нелинейного уравнения
Целевая функция должна быть надежной
Целевая
функция
Ограничения для корней:
• Х1 < -1
• -1 < x2 < 1
• X3 > 1

9.

Решение уравнения
Ограничения для корней:
• Х1 < -1
• -1 < x2 < 1
• X3 > 1

10.

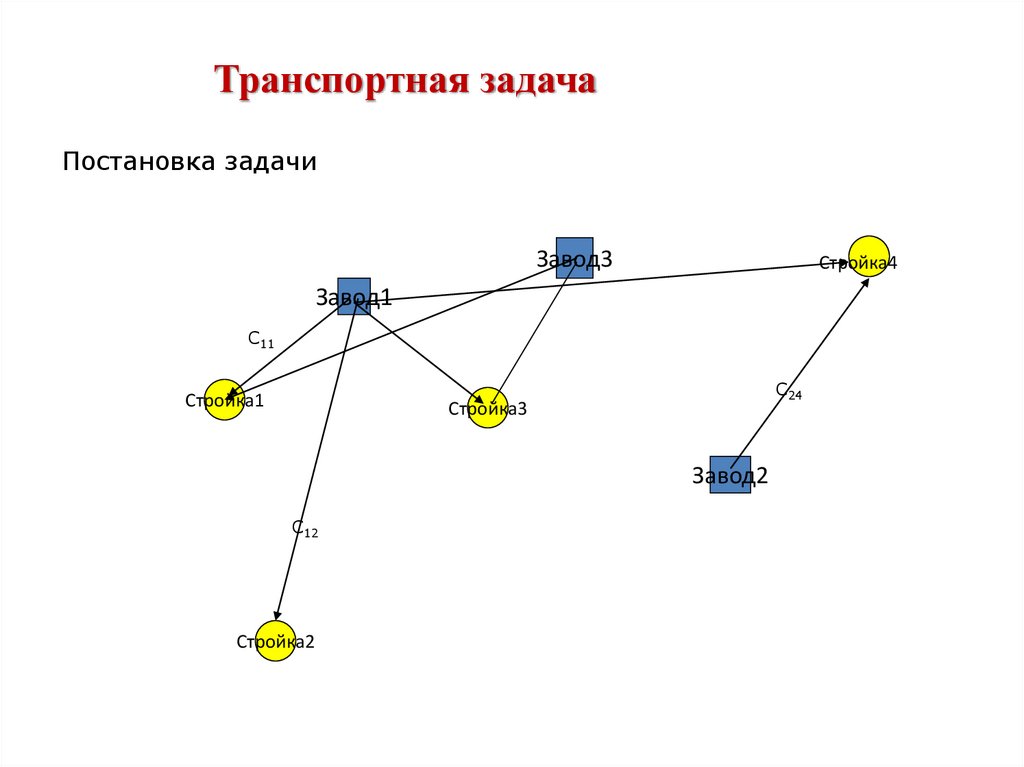
Транспортная задача
Постановка задачи
Завод3
Стройка4
Завод1
С11
Стройка1
С24
Стройка3
Завод2
С12
Стройка2

11.

Матрица перевозок
Целевая функция
(стоимость перевозок)
F
X ij - Количество перевозимых изделий
n
m
C X min
i 1 j 1
Ограничения:
n
X B ;
i 1
ij
j
m
X A
j 1
ij
i
ij
ij
j 1, , m,
i 1, , n,
физические ограничения
Xij 0
Условие замкнутости
задачи:
m
n
A B
i 1
i
j 1
j

12.

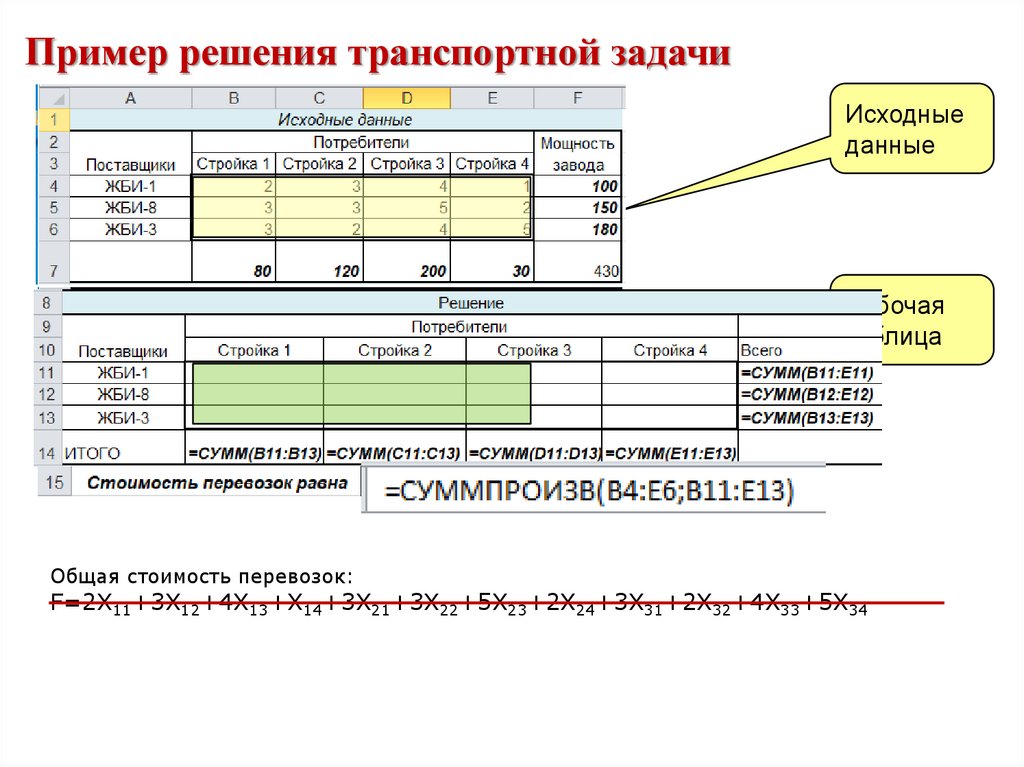
Пример решения транспортной задачи
Исходные
данные
Рабочая
таблица
Общая стоимость перевозок:
F=2X11+3X12+4X13+X14+3X21+3X22+5X23+2X24+3X31+2X32+4X33+5X34

13.

Пример допустимого базисного решения
Количество
перевозок в базисном
решении=
К-во строек+
к-во заводов – 1
=6

14.

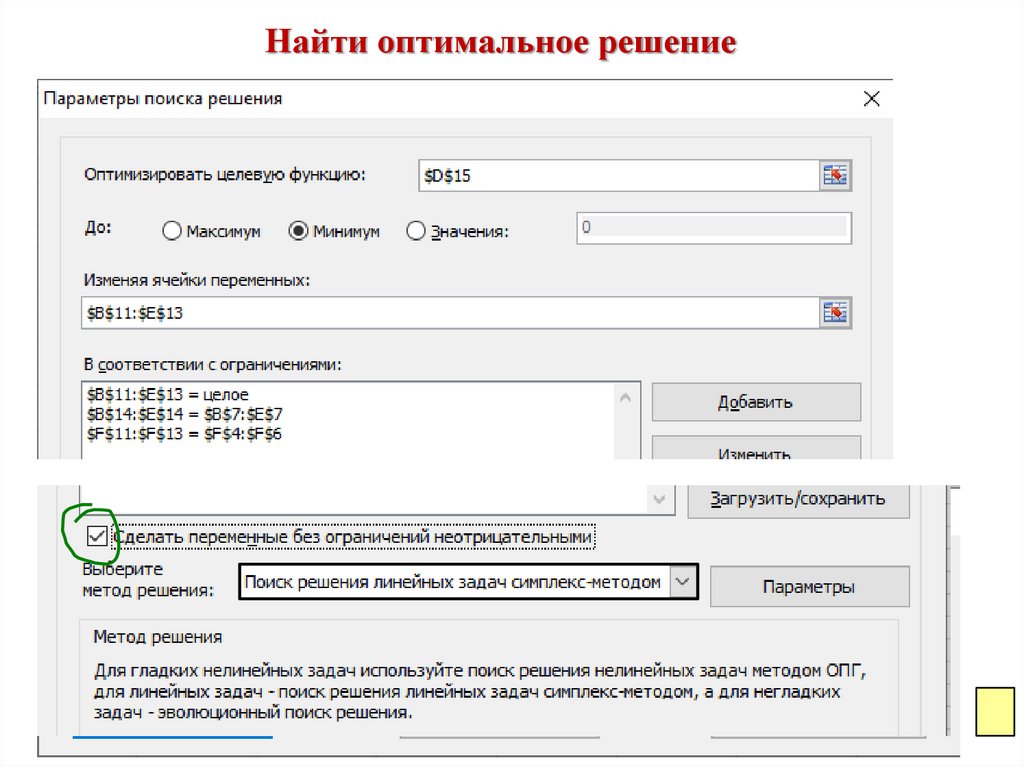
Найти оптимальное решение

15.

Решение готово
Напоминаю:
Стоимость ручного
решения была
1520

16.

Форматирование области решения
Выделить область
Правила выделения ячеек
Условное форматирование
равно
ОК

17.

Задача оптимизации выпуска продукции в
условиях ограниченных запасов сырья
В общем виде задачу можно сформулировать так: сколько
различных изделий нужно произвести, чтобы получить
максимальный доход, если известно количество ресурсов
(например, сырья) и цены, по которым можно реализовать
готовые изделия.
Математическая модель задачи:
• целевая функция – доход от реализации готовой продукции,
т. е. направление оптимизации – на максимум;
• ограничения представлены в виде системы линейных
неравенств;
• требование неотрицательности переменных присутствует.

18.

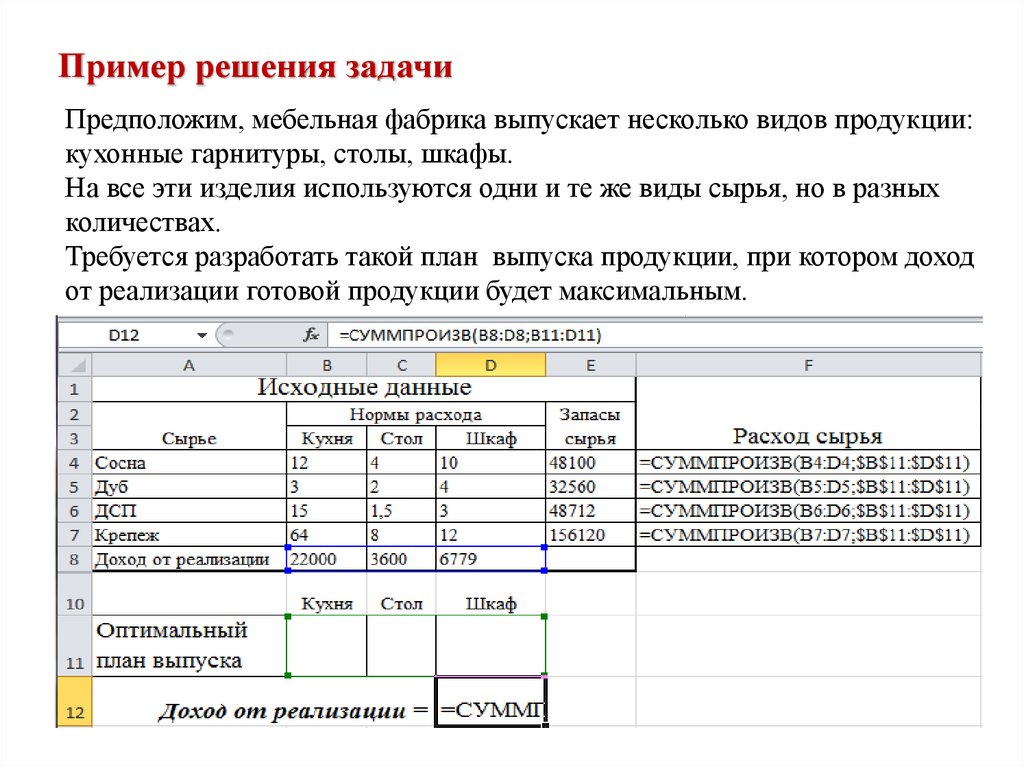
Пример решения задачи
Предположим, мебельная фабрика выпускает несколько видов продукции:
кухонные гарнитуры, столы, шкафы.
На все эти изделия используются одни и те же виды сырья, но в разных
количествах.
Требуется разработать такой план выпуска продукции, при котором доход
от реализации готовой продукции будет максимальным.

19.

Пример решения задачи

20.

Пример решения задачи

21.

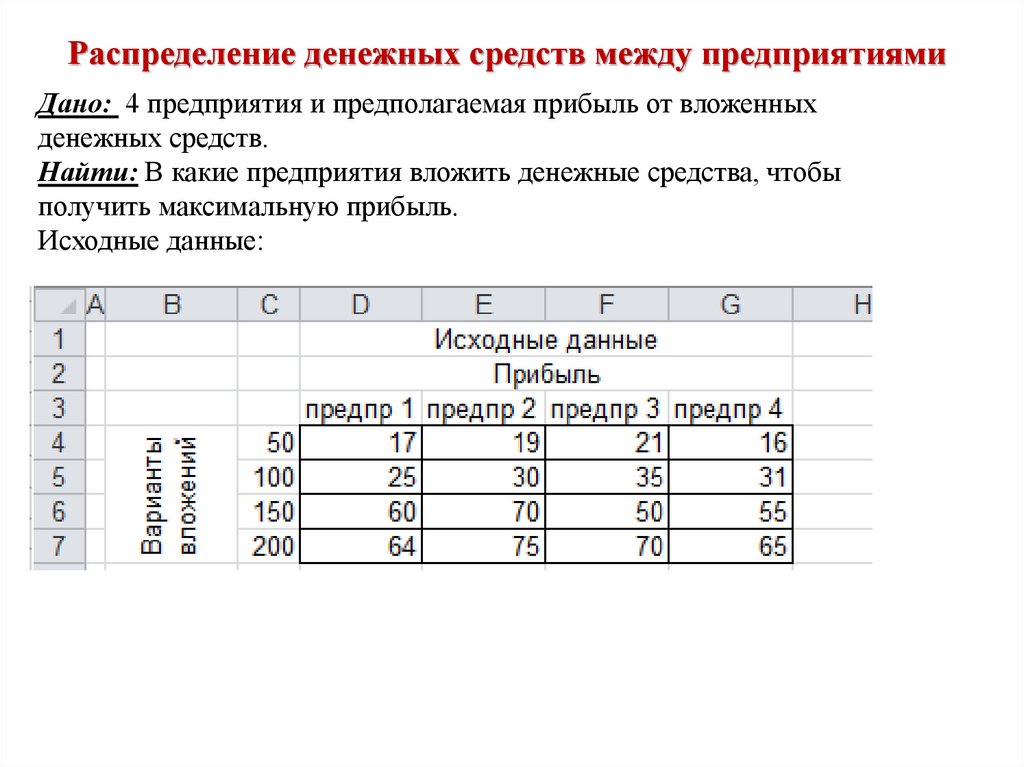
Распределение денежных средств между предприятиями
Дано: 4 предприятия и предполагаемая прибыль от вложенных
денежных средств.
Найти: В какие предприятия вложить денежные средства, чтобы
получить максимальную прибыль.
Исходные данные:

22.

Распределение денежных средств между предприятиями
Подготовка листа к решению задачи.

23.

Распределение денежных средств между предприятиями
Расчетная таблица в режиме значений.

24.

Распределение денежных средств между предприятиями
Важно!!!
Задача является целочисленной, поэтому в
настройках параметров окна «Поиск решений»
следует убрать галочку
Иначе в целях получения максимальной
прибыли программа поставит в ячейки дробные
значения, что не допустимо для данной задачи.

25.

Распределение денежных средств между предприятиями
Результаты решения