Математика
ФизикаПохожие презентации:
Метод конечных разностей. Расчет методом конечных разностей изгибаемых плит
1. Метод конечных разностей
Выполнили:Студенты гр. С-11-17
Любимов А.А
Николаев И.И
2.
Метод конечных разностей — численныйметод решения дифференциальных уравнений,
основанный на замене производных
разностными схемами. Является сеточным
методом.
3. Выражения второй и четвертой производных, которые используются в расчетах изгибаемых плит, в конечных разностях в точке i имеют
вид :Где f – значение функции в узловой точке
λ – шаг вычисления функций.
4. Особенности расчета методом конечных разностей изгибаемых плит.
5. Дифференциальное уравнение Софи Жермен–Лагранжа
Дифференциальное уравнение Софи Жермен–Лагранжа
где,
-цилиндрическая жесткось,
h — толщина плиты, E – модуль упругости, ν –
коэффициент Пуассона, q(x,y) – функция заданной
нагрузки.
6. Изгибающие моменты Mx My
7. Уравнение Софи Жермен–Лагранжа (3) в разностной форме для i-ой точки
где a, b, c, d, e, f, g, h, k, l, m, n –узлы сетки, λ – шаг сетки
(рис. 1).
8. Изгибающие моменты (4) в разностной форме
9. Разностное уравнение вида (5) в матрично-операторной форме
Разностное уравнение вида (5) в матричнооператорной форме10. Разностное уравнение вида (6,7) в матрично-операторной форме
Разностное уравнение вида (6,7) в матричнооператорной форме11.
12. Граничные условия для защемлённого края :
а) прогиб на опоре равен нулю – Wконт= 0;б) угол поворота на опоре равен нулю –
Из этих условий получим:
13. Для шарнирноопёртого края будем иметь:
а) прогиб на опоре равен нулю – Wконт=0;б) изгибающий момент равен нулю –
Откуда:
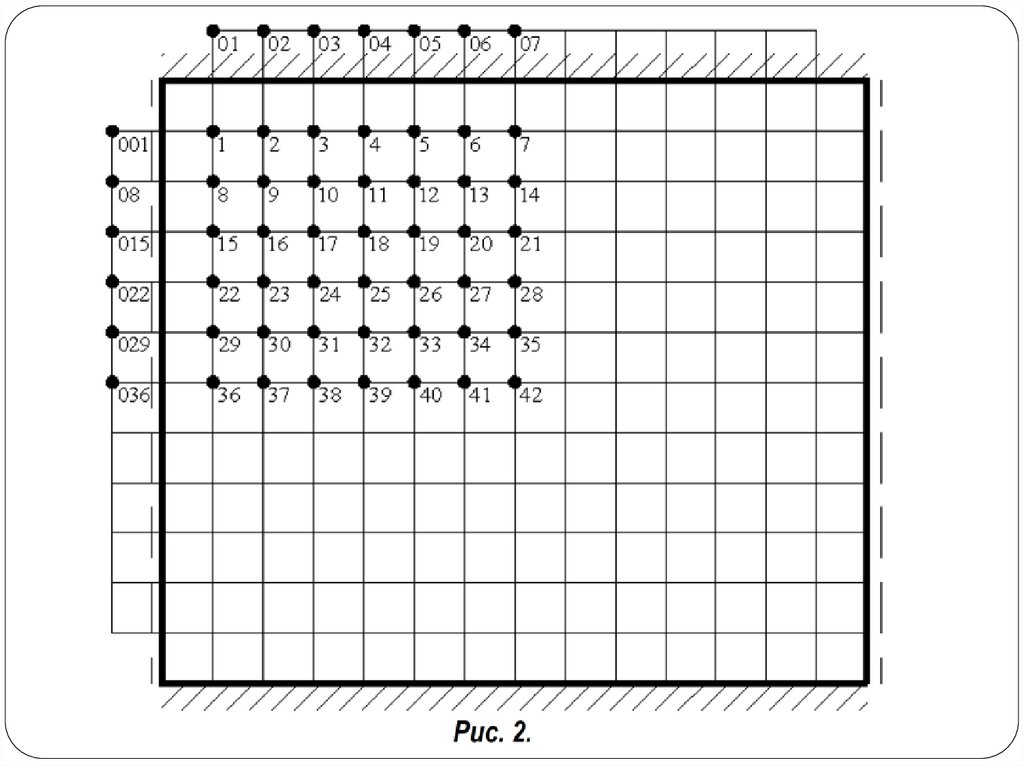
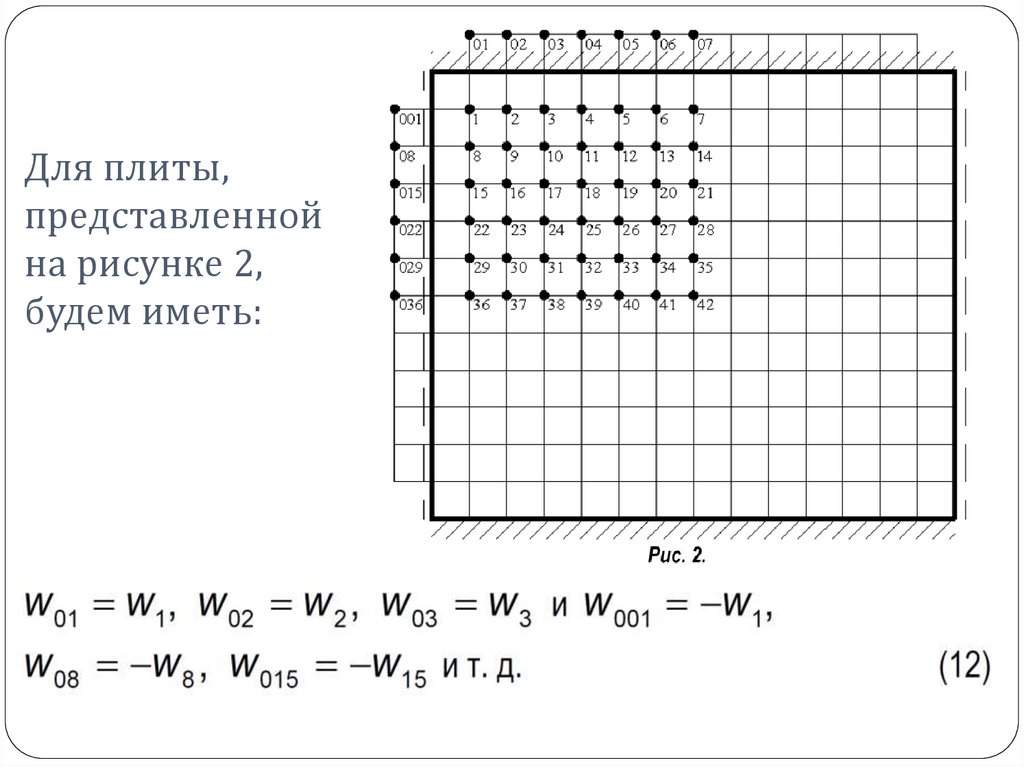
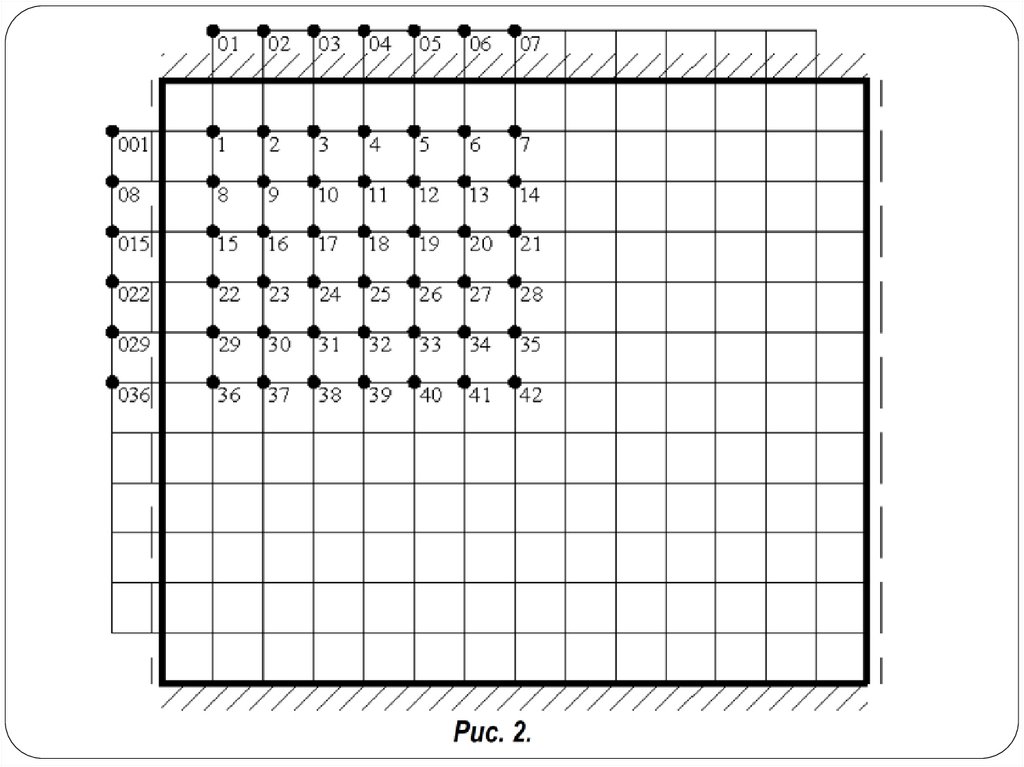
14. Для плиты, представленной на рисунке 2, будем иметь:
15. Расчет изгибаемой плиты, опертой по контуру.
16.
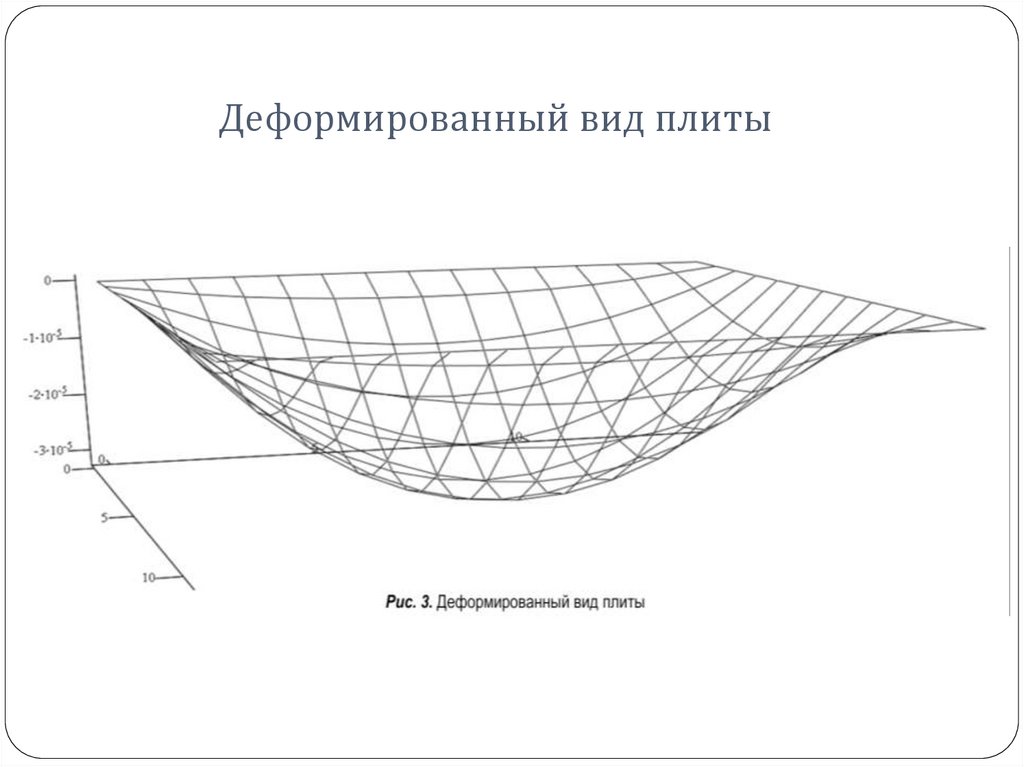
17. Деформированный вид плиты
18. Эпюры изгибающих моментов Mx и My для рассматриваемой плиты
19. Расчет изгибаемой плиты с одной промежуточной опорой.
20.
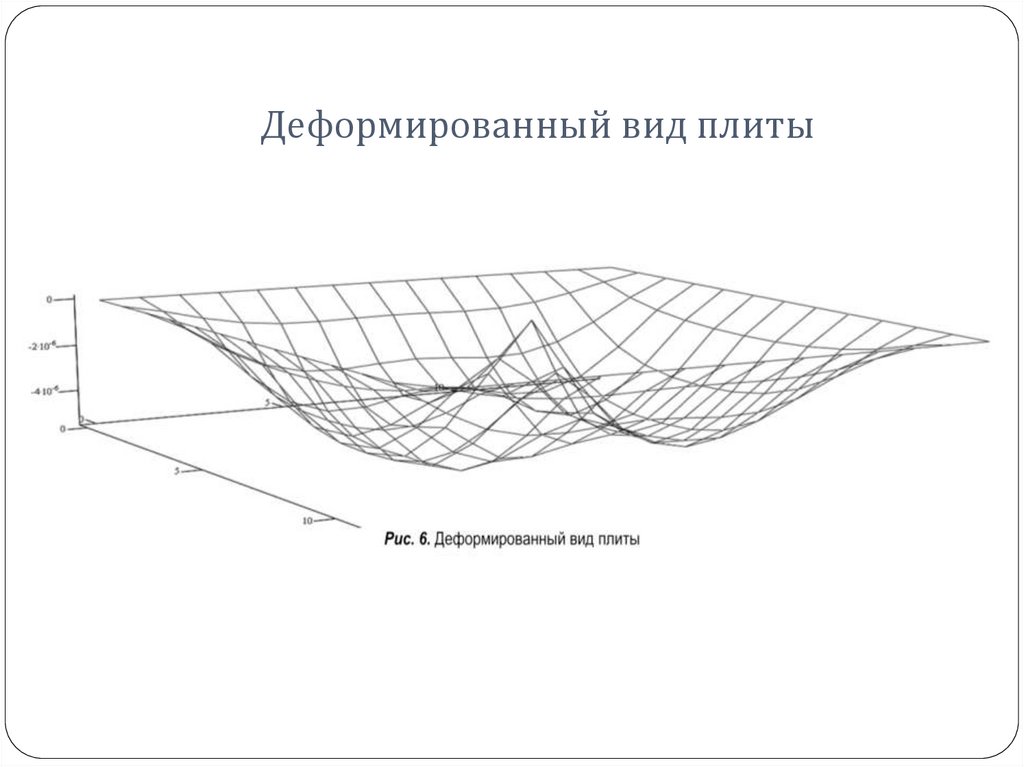
21. Деформированный вид плиты
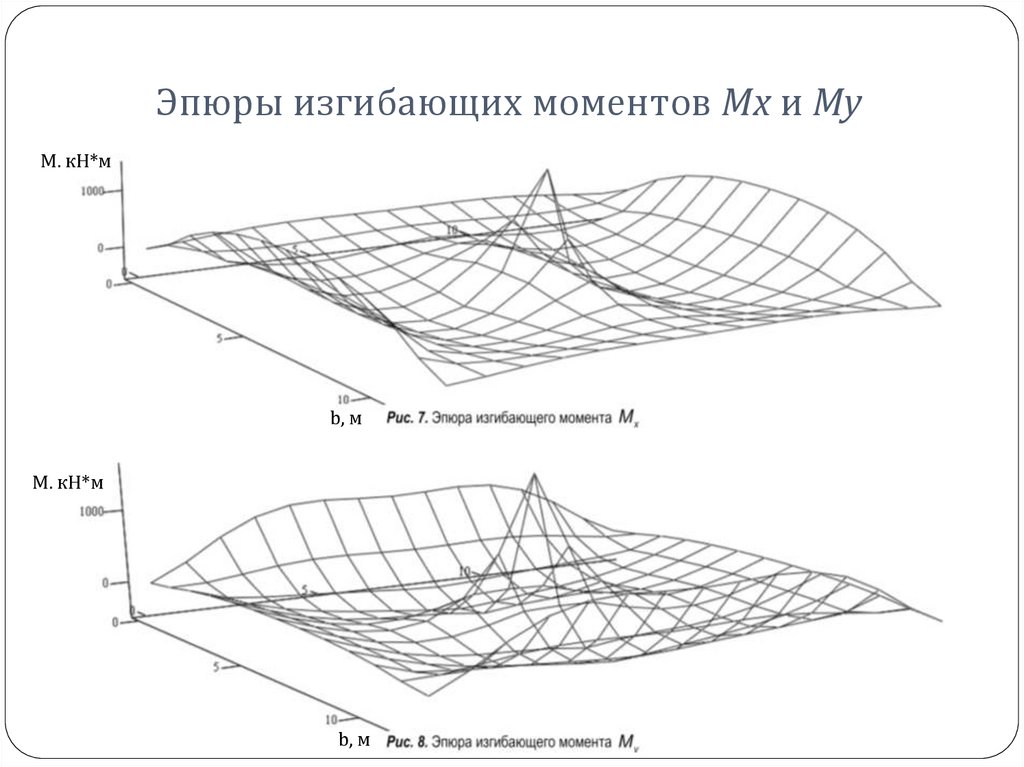
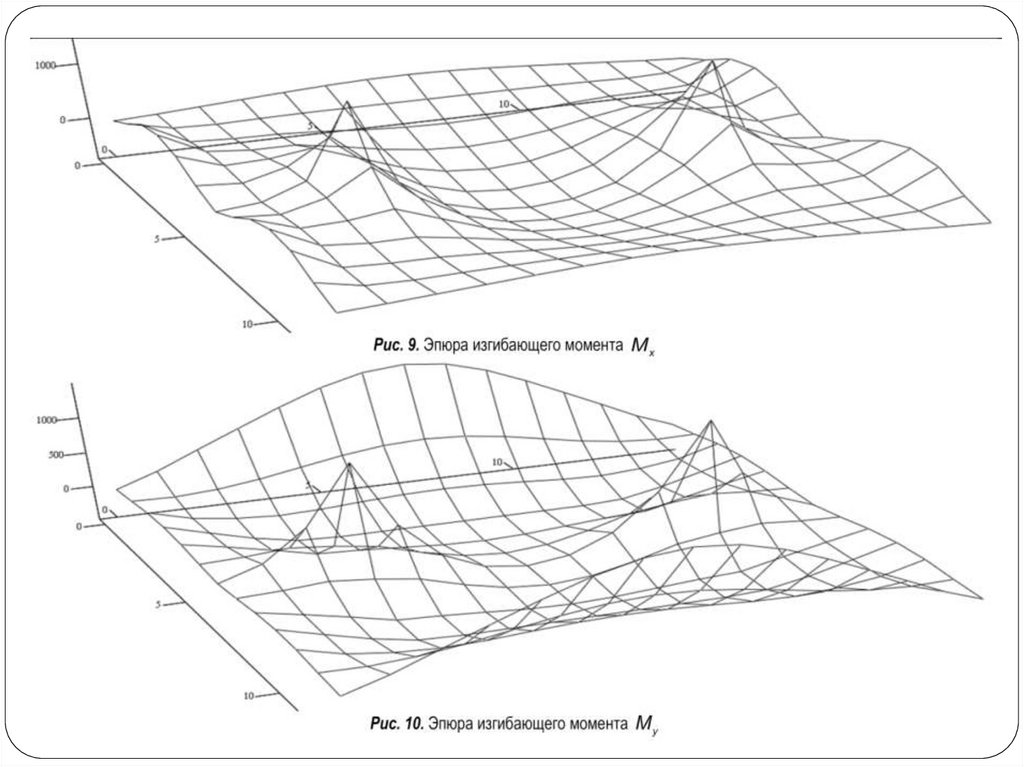
22. Эпюры изгибающих моментов Mx и My
М. кН*мb, м
М. кН*м
b, м