Похожие презентации:
Решение дифференциальных уравнений в частных производных методом конечных разностей
1. Модуль 2. Тема 1. Лекция 1. Решение дифференциальных уравнений в частных производных методом конечных разностей
2. План
1. Постановка задач для ДУЧП параболического типа2. Постановка задач для ДУЧП гиперболического типа
3. Постановка задач для ДУЧП эллиптического типа
4. Конечно-разностные схемы. Основные определения: сеточная
функция, временной слой, шаблон. Явные и неявные схемы для
ДУЧП параболического типа
5. Конечно-разностная аппроксимация задач для ДУЧП
гиперболического типа
6. Конечно-разностная аппроксимация задач для ДУЧП
эллиптического типа
7. Интегро-интерполяционный метод (метод конечных объемов)
8. Основные понятия для разностных схем: аппроксимация и
порядок аппроксимации, сходимость и порядок сходимости,
устойчивость, консервативность и корректность. Анализ порядка
аппроксимации.
3.
План9. Исследование устойчивости методом гармонического анализа.
Условия устойчивости явных схем для основных уравнений
матфизики.
10.Неявно-явная конечно-разностная схема с весами. Схема
Кранка-Николсона
11.Многомерные ДУЧП. Явные и неявные методы. Понятие об
экономичных конечно-разностных схемах
12.Методы расщепления для многомерных уравнений
параболического типа. Расщепление по пространственным
переменным. Расщепление по физическим процессам.
13.Метод переменных направлений
14.Метод дробных шагов
4.
Дифференциальные уравнения в частных производныхu
u 2u 2u
nu
F x1 , x2 ,..., xk , u,
,...,
, 2,
,..., p1 p2
pk
x
x
x
x
x
x
x
...
x
1
k
1
2
1
1
2
k
u ( x1 , x 2 ,..., x k )
n p1 p2 ... pk
0
5.
Линейные ДУЧП второго порядка2u x, t
2u x, t
2u x, t
u x, t
A x, t
2 B x, t
C x, t
D x, t
2
2
x
t x
t
x
u x, t
x, t D
E x, t
F x, t u x, t G x, t ,
t
A x ,t B x ,t C x ,t 0
u x, t
ux
,
x
u x, t
ut
,
t
u x, y
uy
,
y
2 u x, t
u xx
,
2
x
2 u x, t
utt
,
2
t
2 u x, t
u xt
, ...
t x
6.
Линейные ДУЧП второго порядкаAu xx 2 Bu xt Cu tt Du x Eu t Fu G
B 2 AC 0
параболический тип
B 2 AC 0
гиперболический тип
B 2 AC 0
эллиптический тип
Линейные ДУЧП первого порядка
A x, t u x B x, t ut C x, t u G x, t
7.
Примеры ДУЧП1) ut u x 0 ;
2) ut uu xxx sin x ;
3) uxx xutt 0 ;
4) utt с 2uxx 0 ;
5) ut a 2u xx 0 ;
6) uxx uyy 0 ;
7) x ux tut u 2 0 ;
8) uxy 0 ;
9) 3uxx 7uxt 2utt 0 ;
10) ut uxx 3x 2u uxt 3u x u 0
8.
Постановка задач для уравнений параболического типа2
u
2 u
a
, 0 x l, t 0
2
t
x
Уравнение теплопроводности (диффузии)
u( x,0) ( x ), 0 x l , t 0
Начальное условие
u(0, t ) 1 (t ), x 0, t 0
u(l , t ) 2 (t ), x l , t 0
Граничные условия первого рода
u(0, t )
1 (t ), x 0, t 0
x
u(l , t )
2 (t ), x l , t 0
x
Граничные условия второго рода
u (0, t )
u (0, t ) 1 (t ), x 0, t 0
x
u (l , t )
u (l , t ) 2 (t ), x l , t 0
x
Граничные условия третьего рода
9.
Постановка задач для уравнений гиперболического типа2
2u
u
2
a
, 0 x l, t 0
2
2
t
x
u x,0 1 x ,
0 x l, t 0
u 0, t 1 t ,
x 0, t 0
u l , t 2 t ,
x l, t 0
u x,0
2 x , 0 x l, t 0
t
Волновое уравнение
Начальные условия
Граничные условия первого рода
10.
Постановка задач для уравнений гиперболического типа2
2u
u
2
a
, 0 x l, t 0
2
2
t
x
u x,0 1 x ,
0 x l, t 0
u x,0
2 x , 0 x l, t 0
t
u 0, t
1 t ,
x
u l , t
2 t ,
x
Волновое уравнение
Начальные условия
x 0, t 0,
Граничные условия второго рода
x l, t 0
11.
Постановка задач для уравнений гиперболического типа2
2u
u
2
a
, 0 x l, t 0
2
2
t
x
u x,0 1 x ,
0 x l, t 0
u x,0
2 x , 0 x l, t 0
t
u 0, t
u 0, t 1 t , x 0, t 0,
x
u l , t
u l , t 2 t , x l , t 0
x
Волновое уравнение
Начальные условия
Граничные условия третьего рода
12.
Постановка задач для уравнений эллиптического типа2u 2u
x 2 y 2 f x, y ,
u x , y x , y ,
x, y
x, y
Первая краевая задача задача Дирихле
13.
Постановка задач для уравнений эллиптического типа2u 2u
x 2 y 2 f x, y ,
u x, y x, y ,
n
x, y
x, y
u
u
cos n, i cos n, j x, y
x
y
Вторая краевая задача задача Неймана
Эквивалентное представление
граничного условия
14.
Постановка задач для уравнений эллиптического типа2u 2u
x 2 y 2 f x, y ,
u x, y u x, y ,
n
x, y
Третья краевая задача
x, y
15.
Основные определенияКонечно-разностный метод (метод сеток): исходная область пространства
независимых переменных заменяется дискретным множеством точек – сеткой,
а производные аппроксимируются на этой сетке разностными соотношениями.
В результате исходная задача для ДУЧП заменяется конечным числом
алгебраических (разностных) уравнений, которые решаются.
Сетка – конечное множество точек (узлов сетки), принадлежащих области
определения дифференциальной задачи, включая границу, на которой
определяются начальные и граничные условия. Узлы, принадлежащие
внутренней области, называются внутренними, узлы, принадлежащие границе,
называются граничными
Шаг сетки – количественная характеристика плотности размещения узлов
сетки. При стремлении шага сетки к нулю, сетка стремится заполнить область
определения дифференциальной задачи.
Сеточная функция – функция, определенная в узлах сетки
Сеточное представление непрерывной функции – множество значений
функции в узлах сетки
Разностная схема (задача) - совокупность разностных уравнений,
аппроксимирующих ДУЧП во всех внутренних узлах сетки, а также начальные и
краевые условия в граничных узлах сетки.
16.
Основные определенияLu f
0 x l,
Дифференциальная задача с независимыми переменными x и t
Обычно x – пространственная координата, t – время
0 t T
Прямоугольная область
h , x j jh,
h l / N,
j 0 N , t k k , k 0 K
T /K
Прямоугольная сетка
Пространственный и временной шаги сетки
Равномерная (регулярная сетка) – сетка с постоянным шагом по каждой
независимой переменной
Временной слой - множество всех узлов сетки, имеющих одну и ту же
временную координату
uh {u kj u ( x j , t k ),
j 0 N , k 0 K }
Сеточное представление точного
решения дифференциальной задачи
Как правило, вычислить точное решение uh не удается
Lh uˆh f h - разностная схема;
uˆh uh - решение разностной схемы
17.
Разностныесхемы для уравнений параболического типа
2
u
u
a2 2 , 0 x l, t 0
t
x
k
u kj 1 u kj
u
O ( ) ,
t j
k
u
u
2
x j
2
k
j 1
2u u
h
k
j
2
k
j 1
O (h 2 )
Уравнение теплопроводности (диффузии)
Аппроксимация производной по времени
Явная аппроксимация пространственной
производной (используются известные
значения на k-м временном слое)
Одно неизвестное значение может быть явно рассчитано через известные
k
k
k
u kj 1 u kj
u
2
u
u
j
j 1
2
a 2 j 1
O
(
h
),
2
h
j 1, N 1, k 0, K 1
u0k 1 1 (t k 1 ) ,
u 0j ( x j ) ,
uNk 1 2 (t k 1 ) ,
Явная разностная схема
для первой начально-краевой
задачи
k 0, K ;
j 0, N
Схема называется явной, если аппроксимирующее уравнение содержит только
одно неизвестное значение функции на (k+1)-м слое, которое может быть
выражено явно через известные значения на k-м слое.
18.
Разностные схемы для уравнений параболического типаu
x 2
2
k 1
j
u kj 11 2u kj 1 u kj 11
Неявная аппроксимация
2
O (h )
пространственной производной
2
h
(используются неизвестные значения на
(k+1)-м временном слое)
Неизвестные значения
u kj 1 u kj
a
k 1
k 1
k 1
u
2
u
u
j 1
j
j 1
2
h2
O( h2 ) ,
j 1, N 1, k 0, K 1
u0k 1 1 (t k 1 ) ,
u 0j ( x j ) ,
uNk 1 2 (t k 1 ) ,
Неявная разностная схема
для первой начально-краевой
задачи
k 0, K 1 ;
j 0, N
Схема называется неявной, если оператор аппроксимируется с
использованием нескольких неизвестных значений функции на (k+1)-м слое.
19.
Разностные схемы для уравнений параболического типаa1 0;
cN 1 0;
где
b1u1k 1 c1u2k 1 d1 , j 1,
k 1
k 1
k 1
a
u
b
u
c
u
j j 1
j j
j j 1 d j , j 2, N 2,
k 1
k 1
a
u
b
u
N 1 N 2 N 1 N 1 d N 1 , j N 1,
a j , j 2, N 1; b j (1 2 ) , j 1, N 1; c j ,
j 1, N 2; d j u kj , j 2, N 2; d1 (u1k 1 (t k 1 ));
2
a
k
k 1
d N 1 (uN 1 2 (t )); 2 .
h
Система линейных алгебраических уравнений,
полученная по неявной разностной схеме,
может быть решена методом прогонки
20.
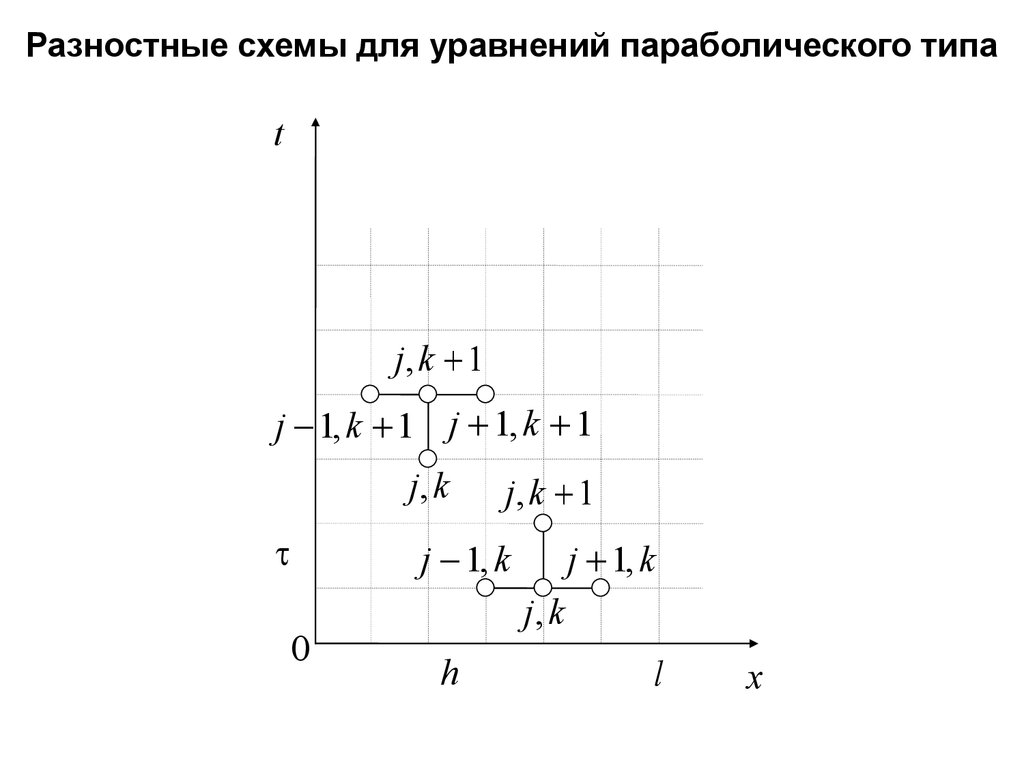
Разностные схемы для уравнений параболического типаt
j, k 1
j 1, k 1 j 1, k 1
j, k
0
j, k 1
j 1, k
j 1, k
j, k
h
l
x
21.
Шаблоны разностных схемдля уравнения теплопроводности
Шаблон – совокупность узлов сетки, значения в которых
используются при аппроксимации дифференциального оператора.
Шаблон, содержащий p узлов называется p-точечным.
j 1
k 1
j 1
j
k
j 1
Шаблон явной схемы
j 1
j
k 1
k
Шаблон неявной схемы
22.
Постановка задач для уравнений гиперболического типа2
2u
u
2
a
, 0 x l, t 0
2
2
t
x
u x,0 1 x ,
0 x l, t 0
u 0, t 1 t ,
x 0, t 0
u l , t 2 t ,
x l, t 0
u x,0
2 x , 0 x l, t 0
t
Волновое уравнение
Начальные условия
Граничные условия первого рода
23.
Разностные схемы для уравнений гиперболического типана примере волнового уравнения
2
2u
2 u
a
, 0 x l, t 0
2
2
t
x
Явная схема для волнового уравнения
u kj 1 2u kj u kj 1
2
a
k
k
k
u
2
u
u
j 1
j
j 1
2
h2
j 1... N 1;
k 1, 2, ...
Неявная схема для волнового уравнения
u kj 1 2u kj u kj 1
2
a
k 1
k 1
k 1
u
2
u
u
j 1
j
j 1
2
h2
j 1... N 1;
k 1, 2, ...
24.
Разностные схемы для уравнений гиперболического типана примере волнового уравнения
2
2u
2 u
a
, 0 x l, t 0
2
2
t
x
Явная схема для волнового уравнения
u kj 1 2u kj u kj 1
2
a
k
k
k
u
2
u
u
j 1
j
j 1
2
h
2
O h
2
2
j 1... N 1;
k 1, 2, ...
Неявная схема для волнового уравнения
u kj 1 2u kj u kj 1
2
a
k 1
k 1
k 1
u
2
u
u
j 1
j
j 1
2
h2
O h2
j 1... N 1;
k 1, 2, ...
25.
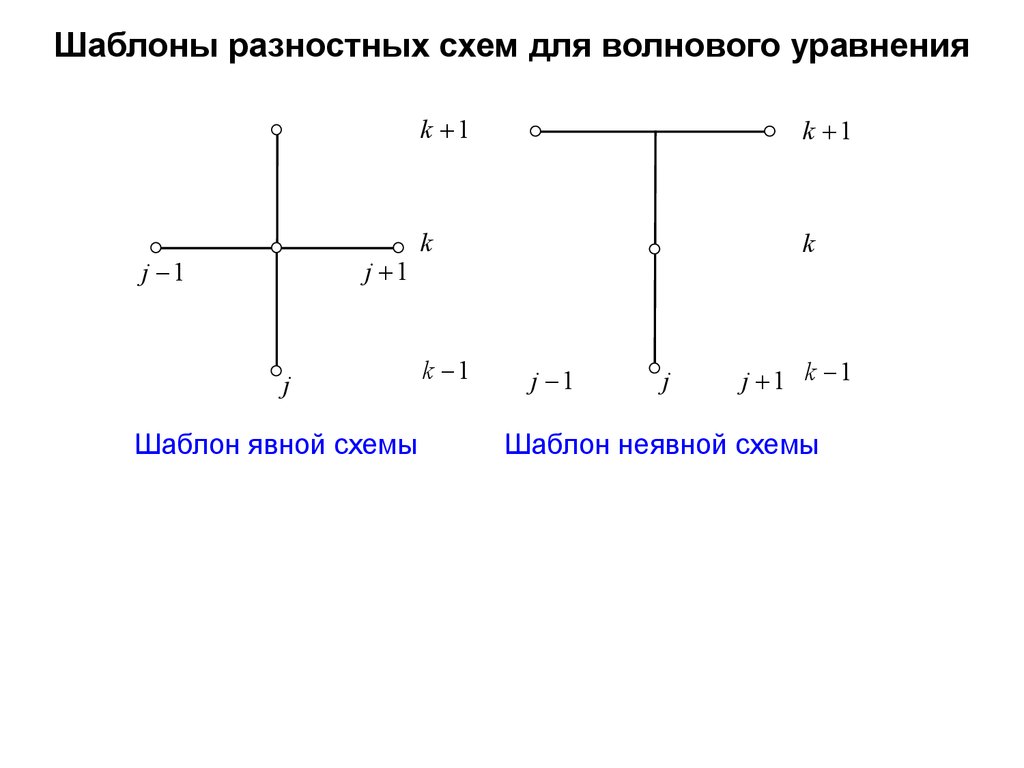
Шаблоны разностных схем для волнового уравненияj 1
j 1
j
Шаблон явной схемы
k 1
k 1
k
k
k 1
j 1
j
j 1 k 1
Шаблон неявной схемы
26.
Разностные схемы для уравнений гиперболического типана примере волнового уравнения
u x,0 1 x ,
0 x l, t 0
u x,0
2 x , 0 x l, t 0
t
u 0j 1 ( x j ),
j 0 ... N
u1j u 0j
2 ( x j ) O ( ), j 0 ... N
u1j 1 ( x j ) 2 ( x j ) O ( 2 )
Начальные условия
Аппроксимация
начальных условий
27.
Разностные схемы для уравнений гиперболического типана примере волнового уравнения
u x,0 1 x ,
0 x l, t 0
Начальные условия
u x,0
2 x , 0 x l, t 0
t
0
0
2
u
u
u1j u x j , 0 u 0j
2
O 3
t j
t j 2
0
2
0
u
2 u
2
a
a
1 x j
2
2
t j
x j
2
2
2
u1j 1 x j 2 x j a 2 1 x j O 3
2
u1j u 0j
2
2 x j a 1 x j O 2
2
Аппроксимация
начальных условий
со вторым порядком
аппроксимации
по времени
28.
Разностные схемы для уравнений эллиптического типа2u 2u
x 2 y 2 f x, y
u x , y x , y
Задача Дирихле
Сетка для
прямоугольной
области
h1 ,h2 xi ih1 , i 0... N1; y j jh2 , j 0... N 2
ui 1, j 2ui , j ui 1, j
2
1
h
ui , j 1 2ui , j ui , j 1
i 1... N1 1; j 1 ... N 2 1
h2
2
O h1 h2 f xi , y j ,
2
2
Разностная схема
для внутренних точек
29.
Шаблон разностной схемыui 1, j 2ui , j ui 1, j
2
1
h
ui , j 1 2ui , j ui , j 1
h2
2
i 1... N1 1; j 1 ... N 2 1
i, j 1
i 1, j
i, j
i, j 1
O h h2 f xi , y j ,
i 1, j
2
1
2
30.
Метод простых итераций для ДУЧП эллиптического типаui 1, j 2ui , j ui 1, j
h1
2
ui , j 1 2ui , j ui , j 1
h2
2
O h1 h2 f xi , y j
2
2
h1 h2 h
ui , j
1
ui 1, j ui 1, j ui , j 1 ui , j 1 h 2 f i , j , i 1... N1 1,
4
j 1... N 2 1
Итерационный процесс Либмана
( n 1)
i, j
u
1 (n)
ui 1, j ui( n1), j ui(,nj) 1 ui(,nj) 1 h 2 f i , j , i 1... N1 1, j 1... N 2 1
4
Итерации сходятся при
n
Сходимость может быть медленной
31.
Итерационные методы решенияДУЧП эллиптического типа
Метод Зейделя
1 (n)
ui 1, j ui( n1 ,1j) ui(,nj 11) ui(,nj) 1 h 2 f i , j ,
4
i 1... N1 1, j 1... N 2 1
ui(,nj 1)
Метод релаксации
1 (n)
u
u (1 ) ui 1, j ui( n1 ,1j) ui(,nj 11) ui(,nj) 1 h 2 f i , j ,
4
i 1... N1 1, j 1... N 2 1
( n 1)
i, j
0 1
1
(n)
i, j
метод нижней релаксации
метод верхней релаксации
32.
Операторное представление дифференциальной задачиLU f
Дифференциальная задача для ДУЧП
Все, связанное с неизвестной
функцией U, помещено в оператор L:
Все, связанное с конкретизацией
задачи, помещено в функцию f :
• Область пространства независимых
переменных
• Дифференциальный оператор
• Тип дифференциальной задачи
• Правая часть
• Начальные условия
• Граничные условия
Пример: начально-краевая задача для уравнения переноса
ut ux , 0 x l , 0 t T
LU u( x,0), 0 x l
u(0, t ), 0 t T
0, 0 x l , 0 t T
f ( x ), 0 x l
( x ), 0 t T
33.
Операторное представлениедифференциальной и конечно-разностной задач
LU f
L
U x, t
дифференциальная задача для ДУЧП
дифференциальный оператор
неизвестная искомая функция
f
LU h
входные данные
fh
дифференциальная задача в узлах сетки
LhU h f h
конечно-разностная схема на точном
(неизвестном) решении
Lh u h f h
uh
конечно-разностная схема
сеточная функция, которую мы находим в
процессе решения по конечно-разностной схеме
34.
Аппроксимация и порядок аппроксимации35.
Устойчивость36.
Устойчивость37.
Сходимость и порядок сходимости38.
Теорема эквивалентности39.
КонсервативностьВсе ДУЧП выведены на основе физических законов сохранения
какой-либо субстанции (массы, энергии, импульса и т.п.). Заменяя
дифференциальную задачу конечно-разностной схемой, можно
нарушить эти законы сохранения.
Определение. Конечно-разностная схема консервативна, если для
нее выполняются законы сохранения, на основе которых поставлена
дифференциальная задача.
В противном случае конечно-разностная схема является
неконсервативной, т.е. решение, полученное на ее основе, не
соответствует решению дифференциальной задачи - решается
другая задача. Поэтому неконсервативными схемами пользоваться
не рекомендуется.
40.
Корректность41.
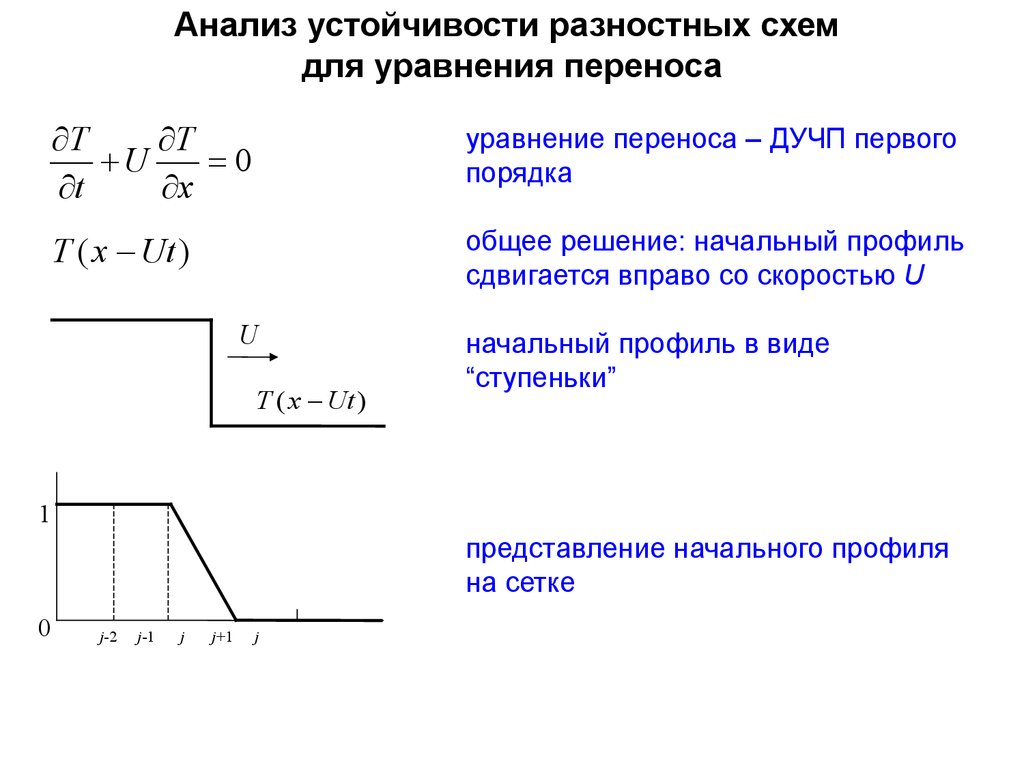
Анализ устойчивости разностных схемдля уравнения переноса
T
T
U
0
t
x
уравнение переноса – ДУЧП первого
порядка
T ( x Ut )
общее решение: начальный профиль
сдвигается вправо со скоростью U
U
T ( x Ut )
начальный профиль в виде
“ступеньки”
1
представление начального профиля
на сетке
0
j-2
j-1
j
j+1
j
42.
Анализ устойчивости разностных схемдля уравнения переноса
T
T
U
0
t
x
уравнение переноса
x , t x j j x , j 0 J ; t k k t , k 0 N
T jk
t
T jk
x
T jk 1 T jk
t
T jk T jk 1
x
O ( t )
O ( x )
T jk T jk 1 T jk
O ( x )
x
x
сетка
аппроксимация производной по времени
варианты аппроксимации
пространственной производной
43.
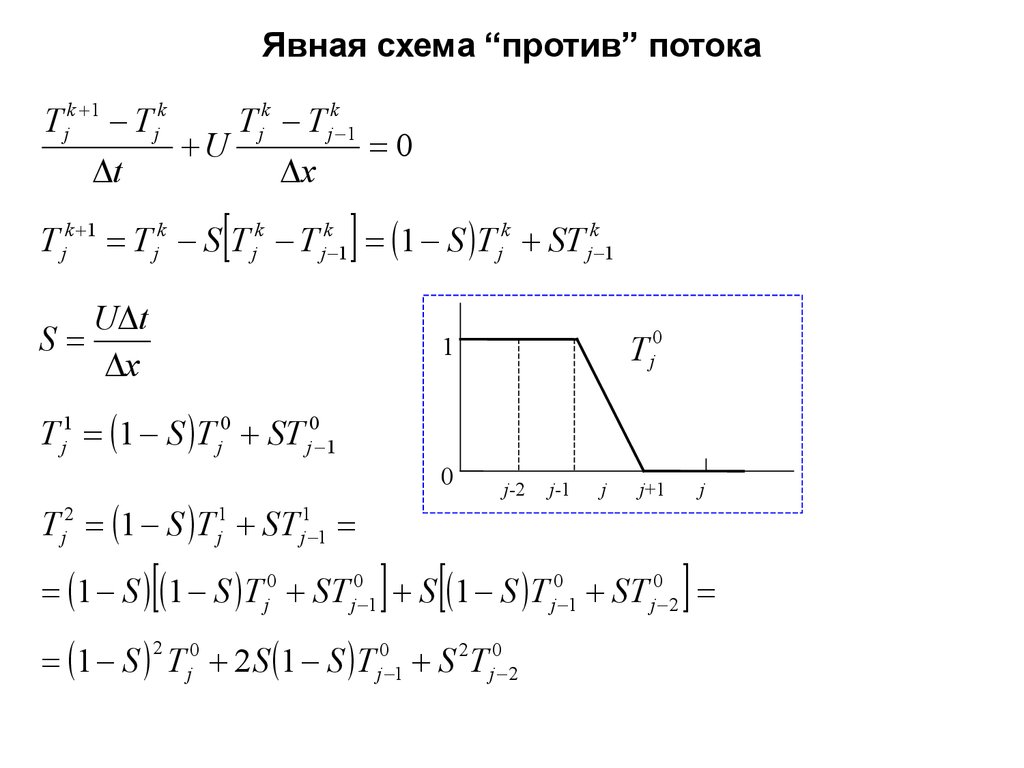
Явная схема “против” потокаT jk 1 T jk
T jk T jk 1
U
0
t
x
T jk 1 T jk S T jk T jk 1 1 S T jk ST jk 1
U t
S
x
T j0
1
T j1 1 S T j0 ST j0 1
T j2 1 S T j1 ST j1 1
0
j-2
j-1
j
j+1
j
1 S 1 S T j0 ST j0 1 S 1 S T j0 1 ST j0 2
2 0
1 S T j 2 S 1 S T j0 1 S 2T j0 2
44.
Анализ устойчивости схемы “против” потокаU t
S
1
x
T jk 1 1 S T jk ST jk 1 T jk 1
S 1
T j1 1 1 S T j0 1 ST j0 2 1,
T j1 1 S T j0 ST j0 1 S 1,
T j1 1 0
S 1
T j1 S 1
T j2 2 S 1 S S 2 S 2 2 S S S 2 S ,
T j2 1 S 2
0 S 1
условие устойчивости схемы “против” потока
45.
Анализ устойчивости схемы “против” потокаS
U t
x
0 S 1
условие устойчивости схемы “против” потока
Uh
x
t
U
S
Uh
скорость распространения возмущения в
конечно-разностной схеме
Uh U
другая формулировка условия устойчивости:
скорость распространения схемного возмущения
должна быть не меньше скорости распространения
возмущения, определяемого физикой процессов
46.
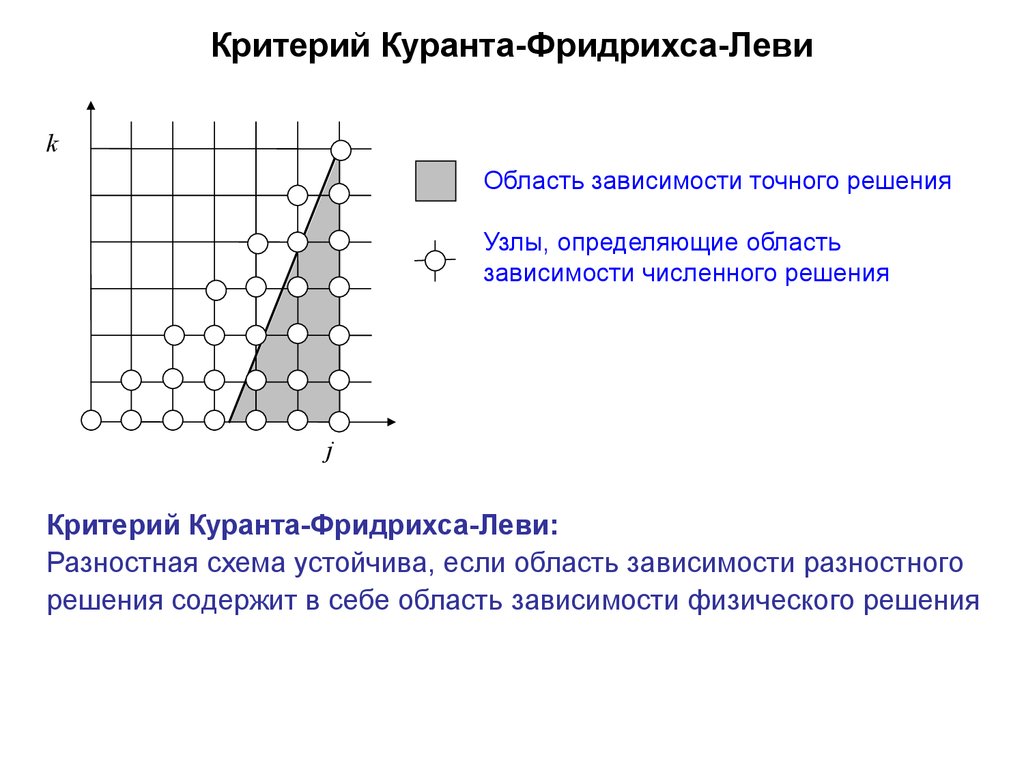
Критерий Куранта-Фридрихса-Левиk
Область зависимости точного решения
Узлы, определяющие область
зависимости численного решения
j
Критерий Куранта-Фридрихса-Леви:
Разностная схема устойчива, если область зависимости разностного
решения содержит в себе область зависимости физического решения
47.
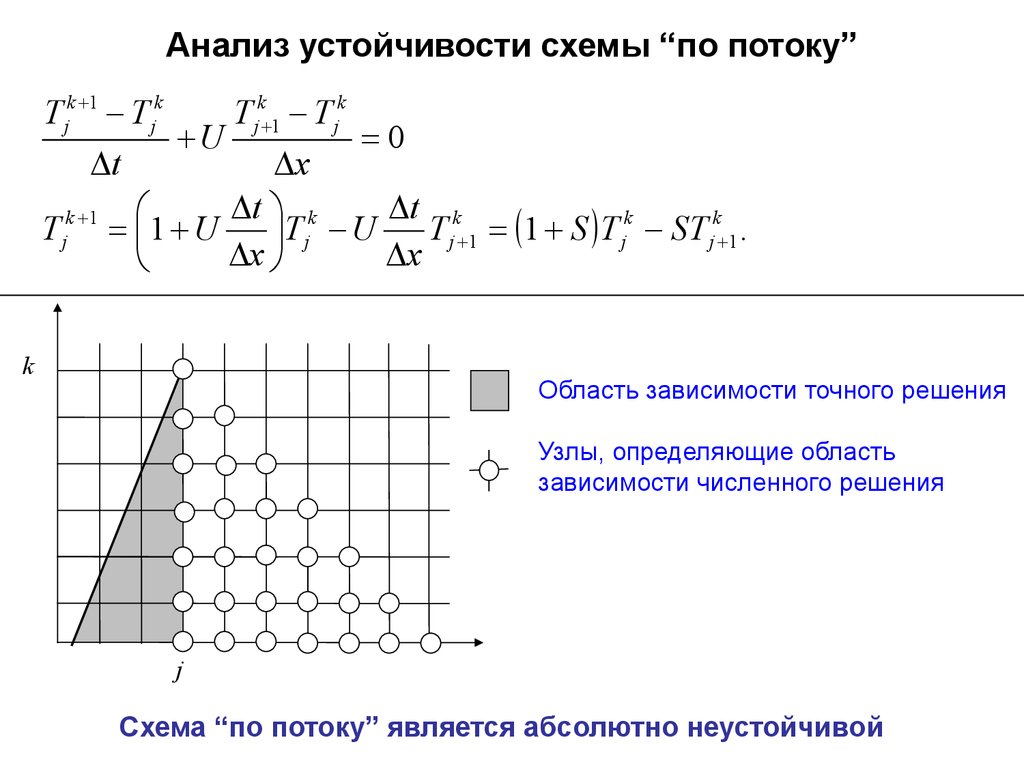
Анализ устойчивости схемы “по потоку”T jk 1 T jk
t
U
T jk 1 T jk
0
x
t k
t k
k 1
T j 1 U
T j 1 1 S T jk ST jk 1.
T j U
x
x
k
Область зависимости точного решения
Узлы, определяющие область
зависимости численного решения
j
Cхема “по потоку” является абсолютно неустойчивой
48.
Интегро-интерполяционный метод2
T
T
T
2
vx
a
0
2
t
x
x
уравнение теплопроводности с конвекцией
x j 1 / 2 0.5 ( x j 1 x j );
[ x j 1 / 2 , x j 1 / 2 ]
x j 1 / 2 0.5 ( x j x j 1 )
[ x j 1 / 2 , x j 1 / 2 ]
x j 1 / 2
Tdx v x T
t x j 1/ 2
x j 1 / 2
x j 1 / 2
a2
T
x
j 1
x j 1 / 2
T k
k
T j x v x T jk 1 / 2 T jk 1 / 2 a 2
t
x
T jk 1/ 2
1 k
T j T jk 1 O x 2
2
j 1 2
j 1/ 2
x j 1 / 2
j
x
x j 1 / 2
T k
x
T jk 1/ 2
j 1
стержень
O x 2
x j 1 / 2
1 k
T j 1 T jk O x 2
2
49.
Интегро-интерполяционный методT k
x
T k
x
x j 1 / 2
x j 1 / 2
T jk 1 T jk
x
T jk T jk 1
x
O x 2
O x 2
k 1
k
T
T
k
j
Tj j
O ( t )
t
t
T jk 1 T jk
t
vx
T jk 1 T jk 1
2 x
k
k
T T j 1 T j 1
O x 2
x
2 x
a
k
k
k
T
2
T
T
j 1
j
j 1
2
x 2
O x 2 t
k
k
k
2T T j 1 2T j T j 1
2
O
x
2
2
x
x
50.
Метод Неймана гармонического анализа устойчивостиu
u
a
Q
t
x
Неоднородное уравнение:
уравнение переноса с источником Q
u
u
точное решение
u u a u u Q
t
x
подстановка решения с возмущением
в уравнение
u
u
a
0
t
x
Однородное уравнение
для возмущения
возмущение точного решения
При анализе устойчивости рассматривают
однородные уравнения для возмущений
51.
Метод Неймана гармонического анализа устойчивостиe qt ei x
Гармоника:
Подставим гармонику в схему для однородного уравнения
и потребуем, чтобы малые возмущения u
не возрастали для любых собственных чисел
Конечно-разностный аналог гармоники на сетке:
qt i x
e e
e
qk t ij x
u jk k eij
e
e
q t k
eij x k eij , x, e q t
.
Необходимое условие устойчивости – отсутствие возрастания
малых возмущений для всех собственных чисел:
1
52.
Анализ устойчивости разностных схем для уравненияпереноса методом Неймана. Схема “против потока”
u
u
a
0
t
x
уравнение переноса
x , t x j j x , j 0 J ; t k k t , k 0 N
u jk 1 u jk
t
a
u jk u jk 1
x
0
схема “против потока”
a t
x
u jk 1 u jk u jk u jk 1 1 u jk u jk 1 ,
u jk k eij
сетка
гармоника
53.
Анализ устойчивости разностных схем для уравненияпереноса методом Неймана. Схема “против потока”
u
k 1
j
1 u u
k
j
u e
k
j
k ij
k
j 1
схема “против потока”
гармоника
k ij
k i [ j 1]
e 1 e e
i
i
e 1 e
i
1 e 1 cos i sin
k 1 ij
54.
Анализ устойчивости разностных схем для уравненияпереноса методом Неймана. Схема “против потока”
1 cos i sin
1 cos sin
2
2
2
1 2 1 cos cos sin
2
2
2
2
2
2
1 2 1 1 2 sin 1 4 1 sin
1
2
2
2
1 4 1 sin
1
2
4 1 0
2
0 1
условие устойчивости схемы “против потока”
55.
Анализ устойчивости разностных схем для уравненияпереноса методом Неймана. Схема “по потоку”
u
u
a
0
t
x
уравнение переноса
x , t x j j x , j 0 J ; t k k t , k 0 N
u jk 1 u jk
t
u
k 1
j
a
u jk 1 u jk
x
0.
сетка
схема “по потоку”
a t
t k
t k
k
k
1 a
u j 1 1 u j u j 1 ,
u j a
x
x
x
u jk k eij
гармоника
56.
Анализ устойчивости разностных схем для уравненияпереноса методом Неймана. Схема “по потоку”
u
k 1
j
1 u u
k
j
u e
k
j
k ij
k
j 1
схема “по потоку”
гармоника
57.
Анализ устойчивости разностных схем для уравненияпереноса методом Неймана. Схема “по потоку”
u
k 1
j
1 u u
k
j
k
j 1
схема “по потоку”
u e
k
j
k 1 ij
e
k ij
гармоника
1 e e
k ij
k i [ j 1]
1 e 1 cos i sin
i
58.
Анализ устойчивости разностных схем для уравненияпереноса методом Неймана. Схема “по потоку”
1 cos i sin
1 2 1 cos 2
2
2
2
2
2
1 2 1 1 2 sin 1 4 1 sin
1
2
2
2
Условие устойчивости всегда не выполнено
Схема “по потоку” абсолютно неустойчивая
59.
Анализ устойчивости разностных схем для уравненияпереноса методом Неймана. Неявная схема
u
u
a
0
t
x
уравнение переноса
x , t x j j x , j 0 J ; t k k t , k 0 N
u jk 1 u jk
u jk 1 u jk 11
a
t
x
1 u jk 1 u jk 11 u jk ,
u jk k eij
сетка
неявная схема “против потока”
a t
x
гармоника
60.
Анализ устойчивости разностных схем для уравненияпереноса методом Неймана. Неявная схема
1 u
k 1
j
u e
k
j
k ij
u
k 1
j 1
u
k
j
неявная схема
“против потока”
гармоника
61.
Анализ устойчивости разностных схем для уравненияпереноса методом Неймана. Неявная схема
1 u
k 1
j
u
k 1
j 1
неявная схема
“против потока”
u
k
j
u e
k ij
k
j
1
гармоника
k 1 ij
e e
1 e
2
k 1 i [ j 1]
i
k ij
e
1
1
1 4 1 sin
2
2
1
условие
устойчивости
всегда выполнено
62.
Анализ устойчивости разностных схем для уравнениятеплопроводности методом Неймана. Явная схема
2
u
u
2
a
t
x 2
h , x j jh, j 0... N ; t k k , k 0...K ,
u jk 1 u jk
u
k 1
j
a
k
k
k
u
2
u
u
j 1
j
j 1
2
h2
O h2
u 1 2 u u ,
k
j 1
u jk k eij
k
j
k
j 1
a 2
2
h
63.
Анализ устойчивости разностных схем для уравнениятеплопроводности методом Неймана. Явная схема
u
k 1
j
u 1 2 u u
k
j 1
k
k ij
uj e
k
j
k
j 1
64.
Анализ устойчивости разностных схем для уравнениятеплопроводности методом Неймана. Явная схема
u
k 1
j
u 1 2 u u
k
j 1
k
j
k
j 1
k
k ij
uj e
k 1 ij
k i [ j 1]
k ij
k i [ j 1]
e e
1 2 e e
e
i
e
i
1 2 2 cos 1 2
1 4 sin
2
2
a 1
2
1 1 4 sin
1 2
2
h
2
2
Условие
устойчивости
явной
схемы
65.
Анализ устойчивости разностных схем для уравнениятеплопроводности методом Неймана. Неявная схема
2
u
u
2
a
t
x 2
h , x j jh, j 0... N ; t k k , k 0...K ,
u jk 1 u jk
u
k 1
j 1
a
k 1
k 1
k 1
u
2
u
u
j 1
j
j 1
2
h2
1 2 u
u jk k eij
k 1
j
u
k 1
j 1
O h2
u ,
k
j
a 2
2
h
66.
Анализ устойчивости разностных схем для уравнениятеплопроводности методом Неймана. Неявная схема
k 1
k 1
k 1
k
u j 1 1 2 u j u j 1 u j
u e
k
j
k ij
67.
Анализ устойчивости разностных схем для уравнениятеплопроводности методом Неймана. Неявная схема
k 1
k 1
k 1
k
u j 1 1 2 u j u j 1 u j
u e
k
j
k ij
k 1 i [ j 1]
e
1 2 e e
k 1 ij
k 1 i [ j 1]
k ij
e
1
i
i
e e 1 2
Неявная
1
1
1 схема
2 cos 1 2 1 4 sin 2 абсолютно
устойчива
2
68.
Анализ устойчивости разностных схем для волновогоуравнения методом Неймана. Явная схема
2
2 u
u
2
a
2
t
x 2
h , x j jh, j 0... N ; t k k , k 0...K ,
k
k
k
u jk 1 2u jk u jk 1
u
2
u
u
j 1
j
j 1
2
2
2
a
O
h
2
2
h
u jk k eij
69.
Анализ устойчивости разностных схем для волновогоуравнения методом Неймана. Явная схема
2 2
a
2
2
2 1 2 m 1 0, 2 , m sin
h
2
1, 2 1 2 m
1 2 m 2 1
1 2 m 1 2 m
1 1 2 m
2
1 1
1 2 m
2
1 1
Правое неравенство
выполнено всегда
m 1 m m 1
a 2 2
2 1
h
Условие устойчивости явной схемы
70.
Анализ устойчивости разностных схем для волновогоуравнения методом Неймана. Неявная схема
2
2 u
u
2
a
2
t
x 2
h , x j jh, j 0... N ; t k k , k 0...K ,
k 1
k 1
k 1
u jk 1 2u jk u jk 1
u
2
u
u
j 1
j
j 1
2
2
a
O
h
2
2
h
u jk k eij
71.
Анализ устойчивости разностных схем для волновогоуравнения методом Неймана. Неявная схема
2 2
a
2
2
1 4 m 2 1 0, 2 , m sin
h
2
1
2 m
1, 2
i
1 4 m 1 4 m
1, 2
1 4 m
1
1 4 m
Неявная схема абсолютно устойчива
72.
Неявно-явные схемы с весами. Схема Кранка-Николсонаu
Lx u f
t
ДУЧП параболического типа
(эволюционное уравнение)
оператор, содержащий
пространственные производные
Lx
u k 1 u k
Lx u k f k O ( )
u k 1 u k
Lx u k 1 f k 1 O ( )
u k 1 u k
Lx u k 1 f k 1 (1 ) Lx u k f k
, (1 );
0 1
явная схема
неявная схема
неявно-явная
схема с весами
веса
73.
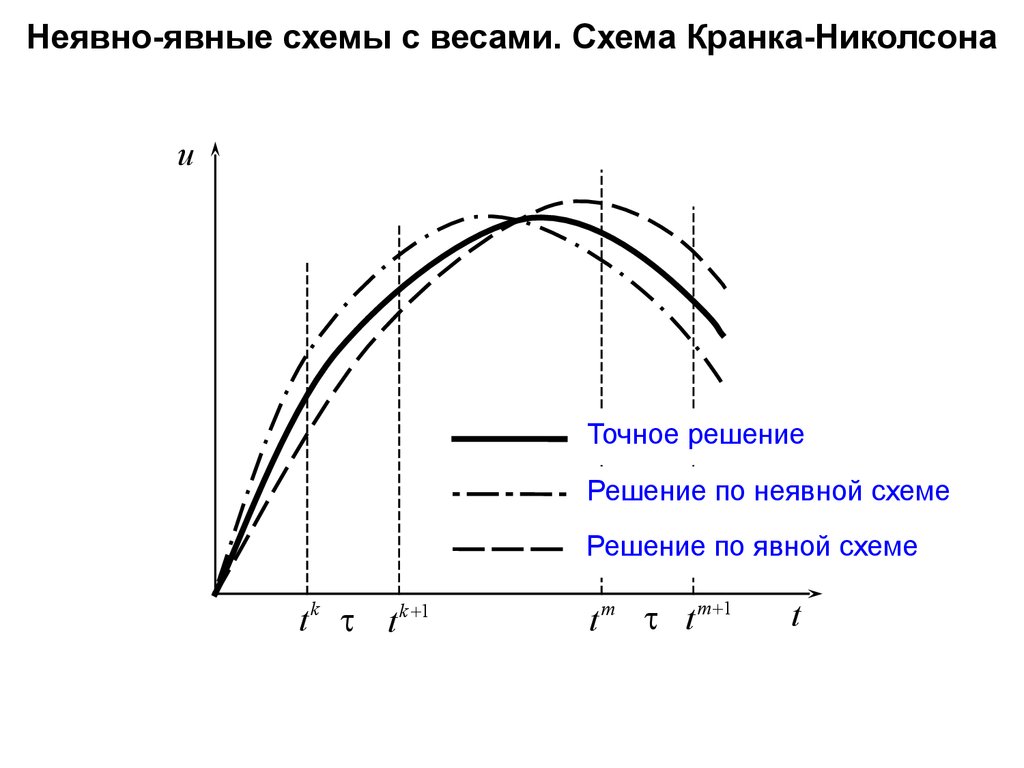
Неявно-явные схемы с весами. Схема Кранка-Николсонаu
Точное решение
Решение по неявной схеме
Решение по явной схеме
t k t k 1
t m t m 1
t
74.
Неявно-явные схемы с весами. Схема Кранка-Николсона1/ 2
u k 1 u k
неявно-явная
Lx u k 1 f k 1 (1 ) Lx u k f k O ( )
схема с весами
1/ 2
u k 1 u k 1
1
Lx u k 1 f k 1 Lx u k f k O 2
2
2
u k 1 / 2
t
t
1
RHS k 1 RHS k
2
Схема
КранкаНиколсона
75.
Схема с весами для уравнения теплопроводностиu kj 1 u kj
a
k 1
k 1
k 1
u
2
u
u
j 1
j
j 1
2
1 4 1
1
1 4
h
2
1 a
k
k
k
u
2
u
u
j 1
j
j 1
2
h2
условие устойчивости
1/ 2 1
абсолютная устойчивость
0 1/ 2
условная устойчивость
1 / 2 : O h2
1 / 2 : O 2 h 2
точность схемы
76.
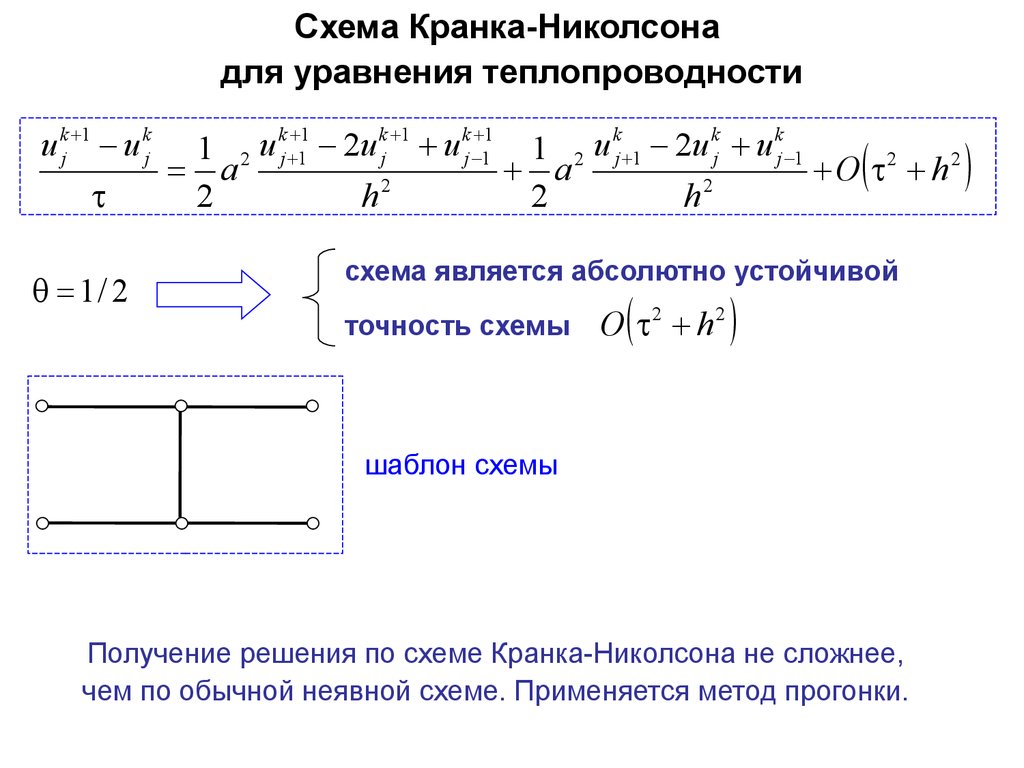
Схема Кранка-Николсонадля уравнения теплопроводности
u kj 1 u kj
1/ 2
k 1
k 1
k 1
k
k
k
1 2 u j 1 2u j u j 1 1 2 u j 1 2u j u j 1
2
2
a
a
O
h
2
2
2
h
2
h
схема является абсолютно устойчивой
точность схемы
O 2 h 2
шаблон схемы
Получение решения по схеме Кранка-Николсона не сложнее,
чем по обычной неявной схеме. Применяется метод прогонки.
77.
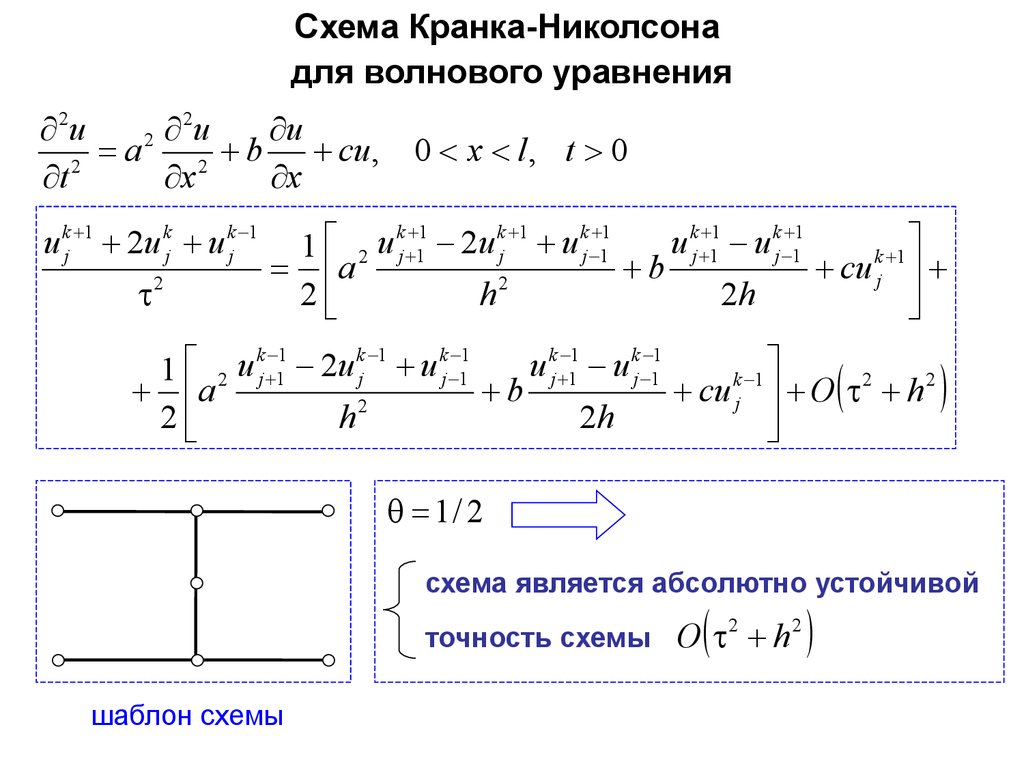
Схема Кранка-Николсонадля волнового уравнения
2
2u
u
u
2
a
b cu,
2
2
t
x
x
u kj 1 2u kj u kj 1
2
0 x l, t 0
k 1
k 1
k 1
k 1
k 1
u
2
u
u
u
u
1 2 j 1
j
j 1
j 1
j 1
k 1
a
b
cu j
2
2
h
2h
k 1
k 1
k 1
u kj 11 u kj 11
1 2 u j 1 2u j u j 1
k 1
2
2
a
b
cu
O
h
j
2
2
h
2h
1/ 2
схема является абсолютно устойчивой
точность схемы
шаблон схемы
O 2 h 2
78.
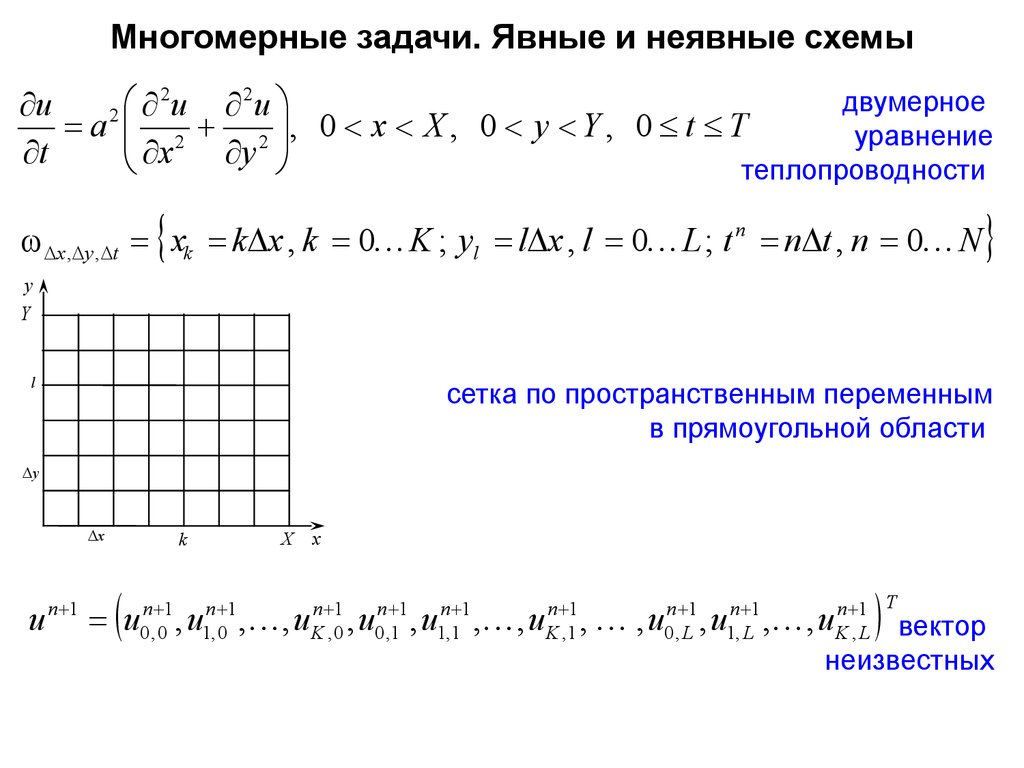
Многомерные задачи. Явные и неявные схемы2
2
двумерное
u
u
u
2
a 2 2 , 0 x X , 0 y Y , 0 t T
уравнение
t
x
y
теплопроводности
x , y , t xk k x , k 0 K ; yl l x , l 0 L ; t n n t , n 0 N
y
Y
l
сетка по пространственным переменным
в прямоугольной области
y
x
u
n 1
X
k
u
n 1
0, 0
n 1
1, 0
,u
, , u
x
n 1
K ,0
n 1
0 ,1
,u
n 1
1,1
,u
, , u
n 1
K ,1
n 1
0, L
, ,u
n 1
1, L
,u
, , u
n 1 T
K , L вектор
неизвестных
79.
Явная схемаu n 1 u n tLh u n u n
Lh ukn, l ukn, l
явная схема, операторное представление
n
n
n
n
n
n
u
2
u
u
u
2
u
u
k 1, l
k ,l
k 1, l
k , l 1
k ,l
k , l 1
2
a
2
2
x
y
n
u n n exp i x k y l
гармоника для
анализа устойчивости
1
1 1
a t 2 2
y 2
x
условие устойчивости
k
2
l
шаблон
явной схемы
80.
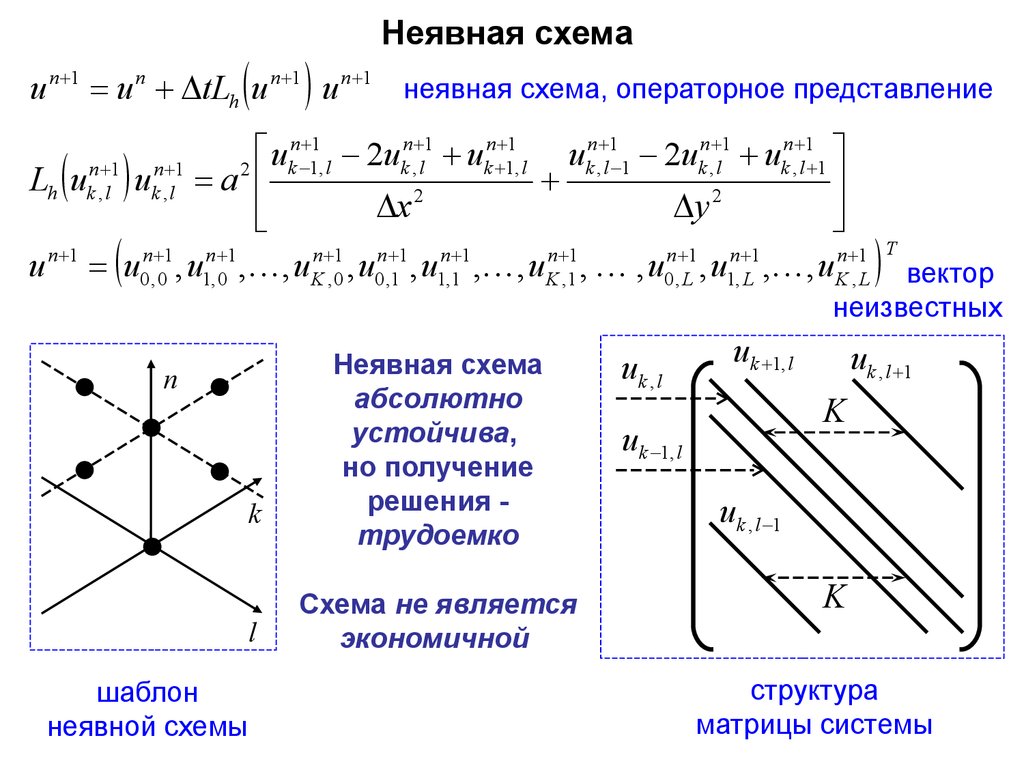
Неявная схемаu n 1 u n tLh u n 1 u n 1 неявная схема, операторное представление
n 1
n 1
n 1
n 1
n 1
n 1
u
2
u
u
u
2
u
u
k 1, l
k ,l
k 1, l
k , l 1
k ,l
k , l 1
n 1
n 1
2
Lh uk , l uk , l a
2
2
x
y
n 1
n 1
n 1
n 1
n 1
n 1
n 1
n 1
n 1
n 1 T
u u0, 0 , u1, 0 , , uK , 0 , u0,1 , u1,1 , , uK ,1 , , u0, L , u1, L , , uK , L вектор
неизвестных
n
k
l
шаблон
неявной схемы
Неявная схема
абсолютно
устойчива,
но получение
решения трудоемко
Схема не является
экономичной
uk , l
uk 1, l
uk , l 1
K
uk 1, l
uk , l 1
K
структура
матрицы системы
81.
Экономичность разностных схем. Методы расщепленияОпределение. Конечно-разностную схему будем называть
экономичной, если число длинных операций (типа умножения)
пропорционально числу узлов сетки.
Явные схемы для многомерных задач –
экономичные, но условно устойчивые
Неявные схемы для многомерных задач абсолютно устойчивые, но не экономичные
Для обеспечения экономичности неявных схем применяют
методы расщепления.
В методах расщепления неэкономичный оператор
переписывают в виде произведения более простых
экономичных операторов, т.е. факторизуют.
82.
Методы расщепленияu n 1 u n tLh u n 1 u n 1
полностью неявная схема
u n 1 u n
Lhx u n 1 Lhy u n 1 O t
t
n 1
hx k , l
L u
u
t
n 1
a
2
n 1
k 1, l
u
2u
n 1
k ,l
2
x
n 1
k 1, l
u
Lhy ukn, l1 a
Lhx u n u n 1 Lhy u n u n 1 O t ,
E t L
hx Lhy
E t L
hx
u
t
n 1
Lhx Lhy u n O t
Lhy E tLhx E tLhy
n 1
n 1
n 1
u
2
u
u
k ,l
k , l 1
2 k , l 1
y 2
u n 1 u n 1 u n
83.
Методы расщепленияE tLhx E tLhy E t Lhx Lhy t 2 Lhx Lhy
E t L
hx Lhy
u
t
n 1
Lhx Lhy u n O t
u
E tLhx E tLhy
t
n 1
u
n
2
Lhx Lhy u t Lhx Lhy
t
u n 1 / 2 E tLhy u n 1
u
E tLhx
t
n 1 / 2
E tLhy u
t
n 1
Lhx Lhy u n
u
t
n 1 / 2
ошибка
расщепления
n 1
O t
84.
Методы расщепленияu n 1 u n
Lhx u n 1 Lhy u n 1
t
u
n 1 / 2
t Lhx Lhy u t Lhx u
n
u n 1 t Lhx Lhy u n 1
n 1 / 2
исходная схема
u n 1 u n 1 / 2 tLhy u n 1
u n 1 / 2 u n t Lhx u n 1 / 2
u n 1 u n 1 / 2 t Lhy u n 1
оба этапа могут быть реализованы
методом прогонки,
что обеспечивает
экономичность
метода расщепления
n 0:
u 0 t Lhx Lhy u 0
n 1:
u n - результат с предыдущего временном слоя
На первом этапе - метод прогонки для каждого отсчета по переменной y
(для всех l), на втором - для каждого отсчета по x (для всех k)
85.
Методы расщепленияu n 1 u n
Lhx u n 1 Lhy u n 1
t
u
n 1 / 2
u n 1 t Lhx Lhy u n 1
t Lhx Lhy u t Lhx u
n
u n 1 u n 1 / 2 tLhy u n 1
u n 1 / 2 u n t Lhx u n 1 / 2
u n 1 u n 1 / 2 t Lhy u n 1
исходная схема
n 1 / 2
u
E tLhx
t
n 1 / 2
E tL u
n 1
hy
t
Lhx Lhy u n
u
t
n 0:
u 0 t Lhx Lhy u 0
n 1:
u n - результат с предыдущего временном слоя
n 1 / 2
На первом этапе - метод прогонки для каждого отсчета по переменной y
(для всех l), на втором - для каждого отсчета по x (для всех k)
86.
Метод расщепления по физическим процессамu n 1 u n
L1 L2 ... LM u n 1
t
E t L1 L2 ... LM u n 1 t L1 L2 ... LM u n
Расщепление
Ошибка имеет второй порядок по шагу по времени
E tL1 E tL2 ... E tLM u n 1 t L1 L2 ... LM u n
E tL1 u n 1 / M t L1 L2 ... LM u n
n 2 / M
u n 1 / M
E tL2 u
n 3 / M
n 2 / M
E
tL
u
u
3
E tL u n 1 u n ( M 1) / M
M
Метод реализуется
за M этапов
87.
Метод переменных направленийu n 1 / 2 u n
Lhx u n 1 / 2 Lhy u n
t / 2
u n 1 u n 1 / 2
Lhx u n 1 / 2 Lhy u n 1
t / 2
u n 1 u n
1
Lhx u n 1 / 2 Lhy u n u n 1
t
2
n
n 1
2
n 1
n
n 1
n
n 1 / 2
u
u
t
u
u
u u 2u
u n 1 / 2
Lhy
Lhy u n 1 u n
2
2
t
t / 2
2
n 1
n
u n 1 u n 1
1
t
u
u
Lhx u n u n 1 Lhy u n u n 1
Lhx Lhy
O ( t 2 )
t
2
2
2
t
O t 2
88.
Метод дробных шаговu n 1 / 2 u n
n 1 / 2
L
u
hx
t
n 1
n 1 / 2
u
u
n 1
L
u
hy
t
E tLhx u n 1 / 2 u n
E tLhy u n 1 u n 1/ 2
E tLhx E tLhy u n 1 u n
E t L
2
n 1
n
L
t
L
L
u
u
hx
hy
hx hy
u n 1 u n
Lhx Lhy u n 1 tLhx Lhy u n 1
t
89.
Фурье-метод расщепления по физическим процессам2
A
A
i A 1 A
2
2
A 2 2 3 3 i A A a1
A A a2 A
.
z 2
2 T
6 T
T
T
2
3
T t z v g t 1 z
A
Dˆ Nˆ A
z
2
3
i
1
ˆ
D 2 2 3 3
2 T
6 T
2
2
2 a
A
2
1
Nˆ i A
A A a2
A T
T
90.
Линейный шаг – применение преобразования ФурьеA ˆ
DA;
z
2
3
i
1
ˆ
D 2 2 3 3
2 T
6 T
2
A( z h, T ) exp( hDˆ ) A( z , T )
exp( hDˆ ) 1 exp hDˆ i
G ( z, ) A( z, T )
A( z, T ) exp[i( )T ]dT
0
1
1
A( z, T ) G ( z, )
G ( z, ) exp[ i ( 0 )T ]d
2
i
i
2
3
ˆ
D i 2 0 3 0
2
6
2
91.
Нелинейный шаг – схема Кранка-Николсона2
2 a
A
2
1
Nˆ i A
A A a2
A T
T
A ˆ
N A A;
z
A( z h, T ) A( z, T )
h
1
Nˆ A( z h, T ) A( z h, T ) Nˆ A( z , T ) A( z, T ) O ( h 2 )
2
A(1) ( z h, T ) A( z, T ) hNˆ A( z , T ) A( z, T )
A( 2 ) ( z h, T )
1 ˆ (1)
A( z, T ) h N A ( z h, T ) A(1) ( z h, T ) Nˆ A( z , T ) A( z, T )
2
92.
Фурье-метод расщепления по физическим процессамТолько дисперсия
Только нелинейность
A z, T
z 0
h

















































































 Математика
Математика