Перпендикулярность прямых и плоскостей в пространстве

1. Перпендикулярность прямых и плоскостей

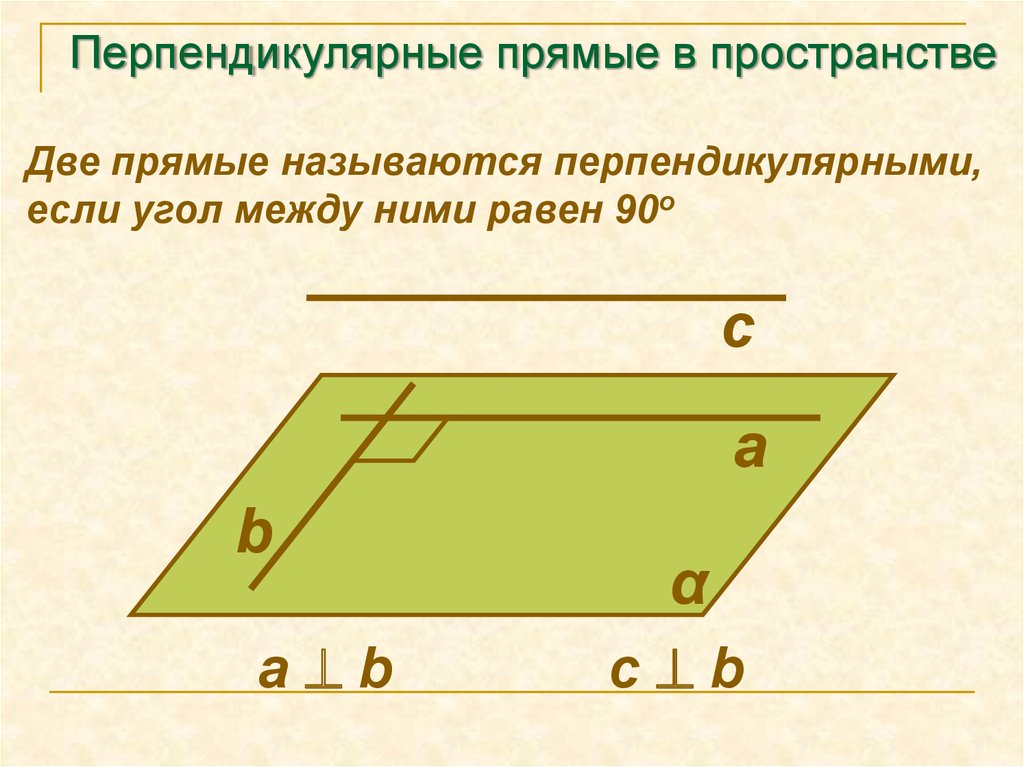
2. Перпендикулярные прямые в пространстве

Две прямые называются перпендикулярными,
если угол между ними равен 90о
с
а
b
а b
α
c b

3. Лемма

Если одна из двух параллельных прямых
перпендикулярна к третьей прямой, то и другая
прямая перпендикулярна к этой прямой.
a
Доказать: b c
b
M
Дано: а || b, a c
A
c
C
α
Доказательство:

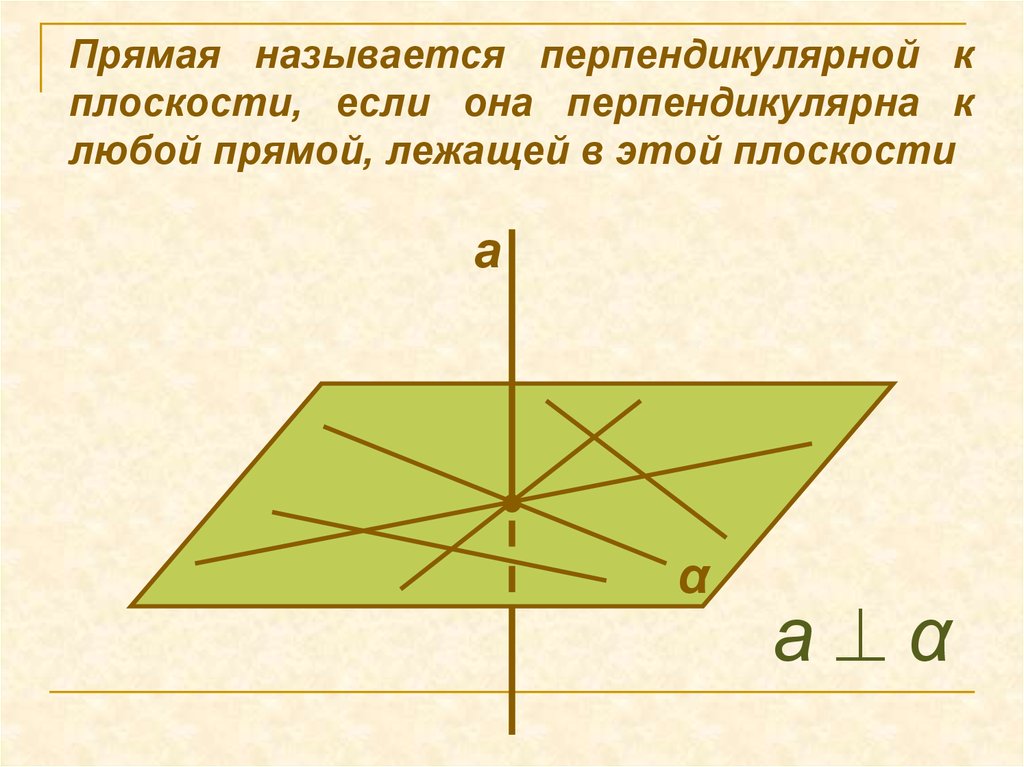
4. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости

а
α
а α

5. Теорема 1

Если одна из двух параллельных прямых
перпендикулярна к плоскости, то и другая
прямая перпендикулярна к этой плоскости.
a
Дано: а || а1; a α
а1
Доказать: а1 α
α
х
Доказательство:

6. Теорема 2

β
Если две прямые
перпендикулярны к
плоскости, то они
параллельны.
M
с
Дано: а α; b α
α
a
b
b1
Доказать: а || b
Доказательство:

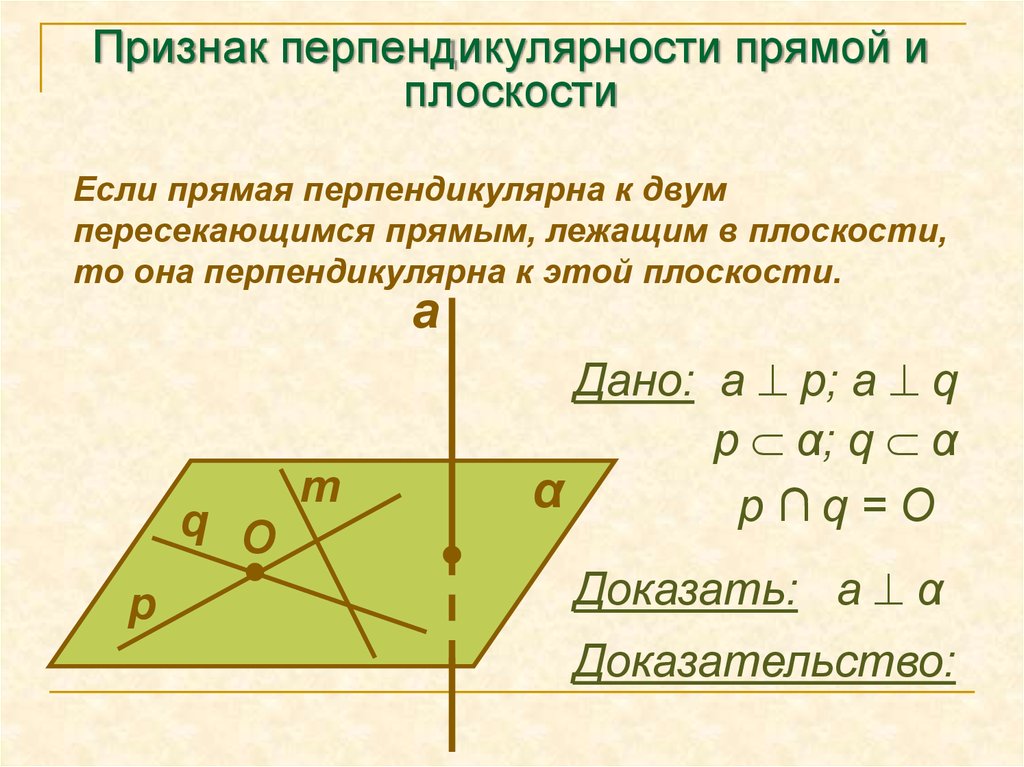
7. Признак перпендикулярности прямой и плоскости

Если прямая перпендикулярна к двум
пересекающимся прямым, лежащим в плоскости,
то она перпендикулярна к этой плоскости.
a
q O
p
m
Дано: а p; a q
p α; q α
α
p∩q=O
Доказать: а α
Доказательство:

8.

Доказательство:
а) частный случай
a
A
P
l
Q
q
O
α
p
m
B
L

9.

Доказательство:
а) общий случай
a1
a
m
q
p
O
α

10.

Теорема 4
Через любую точку пространства проходит
прямая, перпендикулярная к данной плоскости, и
притом только одна.
β
М
b
а
α
с
Дано: α; М α
Доказать:
1) ∃ с, с α, М с;
2) с – !
Доказательство:

11.

Задача
Дано: ABC;
MB BC; MB BA;
MB = BD = a
M
Доказать: МB BD
Найти: MD
a
Решение:
В
А
a
D
C