Похожие презентации:
Процессы переноса в биологических системах
1. Лекция № 5 Процессы переноса в биологических системах
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
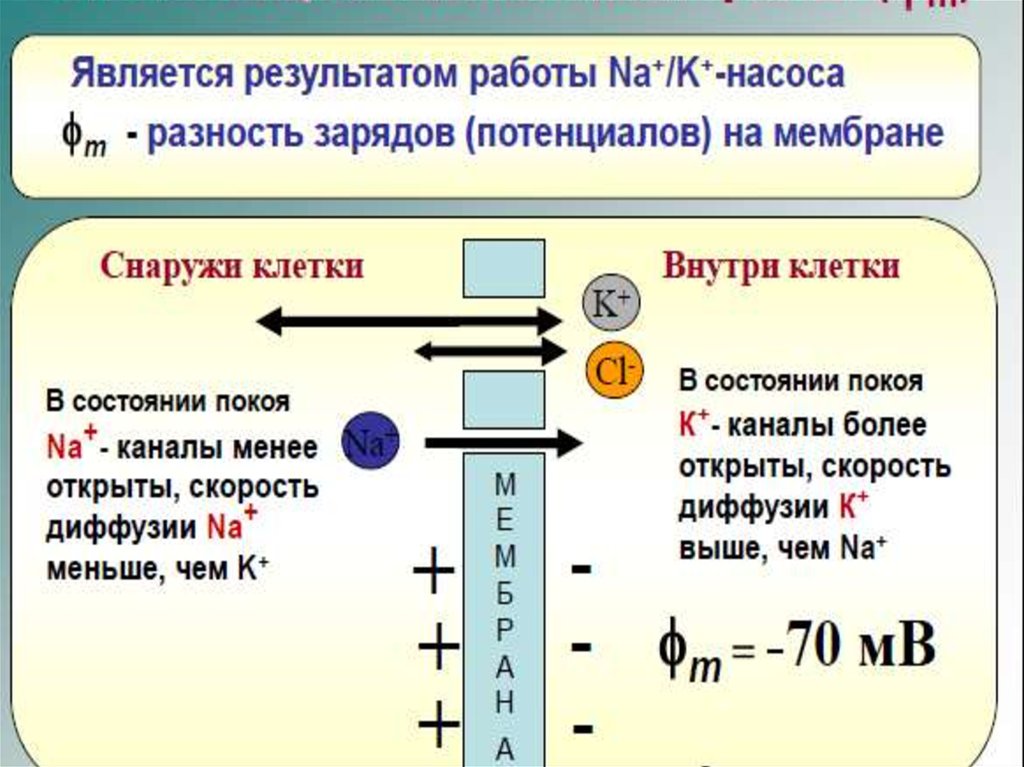
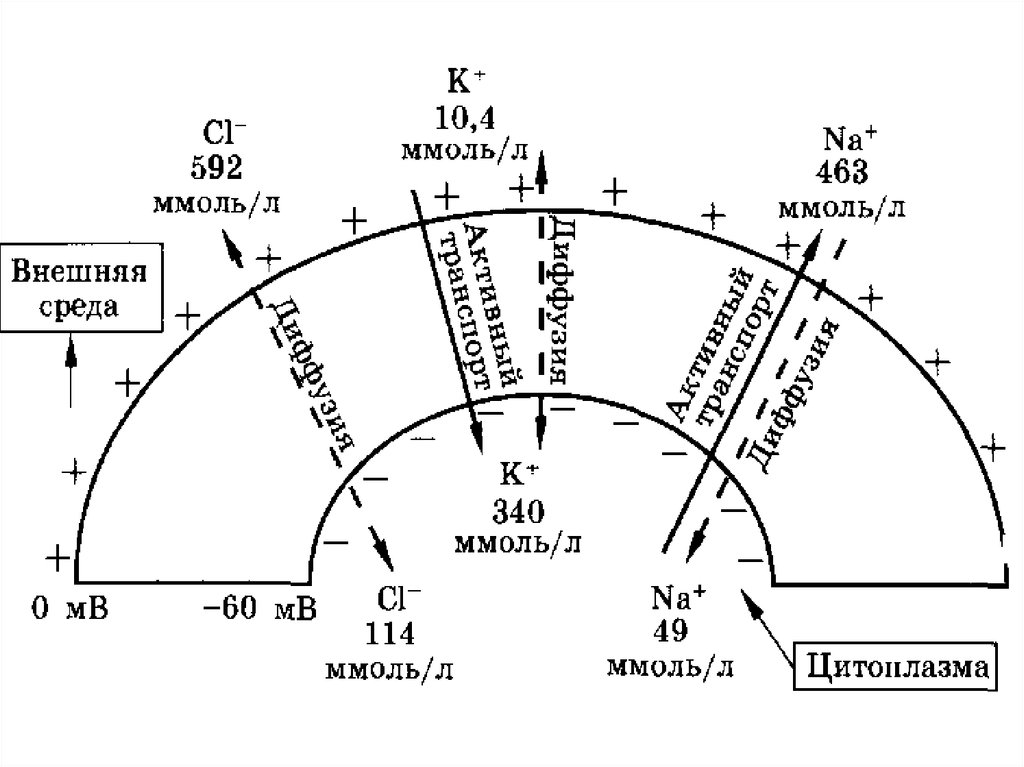
• Натрий-калиевый насос работаетпри условии сопряжения
переноса ионов калия и натрия.
Это означает, что если во
внешней среде нет ионов калия,
не будет активного переноса
ионов натрия из клетки, и
наоборот. Другими словами,
ионы натрия активируют натрийкалиевый насос на внутренней
поверхности клеточной
мембраны, а ионы калия — на
внешней.
15.
• Натрий-калиевый насос переноситиз клетки во внешнюю среду три
иона натрия в обмен на перенос
двух ионов калия внутрь клетки.
Один акт переноса требует затраты
энергии одной молекулы АТФ. При
этом создается и поддерживается
разность потенциалов на мембране,
причем внутренняя часть клетки
имеет отрицательный заряд.
16.
17.
18.
19.
20.
21. Уравнение Нернста-Планка
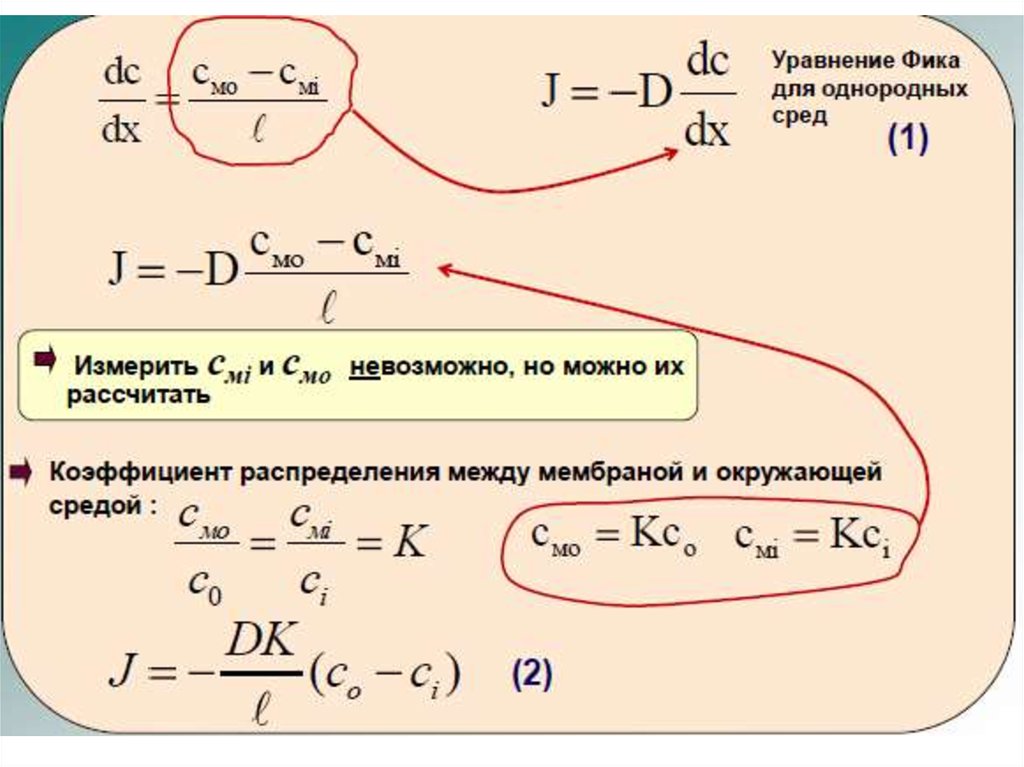
• Уравнение Фика является частным случаемобщего уравнения переноса: J -D dc u zFc d ,
dx
m
dx
где второй член уравнения показывает перенос
заряженных тел. Так как на мембране имеются ионы,
то существует и электрическое поле. Электрическое
поле на мембране влияет на перенос ионов и
электронов. В этом уравнении F – постоянная
Фарадея, φ - потенциал электрического поля, umподвижность, z-заряд и с – концентрация ионов.
Как показал А.Эйнштейн коэффициент диффузии
ионов пропорционален абсолютной температуре
среды и подвижностью ионов, поэтому уравнение
переноса ионов можно написать
dc zFc d
J -D(
dx
T dx
).
22. Уравнение Нернста.
• В условиях равновесия или в стационарныхсостояниях пассивный транспорт ионов
приводит к выравниванию
электрохимического потенциала. Берем
только один сорт иона, например К.
Обозначив концентрацию иона калия [K]o и
[K]i снаружи и внутри мембраны напишем
условие равенства электрохимического
потенциала:
[ K ]i
[ K ]o
RTLn
zF i RTLn
zF o
[ K ]i [ K ]o
[ K ]i [ K ]o
• или
RT
[ K ]i
m i o
Ln
.
zF
[ K ]o
23. Уравнение Гольдмана-Ходжкина-Каца.
Уравнение Гольдмана-ХоджкинаКаца.• В стационарном состоянии суммарный поток
ионов в единицу времени, проходящих через
мембрану равен нулю:
J Na J K J C l 0.
• Интегрируя уравнение Нернста-Планка
было получено:
RT
PNa [ Na]i PK [ K ]i PCl [Cl ]o
m
Ln
.
F
PNa [ Na]o PK [ K ]o PCl [Cl ]i
24.
25.
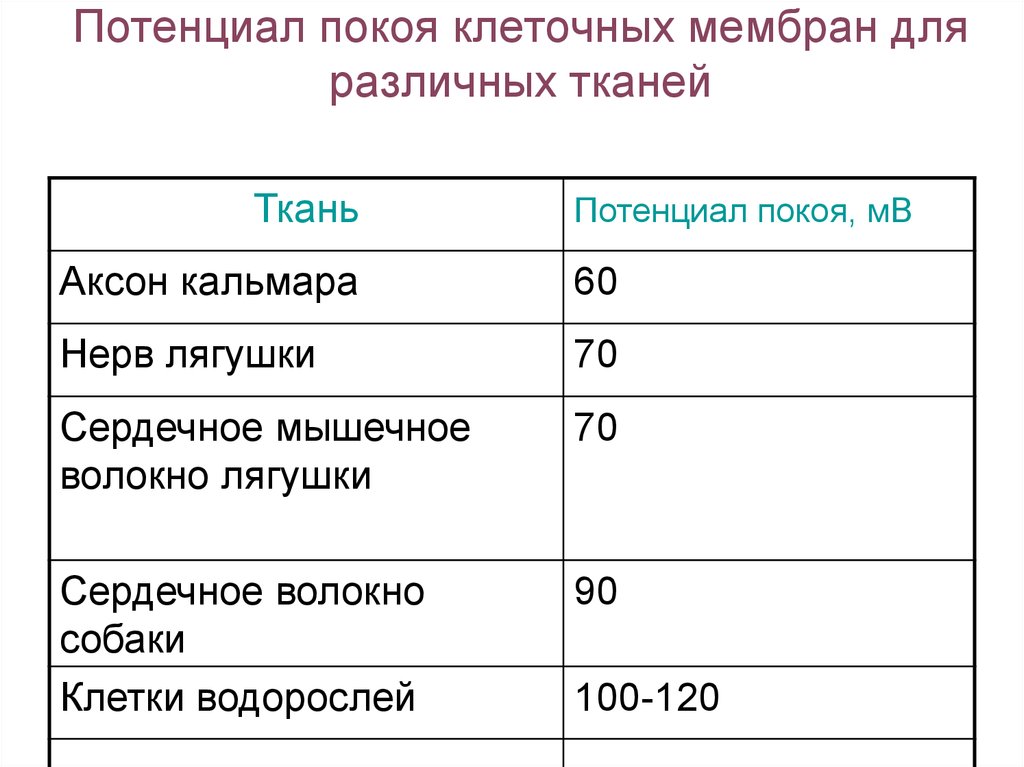
26. Потенциал покоя клеточных мембран для различных тканей
ТканьПотенциал покоя, мВ
Аксон кальмара
60
Нерв лягушки
70
Сердечное мышечное
волокно лягушки
70
Сердечное волокно
собаки
Клетки водорослей
90
100-120
27.
• Возбуждение клетки связано сувеличением электропроводности
клеточной мембраны. При этом
отрицательный относительно
внешней среды потенциал
становится положительным. Если по
уравнению Нернста вычислить
равновесные потенциалы на
мембране аксона кальмара, то
получим соответственно для ионов
К+, Na+ и С1 величины -90, +46 и -29
мВ.
28.
• Следовательно, при возбужденииклетки в начальный период
увеличивается проницаемость
мембран именно для ионов натрия
(проницаемость мембраны
возрастает более чем в 5000 раз) .
«Натриевая теория» возникновения
потенциала действия была
предложена, разработана и
экспериментально подтверждена А.
Ходжкином и А. Хаксли, за что в 1963
г. они были удостоены Нобелевской
премии.














 Биология
Биология








