Решение для атома водорода

1. Решение для атома водорода

Лекция 4

2. Эрвин Шредингер австрийский физик - теоретик

3. Электрон в кулоновском поле ядра (водородоподобный атом)

• Протон закреплен в центре атома и
движение электрона можно рассматривать в поле фиксированного ядра.
• Задачу можно свести к одной частице,
движущейся вокруг неподвижного ядра
под влиянием заряда ядра, но с массой μ
me M n
me
me M n

4. Операторы T и U

• Кинетическая энергия.
Приближение Борна – Оппенгеймера
Т = Ti = Te + Tя ≈ Te, т.к mя /me ≈2000
• Потенциальная энергия
Uij = qi*qj/rij ; Uяе = - Ze2/rяе (CГСЕ)
qe = - e qя = +Ze
Переход к единицам СИ - * 1/4 0
Uяе = - Ze2/rяе*4 0

5. Атомные единицы

Переход к единицам СИ - * 1/4 0 :
квант действия:
=1
масса электрона :
me = 1
заряд электрона :
e =1
длинна: атомный радиус Бора a0 = 1
0 – диэлектрическая проницаемость
вакуума

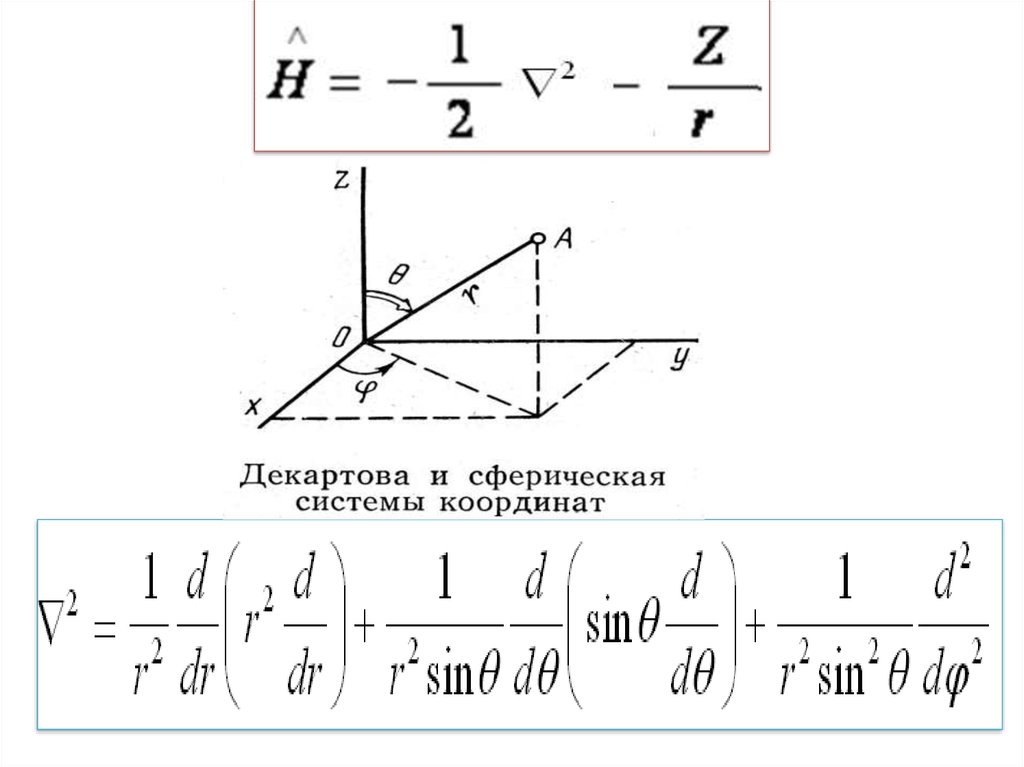
6.

7. Алгоритм решения

ˆ
E 0
H
(
T
(1
1 d
r 2 dr
U ) E
0
Z
) 0
E
2
r
2
1 d
d
1 d 1
2 d
2 2E 0
r
2
sin 2 2
2
d r sin d
r
dr r sin d
2

8. Для простоты вывода  = R**.

Для простоты вывода = R* * .
1/r2* / r*(r2 R/ r) +
+ 1/(r2sin )* / ( sin * / )*R +
+1/(r2sin2 )* 2 / 2)*R + (2 /r + 2E)R =0
Помножим обе части этого уравнения на

9. Алгоритм решения

/ r*(r2 R / r)/R + r2*(2 /r + 2E) +
1/(sin )* / ( sin * / )/ +
+1/(sin2 )* 2 / 2)/ =0
/ r*(r2 R / r)/R + r2*(2 /r + 2E) =
- 1/(sin )* / ( sin * / )/ -1/(sin2 )* 2 / 2)/ = l(l+1)
/ r*(r2 R/ r)/R + r2*(2 /r + 2E) =l(l+1)
Первое уравнение

10. Алгоритм решения

• Второе уравнение
-1/(sin )* / ( sin * / )/ 1/(sin2 )* 2 / 2)/ = l(l+1)
Домножим на sin2 и снова разделим на
две части
-1/(sin )* / ( sin * / )/ - l(l+1) =
1/(sin2 )* 2 / 2)/ = m2

11. Алгоритм решения

• Получим окончательно три уравнения
/ r*(r2 R/ r)/R +r2*(2 /r + 2E) =l(l+1)
1/(sin2 )* 2 / 2)/
d ( )
2
m
( ) 0
2
d
2
=
m2;

12. Результат решения

• Ф( ) = f(m) Фm( )
• ( ) = f(l,m) l,m( )
Y( , ) = l,m( ) *Фm( ) f(l,m)
– угловая часть ВФ
• R(r) = f(n,l) Rn,l(r)
– радиальная часть ВФ

13. Окончательное решение

Волновая функция
Энергия электрона в атоме водорода

14. Физический смысл квантовых чисел

(n) –
описывает наиболее вероятное
расстояние от ядра до электрона
и энергию электрона в атоме Н.
• n = 1,2,3……..
• общее количество АО с n =const
или степень вырождения,
2
равна n

15. Физический смысл квантовых чисел

Меняется от l = 0,1,..(n-1)
• В атоме Н кв. число l определяет форму
АТОМНОЙ ОРБИТАЛИ (АО) и орбитальный
момент количества движения.
–
определяет проекцию АО на выбранную
ось. m=0, 1, 2…. l

16. Атомная орбиталь

АО = nlm

17. Атомная орбиталь

• Название АО определяется l (Малликен)
l
АО
0
1
2
s
p
d
sharp principal diffuse
3
f
fine
Название линии в спектре атома Н
Резкая главная диффузная тонкая

18. Атомная орбиталь

• Рассмотрим пример на атоме N
Электронная конфигурация 1s22s22p3
l = n-1 =0 ; m =0
n =1
l =0 , 1
n =2
, l =0
l =1 ; m =1,0,-1
m=0

19. Способы представления АО.

1. Трехмерное представление или Граничные
поверхности (90-95 % электронной плотности)
2. Контурные диаграммы. Рассчитываем
волновую функцию при различных значениях
r, , . Построим сечения с одинаковыми
значениями функции.

20. Способы представления АО.

• 3. Для удобства изображения приводят
сечение этих орбиталей в плоскости,
проходящих через ядро. Такие сечения
называют часто полярными диаграммами.
( ) Ae
im

21. Форма ns и np-AO

22. Форма nd -AO

23. Анализ угловой части 

Анализ угловой части
• Функцию Yl,m( , ) = l,m( ) m( ) – называют
угловой частью волновой функции.
• В этом случае число l , характеризует
число узловых точек.
n
1
l m
0 0
(1s0) = 1/ *(Z/a0 )3/2 e-
= A * R(r)
;
Y( , )
2 0 0
(2s0) = 1/4 2 *(Z/a0 )3/2(2- ) e- =B* R(r)
2 1 0
(2p0) = 1/4 2 *(Z/a0 )3/2(2- ) e- cos = B* R(r) * cos
2 1 1
2p1 = 1/4 2 *(Z/a0 )3/2(2- ) e- sin cos =B* R(r) *sin cos
где = Zr/a0

24. Вывод

25. Типовая задача

• Атом водорода в квантовой механике.
Этапы решения уравнения Шредингера
для атома водорода. Волновая функция и
разделение переменных. Понятие
атомной орбитали. Физический смысл и
взаимозависимость квантовых чисел
(Покажите на примере атома N). Запишите
все возможные АО и постройте
энергетическую диаграмму

26. Радиальная часть волновой функции

1
2
l
2 3 ( n l 1)!
r / n 2r
2 l 1 2r
R( r )
Ln l ,
e
3
n
n
n 2 n ( n l )!
Полином Лягера

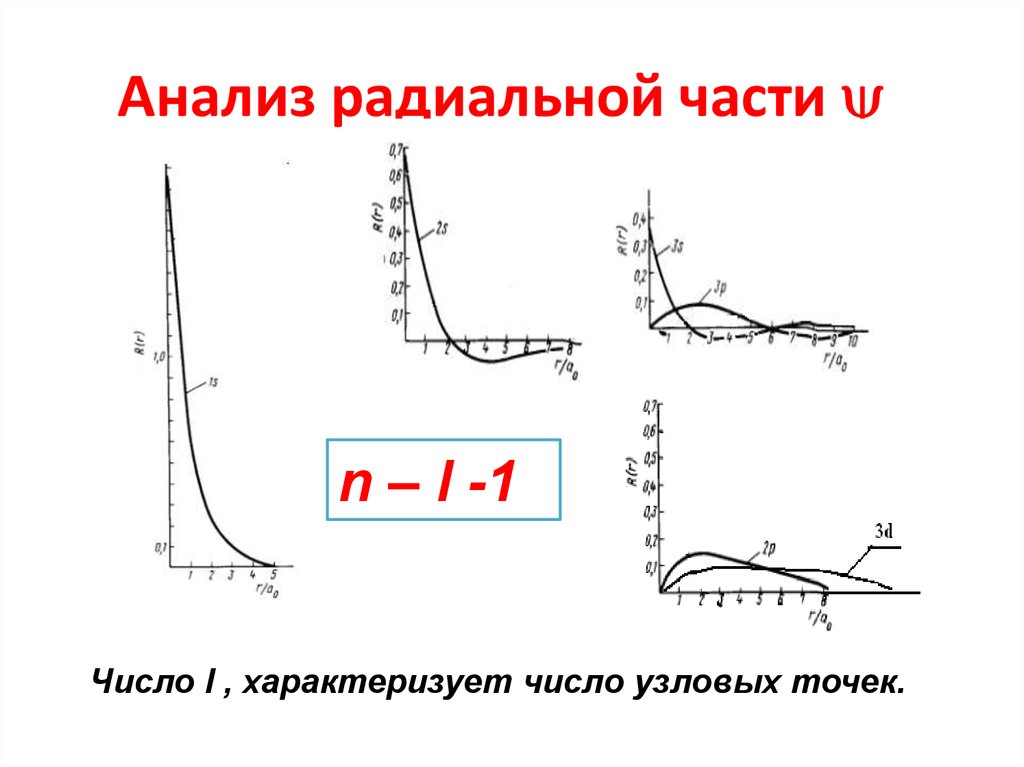
27. Анализ радиальной части 

Анализ радиальной части
n – l -1
Число l , характеризует число узловых точек.

28. Анализ радиальной части 

Анализ радиальной части
= Zr/a0
n
1
l m
0 0 (1s0) = 1/ *(Z/a0 )3/2 e- = B* e-
2 0 0
(2s0) = 1/4 2 *(Z/a0 )3/2(2- ) e- = B’* (2- ) e-
2 1 0 (2p0) = 1/4 2 *(Z/a0 )3/2(2- ) e- cos = B’*Y( , )*(2- ) e-
2 1 1 (2p1 ) = 1/4 2 *(Z/a0 )3/2(2- ) e- sin cos =B’*Y( , )*(2- ) e-

29. Анализ радиальной части 

Анализ радиальной части
Каждый график описывается совокупностью гармоник c
различным значением l

30. Вывод

• Радиальная часть волновой функции
является индивидуальной
характеристикой каждого атома и
распределение электронной
плотности реализуется совокупностью
гармоник с различным значением
азимутального квантового числа l.

31. Энергетическая диаграмма.

E
Z
2
4
me e
2
2n
2
2
( ýðã)
4
2
me e
Z
(äæ ) Z
2n
4
2n 0
2
2
2
2
(àò .åä)
n =1 E = -Z2/2n2 = -1/2 а.е. = -1/2*27,2 эВ = - 13,6 эВ
n =2 E = -Z2/2n2 = -1/8 а.е. = - 3,4 эВ
n =3 E = -1/18 а.е. = - 1,51 эВ