Квантовая теория атома водорода

1.

КВАНТОВАЯ ТЕОРИЯ АТОМА ВОДОРОДА
1. E. Schredinger. Ann. Phisik, 1926, 79, 361. Квантование как задача о собственных значениях. Первое сообщение.
2. E. Schredinger. Ann. Phisik, 1926, 79,489. Квантование как задача о собственных значениях. Второе сообщение*.
Из многочисленных работ, вышедших из под пера Эрвина Шредингера, выделяются две, ссылки на
которые приведены выше, в которых он сформулировал основные положения, как он говорил, волновой
механики, получил волновое уравнение – уравнение Шредингера, и применил их в частности к решению
задачи на отыскание стационарных уровней энергии в атоме водорода и распределении плотности
вероятности для электрона в этих состояниях.
В этих же работах именно он сформулировал стандартные условия, о которых мы уже говорили ранее
при решении задачи о движении частицы в потенциальной яме с бесконечно высокими стенками: именно,
требования конечности и непрерывности волновой функции вместе с её первой производной, а также
условие нормировки волновых функций.
Сам он писал: «В этом сообщении я собираюсь показать, на простейшем примере нерелятивистского
свободного атома водорода, что обычные правила квантования могут быть заменены другими
положениями, в которых уже не вводится каких-либо целых чисел. Целочисленность при этом получается
единственным образом сама по себе подобно тому как сама по себе получается целочисленность числа
узлов при рассмотрении колеблющейся струны. Это новое представление может быть обобщено, и я
думаю, что оно тесно связано с истинной природой квантования».

2.

Квантовомеханическая теория атома, стала фундаментальным вкладом в наши знания о мире. Наряду с коренной
ломкой взглядов на атомные явления, эта теория позволила понять такие близкие проблемы как характер взаимодействия
атомов при образовании стабильных молекул, происхождение периодической системы элементов и наличие характерных
электрических, магнитных, механических и оптических свойств у твёрдых тел. Однако первым продуктивным шагом на
этом пути было решение задачи водорода. В упомянутых выше работах многие математические детали опущены, что
оправдано в научной публикации. Мы же с целью изучения предмета воспроизведем решение во всей его полноте.
Атом водорода состоит из протона, электрический заряд которого +e, в котором сосредоточена практически вся масса
атома, и электрона – частицы с массой в 1836 раз меньшей и зарядом –e, который удерживается вблизи протона
электрическим полем. В первом приближении при таком соотношении масс можно полагать ядро совершенно
неподвижным, однако, если потребуется учесть его движение, то это легко сделать, как делалось в теории Бора, путём
замены массы электрона m на приведённую массу µ=mM/(m+M).
Идеологически совершенно всё равно, каков заряд ядра, поэтому мы будем решать задачу сразу не только для
собственно атома водорода с одним электроном вокруг него, но также и для так называемых водородоподобных атомов
– систем с зарядом ядра ze и движущегося вокруг него электрона. При этом Z полагается целым. В частности при Z = 1
получаем атом водорода.
Потенциальная энергия электрона в таком атоме равна
ze 2
U
,
r
r – расстояние между неподвижным точечным ядром, расположенным в начале отсчета, и электроном.
Общий вид уравнения Шредингера для стационарных состояний
Или
2
2m
2 U E .

3.

2
Ze 2
E ;
2m
r
2
или
2m Ze 2
2 (
E ) 0.
r
2
Поле, в котором движется электрон, является
центральносимметричным, поэтому целесообразно
воспользоваться сферической системой координат, рис.1.
В ней
r x2 y 2 z 2 ;
arccos
z
x y z
2
2
2
;
y
x
arctg .
Оператор Лапласа в сферических координатах имеет вид
1 2
1
1
2
2 (r
) 2
(sin ) 2 2
;
2
r r
r r sin
r sin
2
Рис.1.

4.

Уравнение Шредингера запишется как
1 2
1
1
2 2m
Ze 2
(r
) 2
(sin
) 2 2
2 (E
) 0;
2
2
r r
r
r sin
r sin
r
(Н6)
Уравнение (Н6) является уравнением в частных производных для волновой функции электрона в атоме водорода.
Вместе со стандартными условиями, накладываемыми на волновую функцию и её производную оно однозначно
определяет поведение электрона в данной системе.
Разделение переменных
Преимущество записи уравнения в сферических координатах при решении задачи об атоме водорода заключается в
том, что в таком виде его легко разделить на три уравнения, каждое из которых зависит только от одной координаты.
Попытаемся найти решение уравнения (Н6) в виде произведения трёх различных функций:
R r , зависящей только от r;
T , зависящей только от и
, зависящей только от ,
То есть предположим, что решение имеет вид
(r , , ) = R(r)T ( ) ( ).
(Н7)
Функция R(r) характеризует изменение волновой функции электрона вдоль радиус-вектора при постоянных и .
Функция T описывает изменение в зависимости от угла вдоль меридиана на сфере, центром которой служит
ядро, при постоянных r и .
Функция характеризует изменение в зависимости от азимутального угла вдоль параллели на сфере, центром
которой служит ядро, при постоянных r и .

5.

Далее зависимость введенных выше функций от их аргументов нами указываться не будет: =RTФ.
Подставив (Н7) в уравнение (Н6), получаем:
1
1
T
1
2 2m
Ze 2
2 R
(T r
) 2
(sin R
)
RT 2 2 ( E
) RT 0;
r 2 r
r
r sin
r 2 sin 2
r
Вынося функции, не зависящие от переменных по которым производится дифференцирование, получаем
T 2 R
R
T
RT 2 2m
Ze 2
(r
) 2
(sin ) 2 2
2 (E
) RT 0;
2
2
r r
r
r sin
r sin
r
Разделим уравнение на RTФ, и умножим на r sin :
2
2
sin 2 2 R sin
T
1 2 2mr 2 sin 2
Ze 2
(r
)
(sin )
(E
) 0;
2
2
R r
r
T
r
Перепишем его в виде
sin 2 2 R sin
T
2mr 2 sin 2
Ze 2
1 2
(r
)
(sin )
(E
)
;
2
2
R r
r
T
r
Левая часть зависит от r и , а правая – только от .
И, тем не менее, они равны друг другу. Очевидно, что это может быть только в том случае, если левая и правая часть
равны одной и той же константе. Эту постоянную удобно обозначить как m 2 . Таким образом, имеем два уравнения:

6.

1 2
2
m
и
2
sin 2 2 R sin
T
2mr 2 sin 2
Ze 2
2
(r
)
(sin )
(
E
)
m
.
2
R r
r
T
r
2
Разделим (Н9) на sin
(Н9)
и сгруппируем слева члены, зависящие от r, справа – от .
1 2 R 2mr 2
Ze 2
m2
1
T
(r
) 2 (E
)
(sin );
R r
r
r
sin 2 T sin
Снова получаем уравнение, справа и слева в котором стоят функции разных переменных. Это значит, что каждая из сторон
должна равняться одной и той же постоянной. Обозначим её λ.
Таким образом, имеем три уравнения:
1 2 R 2mr 2
Ze 2
(r
) 2 (E
) ;
R r
r
r
m2
1
T
(sin
) ;
2
sin T sin
1 2
m 2;
2
(Н11)

7.

Каждое из этих уравнений – простое дифференциальное уравнение для одной функции, зависящей от одной
переменной. Следовательно, мы можем заменить символы частных производных на символы полных производных.
Полученное нами упрощение весьма существенно. Перепишем эти уравнения в символах прямых дифференциалов, а
кроме того, первое умножим на R, второе на Т, третье на Ф.
1 d 2 dR 2m
Ze 2 λ
r
2 E
2 R 0;
2
r dr dr
r r
m2
1 d
dT
(sin
) [ 2 ]T 0;
sin d
d
sin
1 d 2
2
m
;
d 2
Решение угловой части
Мы получили три независимых уравнения на собственные значения для соответствующих дифференциальных
операторов. Решение последнего из уравнений общеизвестно:
eim ;
В силу требования однозначности, функция
выполняться равенство
должна быть периодической с периодом 2 . То есть должно
eim eim ( 2πk ) .
так как физически 2 + есть тот же угол, что и . Такая периодичность будет иметь место, если параметр m равен
любому целому числу, включая ноль:
m 0, 1, 2, 3,...

8.

Решим уравнение
1 d
dT
m2
(sin
) [ 2 ]T 0.
sin d
d
sin
(H19)
dx
Обозначим cos = x , тогда -sin d = dx d = -dx/sin , sin2 = 1 – x2.
m2
d
dT
(sin
( sin )) (
)T 0;
2
dx
dx
1 x
Обозначим y x T cos . Область определения x [-1,+1].
m2
d
2 dy
((1 x ) ) (
) y 0.
2
dx
dx
1 x
d
dy
Дифференцируем первую скобку
((1 x 2 ) ) (1 x 2 ) y 2 xy ;
dx
dx
m2
2
(1 x ) y 2 xy (
) y 0;
2
1 x
Так как m входит в квадрате, y может быть функцией только m m .
Будем искать y в виде:
m
2
y (1 x ) V ( x).
2
(Н25)
(Н26)
m
m
1
m
2 2
2 2
y (1 x ) ( 2 x)V (1 x ) V ;
2
y mx(1 x )
2
m
1
2
m
2
V (1 x ) V ;
2
(Н27)

9.

y mx(1 x )
2
y m(1 x )
2
m
1
2
m
1
2
m
2
V (1 x ) V ;
2
m
m
m
m
2
1
1
m
m
2 2
2 2
2 2
2 2
V mx( 1)( 2 x)(1 x ) V mx(1 x ) V (1 x ) ( 2 x) V (1 x ) V ;
2
2
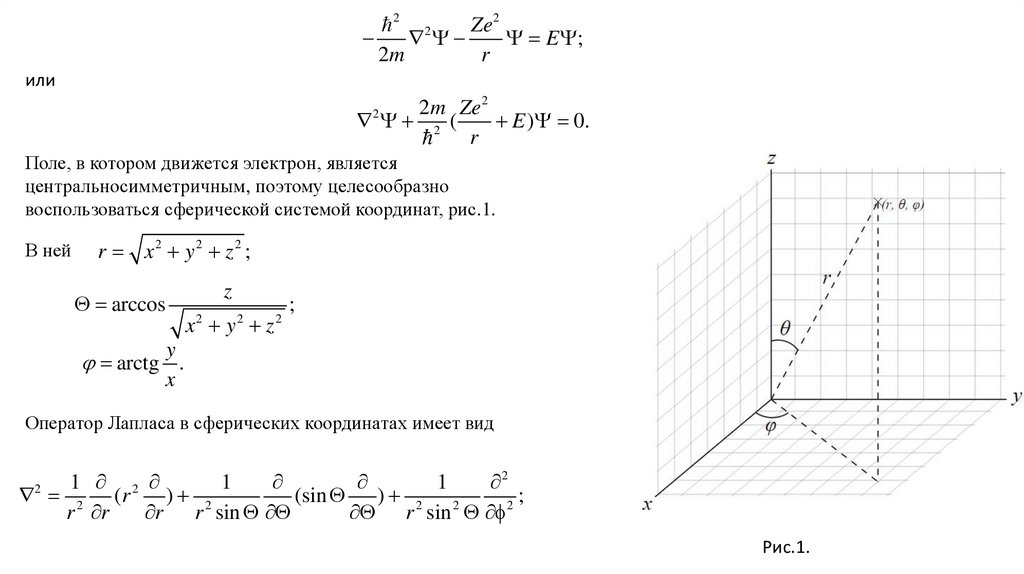
Соберем члены, пропорциональные функции V, первой и второй её производной.
y [ m(1 x )
m
1
2
m
2
2
m
2
2
m
1
2 2
m
2 2
V (1 x ) V ;
2
Для того, чтобы получить первый член в (Н25), умножим левую и правую часть на (1 x )
2
m
2
m x (1 x )
2
2
2
y (1 x ) [ m(1 x ) m x (1 x )
2
2
2
2
2
m
1
2
2mx (1 x )
2
2
2mx (1 x )
2
2
m
1
2
]V 2mx(1 x )
m
2
]V 2mx(1 x ) V (1 x )
2
2
m
1
2
V
*
Для того, чтобы получить второй член в (Н25), умножим левую и правую часть (Н27) на -2x
2 xy 2mx (1 x )
2
2
m
1
2
m
2
V 2 x(1 x ) V ;
2
**
m
2
Подставим выбранный вид решения y (1 x ) V ( x) (Н26) в третий член уравнения (Н25)
2
m
m
1
m2
2 2
2
2 2
(
) y (1 x ) V m (1 x ) V ;
1 x2
***
Подставим три последних выражения (*, **,***)в уравнение (Н25) . Учтем, что все члены пропорциональны (1 x )
2
m
2 2
поэтому сократим на (1 x ) . Соберем члены с соответствующими порядками производных функции V.
m
2,

10.

m
2 2
m
1
2 2
y (1 x 2 ) [ m(1 x ) m 2 x 2 (1 x )
2 xy 2mx (1 x )
2
2
m
1
2
m
1
2 2
2mx 2 (1 x )
m
2
V 2 x(1 x ) V ;
2
m
2 2
m
1
2 2
]V 2mx(1 x ) V (1 x ) V
m
m
1
m2
2 2
2
2 2
(
) y (1 x ) V m (1 x ) V ;
2
1 x
(1 x 2 )V [ 2mx 2 x]V [ m m 2 x 2 (1 x 2 ) 1 2mx 2 (1 x 2 ) 1 2mx 2 (1 x 2 ) 1 m 2 (1 x 2 ) 1 ]V 0
(1 x 2 )V 2(m 1) xV [ m m 2 (1 x 2 ) 1 ( x 2 1) ]V 0
m m
(1 x 2 )V 2( m 1) xV ( m m )V 0;
2
(Н33)

11.

V ( x) a x .
V(x) ищем в виде
(Н34)
0
V a x 1 ;
0
V a ( 1) x 2 ;
0
(Н33)
(1 x 2 )V 2( m 1) xV ( m m )V 0;
2
(Н33) перепишется в виде
(1 x ) a ( 1) x
2
0
2
2( m 1) x a x
0
1
( m m ) a x 0;
2
0
2
2
{
a
(
1)
x
a
(
1)
x
2(
m
1)
a
x
(
m
m
)
a
x
} 0;
0
Эта сумма будет равна нулю, если коэффициенты при всех степенях x будут равны нулю.
Если взять степень равную в первом члене
x 2 x 2,
то во всех остальных степень достигается при ν = . Таким образом номер члена, а соответственно и номер
коэффициента “a” в первом члене на два больше чем во всех остальных.
Приравниваем нулю коэффициент при x и опять обозначая m m , получаем
a 2 ( 2)( 1) a ( 1) a 2(m 1) a ( m m 2 ) 0;

12.

( 1) 2(m 1) m m 2
a 2 a
( 2)( 1)
- рекуррентная формула для коэффициентов ряда (Н34).
Если мы хотим, чтобы наше решение
V ( x) a x . было конечным, непрерывным и однозначным, необходимо,
0
чтобы сумма содержала конечное число членов – была многочленом.
a , a 2 0 если ( 1) 2(m 1) m m 2 0,
или при
( 1) 2(m 1) m m 2 ;
( 1) ( m 1) ( m 1) m( m 1);
[ 1 m 1] (m 1)( m);
( m)( m 1);
Обозначив m , получаем ( 1),
а так как сумма по ν берется по целым положительным числам и
(H45)
m m 0; Кроме того, введенные при интегрировании уравнений константы λ и m оказываются связанными.
0,1, 2,...
m m 0,1, 2,...
0,1, 2,...

13.

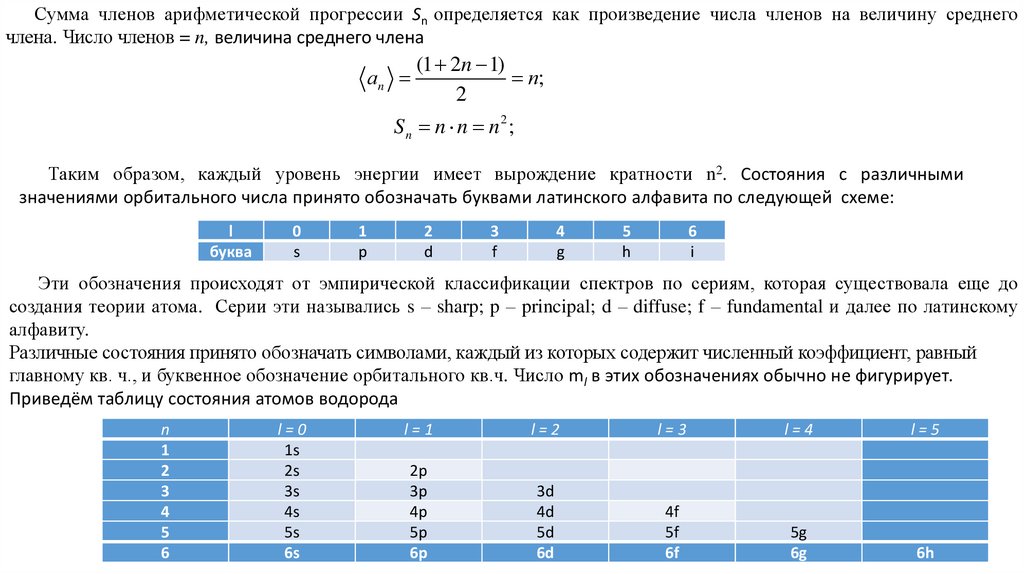
При таких , aν+2 и все последующие коэффициенты одинаковой чётности с aν+2 (в силу (Н41)) будут равны нулю.
Это первое условие, а второе состоит в том, что сумма должна содержать только члены одинаковой чётности.
2
Решение y (1 x )
m
2
V ( x), принадлежащее характеристическим числам
0,1, 2,... и
m 0,1, 2,...,
обозначим через p m ( x), x cos .
Ограничение на m
следует из (Н45), так как >0.
p
где p p
m
m
(1 x )
2
m
2
d
m
dx
m
p ( x),
при m=0
p ( ) называется полиномом Лежандра порядка l.
Коэффициент при нём обычно нормирован так, что p (1) 0, а p
m
( x) - присоединённый полином Лежандра.
Полином Лежандра может быть представлен формулой
p 0 ( x) p ( x)
1
d
( x 2 1) .
2 ! dx
Таким образом, окончательный вид решения уравнения для функции T ( )
T ( ) N m P (cos ),
m
где Nlm - нормированный множитель.

14.

Произведение двух угловых функций
( )T ( ) Y m ( , ).
Y m ( , ) N m P (cos )eim .
m
Функции Y m ( , ) называются сферическими и представляют собой угловую часть семейства ортогональных
решений уравнения Лапласа, записанную в сферических координатах. Они широко используются для изучения
физических явлений в пространственных областях, ограниченных сферическими поверхностями и при
решении физических задач, обладающих сферической симметрией.
Они образуют ортонормированную систему в пространстве функций на двумерной сфере, то есть
применительно к нашей задаче при r = const. Ортонормированность означает выполнение равенств
2
d Y m sin d 1;
2
0
0
2
0 d 0 Y ' m 'Y m sin d ll ' mm ' ,
где ll ' mm ' символы Кронекера.
Совокупность сферических функций для данного уравнения Лапласа Y m ( , ) обладает свойством полноты, то есть
Любая функция ( , ) , имеющая непрерывные вторые производные, может быть равномерно аппроксимирована
некоторым полиномом из сферических функций.
( , ) c mY m ( , ).
0 m

15.

Решение радиальной части
Перейдем к решению уравнения (H18) для радиальной части волновой функции.
1 d 2 dR 2m
Ze 2
r
2 E
2 R 0;
2
r dr dr
r r
Подставляя допустимые значения λ=l l 1 , получаем
1 d 2 dR 2m
Ze 2 l l 1
R 0;
r
2 E
2
2
r dr dr
r
r
Умножим (H56) на
(H56)
2
2m
и приведем к стандартному виду уравнения Шредингера,
1 d 2 dR Ze 2
r
2m r 2 dr dr r
2
l l 1
R ER.
2mr 2
2
Это - уравнение, отвечающее движению в одном измерении с некоторой эффективной потенциальной энергией
2
Ze 2
l (l 1)
U
;
2
r
2m r
(H57)
В аналитической механике при рассмотрении движения в центральном поле для эффективной потенциальной энергии
получается выражение
M2
(H57’)
U U r
;
eff
2mr 2

16.

Сравнивая (H57) с (H57’) , видим, что механический момент в атоме водорода квантуется, причем
M2
где l 0,1, 2,..., lmax .
2
l (l 1); M
l (l 1);
Полученное выражение отличается от боровского условия квантования круговых орбит,
согласно которому M n и нет ограничений на n.
Рассмотрим, как ведет себя эффективная потенциальная энергия (H57). Графики знаменателей даны
на рис.1. При малых значениях аргумента преобладает линейная функция, при больших –
1
квадратичная. Соответственно, при малых r преобладает
, - потенциальная энергия
r2
1
положительна и резко растет с уменьшением радиуса, при больших преобладает
, r
потенциальная энергия отрицательна и с ростом радиуса стремится к нулю, рис.2.
Нас интересуют связанные состояния электрона, то есть такие, когда он находится в
потенциальной яме, поэтому будем рассматривать только случай E 0 .
Поскольку во всех уравнениях складываются члены одинаковой размерности,
2mE
размерность
равняется (длина)-2 , поэтому можно принять
2
Кроме того, обозначим
Ze 2 m
2
2mE
2
1
r
β; r 0
2
0
Рис.1
1
.
α , тогда (H56) приобретет вид
1 d 2 dR 2m
Ze 2 l l 1
R 0;
r
2 E
2
2
r dr dr
r
r
1 d 2 dR 1 2 l l 1
R 0.
r
2
2
2
r dr dr r0
r
r
(H56)
рис.2.

17.

Выполним дифференцирование в первом члене
d 2 R 2 dR 1 2 l (l 1)
2
R 0;
2
2
dr
r dr r0
r
r
В предельном случае r можно пренебречь всеми членами, содержащими r в знаменателе и рассматривать
уравнение
2
Его частные решения имеют вид R e
r
r0
d R R
2 0.
2
dr
r0
, а общее решения является их линейной комбинацией:
r
r0
r
r0
R Ae Be .
В соответствии со стандартными условиями, при r должно быть R 0 , поэтому В = 0 и общее решение (Н61) имеет
вид
R Ae
Учтя