Похожие презентации:
Урок-путешествие. Линейная функция и её график
1. Урок-путешествие
2.
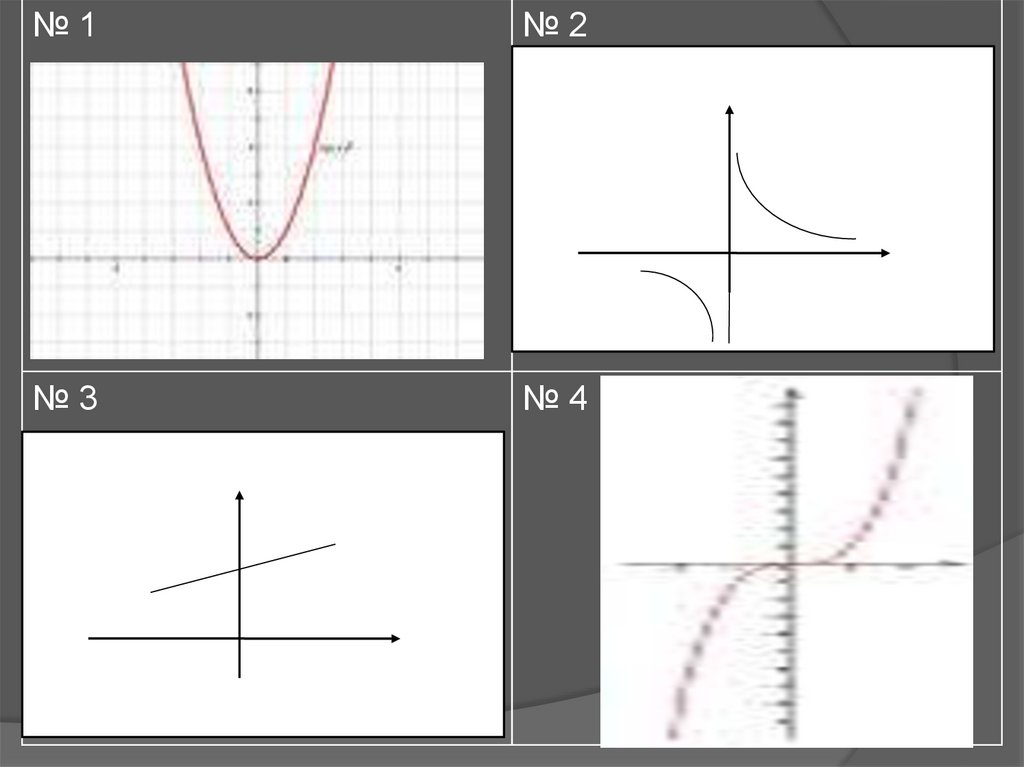
№1№2
№3
№4
3. Тема урока: Линейная функция и её график
4.
Образовательные:а) проверка умений распознавать линейную функцию по формуле, графику,
по словесному описанию; умение задавать формулой линейную функцию,
заданную графически;
б) научить применять знания на практике
Развивающие: расширение кругозора, получение новых знаний:
в) рассмотреть конкретные примеры линейных зависимостей, взятых из
практики и смежных дисциплин.
Воспитательные:
а) повышение интереса к изучению математики
б) воспитание трудолюбия, внимательности, аккуратности и ответственности
при выполнении заданий
в) содействие развитию самоконтроля, любознательности
г) развитие коммуникативной культуры
5. Маршрут
Вход в королевствоГора графиков
Долина точек
Ручей коэффициентов
Дворец Линейной функции
6.
Вход в королевство7.
Какую функция называют линейной?Какое из уравнений задаёт линейную функцию?
1) у = 5х + 3
2) у = - 6
3) у = х2 + 0,5
4) у = + 7
5) у = 16 - 9х
Какую переменную называют аргументом?
Какую переменную называют функцией?
Когда линейная функция является возрастающей
(убывающей)?
8.
9. Гора графиков
10.
у5
3
2
-2
0
-1
1
х
11.
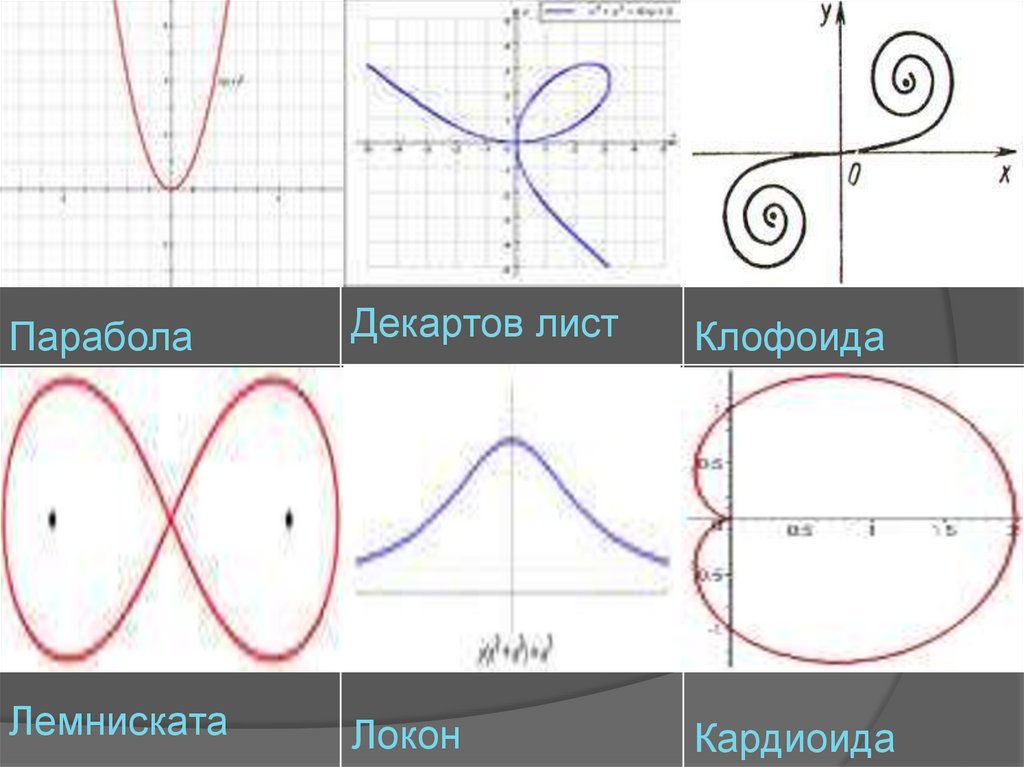
\Парабола
Декартов лист
Клофоида
Лемниската
Локон
Кардиоида
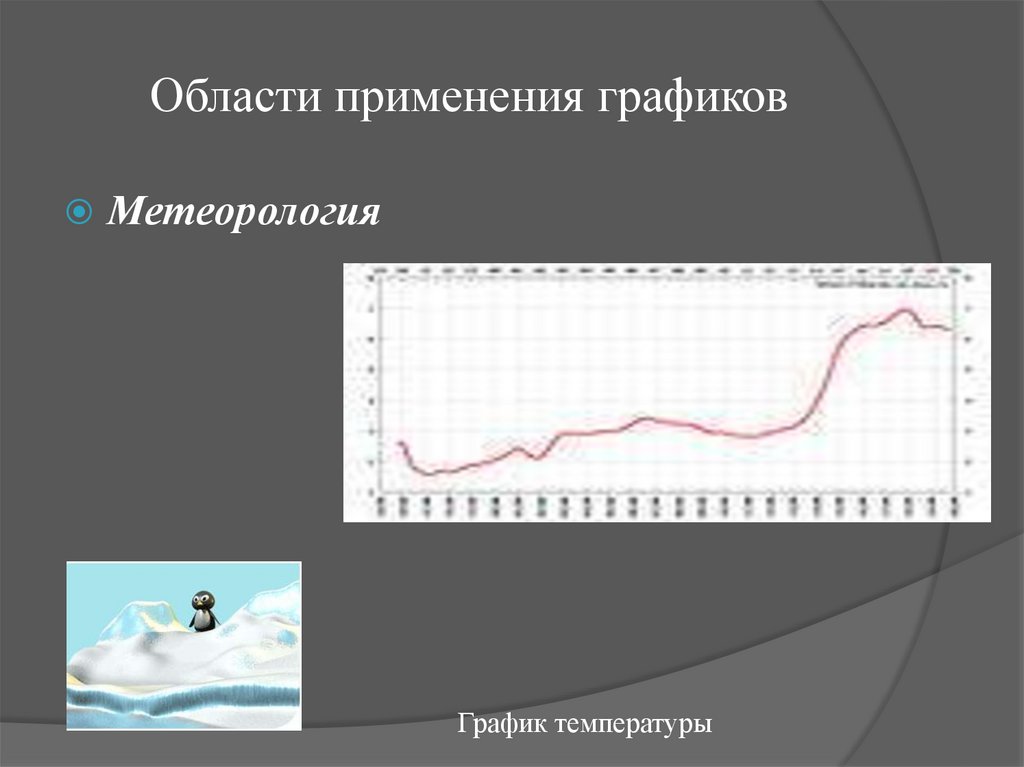
12. Области применения графиков
МетеорологияГрафик температуры
13.
МедицинаКардиограмма сердца
14.
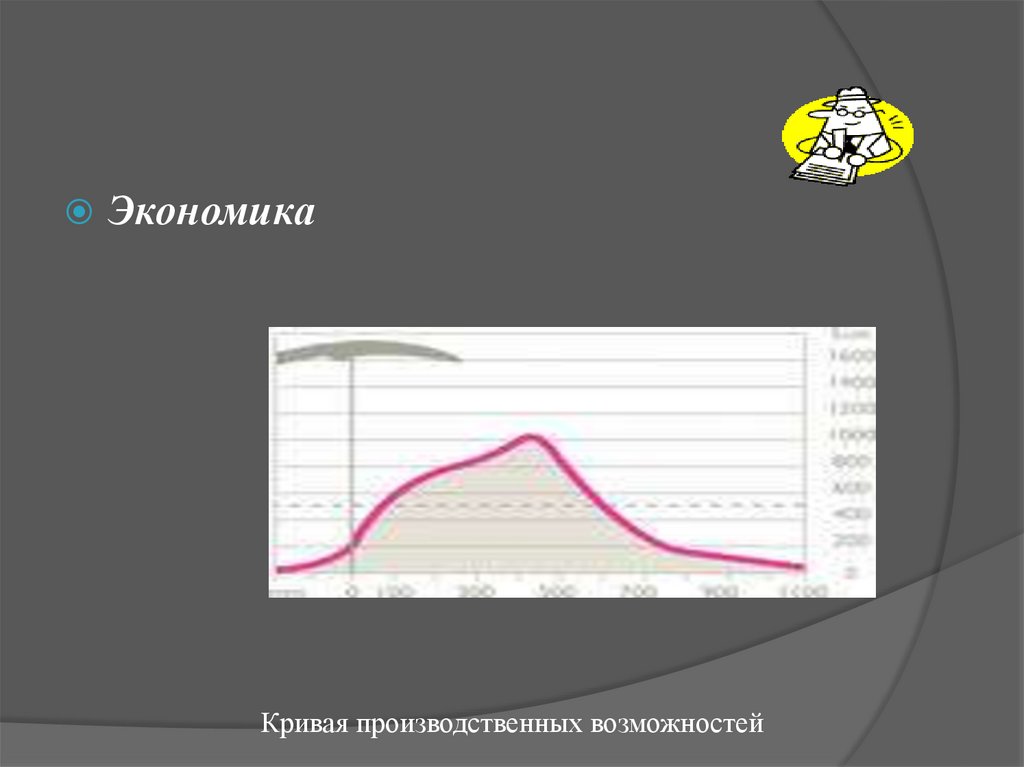
ЭкономикаКривая производственных возможностей
15.
Сейсмологиясейсмограф
сейсмограмма
16. Долина точек
17. Ручей коэффициентов
18. Дворец Линейной функции
19.
Рассмотрим конкретные примеры линейных зависимостей величин,взятые из смежных дисциплин.
При изучении темы «Давление» мы встретились с зависимостью давления жидкости на
дно сосуда (p) от высоты столба жидкости (h).
,
плотность жидкости,
Эта зависимость является линейной функцией, т.к. она вида
, где
h – независимая переменная, - зависимая переменная (функция)
Построим графики давления воды и бензина на дно в зависимости от высоты столба
жидкости
.
20.
Рассмотрим конкретные примеры линейных зависимостей величин,взятые из смежных дисциплин.
Р, кПа
120
вода
бензин
Давление жидкости
100
80
60
40
20
0
0
2
4
6
8
Высота столба жидкости
10
•Почему ученик рисовал только
первый квадрант?
•Что является графиком
функции p=10000h, p=800h?
•Какое давление оказывает
столб воды высотой 8 м?
•При какой высоте столба
бензина его давление на дно
сосуда равно 40 кПа?
•Что оказывает большее
давление – бензин или вода при
высоте столба жидкости 10 м?
•Давление жидкости 70 кПа. Что
больше – высота столба воды
или высота столба бензина? на
12
h, м сколько?
21.
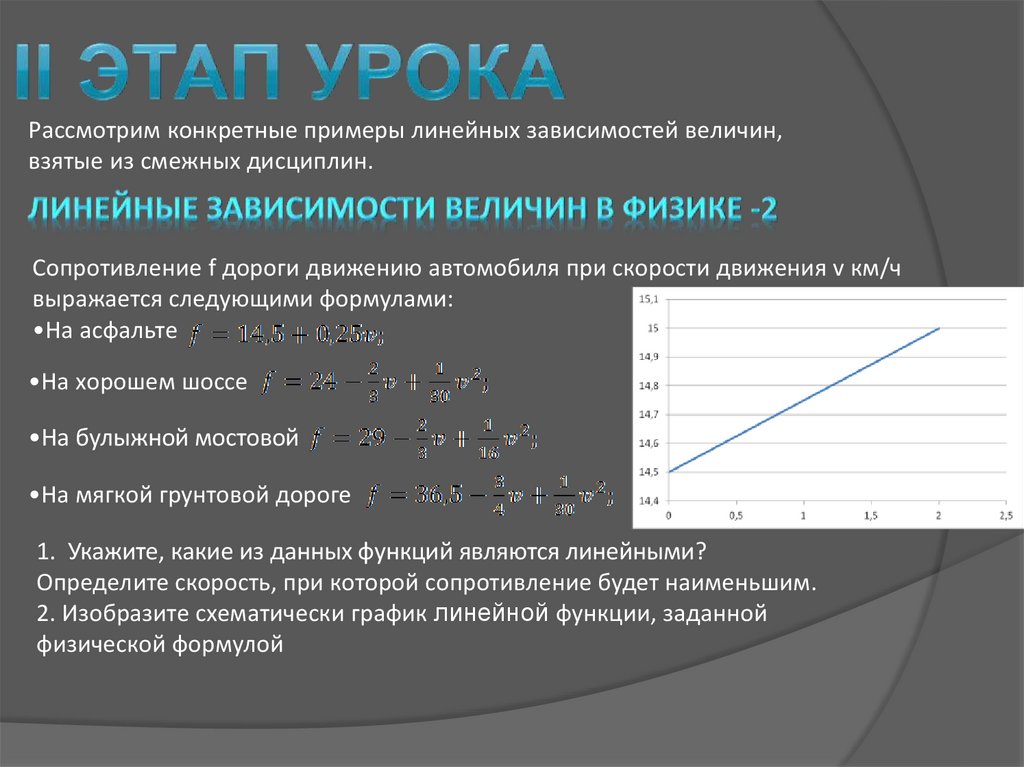
Рассмотрим конкретные примеры линейных зависимостей величин,взятые из смежных дисциплин.
Сопротивление f дороги движению автомобиля при скорости движения v км/ч
выражается следующими формулами:
•На асфальте
•На хорошем шоссе
•На булыжной мостовой
•На мягкой грунтовой дороге
1. Укажите, какие из данных функций являются линейными?
Определите скорость, при которой сопротивление будет наименьшим.
2. Изобразите схематически график линейной функции, заданной
физической формулой
22.
Рассмотрим конкретные примеры линейных зависимостей величин,взятые из смежных дисциплин.
Зависимость численности сине-зеленых водорослей от концентрации общего
фосфора в воде выражается следующей формулой
, где а –
численность сине-зеленых водорослей, а p – концентрация общего фосфора.
Эту зависимость можно использовать для прогнозирования качества воды.
Показателем качества воды служит количество сине-зеленых водорослей. Чем их
больше, тем хуже качество воды. На численность сине-зеленых водорослей влияет
концентрация фосфорного удобрения, стекающего в водоемы вместе с талой водой.
Исходя из этой зависимости, можно дать рекомендации по внесению фосфорных
удобрений для предотвращения ухудшения качества воды.
23.
Рассмотрим конкретные примеры линейных зависимостей величин,взятые из смежных дисциплин.
Изготовление чертежа выкройки.
O m
T
Длина отрезка ОТ зависит от обхвата талии.
Пусть m – длина отрезка ОТ
n – обхват талии.
Тогда зависимость m от n можно записать в виде формулы
,
где 0,64 – коэффициент для юбки.
Построим схематично график данной функции.
24.
Рассмотрим конкретные примеры линейных зависимостей величин,взятые из смежных дисциплин.
n
90
m, см
80
60
120
m 38,
4
76,
8
•Почему только первый
квадрант?
•Какие значения может
принимать n? почему?
•Что является графиком?
Особенность расположения?
76,8
70
60
50
40
На осях n и m масштаб можно
выбрать произвольно!
38,4
30
20
10
0
0
20
40
60
80
100
120
n, см
140
25.
РефлексияУчащиеся высказывают своё мнение о том, что им понравилось на
уроке, что нового они узнали.
Подведение итогов


















 Математика
Математика








