Похожие презентации:
Подготовка к сдаче ОГЭ (геометрический блок)
1. ПРИКАЗ от 17 декабря 2010 г. № 1897 ОБ УТВЕРЖДЕНИИ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО СТАНДАРТА ОСНОВНОГО ОБЩЕГО
ОБРАЗОВАНИЯМинистр
А.ФУРСЕНКО
ПОДГОТОВКА К СДАЧЕ ОГЭ
(ГЕОМЕТРИЧЕСКИЙ БЛОК)
Выполнила: Хаустова Елена Владимировна
Учитель математики
МАОУ «Белостолбовская СОШ»
2018-2019 уч.год.
2. . Федеральный государственный образовательный стандарт основного общего образования (далее – Стандарт) представляет собой
совокупностьтребований, обязательных при реализации основной образовательной программы
основного общего образования.
Стандарт включает в себя требования:
к результатам освоения основной образовательной программы основного
общего образования;
к структуре основной образовательной программы основного общего
образования, в том числе требования к соотношению частей основной
образовательной программы и их объему, а также к соотношению обязательной
части основной образовательной программы и части,
формируемой участниками образовательных отношений;
к условиям реализации основной образовательной программы основного
общего образования, в том числе к кадровым, финансовым, материальнотехническим и иным условиям.
3. Требования к предметным результатам изучения геометрии
овладение геометрическим языком;развитие умения использовать его для описания предметов окружающего
мира; развитие пространственных представлений, изобразительных
умений, навыков геометрических построений;
формирование систематических знаний о плоских фигурах и их
свойствах,
представлений о простейших пространственных телах;
развитие умений моделирования реальных ситуаций на языке геометрии,
исследования построенной модели с использованием геометрических
понятий и теорем;
решения геометрических и практических задач;
4. ТЕОРИЯ ГЕОМЕТРИЯ (повторение)
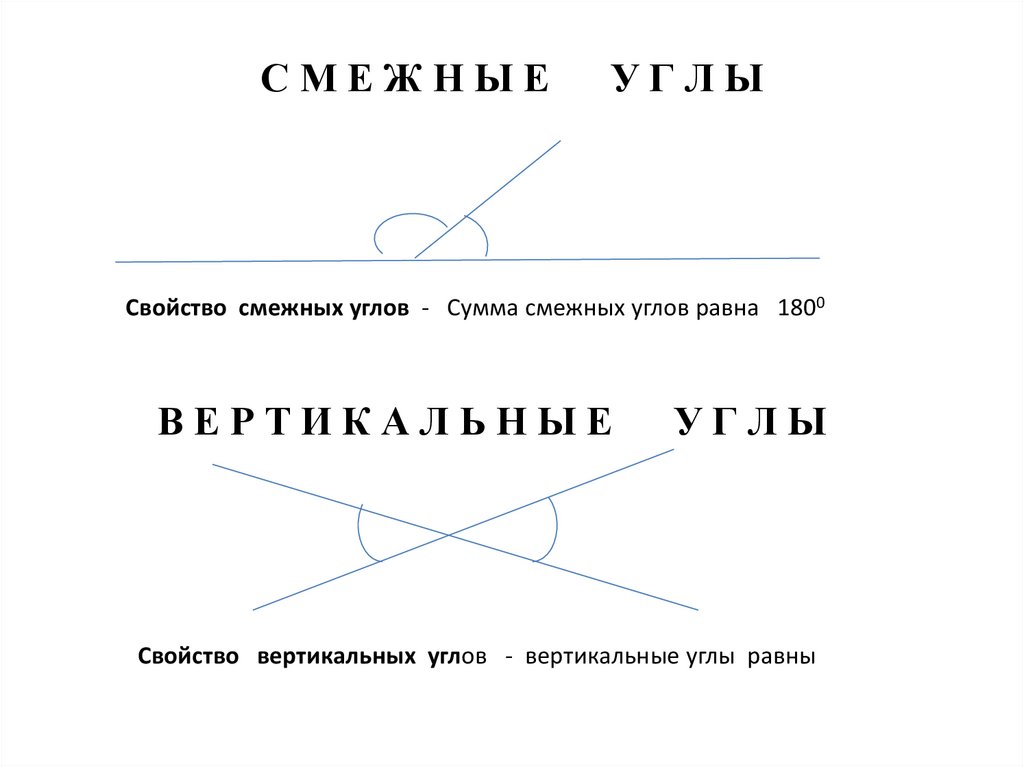
5. С М Е Ж Н Ы Е У Г Л Ы
СМЕЖНЫЕУГЛЫ
Свойство смежных углов - Сумма смежных углов равна 1800
ВЕРТИКАЛЬНЫЕ
УГЛЫ
Свойство вертикальных углов - вертикальные углы равны
6. Т Р Е У Г О Л Ь Н И К В Ы С О Т А
ТРЕУГОЛЬНИКВЫСОТА
Остроугольный
Прямоугольный
Тупоугольный
7. Т О Ч К А П Е Р Е С Е Ч Е Н И Я В Ы С О Т Т Р Е У Г О Л Ь Н И К А
ТОЧКА ПЕРЕСЕЧЕНИЯ ВЫСОТТРЕУГОЛЬНИКА
Остроугольный
Прямоугольный
Тупоугольный
8. Т Р Е У Г О Л Ь Н И К М Е Д И Н А
ТРЕУГОЛЬНИКМЕДИНА
Точка пересечения медиан треугольника
– медианы пересекаются в одной точке и делятся ею в
отношении 2:1, считая от вершины
9. Т Р Е У Г О Л Ь Н И К Б И С С Е К Т Р И С А
ТРЕУГОЛЬНИКБИССЕКТРИСА
Точка пересечения биссектрис треугольника
Биссектрисы треугольника пересекаются в одной точке; эта точка
является центром вписанной окружности
10. СЕРЕДИННЫЙ ПЕРПЕНДИКУЛЯР
Свойство:каждая точка
серединного
перпендикуляра
равноудалена от
концов отрезка
Признак:
если точка равноудалена
от концов отрезка, то
она лежит на
серединном
перпендикуляре
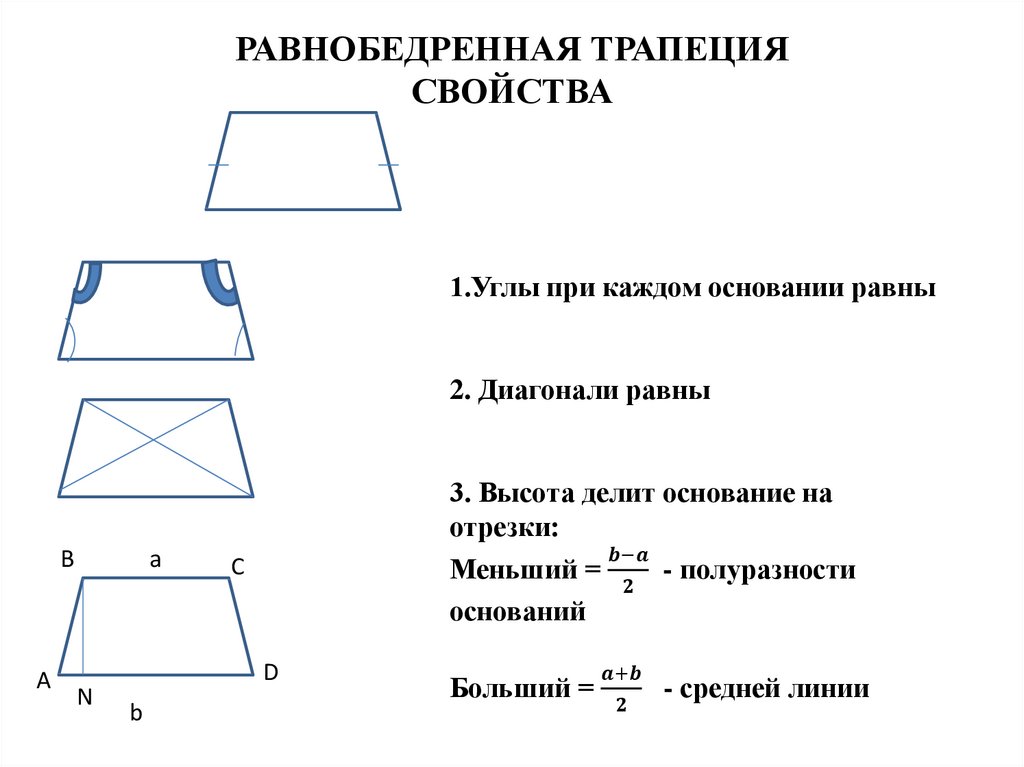
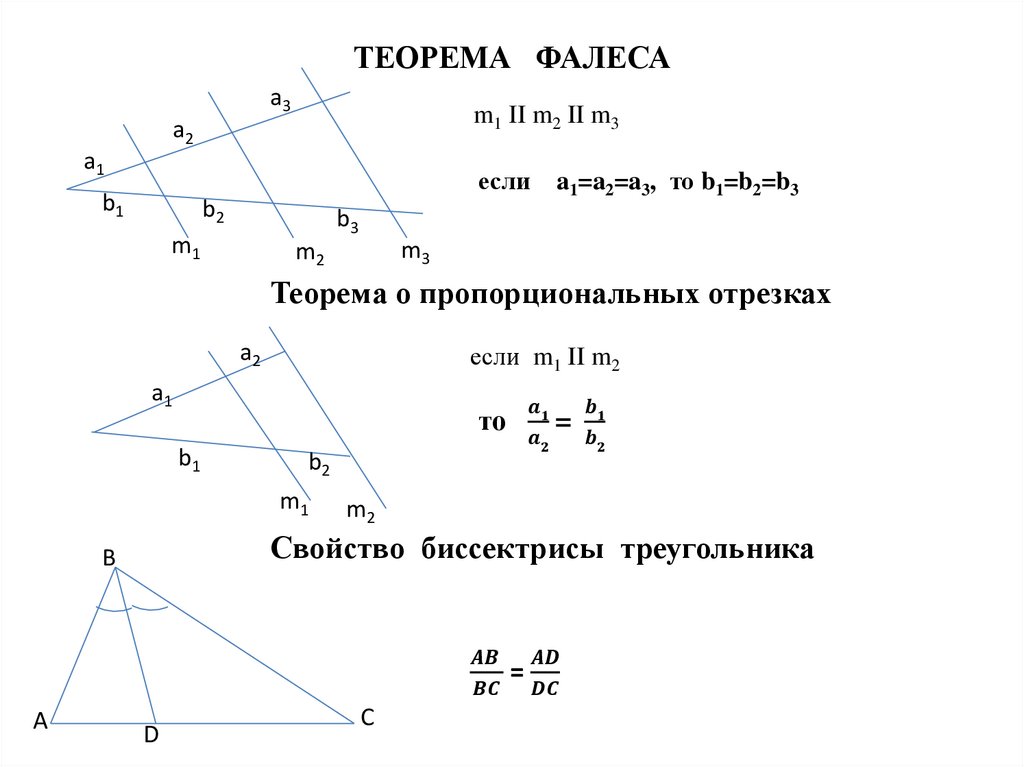
11. РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
Вершина треугольникаСвойства:
1. Углы при основании
равны
2. Биссектриса,
проведенная из вершины
является и медианой, и
высотой
Признаки:
1. Если в треугольнике есть два
равных угла, то он будет
равнобедренным
2. Если биссектриса будет и
высотой, то треугольник будет
равнобедренным
3. Если биссектриса будет и
медианой, то треугольник будет
равнобедренным
4. Если медиана будет и высотой, то
треугольник будет равнобедренным
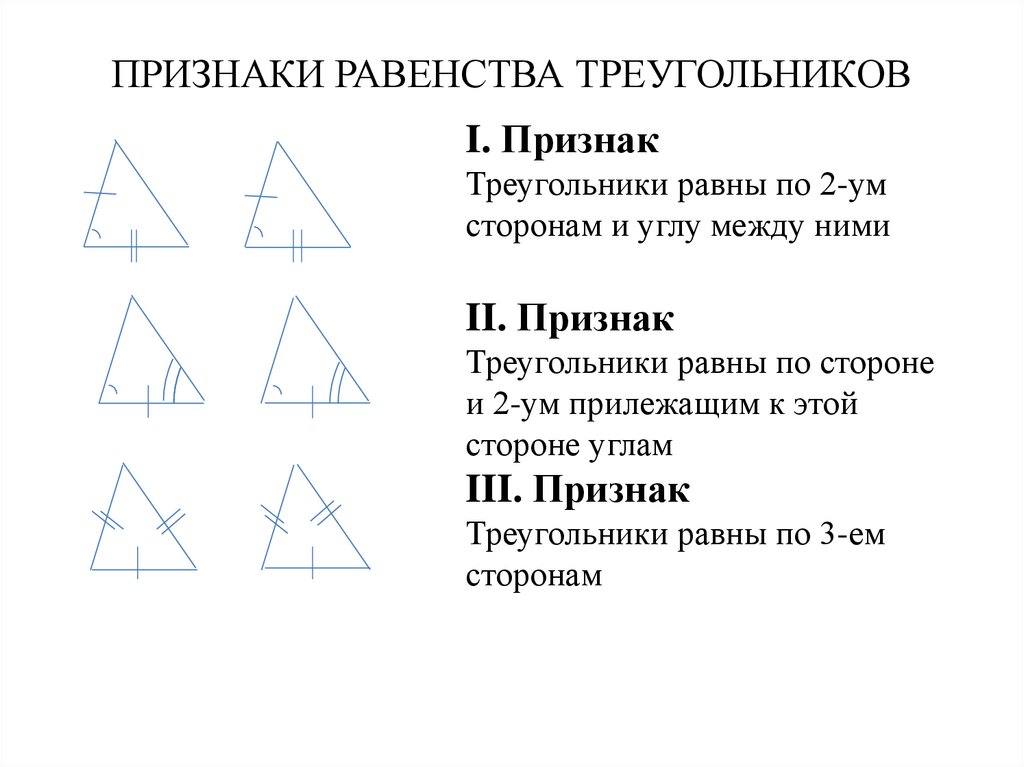
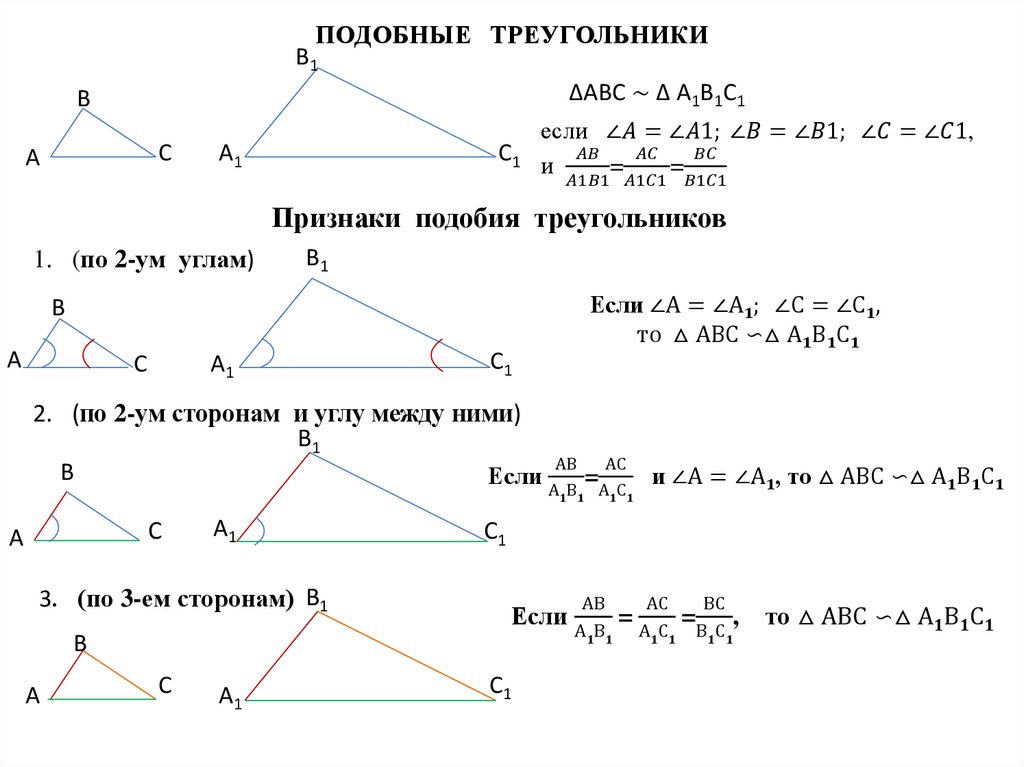
12. ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ
I. ПризнакТреугольники равны по 2-ум
сторонам и углу между ними
II. Признак
Треугольники равны по стороне
и 2-ум прилежащим к этой
стороне углам
III. Признак
Треугольники равны по 3-ем
сторонам
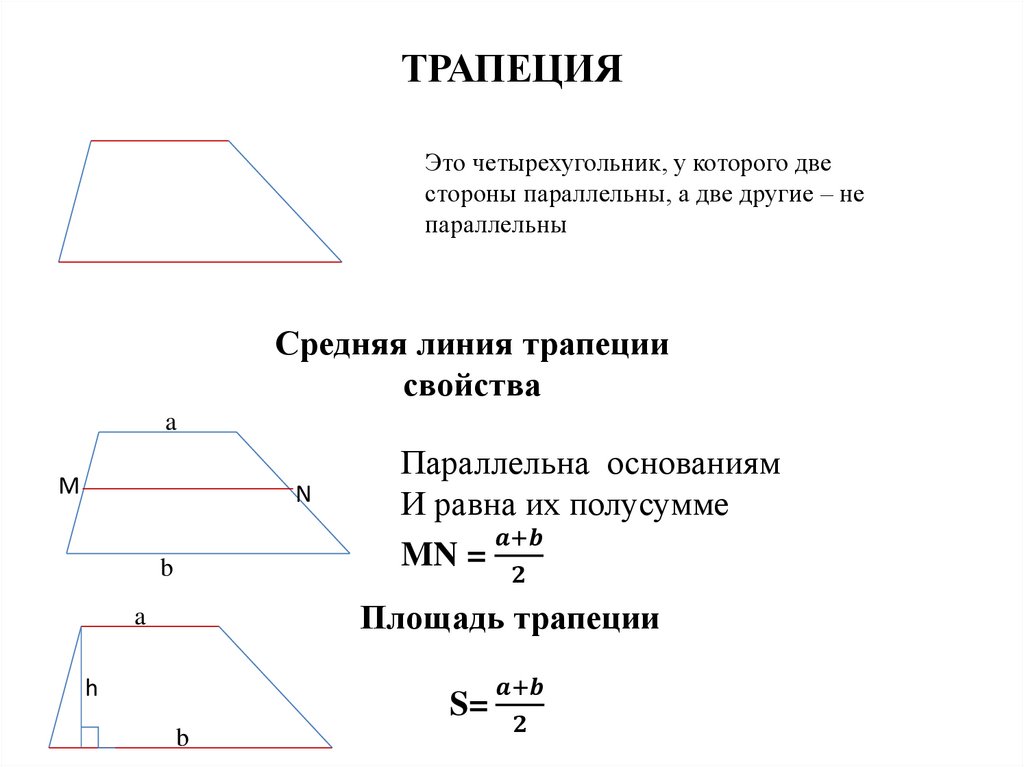
13. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Свойства(если прямые параллельны), то
1.накрест лежащие углы равны
2. соответственные углы равны
3. сумма внутренних односторонних
углов равна 1800
Признаки
1-3. Первые три признака – это
утверждения, обратные свойствам
4. Две прямые, перпендикулярные 3-ей
прямой, параллельны между собой
5. Две прямые, параллельные третьей,
параллельны между собой
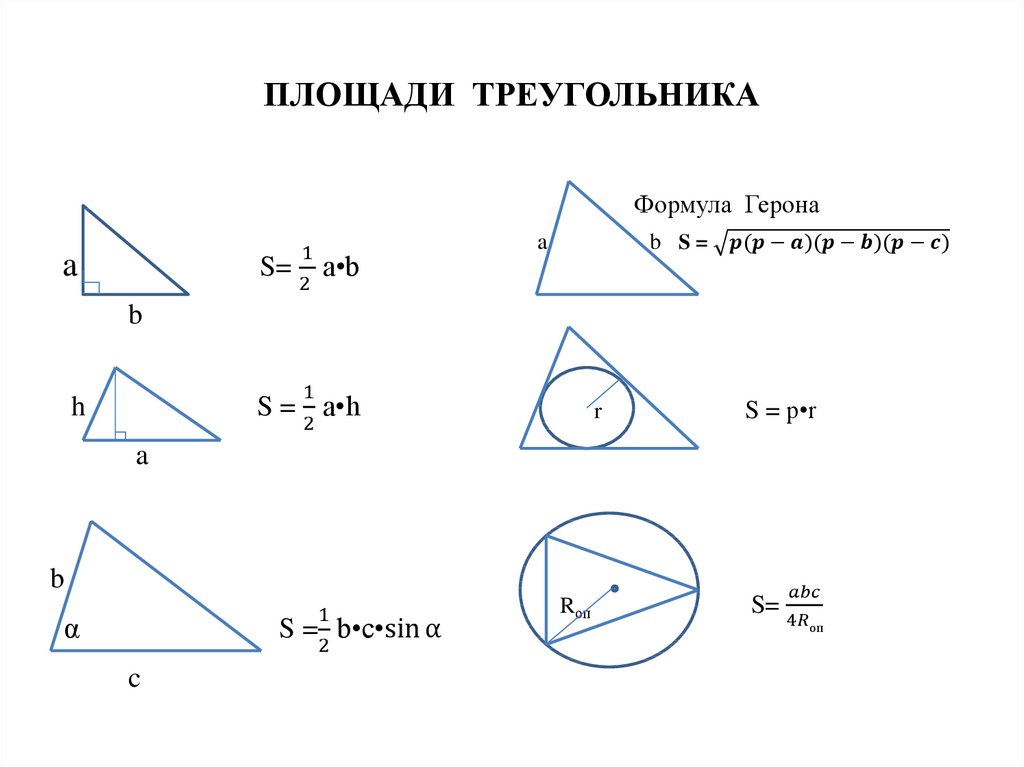
14. СУММА УГЛОВ ТРЕУГОЛЬНИКА
В любом треугольнике суммауглов равна 1800
700
600
1300
Внешний угол треугольника равен
сумме двух углов треугольника, не
смежных с ним
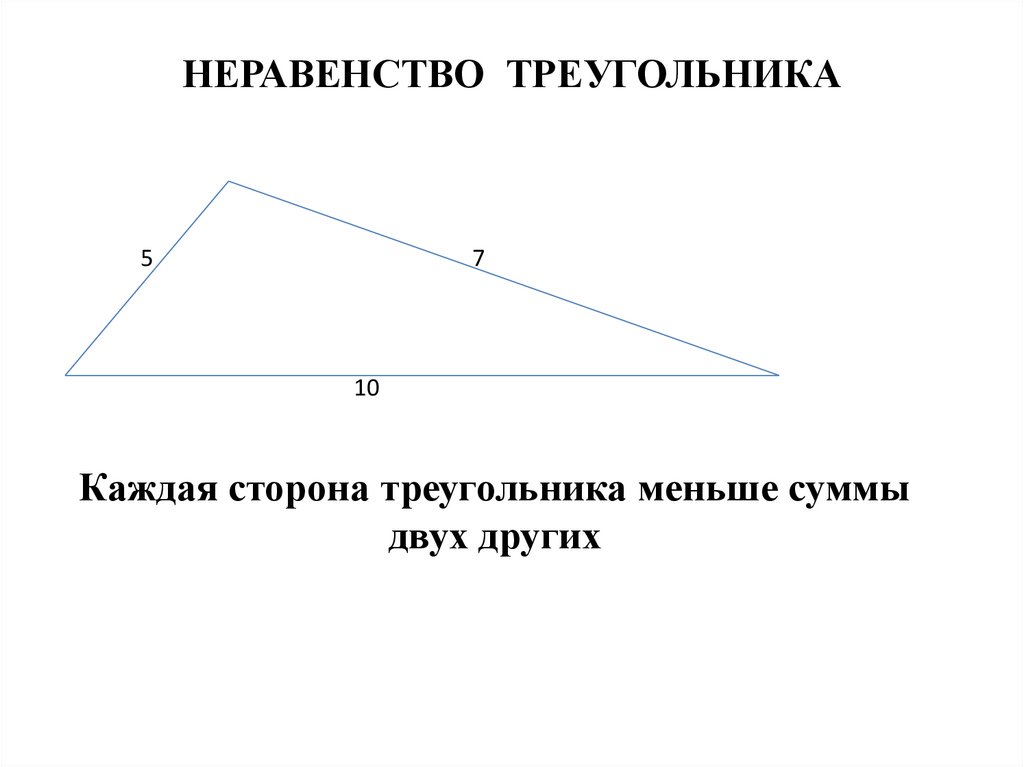
15. НЕРАВЕНСТВО ТРЕУГОЛЬНИКА
57
10
Каждая сторона треугольника меньше суммы
двух других
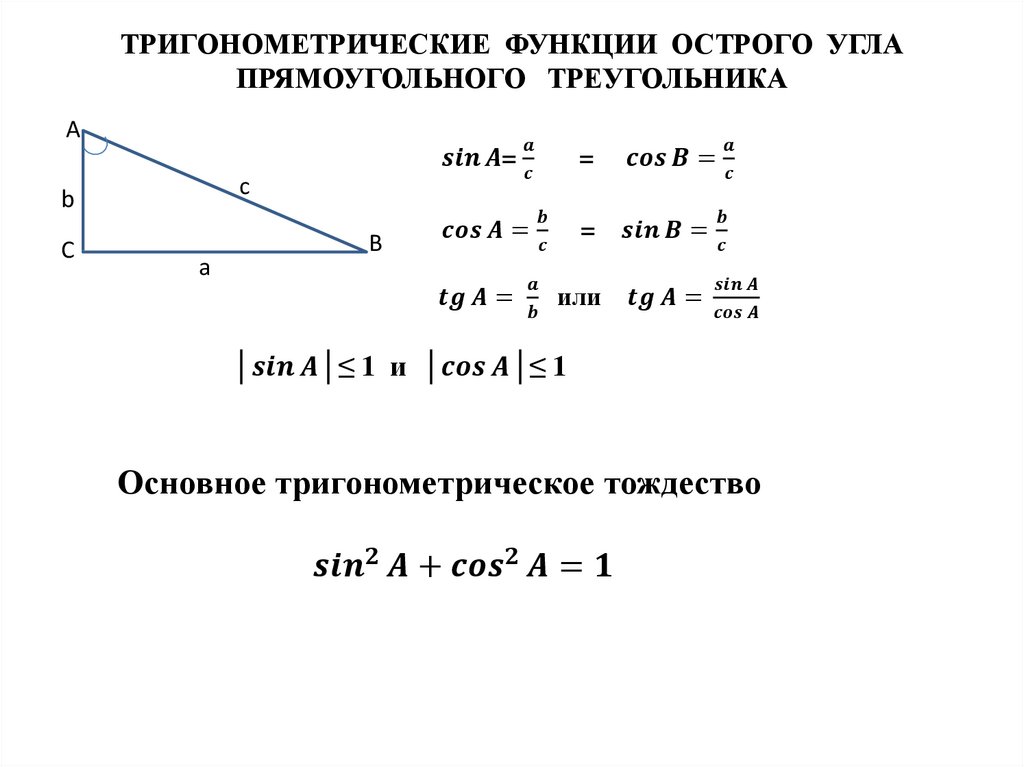
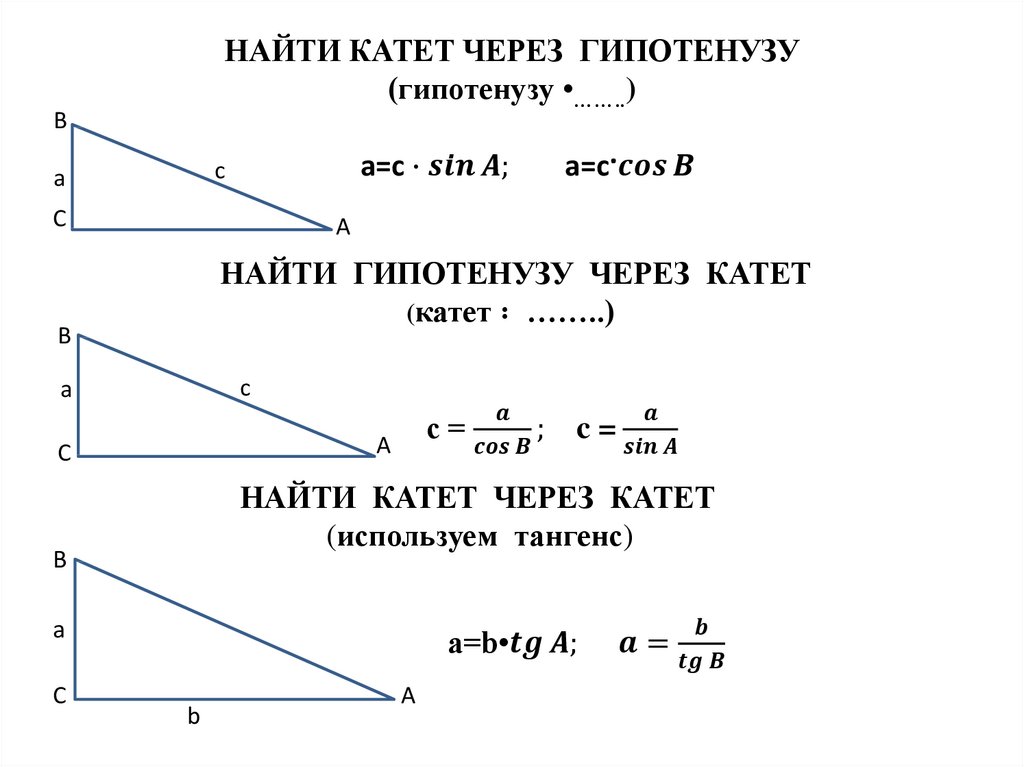
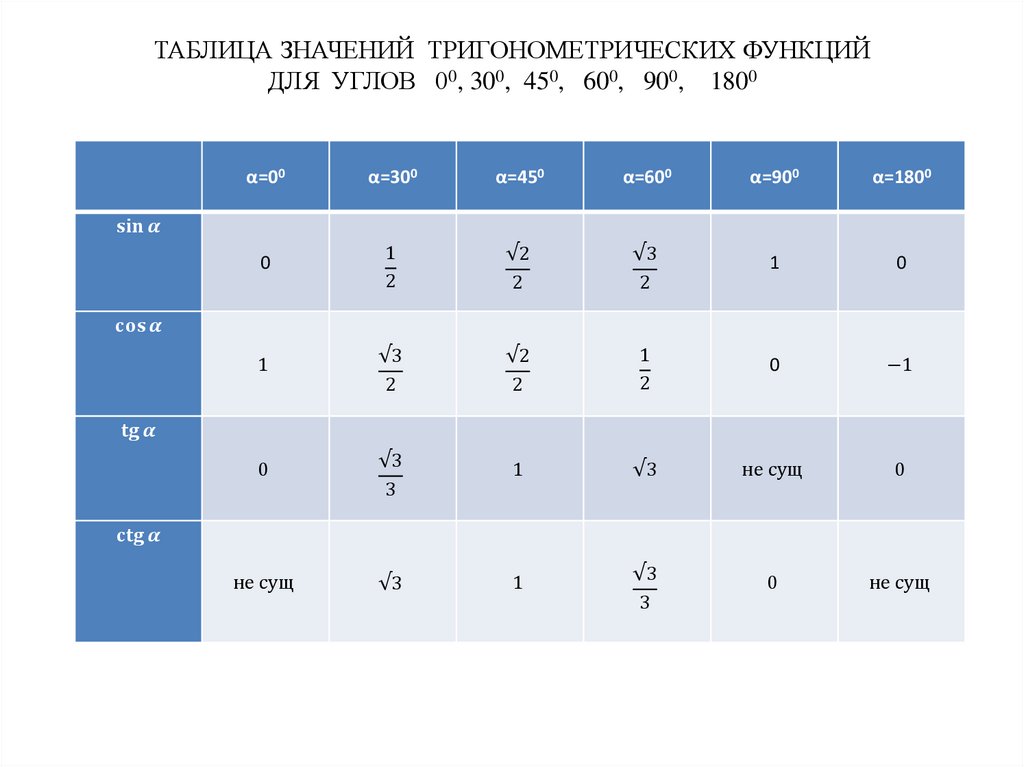
16. ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
гипотенузакатет
катет
Свойства прямоугольного треугольника
1. Сумма двух острых углов равна 900
2. В прямоугольном треугольнике напротив угла в 300
катет в два раза меньше гипотенузы
4
8
300
3. Если в прямоугольном треугольнике катет в два раза меньше
гипотенузы, то он лежит против угла в 300
5
10
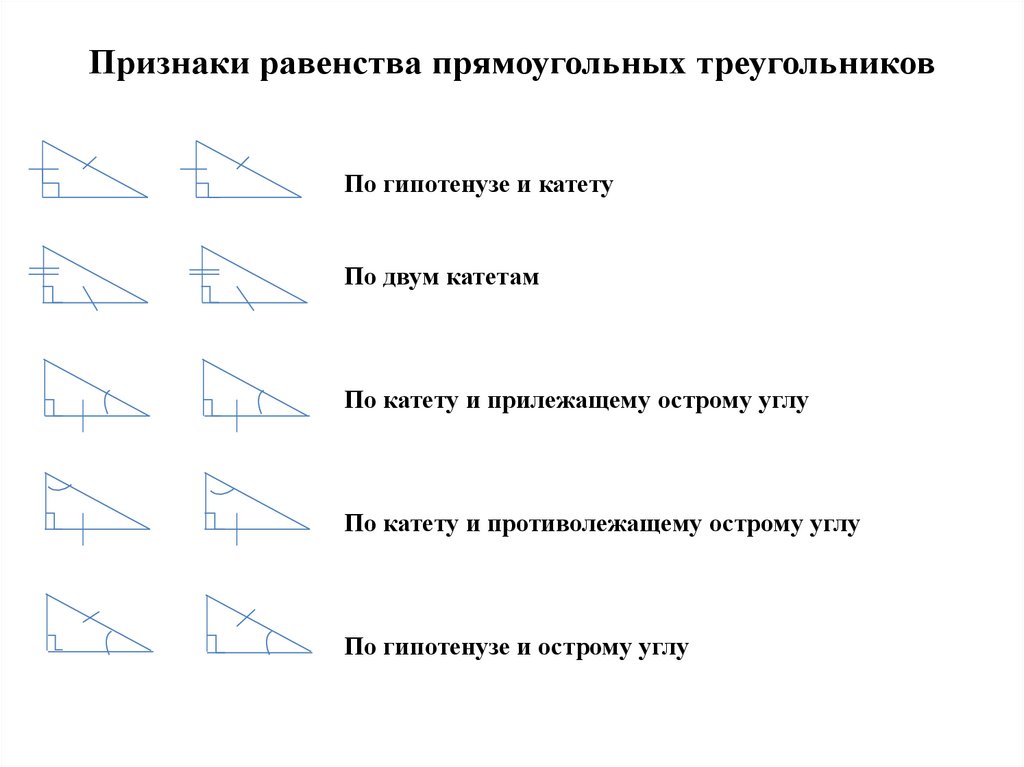
17. Признаки равенства прямоугольных треугольников
По гипотенузе и катетуПо двум катетам
По катету и прилежащему острому углу
По катету и противолежащему острому углу
По гипотенузе и острому углу
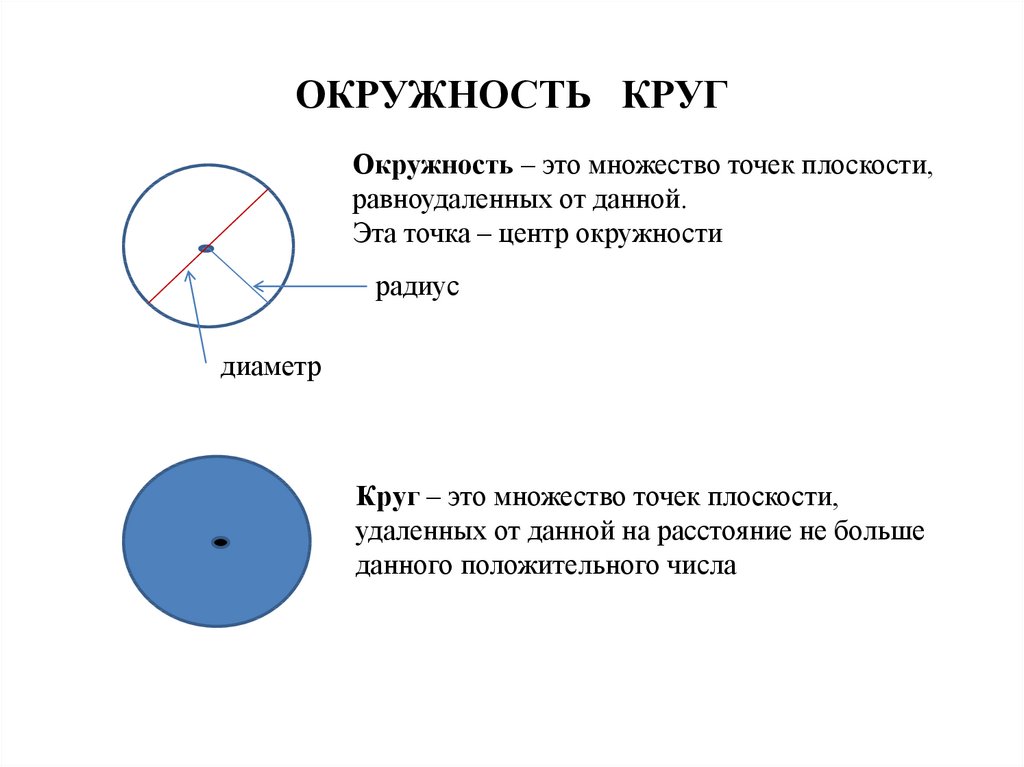
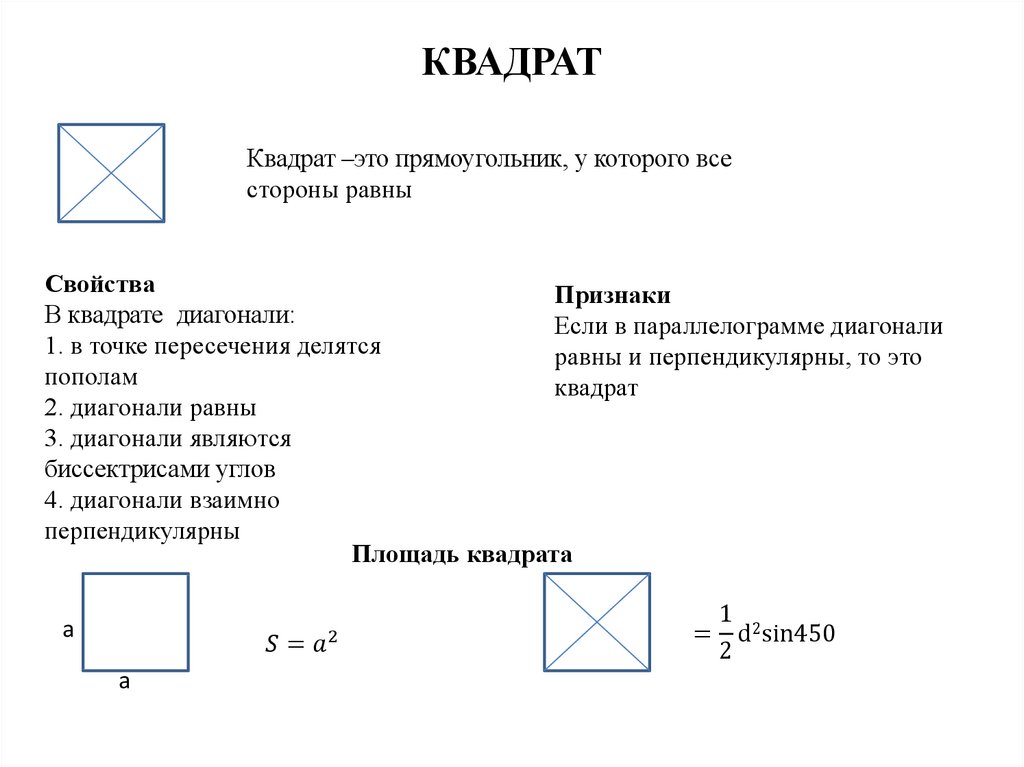
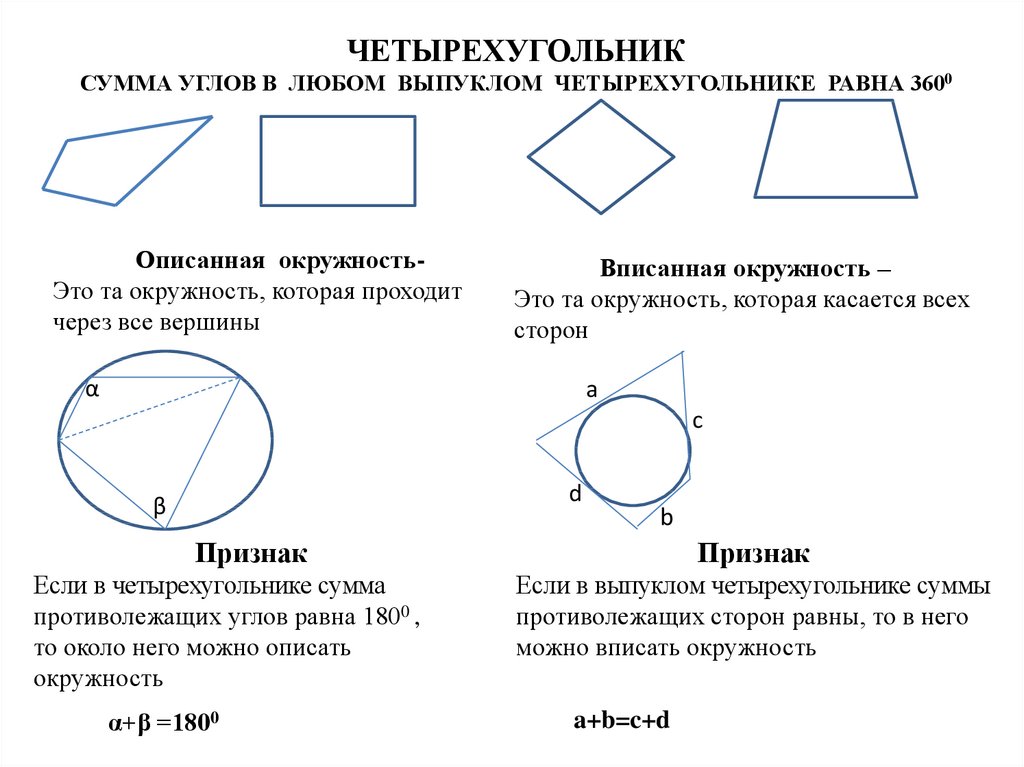
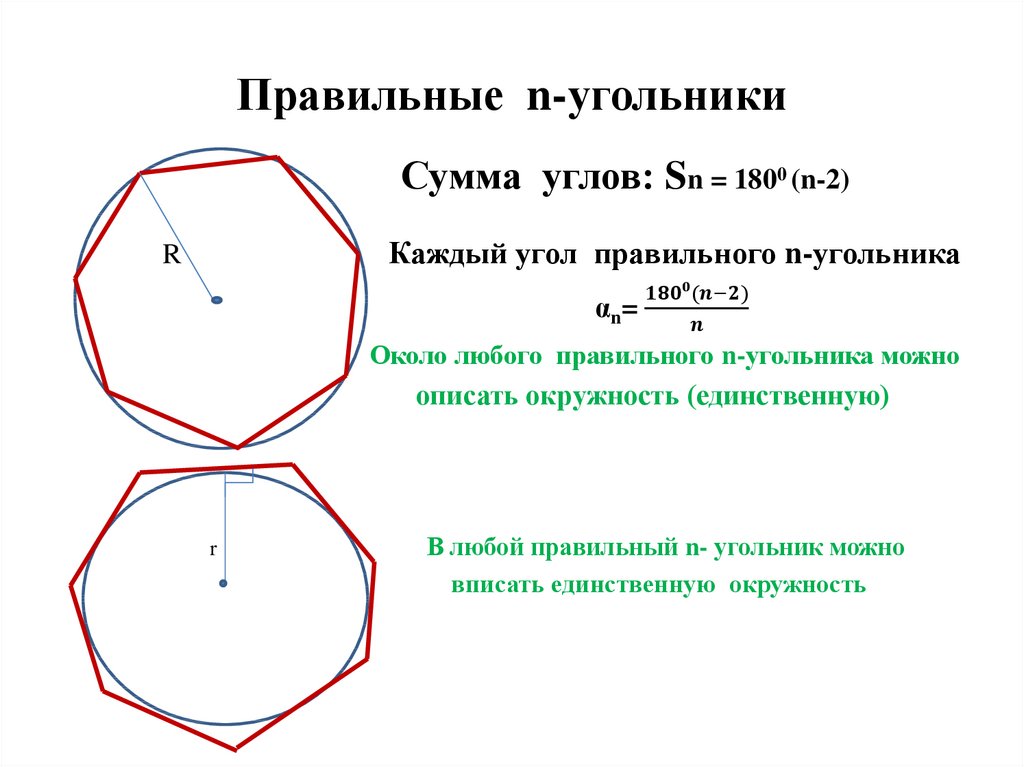
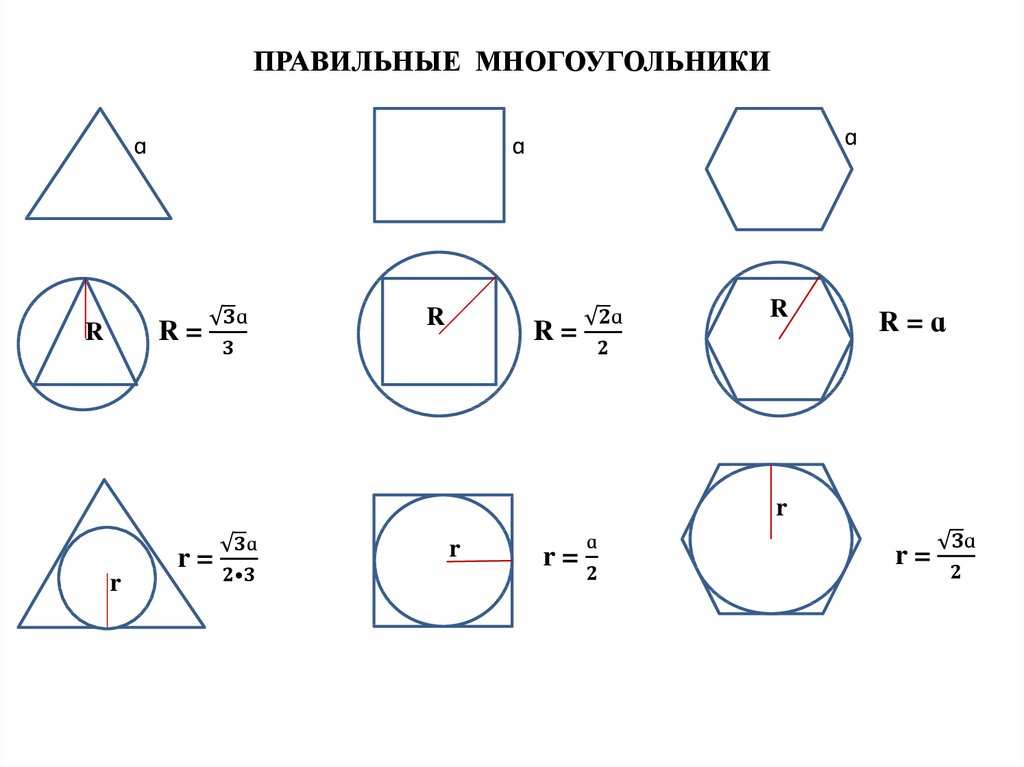
18. ОКРУЖНОСТЬ КРУГ
Окружность – это множество точек плоскости,равноудаленных от данной.
Эта точка – центр окружности
радиус
диаметр
Круг – это множество точек плоскости,
удаленных от данной на расстояние не больше
данного положительного числа
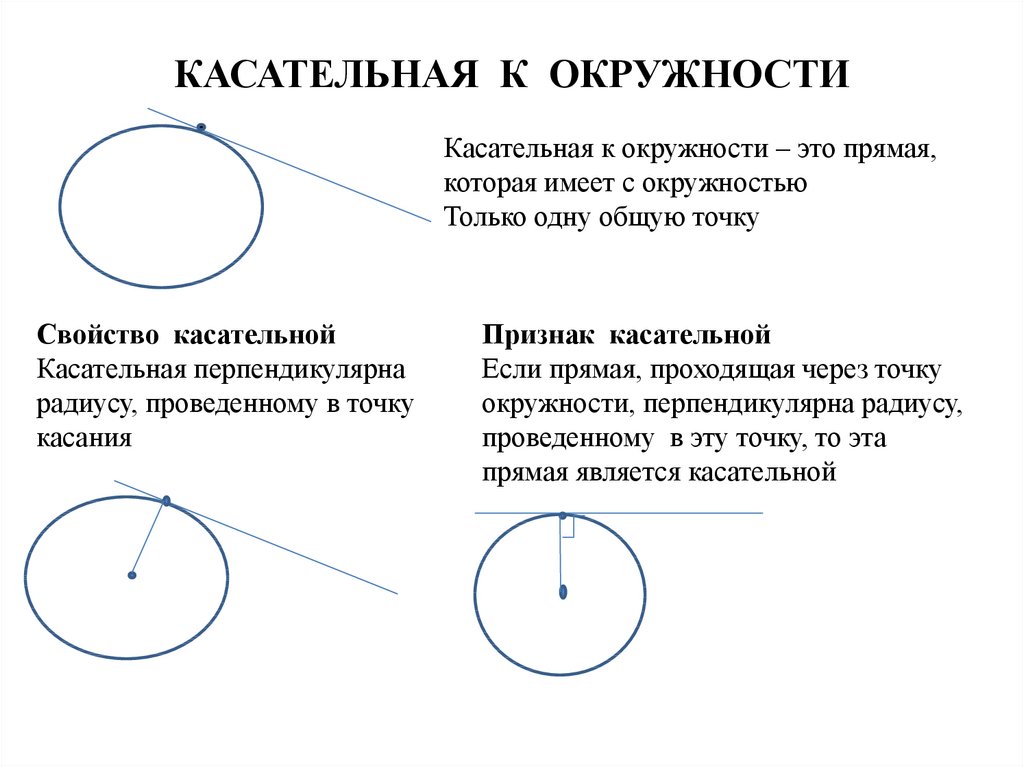
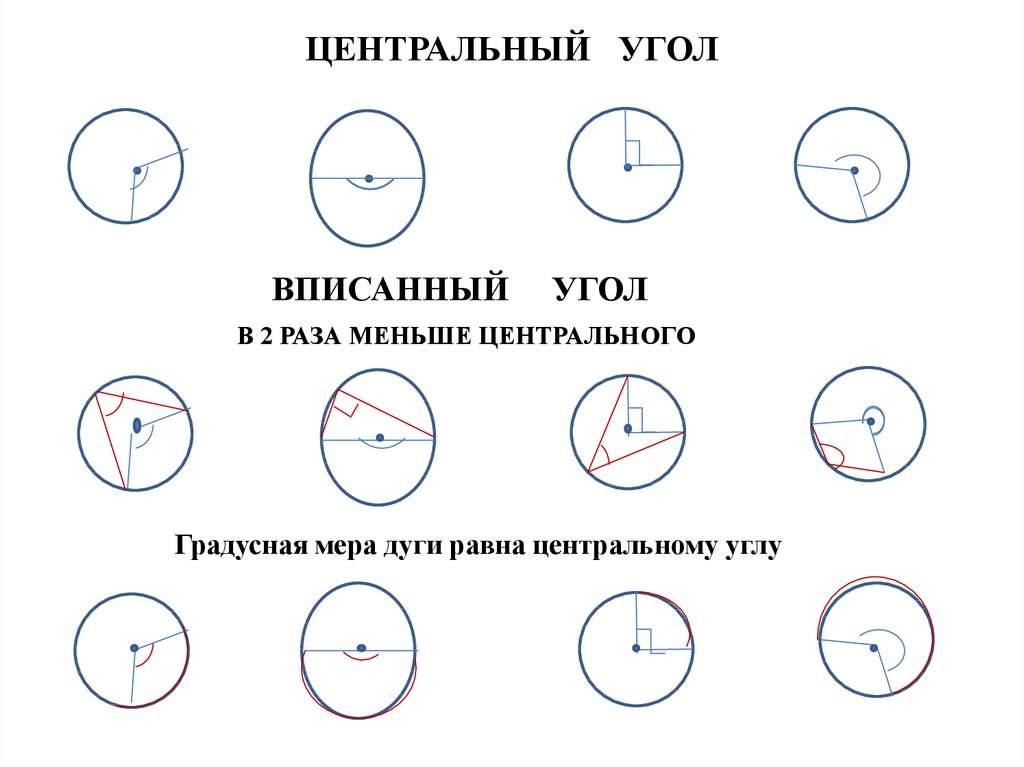
19. КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ
Касательная к окружности – это прямая,которая имеет с окружностью
Только одну общую точку
Свойство касательной
Касательная перпендикулярна
радиусу, проведенному в точку
касания
Признак касательной
Если прямая, проходящая через точку
окружности, перпендикулярна радиусу,
проведенному в эту точку, то эта
прямая является касательной
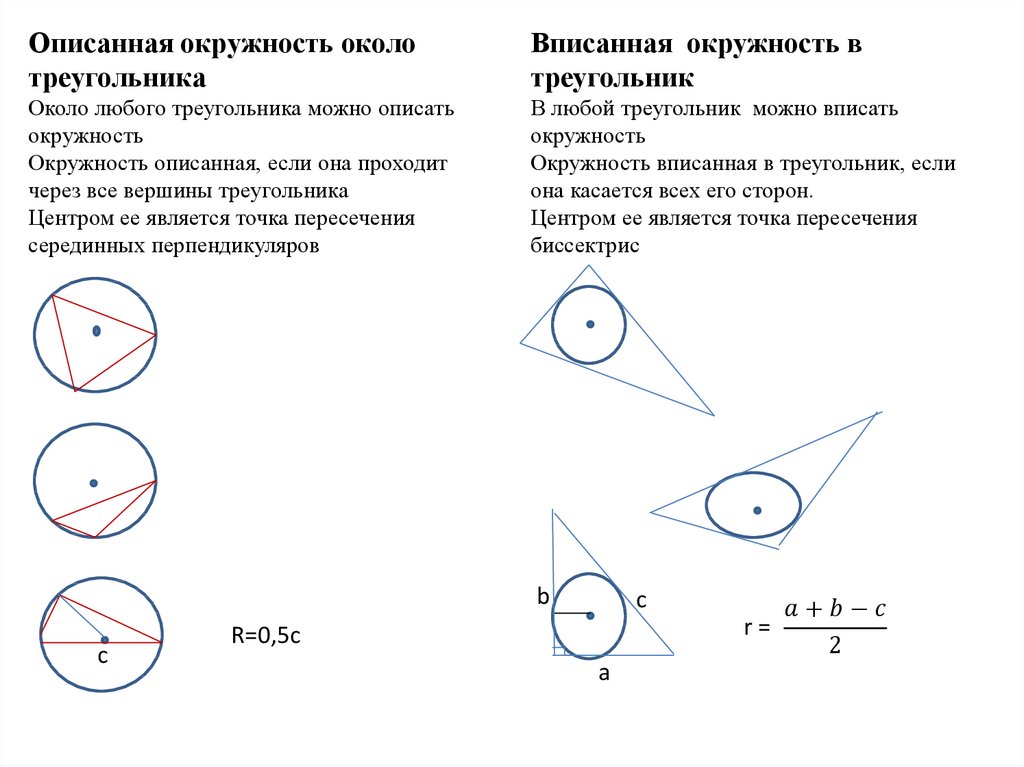
20.
Описанная окружность околотреугольника
Вписанная окружность в
треугольник
Около любого треугольника можно описать
окружность
Окружность описанная, если она проходит
через все вершины треугольника
Центром ее является точка пересечения
серединных перпендикуляров
В любой треугольник можно вписать
окружность
Окружность вписанная в треугольник, если
она касается всех его сторон.
Центром ее является точка пересечения
биссектрис
b
с
с
r=
R=0,5с
a














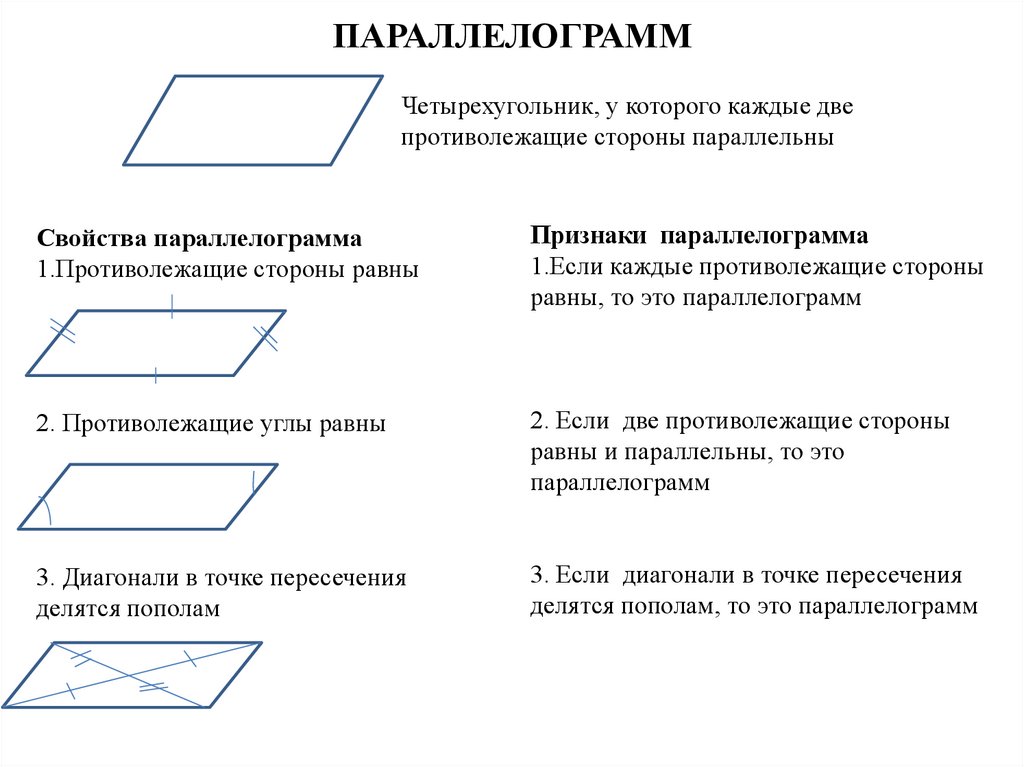
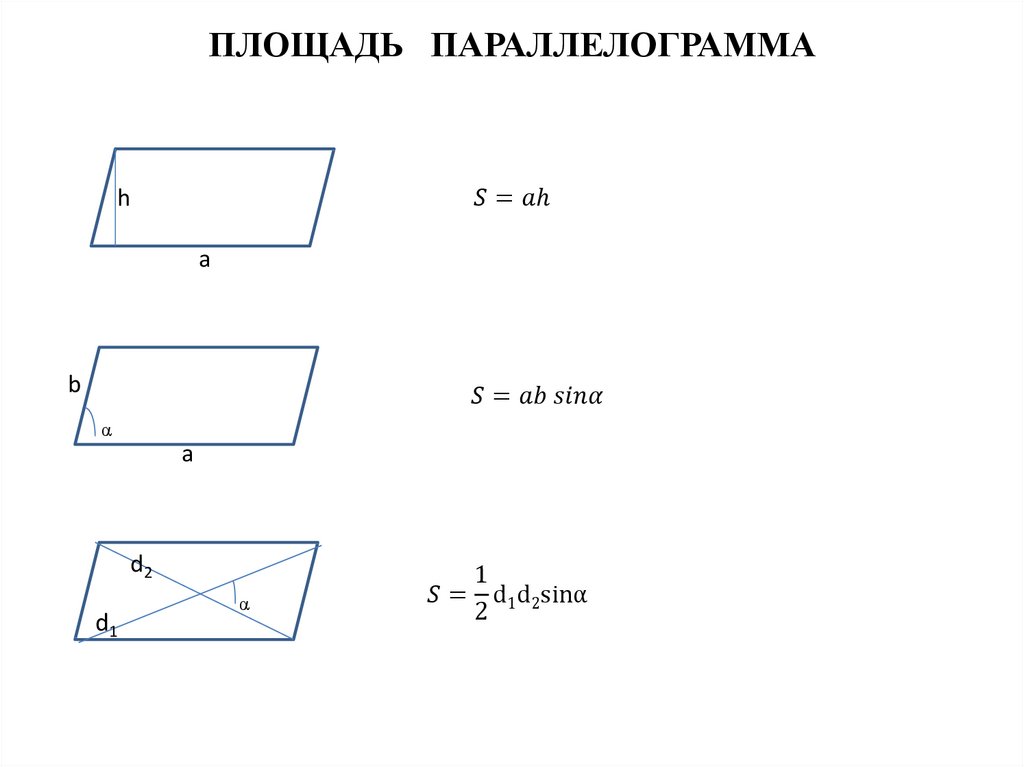
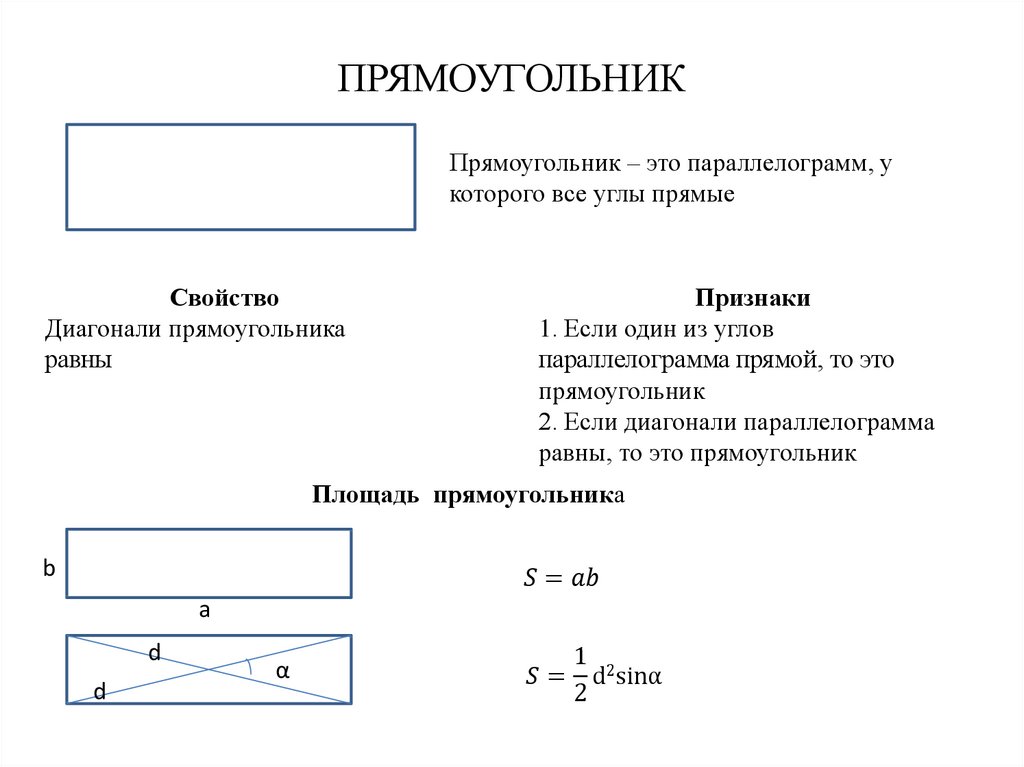
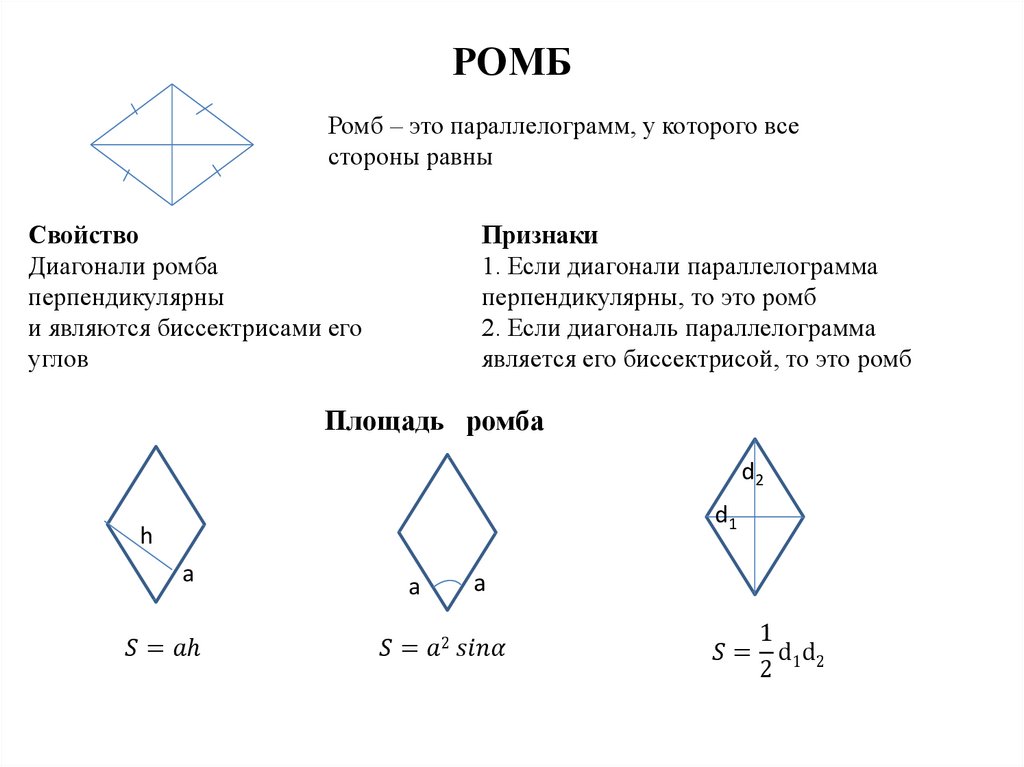







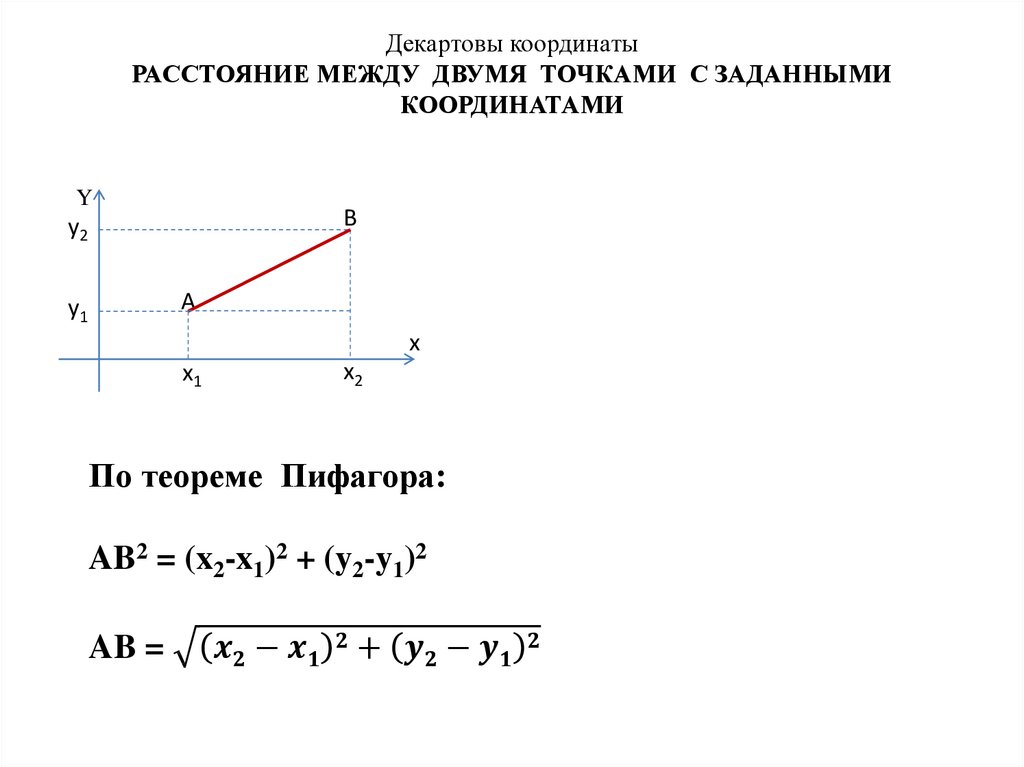
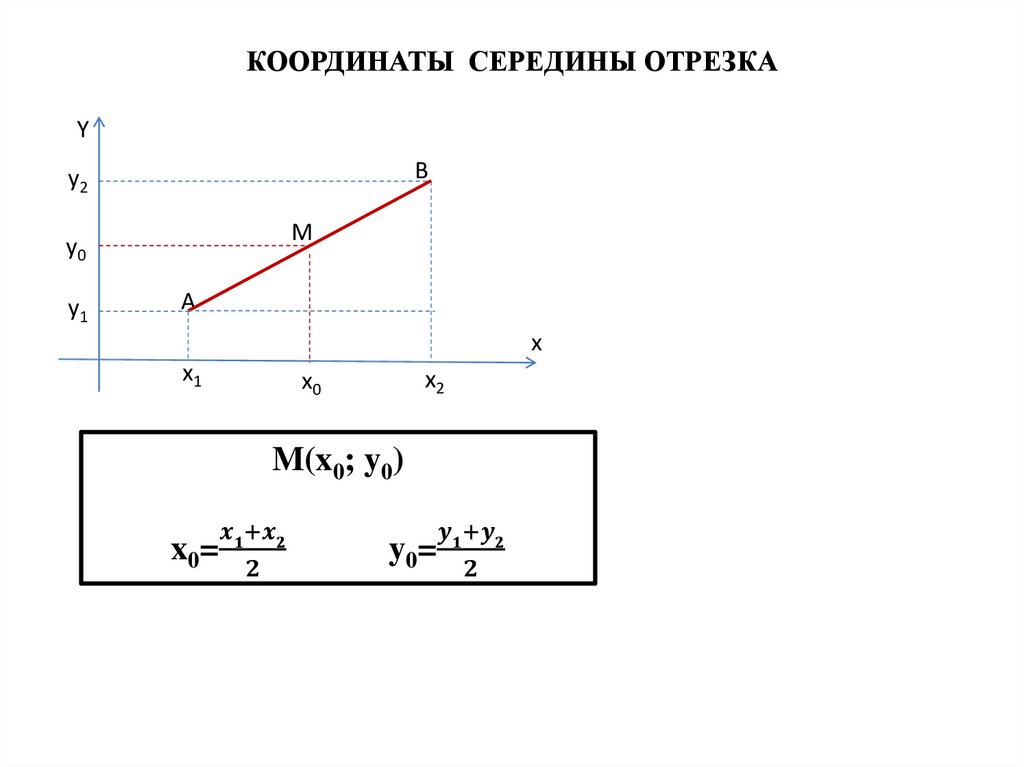
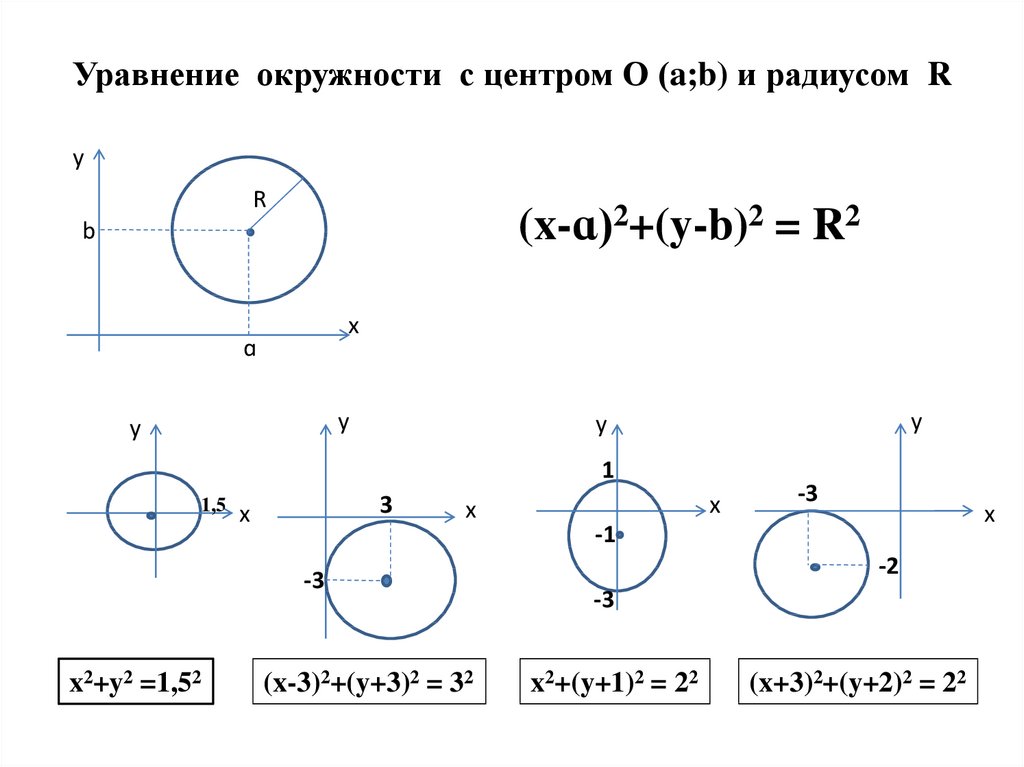

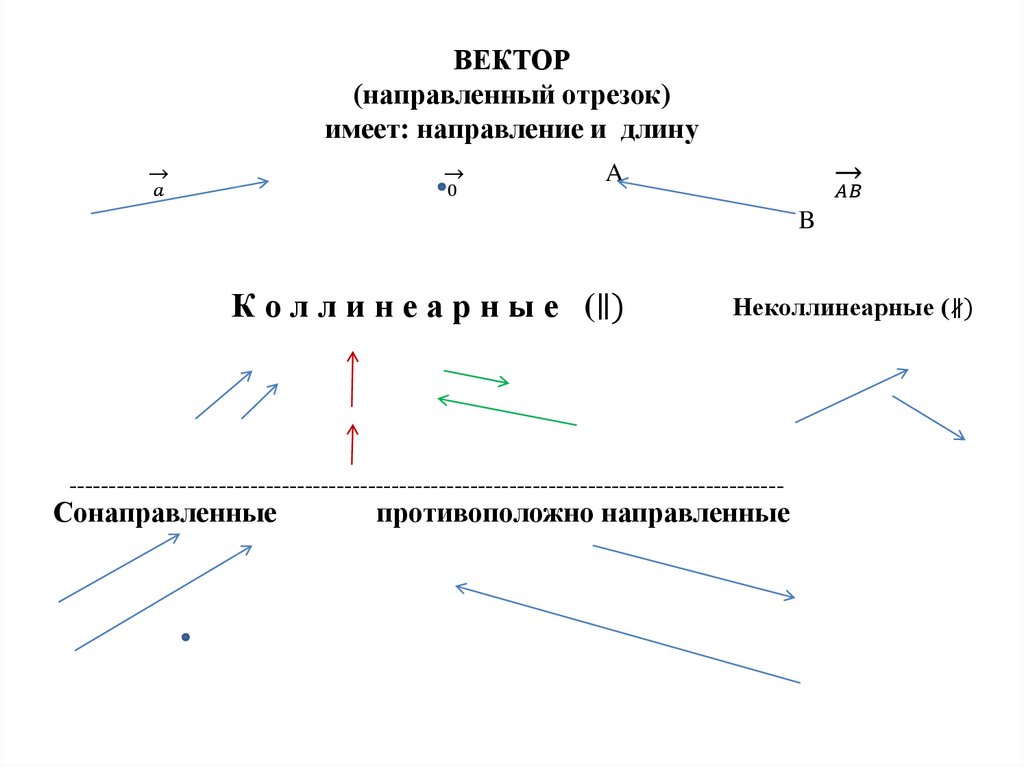

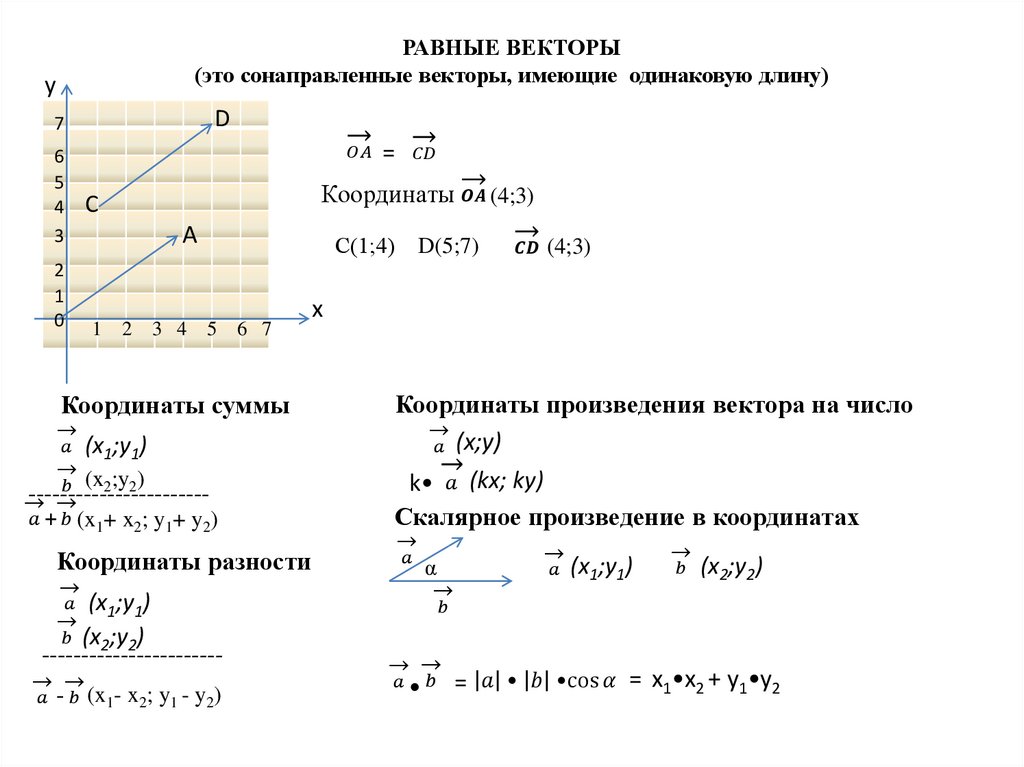

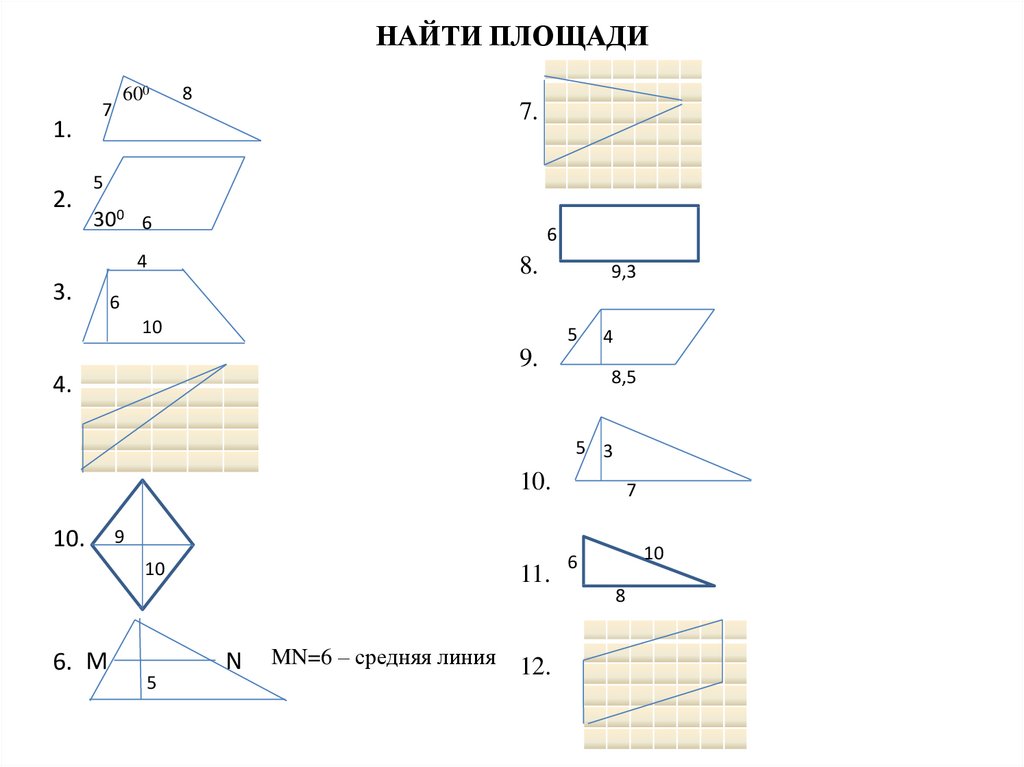
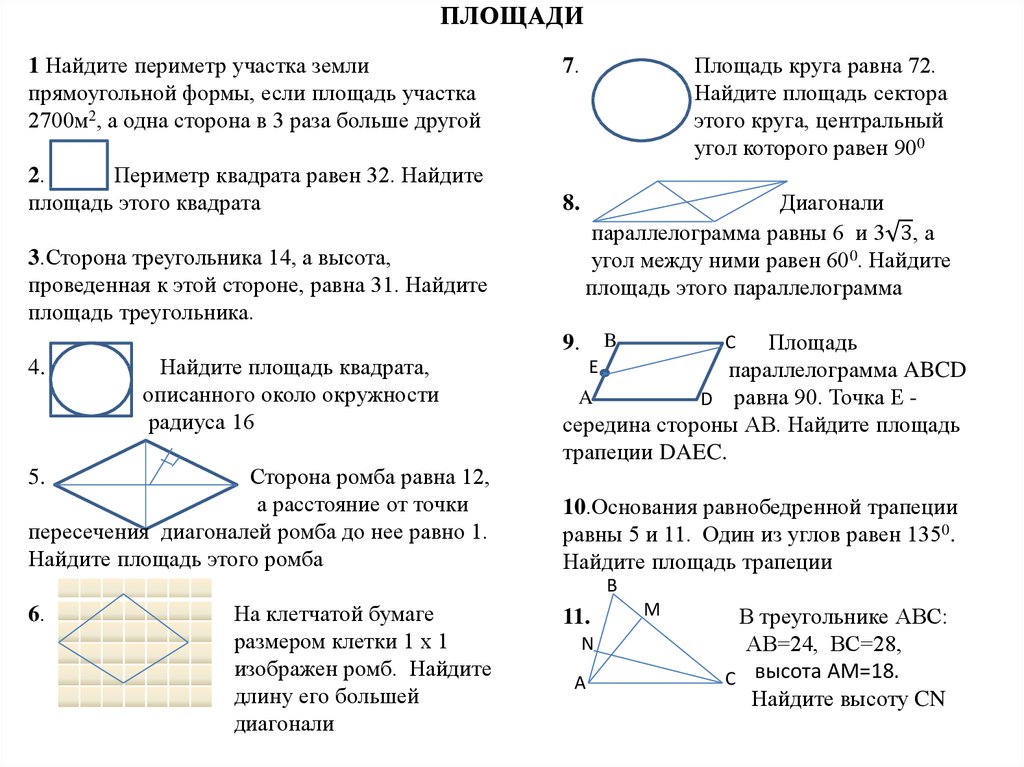
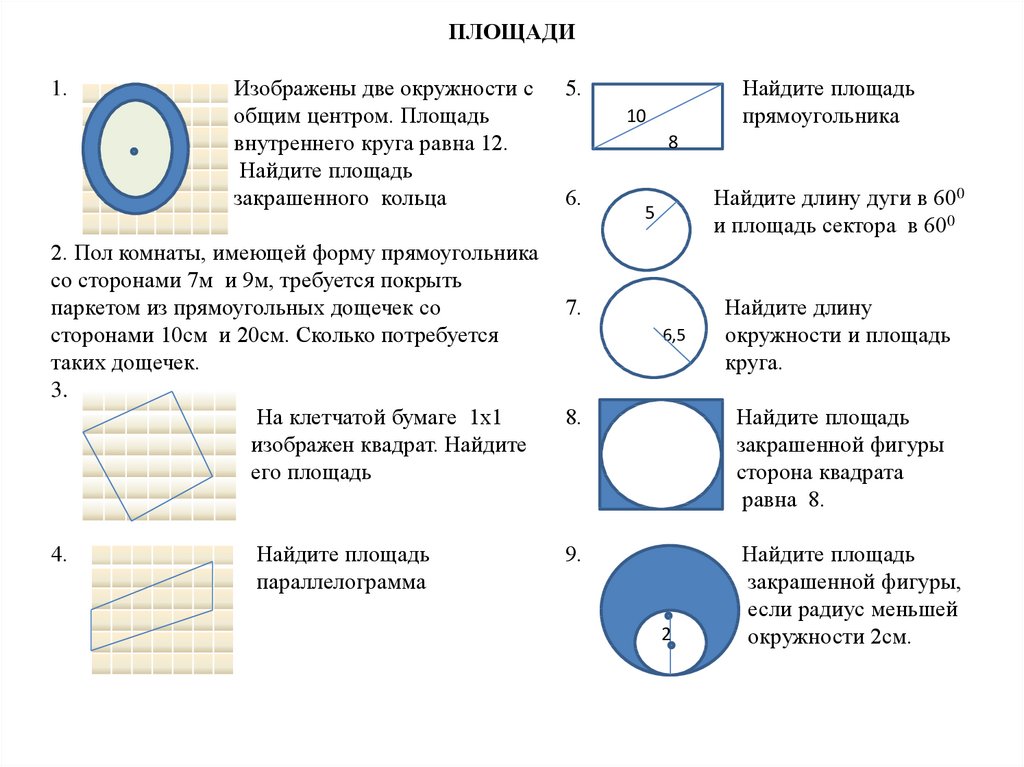
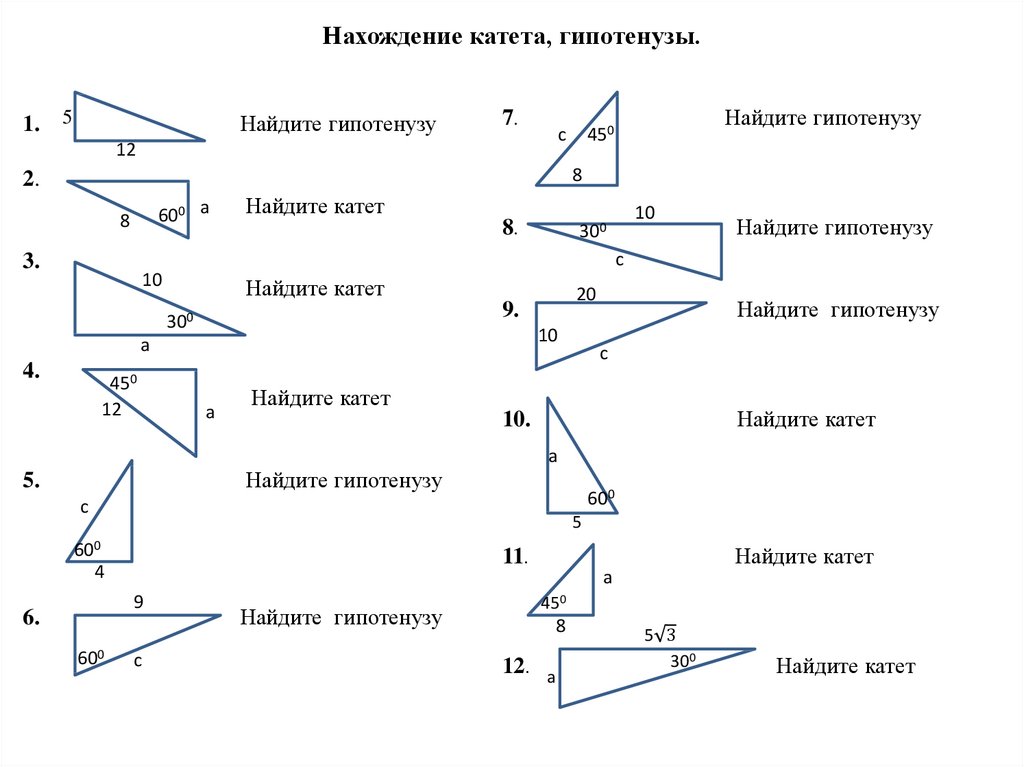
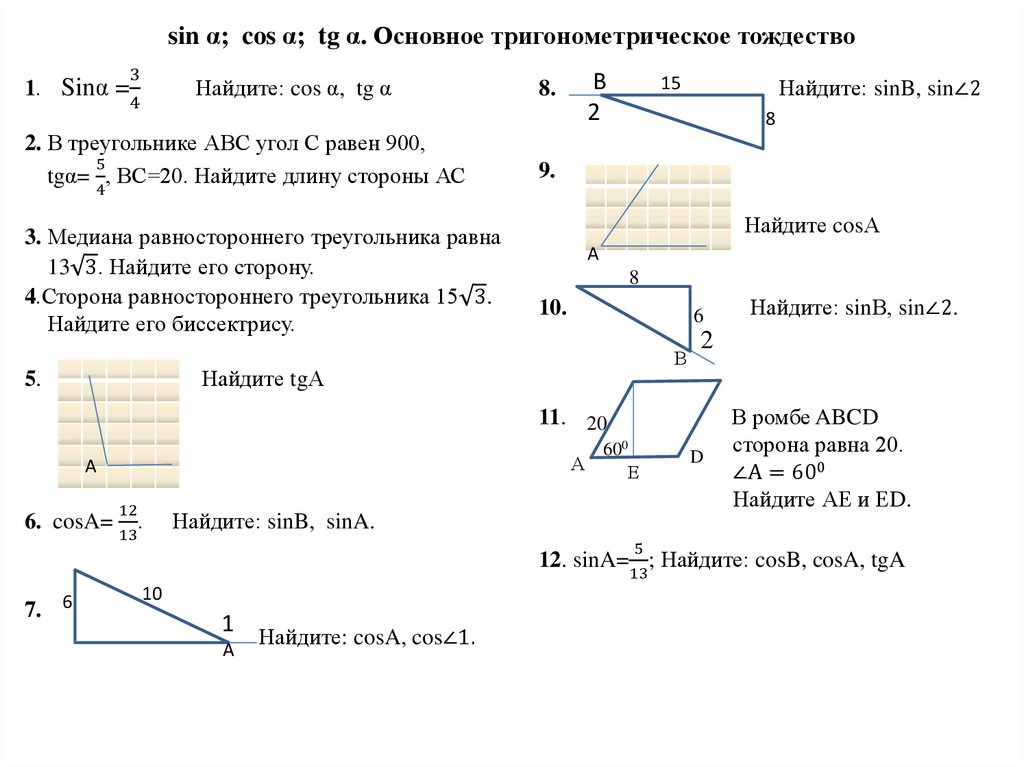
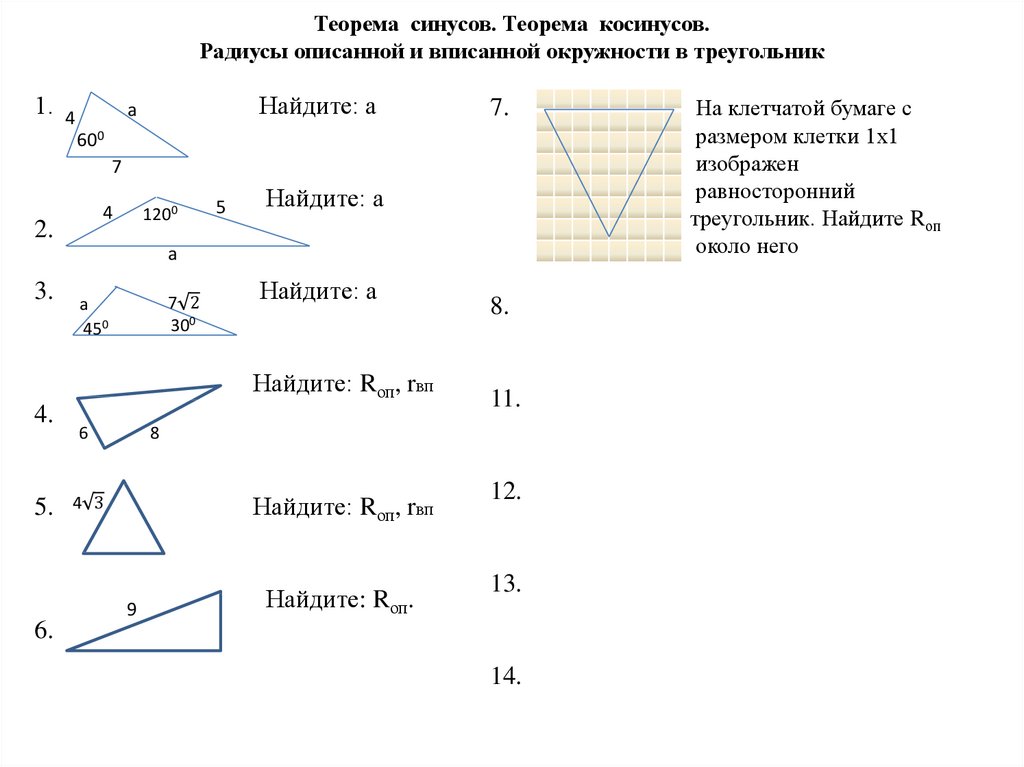
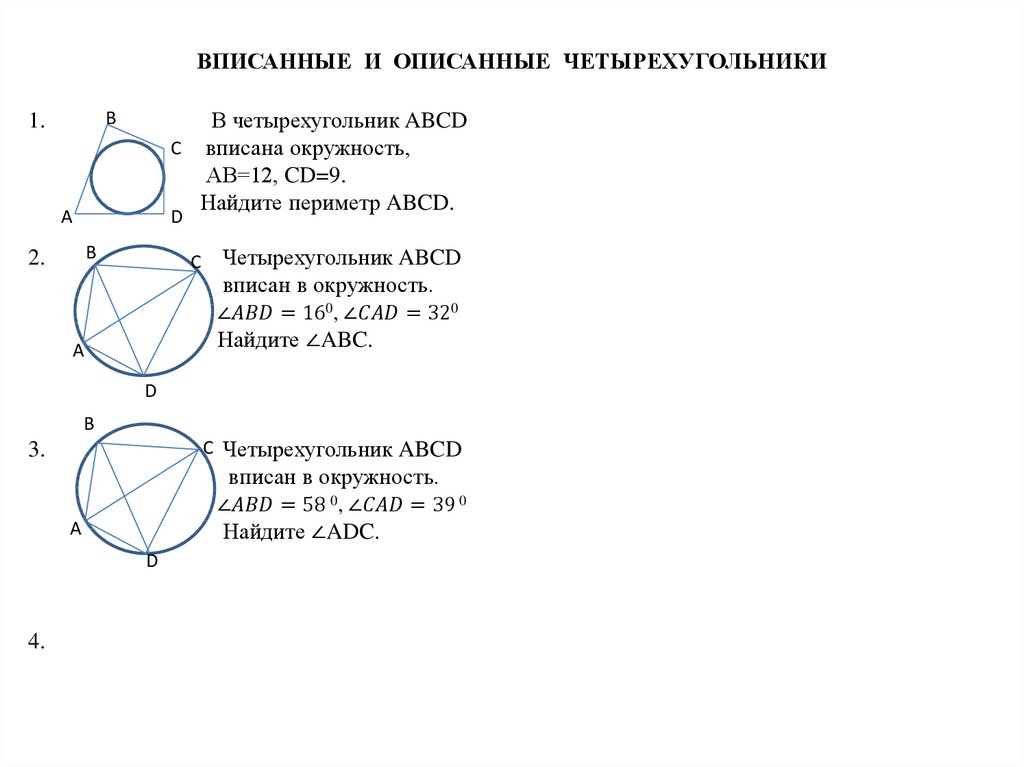
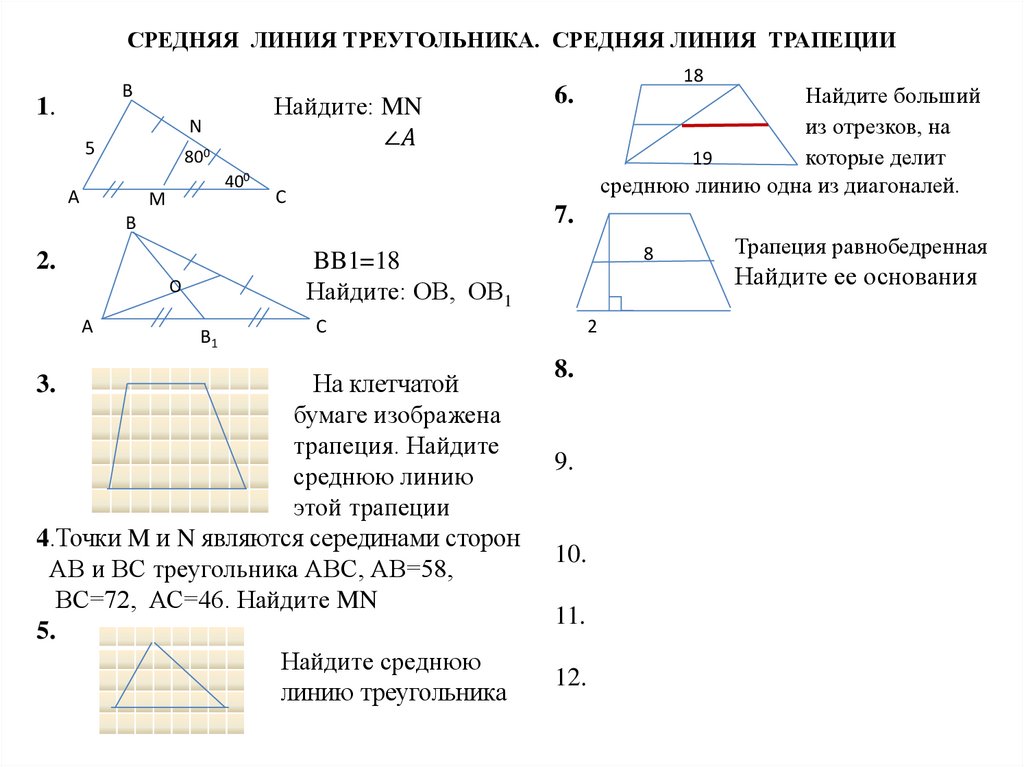
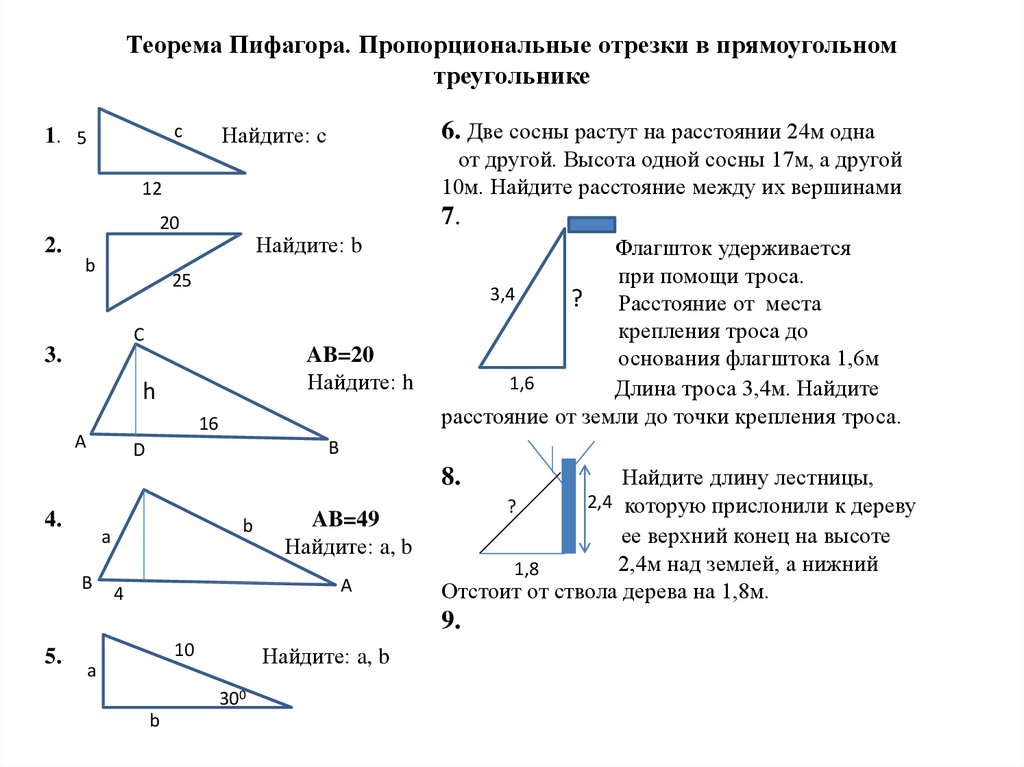
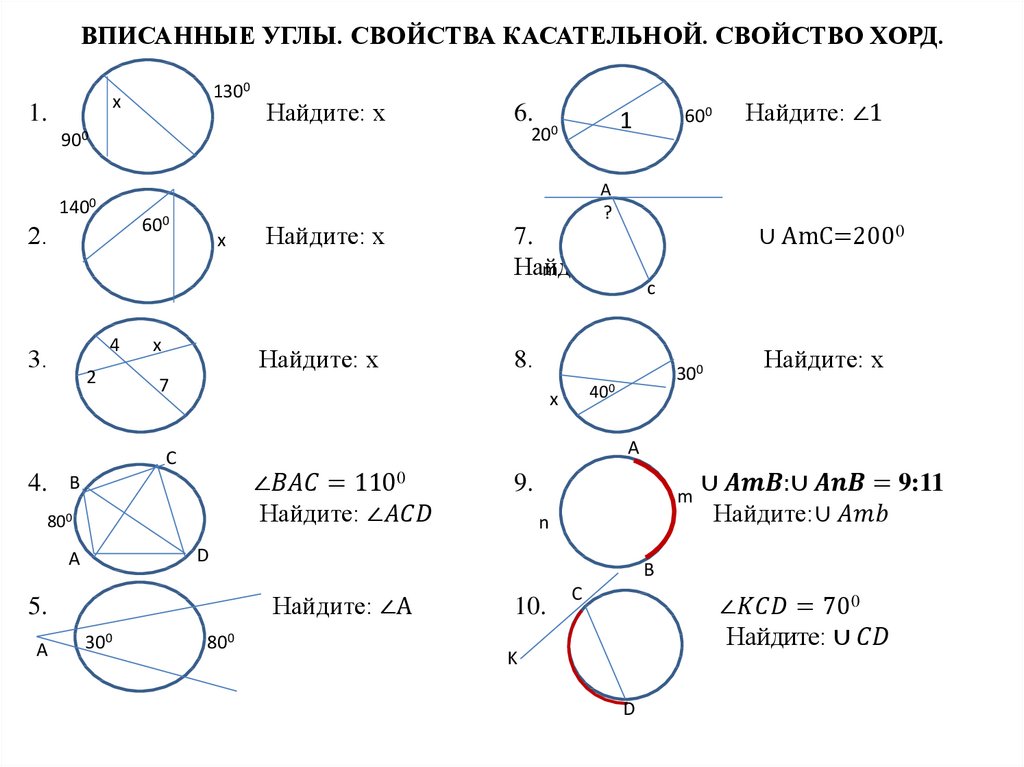
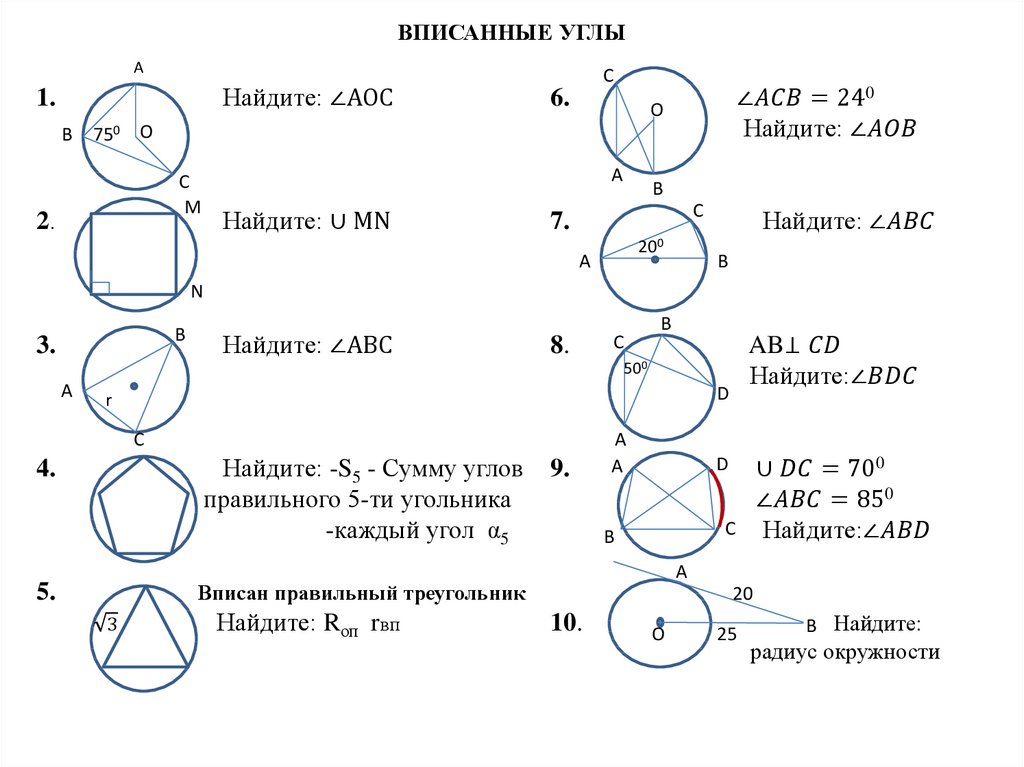
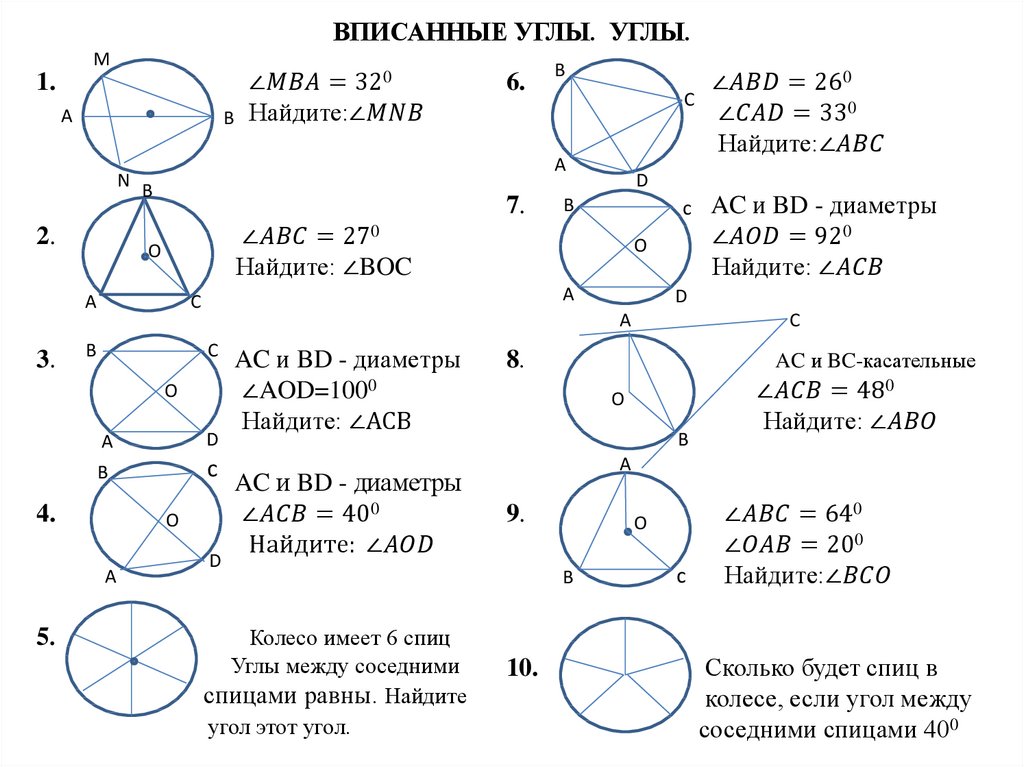
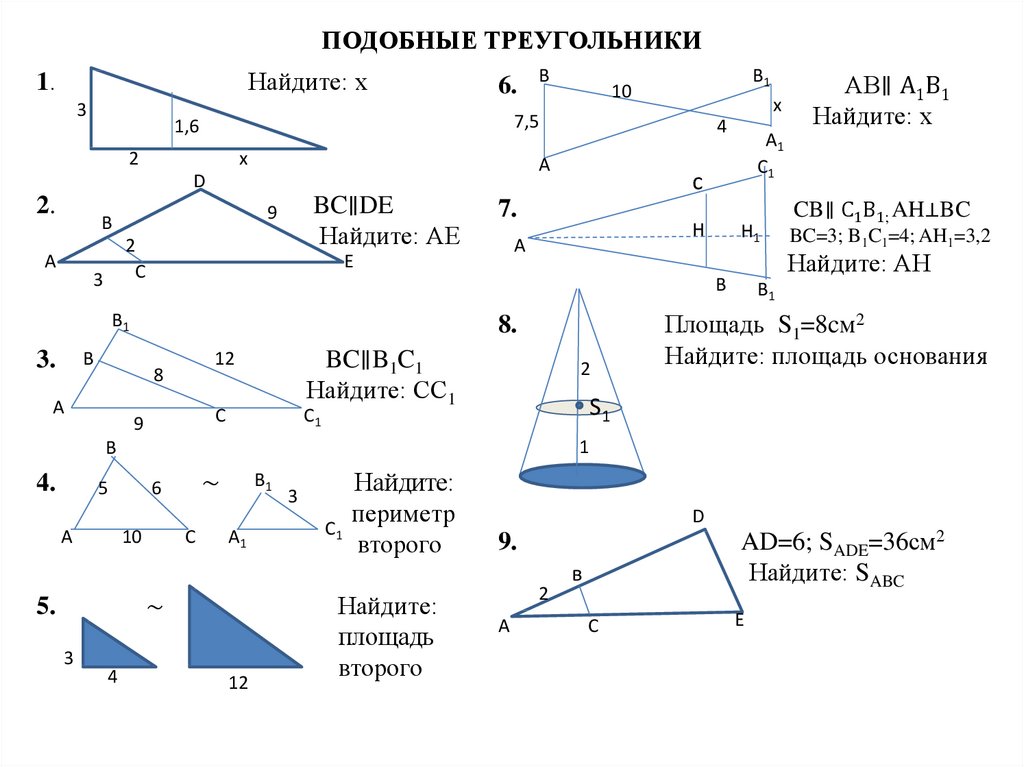
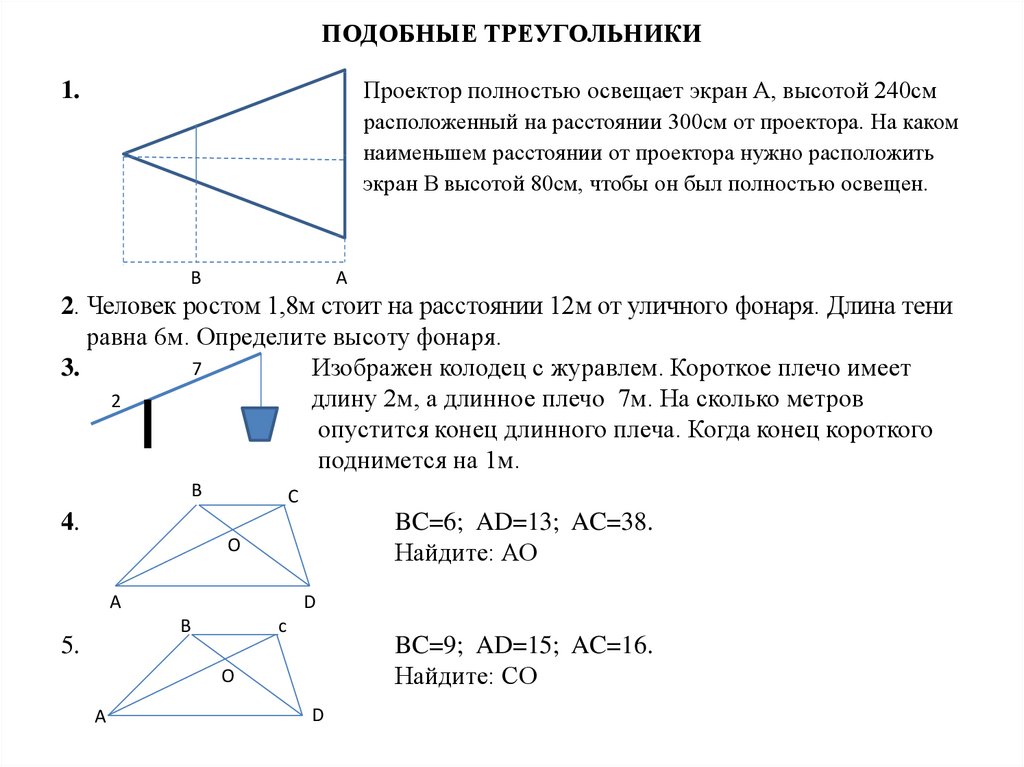
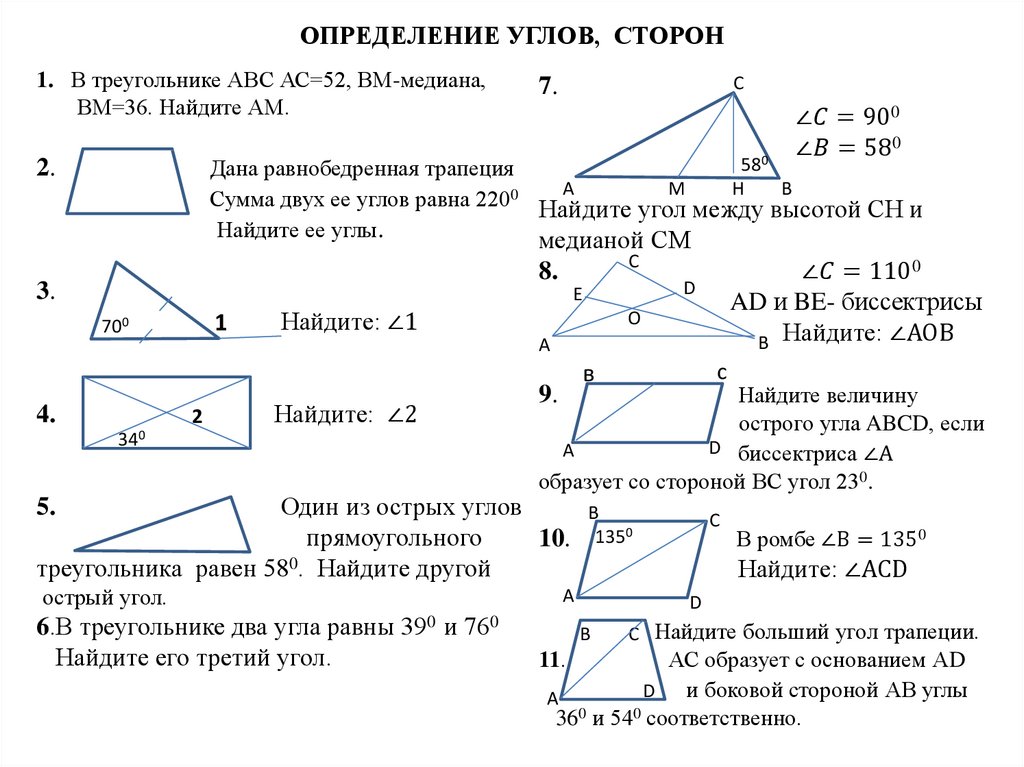
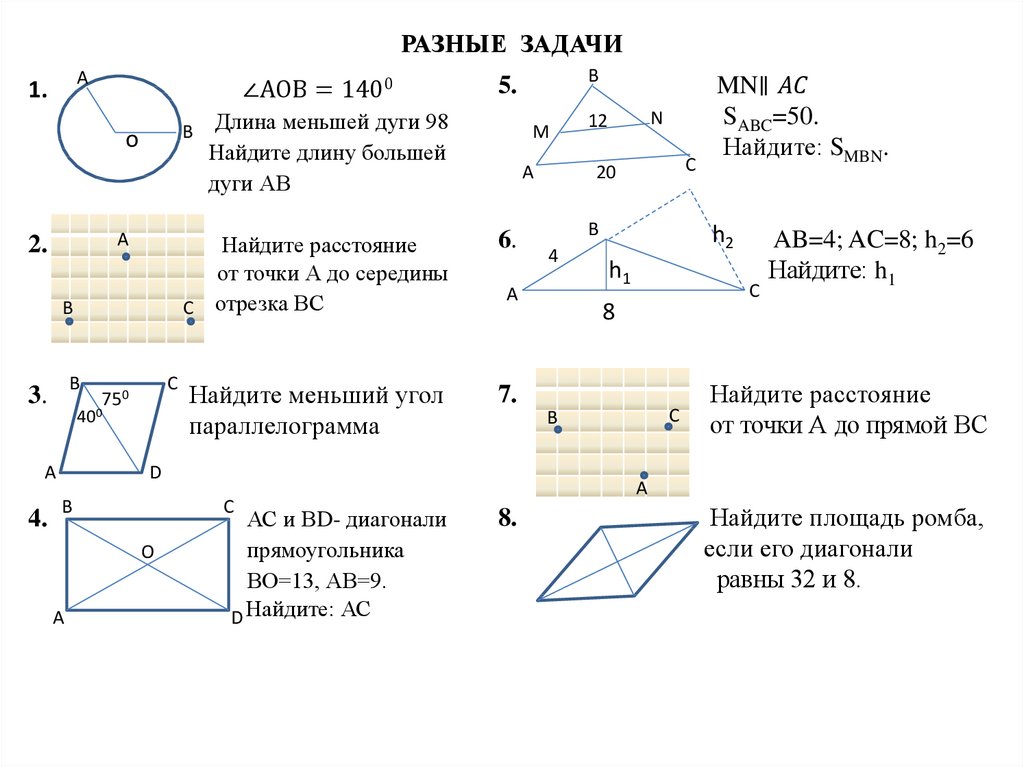
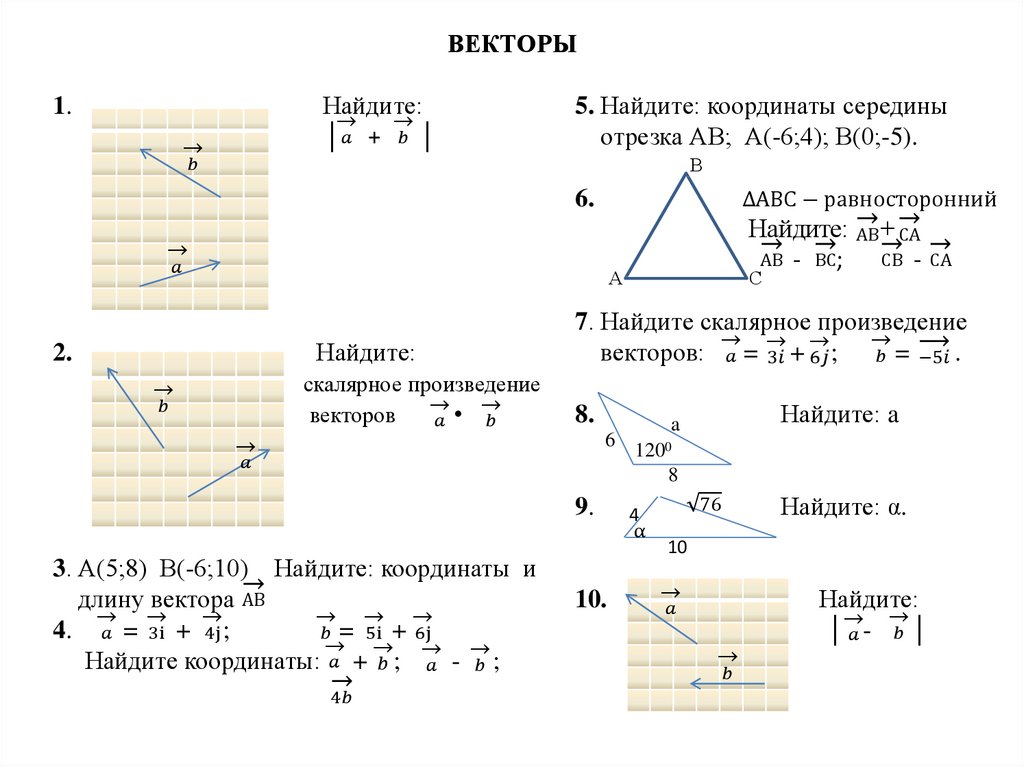
 Математика
Математика