Функция y = kx2 Функция y = k/x. Алгебра 8 класс

1. Функция y = kx2 Функция y = k/x Алгебра 8 класс

МБОУ СОШ №5 – «Школа здоровья и развития»
Учитель математики: Семёнова Елена Юрьевна

2.

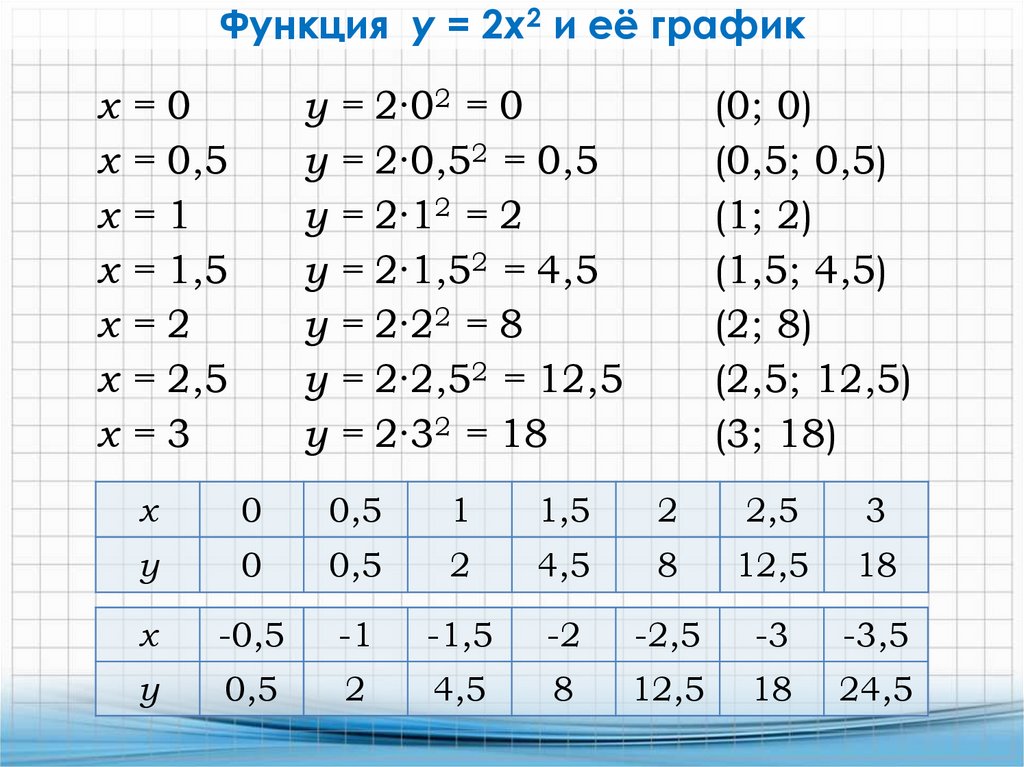
Функция y = 2x2 и её график
х
х
х
х
х
х
х
=0
= 0,5
=1
= 1,5
=2
= 2,5
=3
у=
у=
у=
у=
у=
у=
у=
2·02 = 0
2·0,52 = 0,5
2·12 = 2
2·1,52 = 4,5
2·22 = 8
2·2,52 = 12,5
2·32 = 18
(0; 0)
(0,5; 0,5)
(1; 2)
(1,5; 4,5)
(2; 8)
(2,5; 12,5)
(3; 18)
х
0
0,5
1
1,5
2
2,5
3
у
0
0,5
2
4,5
8
12,5
18
х
-0,5
-1
-1,5
-2
-2,5
-3
-3,5
у
0,5
2
4,5
8
12,5
18
24,5

3.

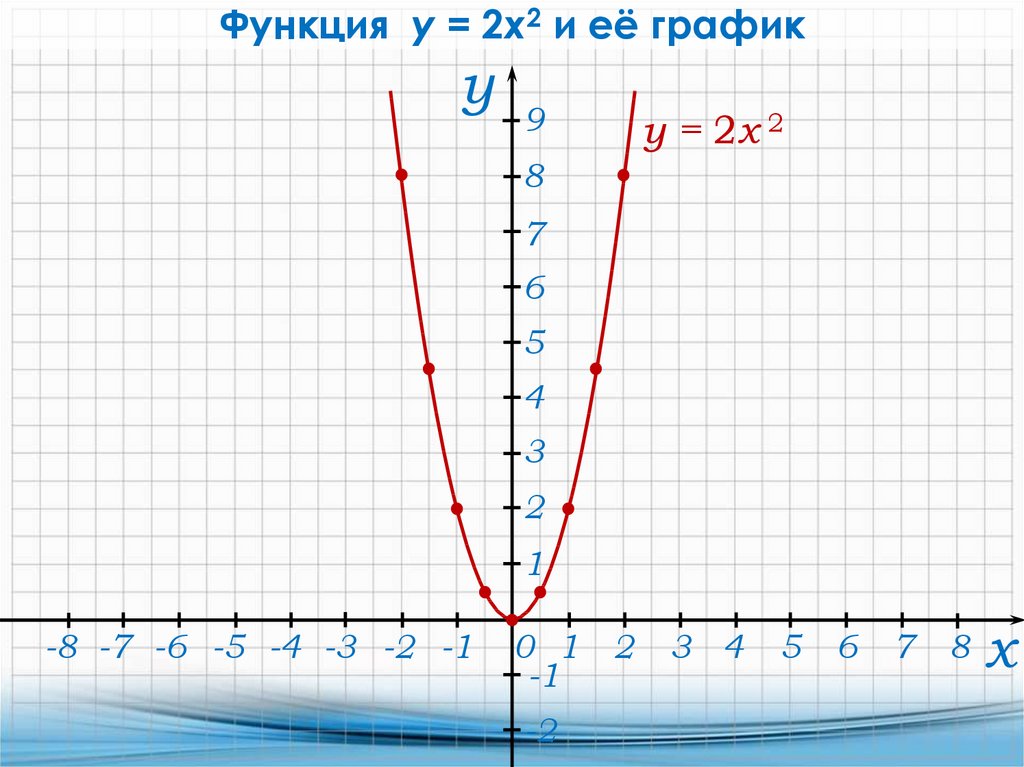
Функция y = 2x2 и её график
у
9
y = 2x 2
8
7
6
5
4
3
2
1
-8 -7 -6 -5 -4 -3 -2 -1
0 1 2
-1
-2
3 4
5
6
7
8
х

4.

Функция y = 0,5x2 и её график
х
х
х
х
х
=0
=1
=2
=3
=4
у=
у=
у=
у=
у=
0,5·02
0,5·12
0,5·22
0,5·32
0,5·42
=
=
=
=
=
0
0,5
2
4,5
8
(0;
(1;
(2;
(3;
(4;
0)
0,5)
2)
4,5)
8)
х
0
1
2
3
4
у
0
0,5
2
4,5
8
х
-1
-2
-3
-4
у
0,5
2
4,5
8

5.

Функция y = 0,5x2 и её график
у
9
y = 0,5x 2
8
7
6
5
4
3
2
1
-8 -7 -6 -5 -4 -3 -2 -1
0 1 2
-1
-2
3 4
5
6
7
8
х

6.

Функция y = kx2 , k > 0 и её свойства
у
-4 -3 -2 -1
9
Функция у = kх 2 – квадратичная
График – парабола,
ветви направлены вверх, если k > 0.
Точка (0; 0) – вершина параболы.
Прямая Оу – ось симметрии
параболы.
D(y) = (‒∞; + ∞); E(y) = [0; + ∞).
унаим. = 0; унаиб. – не существует;
у = 0 при х = 0;
у > 0 при х ≠ 0.
Функция возрастает при х ≥ 0.
Функция убывает при х ≤ 0.
8
7
6
5
4
3
2
1
0 1 2
-1
-2
3 4
5
6
7
8
х

7.

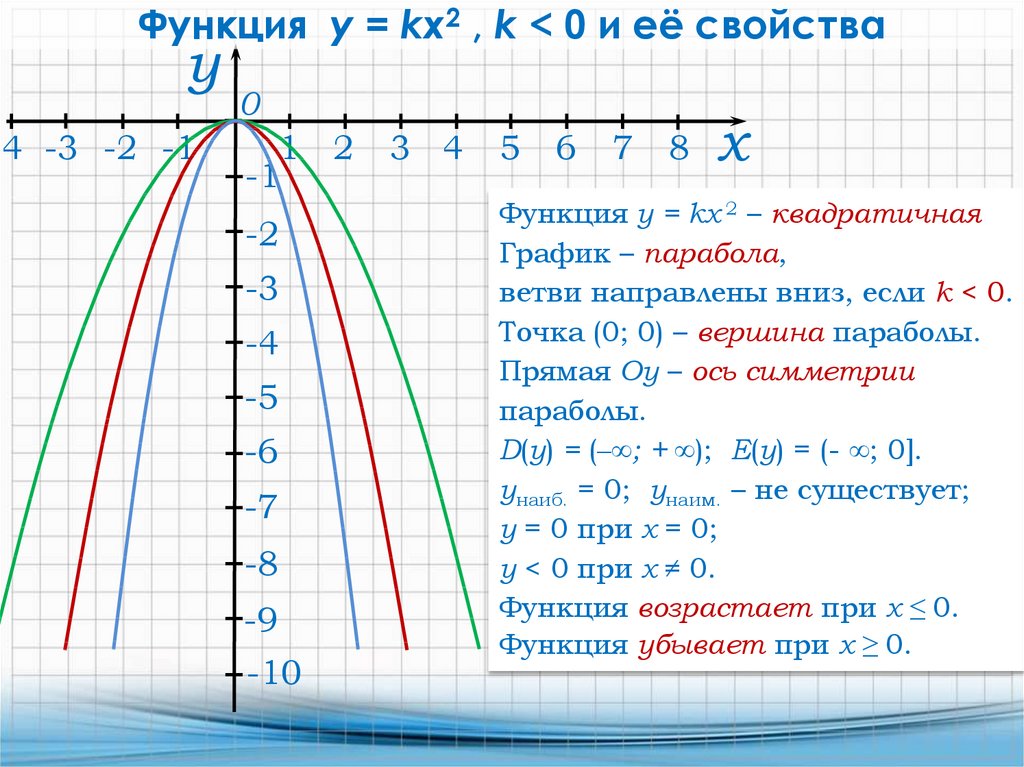
Функция y = kx2 , k < 0 и её свойства
у
-4 -3 -2 -1
0
1 2
-1
-2
-3
-4
-5
-6
-7
-8
-9
-10
3 4
5
6
7
8
х
Функция у = kх 2 – квадратичная
График – парабола,
ветви направлены вниз, если k < 0.
Точка (0; 0) – вершина параболы.
Прямая Оу – ось симметрии
параболы.
D(y) = (‒∞; + ∞); E(y) = (- ∞; 0].
унаиб. = 0; унаим. – не существует;
у = 0 при х = 0;
у < 0 при х ≠ 0.
Функция возрастает при х ≤ 0.
Функция убывает при х ≥ 0.

8.

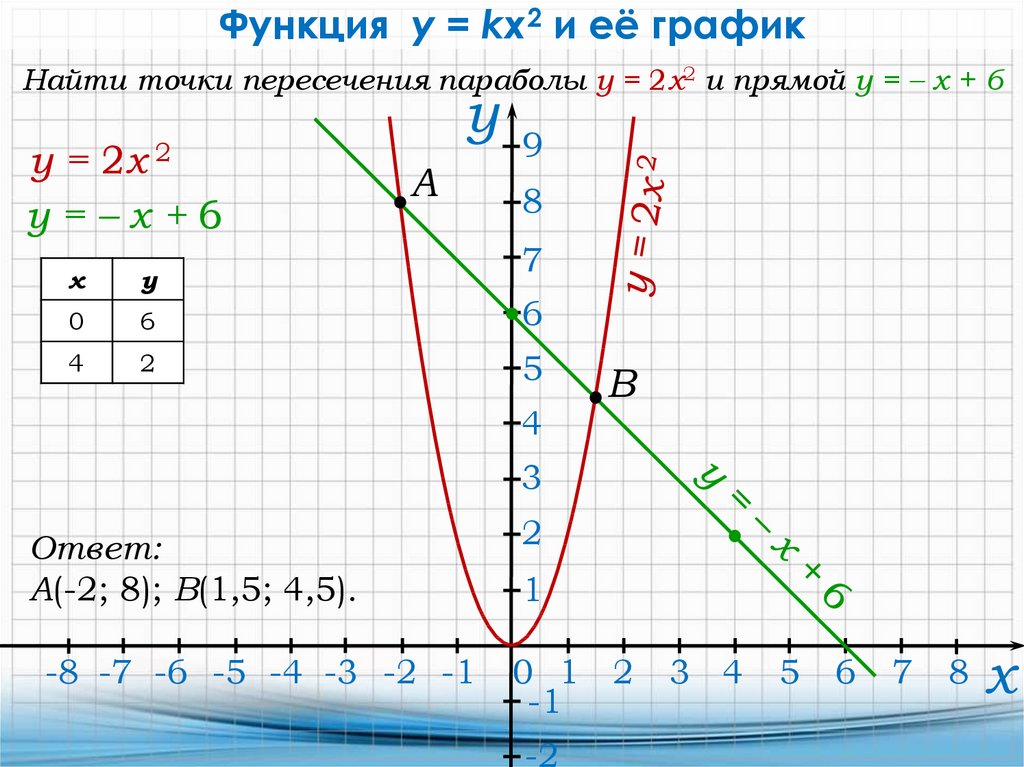
Функция y = kx2 и её график
Найти точки пересечения параболы у = 2х2 и прямой у = – х + 6
y = 2x 2
y=–x+6
у
А
9
8
7
х
у
0
6
6
4
2
5
4
В
3
Ответ:
А(-2; 8); В(1,5; 4,5).
-8 -7 -6 -5 -4 -3 -2 -1
2
1
0 1 2
-1
-2
3 4
5
6
7
8
х

9.

х
х
х
х
х
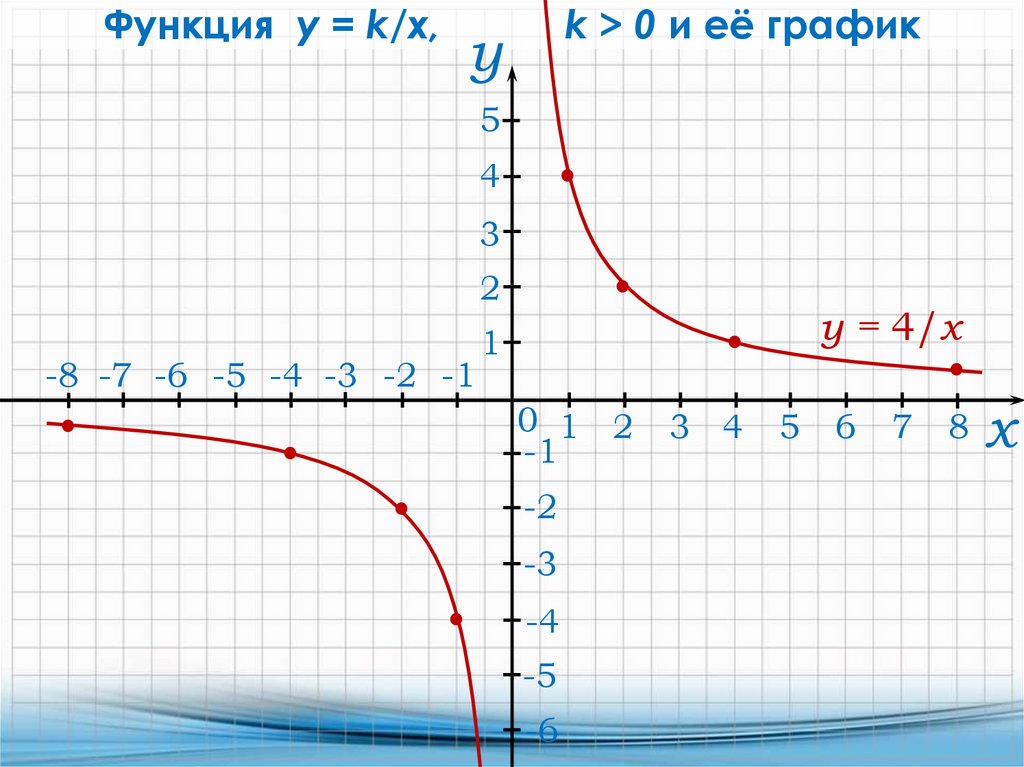
Функция y = k/x и её график
y = 4/x
= 0,5
у = 4:0,5 = 8
(0,5; 8)
=1
у = 4:1 = 4
(1; 4)
=2
у = 4:2 = 2
(2; 2)
=4
у = 4:4 = 1
(4; 1)
=8
у = 4:8 = 0,5
(8; 0,5)
х
0,5
1
2
4
8
у
8
4
2
1
0,5
х
-0,5
-1
-2
-4
-8
у
-8
-4
-2
-1
-0,5

10.

Функция y = k/x,
k > 0 и её график
у
5
4
3
2
-8 -7 -6 -5 -4 -3 -2 -1
y = 4/x
1
0 1 2
-1
-2
-3
-4
-5
-6
3 4
5
6
7
8
х

11.

Функция y = k/x, k > 0 и её график
Функция у = k/х – обратная пропорциональность
График – гипербола, ветви расположены в I и III
координатных углах, если k > 0.
Точка (0; 0) – центр симметрии
Оси координат – асимптоты
D(y) = (‒∞; 0) (0; + ∞); Е(y) = (‒∞; 0) (0; + ∞).
у > 0 при х > 0; у < 0 при х < 0.
Функция убывает при х < 0 и x > 0.
Наибольшего и наименьшего значений функции нет.
Функция не ограничена ни сверху, ни снизу.

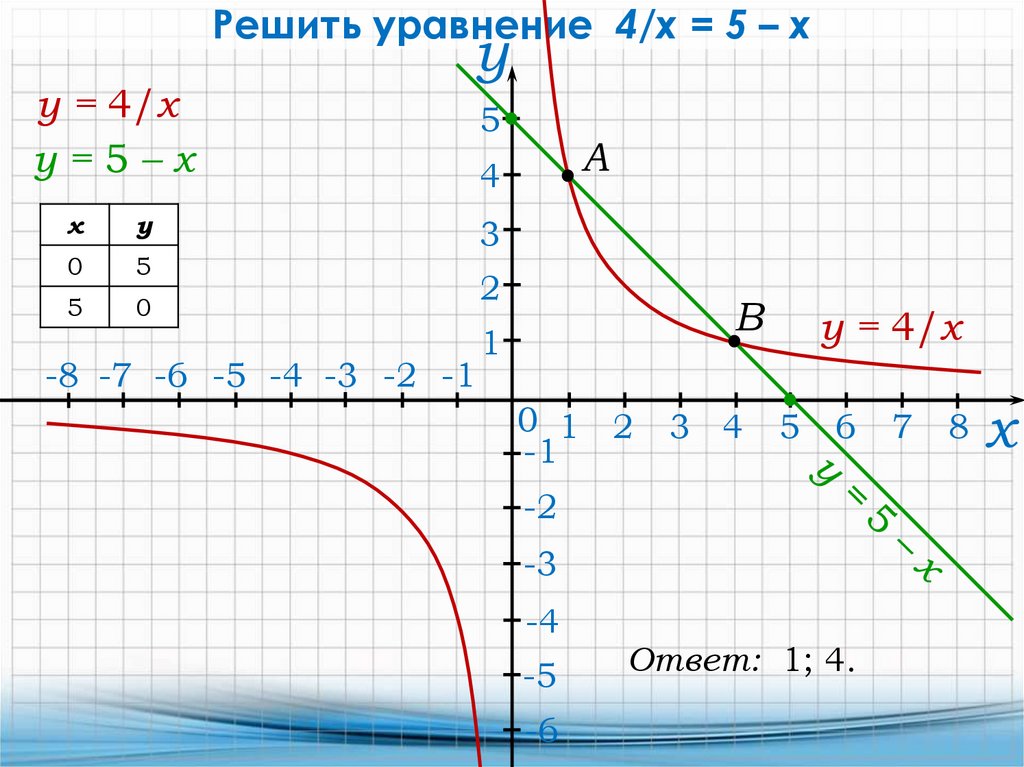
12.

Решить уравнение 4/x = 5 – х
y = 4/x
y=5–x
х
у
0
5
5
0
у
-8 -7 -6 -5 -4 -3 -2 -1
5
А
4
3
2
В
1
0 1 2
-1
3 4
y = 4/x
5
6
-2
-3
-4
-5
-6
Ответ: 1; 4.
7
8
х

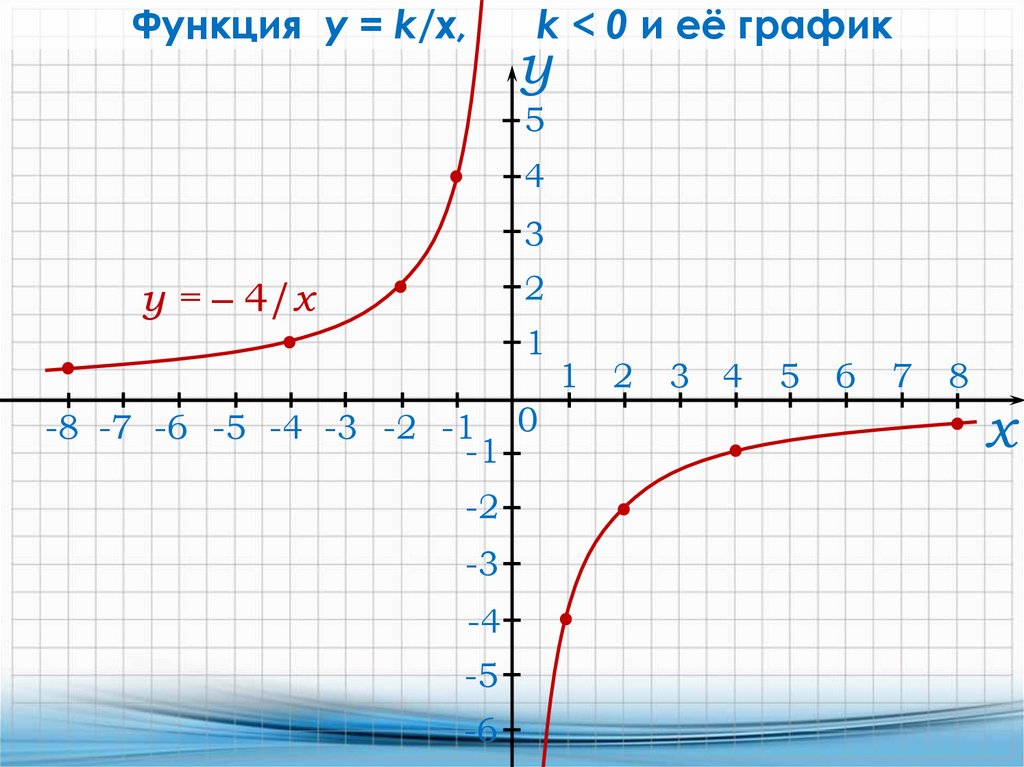
13.

Функция y = k/x,
k < 0 и её график
у
5
4
3
2
y = ‒ 4/x
1
-8 -7 -6 -5 -4 -3 -2 -1 0
-1
-2
-3
-4
-5
-6
1 2
3 4
5
6
7
8
х

14.

Функция y = k/x, k < 0 и её график
Функция у = k/х – обратная пропорциональность
График – гипербола, ветви расположены в II и IV
координатных углах, если k < 0.
Точка (0; 0) – центр симметрии
Оси координат – асимптоты
D(y) = (‒∞; 0) (0; + ∞); Е(y) = (‒∞; 0) (0; + ∞).
у > 0 при х < 0; у < 0 при х > 0.
Функция возрастает при х < 0 и x > 0.
Наибольшего и наименьшего значений функции нет.
Функция не ограничена ни сверху, ни снизу.

15.

Преобразование графика функции у = f(x)
1. Построение графика функции y = f(x – n)
Сдвиг графика функции y = f(x ) вдоль оси х на n
единиц вправо, если n > 0;
Сдвиг графика функции y = f(x ) вдоль оси х на n
единиц, влево если n < 0.
2. Построение графика функции y = f(x ) + m
Сдвиг графика функции y = f(x ) вдоль оси у на т
единиц вверх, если т > 0;
Сдвиг графика функции y = f(x ) вдоль оси у на т
единиц, вниз если т < 0.
3. Построение графика функции y = f(x – n) + m

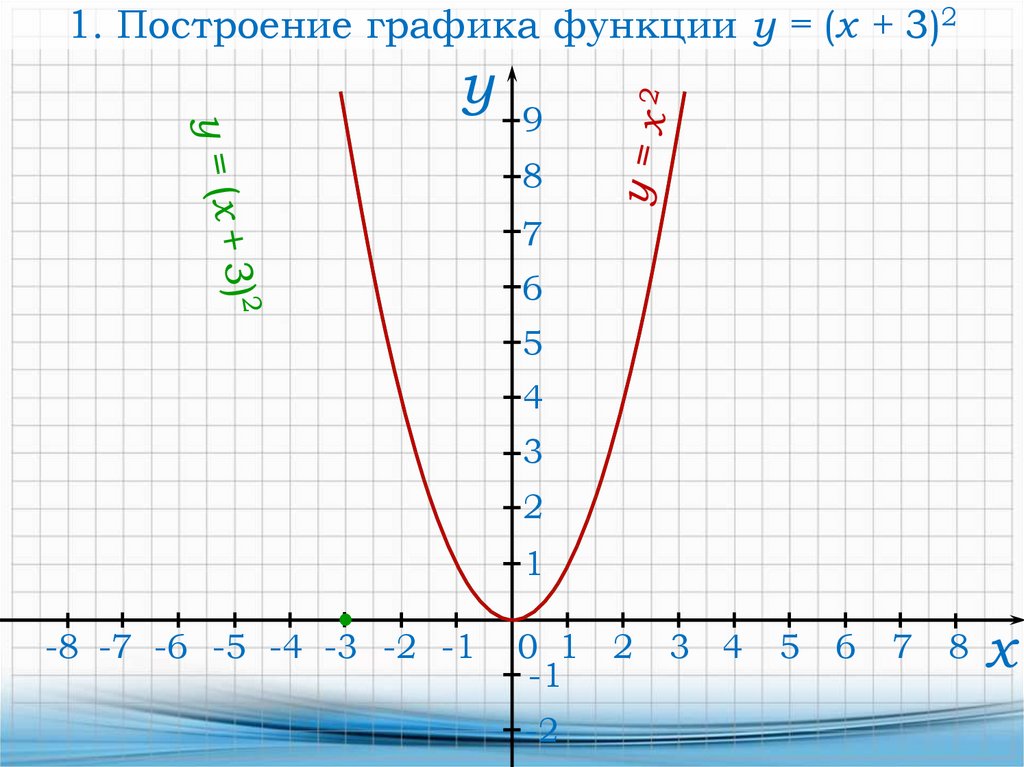
16.

1. Построение графика функции y = (x + 3)2
у
9
8
7
6
5
4
3
2
1
-8 -7 -6 -5 -4 -3 -2 -1
0 1 2
-1
-2
3 4
5
6
7
8
х

17.

у
1. Построение графика функции y = x – 4
9
8
7
6
5
y = x
4
3
2
y = x – 4
1
-1 0
1 2
-1
-2
х
3 4
5
6
7
8 9 10 11 12 13 14 15 16

18.

2. Построение графика функции y = 0,5х – 2,5
у
y = 0,5x
5
х
у
0
0
4
4
2
3
2
1
-8 -7 -6 -5 -4 -3 -2 -1 0
-1
-2
-3
-4
-5
-6
1 2
3 4
5
6
7
8
х

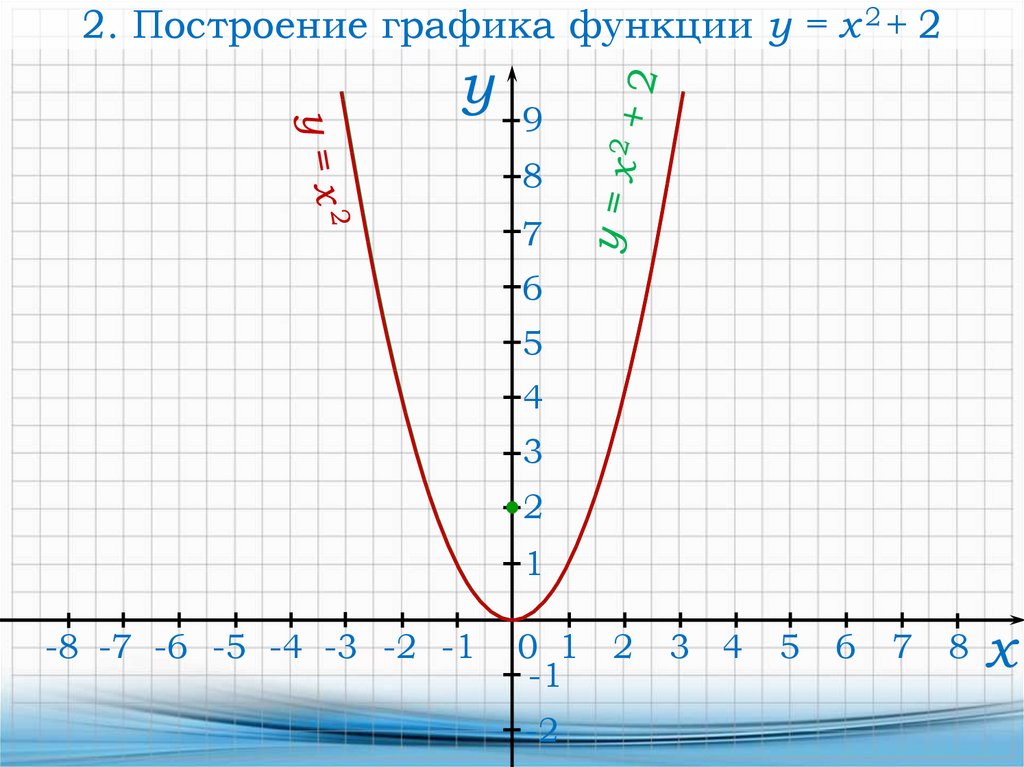
19.

2. Построение графика функции y = x 2+ 2
у
9
8
7
6
5
4
3
2
1
-8 -7 -6 -5 -4 -3 -2 -1
0 1 2
-1
-2
3 4
5
6
7
8
х

20.

2. Построение графика функции y = – 4/х – 1
у
5
4
4
y=‒ x
3
2
1
1 2
3 4
5
6
7
-8 -7 -6 -5 -4 -3 -2 -1 0
-1
-2
-3
-4
-5
-6
4
y=‒ x ‒1
8
х

21.

Алгоритм построения графика функции у = f(x – n) + m
1 способ:
1. Построить график функции y = f(x).
2. Осуществить параллельный перенос графика
функции y = f(x) вдоль оси х на n единиц вправо,
если n > 0; влево если n < 0.
3. Осуществить параллельный перенос
полученного в п. 2 графика вдоль оси у на т
единиц вверх, если т > 0; вниз если т < 0.

22.

3. Построение графика функции y = (x 4)2 + 2
у
9
8
7
6
5
4
3
2
1
-8 -7 -6 -5 -4 -3 -2 -1
0 1 2
-1
-2
3 4
5
6
7
8
х

23.

Алгоритм построения графика функции у = f(x – n) + m
2 способ:
1. Перейти к вспомогательной системе
координат, проведя пунктиром прямые х = n,
у = т, т.е. выбрав в качестве начала новой
системы координат точку (п; т).
2. Построить в «новой» (пунктирной) системе
координат график функции y = f(x).

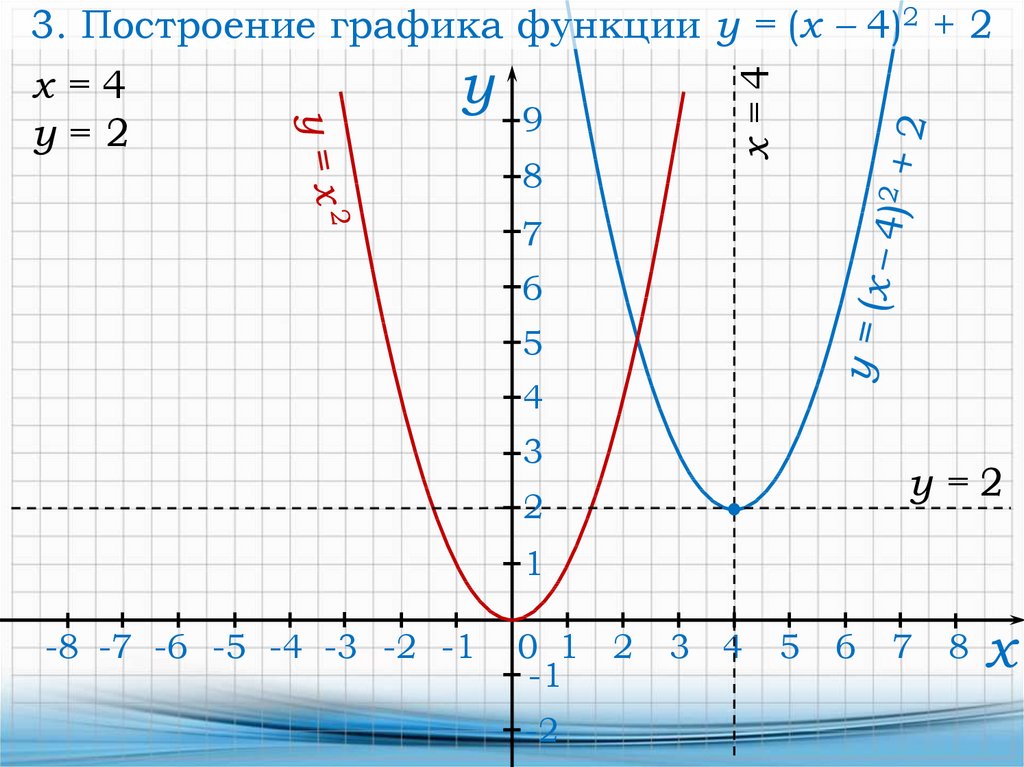
24.

х=4
у=2
у
9
8
х=4
3. Построение графика функции y = (x 4)2 + 2
7
6
5
4
3
y=2
2
1
-8 -7 -6 -5 -4 -3 -2 -1
0 1 2
-1
-2
3 4
5
6
7
8
х

25.

у
7
6
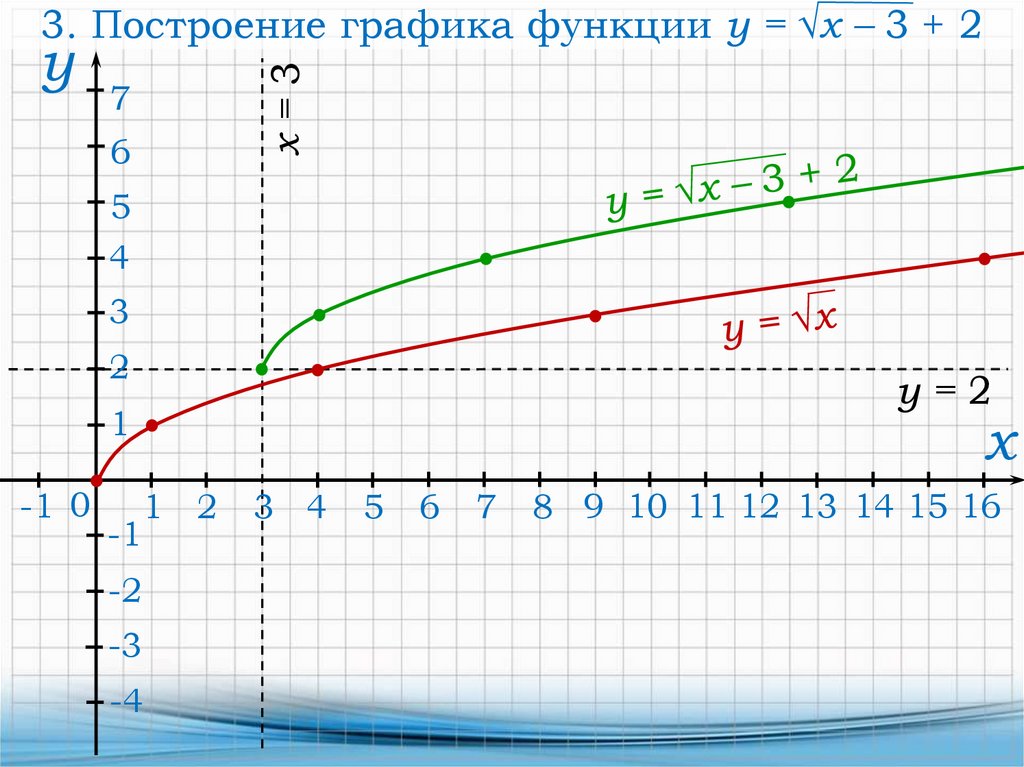
х=3
3. Построение графика функции y = x – 3 + 2
5
4
3
2
y=2
1
-1 0
1 2
-1
-2
-3
-4
х
3 4
5
6
7
8 9 10 11 12 13 14 15 16

26.

Функция у = ах2 + bx + c, ее свойства и график
Функцию у = ах2 + bx + c, где a, b, с – произвольные
числа, причем а ≠ 0, называют квадратичной
функцией.
ах2 + bx + c – называют квадратным трёхчленом
ах2 – старший член квадратного трёхчлена
а – старший коэффициент
с – свободный коэффициент
Если а > 0, то
Если а < 0, то

27.

Функция у = ах2 + bx + c, ее свойства и график
Графиком квадратичной функции у = ах2 + bx + c
является парабола, которая получается из
параболы у = ах2 параллельным переносом.
ax bx c ax
2
2
2
b
a x 2
x
2a
2
2
b
b
a x
2a
4a
2 b
bx c a x x c
a
b2 b2
c
2
2
4a 4a
2
2
b
4
ac
b
c a x
2a
4a
2
2
b
4
ac
b
ax 2 bx c a x
2a
4a

28.

Функция у = ах2 + bx + c, ее свойства и график
ax bx c a x n m
2
2
2
2
b
4
ac
b
2
ax bx c a x
2a
4a
b
n
;
2a
4ac b 2
m
4a
Координаты вершины параболы:
b
xв
;
2a
4ac b 2
ув
4a
b
Ось симметрии параболы: x о
2a

29.

Функция у = ах2 + bx + c, ее свойства и график
Пример 1
у x 2 4x 1
а 1;
b 4;
с 1
Ветви параболы направлены вверх, т.к. а = 1 > 0.
b
4
xв
2;
2a
2 1
4ac b 2 4 1 1 42 4 16
ув
3
4a
4 1
4
(-2; -3) ‒ координаты вершины параболы
у x 2 3
2
Ось симметрии параболы: хо = ‒2.
Доп. точки:
х
0
-1
-3
-4
1
у
1
-2
-2
1
6

30.

у x 2 3
2
у
хв = -2
ув = -3
5
4
3
2
-8 -7 -6 -5 -4 -3 -2 -1
0 1 2
-1
-2
х = -2
-3
-4
-5
-6
3 4
5
6
7
8
х

31.

Функция у = ах2 + bx + c, ее свойства и график
Пример 2
у 2x 2 4x 3
а 2;
b 4;
с 3
Ветви параболы направлены вниз, т.к. а = -2 < 0.
b
4
xв
1;
2a
2 2
4ac b 2 4 2 3 42 24 16
ув
1
4a
4 2
8
(1; -1) ‒ координаты вершины параболы
у 2 x 1 1
2
Ось симметрии параболы: хо = 1.
Доп. точки:
х
0
2
-1
3
у
-3
-3
-9
-9

32.

у 2 x 1 1
2
хв = 1
ув = -1
у
2
1
0 1 2
-1
-2
-3
-4
-5
-6
-7
-8
-9
х=1
-8 -7 -6 -5 -4 -3 -2 -1
3 4
5
6
7
8
х

33.

Решите графически уравнение х2 – 2х – 3 = 0.
1 способ.
у
2
xв
1;
2 1
ув 12 2 1 3 4
1; 4
-8 -7 -6 -5 -4 -3 -2 -1
5
4
3
2
y=0
0 1 2
-1
3 4
5
6
7
-2
х1 1; х 2 3.
-3
-4
-5
-6
Ответ : 1; 3.
8
х

34.

Решите графически уравнение х2 – 2х – 3 = 0.
2 способ.
у
9
х2 – 2х – 3 = 0
8
х2 = 2х + 3
7
1) у = х2
2) у = 2х + 3
6
5
х
у
4
0
3
-2
-1
3
-8 -7 -6 -5 -4 -3 -2 -1
2
х1 1; х 2 3.
1
Ответ : 1; 3.
0 1 2
-1
-2
3 4
5
6
7
8
х

35.

Использованы ресурсы
Алгебра 8 класс. Учебник / А.Г. Мордкович, Т.Н. Мишустина,
Москва: Мнемозина, 2015 г.