Электромагнитные волны в вакууме

1.

Уравнения Максвелла
Электромагнитные волны в вакууме
В отсутствии зарядов
0, j 0
div E 0
B
t
rot(
)
rot rotE
rotB
t
1 E
c 2 t
rot(
)
rot rotB
rotE
t
rot E
div B 0
rot B
rot rotE grad divE E

2.

Уравнения Максвелла
Электромагнитные волны в вакууме
2E
c 2 E 0
2
t
2B 2
c B 0
t 2
2
2
2
2 2 2
x y z
– волновые уравнения
для электромагнитного поля
– лапласиан
Частное решение – плоские бегущие волны
E E(t nr c) , B B(t nr c)
n – единичный вектор (направление распространения бегущей волны)

3.

Уравнения Максвелла
Электромагнитные волны в вакууме
E E(t nr c) , B B(t nr c)
– волна, движущаяся в направлении вектора n со скоростью c.
c
n
Профиль E и B перемещается вдоль n со скоростью c

4.

Уравнения Максвелла
Электромагнитные волны в вакууме
Последовательные картины электрического и магнитного полей,
распространяющихся от вибратора (антенны), соединенного с
источником переменного тока.

5.

Уравнения Максвелла
Электромагнитные волны в вакууме
направление
распространения

6.

Уравнения Максвелла
Электромагнитные волны в вакууме
Гармоническая (монохроматическая) волна
E E0 sin( t kr ) , B B0 sin( t kr )
k – волновой вектор,
k
c
E
B
cT 2 k – длина волны
направление
распространения волны
B
E

7.

Уравнения Максвелла
Электромагнитные волны в вакууме
Свойства гармонических волн
E
E, B, n – правая тройка векторов
nE nB 0
n E cB
n
E = cB
B
Поток энергии
w – объемная плотность электромагнитной энергии
S E H nEH nc 1 2 ( 0 E 2 B 2 0 )
S n cw
скорость переноса энергии плоской гармонической волной
в вакууме равна скорости света

8.

Уравнения Максвелла
Электромагнитные волны в диэлектриках
Среда const, const, 0.
В отсутствии сторонних зарядов и токов проводимости
divE 0
B
rotE
t
divB 0
rotB
v
1 E
v 2 t
c
c
2 E
2
v
E 0
2
t
2 B
v 2 B 0
2
t
– скорость распространения
электромагнитной волны в диэлектрике

9.

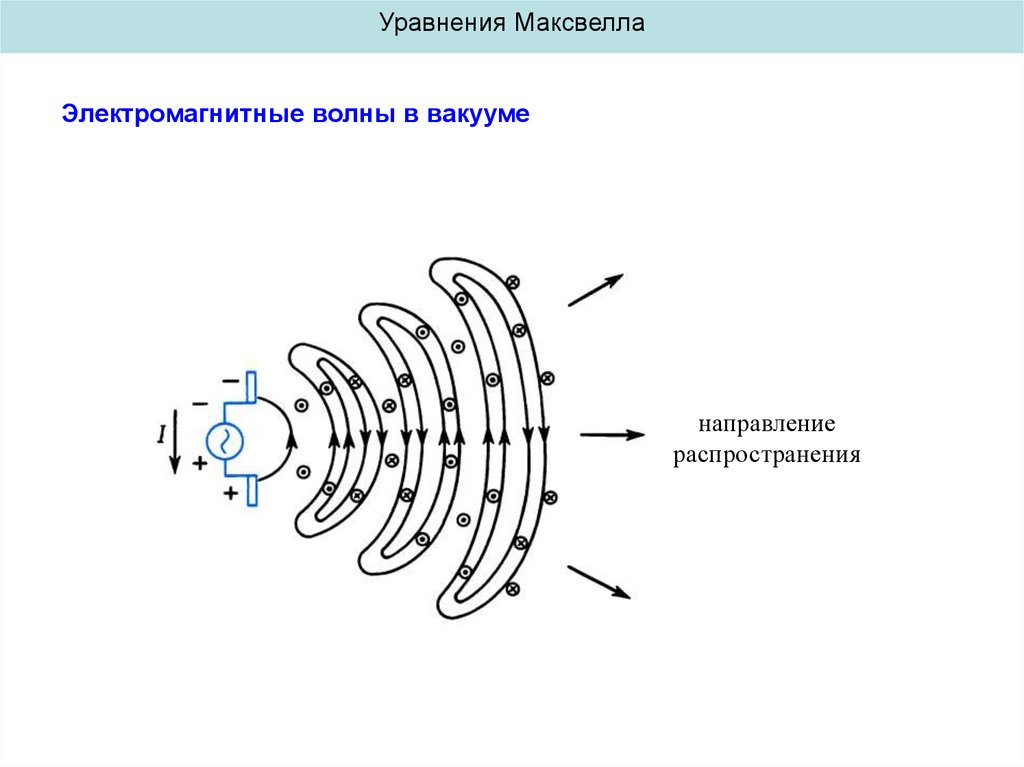
Уравнения Максвелла
Давление и импульс электромагнитных волн
падающая
волна
отраженная
волна
E
E
n
B
n
B
идеальный проводник
0
Внутри проводника
электрическое поле отсутствует
E E 0
B B
на границе

10.

Уравнения Максвелла
Давление и импульс электромагнитных волн
2B
Давление оказывает магнитное поле
i
(2 B )2
P
2 0
( E cB )
B2
0 E 2 2 w
0
P 2w , w – объемная плотность
энергии падающей волны
электромагнитная волна обладает импульсом
g – объемная плотность импульса

11.

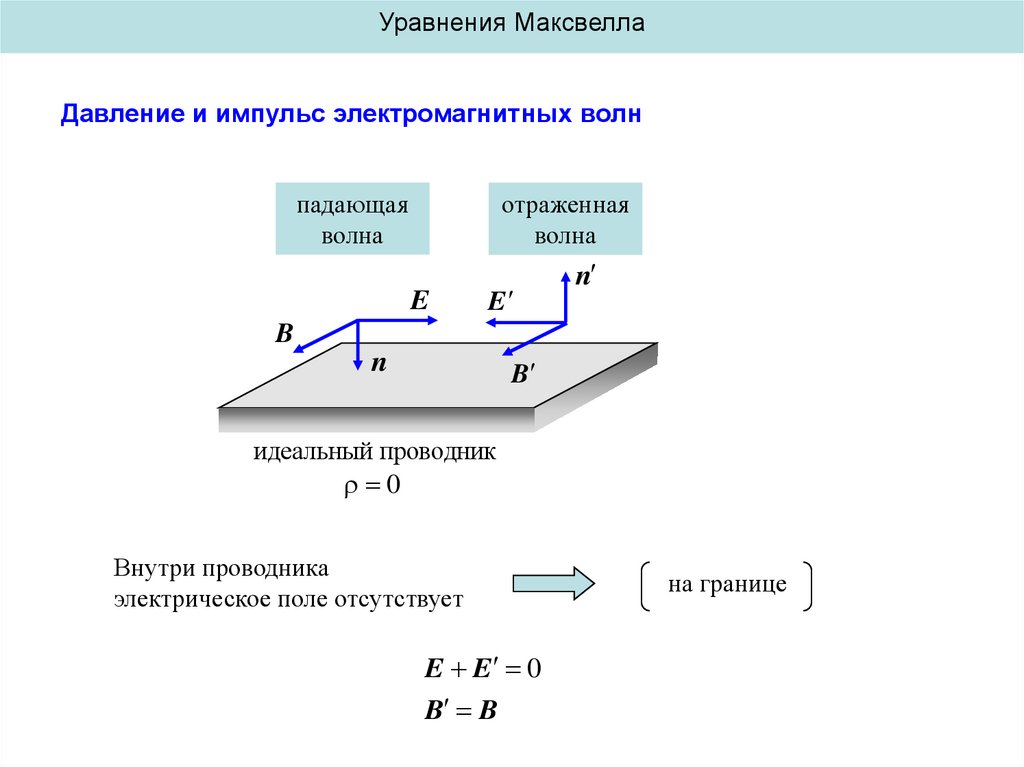
Уравнения Максвелла
Давление и импульс электромагнитных волн
падающая
волна
отраженная
волна
p gSc t g Sc t
g
g
p – импульс, переданный проводнику за t
S
F
p
2 gcS
t
F
2 gc
S
P 2w
P
F
g
w
S
n 2
c
c
g
w
c

12.

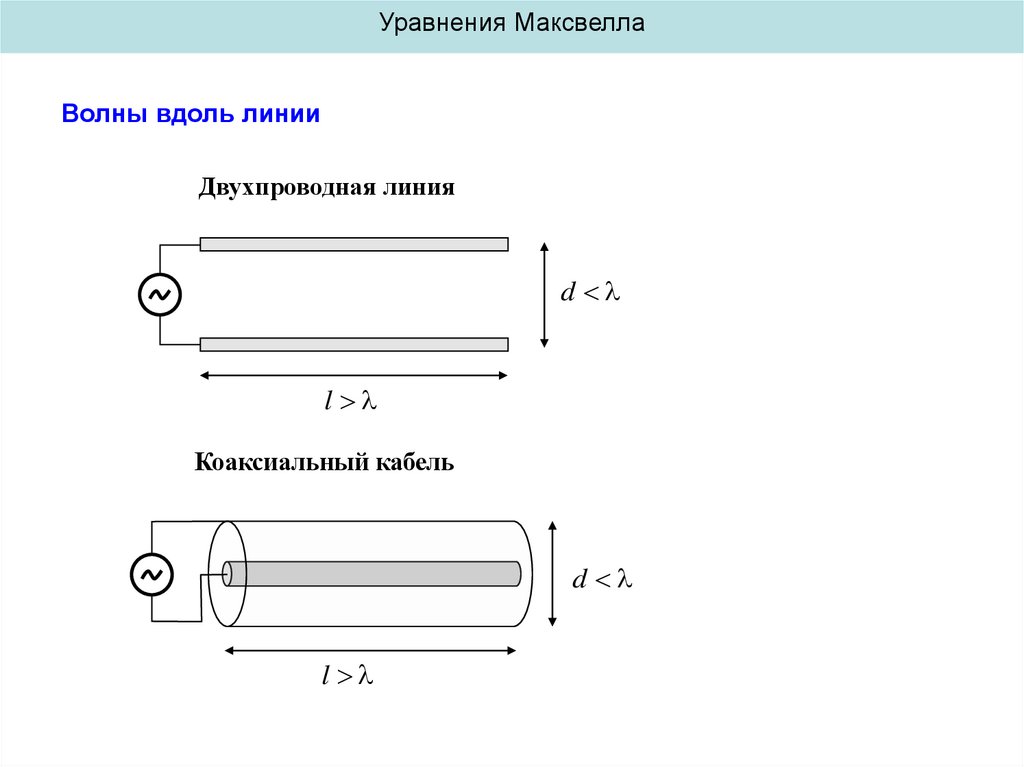
Уравнения Максвелла
Волны вдоль линии
Двухпроводная линия
d
l
Коаксиальный кабель
d
l

13.

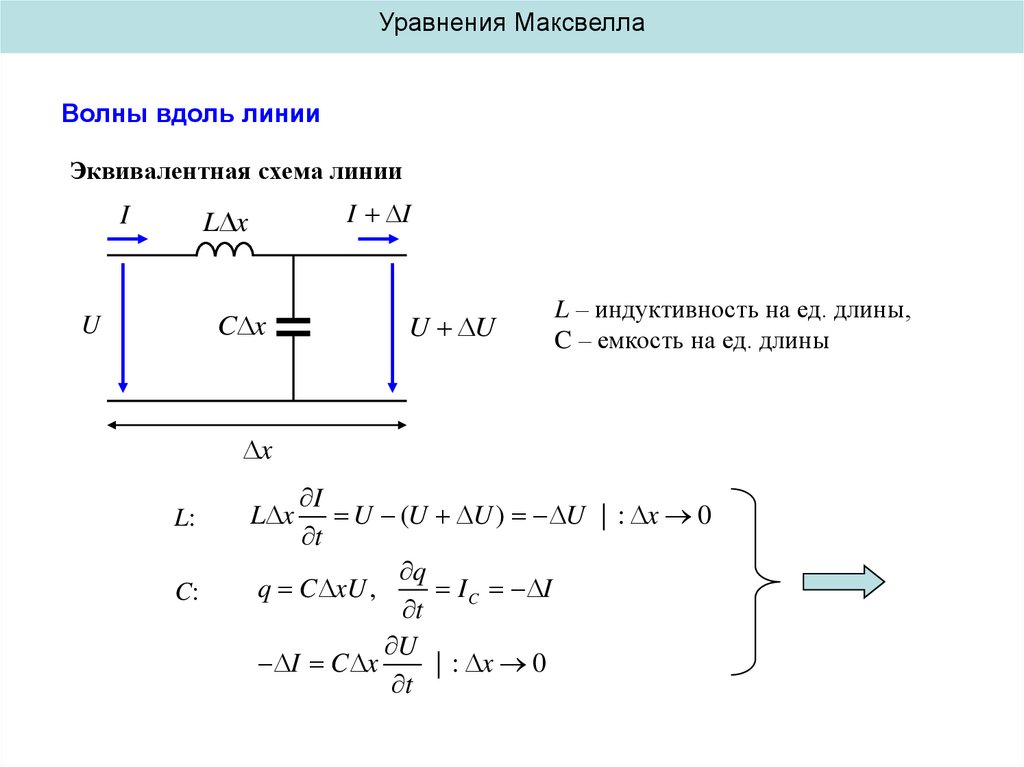
Уравнения Максвелла
Волны вдоль линии
Эквивалентная схема линии
I I
L x
I
C x
U
U U
L – индуктивность на ед. длины,
C – емкость на ед. длины
x
L:
C:
I
U (U U ) U | : x 0
t
q
q C xU ,
I C I
t
U
I C x
| : x 0
t
L x

14.

Уравнения Максвелла
Волны вдоль линии
L
I
U
t
x
2
2U
2 U
v
0
2
2
t
x
I
U
C
x
t
2
2 I
2 I
v
0
2
2
t
x
Общее решение уравнений
U U1 (t x v) U 2 (t x v ),
правая
бегущая волна
I I1 (t x v ) I 2 (t x v )
левая
бегущая волна
– волновые
уравнения
v 1
LC

15.

Уравнения Максвелла
Волны вдоль линии
В бегущей волне
Z LC
“+” – правая волна
“–” – левая волна
U ZI
– волновой импеданс (волновое сопротивление) линии
Коаксиальный кабель
C
2 0
, L 0 ln( R r )
ln( R r )
2
Z
1
0 0 ln( R r ) 60 ln( R r ) Ом
2
R
r
v
с

16.

Уравнения Максвелла
Волны вдоль линии
Согласование линии и нагрузки
Ul , Il
Uн , Iн
Zн
Граничные условия:
Uн Ul
Iн Il
Uн Zн Iн
U l Z l I l
U l Z l I l
1) Zн = Zl – нагрузка и линия согласованы между собой, отражение = 0.
Вся энергия поглощается Zн.
2) Zн ≠ Zl – нагрузка и линия не согласованы между собой, возникает
отражение.

17.

Уравнения Максвелла
Волны вдоль линии
Zг
Zн
Распространение сигнала
Zг
Zн
Отражение сигнала
от нагрузки (при Zн ≠ Zl)
Zг
Zн
Отражение сигнала от генератора
(при Zг ≠ Zl)
Результат многократных отражений – сильное искажение сигнала.

18.

Уравнения Максвелла
Излучение электромагнитных волн. Вибратор Герца
q( t )
I (t )
d (t )
– вибратор Герца (электрический диполь, момент которого
изменяется со временем)
q(t )
Поле, создаваемое вибратором:
1) r < = cT – поле, совпадающее с полем статического диполя
(электрического и магнитного)
2) r > = cT – волновая зона,
B лежит в широтных плоскостях, E – в меридиальных

19.

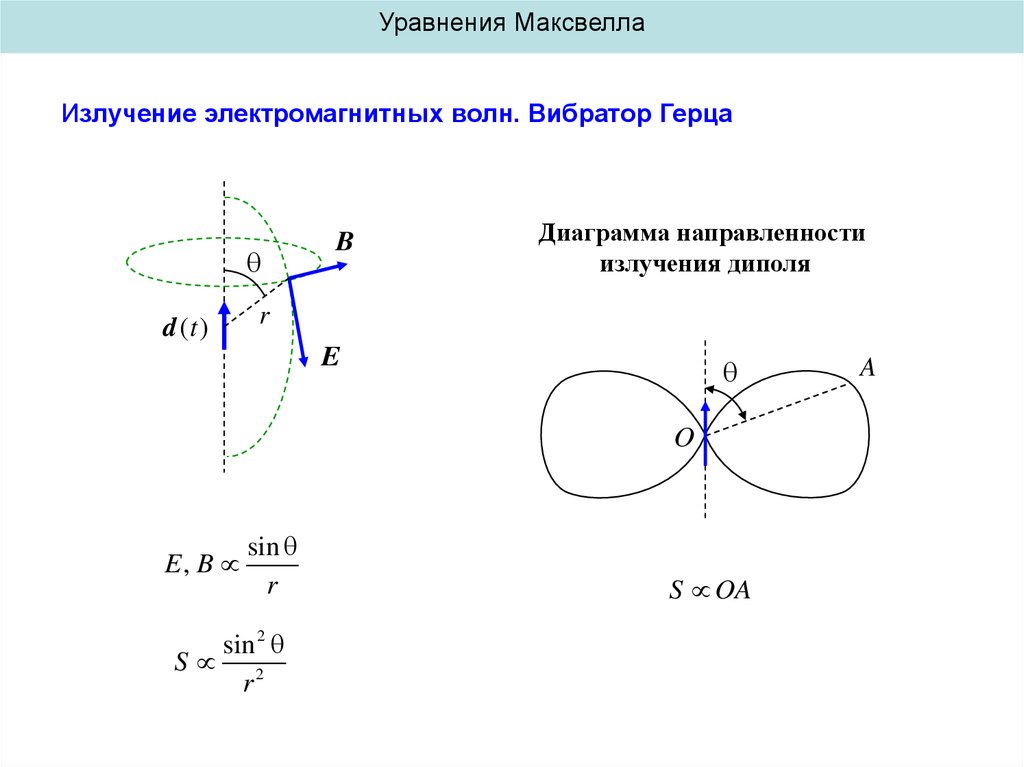
Уравнения Максвелла
Излучение электромагнитных волн. Вибратор Герца
d (t )
B
Диаграмма направленности
излучения диполя
r
E
O
E, B
sin
r
sin 2
S 2
r
S OA
A