Похожие презентации:
Комплексные числа. Алгебраическая форма комплексного числа
1.
КОМПЛЕКСНЫЕЧИСЛА
2.
Алгебраическаяформа
комплексного
числа.
3. Число, квадрат которого равен –1 называется мнимой единицей и обозначается i или j
2j 1
4. Степени мнимой единицы
j 1j 1j j j- 1 ( 11) 1
j j
j j j j 1 j j j
j 1
j 1
0
1
2
4
5
2
2
6
7
8
4
j j j j -j1 j
j j
3
2
9
j
10
1
j
11
j
5.
j4 k 0
1
j
4 k 1
j
j
4 k 2
1
j
4 k 3
j
j
4 k a
j
a
6.
326j
j
4 8 1 2
j
2
-1
326 4 81 2
157
(-j)
157
(-1)
j
4 39 1
(-1) j - j
1
157 4 39 1
(-2j) (-2) j
55
55
4 1 3 3
-2 (-j) 2
55
(-1) 2
55
55
55
j
3
j
55 4 13 3
7. Мнимым числом называется произведение мнимой единицы на действительное число.
Примеры: 2j;-5,3j;
2
j;
7
j 7
8. Комплексным числом называется число вида a+bj, где a и b-произвольные действительные числа, j – мнимая единица.
a –действительная часть КЧ;bj – мнимая часть КЧ
b – коэффициент мнимой части.
9.
z=a+bjалгебраическая
форма кч
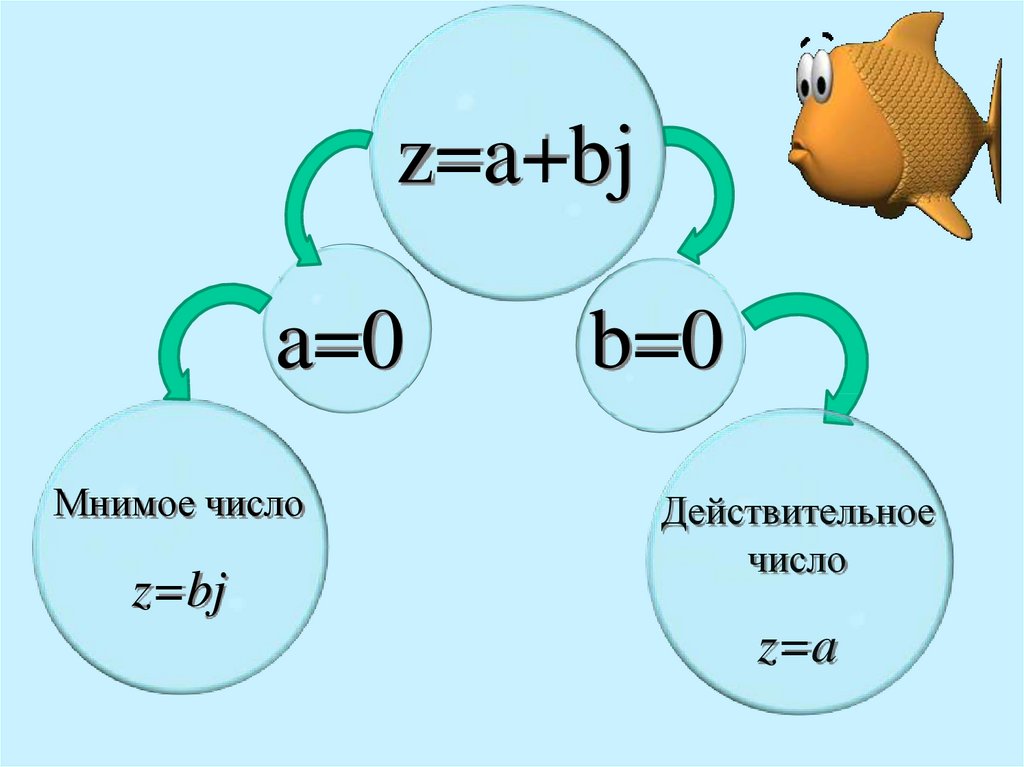
10.
z=a+bja=0
Мнимое число
z=bj
b=0
Действительное
число
z=a
11. Комплексные числа называются равными, если равны их действительные части и коэффициенты мнимых частей.
z1=z2 , если a1=a2 , b1=b212. КЧ равно нулю если равны нулю его действительная часть и коэффициент мнимой части.
z=0 , если a=0 , b=0z=0+0j
13. Модулем комплексного числа называется квадратный корень из суммы квадратов его действительной и коэффициента мнимой части.
ρ a b2
2
14. Найдите модуль кч:
z1=3+4jz2=2-7j
z3=3-4j
z4=-2-3j
ρ1 3 4
2
2
25 5
ρ2 2 ( 7) 53
2
2
ρ3 3 2 ( 4) 2 25 5
ρ4 (-2) ( 3) 13
2
2
15. КЧ называются сопряженными, если они различаются только знаком коэффициента мнимой части.
z=a+bjz=a- bj
Модули сопряженных
чисел равны.
16. Являются ли числа сопряженными?
7+3j и -7+3jнет
да
2-5j и 2+5j
2,4j+11 и -2,4j+11 да
8+6j и -8-6j нет
-7+5j и 7-5j нет
2+3j и 2+3j нет
9-4j и 4j+9 да
17. Каждому комплексному числу в комплексной плоскости ставится в соответствие одна, и только одна точка; или один, и только один
вектор с началом в началекоординат и концом в
точке с координатами
(a; b).
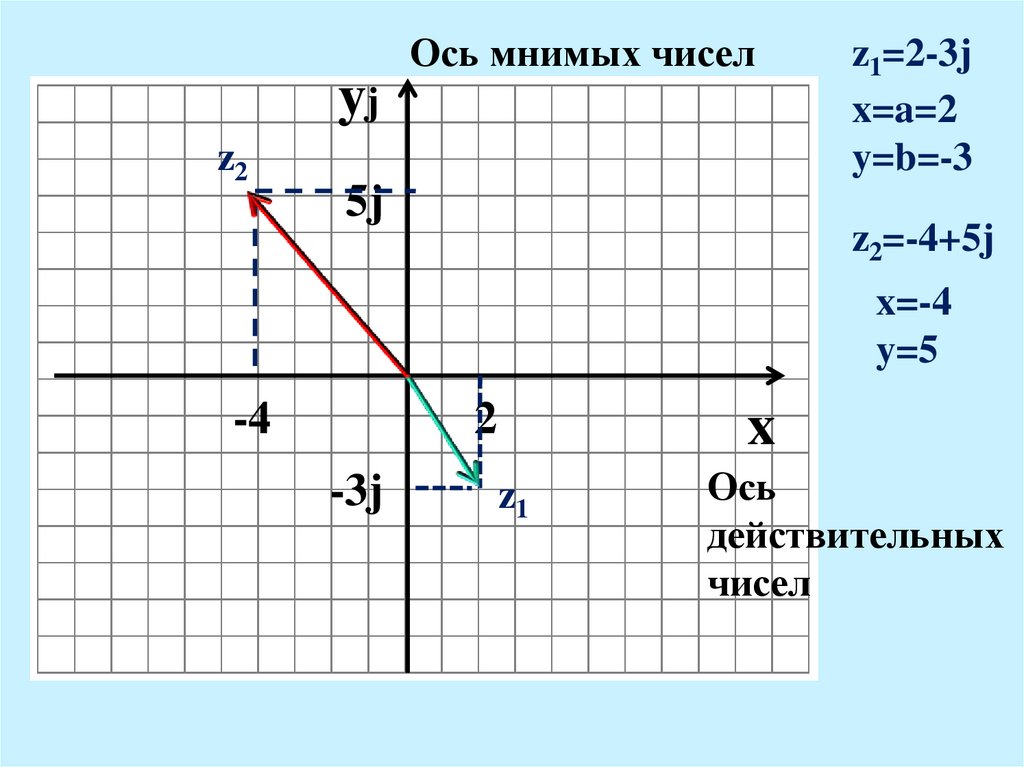
18.
Ось мнимых чиселyj
z2
5j
z1=2-3j
x=a=2
y=b=-3
z2=-4+5j
x=-4
y=5
-4
2
-3j
x
z1
Ось
действительных
чисел
19.
Геометрическая сумма комплексных чиселyj
z1=2-3j
z2=4+5j
z2
5j
z=z1+z2
z=z1+z2
2j
2
-3j
4
z1
6
x
По правилу
параллелограмма
z=6+2j
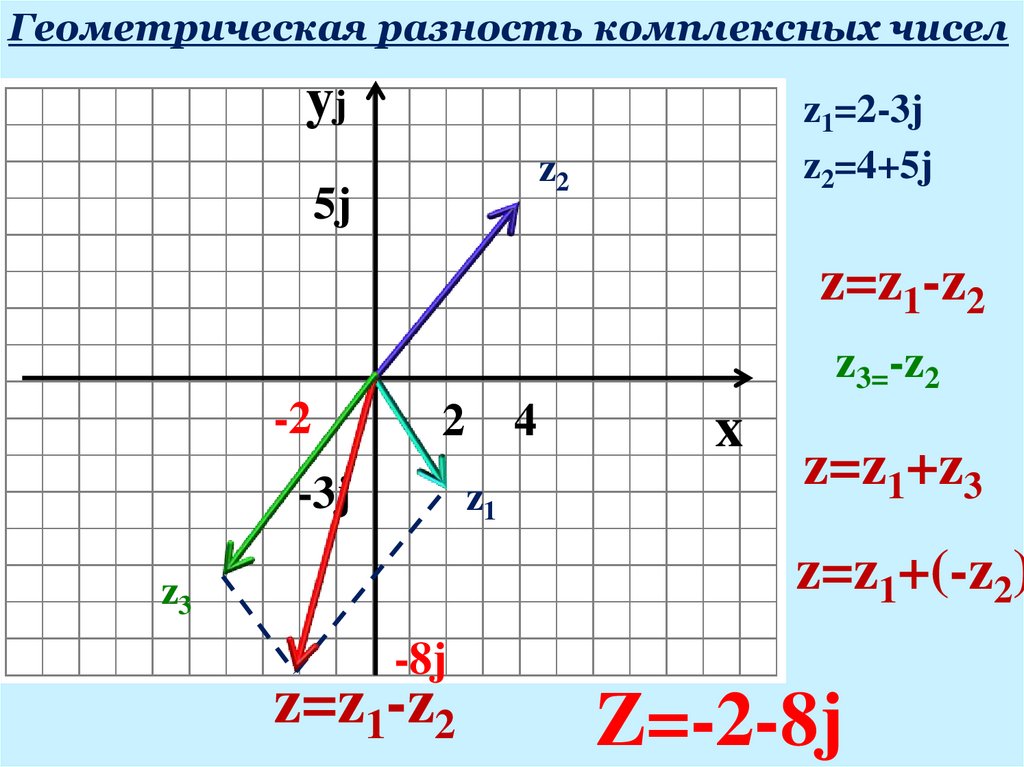
20.
Геометрическая разность комплексных чиселyj
z1=2-3j
z2=4+5j
z2
5j
z=z1-z2
z3=-z2
-2
2
-3j
4
z1
x
z=z1+z3
z=z1+(-z2)
z3
-8j
z=z1-z2
Z=-2-8j
21.
Действия надкомплексными
числами в
алгебраической
форме
22.
Складывать ивычитать КЧ можно
!
только в
алгебраической форме.
Извлечения корня в
алгебраической форме
не делают.
!
!
23.
z1=a1+b1 jz2=a2+b2 j
1) Сумма кч
z1+z2=(a1+b1j)+(a2+b2j)= a1+b1j+a2+b2j= (a1+a2)+ (b1+b2)j
2) Разность кч
z1-z2=(a1+b1j)-(a2+b2j)= a1+b1j - a2 - b2j= (a1 - a2)+ (b1 - b2)j
3) Произведение кч
z1·z2=(a1+b1j)·(a2+b2j)= a1a2+a1b2j+ a2b1j + b1b2j2=
=a1a2+a1b2j+ a2b1j - b1b2= (a1a2 - b1b2)+ (a1b2 + a2b1)j
24.
z1=3+5 jz2=2-6 j
1) Сумма
z1+z2=(3+5j)+(2-6j)= 3+5j+2-6j= (3+2)+ (5-6)j= 5 - j
2) Разность
z1-z2=(3+5j)-(2-6j)= (3 - 2)+(5+6)j=
2)+(5-(-6))j=
1+11j
3) Произведение
z1·z2=(3+5j)·(2-6j)= 3·2+3·(-6)j+ 2·5j + 5·(-6)j2=
=6-18j+ 10j +
– 30·(-1)=
30= (6 +30)+(-18+10)j= 36-8j
25.
z1=a1+b1 jz2=a2+b2 j
4) Деление кч Домножаем числитель и знаменатель на число
сопряженное знаменателю
(a1+b1j) ·(a2-b2j) a1a2-a1b2j+ a2b1j - b1b2j2
z1:z2=
=
=
=
2
a2+b2j (a2+b2j) ·(a2-b2j) a2a2-a2b2j+a2b2j - b2b2j
a1+b1j
=
a1a2-a1b2j+ a2b1j + b1b2
=
(a1a2+ b1b2)+ (a2b1-a1b2)j
a22+b22
=
a1a2+ b1b2
a22+b22
+
a22+b22
a2b1-a1b2
a22+b22
j
5) Возведение в степень производится по формулам
сокращенного умножения
=
26.
z1=3+5 jДомножаем числитель и знаменатель на число
сопряженное знаменателю
4) Деление
z1:z2=
=
z2=2-6 j
3+5j
2-6j
(3+5j) ·(2+6j)
=
(2-6j) ·(2+6j)
6+18j+ 10j + 30(-1)
=
=
40
+
28
40
j =-
22-
62j2
(6-30)+ (18+10)j
4+36
-24
=
3·2+3·6j+ 2·5j + 5·6j2
40
3
5
+
7
10
j = - 0,6+0,7j
=
=
27.
5)121 121 j 121 j 11 j
2
2
x1 11 j
x2 11 j
5 j
10 5 5 j 5 j
6)
5
j
2
( 1)
2 j j j j j
7)
z1=3
z2=5j
z1+z2= ?3+5j
z1=6
z2=-2j
z1+z2= ?6-2j
28. Свойства сопряженных чисел.
доказать самостоятельноСумма двух сопряженных чисел
есть число, равное 2а.
Разность двух сопряженных чисел
есть мнимое число, равное 2bj.
Произведение сопряженных чисел
есть квадрат их общего модуля.
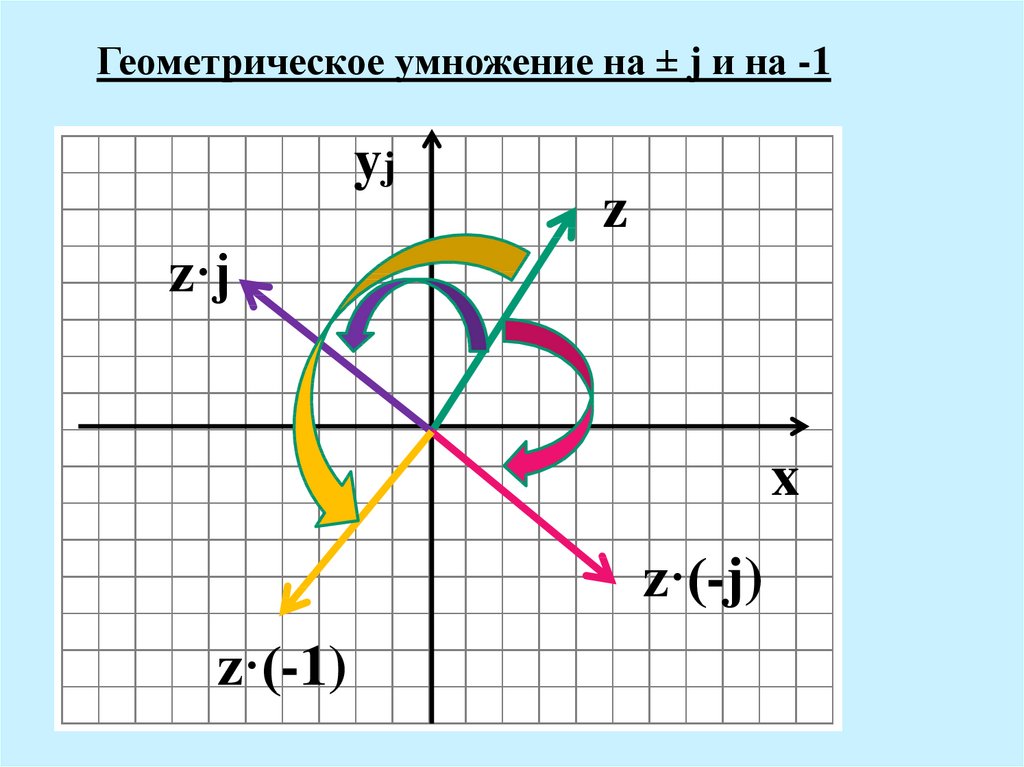
29.
Геометрическое умножение на ± j и на -1yj
z
z·j
x
z·(-j)
z·(-1)
30. Геометрическое умножение на ± j и на -1
Умножению числа на j (-j)соответствует поворот вектора на 900
в положительном (отрицательном)
направлении (против часовой стрелки).
Умножению числа на –1
соответствует поворот вектора на
1800.


























 Математика
Математика








