Диэлектрики в электрическом поле

1. Диэлектрики в электрическом поле

• Свободные и связанные заряды
Связанными зарядами называют заряды, входящие в состав атомов и
молекул, а также заряды ионов в кристаллических веществах с ионной
решеткой. Все остальные заряды называют свободными. Примерами
свободных зарядов могут служить электроны проводимости в металлах, ионы
в газах и электролитах.
Ионами называются атомы или молекулы, имеющие либо избыток, либо
недостаток электронов по сравнению с нормальным состоянием этих атомов
или молекул.
Электроны, оторвавшиеся от атомов при их ионизации, не всегда
присоединяются к другим атомам; часто они остаются свободными.
Диэлектриками называются вещества, в которых отсутствуют свободные
заряды (или их присутствие незначительно и этим присутствием можно
пренебречь в условиях рассматриваемой задачи).
В диэлектрике все заряды связаны.
В диэлектриках свободные заряды отсутствуют. Когда на диэлектрик
переходит свободный электрон, он тут же присоединяется к какому-либо атому
или молекуле.
1

2. Диполь

Диполь – система связанных противоположных зарядов. Если говорить более
точно, система двух одинаковых по величине,
но противоположных по знаку
l r r - плечом диполя (расстояние
зарядов называется диполем, а
между зарядами). При этом заряды не обязательно являются точечными, и
если они не точечные,
и
- радиус-векторы электрических центров зарядов, образующих
диполь.
r
r
Точечный диполь. Пусть размеры заряженных тел, образующих диполь, и
расстояние между ними (плечо диполя) малы по сравнению с расстоянием от
точки наблюдения до центра диполя. (Другими словами, последнее
расстояние так велико, что в условиях рассматриваемой задачи два
противоположных заряда можно считать слившимися в одну точку.) В этом
случае диполь называется точечным.
2

3. Дипольный момент или электрический момент диполя

pe ql
Дипольный
(1)
момент (электрический) определяется вектором
Здесь - l вектор, направленный вдоль оси диполя от отрицательного заряда к
положительному.
3

4. Поляризация диэлектриков

• Поляризация состоит в повороте осей жестких диполей вдоль E
диполь с моментом pe , помещенный во внешнее однородное
электрическое поле , действует пара сил с моментом
,
pe , E
. На
стремящаяся повернуть диполь в направлении напряженности поля.
Потенциальная энергия жесткого диполя, помещенного во внешнее
электрическое поле, равна Wpot pe E
Знак минус показывает, что устойчивым положением диполя,
соответствующим минимуму потенциальной энергии, является
вектора
расположение его
вдоль положительного направления
4
pe
E
.

5. Добавочное поле , созданное диполем, ослабляет внешнее поле.

Добавочное поле E add , созданное диполем, ослабляет внешнее поле.
Вектор поляризации
Молекула поляризованного диэлектрика может рассматриваться как диполь, то
есть как система связанных противоположных зарядов.
P
(r
) или
Мерой поляризации диэлектрика является
вектор поляризации
поляризованность в точке среды M (r )
и определяется по формуле
-
P( r )
p
ei
dV
dV
Здесь суммирование распространяется на все молекулы-диполи,
находящиеся в физически бесконечноdV
малом объеме
,
M
(r
)
содержащем
точку
.
i
pei
- дипольный момент
-й молекулы.
(2)
5

6. Потенциал поляризованного диэлектрика

V
r
Пусть молекулы-диполи распределены в объеме
.
Рассмотрим элемент объема dV , расположенный в точке с радиус-вектором
, как точечный диполь, электрический момент которого равен
pe P
(r )dV
Найдем потенциал, создаваемый этим диполем в точке наблюдения M (r ) .
Запишем приращение потенциала как для точечного заряда
т.з.(r r l ) т.з. (r r ) т.з. r r l o( l )
Если l 0 , то
d (r ) т. з. r r l
1
kq l kpe
r r
Здесь использовали
R r r ,
1
1
kP(r ) dV
r r
R
1
1
q
( ) , т.з.(r ) k
R
r
R
1
- градиент по штрихованным координатам.
R
6

7. Следовательно,

получаем после интегрирования
Рассмотрим действие оператора
1
(r ) k P(r ) dV
R
V
P 1 1
P P
R
R R
1 P 1
• Выразим из этого равенства
P P
R
R R
P(r )
1
• В результате имеем
dV P(r )dV
(r ) k
V
R
V R
P(r ) dS
P(r )
k
dV
R
R
V
S
.
Воспользовались теоремой Остроградского-Гаусса
S - граница области V
В выражении (3) поверхностный интеграл эквивалентен потенциалу
некоторого поверхностного распределения зарядов; объемный интеграл –
потенциалу объемного распределения зарядов. Соответствующие плотности
зарядов равны:
P
P
P
n
P
(3)
(4)
7

8. Плотности зарядов

P
• При неоднородном распределении дипольных моментов представляет
собой плотность тех зарядов, которые нескомпенсированы из-за
неоднородности распределения, а
есть плотность зарядов,
P
возникающих на поверхности ввиду отсутствия компенсирующих
соседей у тех диполей, концы которых лежат на этой поверхности
В общем случае потенциал поляризационных зарядов обоих
видов выражается соотношением:
P (r )dS
P (r )
(r ) k
S
R
V
R
dV
(5)
Вывод. Дипольные моменты, порожденные поляризацией вещества,
представляют собой разновидность источников поля .
Указанные дипольные моменты возникают в веществе под действием
электрического поля, и поведение вещества можно описать с помощью
вектора поляризации .
8

9. Уравнение Пуассона

• Так как источники электрического поля разделены нами на два вида,
то уравнение Пуассона принимает следующий вид:
2
1
E P
0
(6)
Плотность P согласно (4) выражена через дивергенцию поляризации
P , то формула (6) преобразуется к виду: P
E
0 0
(7)
Введем вектор электрической индукции D
, называемый также
электрическим смещением (термин, введенный еще Максвеллом):
D 0E P
(8)
Уравнение (6) можно записать теперь двумя способами:
total P
D
total 1
E
P
0
0
Ур-е Максвелла (9) удобно для расчетов, т.к. чаще всего известна
плотность свободных зарядов.
(9)
(10)
9

10. Теорема Гаусса для потока электрического смещения

С помощью теоремы Гаусса-Остроградского можно получить и
соответствующие интегральные соотношения:
D dS Q
S
Qtotal
E dS
(11.1) (11.2)
0
S
Q dV
Qtotal Q ( P)dV
VS
VS
Здесь S произвольная замкнутая кусочно-гладкая поверхность
внутри диэлектрика V
- объем, ограниченный поверхностью
S
(12)
S
D представляет собой лишь ту часть поля, которая создается свободными
зарядами.
Поле P создается только поляризационными зарядами.
Вектор E описывает поле, создаваемое как свободными,
так и связанными зарядами
10

11. Диэлектрическая проницаемость среды

Будем считать, что при не очень сильном
внешнем
поле в изотропном
диэлектрике вектор поляризации
P E
0
пропорционален напряженности поля.
10 9 Ф
0
36 м
называется электрической постоянной
D 0 1 E a E
( 8)
(14)
диэлектрической восприимчивостью среды
0
для вакуума
1
1
(13)
относительная диэлектрическая проницаемость
(15)
для вакуума
a 0 (1 )
a 0
абсолютная диэлектрическая проницаемость среды
(16)
11

12. Относительная диэлектрическая проницаемость

a
0
Абсолютная диэлектрическая проницаемость вакуума
(17)
a 0 0
Для большинства применяемых в технике диэлектриков
относительная диэлектрическая проницаемость находится в пределах
2 8
Вектор электрической индукции или электрическое
смещение равен
D 0 E
Замечание. Сказанное
относится
к изотропным диэлектрикам,
у которых векторы D, E , P
совпадают по направлению.
12

13. Классификация сред

Свойства среды по отношению к электрическому полю определяются
параметром a
.
Различают следующие среды.
Линейные, в которых параметр
a не зависит от величины электрического поля
нелинейные, в которых параметр a зависит от величины электрического поля
однородными называют диэлектрики,
параметр a которых не зависит от координат
Среды, у которых этот параметр является функцией координат,
называют неоднородными
Если свойства диэлектрика одинаковы по разным направлениям,
то его называют изотропным.
Соответственно среды, свойства которых различны по разным направлениям,
называют анизотропными.
В изотропных диэлектриках векторы
В изотропных диэлектриках
a
P, E
D, E
параллельны
- скалярные величины
В анизотропных этот параметр является тензором (линейным оператором).
D a E
13

14. Теорема Гаусса для различных сред

1
(
E
,
d
S
)
dV
S
V
0
1
( E, dS ) dV
S
0 V
-для линейной изотропной
однородной среды
(18)
(19)
-для вакуума
Для линейной изотропной среды в общем случае (r )
теорема Гаусса в дифференциальной форме имеет вид
div ( 0 (r ) E)
0div ( (r ) grad )
(20)
(21)
Минус в (21) возникает за счет появления потенциала
14

15. Кусочно-однородная среда

Рассмотрим случай кусочно-однородной среды. Пусть для
определенности имеется две различные среды, заполненные
однородными средами с различными
.
Условие сопряженности
Рассмотрим границу раздела двух диэлектриков
с относительными проницаемостями
1 и
Для элементарного контура
pqrs
2
,
расположенного по обе стороны границы раздела, запишем
закон электромагнитной индукции
Bn
(
E
,
d
l
)
S
t
pqrs
Bn нормальная составляющая индукции к площадке S
охваченной контуром интегрирования
(22)
,
15

16. Условие сопряженности

Распределение Bn в пределах малой площадки S принято
считать равномерным.
Такое же предположение примем и в отношении составляющих
напряженности на границах контура qr и ps
16

17. Условие сопряженности Сделанные предположения позволяют (22) записать в виде

Et1 l1 Et2 l2
Et1
Bn
( E , dl )
S
t
pq,rs
(23)
Et2 касательные составляющие вектора напряженности электрического
и
поля на отрезках l1
и
l2
При предельном переходе, когда контур стягивается к границе раздела
.
l
, имеем l1 l
.
l2 l
Длины отрезков qr
и ps
стремятся к нулю, также стремится к нулю и
площадь
Из (23) получаем условие
Et1 = Et2
S
(24)
На границе раздела диэлектриков касательные составляющие вектора
напряженности электрического поля равны.
17

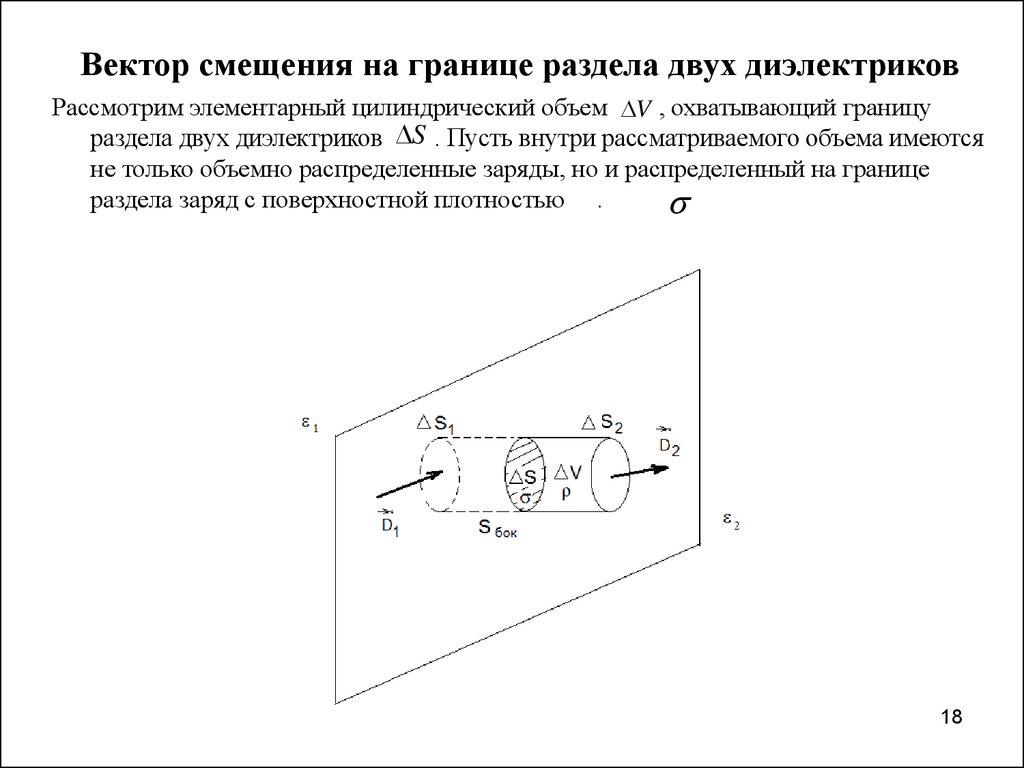
18. Вектор смещения на границе раздела двух диэлектриков

Рассмотрим элементарный цилиндрический объем V , охватывающий границу
раздела двух диэлектриков S . Пусть внутри рассматриваемого объема имеются
не только объемно распределенные заряды, но и распределенный на границе
раздела заряд с поверхностной плотностью .
18

19. В этом случае из постулата Максвелла следует

( D, dS ) S V
(25)
S
Пусть S поверхность цилиндра. Принимая условие постоянства
нормальных составляющих вектора D на малых торцевых
поверхностях цилиндра S , S2, перепишем (25) в виде
1
Dn1 S1
Dn2 S2
( D, dS ) S V
(26)
S бок
При стягивании цилиндра к границе раздела
S
объем цилиндра будет стремиться к нулю:
V 0
Также S1 S , S2 S , Sбок 0 Из (26) получаем
2
Dn
1
Dn
(27)
Условия (24) и (27) являются граничными условиями
на границе раздела диэлектриков
19