Потенциал и напряженность электрического поля на оси тонкого равномерно заряженного кольца

1. Потенциал и напряженность электрического поля на оси тонкого равномерно заряженного кольца

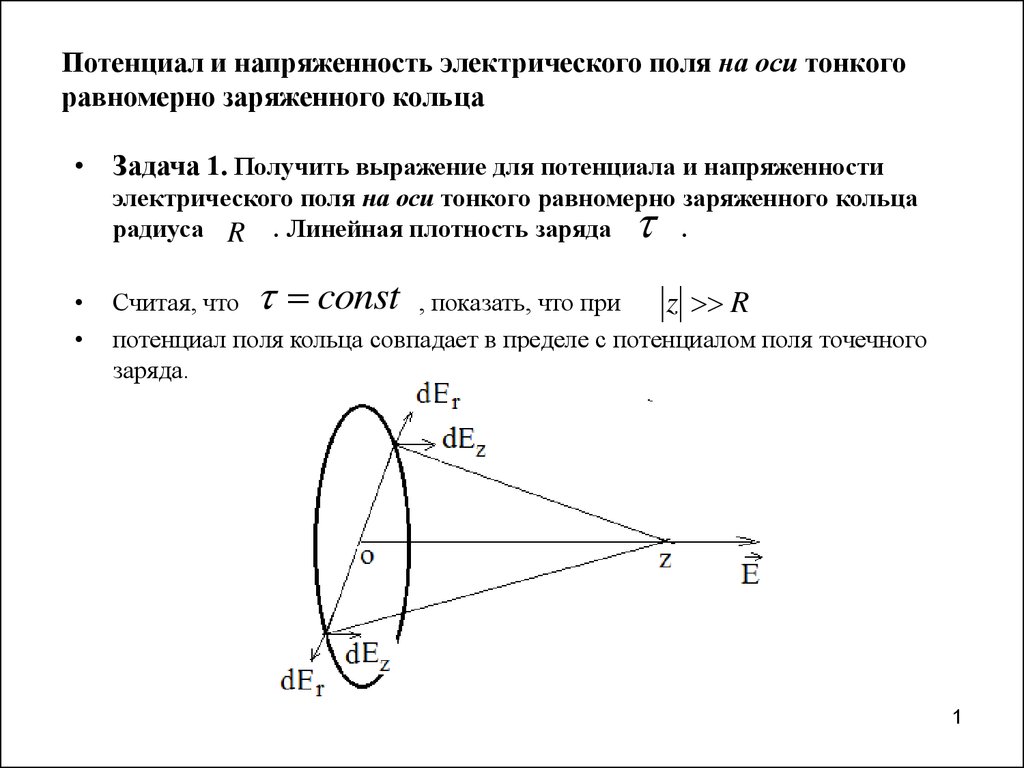
• Задача 1. Получить выражение для потенциала и напряженности
электрического поля на оси тонкого равномерно заряженного кольца
радиуса R . Линейная плотность заряда
.
const , показать, что при z R
Считая, что
потенциал поля кольца совпадает в пределе с потенциалом поля точечного
заряда.
1

2. Ведем цилиндрическую систему координат. Пусть ось совпадает с осью кольца и начало координат с центром кольца, – расстояние от центра коль

Ведем цилиндрическую систему координат. Пусть ось
с осью кольца и начало координат с центром кольца,
от центра кольца до точки наблюдения на оси.
dl
q
2 R
совпадает
– расстояние
Oz
z
dq dl Rd
– элемент длины тонкого кольца
Потенциал для точечного заряда
d
dq
4 0
( z)
2
0
Rd
R 2 z 2 4 0
R
4 0
1
1
R2 z 2
Напряженность поля кольца
d
1
R2 z 2
R
2 0
Ez ( z)
1
R2 z 2
d
R
dz 2 0
E z ( z ) E z ( z )
R
( z ) ( z )
z
2
z
2
3
2

3. Предельный случай

R
( z)
2 0
R
0
z
R
z
1
2
2
2 0
R z
1
2
R
1
z
z
R
R R
q 1
o
o
2 0 z
z 4 0 z
z
Использовали эквивалентную функцию
1 1
0
2
и
R
q
2
z R
Вывод. В предельном случае при
потенциал поля кольца совпадает с потенциалом поля точечного заряда
3

4. Задача 2. Получить выражение для напряженности электрического поля, создаваемое тонкой равномерно заряженной дугой окружности радиуса в е

Задача 2. Получить выражение для напряженности электрического
поля, создаваемое тонкой равномерно заряженной дугой окружности
радиуса R
в ее центре О . Линейная плотность заряда
.
4

5. В силу симметрии и принципа суперпозиции получаем, что

E x 0, E E y e y
• Для точечного заряда
dq dl Rd
1
Rd 1
dE y dE cos
cos
cos
2
2
4 0 R
4 0 R
dq
0
0
cos d
Ey 2
sin
2 0 R
2
0 4 R 0
2
5

6. Задача 3. Найти силу взаимодействия отрезка длиной , равномерно заряженного с линейной плотностью заряда с точечным зарядом , находящимся н

Задача 3. Найти силу взаимодействия отрезка длиной l ,
равномерно заряженного с линейной плотностью заряда
с
точечным зарядом q 0
, находящимся на продолжении отрезка
на расстоянии a от ближайшего его конца.
Пусть ось Ox проходит через отрезок и точечный заряд. Начало
координат совпадает с началом отрезка. Тогда координата точечного
заряда равна
a l
dq dx
.
dq q0
1
dF
4 0 (l a x) 2
q0
q0 a dt
dx
F
2
2
4
4
0 (l a x)
0 l a t
0
l
6

7. Задача 4. Ось равномерно заряженного диска радиуса совпадает с осью . Центр диска находится в начала координат. Диск заряжен равномерно с по

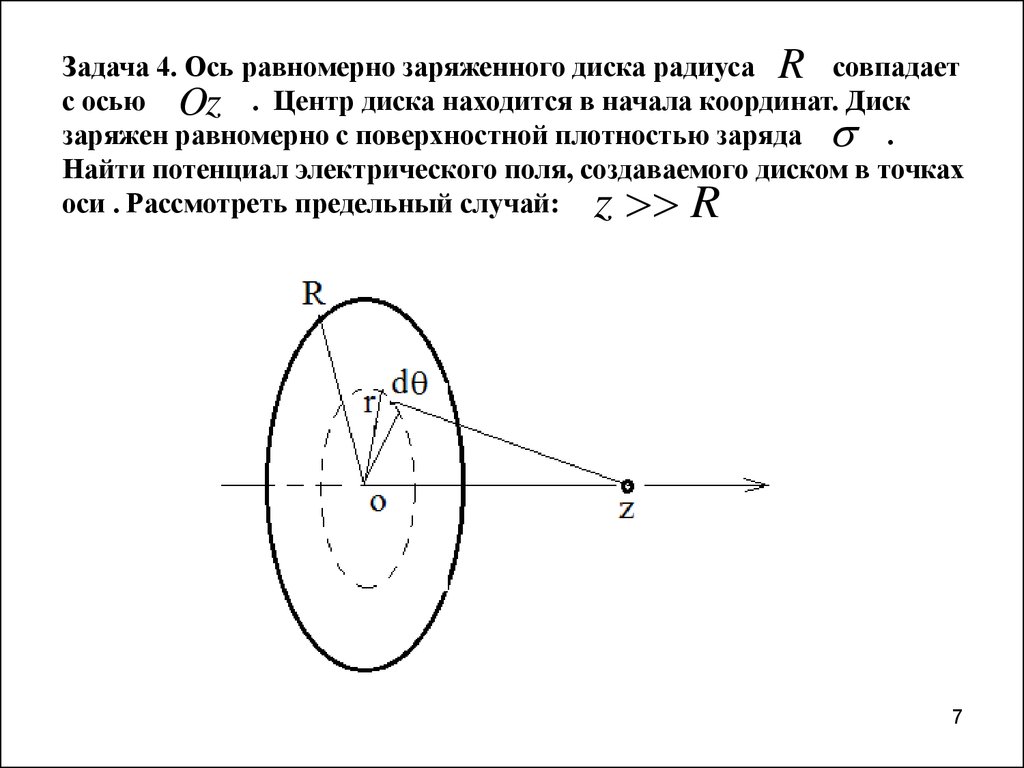
Задача 4. Ось равномерно заряженного диска радиуса R совпадает
с осью Oz . Центр диска находится в начала координат. Диск
заряжен равномерно с поверхностной плотностью заряда .
Найти потенциал электрического поля, создаваемого диском в точках
оси . Рассмотреть предельный случай:
z R
7

8. Введем цилиндрическую систему координат

• Рассмотрим точечный заряд
d
dq
4 0
dq dS rdrd
rdrd
1
4 0 r 2 z 2
r2 z2
1
2 R rdrd
2 R rdr
( z)
4 0 0 0 r 2 z 2 4 0 0 r 2 z 2
4 0
R2 z2
z2
dt
1/ 2
2 0
t
R z
2
2
z
8

9. Предельный случай

lim ( z ) lim
z
z 2
0
2
z
R
1 1
R 2 z 2 z lim
z
z 2
z
0
2
R2
z 1 R 2
R
1
q 1
o
2
2
z 4 0 z 16 0 z
z 2 2 z
z
0
• Вывод. При z потенциал электрического поля заряженного
диска совпадает с точностью до константы с потенциалом поля
точечного заряда.
9

10. Задача 5. Найти потенциал ограниченной цилиндрической поверхности радиуса и длиной с зарядом , равномерно распределенным по поверхности.

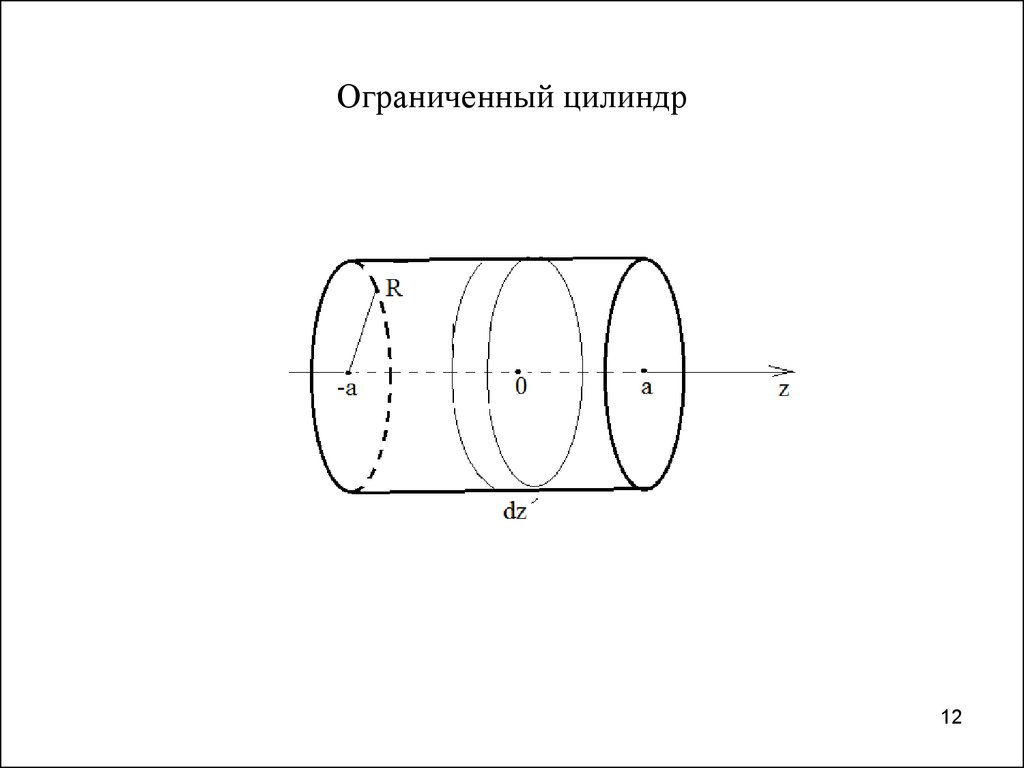
Задача 5. Найти потенциал ограниченной цилиндрической
поверхности радиуса
R и длиной 2a с зарядом q
равномерно распределенным по поверхности.
,
• Способ 1. Нахождение потенциала электрического поля, создаваемого
заряженной цилиндрической поверхностью через потенциал поля
заряженной окружности (тонкого кольца).
qкольца
кольца R
1
1
кольца( z )
, qкольца 2 R кольца
2
2
2
2
4 0 R z
2 0 R z
Рассматриваемая цилиндрическая поверхность – это совокупность
q
заряженных колец с зарядом dq
dz
2a
dq
q
2 R 2a
– заряд цилиндра
dz 2 Rd z
2a
z – координата кольца
10

11. Потенциала поля заряженной цилиндрической поверхности

( z)
a
q / 2a
4
0
a
1
R 2 ( z z ) 2
dz
a
a z (a z )2 R 2
q
d ( z z )
q
ln
8 a 0 a R 2 ( z z ) 2 8 a 0 a z (a z ) 2 R 2
Способ 2. Нахождение потенциала заряженной цилиндрической
поверхности через потенциал поля точечного заряда.
Цилиндрическая поверхность – это совокупность элементарных площадок
поверхности с зарядом
q
q
dq dS
2 R 2a
Rd dz
4 a
d dz
q 2 a
d dz
( z)
4 0 4 a 0 a R 2 ( z z ) 2
1
11

12. Ограниченный цилиндр

12