Похожие презентации:
Модель парной нелинейной регрессии
1.
Модели нелинейной регрессии№
домохозяйства
Среднедушевой
доход
Объем спроса, кг в
домохозяйства, месяц
тыс. д.е.
1
1
1,71
2
2
6,88
3
3
8,25
4
4
9,52
5
5
9,81
6
6
11,43
7
7
11,09
8
8
10,87
9
9
12,15
10
10
10,94
2.
14x
Спрос (y), кг
12
y
10
1
1,71
8
2
6,88
3
8,25
2
4
9,52
0
5
9,81
6
11,43
7
11,09
8
10,87
9
12,15
10
10,94
6
4
0
Доход (x),тыс. д.е.
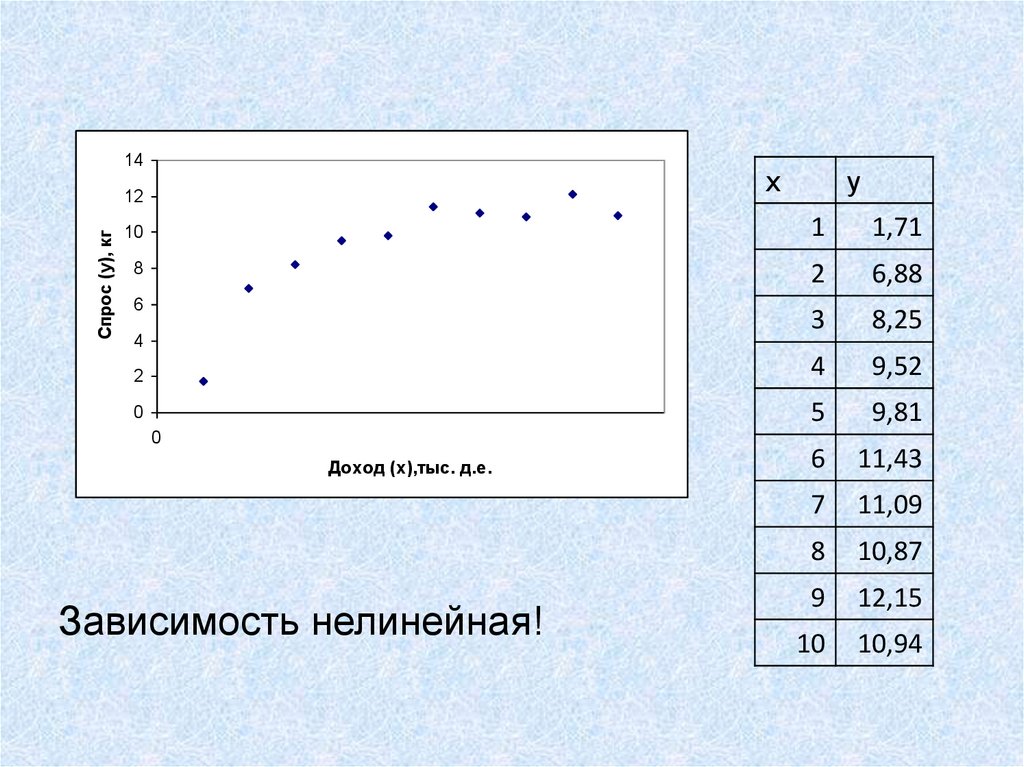
Зависимость нелинейная!
3.
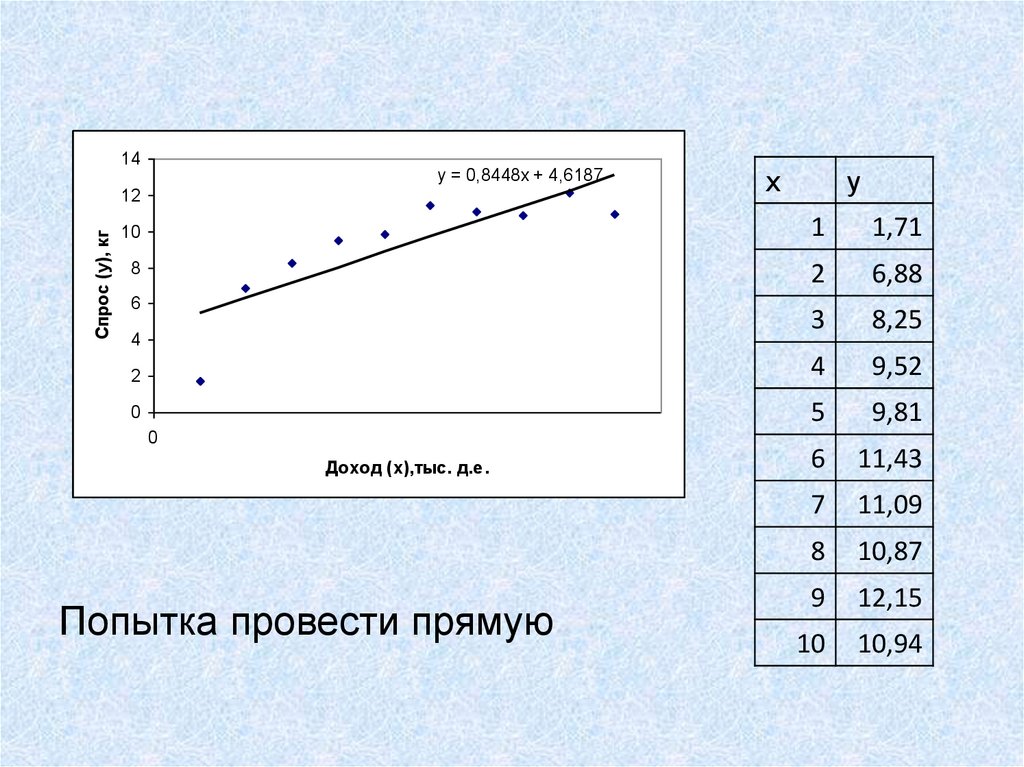
14y = 0,8448x + 4,6187
Спрос (y), кг
12
x
y
10
1
1,71
8
2
6,88
3
8,25
2
4
9,52
0
5
9,81
6
11,43
7
11,09
8
10,87
9
12,15
10
10,94
6
4
0
Доход (x),тыс. д.е.
Попытка провести прямую
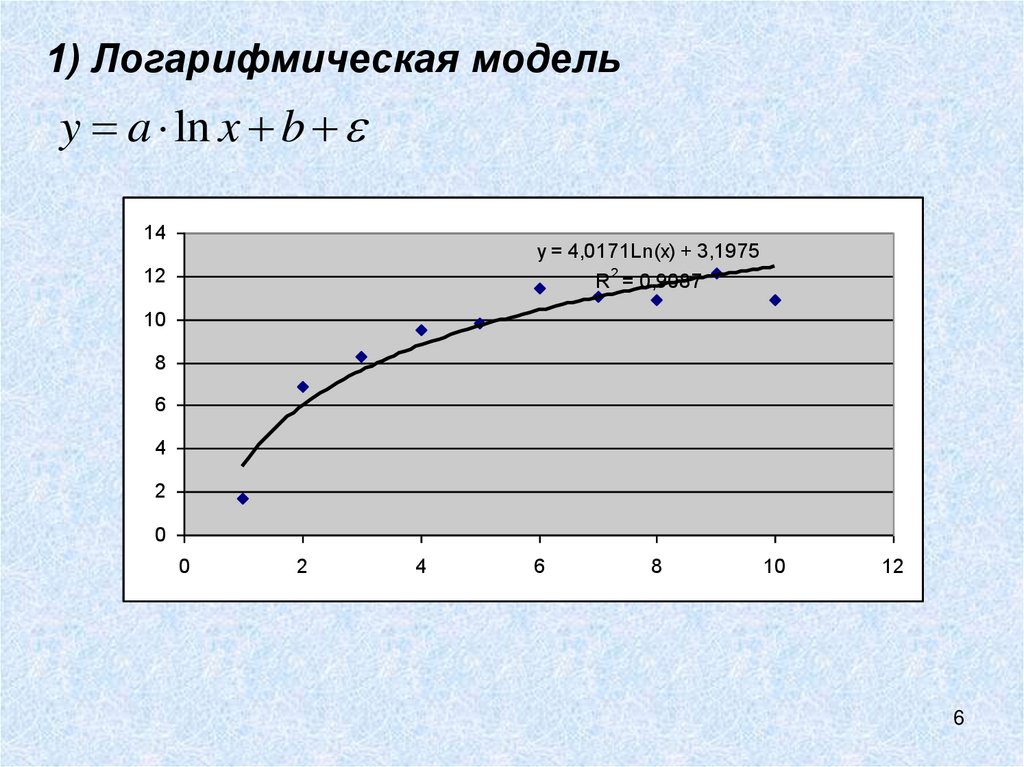
4. 1) Логарифмическая модель
y a ln x bДля оценки такой зависимости создаем столбец с ln(x)
4
5. 1) Логарифмическая модель
y a ln x bИспользуя сервис Анализ данных построим модель линейной регрессии,
используя в качестве зависимой переменной y, а в качестве независимой ln(x).
Y=4.017ln(x)+3.197
5
6. 1) Логарифмическая модель
y a ln x b14
y = 4,0171Ln(x) + 3,1975
12
2
R = 0,9087
10
8
6
4
2
0
0
2
4
6
8
10
12
6
7. 1) Логарифмическая модель
y a ln x bИнтерпретация коэффициента а: при увеличении х на 1% y увеличится на
а/100 единиц.
Y=4.017ln(x)+3.197
При увеличении дохода на 1% спрос на товар увеличится на
0,0417 единиц.
7
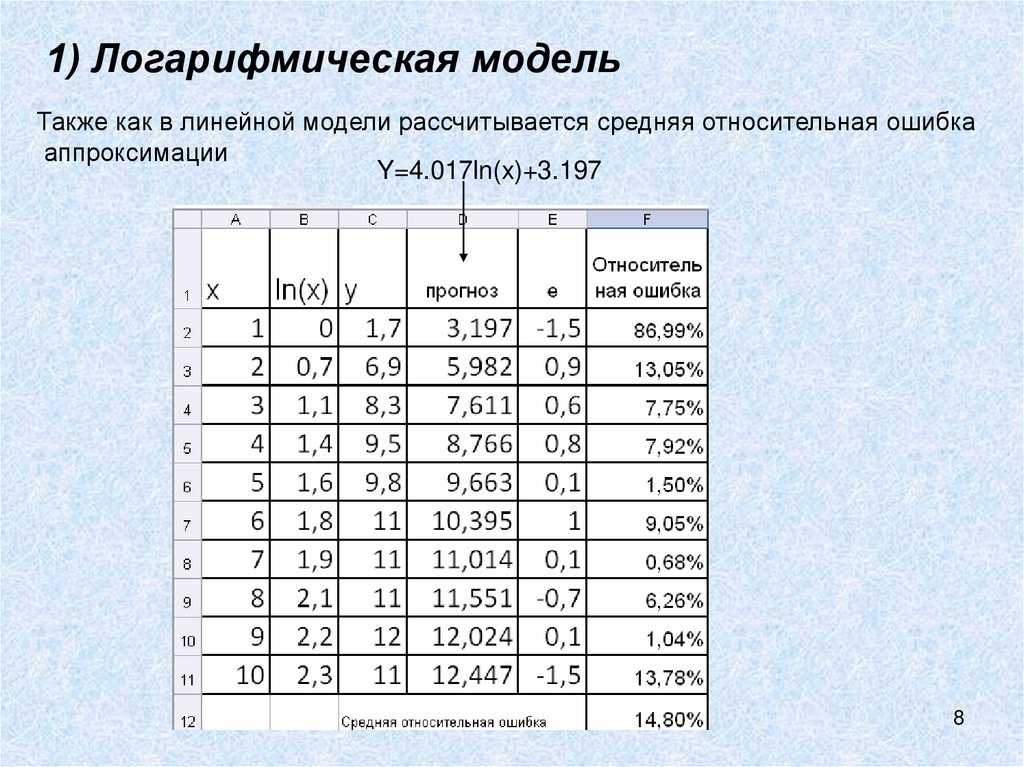
8. 1) Логарифмическая модель
Также как в линейной модели рассчитывается средняя относительная ошибкааппроксимации
Y=4.017ln(x)+3.197
8
9.
14x
Спрос (y), кг
12
y
1
1,71
2
6,88
3
8,25
4
9,52
2
5
9,81
0
6
11,43
7
11,09
8
10,87
9
12,15
10
10,94
10
8
6
4
0
Доход (x),тыс. д.е.
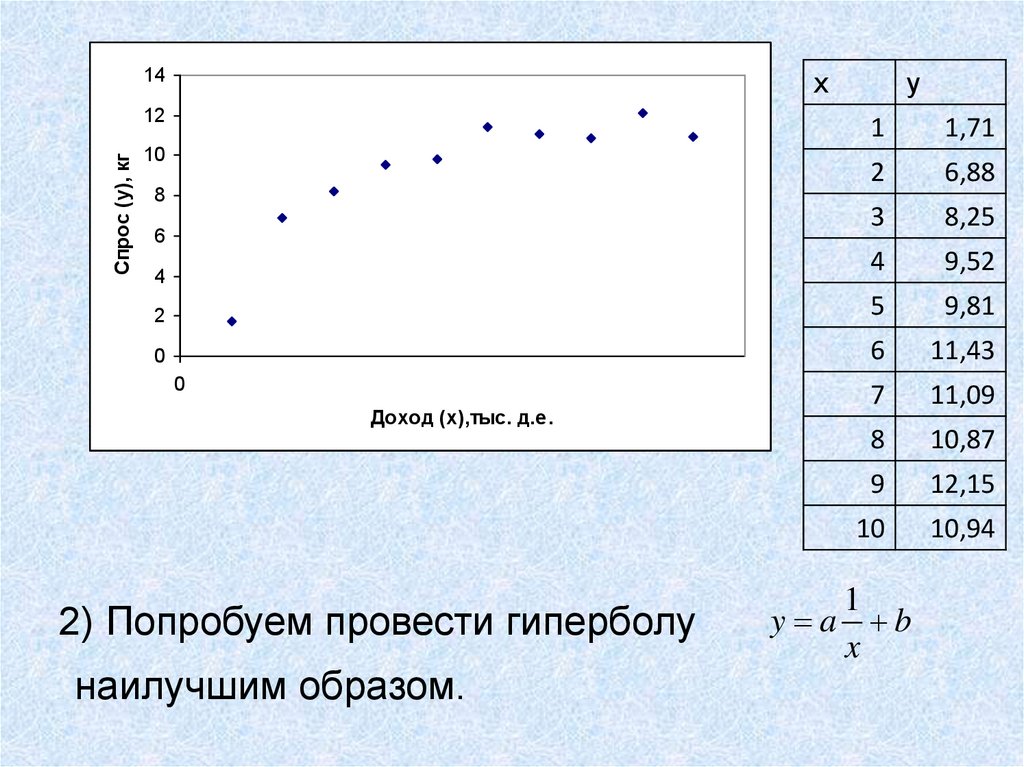
2) Попробуем провести гиперболу
наилучшим образом.
1
y a b
x
10.
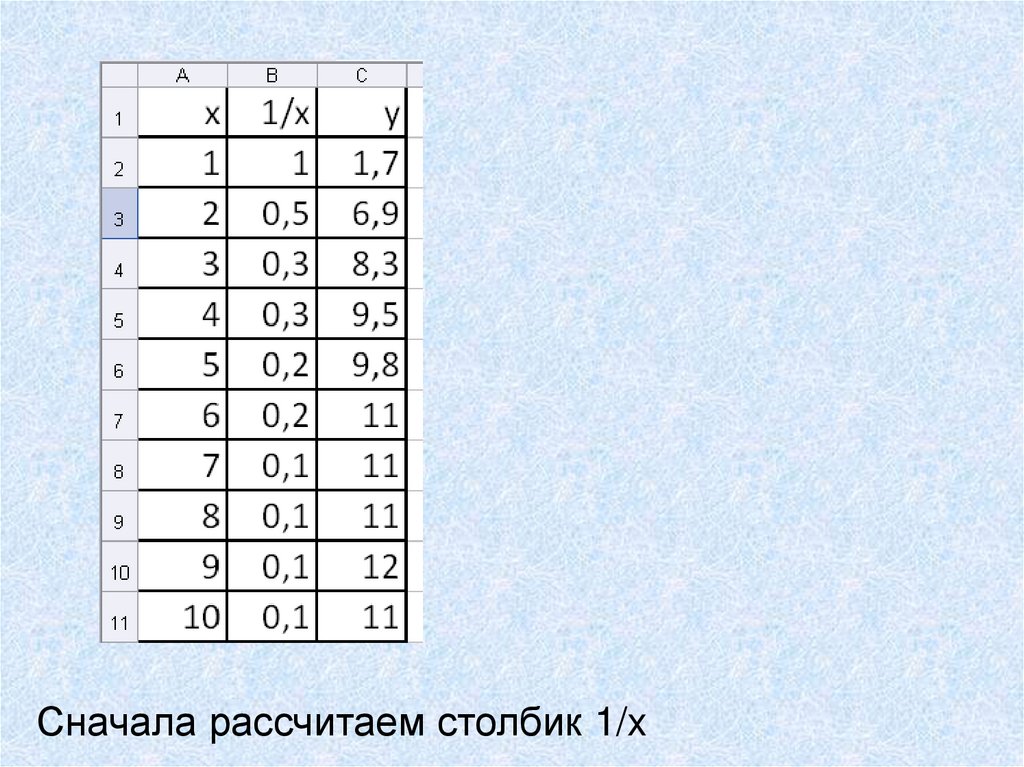
Сначала рассчитаем столбик 1/x11.
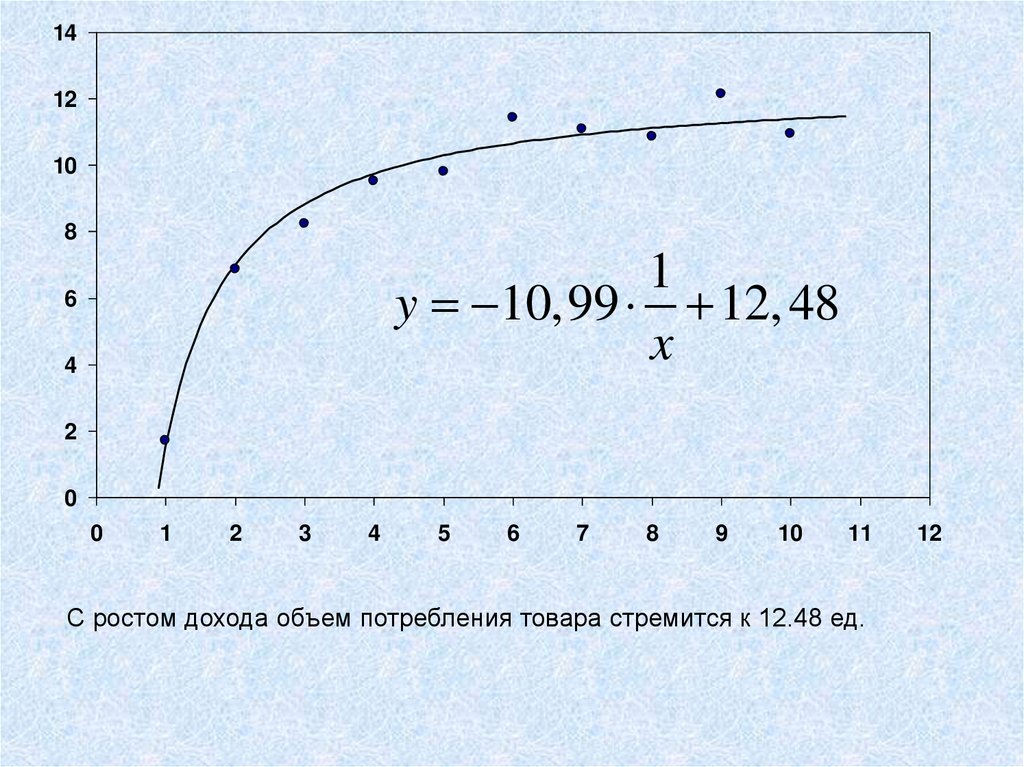
1y 10,99 12, 48
x
12.
1412
10
8
1
y 10,99 12, 48
x
6
4
2
0
0
1
2
3
4
5
6
7
8
9
10
11
С ростом дохода объем потребления товара стремится к 12.48 ед.
12
13.
Вычисляем ошибку аппроксимации1
y 10,99 12, 48
x
14. 3) Степенная модель
y bxa
Интерпретация коэффициента a – эластичность
зависимой переменной по объясняющей переменной
a показывает, на сколько процентов возрастает y при
возрастании x на 1%.
14
15. Степенная модель
y bxa
Сводится к линейной модели логарифмированием
ln y ln b a ln x
15
16. Степенная модель
Создаем столбцы с логарифмами16
17.
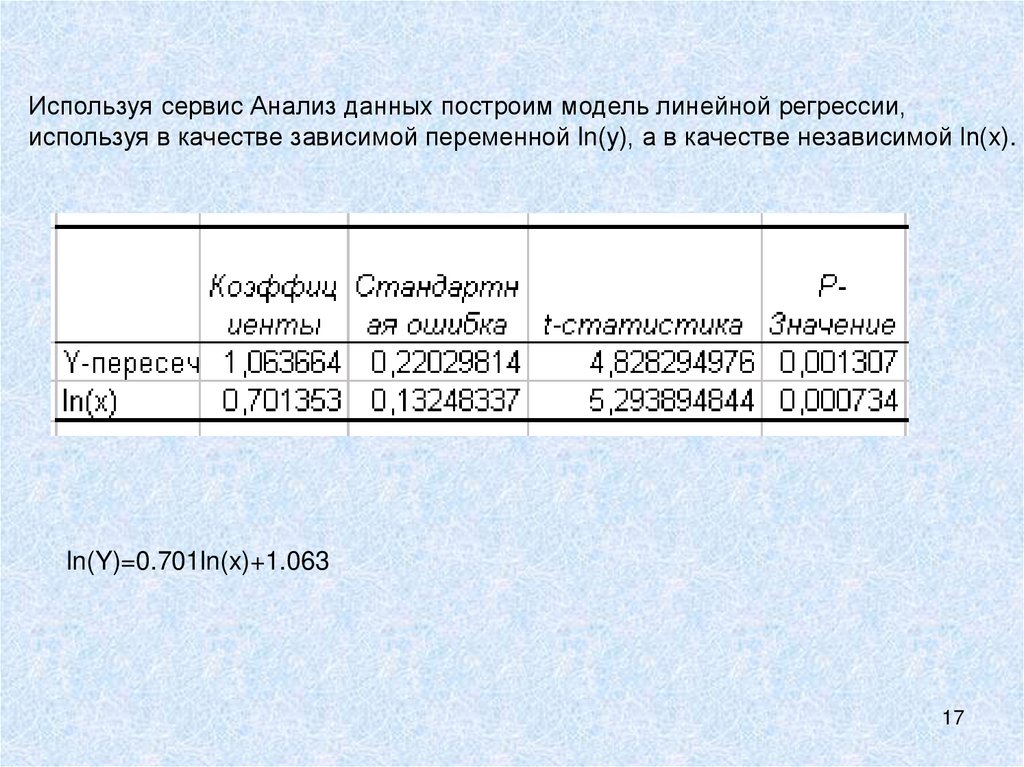
Используя сервис Анализ данных построим модель линейной регрессии,используя в качестве зависимой переменной ln(y), а в качестве независимой ln(x).
ln(Y)=0.701ln(x)+1.063
17
18.
Используя сервис Анализ данных построим модель линейной регрессии,используя в качестве зависимой переменной ln(y), а в качестве независимой ln(x).
ln(Y)=0.701ln(x)+1.063
ln y a ln x ln b
ln b 1.063 b exp(1.063) 2.9
18
19.
Используя сервис Анализ данных построим модель линейной регрессии,используя в качестве зависимой переменной ln(y), а в качестве независимой ln(x).
ln(Y)=0.701ln(x)+1.063
y bx
a
b exp(1.063) 2.9
y 2.9 x
0.701
19
20.
16y = 2,897x0,7014
14
R = 0,7779
2
12
10
8
6
4
2
0
0
2
y 2.9 x
4
6
8
10
12
0.701
20
21.
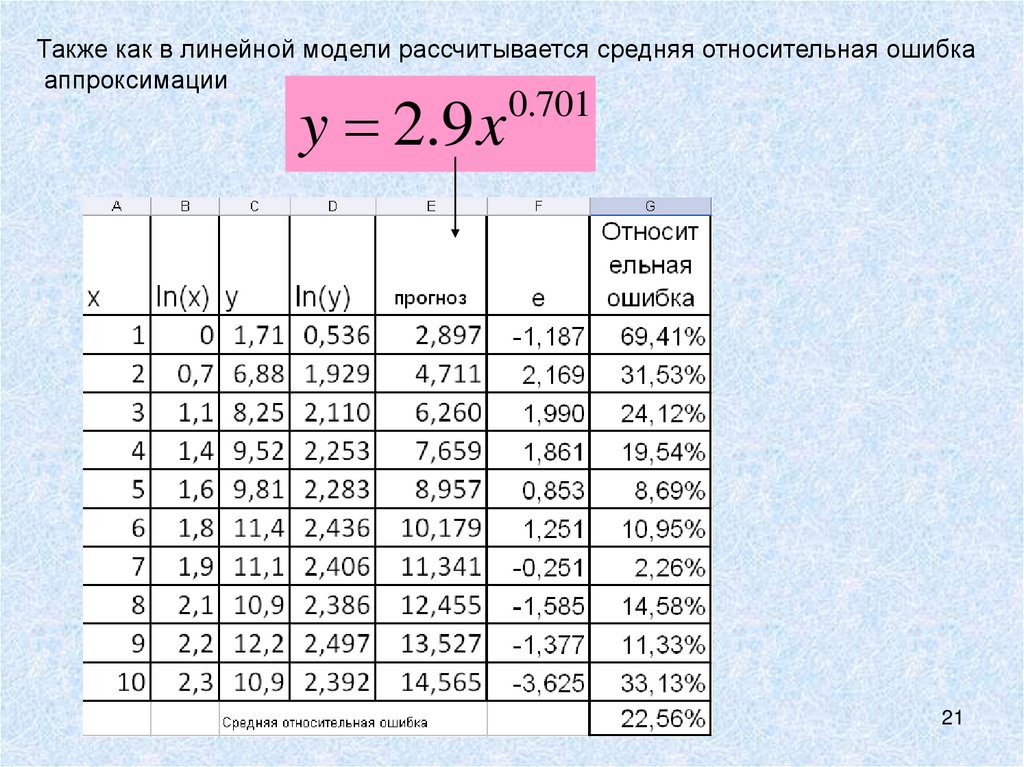
Также как в линейной модели рассчитывается средняя относительная ошибкааппроксимации
y 2.9 x
0.701
21
22.
1y 10,99 12, 48 - наилучшая функция спроса
x
в зависимости от дохода.
1)Выполнить прогноз потребления продукта
домохозяйством с доходом 4 тыс.д.е.
2) Имеется ли уровень насыщения для данного
продукта? Если да, найти его.
2)Найти предельную склонность к потреблению
продукта.
3) Найти эластичность спроса по доходу при
доходе 1000 д.е. и 10000 д.е.













 Математика
Математика








