Похожие презентации:
Анализ многосвязных динамических систем
1.
Анализ многосвязных динамических системОсновные вопросы лекции #2
1. Основные задачи анализа динамических систем
2. Нули системы и определяемые ими структурные свойства
3. Вычисления и идентификация типа нулей
4. Примеры ???
1
2.
Анализ многосвязных динамических систем.Ана́лиз (др.-греч. ἀνάλυσις «разложение, расчленение, разборка») — метод исследования,
характеризующийся выделением и изучением отдельных частей объектов исследования.
Под анализом понимается процесс исследования системы управления, основанный на ее декомпозиции
с последующим определением статических и динамических характеристик составляющих элементов,
рассматриваемых во взаимосвязи с другими элементами системы и окружающей средой.
Целью анализа системы управления является:
детальное изучение системы управления для более эффективного использования и принятия решения по ее
дальнейшему совершенствованию или замене;
исследование альтернативных вариантов вновь создаваемой системы управления с целью выбора наилучшего
варианта.
В отличие от анализа, когда исследуется заданная система управления, в процессе
синтеза необходимо создать новую систему путем определения ее рациональных или
оптимальных свойств и соответствующих показателей.
2
3.
К задачам анализа системы управления относятся:выделить анализируемую систему управления;
определение объекта анализа;
определить цели и задачи управления;
произвести первичную декомпозицию системы с выделением управляющей подсистемы
(органов управления), объектов управления (исполнителей) и окружающей среды.
структурирование системы;
Современные системы характеризуются
сложностью,
большим числом взаимосвязанных элементов,
большим числом функций,
сложными алгоритмами,
иерархичностью,
сложными структурными и функциональными взаимоотношения между элементами системы.
Целью решения задачи структурирования является детальное изучение системы
управления, установление связей и отношений между ее элементами.
определение функциональных особенностей системы управления;
определение количественных и качественных показателей системы управления;
оценивание и оценка эффективности системы управления;
обобщение и оформление результатов анализа.
3
4.
Фундаментальные свойства линейных динамических систем1. Устойчивость
2. Управляемость
3. Наблюдаемость
Устойчивость системы – способность системы после прекращения
внешнего воздействия по истечении некоторого времени
возвращаться к тому состоянию равновесия или вынужденного
движения, в котором она находилась до начала воздействия.
4
5.
Математический анализ свойства устойчивости системыопирается на вычисление характеристических корней (полюсов)
системы. Для нахождения полюсов составляется характеристическое
уравнение, а затем ищутся его корни.
Полюс системы это корень характеристического уравнения
( p) 0 .
SISO:
MIMO:
На устойчивость скалярной системы оказывают влияние все
полюсы. При этом
Re i 0 i 1, n – система устойчива;
если
если
если
i Re i 0,
i Re i 0,
i 1, n система нейтральная;
i 1, n система неустойчива.
5
6.
Иллюстрации устойчивости\неустойчивости6
7.
Управляемость характеризует принципиальную возможностьизменения состояния системы с помощью входных сигналов.
Динамическая система называется управляемой, если
существуют управляющие сигнала u(t ) , позволяющие перевести ее
за конечное время T в любое наперед заданное состояние
x(T ) Rn .
Критерий Калмана: для полной управляемости динамической
системы необходимо и достаточно, чтобы матрица управляемости
имела полный ранг:
rank R rank B AB A2 B ... An 1B n .
7
8.
Наблюдаемость характеризует принципиальную возможностьопределения состояния системы по наблюдениям за ее входными и
выходными сигналами u(t ) , y (t ) на конечном интервале времени
0 t T .
Критерий Калмана: для полной наблюдаемости динамической
системы необходимо и достаточно, чтобы матрица наблюдаемости
имела полный ранг: rank D rank C T (CA)T (CA2 )T ...(CAn 1 )T n
Рудольф Калман
По теореме о канонической декомпозиции Р. Калмана для линейных
динамических систем любую систему S можно рассматривать как
прямую сумму следующих четырех подсистем: полностью
управляемую и наблюдаемую подсистему S11 ; полностью
управляемую, но ненаблюдаемую подсистему S10 ; полностью
неуправляемую, но наблюдаемую подсистему S 01 ; полностью
неуправляемую и ненаблюдаемую подсистему S00 .
8
9.
Анализ линейных МСУ. Вычисление характеристик.Характеристики
Импульсная функция\характеристика
Переходная функция\характеристика
Частотные характеристики
Быстродействие (время переходного процесса)
Динамическая точность (перерегулирование)
Статическая точность
Запасы устойчивости (по амплитуде и по фазе)
и т.д.
Все характеристики для линейной МСУ вычисляются по правилам и алгоритмам для односвязных систем,
НО для каждого канала управления, для каждой взаимосвязи ОТДЕЛЬНО.
9
10.
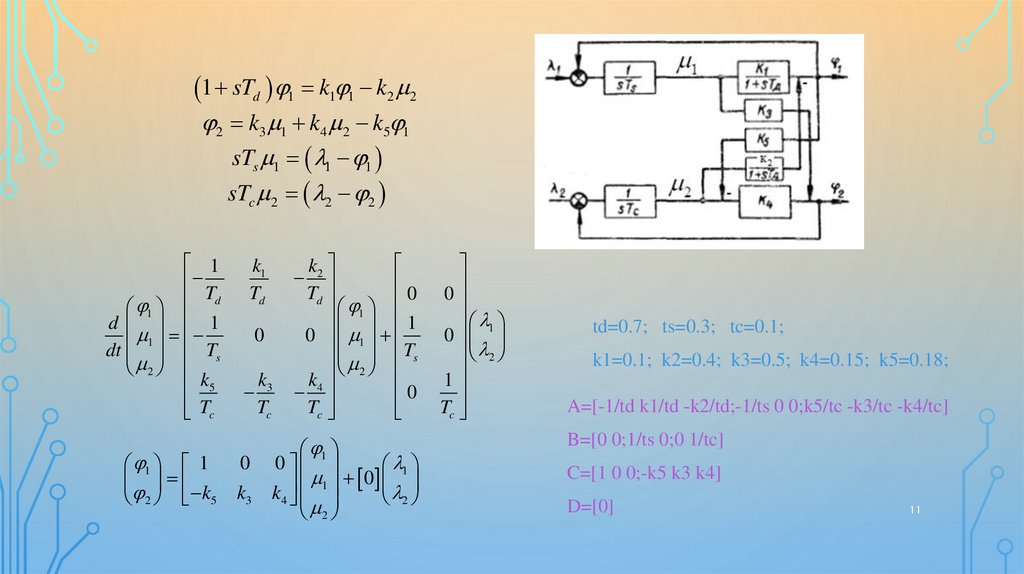
Пример.Турбореактивный двигатель с форсажной камерой (ТРДФ)
[Морозовский В.Т.]
В двигателе регулирование скорости вращения вала
турбины осуществляется посредством изменения подачи
топлива в двигатель, а регулирование температуры газа
посредством изменения подачи топлива в форсажную
камеру.
Математическая модель ТРДФ (полученная при целом ряде
допущений и ограничений)
объект
И-регулятор
1 sTd 1 k1 1 k2 2
2 k3 1 k4 2 k5 1
sTs 1 1 1
sTc 2 2 2
1 - скорость вращения; 2 - температура газа;
1 - расход топлива в основной камере сгорания;
2 - расход топлива в форсажной камере;
Td - постоянная времени двигателя;
1 2 - заданные значения скорости и температуры
10
11.
1 sTd 1 k1 1 k2 22 k3 1 k4 2 k5 1
sTs 1 1 1
sTc 2 2 2
1
T
1 d
d 1
1
dt Ts
2
k5
Tc
1 1
k
2 5
k1
Td
0
0
k3
k2
Td
0
1
1
0 1
Ts
2
k4
0
Tc
k3
Tc
1
0
1
0
k4 1
2
2
0
1
0
2
1
Tc
td=0.7; ts=0.3; tc=0.1;
k1=0.1; k2=0.4; k3=0.5; k4=0.15; k5=0.18;
A=[-1/td k1/td -k2/td;-1/ts 0 0;k5/tc -k3/tc -k4/tc]
B=[0 0;1/ts 0;0 1/tc]
C=[1 0 0;-k5 k3 k4]
D=[0]
11
12.
A = -1.4286 0.1429 -0.5714-3.3333
0
B=
0
1.8000 -5.0000 -1.5000
eig(A)
0
3.3333
C=
0
1.0000
0
0 10.0000
D= 0
0
0
-0.1800 0.5000 0.1500
ans =
-0.0185 + 1.8816i
-0.0185 - 1.8816i
-2.8916 + 0.0000i
From input 1 to output...
0.4762 s + 10.24
sys=ss(A,B,C,D)
tfsys = tf(sys)
1: ---------------------------------
=W11
s^3 + 2.929 s^2 + 3.648 s + 10.24
1.667 s^2 + 2.295 s - 5.096e-16
2: ---------------------------------
=W12
s^3 + 2.929 s^2 + 3.648 s + 10.24
12
13.
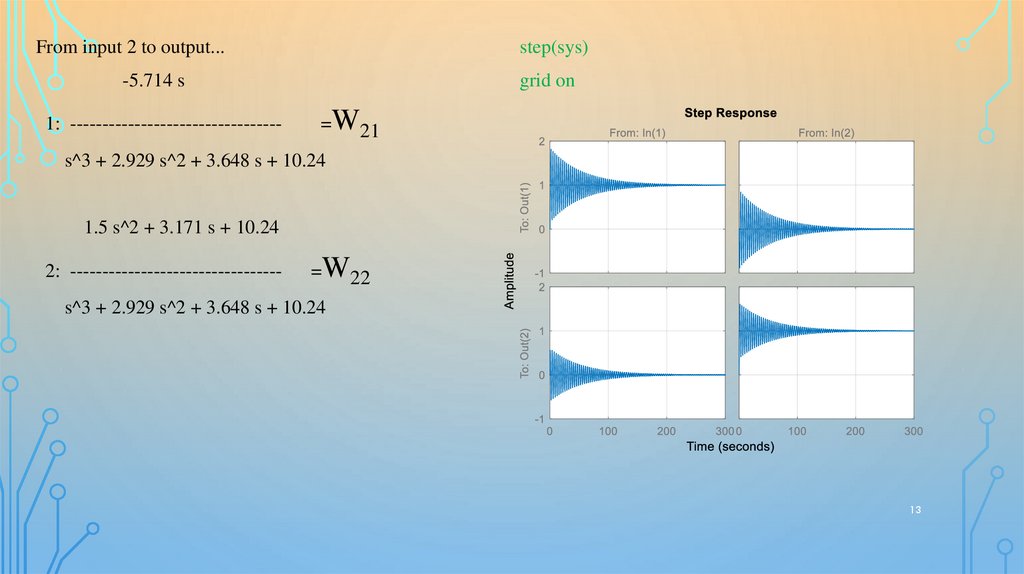
From input 2 to output...step(sys)
-5.714 s
1: ---------------------------------
grid on
=W21
s^3 + 2.929 s^2 + 3.648 s + 10.24
1.5 s^2 + 3.171 s + 10.24
2: ---------------------------------
=W22
s^3 + 2.929 s^2 + 3.648 s + 10.24
13
14.
Структурные свойства динамических системНули системы и определяемые ими структурные свойства
x1 a11
d x2 a21
dt ... ...
xn an1
... a1n x1 b11 b12
... a2 n x2 b21 b22
... ... ... ... ...
... ann xn bn1 bn 2
a12
a22
...
an 2
y1 c11 c12
y c
c22
2 21
... ... ...
ym cm1 cm 2
cn x1
... c2 n x2
.
... ... ...
... cmn xn
...
X (t ) AX (t ) BU (t ),
X (0) X 0 ,
Y (t ) CX (t ),
Y ( p) Fyu ( p)U ( p)
где
... b1s u1
... b2 s u2
,
... ... ...
... bns us
Fyu ( p) C pI A B
1
bmij p m ... b1ij p b0ij bij ( p )
F ( p ) ij n
ij
ij
ij
an p ... a1 p a0 aij ( p )
u
y
14
15.
Согласно классическому определению нулями системы с однимвходом и выходом называются корни полинома b( p) числителя скалярной передаточной функции
Классический нуль – это такое комплексное число a j , при
котором передаточная функция обращается в нуль.
Это означает, что при подаче на вход системы сигнала вида eat
реакция на ее выходе после окончания переходного процесса будет
отсутствовать.
Нулями системы называют корни полиномов, стоящих в числителе
передаточной функции.
Конечными нулями принято называть нули системы, принимающие
конечные значения комплексных частот.
Минимально-фазовым нулем принято
отрицательной действительной частью.
называть
нуль
с
15
16.
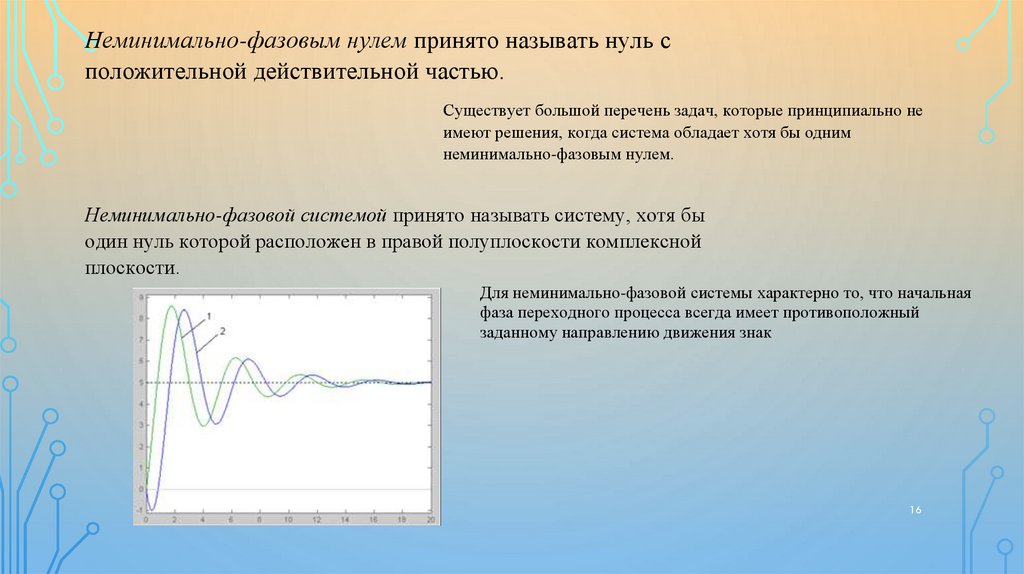
Неминимально-фазовым нулем принято называть нуль сположительной действительной частью.
Существует большой перечень задач, которые принципиально не
имеют решения, когда система обладает хотя бы одним
неминимально-фазовым нулем.
Неминимально-фазовой системой принято называть систему, хотя бы
один нуль которой расположен в правой полуплоскости комплексной
плоскости.
Для неминимально-фазовой системы характерно то, что начальная
фаза переходного процесса всегда имеет противоположный
заданному направлению движения знак
16
17.
По влиянию на динамические свойства системы, а также поустойчивости к различным воздействиям на систему, нули
многосвязных систем могут быть классифицированы следующим
образом:
Обычные нули это нули числителей скалярных функций
элементов матричной передаточной функции
bm p m ... b1 p b0 b( p)
F ( p)
n
ij
an p ... a1 p a0 a ( p )
u
y
17
18.
Обычный нуль многомерной системы — это такое значениекомплексной частоты a , при котором передача гармонического (экспоненциального) сигнала от входа к выходу блокируется.
Блокирование системой входного сигнала означает отсутствие на
выходе системы вынужденной составляющей, которая определяет
установившуюся реакцию системы.
Структурными свойствами обычные нули не обладают.
Передаточные нули. Нуль передачи (передаточный нуль)
соответствуют значению комплексного числа a , при котором
происходит уменьшение ранга матричной передаточной функции.
Передаточные нули вызывают «запирание» столбца или строки
матричной передаточной функции целиком, но для входного сигнала
с определенной частотой и амплитудой (точнее, с определенным
распределением воздействий на входы).
18
19.
Отличие «многомерного» нуля от классического заключается в том,что скалярная система не пропускает на выход все входные сигналы,
пропорциональные eat , в многомерном же случае существуют
входные сигналы, пропорциональные eat , которые передаются на
выход.
Передаточные нули вызывают «запирание» столбца или строки
матричной передаточной функции целиком, но для входного сигнала
с определенной частотой и амплитудой (точнее, с определенным
распределением воздействий на входы).
Возникающая линейная зависимость, например, столбцов
матричной передаточной матрицы приводит к тому, что будет
существовать такой входной сигнал с определенной частотой и
амплитудой, при котором на всех выходах одновременно имеются
нули.
19
20.
Развязанные нули. Понятие развязанного нуля связано с наличиемнеуправляемой (ненаблюдаемой) подсистемы. Развязанные по входу
нули совпадают с неуправляемыми полюсами, а развязанные по выходу нули – с ненаблюдаемыми полюсами системы.
Развязанные нули вызывают «запирание» строки матричной
передаточной функции по выходу, столбца по входу, но на
произвольных сигналах.
Нулем, развязанным по входу, называется комплексная частота
p kPвх , при которой уменьшается строчный ранг матрицы
Rid ( p) pI n A, B
или, что равносильно, обнуляется один или более столбцов матрицы
Fxu ( p)
P
Поскольку при p kвх один и более скалярных входов перестают
влиять на поведение системы, то система частично теряет
управляемость и сигналы с комплексной частотой kPвх не воздействует
на систему.
20
21.
Нулем, развязанным по выходу, называется комплексная частотаp kPвых , при которой уменьшается столбцовый ранг матрицы
или, что равносильно, обнуляется одна или более строк матричной
функции Fyx0 ( p) .
Так как при p kPвых система теряет наблюдаемость, то комплексная
частота aod никогда не появится на выходе системы.
На этой частоте один и более соответствующих выходов системы
обнуляются, независимо от амплитуды входных сигналов.
Нулем, развязанным по входу-выходу, называют комплексные
числа p kP , при которых уменьшаются как ранг матрицы Rid ( p ) , так
и ранг матрицы Rod ( p ) .
21
22.
Наличие развязанных нулей всегда связано с неуправляемостью иненаблюдаемостью системы:
наличие развязанных по входу нулей означает, что система
неуправляема (не полностью управляема);
наличие развязанных по выходу нулей означает, что система
ненаблюдаема (не полностью наблюдаема);
наличие развязанных по входу и выходу нулей означает, что
система не управляема и не наблюдаема одновременно.
Совокупность развязанных и передаточных нулей принято называть
системными нулями и связано это с тем, что регулярные законы
управления не могут изменить положения этих нулей.
22
23.
Инвариантные нули. Инвариантные нули вызывают «запирание»системы при определенном сочетании входного сигнала и начальных
условий.
Инвариантные нули это комплексные частоты p иk , на которых
происходит взаимно компенсирующее влияние входного сигнала и
ненулевых начальных условий.
Это означает, что при определенном сочетании входных сигналов и
ненулевых начальных условий в многосвязной системе происходит
понижение ранга матричной передаточной функции.
Поскольку выходной сигнал формируется по правилу
следовательно, Fyu ( иk )u( иk ) Fyx0 ( иk ) x0 ( иk ) 0 для фиксированной
пары (u и , x0и ) .
23
24.
Инвариантным нулем называется комплексная частота p иk ,при которой ранг матрицы Розенброка становится меньше
номинального n min(s, m) .
Множество инвариантных нулей содержит полное множество передаточных нулей и часть развязанных нулей.
Свойства нулей линейных динамических систем
Одним из замечательных свойств нулей является их
инвариантность к различным эквивалентным преобразованиям
объекта, таким как замена базиса в пространстве состояний,
невырожденное преобразование входов и выходов, замыкание объекта
обратными связями по состоянию и выходу.
Рассмотрим невырожденную замену переменных состояния
X TX , в результате которой матрицы описания в пространстве
состояний примут вид
24
25.
Такое преобразование не затрагивает матричной передаточнойфункции системы
и, следовательно, не изменяет ее передаточных нулей.
Кроме того, указанное преобразование не изменяет собственных
чисел матрицы A , а так как развязанные нули совпадают с
неуправляемыми (ненаблюдаемыми) полюсами, то преобразование
сохраняет неизменными и развязанные нули системы.
Отсюда вытекает, что нули системы инвариантны к невырожденному
изменению базиса в пространстве состояний.
Можно показать, что при схватывании линейной системы обратной
связью по состоянию (или по выходу) системные нули не
изменяются, т.е. системные нули инвариантны к замыканию
системы обратной связью по состоянию
25
26.
).Вычисления и идентификация типа нулей
Существуют различные определения и способы вычисления нулей многомерной
динамической системы, опирающиеся на различные свойства систем и их нулей.
Но вычисления нулей системы через соответствующие определения – сопряжен с большой
трудоемкостью из-за необходимости использования специальных форм матриц R( p ) R0 ( p )
Ri ( p ) Ô( p) – форм Смита и Смита-Макмиллана
На практике для вычисления нулей можно использовать свойства
квадратных систем (число входов совпадает с числом выходов, т.е.
m s ).
В теории систем доказано, что множество нулей исходной системы
является подмножеством нулей квадрированной системы, т.е.
или
y Ly LCx
при s m ,
rank Ls,m s
u Du
при m s ,
rank Ds ,m m .
В теории систем доказано, что множество нулей исходной системы является подмножеством нулей
квадрированной системы, т.е.
A, B, C A, B, LC или
A, B, C A, B, C , D ,
где ... – множество нулей системы.
26
27.
Тогда возможен следующий прием:1) система дважды квадрируется различными матрицами, каждый раз находится
множество нулей,
2) искомое множество нулей исходной системы находится как пересечение двух
квадрированных систем.
Вычисления нулей:
1-й подход.
Используется асимптотическое свойство нулей замкнутой системы:
при k нули системы совпадают с конечными собственными числами матрицы A(k ) A kBKC
где K – некоторая произвольная ограниченная матрица.
Поэтому нули можно вычислять путем выбора некоторой матрицы K умноженной на большой скаляр,
например, k 1015 и последующего определения собственных чисел матрицы An,n (k )
Ограниченные собственные числа A(k ) и будут искомыми передаточными нулями.
Достоинством данного метода является то, что проблема вычисления нулей сводится к проблеме собственных значений
матрицы, для решения которой существуют апробированные численные процедуры, а недостаток заключается в том,
что метод имеет численные погрешности из-за использования больших чисел
27
28.
2-й подход.Используется свойство квадратных систем, что нули такой системы являются корнями полинома ( p)
( p) det pI n A det C pI n A B q
1
дальнейшее см в [3]
После получения полного множества нулей системы проводится определение типа нулей.
Определение типов нулей происходит путем последовательной их подстановки в матрицы
R( p) , R0 ( p ) , Ri ( p ) , Ô( p) и проверки условий – определений различных типов нулей.
28
МЕТОДЫ СОВРЕМЕННОЙ ТЕОРИИ УПРАВЛЕНИЯ _ АСАНОВ А.З. _
29.
Вопросы для самостоятельной проработки1. Основные законы управления, их синтез и свойства для SISO-объектов [5];
2. Основные методы, математический аппарат для синтеза алгоритмов управления SISO-объектами [2];
3. Разработать математическую модель объекта управления (ОУ) (индивидуально, по вариантам):
• в пространстве состояний;
• в форме матричной передаточной функции;
• в форме проматрицы;
4. Обосновать\доказать адекватность полученных математических\компьютерных моделей;
5. Обосновать\доказать идентичность\соответствие различных форм математических моделей ОУ
29


























 Информатика
Информатика








