Трёхфазные электрические цепи Соединение треугольником. Лекция 7

1. БГТУ «ВОЕНМЕХ» им. Д.Ф. Устинова кафедра электротехники, О8

Лекция 7
Трёхфазные электрические цепи
Соединение треугольником
1

2.

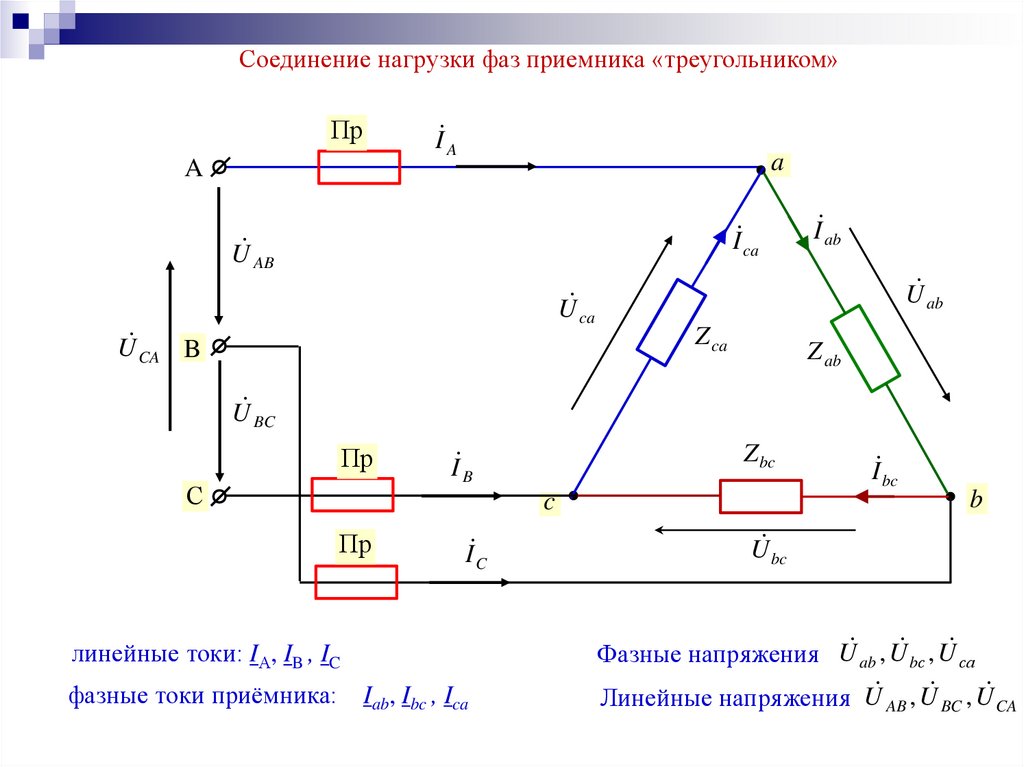
Соединение нагрузки фаз приемника «треугольником»
Пр
I A
a
A
I ca
U AB
I ab
U ab
U ca
Z ca
U CA B
Z ab
U BC
Пр
С
Z bc
I B
I bc
b
c
Пр
I C
линейные токи: IА, IB , IC
фазные токи приёмника: Iab, Ibc , Ica
U bc
Фазные напряжения U ab , U bс , U сa
Линейные напряжения U , U , U
AB
BC
CA

3.

Фазные токи и напряжения при соединении нагрузки треугольником
При соединении нагрузки треугольником фазные напряжения равны линейным
напряжениям:
U AB U ab
U BC U bc
U U
CA
UЛ UФ
ca
Фазные токи приемника определяются по закону Ома:
Комплексные значения
фазных токов:
ab
U
I ab
U ab Yab I ab e j
Z ab
bс
U
I bс
U bс Ybс I bс e j
Z bс
I сa U сa U сa Yсa I сa e j
Z сa
ab arctg
xab
rab
-фазовый сдвиг
ab
bc
ca
Действующие значения
фазных токов:
U
I ab ab U ab y ab
z ab
I bc
U bc
U bc ybc
zbc
I ca
U ca
U ca yca
zca
ab AB ab
ab -
начальная фаза
тока
AB - начальная фаза
напряжения

4.

Линейные токи (для узлов а, b, c) определяются по первому закону Кирхгофа:
I A I ca I ab 0
I B I ab I bc 0
I I I 0
C
bc
I A I ca I ab
I B I ab I bc
I I I
C
ca
bc
В векторной форме:
ca
I B
I ca
Из системы уравнений получим:
I A I B I C 0
I bc
При симметричной нагрузке, когда
Z ab Z bc Z Ca Z
Фазные токи тоже равны и рассчитываются:
I ab I bc I ca I Ф
UФ
ZФ
Линейные и фазные токи связаны соотношением:
I Л Iф 3
I B
I ab
I A

5.

Несимметричные режимы работы трехфазного соединения нагрузки
Когда комплексы фазных сопротивлений имеют различные значения:
Z ab Z bc Z сa
Комплексы фазных токов находим по закону Ома:
I U ab
ab
Z ab
I U bс
bс
Z bс
I U сa
сa
Z сa
I С
I bc
I B
I ca
I ab
I A
Линейные токи определяются на основании первого закона Кирхгофа:
I A I ca I ab
I B I ab I bc
I I I
C
bc
ca
При несимметричной нагрузке линейные и фазные токи тоже насимметричны!

6.

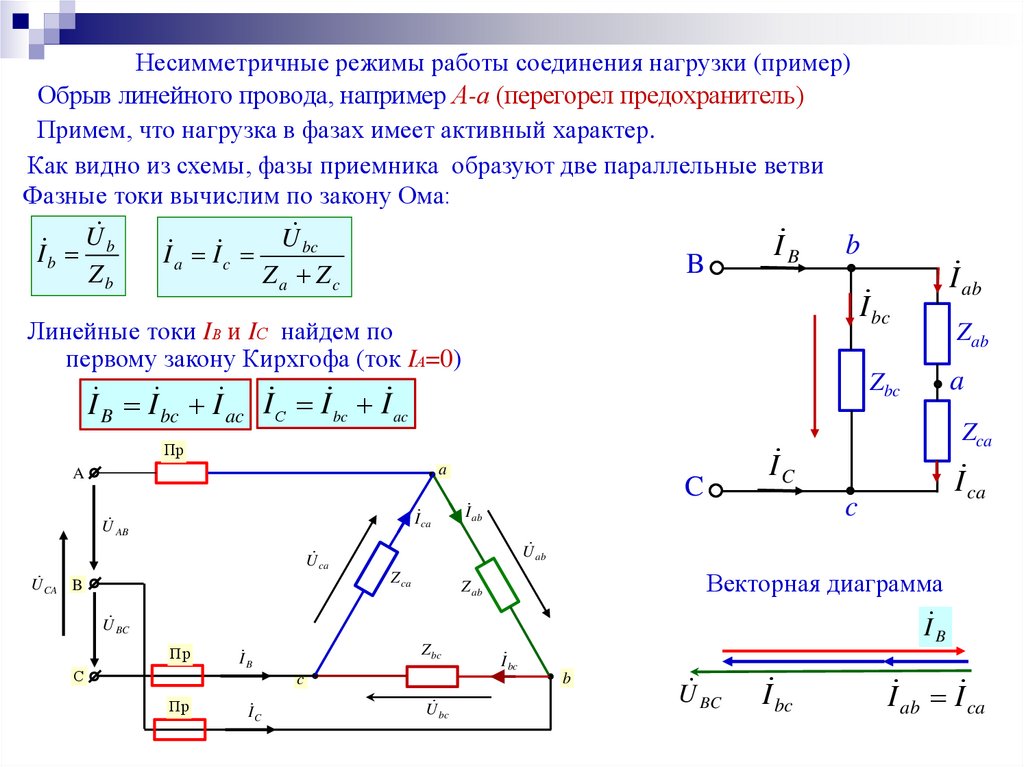
Несимметричные режимы работы соединения нагрузки (пример)
Обрыв линейного провода, например А-а (перегорел предохранитель)
Примем, что нагрузка в фазах имеет активный характер.
Как видно из схемы, фазы приемника образуют две параллельные ветви
Фазные токи вычислим по закону Ома:
U bc
b
I U b
I
B
I
I
b
a
c
B
Zb
Za Zc
I bc
Линейные токи IВ и IС найдем по
первому закону Кирхгофа (ток IА=0)
Пр
a
A
I ca
I ab
С
Z bc
c
Пр
I C
I ca
c
Векторная диаграмма
I
Z ab
U BC
I B
Zca
U ab
Z ca
Пр
a
I C
C
U ca
U CA B
Zab
Zbc
I B I bc I ac I С I bc I ac
U AB
I ab
U bc
B
I bc
b
U BC
I bc
I ab I ca

7.

Мощность трёхфазной цепи
Активная P,
реактивная Q
полная S
мощности трёхфазной цепи определяются также, как и в однофазных цепях:
Полная комплексная мощность фазы
*
SФ U Ф I Ф PФ jQФ
*
IФ
- сопряженный ток фазы
Активная мощность фазы
PФ UI cos
Реактивная мощность фазы
QФ UI sin
Полная мощность фазы
S Ф PФ2 QФ2
Полная комплексная мощность трёхфазной нагрузки вычисляется
как сумма комплексов полных мощностей фаз:
S S A S B S C ( Pa Pb Pc ) j (Qa Qb Qc )

8.

Мощность трёхфазной цепи
Мощность трёхфазной цепи удобнее считать используя линейные токи и напряжения
Соединение «Звезда»
U
Uф Л
3
Соединение «Треугольник»
Uф U Л
Iф
Iф I Л
S 3U Ф I Ф 3U Л I Л
ВА
P 3U Ф I Ф cos 3U Л I Л sin Вт
Q 3U Ф I Ф sin 3U Л I Л sin
ВАр
IЛ
3

9.

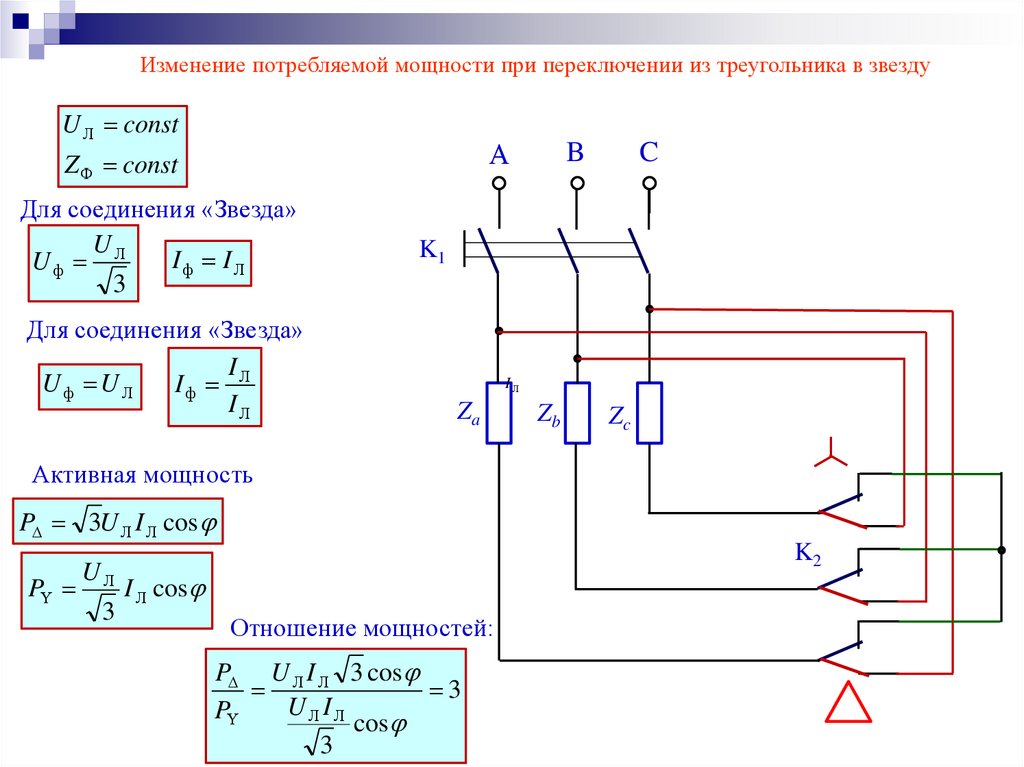
Изменение потребляемой мощности при переключении из треугольника в звезду
U Л const
А
Z Ф const
Для соединения «Звезда»
U
Iф I Л
Uф Л
3
Для соединения «Звезда»
I
Uф U Л
Iф Л
IЛ
B
C
K1
IЛ
Za
Zb
Zc
Активная мощность
P 3U Л I Л cos
P
UЛ
3
K2
I Л cos
Отношение мощностей:
P U Л I Л 3 cos
3
U
I
P
Л Л
cos
3