Механическая работа. (Лекция 4)

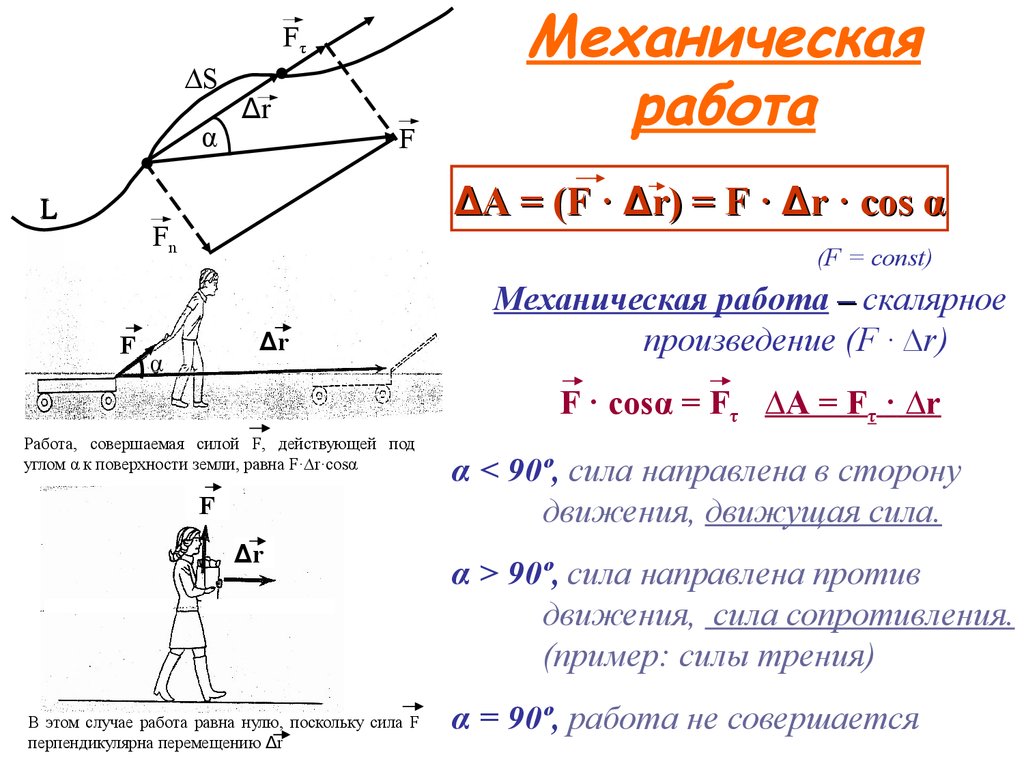
1. Механическая работа

Fτ
∆S
α
L
∆r
F
∆A = (F · ∆r) = F · ∆r · cos α
Fn
F
Механическая
работа
(F = const)
∆r
α
Механическая работа – скалярное
произведение (F · ∆r)
F · cosα = Fτ ∆A = Fτ · ∆r
Работа, совершаемая силой F, действующей под
углом α к поверхности земли, равна F·∆r·cosα
F
∆r
В этом случае работа равна нулю, поскольку сила F
перпендикулярна перемещению ∆r
α < 90º, сила направлена в сторону
движения, движущая сила.
α > 90º, сила направлена против
движения, сила сопротивления.
(пример: силы трения)
α = 90º, работа не совершается

2. Механическая работа

В общем случае:
A
N
A
i 1
i
F dr
L
Работа силы F при перемещении тела вдоль некоторой траектории L
[A] = Дж = Н ·
м
dA
N=
dt
мощность [N] =Дж/с = вт

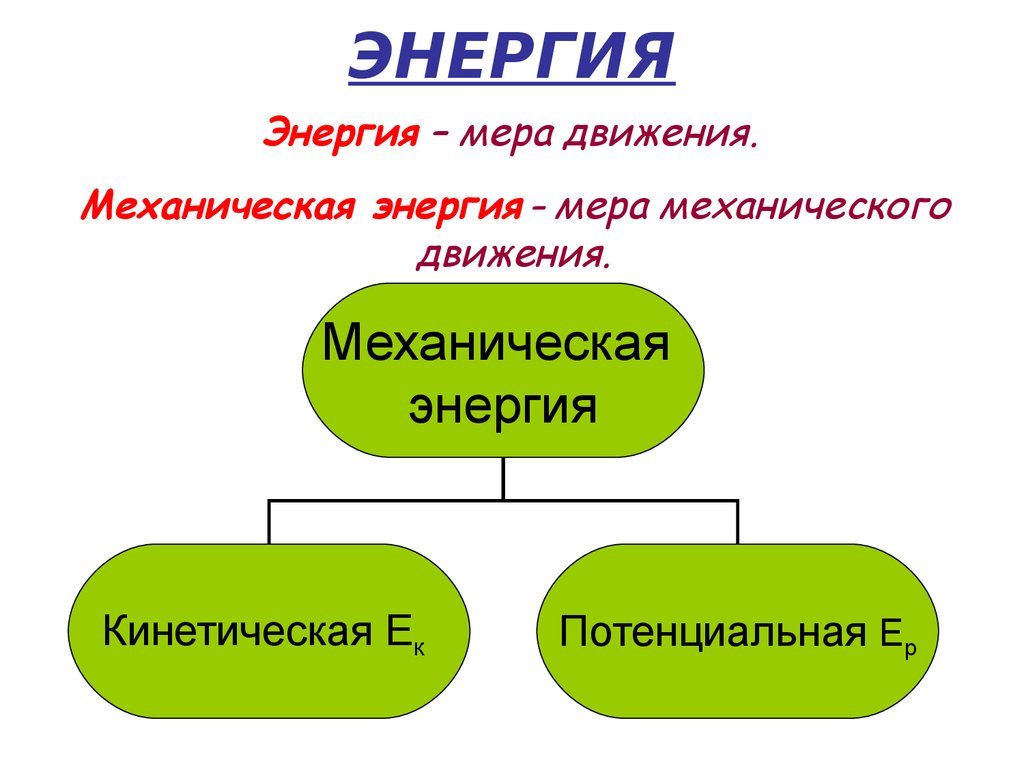
3. ЭНЕРГИЯ

Энергия – мера движения.
Механическая энергия – мера механического
движения.
Механическая
энергия
Кинетическая Ек
Потенциальная Ер

4.

Потенциальная энергия – это энергия
взаимодействия тел, она определяется
взаимным расположением тел
Пример потенциальной энергии: энергия поднятого над землёй тела.
∆A = mg·∆r cosα на элементарном перемещении ∆r
∆r cosα = ∆h
∆A = mg·∆h
A = ∑mg·∆hi = mg(H2 – H1 )
i
A = (mg·ΔH);
Ер= mg·H
Работа равна изменению потенциальной энергии

5.

Кинетическая энергия – энергия движущегося тела.
Предположим, что материальная точка, движущаяся под действием силы F
изменяет свою скорость за время t от V1 до V2. Подсчитаем работу этой силы,
если F || ∆r ( ∆r – перемещение тела).
A = F·∆r = F
F = ma
2
a=
V2-V1
V1+V2
2
·t =
F ·t (V1+V2)
2
;
;
t
2
2
m (V2-V1) t (V2+V1)
mV1
m V2
A=
=
;
t
2
2
2
mV1
= Eк1
2
2
m V2
Eк2
=
2
Кинетическая энергия – положительная
величина.
Кинетическая энергия зависит от выбора
системы
единиц,
т.е.
является
относительной величиной.
A = Eк1 – Eк2
Работа
–
разность
кинетических энергий в начале
и конце пути.

6.

Работа есть мера перехода
энергии от одного тела к
другому, есть процесс или
форма передачи энергии от
одного тела к другому или
превращения энергии из одной
формы в другую

7.

Если
работа,
которую
совершают
силы,
зависит только от начального и конечного
положений тела, то такие силы называются
консервативными.
Источник консервативных сил – потенциальные
поля.
Примеры: гравитационное поле, электрическое
поле.

8.

•Закон сохранения и превращения энергии
Емех = Eпот+ Екин
I: Емех= Eпот1+ Екин1
II: Емех = Eпот2+ Екин2
Полная механическая энергия системы
тел,
в
которой
действуют
только
консервативные
силы,
остается
постоянной, т.е. не изменяется с течением
времени
Епот + Екин = Емех = const

9.

Механические системы, на тела которых действует
только консервативные силы (внутренние и внешние)
называются консервативными системами
Тогда
закон
сохранения
механической
энергии
формулируется так: в консервативных системах полная
механическая энергия сохраняется

10.

Существует ещё один вид систем –
диссипативные системы
В диссипативных системах механическая энергия
постепенно уменьшается за счёт преобразования в
другие (немеханические) формы энергии. Этот
процесс называется диссипацией (рассеянием)
энергии
В диссипативных системах полная механическая
энергия не сохраняется, однако она превращается в
другие виды энергии
Энергия не создается и не уничтожается, она
может только переходить из одной формы в
другую – фундаментальный закон природы,
закон сохранения и превращения энергии