Похожие презентации:
Работа и кинетическая энергия. Закон сохранения полной механической энергии в поле консервативных сил. (Лекция 4)
1. Лекция 4
12.
Содержание предыдущей лекцииДинамика поступательного движения.
Закон сохранения импульса.
• Движение тел переменной массы. Формула
Циолковского.
Механическая энергия
• Сила, работа и потенциальная энергия, связь между
силой и потенциальной энергией.
• Консервативные и неконсервативные силы.
2
3.
Содержание сегодняшней лекцииМеханическая энергия
• Работа и кинетическая энергия.
• Закон сохранения полной механической энергии в поле
консервативных сил.
• Столкновение тел.
Кинематика и динамика вращательного движения
• Кинематика вращательного движения: угловая скорость и
угловое ускорение, их связь с линейной скоростью и
ускорением.
• Момент силы. Уравнение моментов.
3
4.
Поле консервативных силРабота и кинетическая энергия
Уравнение движения частицы mv F .
ds vdt
mvvdt Fds
v2
mv 2
mvvdt mvdv md d
Fds dA
2
2
4
5.
Поле консервативных силРабота и кинетическая энергия
mv 2
p2
d
d
2
2m
p2
Т
– кинетическая энергия частицы.
2m
Зависимость кинетической энергии (энергии движения)
от массы и скорости рассматриваемого тела.
5
6.
mv 2Fds dA
d
2
Поле консервативных сил
Работа и кинетическая энергия
mv mv
Т 2 T1
Fds A12 .
2
2
1
2
2
2
1
2
Равенство работы результирующей консервативных сил,
действующих на частицу,
приращению кинетической энергии частицы
A12 Т 2 T1.
6
7.
Закон сохранения полной механической энергиив поле консервативных сил
A12 U1 U 2
A12 Т 2 T1
Т 2 T1 U1 U 2
Т 2 U 2 T1 U1
Постоянство полной механической энергии E T U
частицы, находящейся в поле консервативных сил.
7
8.
Закон сохранения полной механической энергиив поле консервативных сил
Постоянство полной механической энергии
системы невзаимодействующих частиц,
на которые действуют только консервативные силы.
8
9.
Столкновение телДва крайних случая соударения –
абсолютно упругий и абсолютно неупругий удары.
9
10.
Абсолютно упругий ударДо удара
После удара
Условие упругого удара: механическая энергия
взаимодействующих тел
не переходит в другие (немеханические) виды энергии.
Переход кинетической энергии тел
в потенциальную энергию упругой деформации тел и обратно.
Выполнение законов
сохранения полной энергии и полного импульса системы тел.
10
11.
Абсолютно упругий ударЗамкнутая система из двух частиц
Отсутствие вращения частиц (поступательное движение)
Выполнение закона сохранения механической энергии
2
2
2
2
m1v10 m2v20 m1v1 m2v2
.
2
2
2
2
Выполнение закона сохранения суммарного импульса частиц
m1v10 m2v20 m1v1 m2v2 .
11
12.
Абсолютно упругий удар2
2
2
2
m1v10 m2v20 m1v1 m2v2
m1v10 m2v20 m1v1 m2v2
2
2
2
2
2 2
a b (a b )(a b )
m1 v10 v1 v10 v1 m2 v2 v20 v2 v20
m1 v10 v1 m2 v2 v20
v10 v1 v2 v20
12
13.
v10 v1 v2 v20m1 v10 v1 m2 v2 v20
Абсолютно упругий удар
m1 v10 v1 m2 v2 v20
m1 v10 v1 m2 v2 v20
m
m
-
2
v10 v1 v2 v20
+
1
v10 v1 v2 v20
2m2 v20 m1 m2 v10
2m1v10 m2 m1 v20
v1
, v2
.
m1 m2
m1 m2
Частный случай: m1 m2
v1 v20 v2 v10
13
14.
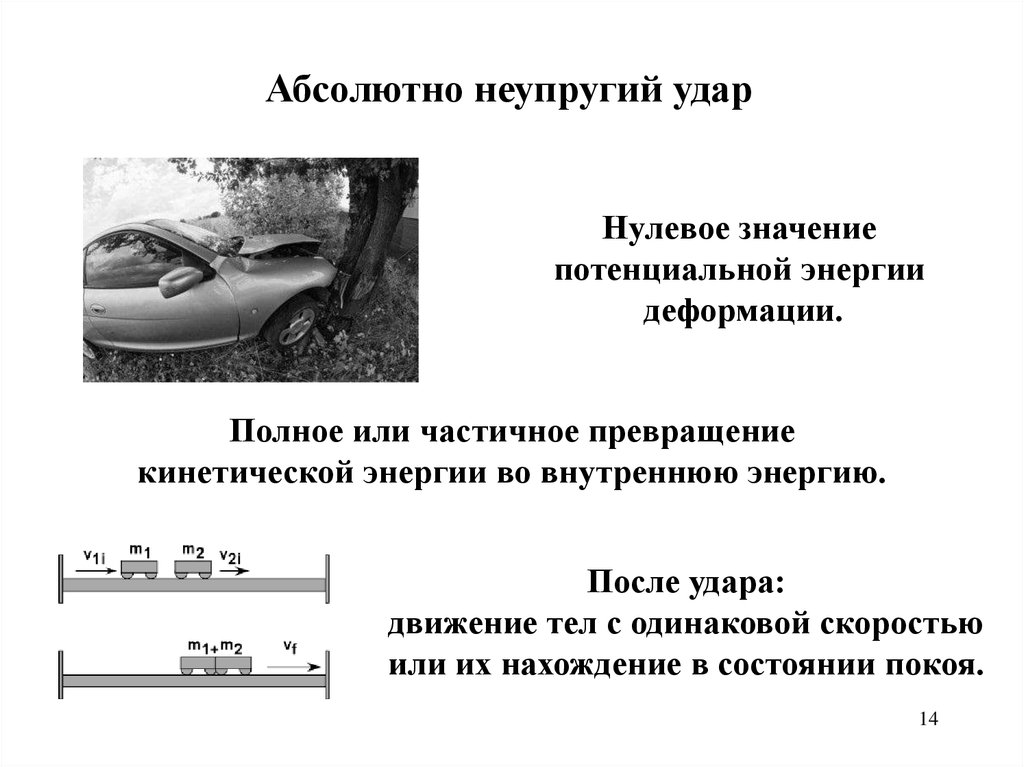
Абсолютно неупругий ударНулевое значение
потенциальной энергии
деформации.
Полное или частичное превращение
кинетической энергии во внутреннюю энергию.
После удара:
движение тел с одинаковой скоростью
или их нахождение в состоянии покоя.
14
15.
Абсолютно неупругий ударВыполнение закона сохранения импульса.
Невыполнение закона сохранения механической энергии.
Выполнение закона сохранения суммарной энергии
различных видов - механической и внутренней.
15
16.
Абсолютно неупругий ударЗакон сохранения
суммарного импульса двух частиц,
образующих замкнутую систему,
m1v10 m2v20 m1v m2v (m1 m2 )v
до удара
после удара
m1v10 m2 v20
v
.
m1 m2
16
17.
Вращательное движение17
18.
Вращательное движение – движение,при котором все точки тела совершают движение по
концентрическим окружностям.
18
19.
Кинематика вращательного движения19
20.
Кинематика вращательного движенияВектор
характеристика поворота материальной точки (тела)
на некоторый угол относительно некоторой
фиксированной в пространстве оси.
Длина вектора – угол поворота.
Направление вектора – ориентация оси.
Неоднозначность в выборе направления поворота
– поворот возможен по или против часовой стрелки.
20
21.
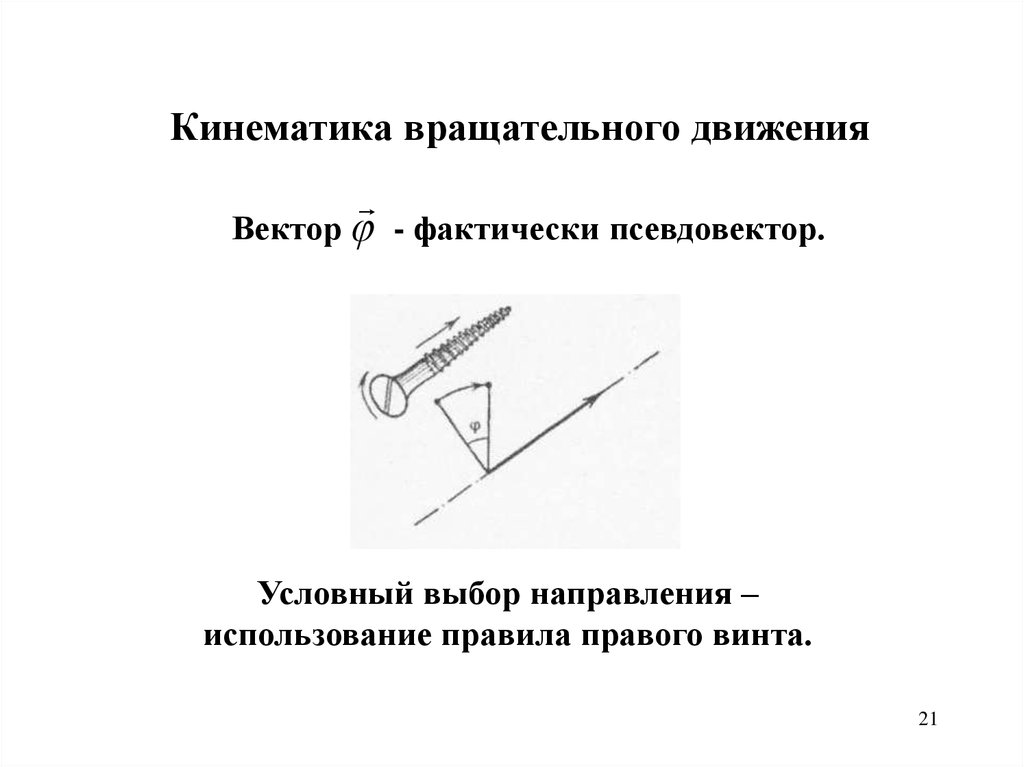
Кинематика вращательного движенияВектор
- фактически псевдовектор.
Условный выбор направления –
использование правила правого винта.
21
22.
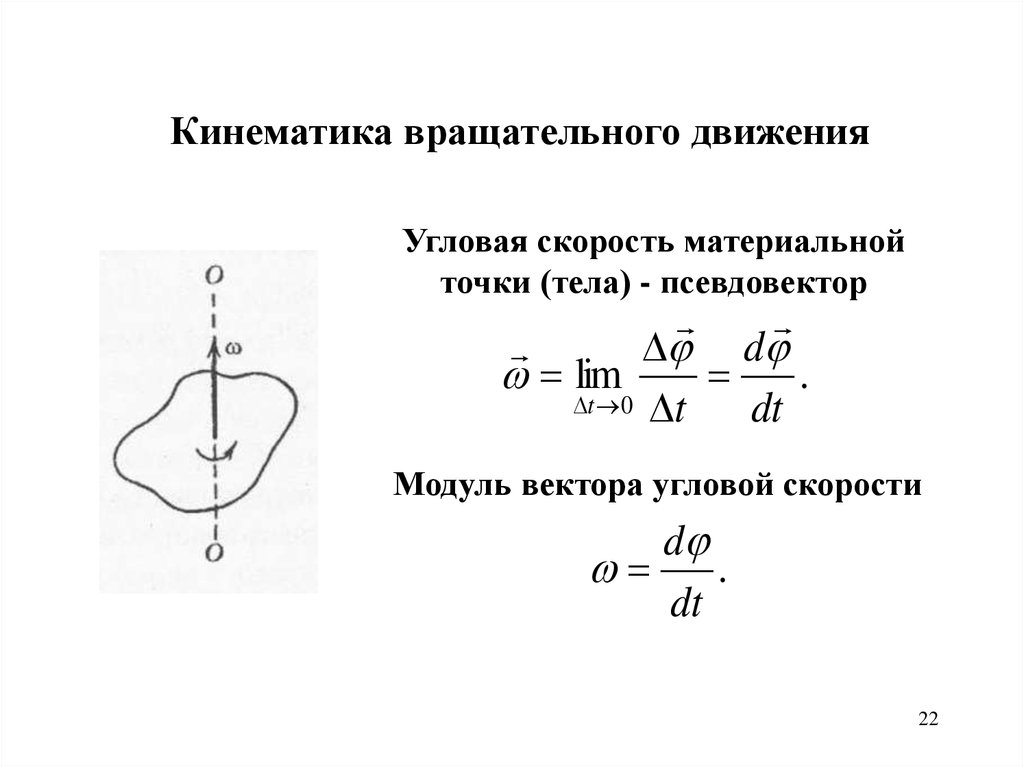
Кинематика вращательного движенияУгловая скорость материальной
точки (тела) - псевдовектор
d
lim
.
t 0 t
dt
Модуль вектора угловой скорости
d
.
dt
22
23.
Кинематика вращательного движенияРавномерное вращательное движение –
вращение с постоянной скоростью
.
t
Период обращения Т при равномерном вращении –
время, за которое тело делает один оборот.
t T
2
2 / T
Число оборотов в единицу времени
Угловая скорость
T 2 /
v 1/ T / 2 .
2 .
23
24.
Кинематика вращательного движенияВозможность изменения
за счет изменения
скорости вращения тела вокруг оси (модуль) и
за счет поворота оси (направление).
Угловое ускорение (псевдовектор)
d
ε lim
t 0 t
dt
- характеристика скорости изменения вектора угловой
скорости во времени.
24
25.
Кинематика вращательного движенияРазная линейная скорость
у различных точек
вращающегося тела.
v
s
d
v lim
lim R
R
R .
t 0 t
t 0
t
dt
v R .
25
26.
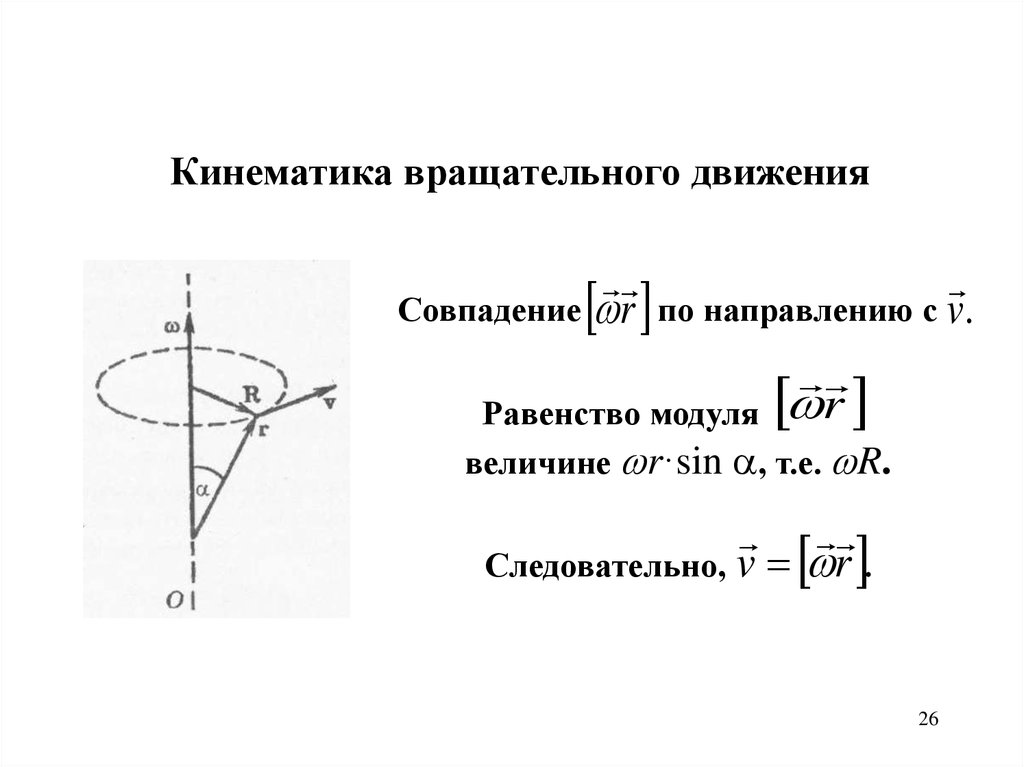
Кинематика вращательного движенияСовпадение r по направлению с v .
Равенство модуля r
величине r·sin , т.е. R.
Следовательно, v r .
26
27.
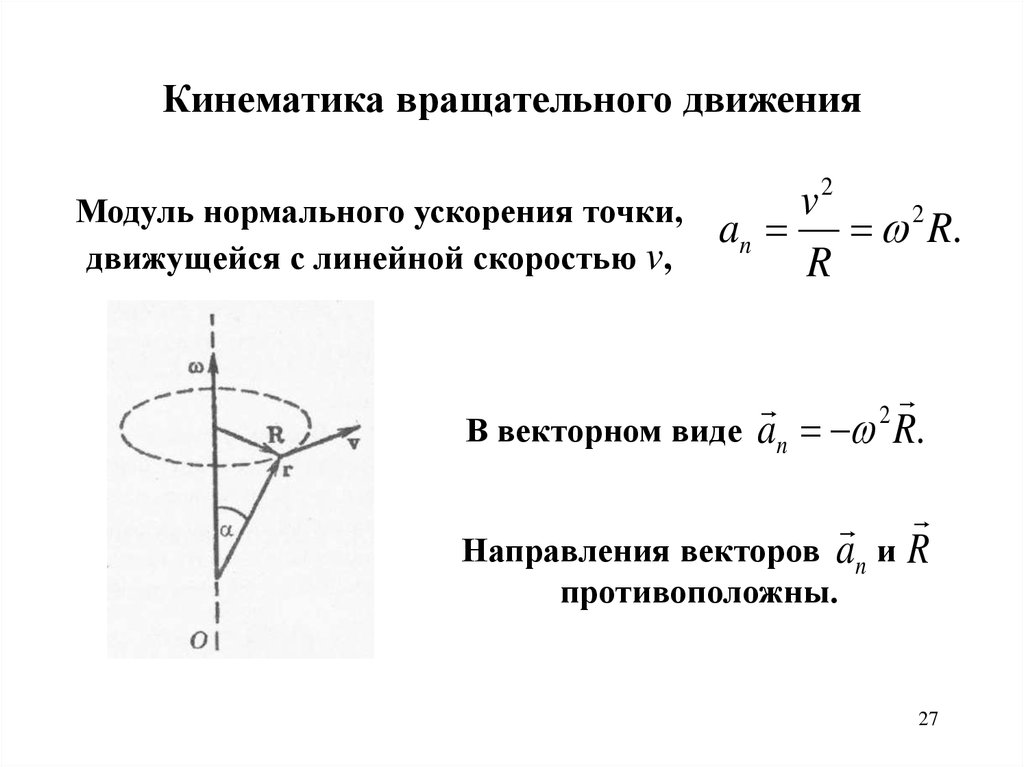
Кинематика вращательного движенияМодуль нормального ускорения точки,
движущейся с линейной скоростью v,
v2
an 2 R.
R
В векторном виде
2
an R.
an и R
Направления векторов
противоположны.
27
28.
Кинематика вращательного движенияУсловие: ось тела не поворачивается в пространстве.
Модуль тангенциального ускорения
a dv / dt .
Линейная скорость точки на расстоянии R от оси вращения
v R.
v
( R)
a lim
lim
lim R
R lim
R .
t 0 t
t 0
t 0
t 0 t
t
t
a R .
28
29.
Динамика вращательного движения29
30.
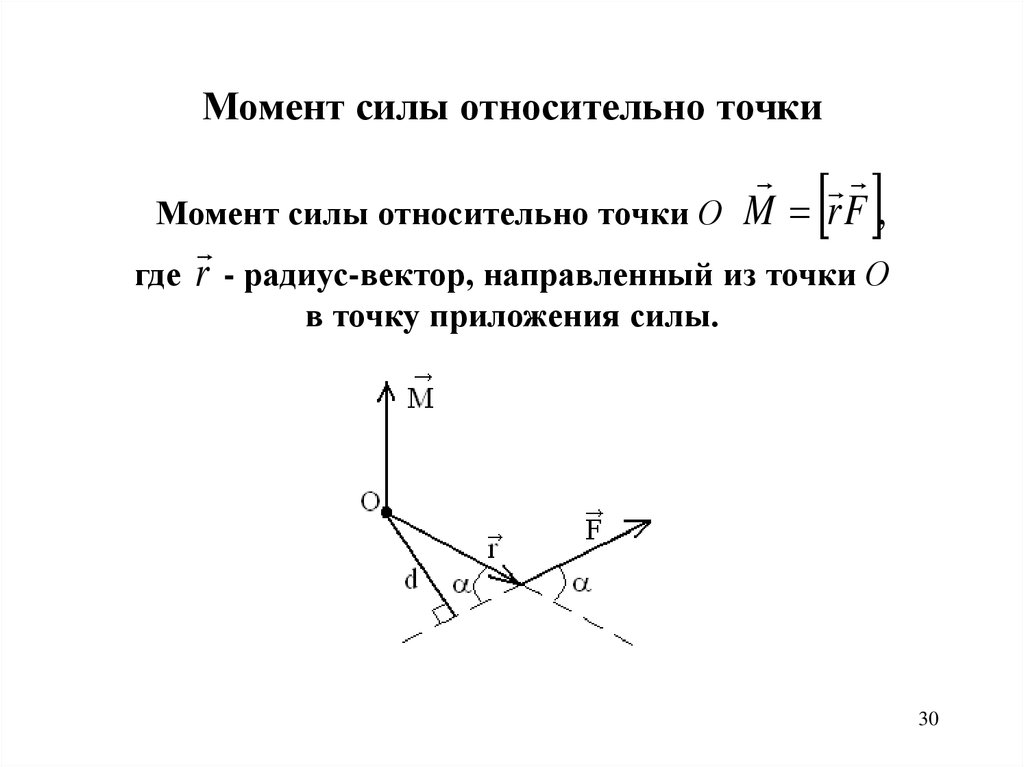
Момент силы относительно точкиМомент силы относительно точки О
где
M rF ,
r - радиус-вектор, направленный из точки О
в точку приложения силы.
30
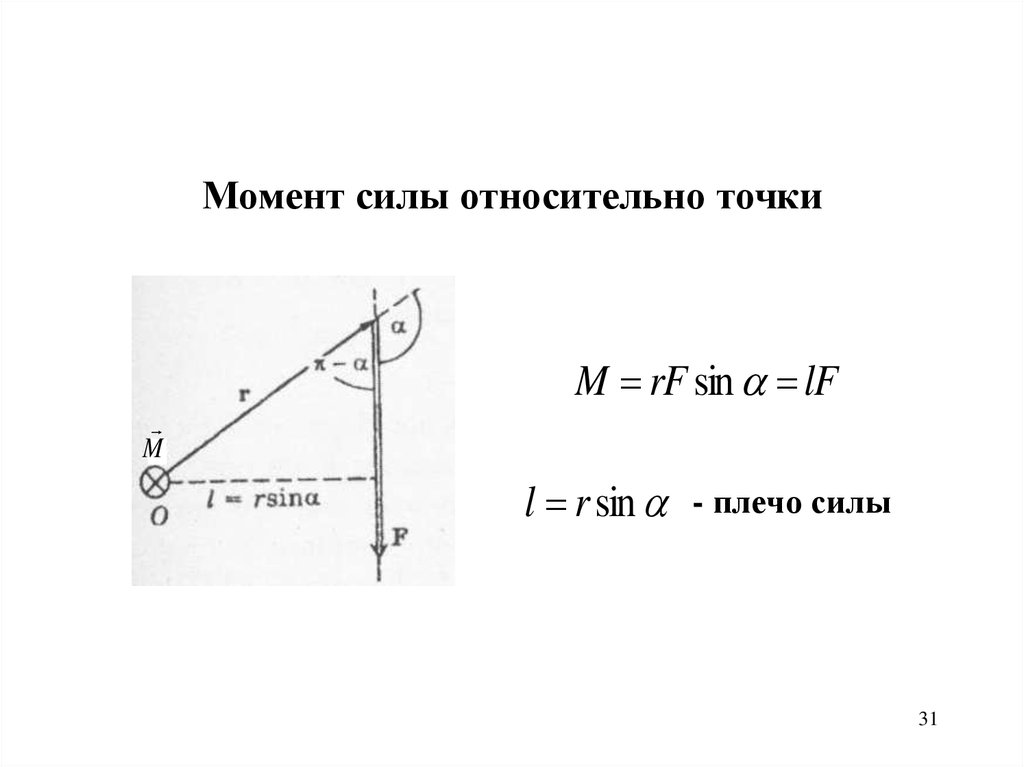
31.
Момент силы относительно точкиM rF sin lF
M
l r sin
- плечо силы
31
32.
Контрольный вопросДве частицы обладают одинаковыми кинетическими
энергиями. Величины их импульсов соотносятся как:
а) p1 < p2,
б) p1 = p2,
в) p1 > p2,
г) невозможно определить.
32

























 Физика
Физика








