Молекулярная физика. Основы термодинамики. Элементы молекулярно-кинетической теории. Уравнение состояния идеального газа

1.

МОЛЕКУЛЯРНАЯ ФИЗИКА.
ОСНОВЫ ТЕРМОДИНАМИКИ
ЭЛЕМЕНТЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ.
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
1. Основные понятия
Молекулярная физика эта наука о строении, агрегатных состояниях и
физических свойствах вещества, рассматриваемого как совокупность
большого количества молекул (атомов и ионов), которые
взаимодействуют между собой и находятся в непрерывном
хаотическом движении.
Задачами молекулярной физики являются:
1) исследование строения
вещества и его изменение под
влиянием внешних воздействий;
2) изучение фазовых превращений
(испарение и конденсация,
плавление и кристаллизация);
3) исследование поверхностных
явлений на границах различных
фаз;
4) изучение явлений переноса
(диффузия, теплопроводность,
внутреннее трение и др.)

2.

Молекулярно-кинетическая теория
(МКТ), используя статистический метод
исследования вещества, описывает
наблюдаемые на практике свойства
систем состоящих из большого числа
молекул (макроскопических тел)
давление, температура,
диффузия,
явления переноса,
законы распределения
молекул по скоростям,
теплоемкость, и т.д.
Статистический метод основывается на
определенных представлениях о строении вещества
и лежит в основе молекулярной физики

3.

Термодинамика есть феноменологическая теория
макроскопических процессов, сопровождающихся
превращениями энергии
Предметом изучения термодинамики являются закономерности
превращения энергии в различных физических, химических и
других процессах.
Можно сказать, что термодинамика представляет собой, в
самом общем смысле, науку о энергии
Термодинамический подход, основывается на небольшом числе
экспериментально установленных фактах (постулат, закон)
В термодинамике поведение макросистем характеризуется
макроскопическими (термодинамическими) параметрами –
физические величины, характеризующие состояние ТС, а
следовательно, и ее свойства без учета его молекулярного строения

4.

Каждому состоянию ТС отвечают определенные
значения термодинамических параметров
Термодинамическая система – совокупность
материальных тел, а также полей, находящихся в
механическом и/или тепловом взаимодействии, а также
обменивающихся друг с другом веществом
Механическое взаимодействие между телами
осуществляется посредством механических сил
Тепловое взаимодействие состоит в передаче тепла
(теплопередачи) и осуществляется путем теплопроводности,
конвекции и/или излучением
Обмен веществом состоит в переносе вещества через
границы термодинамической системы

5.

Системы, в которых возможны все три типа взаимодействия,
называются открытыми
Системы, в которых обмен веществ не происходит,
называются закрытыми
Если термодинамическая система не может обмениваться
теплотой с другими системами (окружающей средой), то ее
называют теплоизолированной или адиабатической
системой.
Систему, совершено не взаимодействующую с другими
системами (окружающей средой), называют изолированной
системой
Система, имеющая во всех своих частях одинаковые
свойства, называется однородной

6.

Состояние ТС, при котором все его термодинамические параметры при
неизменных внешних условиях остаются постоянными сколь угодно
долго, будем называть равновесным
Уравнением состояния ТС
называется уравнение,
связывающее все
макропараметры системы
Всякое изменение в ТС, связанное с
изменением хотя бы двух из ее
макропараметров, называется
термодинамическим процессом
Термодинамические процессы, состоящие из непрерывной
последовательности близлежащих равновесных состояний,
называют квазиравновесным, в противном случае процесс
называют неравновесным
Изопроцессами называются термодинамические процессы,
происходящие в системе с постоянной массой и типом газа, при
каком либо одном постоянном параметре состояния.

7.

2. Основные положения и понятия МКТ
В основе МКТ лежат три основных положения:
а) все тела состоят из большого числа частиц – молекул, атомов и ионов
б) атомы, молекулы и ионы находятся в непрерывном тепловом движении, т.е.
обладают кинетической энергией (броуновское движение, диффузия);
в) частицы любого тела взаимодействуют между собой.
1. Относительная атомная (молекулярная)
масса Mr вещества
1 а.е.м. 1,66 10-27 кг
2. Количество вещества системы
3. Молярная масса
4. Масса вещества

8.

3. Основное уравнение МКТ идеального газа
Идеальным газом в МКТ называется газ, удовлетворяющий
следующим условиям:
– силы взаимодействия между молекулами ничтожно малы,
и ими можно пренебречь (Ер = 0);
– молекулы взаимодействуют между собой и со стенками
сосуда только при непосредственном соприкосновении, при
этом они ведут себя как абсолютно упругие шарики, т.е. эти
взаимодействия, подчиняются законам абсолютно упругого
удара;
– время столкновения молекул друг с другом и со стаканами
сосуда пренебрежимо мало по сравнению со временем
между двумя последовательными столкновениями;
– объёмом всех молекул газа можно пренебречь по
сравнению с объёмом сосуда, в котором этот газ находится

9.

Fn
p
S
Давление
пост
Ek
m0
2
2
1
2
p nm0
3
2
пост
p n Ek
3

10.

4. Температура. Средняя энергия теплового движения молекул.
Степень свободы
Природа теплого и холодного
В термодинамике, теплота
рассматривается как род
некоторого внутреннего
движения, но что это за
движение, какова его природа,
она не конкретизирует
Молекулярная физика
рассматривает теплоту как меру
непрерывного, беспорядочного
движения атомов и молекул
Температура количественная
характеристика различной
степени нагретости тел.
(относительность)
Для изучения тепловых явлений
вводится новая физическая
величина – температура
В физике к понятию температуры
приходят через понятие
теплового равновесия
Для теоретических исследований
пользуются термодинамической
шкалой температур
(шкала У. Томсон (лорд Кельвин))

11.

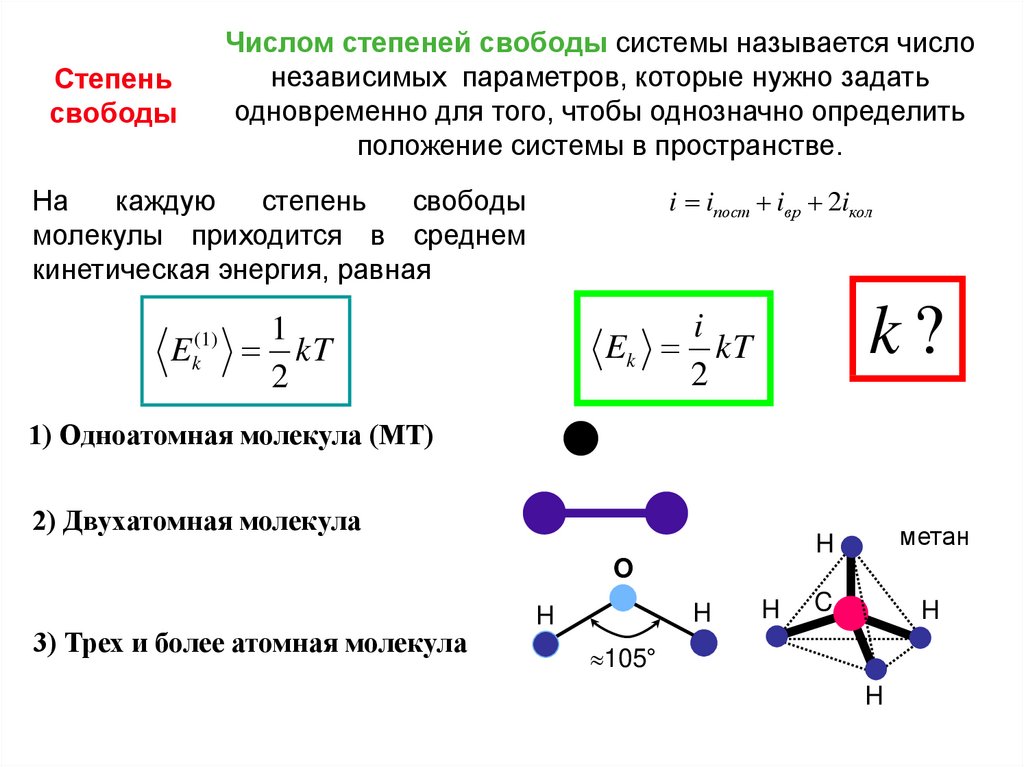
Числом степеней свободы системы называется число
независимых параметров, которые нужно задать
одновременно для того, чтобы однозначно определить
положение системы в пространстве.
Степень
свободы
i iпост iвр 2iкол
На
каждую
степень
свободы
молекулы приходится в среднем
кинетическая энергия, равная
E
( 1)
k
k?
i
Ek kT
2
1
kT
2
1) Одноатомная молекула (МТ)
2) Двухатомная молекула
H
метан
C
H
O
3) Трех и более атомная молекула
H
H
H
105°
H

12.

Основное уравнение МКТ
идеального газа
i
Ek kT
2
1
2
2
P nm0 n Ekпост
3
3
p nkT
2
Ekпост
m0 2
2
3kT
m0
p
V
p const
n
N
с к
2
3kT
m0

13.

5. Уравнение состояния идеального газа. Изопроцессы
pV
m
RT
pV
const
T
pV RT
p RT
Фр. физик Б. Клапейрон (1834 г.)
Уравнение состояния газовой смеси
Смесью газов называют совокупность нескольких химически
различных газов, которые не вступают в химическую реакцию
между собой
Давление, оказываемой какой-либо компонентой смеси на стенки сосуда, без
учета других компонент смеси, называют
парциальным давлением

14.

Английский физик Джон Дальтон (1801 г.) экспериментально установил,
что для достаточно разряженных газов давление газовой смеси равно
сумме парциальных давлений
p p1 p2 pn pi
i 1
закон Дальтона
а парциальные давления каждой из компонент смеси подчиняются при
этом уравнению Менделеева – Клапейрона:
p1V
m1
1
RT , p2V
m2
2
RT piV
mi
i
RT

15.

Изопроцессами называются термодинамические процессы, происходящие в
системе с постоянной массой и типом газа, при каком либо одном
постоянном параметре состояния
1. Изотермический процесс (закон Бойля – Мариотта, 1662 г).
2. Изохорический процесс (закон Шарля, 1802 г).
3. Изобарный процесс (закон Гей-Люссака, 1802 г.).

16.

2. СТАТИСТИЧЕСКИЕ ЗАКОНОМЕРНОСТИ В МКТ
2.1. Общие понятия
Событием называется любое
явление, которое в данных условиях
может произойти или не произойти
«Измерение» физической
величины называется
испытанием
Достоверное и невозможное события
Случайным называется событие, которое при данном
испытании может или произойти, или не произойти
Отношение Ni /N называется относительной частотой
появления значения x = xi
Пример: кубик

17.

Вероятностью данного события (наблюдения значения х = xi)
Ni
ωi xi lim
N N
Ni – число испытаний в результате которых наблюдалось значение x = xi
N – полное число испытаний
Т.к.
N Ni
i
Ni N
Ni
ωi xi
i
1
N
N
i
i N
ωi xi 1
i
Это утверждение носит название
т.е. сумма вероятностей всех
возможных событий равна единице
условия нормировки!!!

18.

Если величина х имеет непрерывный спектр значений
d ( x ) f ( x )dx
f(x) – функция распределения вероятностей
f ( x)
d ( x )
dx
плотность вероятности того события, что
испытание даст значение величины, равное x
Отсюда, количество молекул dN, для которых величина x, характеризующая их,
заключена в интервале значений от x, до x+dx, равна:
dN Nd x Nf ( x)dx
Вероятность 12 обнаружить значение величины x
в заданном интервале значений х1 х х2
условие
нормировки
x max
Свойства функции распределения
f ( x )dx 1
x min
x2
12 f ( x )dx
x1

19.

2.2. Закон распределение молекул идеального
газа по скоростям теплового движения
NА 6,03 1023 моль-1
Число столкновений одной молекулы
газа при нормальных условиях в среднем
порядка 108 столкн/с
Скорость молекул
Молекулы газа, находящегося в равновесном состоянии движутся с
различными скоростями, причем как модуль так и направление их
скорости непрерывно изменяются
В газе различают две непрерывные функции
распределения молекул по скоростям
1) По компоненте скорости
2) По модулю скорости

20.

1) Функция распределения молекул ИГ
по компоненте скорости
dω
dN x
N
ΔN
f x d x
N
1
2
m
1 dN m0
f x
exp
N d x 2 kT
2kT
2
0 x
x
ω12
x1
f d
x
x
x1
1
2
2
m
m
0
0 y
f y
exp
2
kT
2πkT
1
2
m0 z2
m0
f z
exp
2 kT
2kT

21.

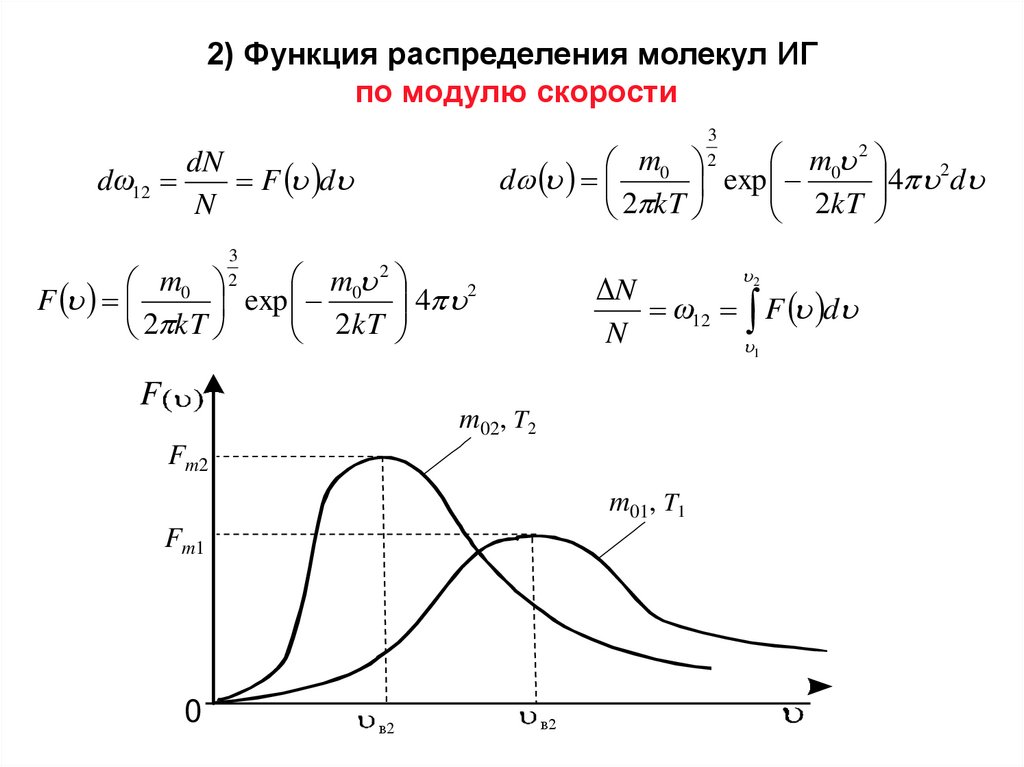
2) Функция распределения молекул ИГ
по модулю скорости
3
2
m0 2
m0
4 2d
d
exp
2 kT
2kT
dN
dω12
F d
N
3
2
m0 2
m0
4 2
F
exp
2 kT
2kT
F
2
ΔN
ω12 F d
N
1
m02, T2
Fm2
m01, T1
Fm1
0
в2
в2

22.

2.3. Характерные скорости молекул ИГ
3
2
2
m
m
2
0
0
F
exp
4
2kT
2 kT
1)
2kT
2 RT
вер
m0
dF
0
d
Fmax
вер
4 m0
e 2πkT
3
2
2
m
m
3
0
0
υF
d
d
2)
2π
2 exp
2πkT 0
0
2kT
8kT
8RT
m0
3) F d
2
0
2
ск
2
3kT
3RT
m0
1
2

23.

Пример 2. Получить выражение для функции распределения
Максвелла по относительным скоростям.
m0 2
m0
4 2
F
exp
2 kT
2kT
32
d
dN
F d
N
u
в
dN
Найти: d u
F u du
N
2 2
8m0
F
exp 2 2
kT
в в
du
в
d du в
2kT
m0
dN N
8m
F u 0 exp u 2 u 2
kT
d u
4
2kT 2 RT
m0
12
12
d
в2
dN
4
exp u 2 u 2 du
N
exp u 2 u 2 du
u u N N
4
exp u 2 u 2 u

24.

2.4. Барометрическая формула
p dp
p (p dp) ρgdh
h dh
g
pV
m
RT
p
p RT
RT
dp p gdh/RT
p
h
dp
g
p RT dh
dp
g
p RT dh
ln p μgh/RT ln C p C exp μgh/RT
p p0e μgh/RT
p p0e
m0 gh/kT