Похожие презентации:
Молекулярная физика и термодинамика
1.
МОЛЕКУЛЯРНАЯ ФИЗИКАИ
ТЕРМОДИНАМИКА
2.
Системы, состоящие из очень большого числа частиц (атомов,макросистемами. Примером макросистемы может служить газ.
молекул
и
т.д.),
называют
Два метода изучения макросистем:
статистический
термодинамический
изучает строение и свойства вещества, исходя из
молекулярно-кинетических
представлений:
любое тело (твердое, жидкое или газообразное)
состоит из большого числа малых частиц (атомов,
молекул или ионов), находящихся в состоянии
непрерывного беспорядочного движения. МКТ
истолковывает наблюдаемые свойства тел как
суммарный
результат
действия
молекул,
пользуясь статистическими методами: т.е. МКТ не
интересуется движением отдельных молекул, но
оперирует
со
средними
величинами,
характеризующими движение всей совокупности
молекул.
изучает свойства веществ и изменение их
состояний путем анализа процессов превращения
энергии в них без рассмотрения движения
отдельных частиц, из которых они состоят. В
основе
термодинамики
лежит
несколько
фундаментальных законов, установленных в
результате обобщений опытных фактов.
Молекулярно-кинетическая теория (МКТ) и термодинамика,
подходя к рассмотрению изменений состояния вещества с различных точек зрения, дополняют друг друга,
образуя по существу одно целое.
3.
Состояние системы. Термодинамические параметры и процессыТермодинамическими параметрами (или параметрами состояния) системы называются физические
величины, служащие для характеристики состояния системы. В качестве термодинамических параметров
используются температура Т, давление р и объем V.
Состояние системы называется равновесным, если все ее параметры остаются неизменными
произвольно долгое время при постоянных внешних условиях. Состояние системы, в котором хотя бы
один из параметров не имеет определенного значения, называется неравновесным.
Термодинамическим процессом называется процесс перехода системы из одного состояния в другое.
Всякий термодинамический процесс связан с нарушением равновесия системы. Следовательно, при
протекании какого-либо процесса система последовательно проходит через неравновесные состояния.
Однако, при достаточно медленном протекании реального процесса (например, медленное сжатие газа,
находящегося в цилиндре под поршнем) состояние системы в каждый момент времени можно считать
равновесным, и бесконечно медленный процесс будет состоять из последовательных равновесных
состояний. Таким образом, процесс называется равновесным или квазистатическим, если он
состоит из последовательных равновесных состояний.
При изменении направления равновесного процесса (например, замене сжатия газа расширением)
система будет проходить через те же состояния, что и при прямом процессе, но в обратной
последовательности. Поэтому равновесные процессы являются обратимыми.
Круговым процессом или циклом называют такой процесс, в результате которого термодинамическая
система возвращается в исходное состояние.
4.
12
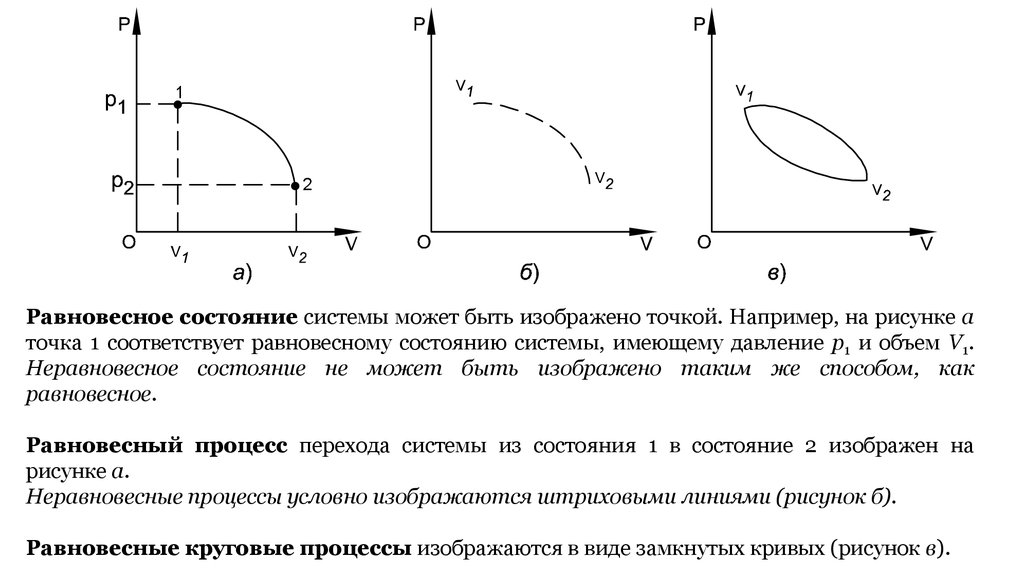
Равновесное состояние системы может быть изображено точкой. Например, на рисунке а
точка 1 соответствует равновесному состоянию системы, имеющему давление p1 и объем V1.
Неравновесное состояние не может быть изображено таким же способом, как
равновесное.
Равновесный процесс перехода системы из состояния 1 в состояние 2 изображен на
рисунке а.
Неравновесные процессы условно изображаются штриховыми линиями (рисунок б).
Равновесные круговые процессы изображаются в виде замкнутых кривых (рисунок в).
5.
Уравнение состояние. Основные положения МКТПараметры состояния системы, находящейся в равновесном состоянии, связаны между собой определенной
функциональной зависимостью типа
f p,V , T 0
Соотношение, определяющее связь между параметрами состояния какой-либо системы, называется
уравнением состояния системы.
Уравнение состояния в статистической физике выводится теоретически, а в термодинамике получается
опытным путем, и в этом состоит взаимосвязь статистического метода исследования с термодинамическим
методом.
Молекулярная физика базируется на молекулярно-кинетической теории строения вещества (МКТ),
исходными положениями которой являются следующие:
все вещества состоят из очень большого числа частиц (атомов, молекул или ионов)
частицы вещества находятся в непрерывном хаотическом движении (это движение называется
тепловым);
частицы вещества взаимодействуют между собой, причем это взаимодействие существенно зависит от
типа частиц и расстояния между ними.
6.
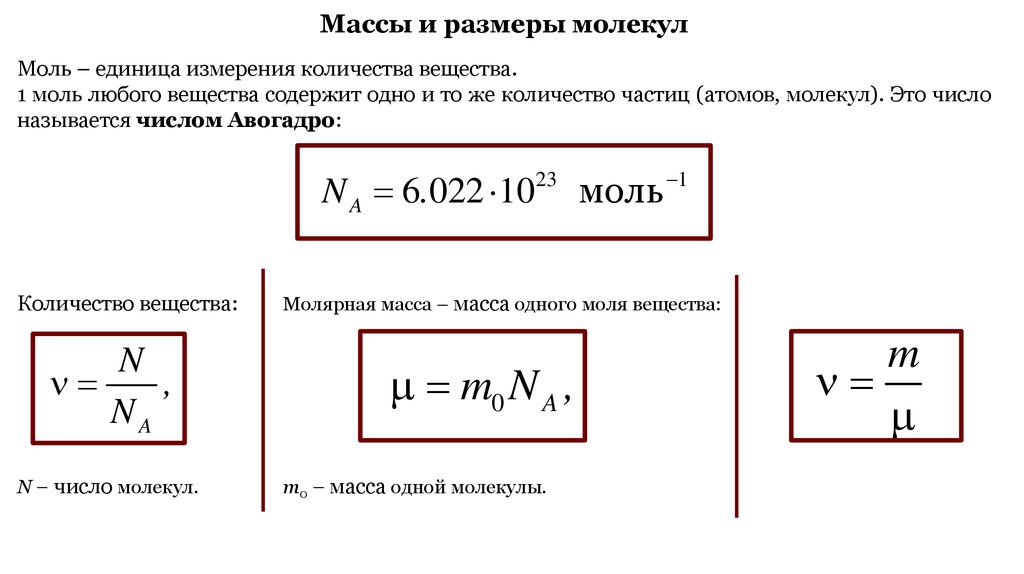
Массы и размеры молекулМоль – единица измерения количества вещества.
1 моль любого вещества содержит одно и то же количество частиц (атомов, молекул). Это число
называется числом Авогадро:
N A 6.022 10
Количество вещества:
N
,
NA
N – число молекул.
23
моль
1
Молярная масса – масса одного моля вещества:
m0 N A ,
m0 – масса одной молекулы.
m
7.
Идеальный газДля описания свойств каких-либо объектов обычно пользуются модельными представлениями. Вид
модели выбирается в зависимости от характера решаемой задачи. В частности, при исследовании свойств
достаточно разреженных газов в молекулярной физике применяется модель так называемого
идеального газа.
Идеальным газом называется газ, молекулы которого не взаимодействуют друг с другом на
расстоянии и имеют малые собственные размеры.
Кроме того, считается, что:
молекулы идеального газа при взаимных столкновениях и ударах о стенки сосуда ведут себя как
абсолютно упругие шарики;
движение каждой молекулы идеального газа подчиняется законам классической механики, при этом
между столкновениями каждая молекула движется равномерно и прямолинейно;
связи между атомами в многоатомных молекулах идеального газа абсолютно жесткие (это положение
нарушается при высоких температурах газа: атомы получают возможность совершать колебания друг
относительно друга, и связи между ними в этом случае следует считать упругими).
8.
ОСНОВНОЕ УРАВНЕНИЕ МКТ.Давление идеального газа.
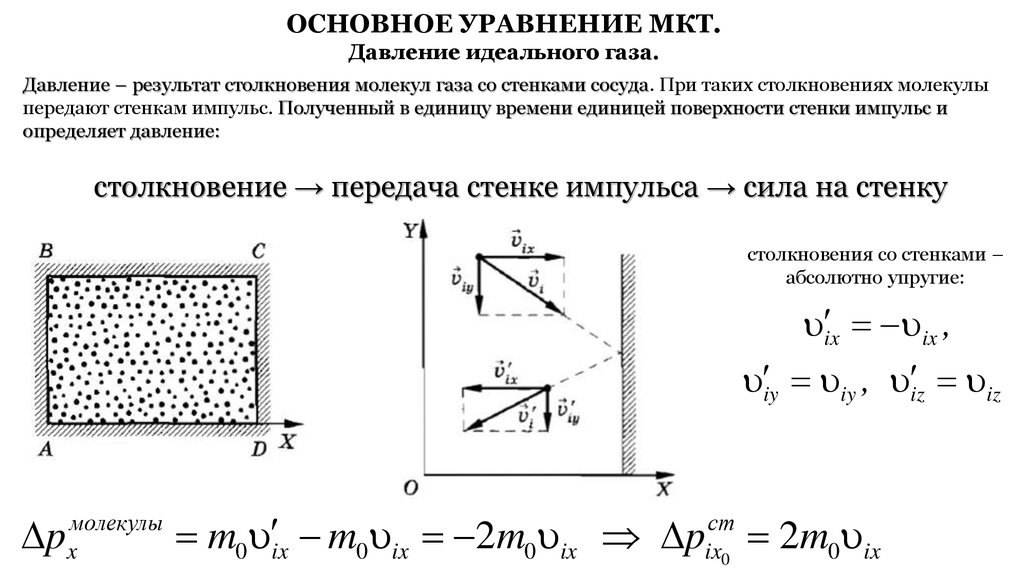
Давление – результат столкновения молекул газа со стенками сосуда. При таких столкновениях молекулы
передают стенкам импульс. Полученный в единицу времени единицей поверхности стенки импульс и
определяет давление:
столкновение → передача стенке импульса → сила на стенку
столкновения со стенками –
абсолютно упругие:
ix ix ,
iy iy , iz iz
p
молекулы
x
ст
m0 ix m0 ix 2m0 ix pix0 2m0 ix
9.
число молекул со скоростями υix > 0,которые за время Δt долетят до
рассматриваемой стенки сосуда:
N i ni ix S t
ni - концентрация молекул i-той группы
(число молекул в единице объема, xсоставляющие
скоростей
которых
близки к υix > 0 )
Импульс, который молекулы со скоростями, близкими к υix>0, передают стенке за время Δt:
p
ст
ix
2ni m0 ix S t
2
Импульс, который все молекулы, летящие к стенке, передают за время Δt:
p
ст
x
2m0 S t ni ix
2
ix 0
10.
Средний квадрат проекции скорости на ось Х:2
x
ni
2
ix
ix
n
Все направления равновероятны::
1
2
n
n
i ix
i ix ,
2 ix
ix 0
2
2x 2y 2z ,
2x 2y 2z 2 ,
2
x
1 2
3
ст
x
2m0 S t ni ix ,
ст
x
m0 S t ni ix ,
p
ст
x
nm0 S t,
p
ст
x
1
2
nm0 S t
3
p
p
2
ix 0
2
ix
2
x
1
2
p nm0
3
Давление – импульс,
переданный в единицу
времени единице
поверхности
11.
Средняя квадратичная скорость:2
n
i
2
i
n
Давление идеального газа:
1
2
p nm0
3
Средняя кинетическая энергия
поступательного движения молекулы:
пост
m0
2
2
2
p n пост
3
12.
ТЕМПЕРАТУРАТемпература характеризует состояние теплового равновесия макроскопической
системы: во всех частях системы, находящейся в состоянии теплового
равновесия, температура имеет одно и то же значение.
К отдельным молекулам понятие температуры неприменимо.
С точки зрения МКТ температура – мера средней кинетической энергии
хаотического движения молекул в макроскопических телах:
пост
3
kT
2
средняя кинетическая энергия
поступательного движения
молекул
пост
k 1.38 10
23
Дж/К – постоянная Больцмана
13.
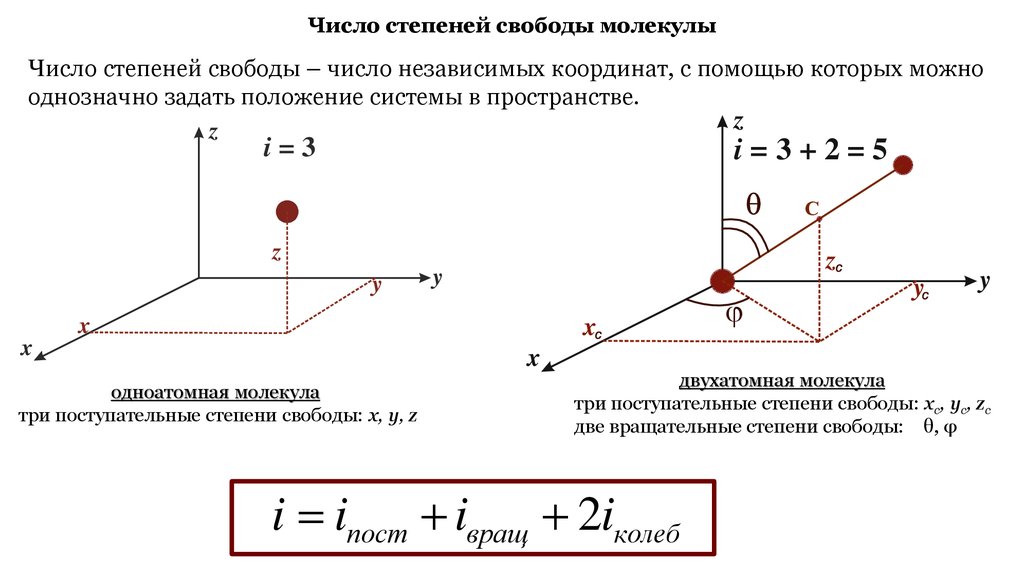
Число степеней свободы молекулыЧисло степеней свободы – число независимых координат, с помощью которых можно
однозначно задать положение системы в пространстве.
z
z
i=3
i=3+2=5
С
z
y
z
y
x
x
x
x
одноатомная молекула
три поступательные степени свободы: x, y, z
y
y
двухатомная молекула
три поступательные степени свободы: xc, yc, zc
две вращательные степени свободы: θ, φ
i iпост iвращ 2iколеб
14.
Теорема о равномерном распределении кинетической энергии по степеням свободы:в состоянии теплового равновесия на каждую степень свободы
приходится в среднем одна и та же кинетическая энергия
пост
3
kT , iпост 3
2
Т.е. на каждую поступательную степень
свободы приходится в среднем энергия
i
kT
2
средняя энергия
молекулы
1
kT
2
15.
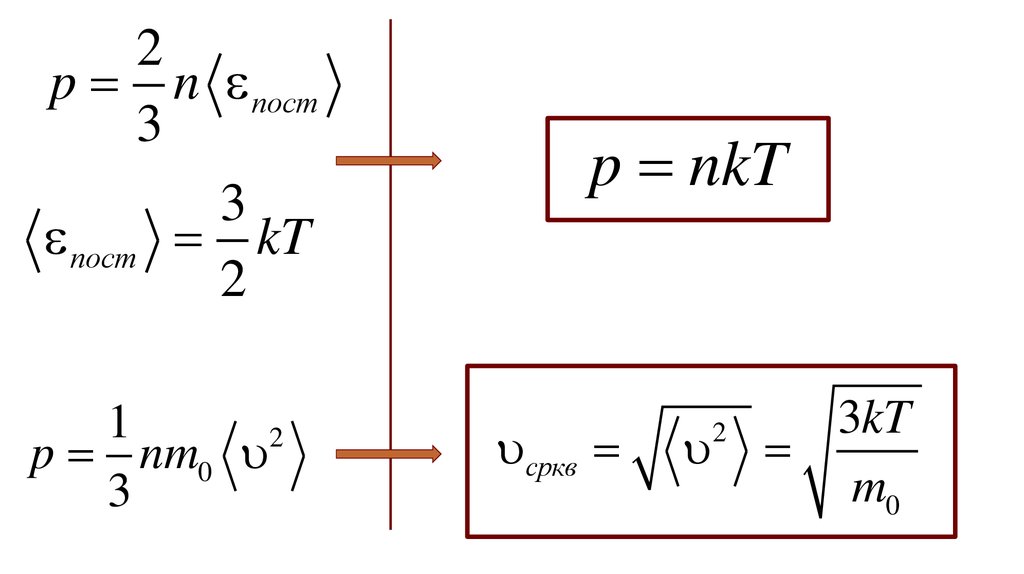
2p n пост
3
3
пост kT
2
1
2
p nm0
3
p nkT
сркв
2
3kT
m0
16.
Уравнение состояния идеального газа.Газовые законы.
N
p nkT kT ,
V
N
n , N N A ,
V
pV N AkT
R N Ak 8.31
Дж/моль∙К –
универсальная газовая постоянная
pV RT
17.
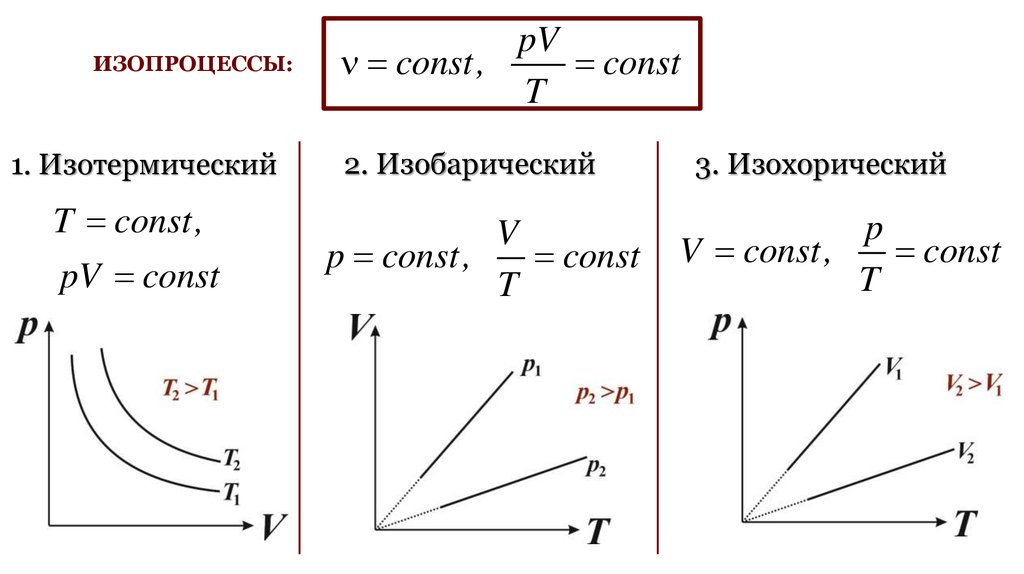
ИЗОПРОЦЕССЫ:1. Изотермический
T const,
pV const
pV
const,
const
T
2. Изобарический
V
p const,
const
T
3. Изохорический
p
V const,
const
T
18.
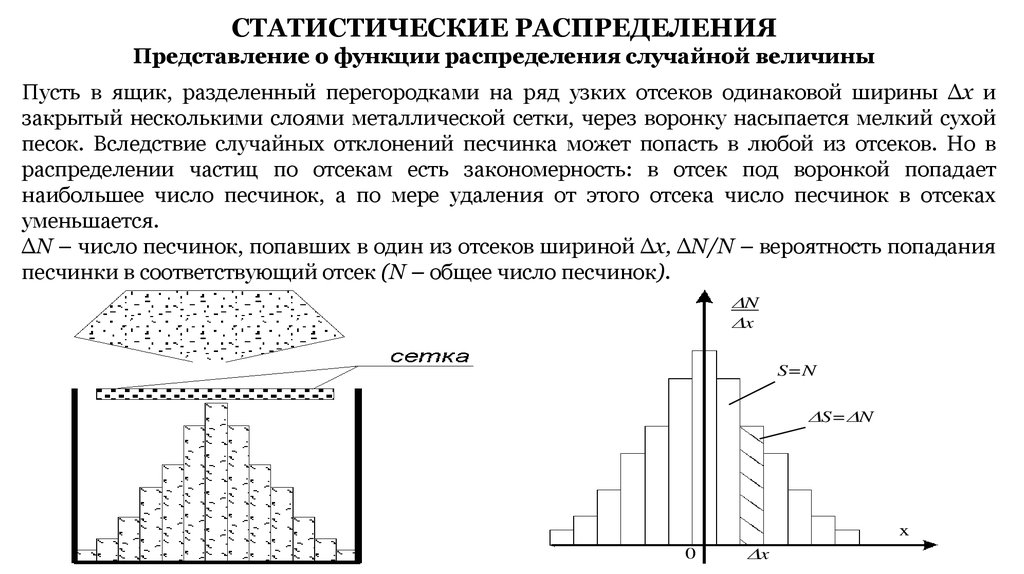
СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯПредставление о функции распределения случайной величины
Пусть в ящик, разделенный перегородками на ряд узких отсеков одинаковой ширины Δx и
закрытый несколькими слоями металлической сетки, через воронку насыпается мелкий сухой
песок. Вследствие случайных отклонений песчинка может попасть в любой из отсеков. Но в
распределении частиц по отсекам есть закономерность: в отсек под воронкой попадает
наибольшее число песчинок, а по мере удаления от этого отсека число песчинок в отсеках
уменьшается.
ΔN – число песчинок, попавших в один из отсеков шириной Δx, ΔN/N – вероятность попадания
песчинки в соответствующий отсек (N – общее число песчинок).
N
x
S=N
S= N
x
0
x
19.
При уменьшении ширины отсека (в пределе Δx→0) ступенчатая диаграмма перейдет вплавную линию f(x).
Функция f(x) называется функцией распределения:
dN
f x dx
dP
N
вероятность попадания песчинки в точку,
имеющую координату в интервале
от x до x+dx
Площадь под кривой:
Среднее значение х:
Среднее значение
х2:
f x dx 1
x xf x dx
x
2
x 2 f x dx
20.
РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО СКОРОСТЯМ(РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА)
Молекулы газа, участвуя в непрерывном хаотическом движении, сопровождающемся
многочисленными столкновениями их друг с другом, в каждый момент времени обладают
разными по модулю и направлению скоростями. То, что в газе имеются молекулы как с очень
большими, так и с очень малыми скоростями, подтверждается опытами по их измерению.
И хотя скорости отдельных молекул газа непостоянны, в состоянии теплового
равновесия существует некоторое стационарное распределение молекул по
модулям скоростей, то есть доля молекул со скоростями в том или ином
диапазоне не изменяется.
dN
f dw f d x d y d z
N
доля молекул,
компоненты скоростей которых
лежат в интервалах между
υx и υx +dυx, υy и υy +dυy, υz и υz +dυz.
21.
x d xy d y
z d z
вероятность того,
что х-составляющая
скорости молекулы
лежит в интервале от
υx до υx +dυx
вероятность того,
что y-составляющая
скорости молекулы
лежит в интервале от
υy до υy +dυy
вероятность того,
что z-составляющая
скорости молекулы
лежит в интервале от
υz до υz +dυz
(две другие составляющие
при том могут быть какими
угодно)
(две другие составляющие
при том могут быть какими
угодно)
(две другие составляющие
при том могут быть какими
угодно)
Идея Максвелла:
попадания компонент скорости молекулы в интервалы
(υx; υx +dυx), (υy; υy +dυy) и (υz; υz +dυz) – независимые события:
f x y z
22.
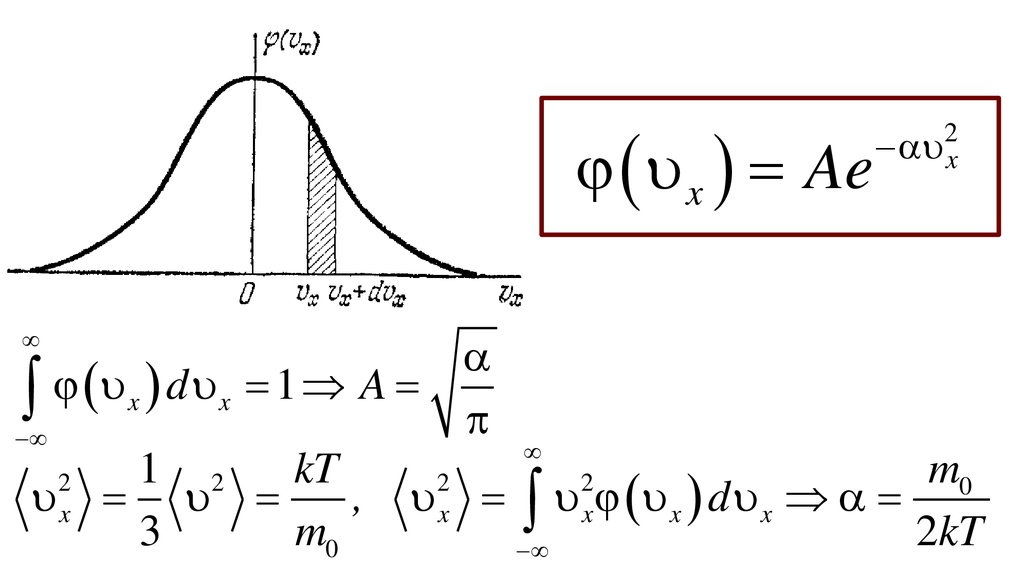
x Ae2
x
d
1
A
x
x
1 2
kT
m0
2
2
2
x
, x x x d x
3
m0
2kT
23.
m0x
exp
2 kT
m0 2x
2 kT
f x y z
m0 2y
m0
y
exp 2 kT
2 kT
m0
z
exp
2 kT
m0 2z
2 kT
m0
f
2 kT
3/ 2
m0
exp
2kT
2
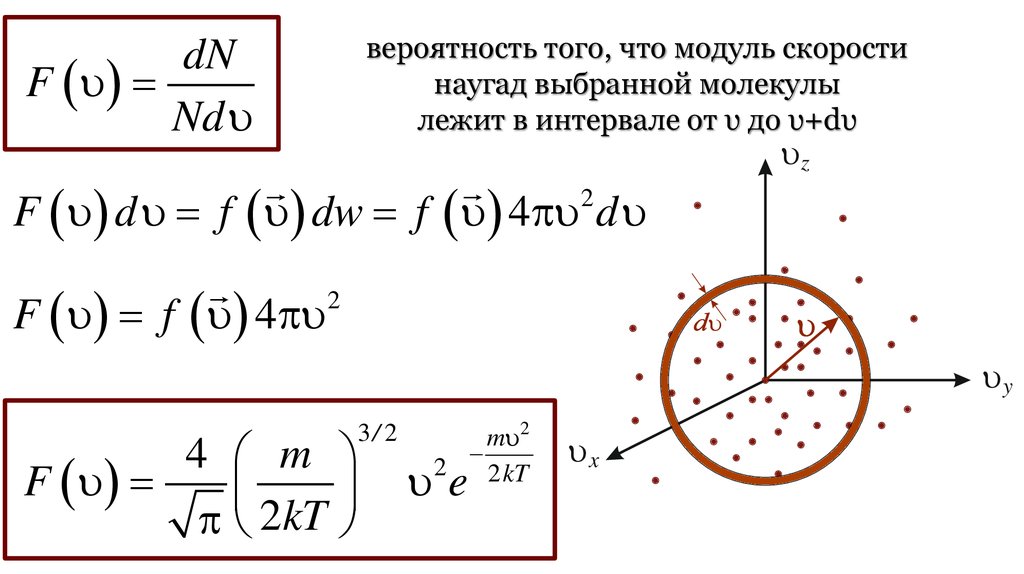
24.
вероятность того, что модуль скоростинаугад выбранной молекулы
лежит в интервале от υ до υ+dυ
dN
F
Nd
z
F d f dw f 4 d
2
F f 4
2
y
4 m
F
2kT
3/ 2
m 2
2
2 kT
e
x
25.
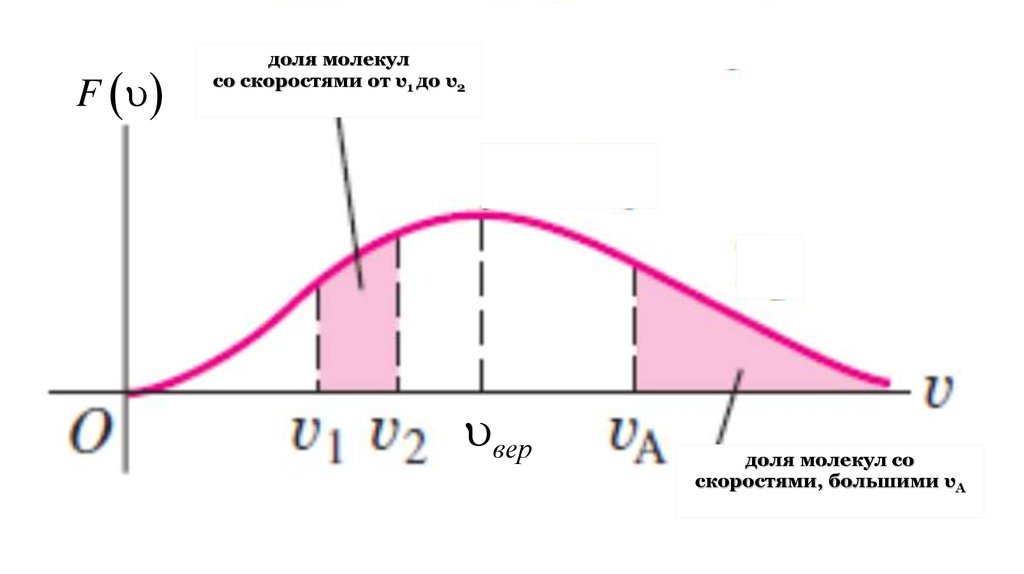
Fдоля молекул
со скоростями от υ1 до υ2
вер
доля молекул со
скоростями, большими υА
26.
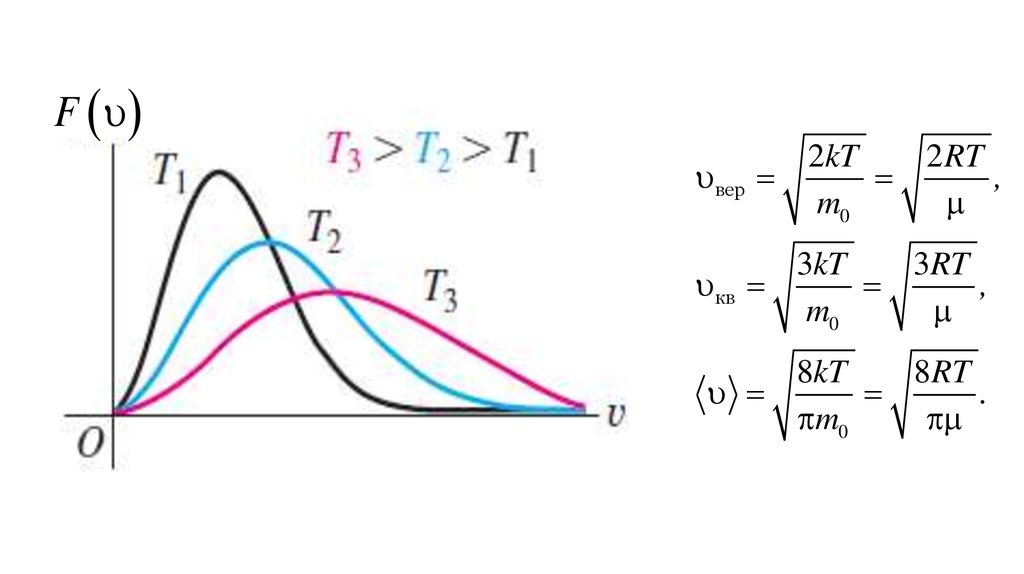
Fвер
2kT
2 RT
,
m0
3kT
3RT
кв
,
m0
8kT
8 RT
.
m0
27.
РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ В ПОТЕНЦИАЛЬНОМ СИЛОВОМ ПОЛЕ(РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА)
Выделим мысленно вертикальный столб воздуха с площадью основания S. Пусть на высоте h давление
равно p, тогда на высоте (h+dh) давление равно (p+dp). Так как давление с увеличением высоты падает, то
его приращение будет отрицательным (dp< 0).
p+dp
Условие равновесия выделенного столба газа имеет вид:
S
dh
p
h0=0; P0
dmg S p p dp Sdp.
Для идеального газа давление равно
p nkT
h
dp dnkT ,
где n – концентрация молекул газа.
Масса dm может быть записана как
dm m0 dN m0 ndV m0 nSdh,
где m0 – масса одной молекулы, dN – число молекул в
объеме столба dV.
28.
Тогдаdn m0 gdh
.
n
kT
n
Интегрируя, получим:
h
m0 g
n0 m0 gh
dn
dh ln
n n0 e
n 0 kT
n
kT
n0
m0 gh
kT
,
где n0 - концентрация на высоте h = 0.
m0 gh U
n n0 e
- потенциальная энергия молекулы газа в поле силы тяжести.
U
kT
распределение
Больцмана
U – потенциальная энергия
молекулы газа в потенциальном
силовом поле,
n0 – концентрация при U = 0.
29.
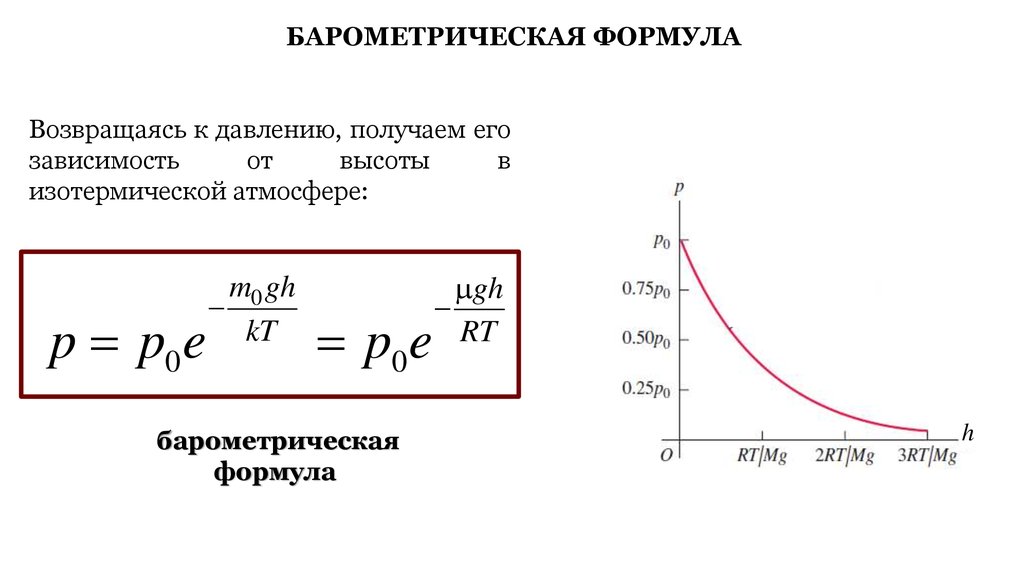
БАРОМЕТРИЧЕСКАЯ ФОРМУЛАВозвращаясь к давлению, получаем его
зависимость
от
высоты
в
изотермической атмосфере:
p p0 e
m0 gh
kT
p0 e
барометрическая
формула
gh
RT
h
30.
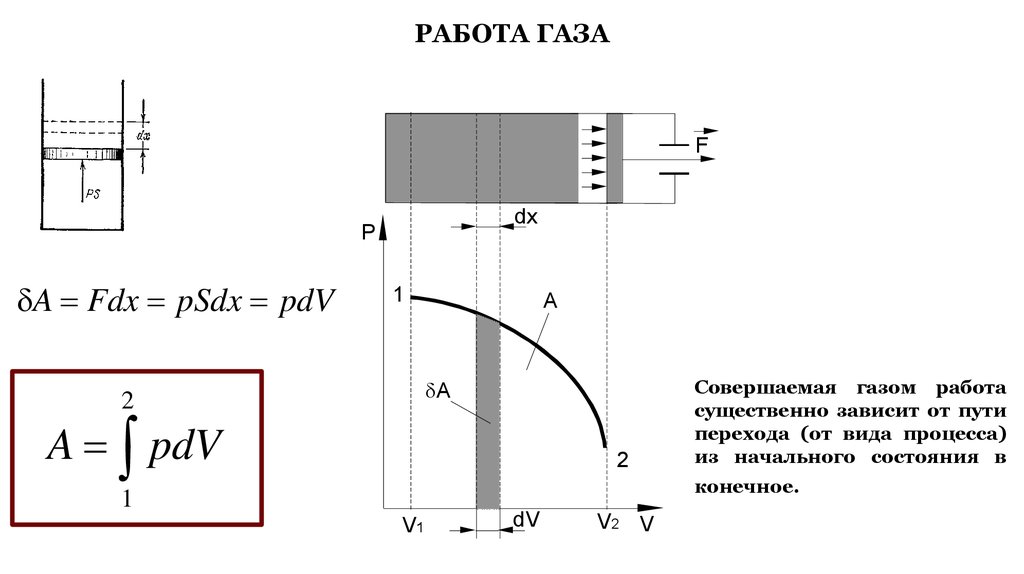
РАБОТА ГАЗАF
dx
P
A Fdx pSdx pdV
1
A
A
2
A pdV
2
Совершаемая газом работа
существенно зависит от пути
перехода (от вида процесса)
из начального состояния в
конечное.
1
V1
dV
V2 V
31.
АДИАБАТИЧЕСКАЯ ОБОЛОЧКАОболочка называется адиабатической, если состояние заключенной в ней
системы остается неизменным при любых изменениях температуры
окружающих тел, если только значения внешних параметров поддерживаются
постоянными. Т.е. изменить состояние системы в адиабатической оболочке
можно только путем изменения внешних параметров.
Система, заключенная в адиабатическую оболочку, называется адиабатически
изолированной.
Если система тел адиабатически изолирована, то работа внешних
сил над этой системой зависит только от ее начального и
конечного состояний, но не зависит от способа (пути) перехода.
32.
ВНУТРЕННЯЯ ЭНЕРГИЯ СИСТЕМЫВнутренней энергией системы U называется функция
состояния,
приращение
которой
во
всяком
процессе,
совершаемом системой в адиабатической оболочке, равно
работе внешних сил над системой при ее переходе из начального
состояния в конечное.
U U 2 U1 A12внеш
A12внеш A12
U1 U 2 A12
Понятие внутренней энергии относится только к равновесным состояниям термодинамических систем.
33.
КОЛИЧЕСТВО ТЕПЛОТЫПроцесс обмена внутренними энергиями соприкасающихся тел, не
сопровождающийся производством макроскопической работы, называется
теплообменом.
Энергия, переданная телу окружающей средой в результате теплообмена,
называется количеством теплоты Q.
Количество теплоты – функция процесса.
34.
ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИСистема (I+II) заключена в адиабатическую оболочку.
Граница АВ – теплопроводящая.
Оболочка системы II – жесткая.
A12 U1 U 2 U I1 U II1 U I 2 U II 2 ,
A12 AI ,
U II1 U II 2 QI ,
AI U I1 U I 2 QI или QI U I AI .
Тепло, полученное системой, идет на приращение ее внутренней
энергии и на совершение ею работы.
35.
Q U A U 2 U1 A,Q dU A dU pdV
Если U1 = U2 и Q = 0, то А = 0.
Т.е. невозможен процесс, единственным результатом которого
является производство работы без каких бы то ни было изменений
в других телах (невозможность вечного двигателя первого рода).
36.
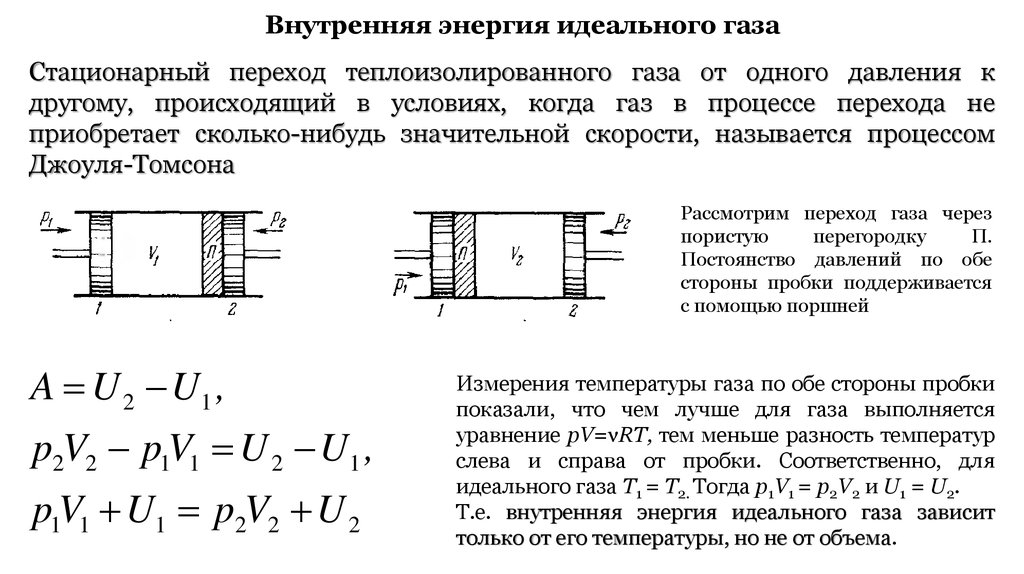
Внутренняя энергия идеального газаСтационарный переход теплоизолированного газа от одного давления к
другому, происходящий в условиях, когда газ в процессе перехода не
приобретает сколько-нибудь значительной скорости, называется процессом
Джоуля-Томсона
Рассмотрим переход газа через
пористую
перегородку
П.
Постоянство давлений по обе
стороны пробки поддерживается
с помощью поршней
A U 2 U1 ,
p2V2 p1V1 U 2 U1 ,
p1V1 U1 p2V2 U 2
Измерения температуры газа по обе стороны пробки
показали, что чем лучше для газа выполняется
уравнение pV=νRT, тем меньше разность температур
слева и справа от пробки. Соответственно, для
идеального газа Т1 = Т2. Тогда p1V1 = p2V2 и U1 = U2.
Т.е. внутренняя энергия идеального газа зависит
только от его температуры, но не от объема.
37.
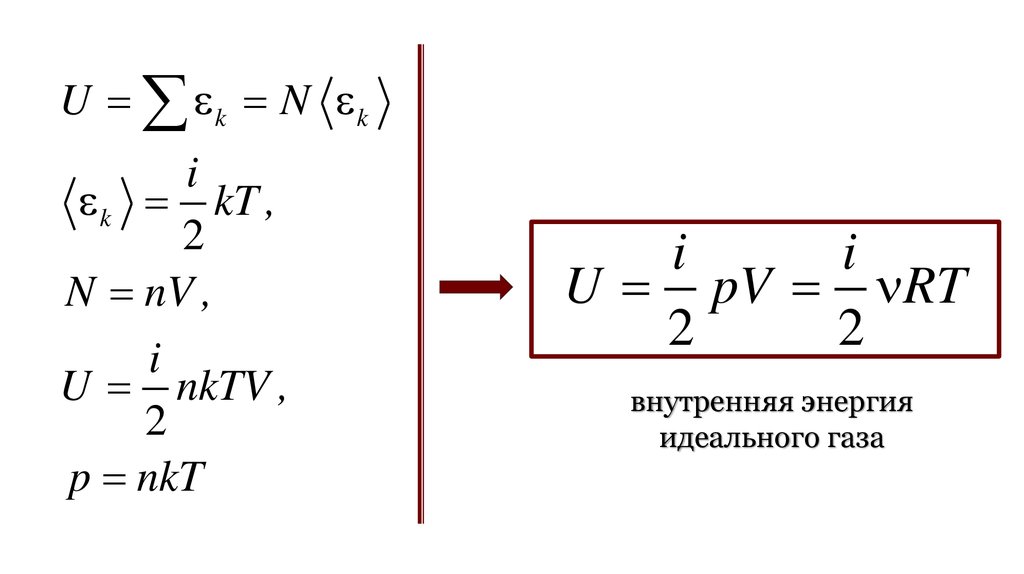
U k N ki
k kT ,
2
N nV ,
i
U nkTV ,
2
p nkT
i
i
U pV RT
2
2
внутренняя энергия
идеального газа
38.
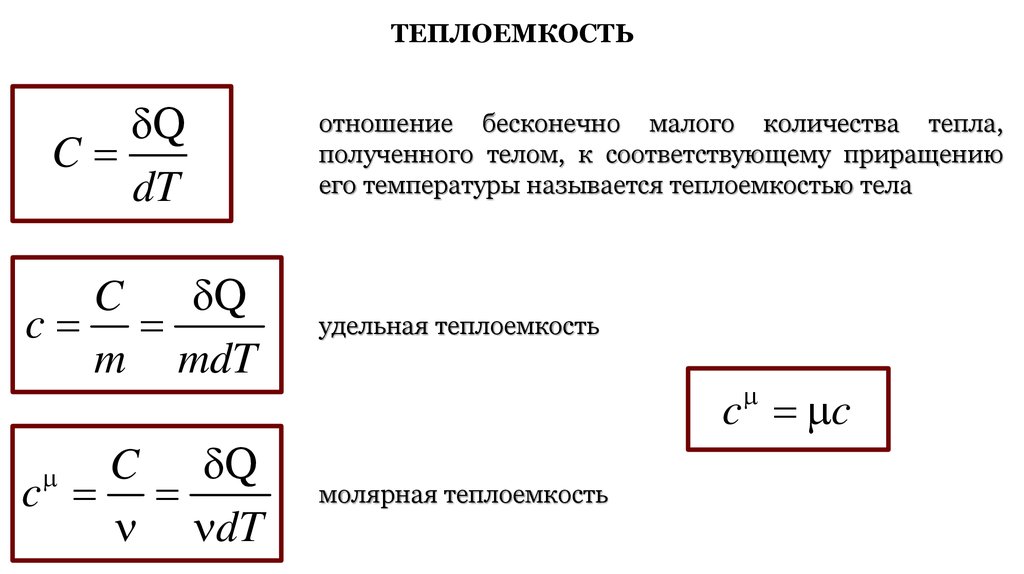
ТЕПЛОЕМКОСТЬQ
C
dT
отношение бесконечно малого количества тепла,
полученного телом, к соответствующему приращению
его температуры называется теплоемкостью тела
C
Q
c
m mdT
удельная теплоемкость
C Q
c
dT
молярная теплоемкость
c c
39.
Молярные теплоемкости идеального газапри постоянном объеме и постоянном давлении
Q dU A dU pdV
C
,
dT
dT
dT
dT
U
U
dU
dV
dT ,
V T
T V
dV
U U
C
p
T V V T
dT
40.
UCV
,
T V
U
V
C p CV
p
V T
T p
U
У идеального газа внутренняя энергия от объема не зависит, поэтому
0.
V T
dU
CV
,
dT
V
C p CV p
T p
Для одного моля идеального газа:
R
V
pV RT
,
T p p
C p CV R
уравнение Майера
i
U RT ,
2
i
i 2
CV R, C p
R
2
2
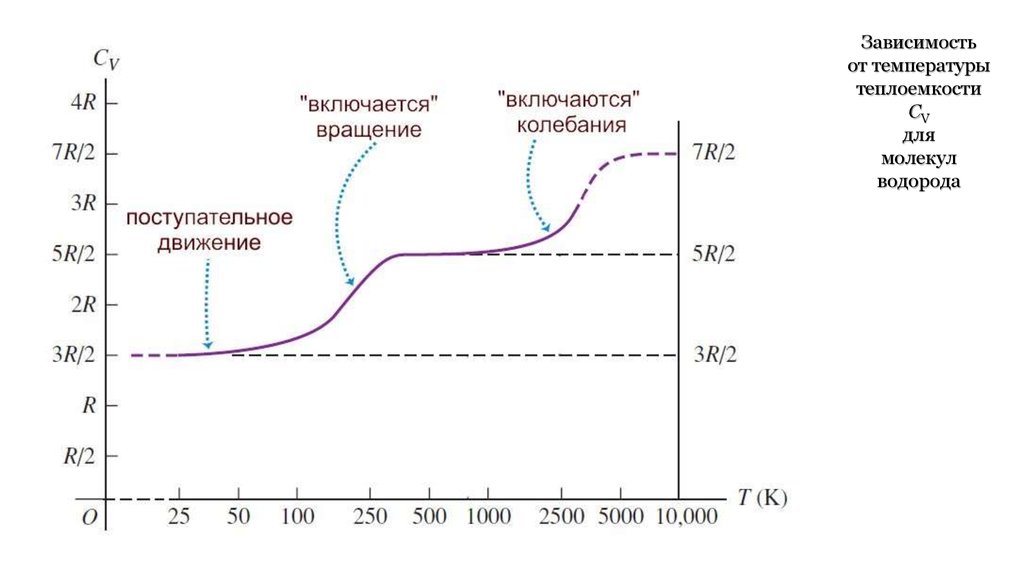
41.
Зависимостьот температуры
теплоемкости
СV
для
молекул
водорода
42.
АДИАБАТНЫЙ ПРОЦЕССПроцесс, происходящий без подвода и отвода тепла, называется адиабатным:
Q 0 ,
dU CV dT ,
dU A pdV
CV R C p ,
pV RT d pV RdT ,
Cp
dpV pdV RdT ,
CV
CV
dpV pdV pdV ,
R
CV R
dpV
pdV 0,
CV
,
dpV pdV 0 ,
dp
dV
0,
p
V
pV const
43.
i 2CV
i
Cp
pV const
TV
Tp
1
1
const,
const
показатель адиабаты
уравнение Пуассона
(уравнение адиабаты
в координатах (p, V))
уравнения адиабаты
в координатах
(T, V) и (p, T)
при адиабатическом
расширении температура
газа понижается
44.
ПОЛИТРОПНЫЙ ПРОЦЕССПроцесс, в котором теплоемкость остается постояннной, называется адиабатным:
Q dU A, CdT CV dT pdV
pV RT d pV RdT ,
dpV pdV
dT
,
R
C CV Vdp C CV R pdV 0,
C p CV R,
Vdp
C Cp
C CV
pdV 0 ,
n
C Cp
C CV
,
dpV npdV 0,
dp
dV
n
0,
p
V
pV const
n
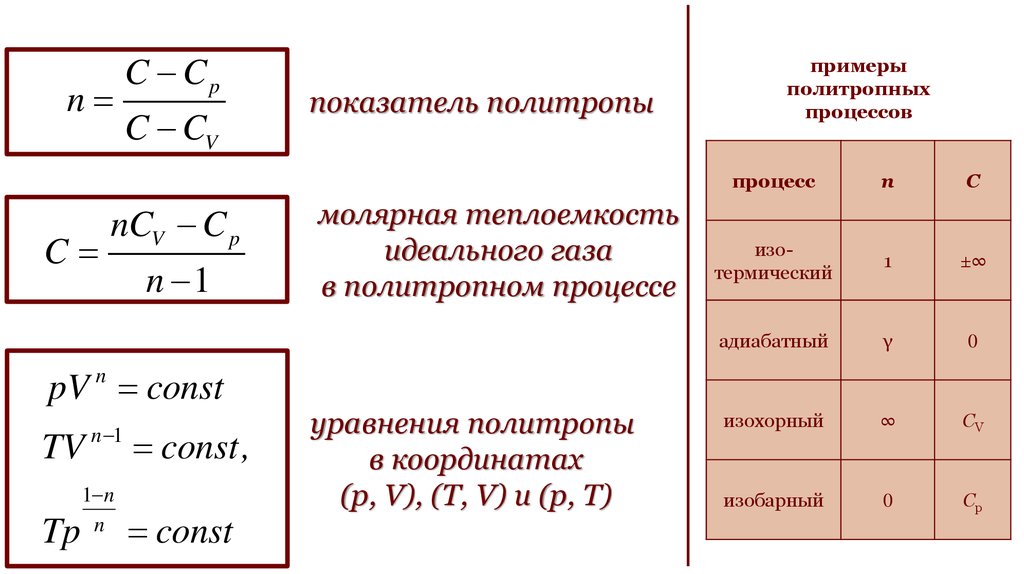
45.
nC
C Cp
C CV
nCV C p
n 1
pV const
показатель политропы
молярная теплоемкость
идеального газа
в политропном процессе
примеры
политропных
процессов
процесс
n
C
изотермический
1
±∞
адиабатный
γ
0
изохорный
∞
CV
изобарный
0
Cp
n
TV
Tp
n 1
1 n
n
const,
const
уравнения политропы
в координатах
(p, V), (T, V) и (p, T)
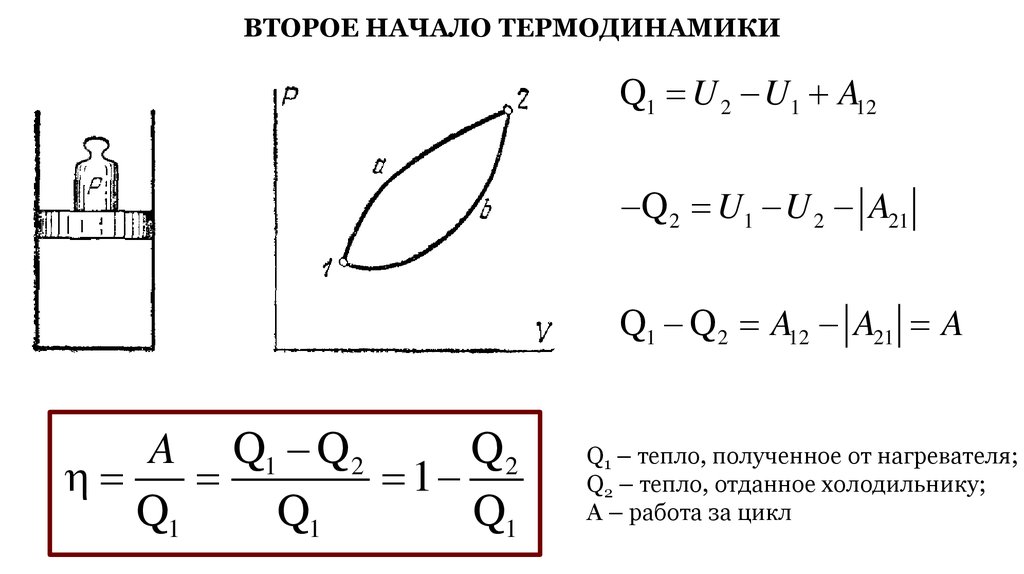
46.
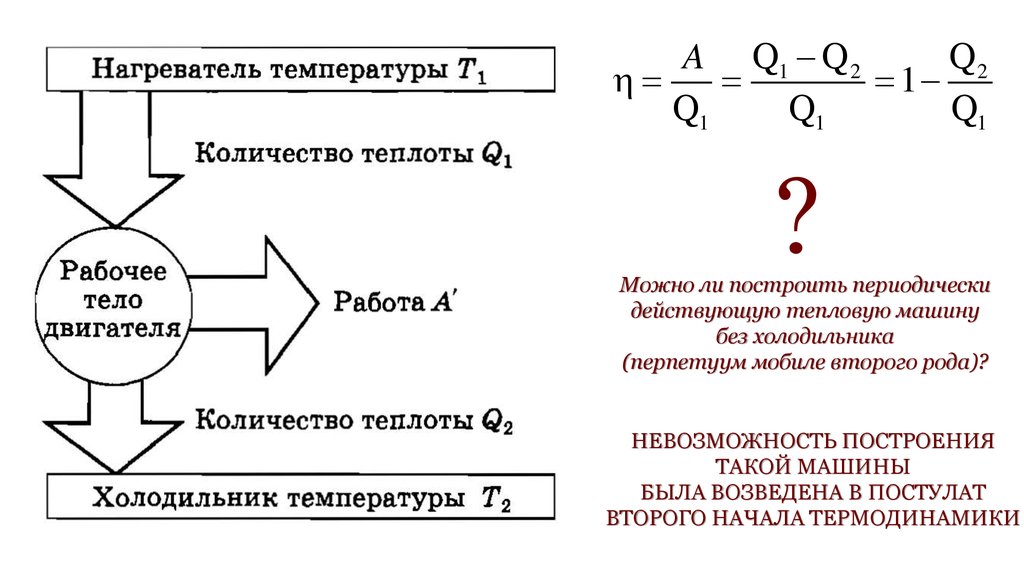
ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИQ1 U 2 U1 A12
Q 2 U1 U 2 A21
Q1 Q 2 A12 A21 A
A Q1 Q 2
Q2
1
Q1
Q1
Q1
Q1 – тепло, полученное от нагревателя;
Q2 – тепло, отданное холодильнику;
A – работа за цикл
47.
A Q1 Q 2Q2
1
Q1
Q1
Q1
?
Можно ли построить периодически
действующую тепловую машину
без холодильника
(перпетуум мобиле второго рода)?
НЕВОЗМОЖНОСТЬ ПОСТРОЕНИЯ
ТАКОЙ МАШИНЫ
БЫЛА ВОЗВЕДЕНА В ПОСТУЛАТ
ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ
48.
ФОРМУЛИРОВКИ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ1. Формулировка Планка:
невозможно построить периодически действующую машину, единственным
результатом которой было бы поднятие груза за счет охлаждения
теплового резервуара
2. Формулировка Томсона:
невозможен круговой процесс, единственным результатом которого было бы
производство работы за счет охлаждения теплового резервуара
3. Формулировка Клаузиуса:
Теплота не может самопроизвольно переходить от тела менее нагретого к
телу более нагретому
49.
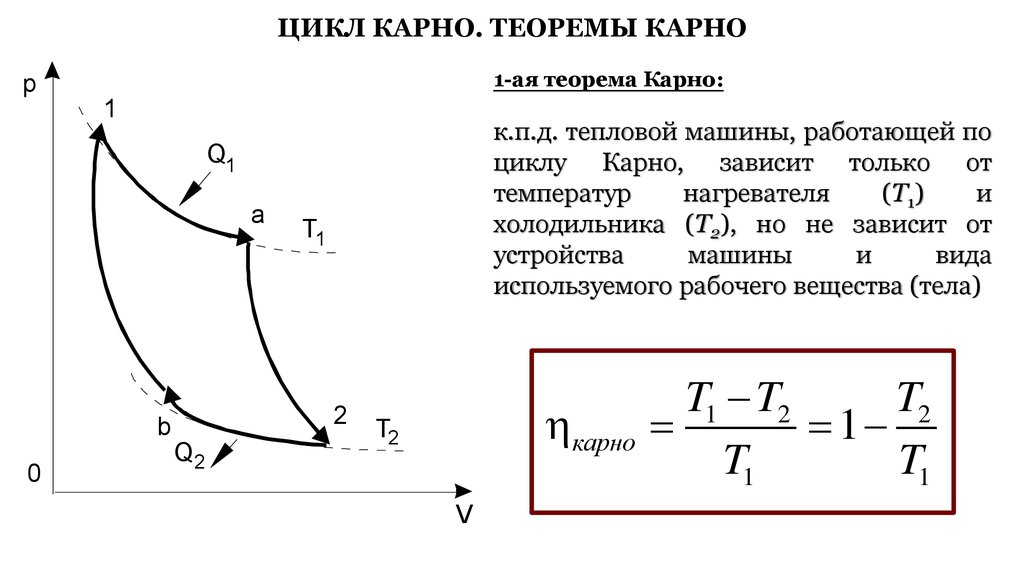
ЦИКЛ КАРНО. ТЕОРЕМЫ КАРНОp
1-ая теорема Карно:
1
к.п.д. тепловой машины, работающей по
циклу Карно, зависит только от
температур
нагревателя
(Т1)
и
холодильника (Т2), но не зависит от
устройства
машины
и
вида
используемого рабочего вещества (тела)
Q1
a
b
0
T1
2
Q2
карно
T2
V
T1 T2
T2
1
T1
T1
50.
НЕРАВЕНСТВО КЛАУЗИУСА (ЧАСТНЫЙ СЛУЧАЙ)2-ая теорема Карно:
к.п.д. всякой тепловой машины не может превосходить к.п.д. идеальной
машины, работающей по циклу Карно с теми же самыми температурами
нагревателя (Т1) и холодильника (Т2):
Q2
T2
Q1 Q 2
карно , 1
1 ,
0
Q1
T1
T1 T2
Не будем далее различать, какой тепловой резервуар является нагревателем, а
какой – холодильником. Условимся считать количество теплоты, полученное
системой (и, соответственно, отданное резервуаром), положительным. Тогда:
Q1 Q 2
0
T1 T2
неравенство Клаузиуса
в частном случае
51.
НЕРАВЕНСТВО КЛАУЗИУСА (ОБЩИЙ СЛУЧАЙ).РАВЕНСТВО КЛАУЗИУСА. ЭНТРОПИЯ
Q
0
T
При окончательной формулировке неравенства можно
пользоваться представлением о теплообмене между
рассматриваемой системой и окружающей средой. В
таком представлении Т – температура среды, δQ –
бесконечно малое количество тепла, переданное системе
при температуре Т. Процесс, совершаемый системой,
должен быть круговым.
Пусть совершаемый системой круговой процесс квазистатический. Тогда он обратим и может
идти в обратном направлении:
в прямом направлении:
в обратном направлении:
Q
T 0
Q
T 0
Q Q,
Q
0
T
Q
0
T
52.
Q0
T
Q
0
T
Q
0
T
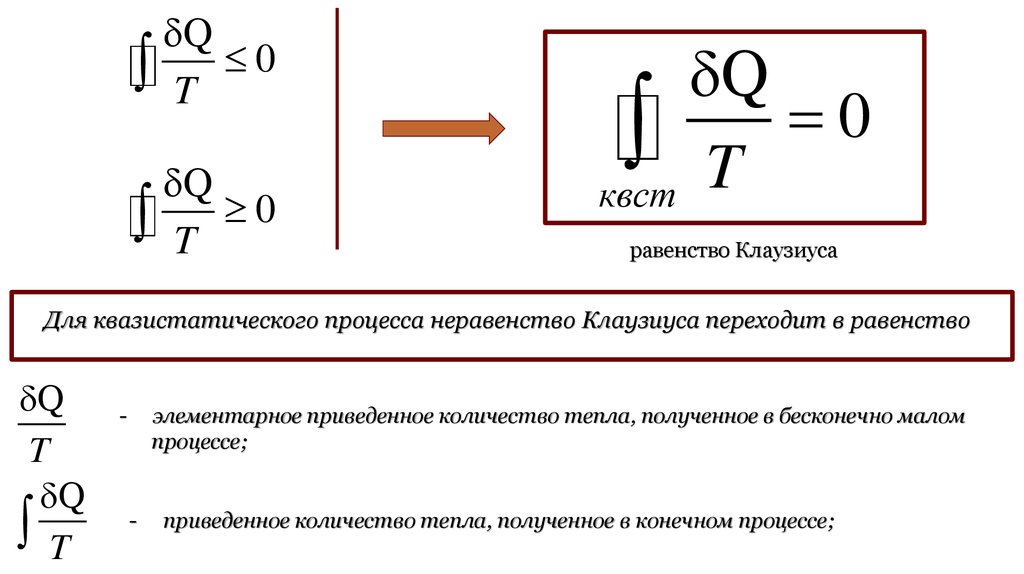
квст
равенство Клаузиуса
Для квазистатического процесса неравенство Клаузиуса переходит в равенство
Q
T
Q
T
-
элементарное приведенное количество тепла, полученное в бесконечно малом
процессе;
-
приведенное количество тепла, полученное в конечном процессе;
53.
QQ
Q
0
,
T
T 2 II 1 T
1I 2
пути I и II перехода системы из
состояния 1 в состояние 2 –
квазистатические
Q
Q
Q
Q
2 II 1 T 1II 2 T , 1 I 2 T 1II 2 T 0,
Q
Q
1I 2 T 1II 2 T
приведенное количество тепла,
квазистатически полученное системой,
не зависит от пути перехода, а
определяется лишь начальным и конечным
состояниями системы
54.
ЭНТРОПИЯЭнтропия – функция состояния системы. Разность энтропий в двух
равновесных состояниях равна приведенному количеству тепла, которое
нужно сообщить системе, чтобы перевести ее из состояния 1 в состояние 2 по
любому квазистатическому пути:
Q
dS
,
T квст
Q
S S 2 S1
T
квст
1 2
55.
:Приращение энтропии идеального газа:Q
dS
, Q dU A CV dT pdV ,
T квст
Q
dT p
dT
dV
CV
dV CV
R
,
T
T T
T
V
S
1 2
квст
Q
T2
V2
CV ln Rln
T
T1
V1
56.
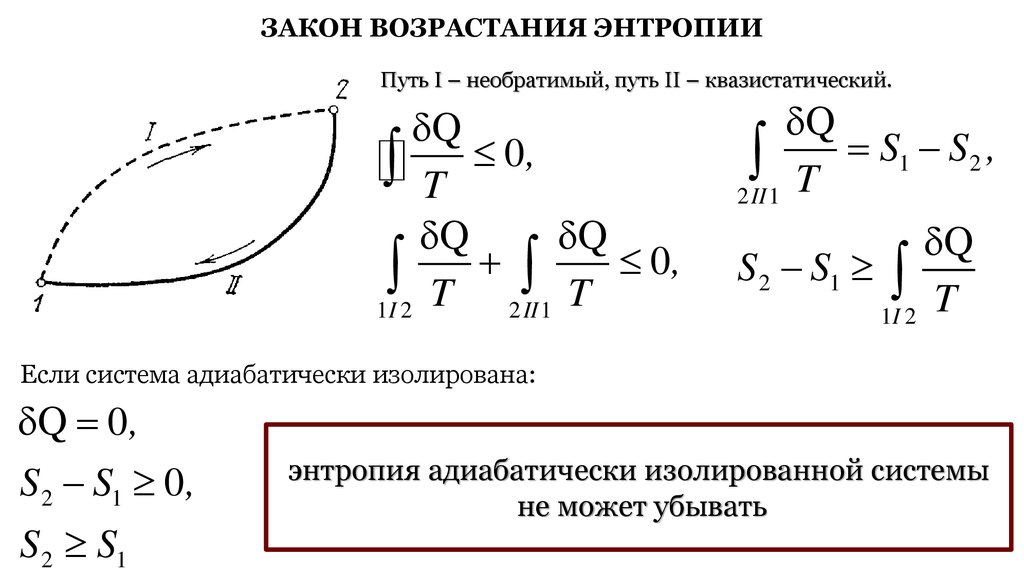
ЗАКОН ВОЗРАСТАНИЯ ЭНТРОПИИПуть I – необратимый, путь II – квазистатический.
Q
T 0,
Q
Q
1I 2 T 2 II 1 T 0,
Q
S
S
,
1
2
2 II 1 T
Q
S 2 S1
T
1I 2
Если система адиабатически изолирована:
Q 0 ,
S 2 S1 0 ,
S 2 S1
энтропия адиабатически изолированной системы
не может убывать
57.
СТАТИСТИЧЕСКИЙ СМЫСЛВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ
Состояние системы может быть задано с помощью макроскопических (то есть
характеризующих систему в целом) параметров: объема, давления, температуры.
Охарактеризованное таким образом состояние называется макросостоянием.
Если состояние системы охарактеризовано настолько детально, что оказываются
заданными состояния всех ее частиц, то состояние называют микросостоянием.
Всякое
макросостояние
микросостояниями.
может
быть
реализовано
Число
различных
микросостояний,
соответствующих
макросостоянию, называется его статистическим весом.
различными
данному
58.
МакросостояниеМикросостояние
Стат.
вес
Число молекул
Номера молекул
( )
Вероятность
(Р)
1
1/16
4
4/16
6
6/16
4
4/16
1
1/16
слева
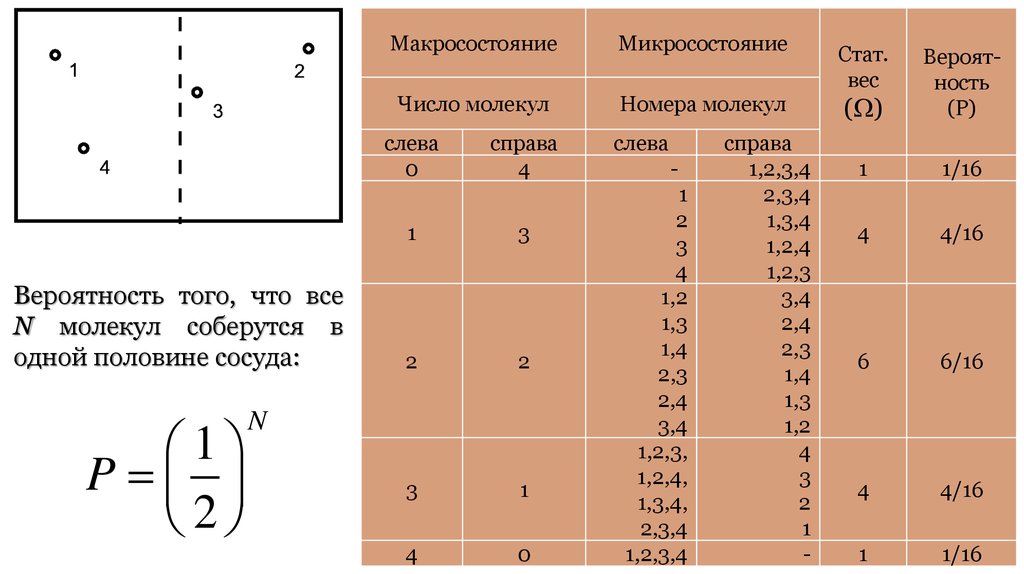
0
Вероятность того, что все
N молекул соберутся в
одной половине сосуда:
1
P
2
справа
4
1
3
2
2
3
1
4
0
N
слева
1
2
3
4
1,2
1,3
1,4
2,3
2,4
3,4
1,2,3,
1,2,4,
1,3,4,
2,3,4
1,2,3,4
справа
1,2,3,4
2,3,4
1,3,4
1,2,4
1,2,3
3,4
2,4
2,3
1,4
1,3
1,2
4
3
2
1
-
59.
Предоставленнаясамой
себе
система стремится переходить от
менее вероятных состояний к
более вероятным.
Самопроизвольные процессы в
изолированных
системах
сопровождаются
возрастанием
энтропии.
идея: наличие связи между энтропией и вероятностью состояния (статистическим весом)
S k ln
формула Больцмана
энтропия характеризует степень беспорядка в системе














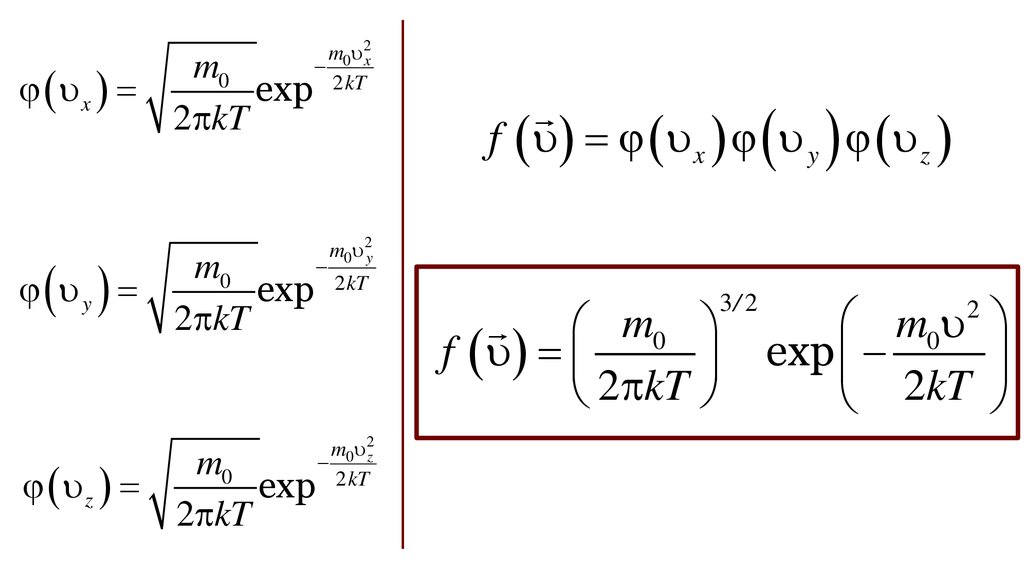




















 Физика
Физика








