Похожие презентации:
Кинематика сложного движения
1. КИНЕМАТИКА сложного движения
2. Сложное движение точки (тела) –
это такое движение, при которомточка (тело) одновременно
участвует в двух или более
движениях.
3.
Mr
О1
0
z
k О i
x
y
j
4.
• Движение тела относительно подвижнойсистемы координат называется
относительным движением (relatif).
• Движение тела относительно неподвижной
системы координат называется
абсолютным движением.
• Движение подвижной системы координат
относительно неподвижной системы координат
называется переносным движением (emporter).
5.
• Скорость и ускорение тела относительноподвижной системы координат называются
относительной скоростью vr
и относительным ускорением W
r
• Скорость и ускорение тела относительно
неподвижной системы координат называются
абсолютной скоростью va
и абсолютным ускорением Wа
6.
• Скорость и ускорение точки неразрывносвязанной с подвижной системой координат
называются переносной скоростью ve
и переносным ускорением Wе
7. Теорема о сложении скоростей
8. Во все время движения точки радиусы-векторы связаны зависимостью:
Во все время движения точки радиусывекторы ; 0 ; r связаны
зависимостью:
0 r 0 ( xi yj zk )
1
9.
Вектор абсолютной скорости точки равен:d
va
dt
Продифференцируем векторное равенство (1):
d d 0 dr d 0 d
va
( xi yj zk )
dt
dt
dt
dt dt
d 0 dx dy dz
di
dj
dk
i
j k x y z
dt
dt
dt
dt
dt
dt
dt
10.
По формулам Пуассона:di
e i
dt
dk
e k
dt
dj
e j
dt
Подставим в равенство (1):
d 0 dx dy dz
i
j k
dt
dt
dt
dt
x e ; i y e ; j z e ; k
2
11.
Выясним механический смысл входящих вформулу (2) слагаемых:
1) Остановилась подвижная система координат:
va vr
0 const
i const
j const
k const
0
d 0 dx
dy dz
i
j k
dt
dt
dt
dt
0 0 0
di
dj
dk
x y z
dt
dt
dt
12.
2) Остановилась точка:va ve
y const
x const
0
z const
0
0
d 0 dx dy dz
i
j k
dt
dt
dt
dt
di
dj
dk
x y z
dt
dt
dt
13.
Таким образом:va vo e r vr
Абсолютная скорость точки при ее
сложном движении равна
геометрической сумме ее
переносной и относительной скорости.
14. Теорема о сложении ускорений
Теорема Кориолиса15. Гаспар-Гюстав Кориолис Gaspard-Gustave de Coriolis
Дата рождения:21 мая 1792(1792-05-21)
Место рождения:
Париж, Франция
Научная сфера:
математика, физика
16.
Mr
О1
0
z
k О i
x
y
j
17. Во все время движения точки радиусы-векторы связаны зависимостью:
Во все время движения точки радиусывекторы ; 0 ; r связаны
зависимостью:
0 r 0 ( xi yj zk )
1
18.
Вектор абсолютного ускорения точки равен:2
dva d
Wa
2
dt
dt
Продифференцируем дважды векторное
равенство (1):
2
dv a d d d 0 dr
Wa
2 (
)
dt
dt dt
dt
dt
2
2
d 0 d
2 ( xi yj zk )
2
dt
dt
19.
22
d 0 d x
d z
d y
k
j
i
2
2
2
2
dt
dt
dt
dt
2
2
2
d k
d j
d i
x 2 y 2 z 2
dt
dt
dt
dx di dy dj dz dk
)
2(
dt dt dt dt dt dt
2
2
3
20.
Выясним механический смысл входящих вформулу (3) слагаемых:
1) Остановилась
подвижная
система
координат:
0 const
Wa Wr
i const 0 j const
k const
2
2
d 0 d x
d y
d z
2 i 2 j 2 k
2
dt
dt
dt
dt
0
0
0
2
2
2
d i
d j
d k
x 2 y 2 z 2
dt
dt
dt
0 0 0
dx di dy dj dz dk
2(
)
dt dt dt dt dt dt
2
2
21.
2) Остановилась точка:x const
Wa We
y const
z const
0
0
0
2
2
2
d 0 d x
d y
d z
2 i 2 j 2 k
2
dt
dt
dt
dt
d 2i
d2 j
d 2k
x 2 y 2 z 2
dt
dt
dt
0
0
0
dx di dy dj dz dk
2(
)
dt dt dt dt dt dt
2
22.
По формулам Пуассона:2
d i d d e di
( e i )
i e
2
dt
dt
dt
dt
e i e ( e i )
Аналогично:
2
d j
e j e ( e j )
2
dt
2
d k
e k e ( e k )
2
dt
4
23. Симео́н Дени́ Пуассо́н Siméon Denis Poisson
21 июня 1781, Питивье, Франция —25 апреля 1840, Со) —
знаменитый французский физик и
математик.
Число учёных трудов Пуассона
превосходит 300. Они относятся к
разным областям чистой
математики, математической
физики, теоретической и небесной
механики.
Наиболее известными его
учениками были П.Г.ЛежёнДирихле, Ж.Лиувилль и М.Шаль.
24.
Подставим формулы (4) в равенство (3):Wr
2
2
2
2
d 0 d x d y d z
2 i 2 j 2 k
Wa
2
dt
dt
dt
dt
x( e i e ( e i ))
y ( e j e ( e j ))
z ( e k e ( e k ))
dx dy dz
2( ( e i ) ( e j ) ( e k ))
dt
dt
dt
We a0 e r e ( e r )
25.
Таким образом,Wa We Wr 2( e vr )
Здесь,
Wc 2( e vr )
Кориолисово ускорение
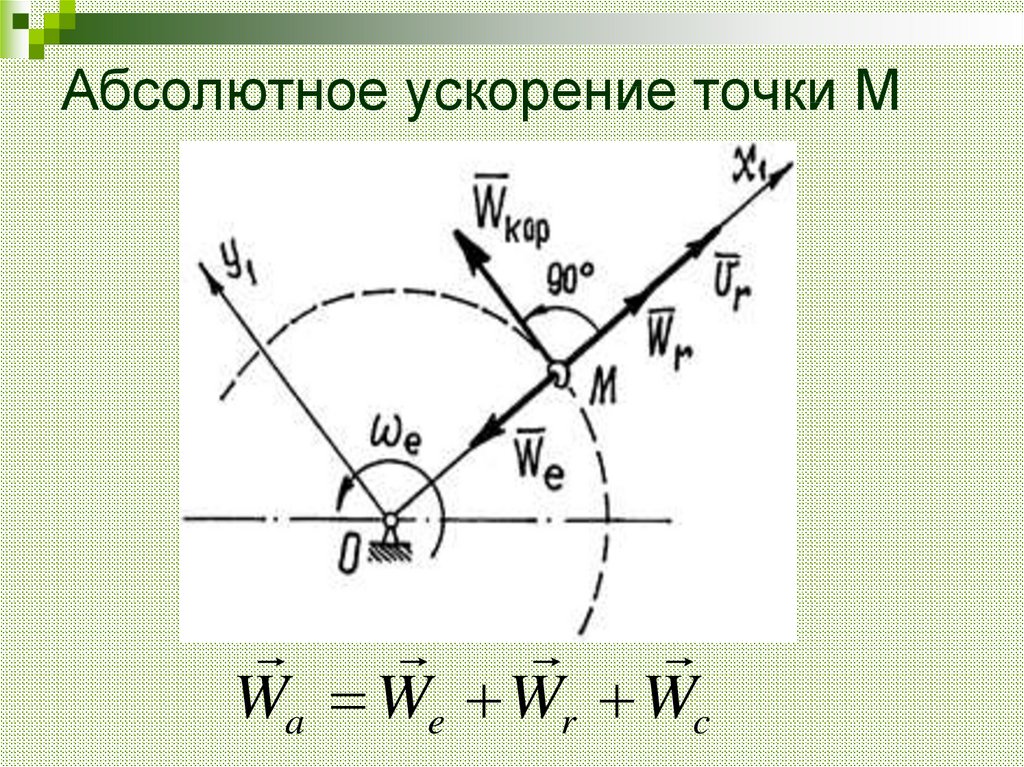
26. Теорема Кориолиса
Абсолютное ускорение точки при еесложном движении равно
геометрической сумме ее
переносного, относительного
и кориолисова ускорений.
Wa We Wr Wc
27. Модуль и направление кориолисова ускорения
28. Кориолисовым или поворотным ускорением называется составляющая абсолютного ускорения точки в сложном движении, равная
удвоенному векторному произведениюугловой скорости переносного вращения на
относительную скорость точки:
Wc 2( e vr )
29. Кориолисово ускорение характеризует: 1) изменение модуля и направления переносной скорости точки вследствие ее относительного
движения;2) изменение направления относительной
скорости точки вследствие вращательного
переносного движения.
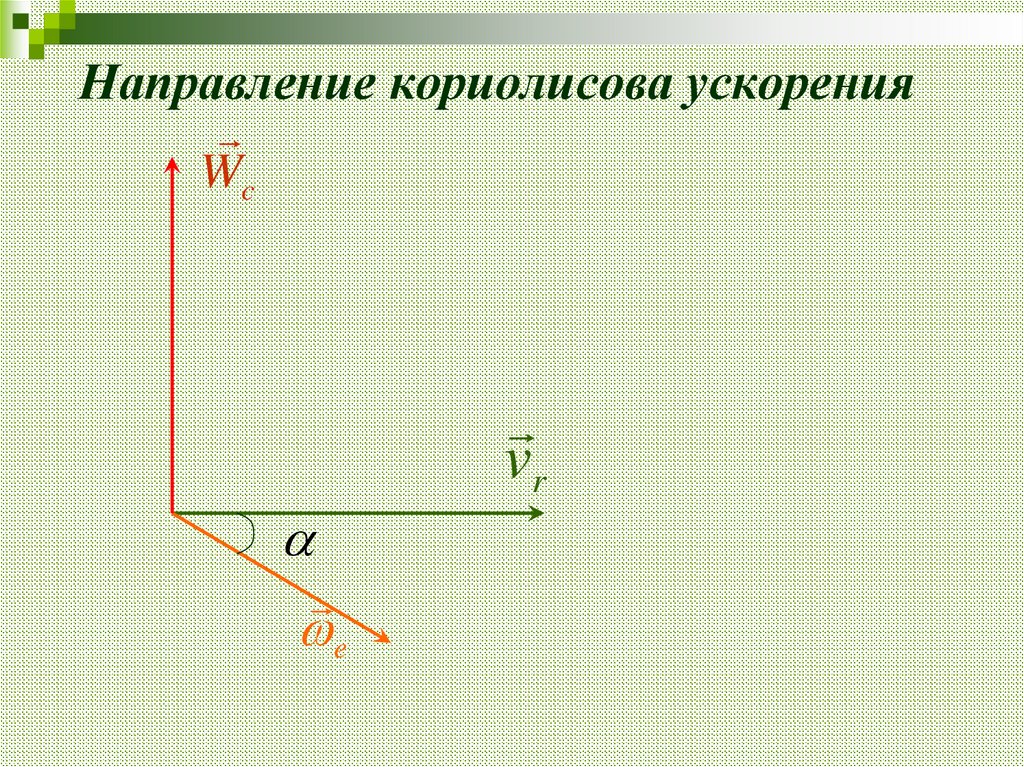
30. Модуль кориолисова ускорения определяется как удвоенный модуль векторного произведения:
Wc 2 e vr sin31. Кориолисово ускорение равно нулю:
1) Если e 0 - поступательноепереносное движение;
2) Если vr 0 - относительный покой точки;
3) Если sin 0 - относительная скорость
точки параллельна оси переносного
вращения.
32. Направление кориолисова ускорения
Wcvr
e
33. Пример 1
Колесо М движется повращающемуся стержню так,
что OM=s=3t2 (см) и φ=2t (рад).
Определить абсолютную скорость
точки в момент времени t=2 c.
34.
35. Решение
относительная скорость направлена покасательной к траектории вдоль стержня
vr S 6t 12cм / с
Переносная скорость направлена по
касательной к траектории переносного
движения, перпендикулярно стержню.
ve OM S 3t 2 6t 24cм / с
2
2
36.
Абсолютную скорость, так как ve v rвычислим по теореме Пифагора
vM v v 12 24 26.83cм / с
2
e
2
r
2
2
37. Абсолютное ускорение точки М
Wa We Wr Wc38.
Переносное ускорение при движенииколеса по окружности радиусом OM=s:
n
We We We
We S e S 0
We W S S
n
e
2
e
12 2 48см / с
2
2
2
39. Кориолисово ускорение, перпендикулярно стержню и направлено в сторону вращения
Относительное ускорение2
Wr S 6см / с
Кориолисово ускорение,
перпендикулярно стержню и
направлено в сторону вращения
Wс 2 e v r sin 90 2 2 12 48см / с
2
40.
Величину абсолютного ускорениякольца М найдем с помощью проекций
на подвижные оси x1 и y1
Wx1 Wr We 6 48 42см / с
Wу1 Wс 48см / с
WМ W W
2
x1
2
y1
2
( 42) 48 63,78cм / с
2
2
2
2










































 Физика
Физика








