Похожие презентации:
Растровые алгоритмы
1. Растровые алгоритмы
Лекция 22. Растровое представление линий
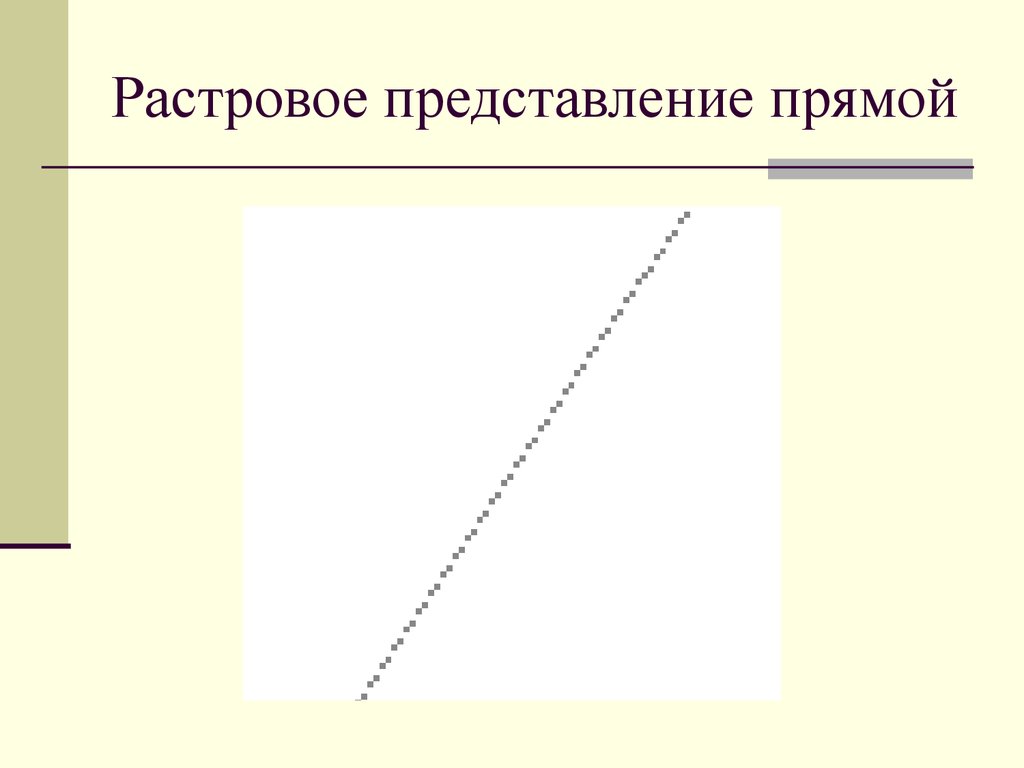
Из-за необходимости производитьокругление при переходе от бумажных к
экранным координатам вместо плавной и
непрерывной кривой на экране получается
ступенчатая и прерывистая линия
В качестве линии на растровой сетке
выступает набор пикселей P1, P2,…, Pn, где
любые два пикселя Pi, Pi+1 являются
соседними
3. Связность пикселей
Два пикселя (x1,y1) и (x2,y2) считаютсясоседними, если они являются связными.
Под связностью пикселей понимается
возможность соединения их растровой
линией, т. е. последовательным набором
пикселей.
Различают два вида связности:
4-связность и
8-связность
4. Связность пикселов
Условие 4-связности:|X2-X1|+|Y2-Y1|=1
x
Условие 8-связности:
|X2-X1|≤1,
|Y2-Y1|≤1
y
5. Линии на растровой сетке
Линия называется 4(8)-связной, еслилюбые два ее соседних пикселя являются
4(8)-связными
Понятие 4-связности является более
сильным, поэтому 4-связная линия
является и 8-связной, но не наоборот
6. Растровое представление прямой
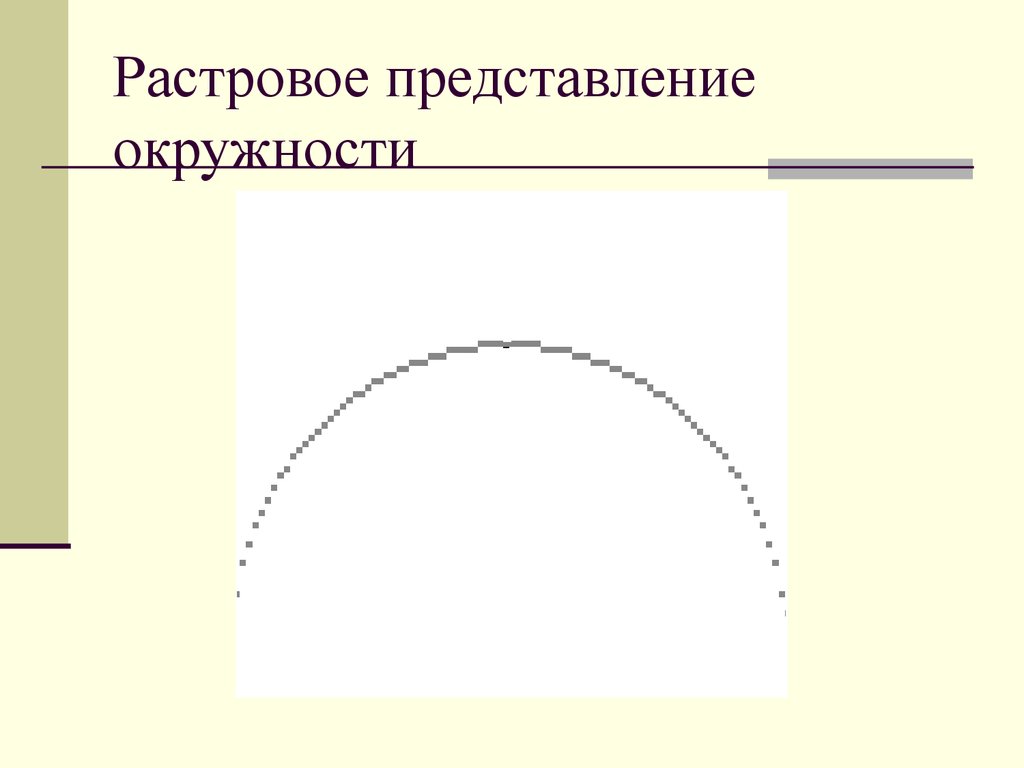
7. Растровое представление окружности
8. Алгоритм Брезенхейма
Проблемакорректной
реализации
растрового
представления
отрезка прямой
линии была
решена в 1962 году
Дж. Брезенхеймом
(Jack E.
Bresenham)
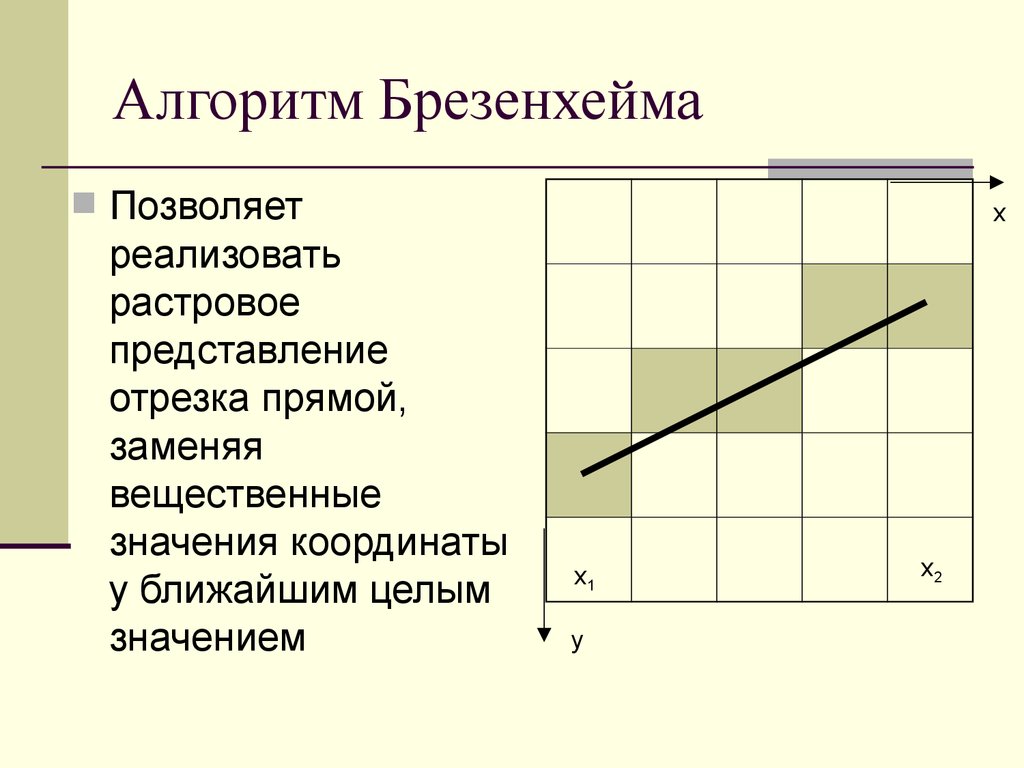
9. Алгоритм Брезенхейма
Позволяетреализовать
растровое
представление
отрезка прямой,
заменяя
вещественные
значения координаты
y ближайшим целым
значением
x
x1
y
x2
10. Алгоритм Брезенхейма
Пусть требуется построить отрезок,соединяющий точки (x1,y1) и (x2,y2). Будем
считать, что
0 ≤ y2 - y1 ≤ x2 - x1
(случай 0 ≤ x2 - x1 ≤ y2 - y1 сведется к
предыдущему перестановкой координат x
и y).
Отрезок описывается уравнением:
y= y1 + (x - x1) * (y2 - y1 )/(x2 - x1).
11. Алгоритм Брезенхейма
Идея алгоритма заключается в том, чтоодна координата изменяется на единицу, а
другая – либо не изменяется, либо
изменяется на единицу в зависимости от
расстояния соответствующей точки до
ближайшего узла координатной сетки
12. Алгоритм Брезенхейма
Расстояниеот
точки
отрезка
до
ближайшего узла по соответствующей
ортогональной координате называется
ошибкой
Алгоритм организован таким образом, что
для вычисления второй координаты
требуется знать только знак этой ошибки
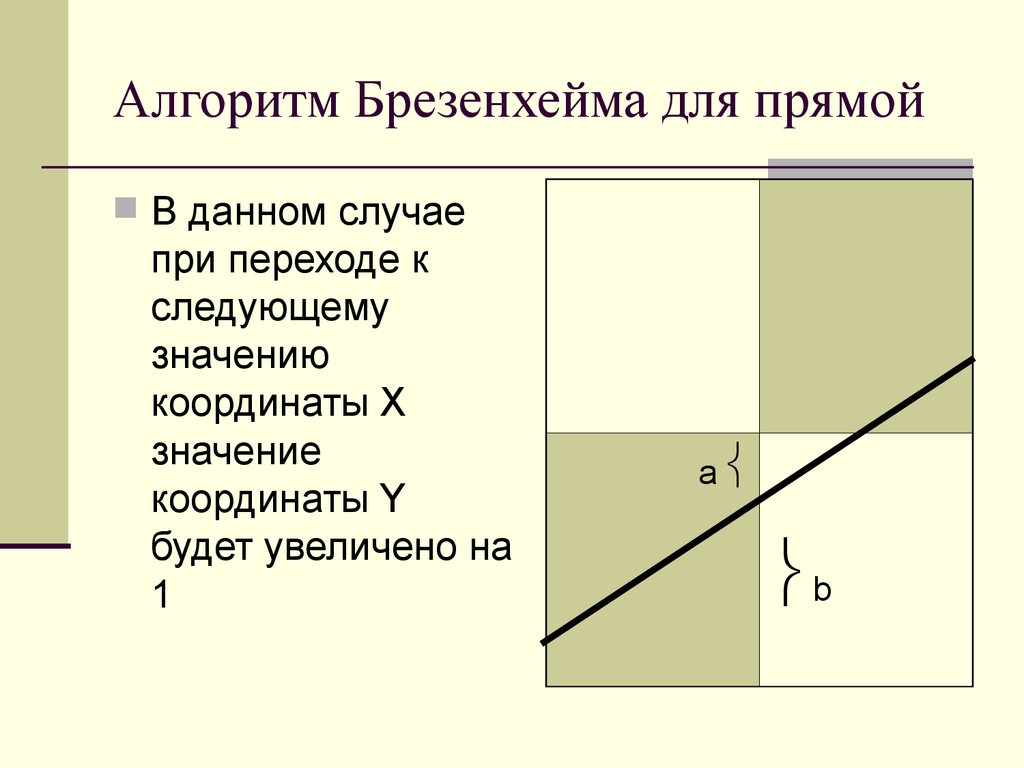
13. Алгоритм Брезенхейма для прямой
В данном случаепри переходе к
следующему
значению
координаты X
значение
координаты Y
будет увеличено на
1
a
b
14. Алгоритм Брезенхейма для прямой
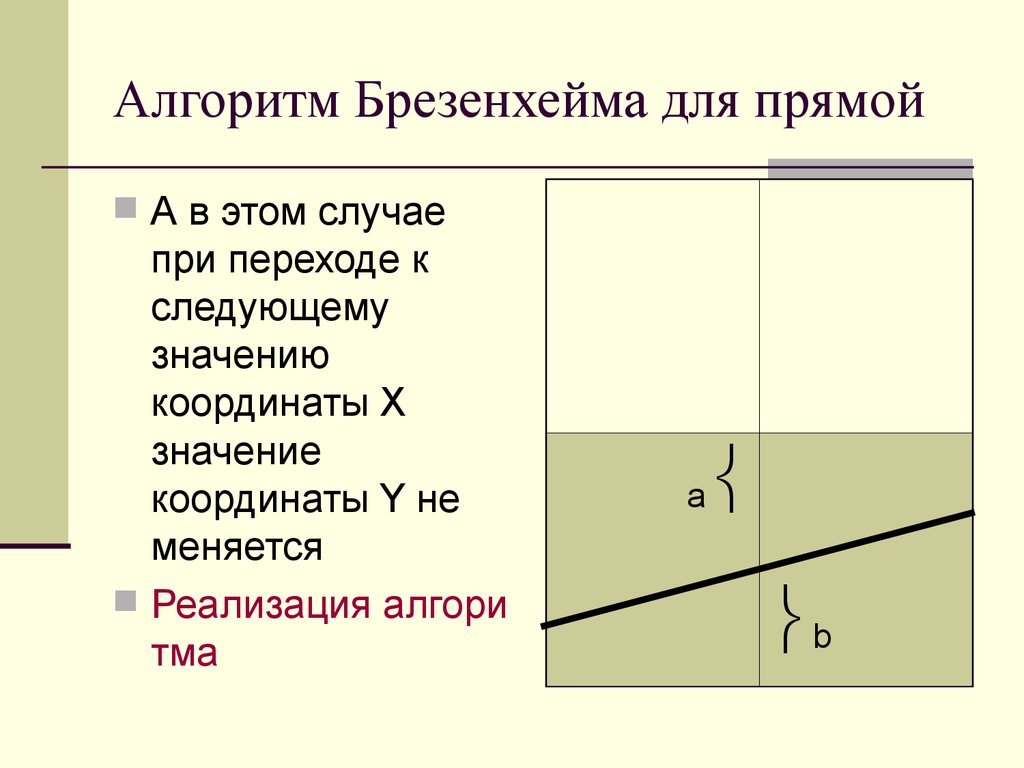
А в этом случаепри переходе к
следующему
значению
координаты X
значение
координаты Y не
меняется
Реализация алгори
тма
a
b
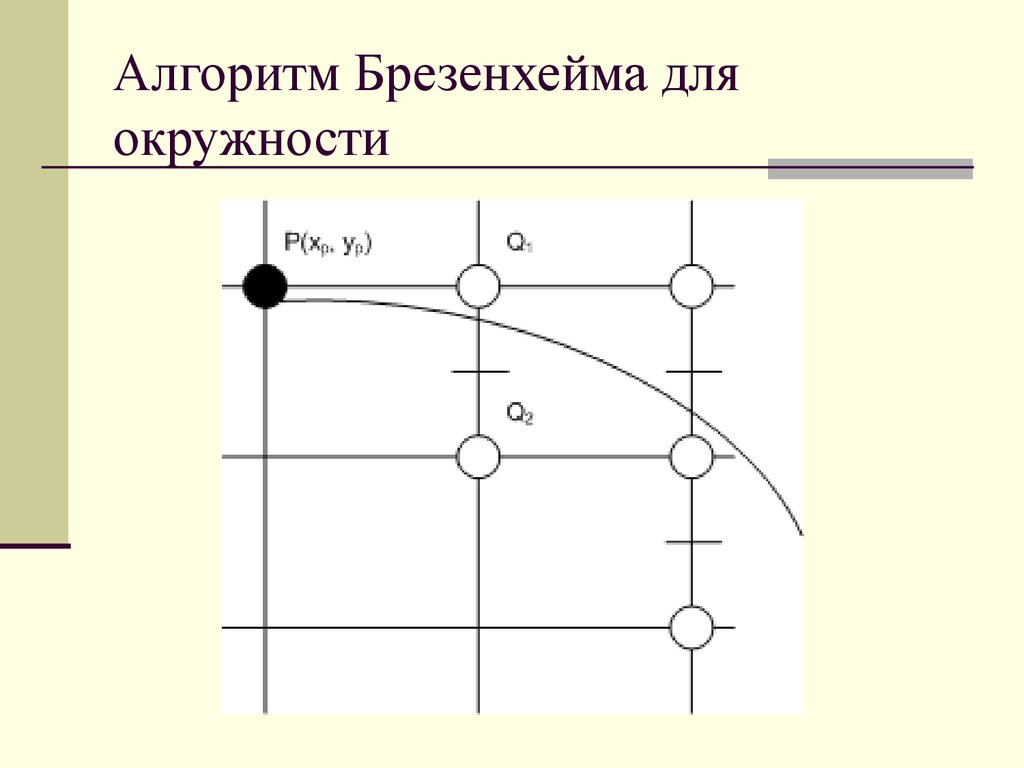
15. Алгоритм Брезенхейма для окружности
16. Алгоритм Брезенхейма для окружности
Описание алгоритма Брезенхейма для окружности











 Информатика
Информатика








