Похожие презентации:
Теоремы сложения и умножения вероятностей
1. Теоремы сложения и умножения вероятностей
2. Теорема сложения вероятностей
События А и В называются несовместными,если в результате данного испытания появление
одного из них исключает появление другого
( испытание: стрельба по мишени
А-выбивание четного числа очков;
В- не четного).
Вероятность появления одного из двух
несовместных событий, равна сумме вероятностей
этих событий:
Р(А+В)=Р(А)+Р(В)
3.
В урне 30шаров :10 красных,5 синих и 15
белых. Найти вероятность
появления цветного шара
4.
Вероятностьпоявления красного шара
(событие А)
10 1
P( A)
30 3
Вероятность
появления синего
5 1
P( B)
30 6
1 1 1
P( A B) P( A) P( B)
3 6 2
5. Теорема сложения вероятностей
Сумма вероятностей противоположных___
событий равна 1
Р( А) Р( А ) 1
События А и В называются совместными,
если в результате данного испытания появление
одного из них не исключает появление другого(
А- в аудиторию вошел учитель; В- вошел
студент).
Вероятность появления хотя бы одного из двух
совместных событий равна сумме вероятностей
этих событий без вероятности их совместного
наступления:
Р( А В) Р( А) Р( В) Р( АВ)
6. Задача 1
В лотерее участвуют 100 билетов, из которых на 5билетов падает выигрыш 20 рублей, на 10 билетов – 15
руб., на 15 билетов – 10 руб., на 25 билетов – 2 рубля.
Найти вероятность того, что на купленный билет будет
получен выигрыш не менее 10 рублей.
Решение.
Пусть А,В,С – события, состоящие в том, что на
купленный билет падает выигрыш, равный соответственно
20,15 и 10 руб.
Т.к. события А,В и С несовместны, то
Р(А+В+С) = Р(А)+Р(В)+Р(С) = 5 + 10 + 15 = 0,3
100 100 100
Ответ: 0,3.
7. Задача 2
В коробке 250 лампочек, из них100 по 100 Вт, 50 – по 60 Вт, 50 - по 25 Вт,
50 - по 15 Вт.
Вычислить вероятность того, что мощность
любой взятой наугад лампочки
не превысит 60 Вт.
8. Решение
Пусть А – событие, состоящее в том, что мощностьлампочки равна 60 Вт, В – 25 Вт, С – 15 Вт, D – 100 Вт.
События А,В,С,D образуют полную систему, т.к.все
они несовместны и одно из них обязательно наступит в
данном испытании (выборе лампочки), т.е.
Р(А)+Р(В)+Р(С)+Р(D) = 1.
События «мощность лампочки не более 60 Вт» и
«мощность лампочки более 60 Вт» – противоположные.
По свойству противоположных событий
Р(А)+Р(В)+Р(С) = 1- Р(D),
Р(А+В+С) = 1- 100 = 150 = 3
250 250 5
Ответ: 0,6
9.
Изурны , в которой находится 12 белых и 8
черных шара вынимают наудачу 2 шара.
Найти вероятность того, что оба шара
окажутся черными?
10.
n C2
20
m C
2
8
11. Задача 3
В коробке лежат 30 галстуков, причем 12 изних красные, остальные белые. Определить
вероятность того, что из 4 наудачу вынутых
галстуков все они окажутся одного цвета.
Решение
Пусть А – событие, состоящее в том, что все 4
галстука будут красные,
В – все 4 галстука будут белыми
4 галстука из 30 можно выбрать
12.
4 галстука из 30 можно выбрать30!
27 28 29 30
4
С30
27405 способами
4!26!
2 3 4
4 галстука из 12 красных можно выбрать
12! 9 10 11 12
4
С12
495 способами, аналогично
4!8!
2 3 4
18! 15 16 17 18
4
3060 способами.
4 белых - С18
4!14!
2 3 4
Вероятность того, что все 4 галстука будут красные, равна
495
3060
79
Р Р( А) Р ( В )
0,13
27405 27405 609
Ответ: 0,13
13. Решение задач
4. Производят три выстрела по одной мишени. Вероятностьпопадания при одном выстреле равна 0,5. Найти
вероятность того, что в результате этих выстрелов
произойдет только одно попадание.
5. У продавца имеется 10 оранжевых,8 синих, 5 зеленых
и 15 желтых шаров. Найти вероятность того, что
купленный шар окажется оранжевым, синим или зеленым.
6. В денежно-вещевой лотерее на каждые 10000 билетов
разыгрывается 150 вещевых и 100 денежных выигрышей.
Найти вероятность выигрыша денежного или вещевого
на один лотерейный билет.
14. ответы
4.0,375
5.
23
38
6.
0,025









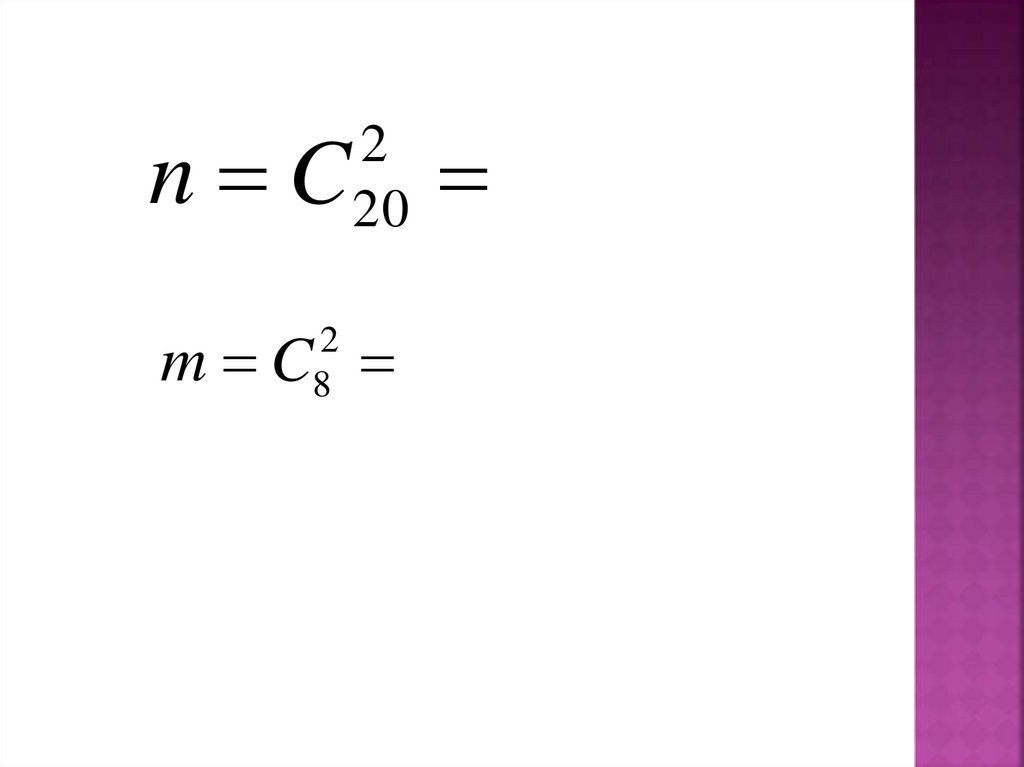




 Математика
Математика








