Похожие презентации:
Теоремы сложения и умножения вероятностей
1. ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ
2. Суммой А + В двух событий А и В называют новое событие, состоящее в появлении либо события А, либо события В, либо обоих этих
событий.3. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий
4. Теорема: вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий.
Р(А+В)=Р(А)+Р(В)5. Следствие: вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме
вероятностей этихсобытий.
6.
Р( А1 А2 ... Ат )Р( А1 ) Р( А2 ) ... Р( Ат )
7. Задача 1 В корзине 30 шаров: 10 красных, 5 синих и 15 белых. Найдите вероятность появления цветного шара.
8. Решение:
10 1Р( А)
;
30 3
9.
5 1Р( В)
;
30 6
10.
1 1 1Р( А В)
3 6 2
11. Задача 2 Стрелок стреляет по мишени, разделённой на три области. Вероятность попадания в первую область равна 0,45, во вторую –
0,35. Найдите вероятностьпопадания того, что стрелок при
одном выстреле попадёт либо в
первую, либо во вторую области.
12. Р(А+В) = 0,45 + + 0,35 =0,8.
13. ПОЛНАЯ ГРУППА СОБЫТИЙ
14. Теорема: Сумма вероятностей событий образующих полную группу, равна единице
Теорема:Сумма вероятностей событий
А1 , А2 ,..., Ат ,
образующих полную группу,
равна единице
15.
Р( А1 ) Р( А2 ) ... Р( Ат ) 116. Задача 3 Консультационный пункт института получает пакеты с контрольными работами из городов А, В и С. Вероятность получения
пакета изгорода А равна 0,7, из города В –
0,2. Найдите вероятность того, что
очередной пакет будет получен из
города С.
17. Решение: 0,7 + 0,2 + р = 1; р = 0,1.
18. ПРОТИВОПОЛОЖНЫЕ СОБЫТИЯ
19. Противоположными называют два единственно возможных события, образующих полную группу. Если одно из противоположных событий
АПротивоположными называют
два единственно возможных
события, образующих полную
группу. Если одно из
противоположных событий
обозначить через А, то другое
принято обозначать -
A
20. Попадание и промах при выстреле по цели – противоположные события. А – попадание,
21. - промах
A-
промах
22. Задача 4 Вероятность того, что день будет дождливым, равна 0,7. Найти вероятность того, что день будет ясным.
23. Решение: =1-0,7=0,3
Решение:p
=1-0,7=0,3
24. Задача 5 В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди наудачу извлечённых двух деталей есть хотя бы
однастандартная.
25. Решение: А – хотя бы одна стандартная - стандартных нет
Решение:А – хотя бы одна
стандартная
A- стандартных нет
26.
С1
Р( А)
;
45
С
2
2
2
10
27. Р(А) =
44Р(А) =
45
28. Задача 6 Два стрелка, для которых вероятности попадания в мишень равна соответственно 0,7 и 0,8, производят по одному выстрелу.
Определите вероятность 1) хотябы одного попадания в мишень.
2) одного попадания в мишень
29. Решение: 1) - первый попал, второй не попал;
Решение:1)
первый
попал,
1
второй не попал;
А
30. второй попал, первый не попал;
А2 -второй попал,первый не попал;
31. первый попал, второй попал;
А-первый попал,
3
второй попал;
32.
Р( А1 ) 0,7 0,20,14
33.
Р( А2 ) 0,8 0,30,24;
34.
Р( А3 ) 0,7 0,80,56
35. Р(А) = 0,14 + 0,24 + 0,56 = 0,94 или Р(А) =
1 0,2 0,3 0,94.36.
2) Р( А) Р( А1 ) Р( А2 )0,38
37. Задача 7 Студент знает 20 из 25 вопросов программы. Вычислите вероятность того, что студент знает предложенные ему
экзаменатором два вопроса.38. Решение: - студент знает первый вопрос;
АРешение:
- студент знает
1 первый вопрос;
39. студент знает второй вопрос
А-студент знает
2 второй вопрос
40.
Р( А) Р( А1 ) Р( А2 )41.
20Р( А1 )
;
25
42.
19Р ( А2 )
24
43.
19Р ( А) .
30
44. Теорема: если события А и В совместны, то вероятность их суммы выражается формулой Р(А+В) = Р(А) + Р(В) - – Р(АВ)
Теорема: если события А иВ совместны, то
вероятность их суммы
выражается формулой
Р(А+В) = Р(А) + Р(В) – Р(АВ)
45. ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
46. Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении этих событий.
47. Например, если А -деталь годная, В -деталь окрашенная, то АВ -деталь годна и окрашена.
48. Условной вероятностью
PA B-называют вероятность
события В, вычисленную в
предположении, что
событие А уже наступило.
49. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно.
50. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар
(событие А).51. Условная вероятность события В при условии, что событие А уже наступило, по определению, равна
52.
P ( AB)PA ( B )
,
P ( A)
P ( A) 0
53. Теорема: Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность
другого,54. вычисленную в предположении, что первое событие уже наступило:
P( AB) P( A) PA ( B)55. По определению условной вероятности
P ( AB)PA ( B )
, отсюда
P ( A)
P ( AB) PA ( B ) P ( A)
56. Вероятность совместного проявления нескольких событий равна произведению вероятности одного из них на условные вероятности всех
остальных,57. причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились
58.
P( A1 A2 A3 ... An )P( A1 ) PA1 ( A2 ) PA1 A2 ( A3 )...
...PA1 A2 ... An 1 ( An )
59. В частности, для трех событий
P( ABC ) P( A) PA ( B) PAB (C)60. Задача 8. В урне 5 белых, 4 чёрных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая
егообратно.
61. Найдите вероятность того, что при первом испытании появится белый шар (А), при втором – чёрный (В), при третьем – синий (С).
62.
5P ( A) ;
12
4
PA ( B ) ;
11
3
PAB (C ) .
10
63.
5 4 3P( ABC )
12 11 10
1
22
64. НЕЗАВИСИМЫЕ СОБЫТИЯ
65. Событие В называют независимым от события А, если появление события А не изменяет вероятности события В,
66. т.е. условная вероятность события В равна его безусловной вероятности
PA ( B) P( B)67. Для независимых событий теорема умножения имеет вид
68.
P( AB) P( A) P( B)69. ВЕРОЯТНОСТЬ ПОЯВЛЕНИЯ ХОТЯ БЫ ОДНОГО СОБЫТИЯ
70. Вероятность появления хотя бы одного из событий
А1 , А2 ,..., Ат ,71. Независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
72.
P( A) 1 q1 q2 ... qm73. В частности,
P( A) 1 qm
74. Задача 9 вероятность того, что при одном выстреле стрелок попадёт в цель, равна 0,4. сколько выстрелов должен произвести
стрелок,75. Чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?
76. Р(А) ≥ 0,9
77.
1 0,6 0,9m
0,6 0,1
m
m 4,5
78. Значит, стрелок должен произвести не менее 5 выстрелов
79. Задача 10 Из партии бюллетеней, доставленных с 3 избирательных участков, эксперт отбирает только действительные бюллетени.
Вероятность того, что бюллетень с первогоучастка окажется действительным, равна 0,95
со второго – 0,9 с третьего – 0,85. Найдите
вероятность того, что из трех выбранных
бюллетеней (по одному с каждого участка): а)
только два действительных, б) хотя бы один
действительный.
80.
81.
82.
83. Задача 11 Для успешной сдачи экзамена необходимо ответить хотя бы на один из двух предложенных теоретических вопросов и решить
задачу. Вероятностьтого, что студент правильно ответит на
теоретический вопрос, равна 0,7, решит
задачу 0,8. Найдите вероятность того,
что студент сдаст экзамен.









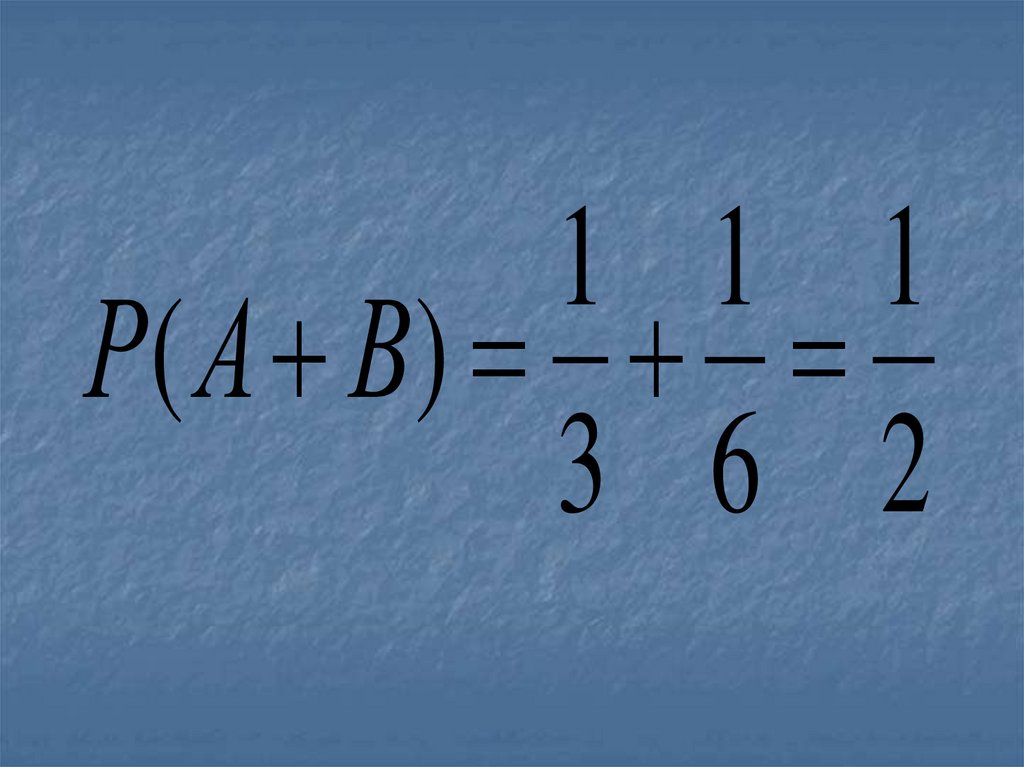






















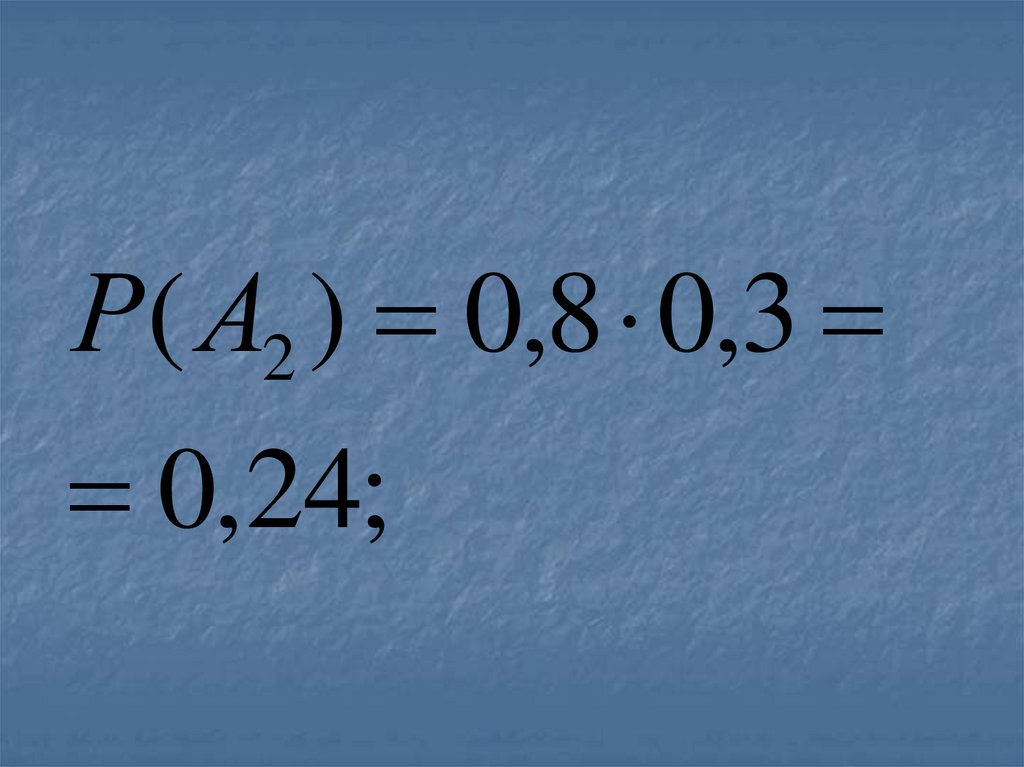

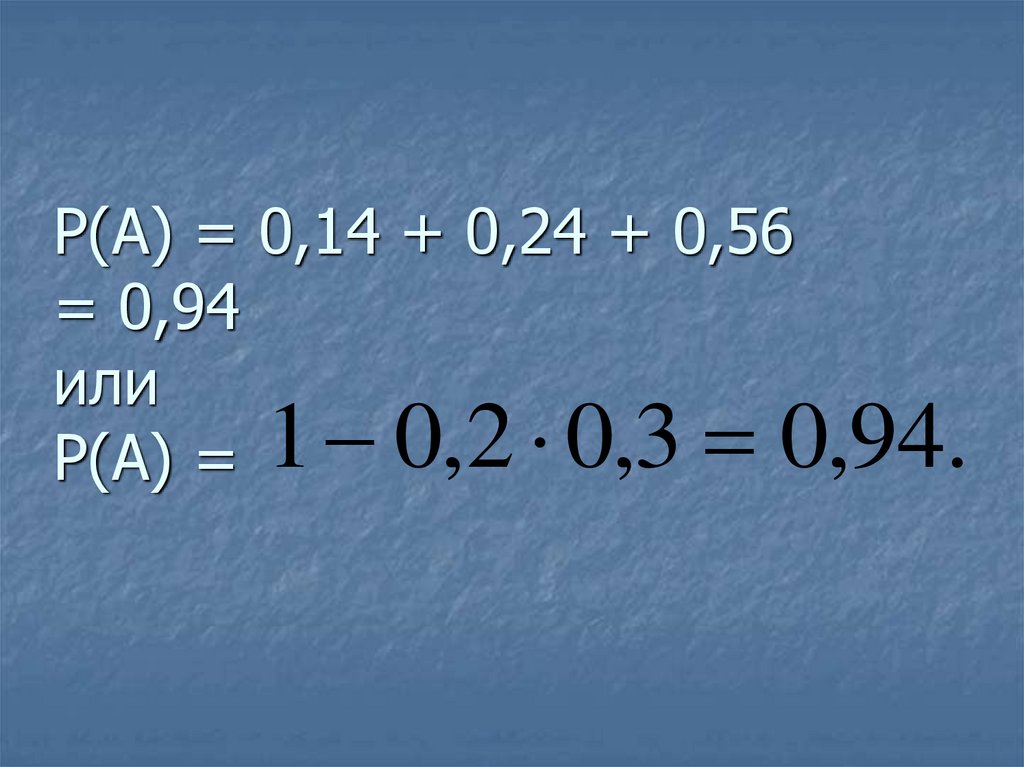
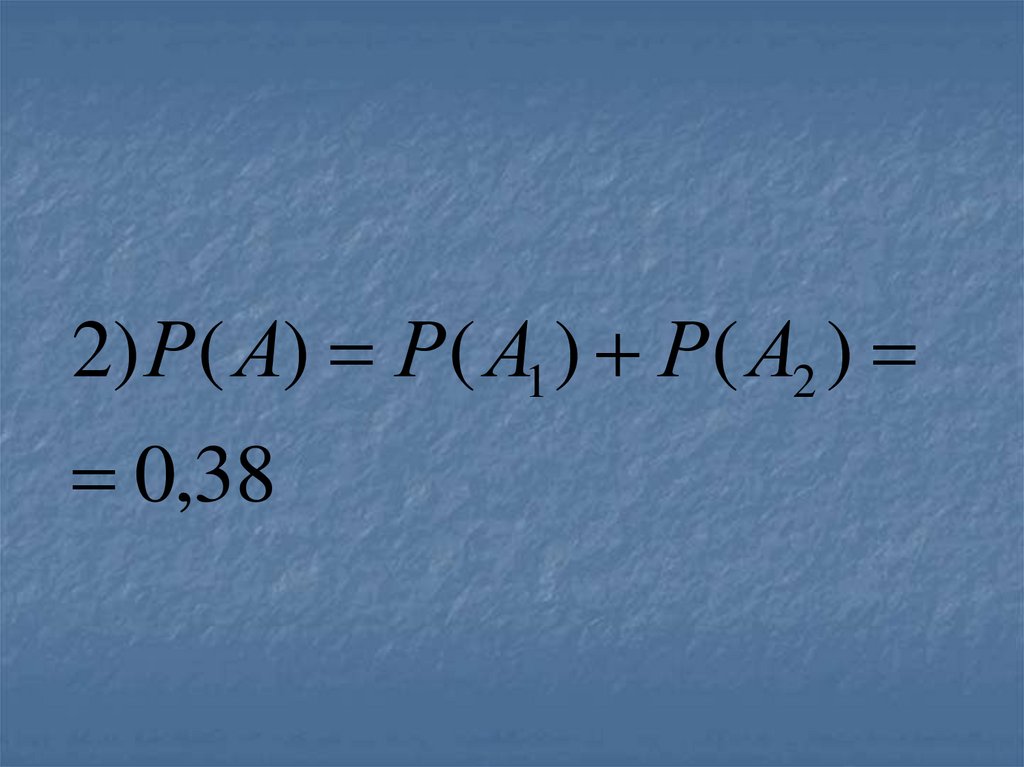



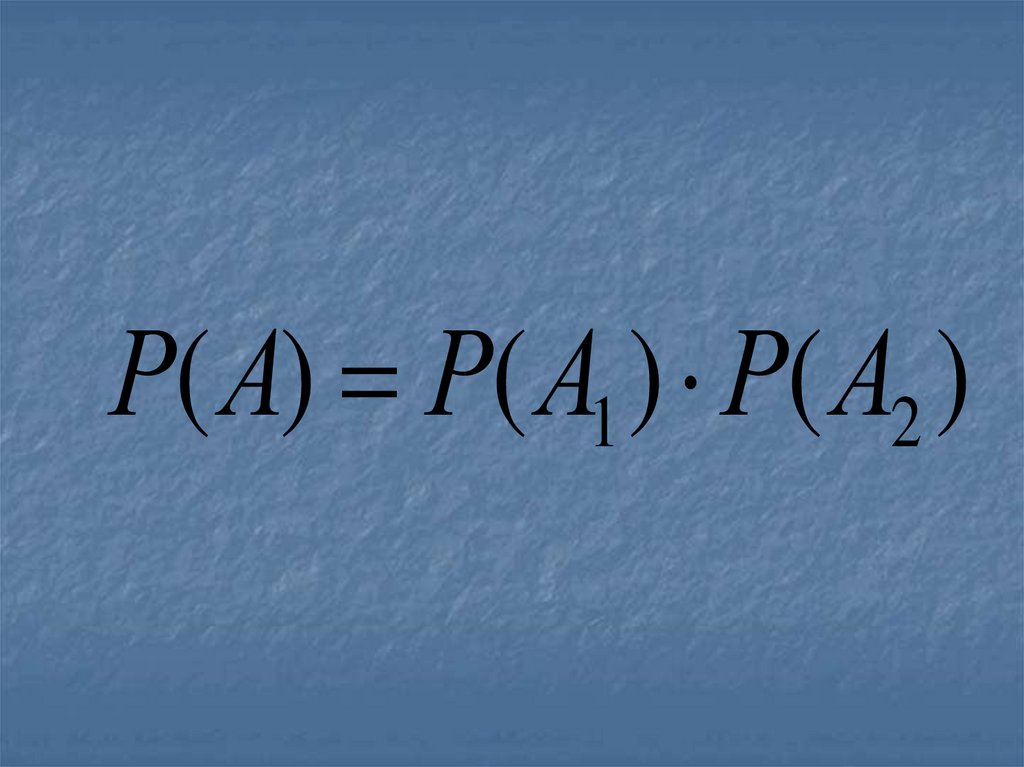
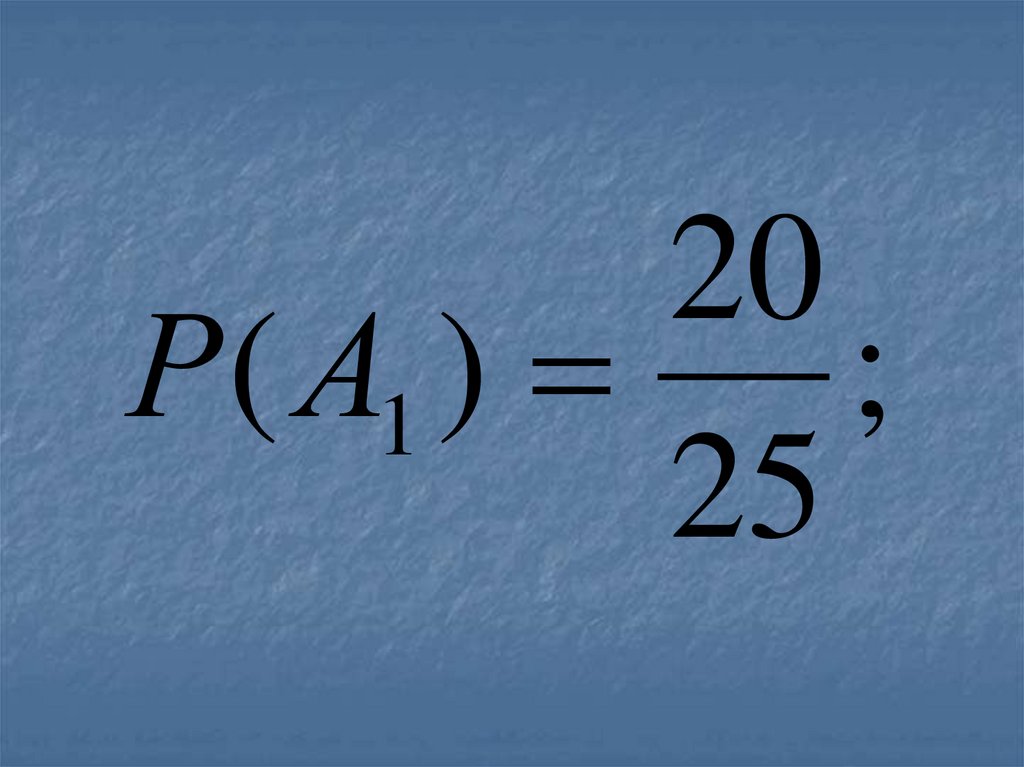
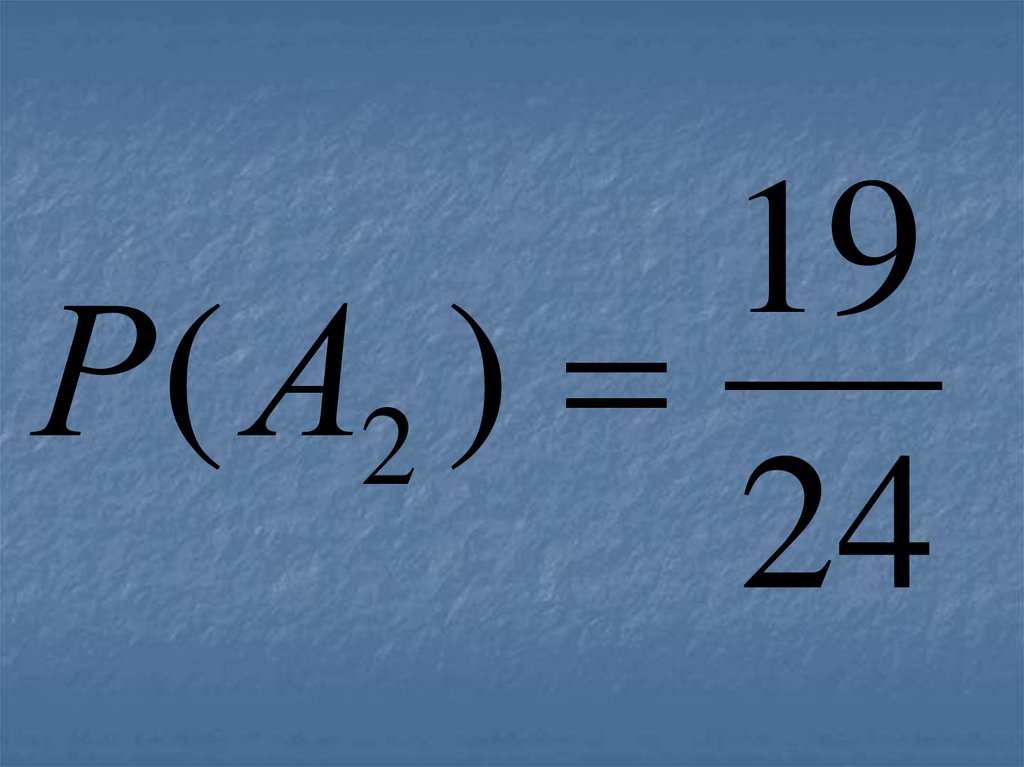
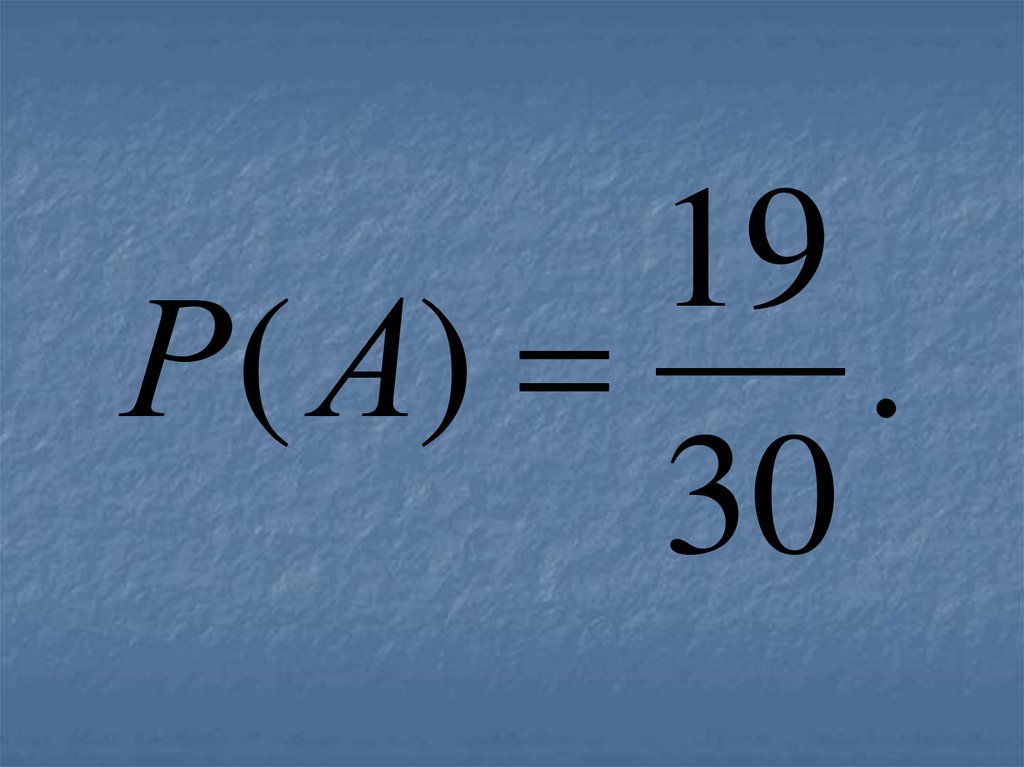








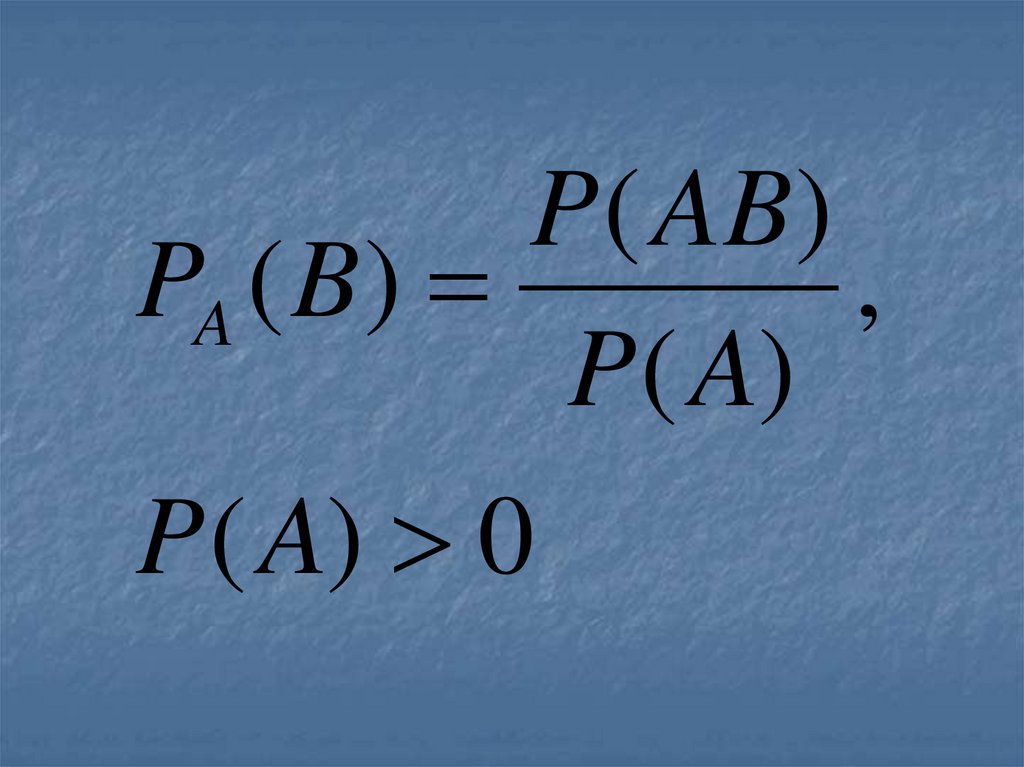






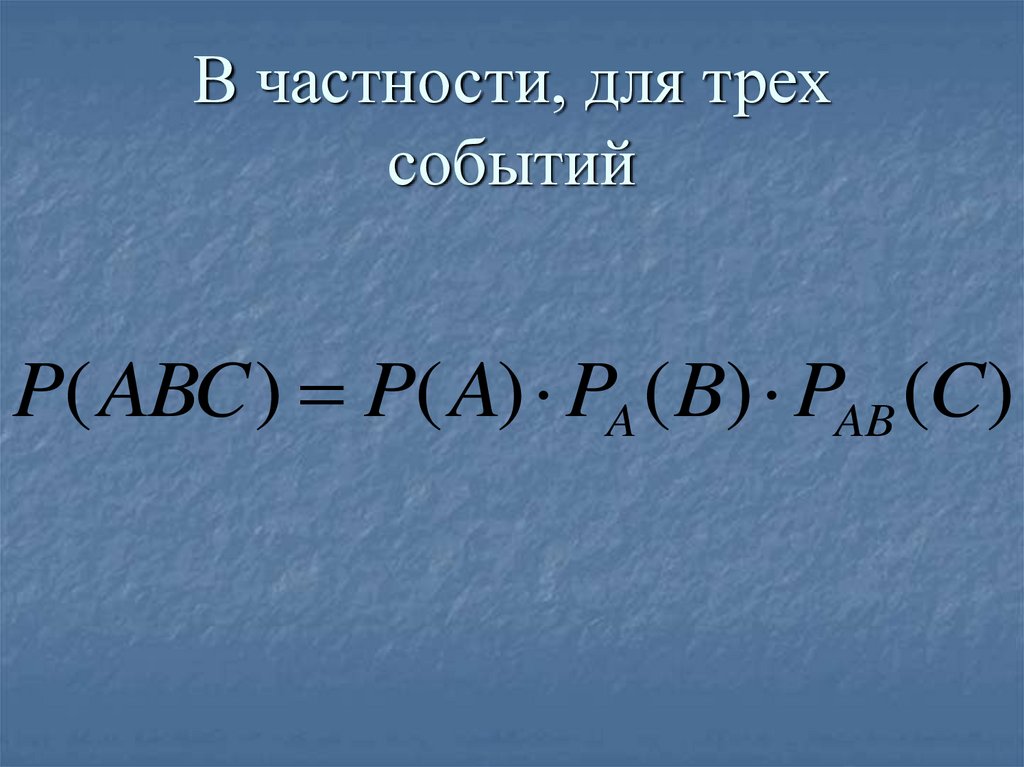


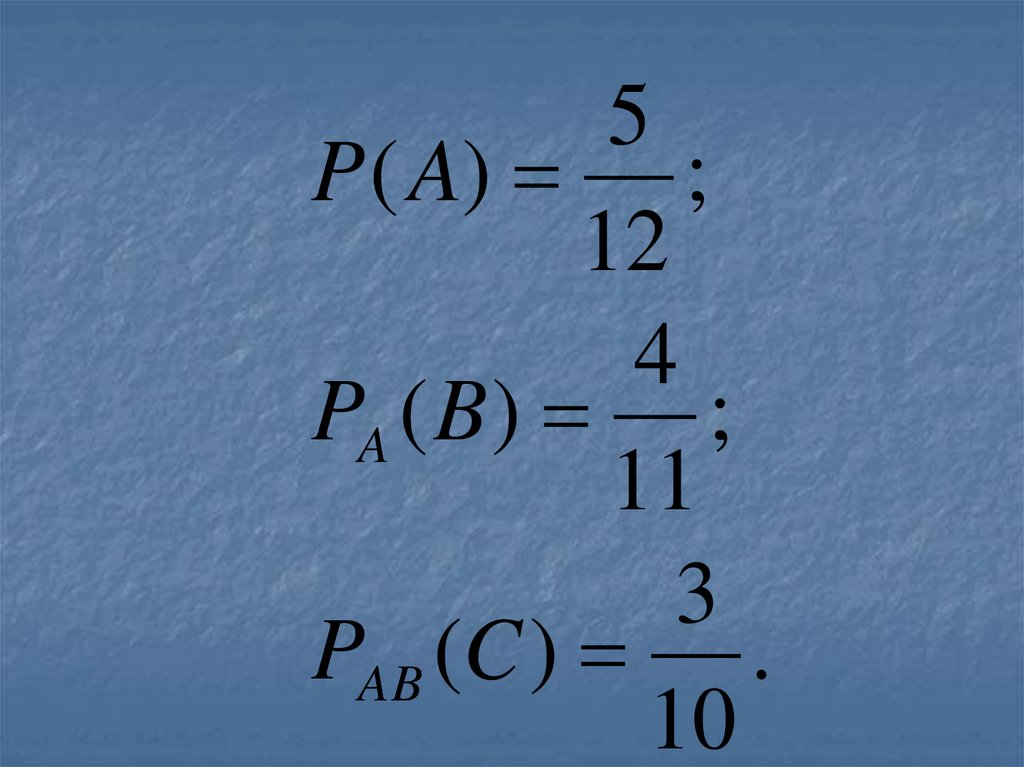





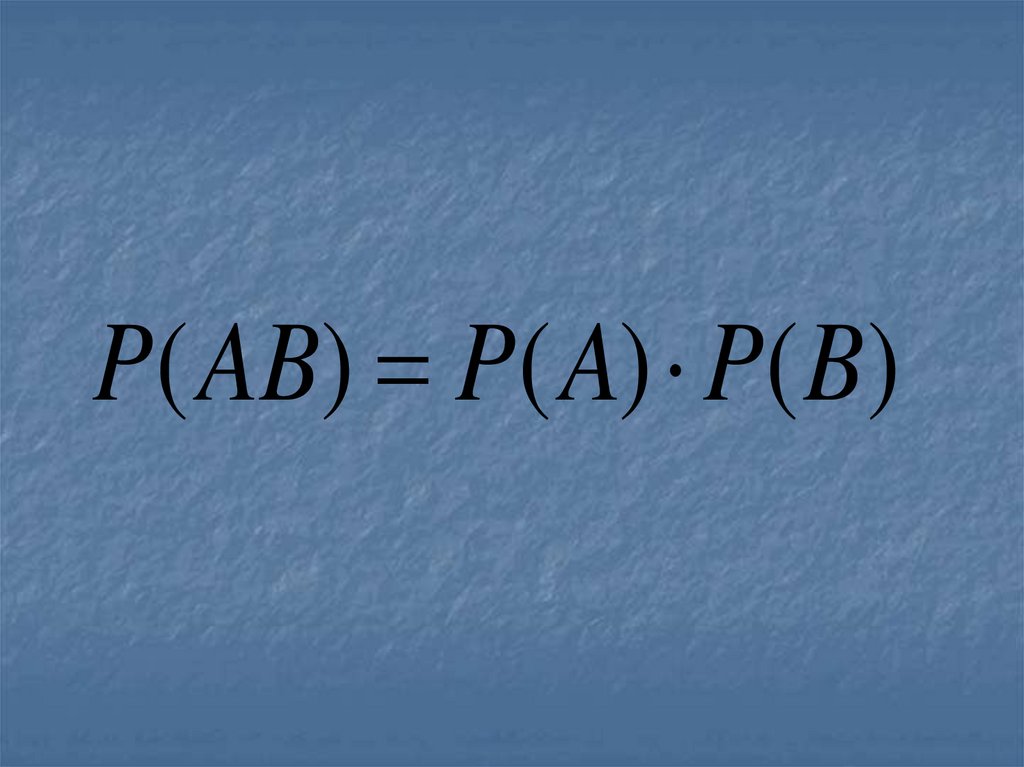




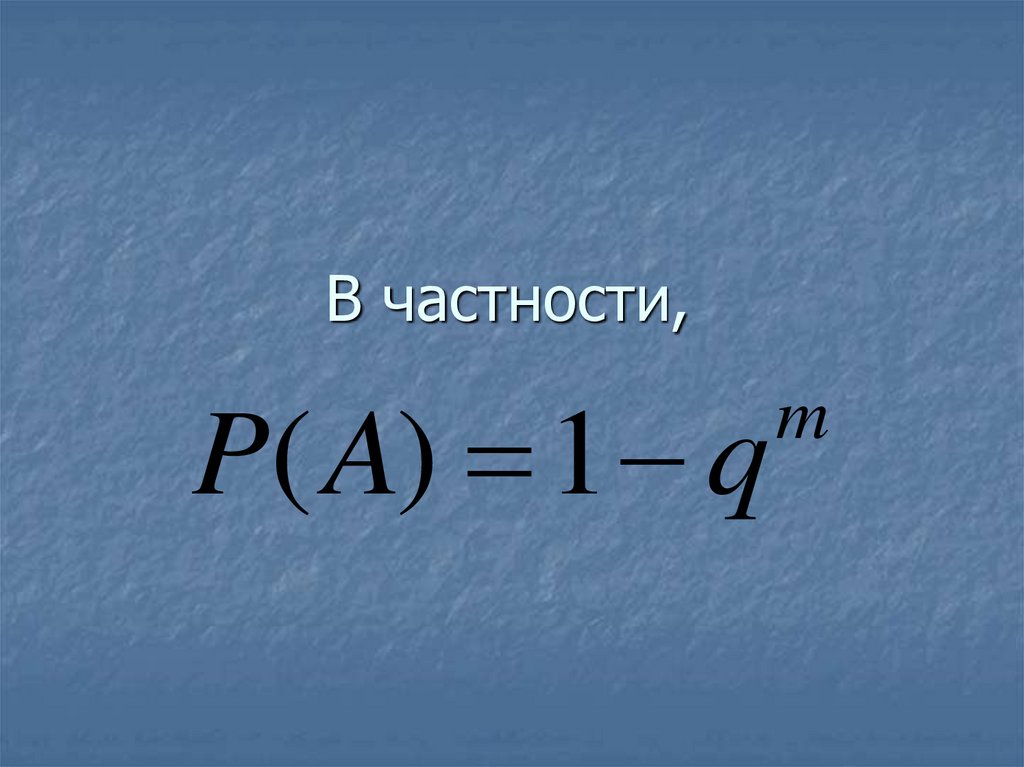



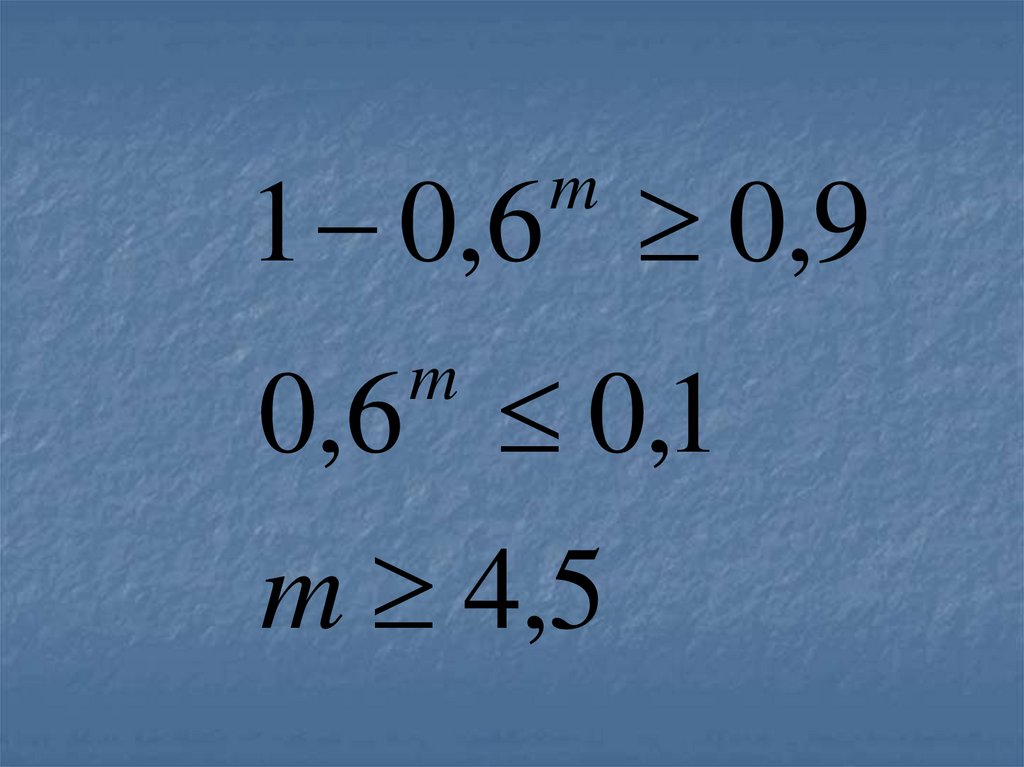








 Математика
Математика








