Похожие презентации:
Обоснования асимптотики для системы эллиптических уравнений в случае обратной квазимонотонности
1.
Физический факультет МГУ им. Ломоносовакафедра математики
ОБОСНОВАНИЯ АСИМПТОТИКИ ДЛЯ СИСТЕМЫ
ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ В СЛУЧАЕ
ОБРАТНОЙ КВАЗИМОНОТОННОСТИ
Петровская Е.С.
Левашова Н.Т.
Москва
30.10.2013
2.
Рассматривается краевая задача для системы двухуравнений второго порядка с разными степенями
0
малого параметра
2
u f (u, v, x , ), v g(u, v, x , ),
4
u 0 u 1 0, v 0 v 1 0.
f и g – достаточно гладкие функции.
x 0, 1
3.
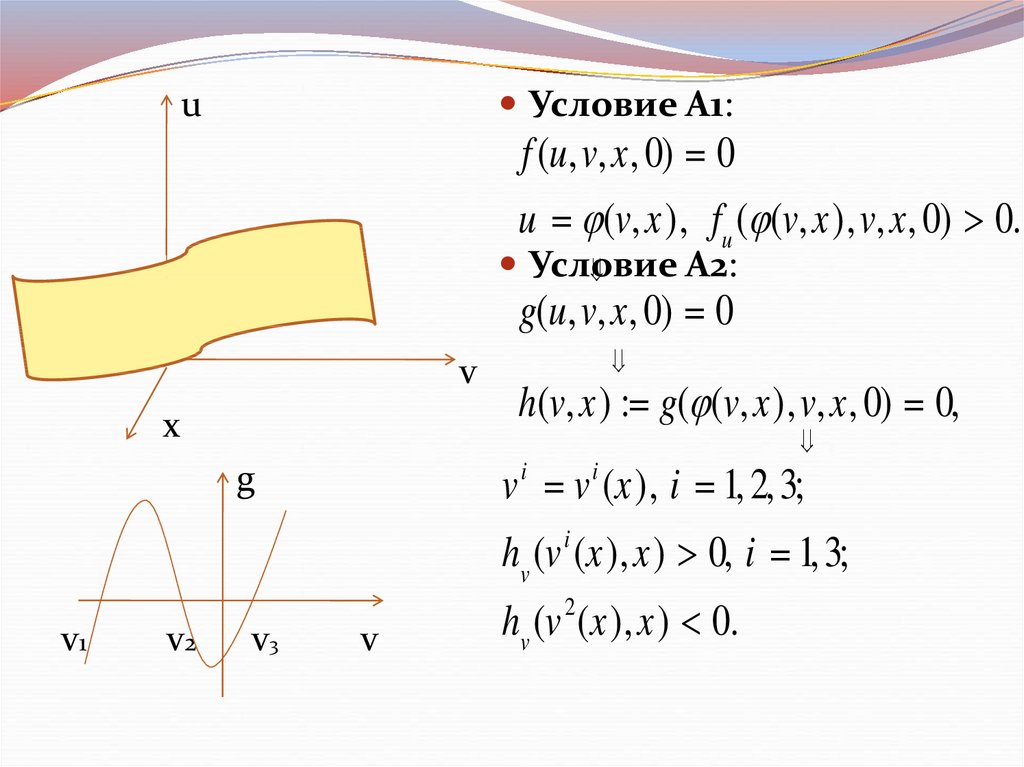
Условие А1:u
f (u, v, x , 0) 0
u (v, x ), fu ( (v, x ), v, x , 0) 0.
Условие
А2:
g(u, v, x , 0) 0
v
x
h(v, x ) : g( (v, x ), v, x , 0) 0,
v i v i (x ), i 1, 2, 3;
g
hv (v i (x ), x ) 0, i 1, 3;
v1
v2
v3
v
hv (v 2 (x ), x ) 0.
4.
v 3 (x )Обозначим
J (x ) :=
т
h (v, x )dv.
v1 ( x )
Условие А3: Пусть существует
уравнения
J (x 0 ) = 0, причем
- )решение
x 0 О (0,1
dJ
x 0 ) < 0.
(
dx
5. ОБРАТНАЯ КВАЗИМОНОТОННОСТЬ
Условие A4fv (u, v, x , 0) > 0, gu (u, v, x , 0) > 0
всюду в области (u, v, x ) О I u ґ
Iv ґ
й0;1щ.
кл ы
ъ
6.
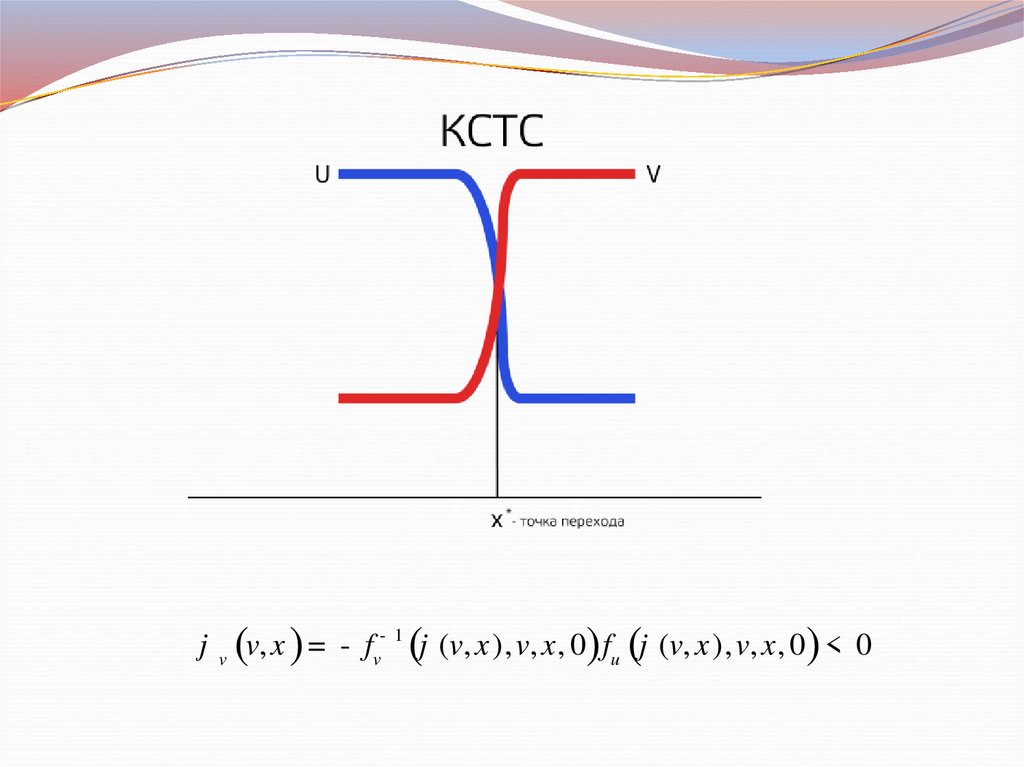
jv
(v, x ) =
- fv- 1 (j (v, x ), v, x , 0) fu (j (v, x ), v, x , 0) < 0
7. Асимптотика
v x *, v 2 x *Точка перехода:
x * ( ) x 0 x 1 2x 2 ...
Асимптотика решения задачи строится
отдельно справа
*
: x (t , )
и слева от точки перехода
(- )
*
м
п
u
,
x
О
[0,
x
]
п
U = н (+ )
*
п
u
,
x
О
[
x
,1]
п
п
о
м
ппv (- ) , x О [0, x * ]
V = н (+ )
ппv , x О [x *,1]
по
где
u
x , Q u , Pu 1,2, R u 1,2, ,;
v v
x , Q ( )v , Pv 1,2, R v 1,2 , ,,
u
x x*
1
x
, 2
1 x
, 1
x
2
, 2
1 x
2
8.
Условия непрерывности асимптотического*
x
(t , )
разложения v – компоненты решения в точке
:
v (- ) (x *, e) + Q (- )v(0, e) = v 2 (x * ), v ( + ) (x *, e) + Q ( + )v(0, e) = v 2 (x * ).
Условия непрерывности производных
*
асимптотических разложений в точке x (t , ) .
dv (- )
dx
du (- )
dx
x*
x*
1 dQ (- )v
+
e dt
1 dQ (- )u
+
e dt
t=0
t=0
dv ( + )
=
dx
du ( + )
=
dx
x*
x*
1 dQ ( + )v
+
e dt
1 dQ ( + )u
+
e dt
t=0
t=0
9. Регулярные члены асимптотики
Для функций u 0( ) , v 0( ) получается вырожденнаясистема:
f x f (u 0( ) , v 0( ) , x , 0) 0 g x g(u 0( ) , v 0( ) , x , 0) 0
Из условий У1 и У2 получаем:
v
u
(- )
0
(- )
0
v 0( + ) = v 3 (x ),
1
= v (x ),
= j (v (x ), x ) = : j (x )
1
1
u
(+ )
0
3
= j (v (x ), x ) = : j
3
(x )
10. Система уравнений для функций переходного слоя
( ( )f j
(± )
)
(± )
( )
x * + Q 0 u (t ), v 3,1 x * + Q 0 v (t ), x *, 0 = 0, (1)
3,1
j
1,3
(x ) + Q
*
( ( )
u (t ) = j v 1,3 x * + Q0( m)v (t ), x *
( m)
0
м
2 (± )
п
d
Q0 v
п
(± )
3,1
*
*
п
=
h
v
x
+
Q
v
t
,
x
,
(
)
п
0
2
н dt
п
(± )
(± )
3,1
*
2
*
3,1
*
п
v
x
+
Q
v
0
=
v
x
;
v
x
+
Q
v (± Ґ
п
(
)
0
0
п
о
( ( )
)
( )
( )
1
2
й v (x 0 )
щ
к
ъ
к2 т h (v, x 0 )dv ъ =
к 1
ъ
кл v (x 0 )
ъ
ы
2
)
( )
1
2
)=
v
3,1
й v (x 0 )
щ
к
ъ
к2 т h (v, x 0 )dv ъ Ю J (x 0 ) = 0
к 3
ъ
кл v (x 0 )
ъ
ы
2
(x ).
*
(2)
11.
ddv 3
J (x )
x1 =
dx
dx
x= x
0
dv 1
dx
x0
x0
жdQ ( + )v dQ (- )v ч
ц
з
1
ч
+ зз 1
ч
ч
зи d t
ч
dt ш
t=0
d
J (x )
x k = S k (x 0 )
dx
x= x
0
12. Обоснование асимптотики
Теорема. При выполнении условий A1-A4 для достаточномалого e > 0 существует решение u(x, e), v(x, e) задачи , для
которого функции U n (x , e), V n (x , e)являются равномерным на
[0;1] асимптотическим приближением с точностью порядка
O ( en + 1 )
U n (x , e), V n (x , e) - построенная асимптотика n-ого порядка
13.
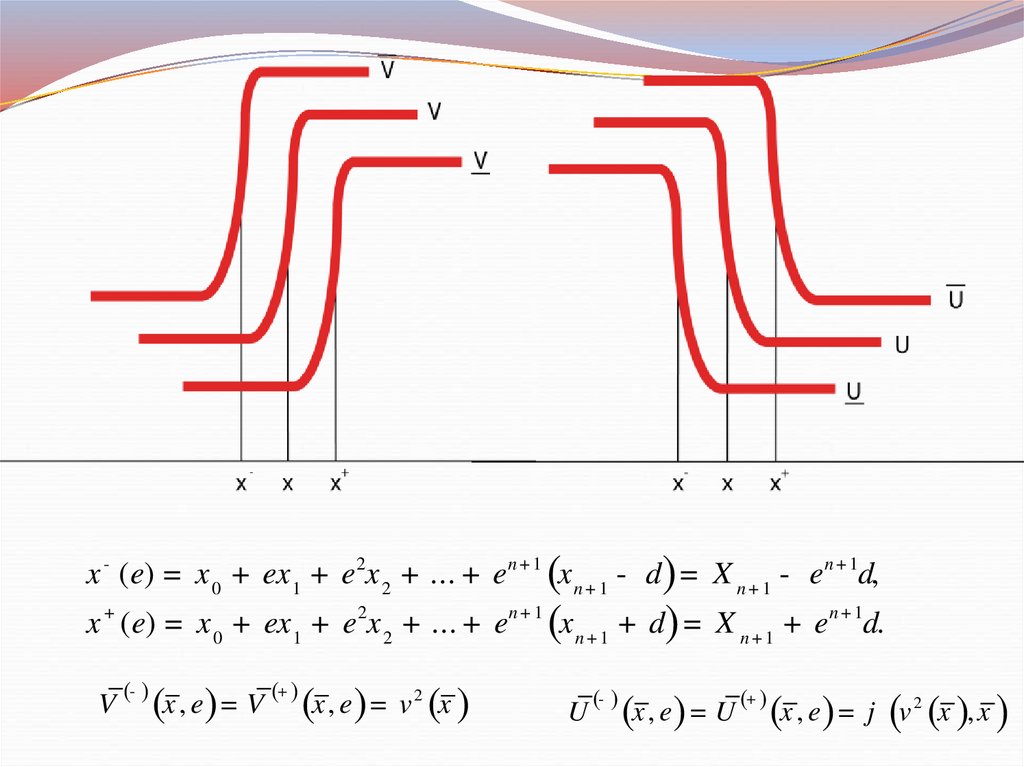
x - ( e) = x 0 + ex 1 + e 2x 2 + ... + en + 1 (x n + 1 - d) = X n + 1 - en + 1d,x + ( e) = x 0 + ex 1 + e 2x 2 + ... + en + 1 (x n + 1 + d) = X n + 1 + en + 1d.
V
(- )
(x , e) = V ( ) (x , e) = v (x )
+
2
U
(- )
(x , e) = U
(+ )
(x , e) = j (v (x ), x )
2
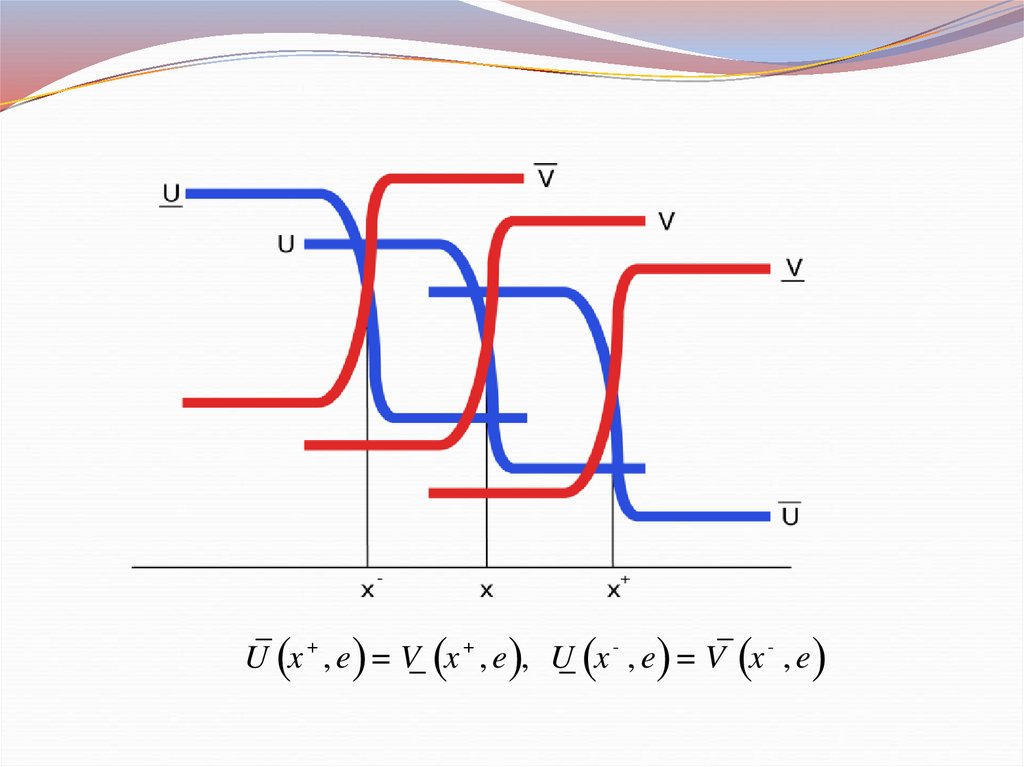
14.
()
(
)
(
)
(
U x+ , e = V x+ , e , U x- , e = V x- , e
)
15. Дифференциальные неравенства
щU Ј U; V Ј V , x О й
0,1
к
ъ
л ы
щ;
L1e (U ,V ) := e 4U ўў- f (U ,V , x , e) < 0, x О й
0;1
к
ъ
л ы
щ;
L2e (U ,V ) := e2V ўў- g (U ,V , x , e) < 0; x О й
0;1
к
л ъ
ы
dU (- ) dU ( + )
> 0,
dx
dx
dV ( - ) dV ( + )
< 0,
dx
dx
16. Верхние и нижние решения
(+ )U (+ ) = U n + 1
V
(+ )
V
(+ )
+
+ en + 1
t+
(+ )
= Vn+1
+ en + 1
t+
(+ )
U (+ ) = U n + 1
(+ )
t-
(+ )
= Vn+1
( ))
(
(
)
()
()
()
%
b
x
+
Q
v
t
+
e
P
v (V );
( ( ) ( ))
()
()
()
()
%
%
a
x
+
Q
u
t
+
e
P
u
V
+
R
( ( ) ( )) ( ( ) u (x )) + e
()
()
()
%
b
x
+
Q
v
t
+
e
P
v (V );
( ( ) ( ))
+ en + 1 - a
+ en + 1
t-
(+ )
(x ) + Q u t +
(+ )
(+ )
(+ )
+ en + 2 P%n + 2u (V2 ) + R%n + 2u (x2 ) + en + 3R%n + 3u (x2 ),
+
+
n+ 2
n+ 2
+
+
+
2
+
n+2
+
n+ 2
+
+
-
n+ 2
+
n+ 2
x x
;
2
2
x x
n+ 2
2
(+ )
R%n + 3u (x2 ),
n+ 3
17.
(- )(- )
+
+
a (x ) + Q u ( t ) = j
-a
(- )
( )
(- )
( )
x- + Q u t - = j
(- )
d 2Q v
=
g
t
u
dt - 2
(- )
d 2Q v
dt
+2
v
(v%(t
+
,x
+
(- )
b
(- )
(- )
+
) )( ( )
((
v% t - , x - , x -
v
A
- b (x ) + Q v( t ) +
fu (t + )
), x )(
+
(- )
+
( ))
x- + Q v t -
-
)
A
( )
fu t -
( )(- a ( ) (x ) + Q ( )u (t )) + g (t )(b ( ) (x ) + Q ( )v (t )) -
-
-
-
-
(
(- )
-
-
-
v
( )( ( )
= gu t + a
-
(- )
(- )
( ))
x+ + Q u t +
+ gv (t ) - b
( )
(- )
B
( )) + B
x+ + Q v t +
18.
Определим функции a(± )
(x ), b
(± )
(x ) как решения систем
(± )
(± )
(± )
(± )
уравнений fu (x )a - fv (x )b = A,
где A и B – положительные числа.
Запишем решение системы:
(± )
a
где
(± )
(x ) =
gv
(x )A +
D
(± )
fv
(± )
(x )
(x )B
b
(± )
(± )
- gu (x )a
(x ) =
fu
(± )
(± )
(± )
+ gv (x )b
(± )
(± )
(x )B - gu
D
(± )
ж
ц
ч
зз
ч
ч
з
f
(± )
з
v ч
D (x ) = fu gv - gu fv = ззhv + gu ч
fu - gu fv = hv fu > 0
ч
ч
fu ч
зз
ч
14442
4443
ч
зз
ч
g
и
ш
v
(x )
= B,
(x )A
,
19. Проверка диф.неравенств
( )( )
L1e (U ,V ) = - en + 1A + O en + 2 , L2e (U ,V ) = - en + 1B + O en + 2 ,
жdV (- ) +
dV ( + ) + ц
ч
зз
ч
x
,
e
x
,
e
=
ч
зз dx
ч
dx
и
ш
+Ґ
жg ( t + )A
ц
1 dJ
1
ч
з
n
n
+
n+1
u
ч
з
= e d
x0 )+ e
F
(
t
)
B
d
t
+
O
e
< 0
(
ч
з
т
+
ч
зи fu ( t )
ч
F (0) - Ґ
F (0) dx
ш
(
)
(
)
( )
dU (- ) +
dU ( + ) +
x ,e x ,e = j
dx
dx
(
)
(
j
)
(
)
(
(v , x ) = - f (0)f (0) < 0
2
v
v
жdV ( - ) +
dV ( + ) +
з
v , x 0 зз
x ,e x ,e
зи dx
dx
2
0
- 1
v
u
)
(
ц
ч
ч
+ O en + 1 > 0.
ч
ч
ш
)
( )








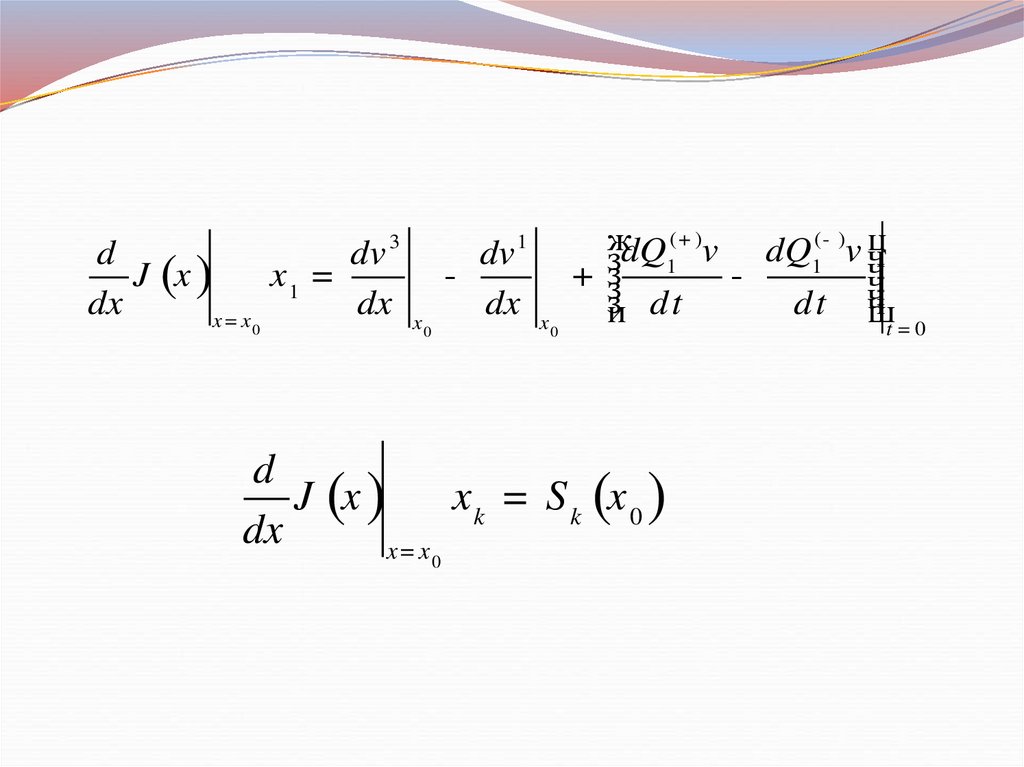



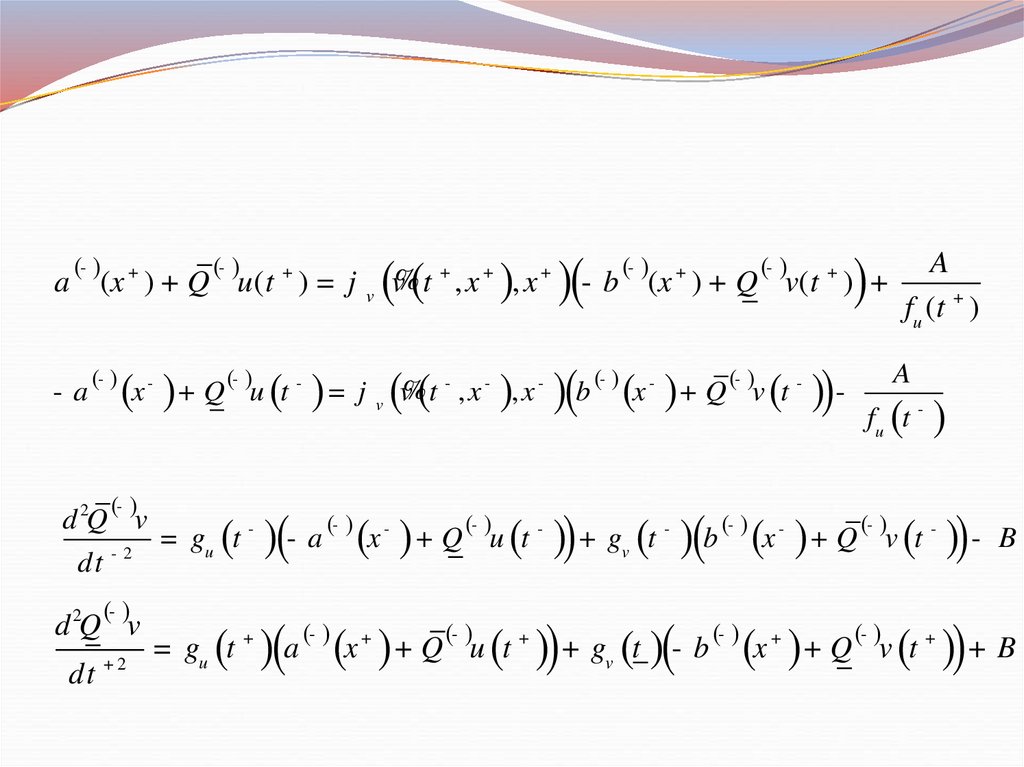



 Математика
Математика








