Лекция 41. Рентгеновская трубка. Эффект Комптона. Введение в квантовую механику

1. Лк - 41

Рентгеновская трубка. Эффект
Комптона. Введение в квантовую
механику

2.

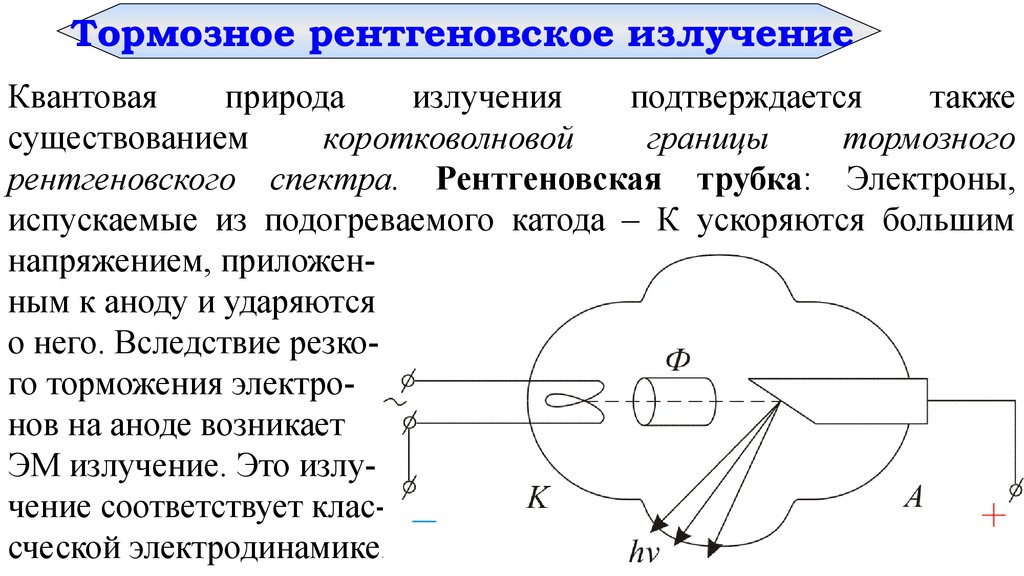
Тормозное рентгеновское излучение 
Квантовая
природа
излучения
подтверждается
также
существованием
коротковолновой
границы
тормозного
рентгеновского спектра. Рентгеновская трубка: Электроны,
испускаемые из подогреваемого катода – К ускоряются большим
напряжением, приложенным к аноду и ударяются
о него. Вследствие резкого торможения электронов на аноде возникает
ЭМ излучение. Это излучение соответствует классческой электродинамике.

3.

Но она не может объяснить наличие
коротковолновой границы тормозного
излучения -λmin. В тоже время это ограничение напрямую вытекает из квантовой природы излучения. если излучение возникает за счёт энергии, теряемой электроном при торможении, то
энергия кванта hω не может превысить энергию электрона: hν ≤ eU, отсюда λ≥Ch/(eU). (С- скорость
света).
Т.о. Квантовые свойства света при излучении и поглощении не
вызывали сомнений. Однако, в каком же виде существует и
распространяется свет?.

4.

Эффект Комптона. В этом опыте фотоны ведут себя подобно
биллиардным шарам, сталкиваясь со свободными электронами.
?????  ????????  ????????????  ??  ???.   ?????????????  ?????????  ?  ??????  ????? λ0,  ?????????  ??  ????????????? 
?????? R,  ????????  ?????  ?????????  ?????????  ?  ?  ????  ??????  ?????  ????????????  ??  ????????????  ????????­
?????? P (??????).  ?????????,  ??????????  ???  ?????????  ????? θ,  ?????????????  ?  ???????  ???????????? 
?????????????
????? S, ? ??????? ???? 
????????????? ??????? ??????
???????? K, ???????????? ?? ??­
???????? ???????.   

5.

???? ???????, ??? ? ?????????? ???? ?????? ? ???????? ?????? ???????????? ??? ????, ??????? ??????? ????? ?????, 
????????? ?? ???? ?????????. 
Если принять, что
излучение представляет собой поток фотонов,
то эффект Комптона
есть результат упругого столкновения рентгеновских фотонов со
свободными электронами вещества. У легких атомов электроны
слабо связаны с ядрами атомов, поэтому их можно считать
свободными. В процессе столкновения фотон передает электрону
часть своей энергии и импульса в соответствии с законами
сохранения.

6.

??????? ???????????? ???? ?????? – ??????????? ??????, 
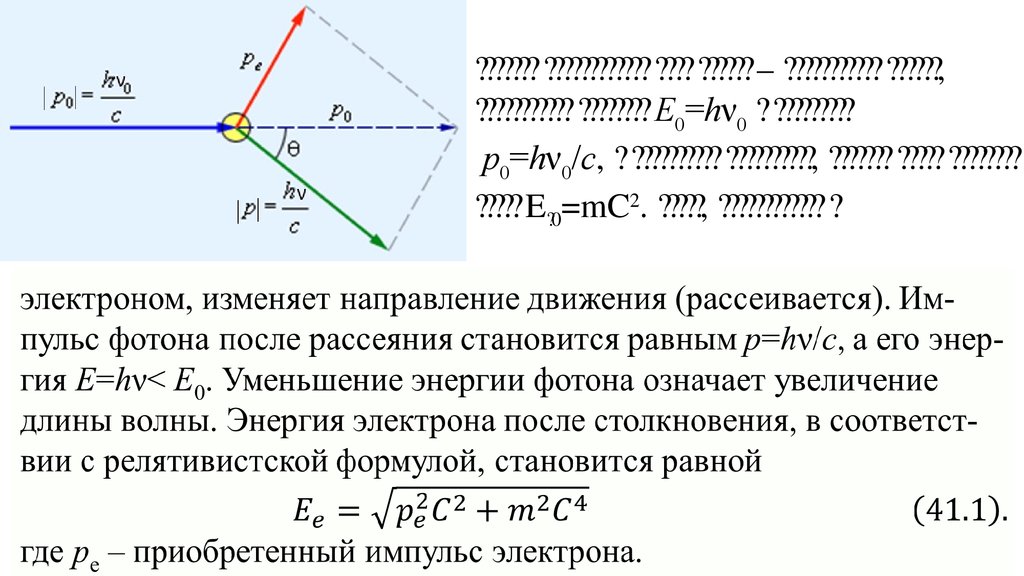
??????????? ???????? E0=hν0 ? ????????? 
 p0=hν0/c, ? ?????????? ??????????, ??????? ????? ???????? 
????? E?0=mC2. ?????, ???????????? ?  

7.

8.

9.

10.

Это заявление было неожиданным. Но вскоре опыты Дэвиссона
обнаружили волновые свойства электрона. При отражении потока
электронов от кристалла никеля на экране, где фиксировались отраженные электроны, возникала дифракционная картина, аналогичная
картине, даваемой рентгеновскими лучами. Следовательно, некая
сопутствующая движению частицы волна не является пустой абстракцией. Оценим длину этой волны по формуле де-Бройля. Пусть
масса частицы m=0.1 г, а скорость v=10 м/c. Тогда
λ=6.6*10-34Дж*с/(10-4Кг*10м/с)=6.6*10-29м. Это невообразимо малая
длина, на много порядков меньшая размеров атомов. Следовательно
для обычных макро частиц длина сопутствующей волны, практически, нулевая, и обнаружить волновые эффекты невозможно. Другое
дело – микрочастицы. Например для электрона со скоростью 100 м/с
λ=6.6*10-34Дж*с/(9.1-31Кг*100м/с)=6*10-6м .

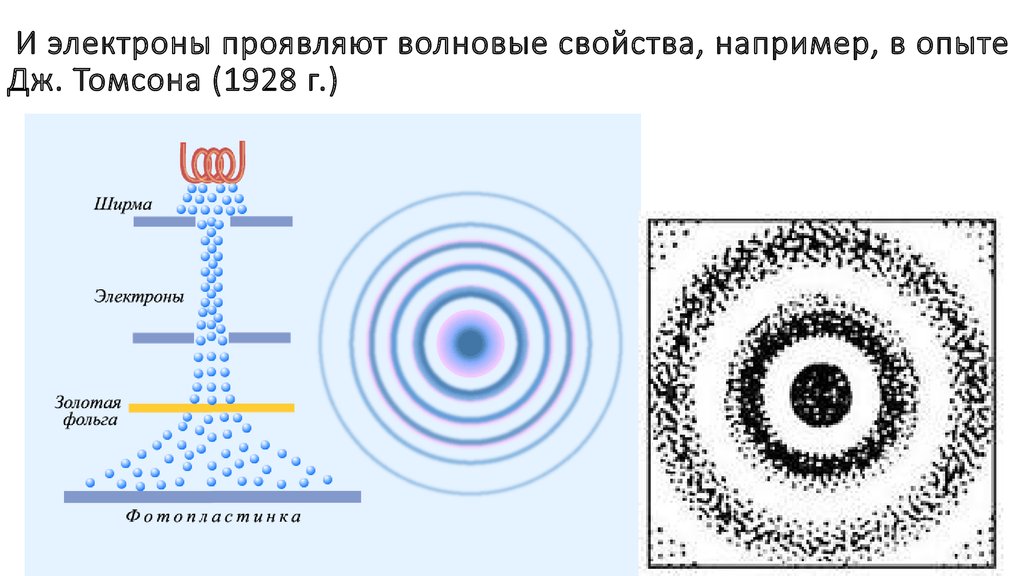
11. И электроны проявляют волновые свойства, например, в опыте Дж. Томсона (1928 г.)

12.

Мы получаем критерий разграничения между микро и макро
частицами: к микрочастицами отнесем те, для которых длина волны
де-Бройля – наблюдаемая величина, макро частицы имеют очень
малую длину волны, которая не может наблюдаться. И те и другие
частицы движутся по общим законам. Но в опытах с макро
частицами эти общие законы дают результат, близкий к законам
классической механики. В опытах с микрочастицами результат
будет существенно отличиться от законов классической механики.
Новая механика для микрочастиц получила два названия: иногда ее
называют волновой, а иногда – квантовой механикой. Отличие ее от
классической состоит в том, что она определяет не координаты
движущейся частицы, а сопутствующую движению волну.
Математическое выражение этой волны назвали волновой функцией
и обозначается буквой ψ (пси).

13.

Элементы квантовой механики.
Начальный этап развития опирался на известные законы оптики,
которые описывают движение одной из микрочастиц – фотона.
Свободный фотон движется вдоль оси Z со скоростью света – c ,
имеет энергию E импульс p=E/c. Ему соответствует плоская
электромагнитная волна, распространяющаяся в ту же сторону с
частотой колебаний ω=Е/ħ и длиной волны λ=2πħ/p. (Здесь использована ħ=h/2π≈10-34Дж*с). Уравнение этой волны для светового
вектора: E=Emcos(ωt-kz), где k=2π/λ=p/ħ – волновой вектор.
По аналогии, для любой свободно движущийся частицы с энергией
E=mv2/2 и импульсом p=mv можем написать уравнение
сопутствующей волны a=Amcos(ωt-kz), где ω=Е/ħ, k=p/ħ. Но если для
света величина E– это световой вектор, то какой смысл величины

14.

Ответ на этот вопрос также вытекает из аналогии с оптикой. Там нас
интересовало не мгновенное значение светового вектора, а
интенсивность света в некоторой точке, которая пропорциональна
квадрату амплитуды (Sm)2. Точно также следует толковать и волну
произвольной частицы, интересуясь только квадратом ее амплитуды – (Am)2 в некоторой точке пространства.
Интенсивность света определяется количеством фотонов, попадающих в данную область пространства в единицу времени.
Следовательно, квадрат амплитуды волновой функции (Am)2 будет
пропорционален количеству частиц, попадающих в данную область
в единицу времени. Если же речь идет об одной движущейся
частице, то (Am)2 представляет собой вероятность попадания
частицы в данную область пространства. Таков физический

15.

Для свободной частицы амплитуда Am не зависит от координаты,
следовательно, вероятность нахождения частицы в любой точке оси
Z одинакова (не зависит от координаты z).
Ограничим свободу частицы двумя стенками, перпендикулярными
оси Z. Расстояние между стенками – l и они упруго отражают
частицу. Классическая частица может иметь любую скорость. Она
ударяется о стенку, отскакивает без потери скорости, ударяется о
другую стенку и т.д.
С точки зрения квантовой механики ситуация иная. Движению частице вправо соотВетствует волновая функция ψ1=Amcos(ωt-kz)
А движению влево – ψ2=Amcos(ωt+kz). Общая волновая функция равна сумме ψ=ψ1+ψ2

16.

17.

18.

Принцип неопределенности. На первый взгляд этот принцип кажется довольно странным, однако по сути он прост. В квантовой механике, где положение частицы определяется квадратом амплитуды, а импульс – длиной волны волновой функции, это принцип выражает факт, характерный для всех волн. Если волна имеет одну определенную длину волны, она бесконечна в пространстве (вспомним случай свободной частицы). Если же волна локализована в пространстве интервалом координаты - Δz, т.е. только в этой области ее
амплитуда не равна нулю а в остальных областях – ноль, то она
представляет собой сумму многих волн с разными длинами волн.
При этом ее импульс не имеет определенного значения и
распределен в некотором интервале –Δp. Гейзенберг вычислил эти
неопределенности:
Δp Δz≈h
(41.8)

19.

Можно получить соотношение неопределенности для частицы,
движущейся между двумя стенками. Ее волновая функция представляет сумму двух волн, распространяющихся навстречу друг другу.
Импульс первой волны р1=h/λ, импульс второй р2=-h/λ.
Следовательно, неопределенность импульса Δp=2h/λ.
Неопределенность координаты равна расстоянию между стенками –
Δz=l. Произведение ΔpΔz= 2lh/λ. В основном состоянии длина
волны λ=2l, следовательно ΔpΔz= h.
Пусть поток электронов проходит через узкую щель. Казалось бы
это поток, пройдя щель, засветит на экране узкую
полоску, с шириной, равной ширине щели Δх.
Однако, вследствие принципа неопределенности
после прохождения щели импульс электронов в
направлении оси Х станет неопределенным: ΔхΔр =h.

20.

Эта неопределённость означает наличие у прошедших электронов
скорости в направлении оси Х: Δvx=h/(mΔx). Время пролета
электронов от щели до экрана равно t=L/vy. За это время электроны
пройдут вдоль оси Х расстояние f= tΔvx=hL/(mvy Δx). Но mvy=ру=h/λ
А отношение f/L=α – угол, на который рассеется электронный поток
после щели: α= λ/ Δx. Эта формула для ширины главного дифракционного максимума при дифракции на щели. Т.о. соотношение
неопределенностей позволяет в упрощенной форме определить
некоторые параметры дифракции микрочастиц.
А что можно сказать об обычных макрочастицах, действует ли для
них соотношение неопределенностей. Конечно действует. Однако,
огромная их масса и размеры пространства делает неопределенность импульса и скорости столь малыми, что обнаружить их

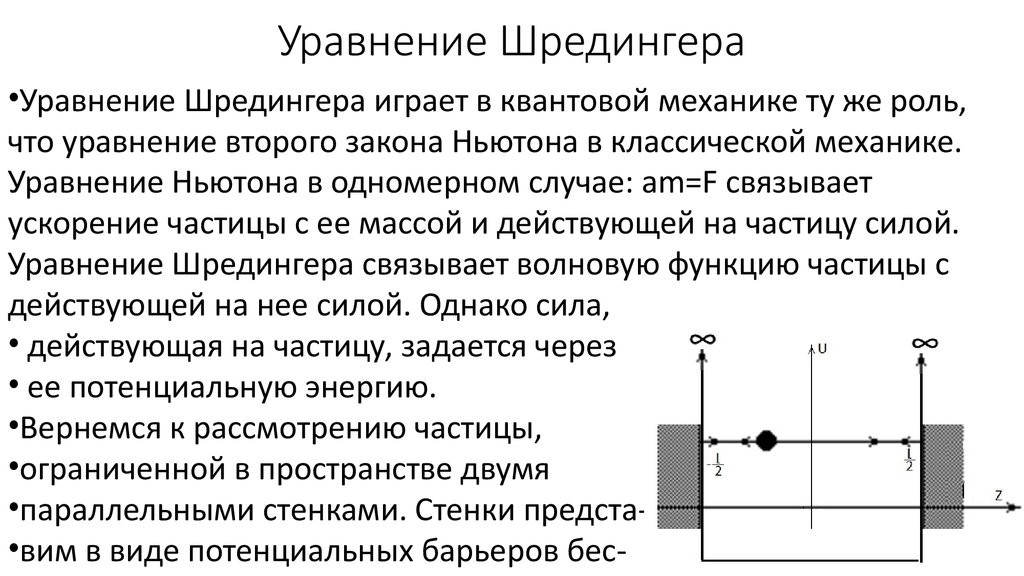
21. Уравнение Шредингера

•Уравнение Шредингера играет в квантовой механике ту же роль,
что уравнение второго закона Ньютона в классической механике.
Уравнение Ньютона в одномерном случае: am=F связывает
ускорение частицы с ее массой и действующей на частицу силой.
Уравнение Шредингера связывает волновую функцию частицы с
действующей на нее силой. Однако сила,
• действующая на частицу, задается через
• ее потенциальную энергию.
•Вернемся к рассмотрению частицы,
•ограниченной в пространстве двумя
•параллельными стенками. Стенки предста•вим в виде потенциальных барьеров бес-

22.

23.

24.

Решение уравнения Шредингера определяется не только видом
потенциальной функции U(z), но и граничными условиями. Это те
условия, которым должна соответствовать частица на границах
области решения.
Если частица находится в потенциальной яме, то вероятность найти
ее вне ямы обращается в нуль; следовательно, здесь
граничное условие состоит в том, что вероятность найти частицу при
значениях, больших | l/2 | обращается в нуль. Этому граничному
условию удовлетворяют лишь определенные значения Е (будем
обозначать их Еn) и соответствующие ψn. Значения Еn называются
собственными значениями, а cответствующие волновые функции —
ψn собственными функциями.
Рассмотрим простейшие примеры решения уравнения Шредингера.

25.

Движение частиц в прямоугольной потенциальной яме
Одна из простейших задач о движении микрочастиц – это задача о
движении в прямоугольной потенциальной яме с очень высокими
стенками. Рассмотрим одномерный случай
Изменение потенциальной энергии по оси z
описывается формулой:
U=0 при 0<z<l
U=∞ при z<0 или z>l
В мире микрочастиц взаимодействие протона
и нейтрона в ядре приближенно описывается
прямоугольным потенциалом. Этот же
потенциал очень грубое приближение к
задаче о движении электрона в атоме.

26.

27.

28.

29.

Скорость частицы не
может быть нулевой. Это
общий результат
квантовой механики,
справедливый для всех
ее задач и полностью
чуждый для классической механики. Расстояние между соседними
уровнями энергии