Похожие презентации:
Магнитный момент атома. Периодическая система элементов Д.И. Менделеева
1. Магнитный момент атома. Периодическая система элементов Д.И.Менделеева
Тема 4.2 «КВАНТОВОМЕХАНИЧЕСКАЯМОДЕЛЬ АТОМА»
Магнитный момент атома.
Периодическая система
элементов
Д.И.Менделеева
2. Магнитный момент атома. Периодическая система элементов Д.И. Менделеева
1. Магнитный момент атома.2. Опыт Штерна и Герлаха. Спин электрона.
3. Распределение электронов по энергетическим
уровням в атоме. Принцип Паули. Электронная
оболочка и подоболочка.
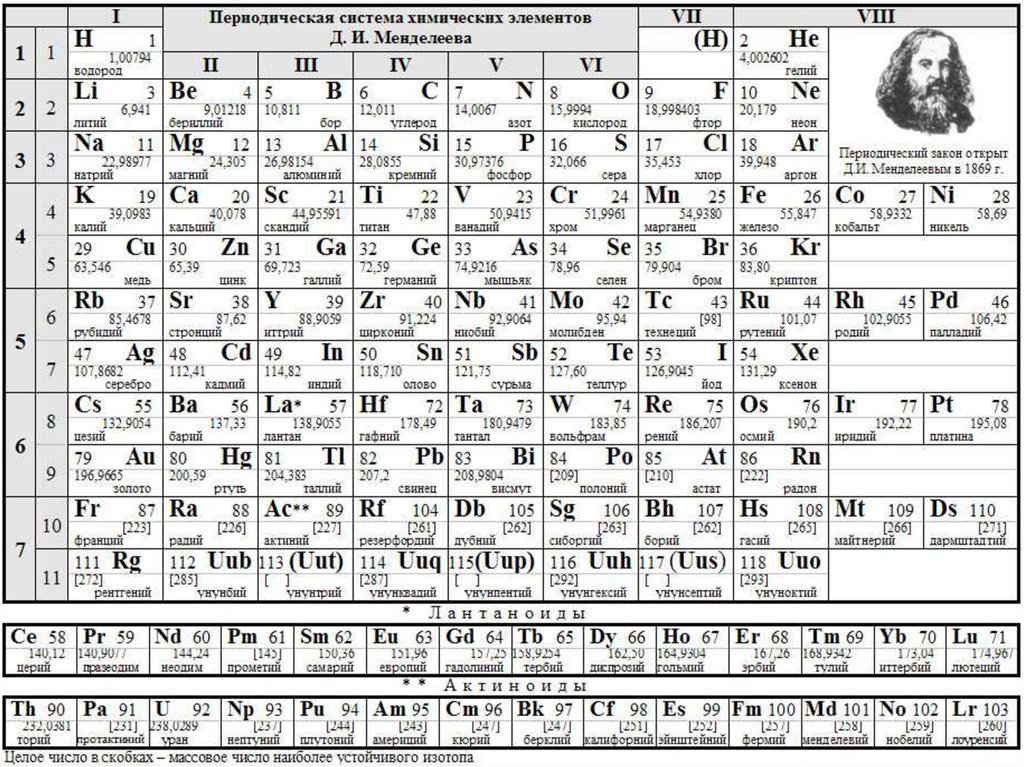
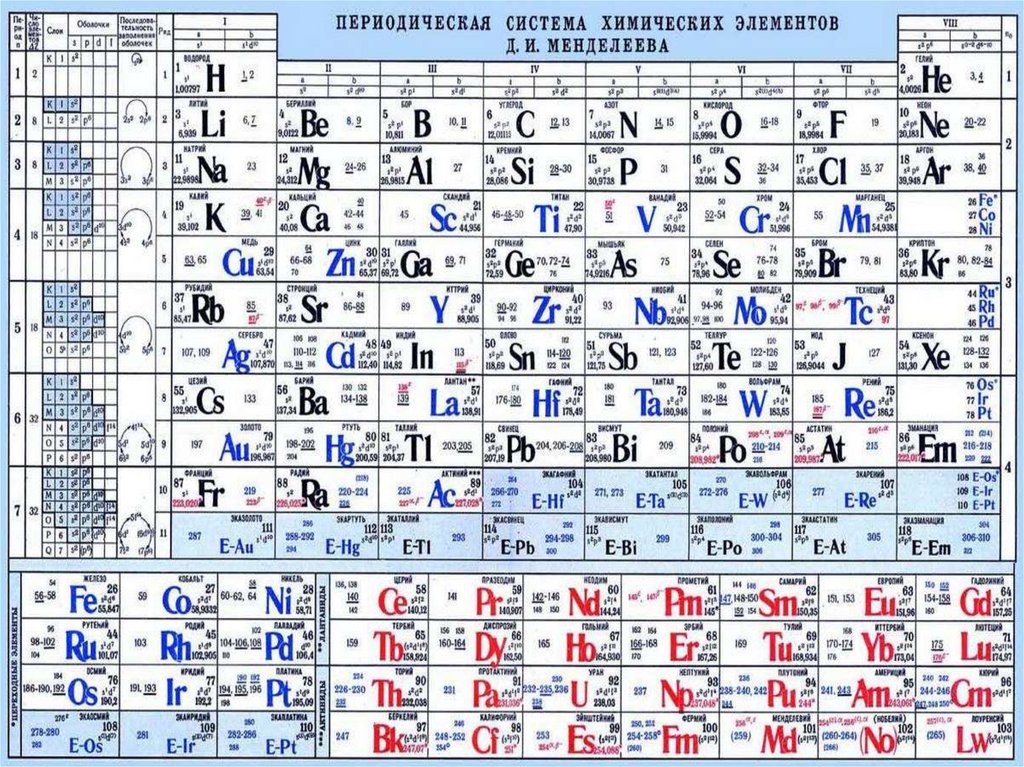
4. Периодическая система элементов.
3. 1. Магнитный момент атома.
Величина орбитального механического момента атома:Le me r
Круговому движению электрона соответствует замкнутый ток:
e e
I
T 2 r
Микроток характеризуется магнитным моментом:
e r
pm I r
2
2
Гиромагнитное отношение:
pm
e
g
L e 2m e
I
pm
4.
Т.о. в любом квантовом состоянии атом обладает, кромемеханического, магнитным моментом:
pm g Le Á l l 1
Б – магнетон Бора – единица измерения магнитных моментов:
e
Á
2m e
из общих положений квантовой механики следует, что проекция
момента импульса электрона на выделенное в пространстве
направление z может иметь только определенные значения:
Lez ml
где ml – магнитное квантовое число.
5.
Lez ml-
формула пространственного квантования определяет
возможные
дискретные
расположения
электронных
орбит
в
пространстве по отношению к направлению
внешнего магнитного поля.
В зависимости от значения магнитного
квантового числа, возможные значения
проекции магнитного момента атома на
выделенное направление z:
p mz g Lez ml Á
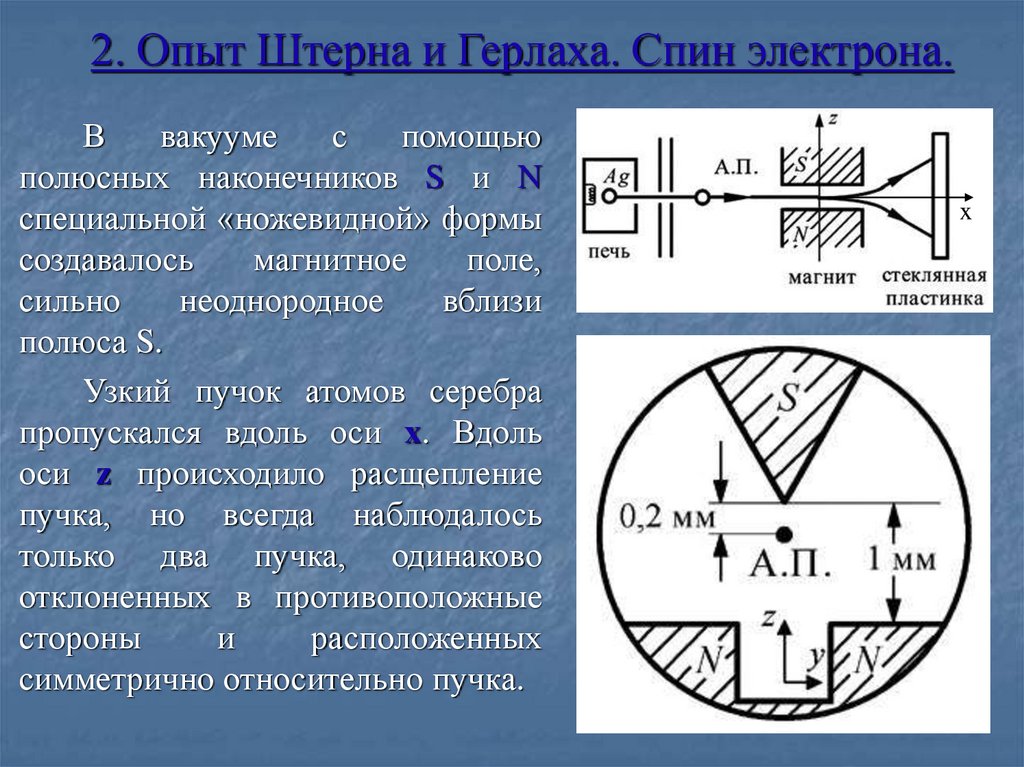
6. 2. Опыт Штерна и Герлаха. Спин электрона.
Ввакууме
с
помощью
полюсных наконечников S и N
специальной «ножевидной» формы
создавалось
магнитное
поле,
сильно
неоднородное
вблизи
полюса S.
Узкий пучок атомов серебра
пропускался вдоль оси x. Вдоль
оси z происходило расщепление
пучка, но всегда наблюдалось
только два пучка, одинаково
отклоненных в противоположные
стороны
и
расположенных
симметрично относительно пучка.
x
7.
Спин электрона – LS – cобственный механический моментимпульса - квантовая величина, у нее нет классического
аналога; это внутреннее неотъемлемое свойство электрона,
подобно его заряду и массе.
Квантование спина:
Ls s(s 1)
Квантование проекции
магнитного поля:
спина
на
направление
внешнего
Lsz ms
Вектор LS может принимать 2s + 1 ориентаций. Т.к.
расщепление происходит на два подуровня, 2s + 1 = 2,
следовательно спиновое квантовое число s = 1/2.
Магнитное спиновое квантовое число:
1
mS s
2
8.
Собственный (спиновый) магнитный момент:p ms gLs
Гиромагнитное отношение для спиновых моментов:
p ms
e
g
Ls
me
9. 3. Распределение электронов по энергетическим уровням в атоме. Принцип Паули. Электронная оболочка и подоболочка.
Состояние электрона в атоме однозначно описывается наборомиз четырех квантовых чисел:
Главное
Орбитальное
Магнитное
Магнитное спиновое
n = 1,2, 3, ...
l = 0, 1, 2, ... , n - 1
ml = 0, ± 1, ± 2,..., ± l
ms = ± 1/2
10.
Принцип Паули:В одном а томе не может быть более одного электрона с
одинаковым набором четырех квантовых чисел:
Z(n , l, ml , ms ) 1
или
Z(n , l, ml , ms ) 0
Принцип Паули (квантовомеханическая формулировка):
Системы фермионов встречаются в состояниях, описываемых
антисимметричными волновыми функциями.
11.
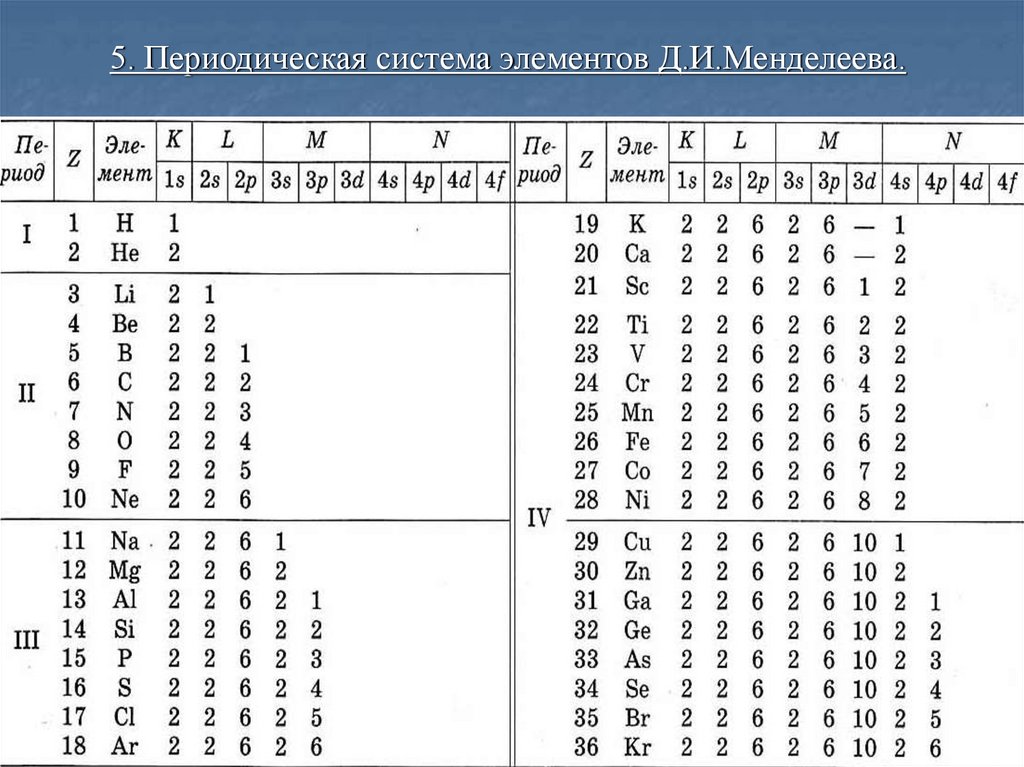
Распределение электронов по оболочкам и подоболочкам.Максимальное число электронов в состоянии, определяемом
главным квантовым числом n:
Z( n )
n 1
2( 2l
l 0
1) 2n 2
Электронная оболочка
Совокупность электронов в многоэлектронном атоме, имеющих
одно и то же главное квантовое число n.
Подоболочка
Совокупность электронов в каждой из оболочек,
соответствующих данному значению l.
12.
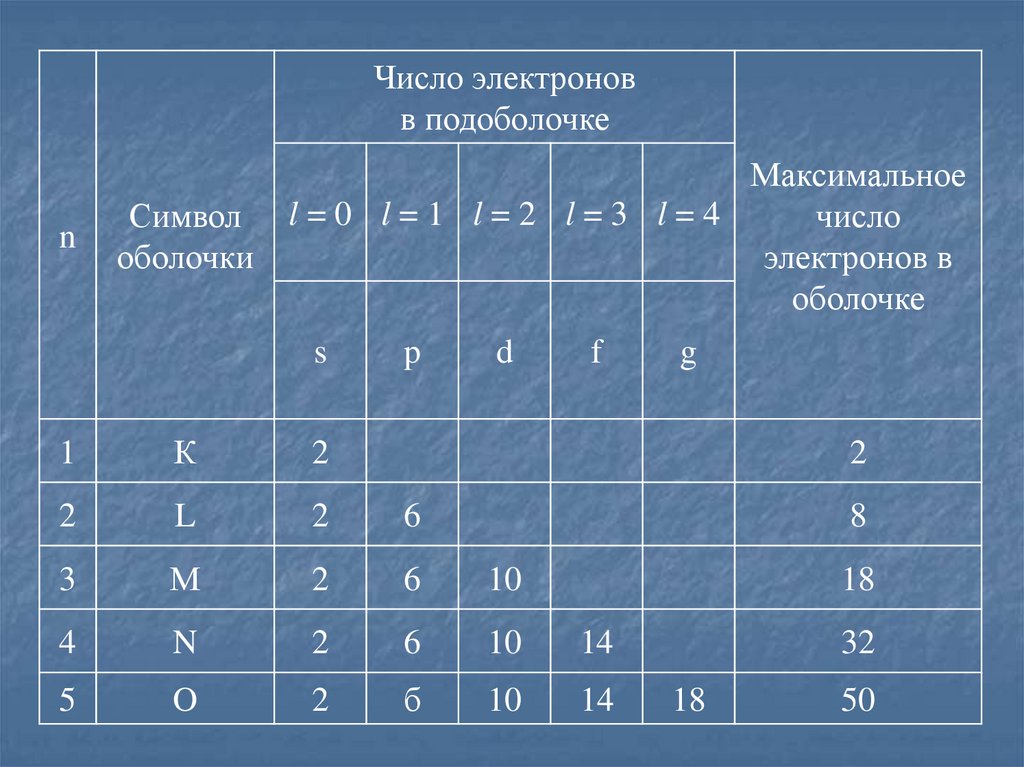
Число электроновв подоболочке
n
Символ
оболочки
Максимальное
l=0 l=1 l=2 l=3 l=4
число
электронов в
оболочке
s
p
d
f
1
К
2
2
L
2
6
3
М
2
6
10
4
N
2
6
10
14
5
O
2
б
10
14
g
2
8
18
32
18
50











 Химия
Химия








