Похожие презентации:
Специальные случайные распределения, используемые в математической статистике
1. Специальные случайные распределения, используемые в математической статистике
2. Гамма-функция
Интегральное представление:( x)
0
t x 1
e t
dt
3.
Основное свойство :(x+1) = x (x)
где х – любое действительное число.
Частные свойства.
(n+1) = n ! , где n - натуральное число.
(1) = (2) = 1.
(1 / 2 ) 1, 77245 ...
( 3 / 2 ) / 2 0 ,88623 ...
4.
Асимптотика( x ) e
x
x x
x
2 / x
5.
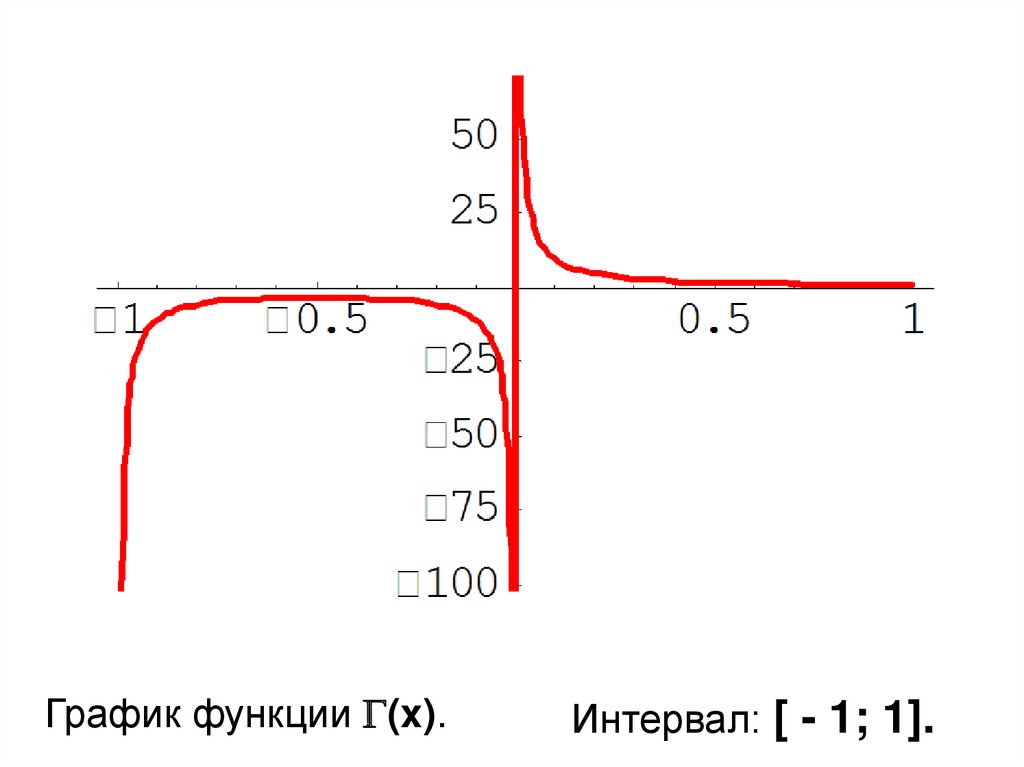
График функции (x).Интервал: [ - 1; 1].
6.
105
4
2
2
4
5
10
График функции (x).
Интервал: [ - 5; 5].
7.
42
4
2
2
4
2
4
График функции
1 / (x).
8.
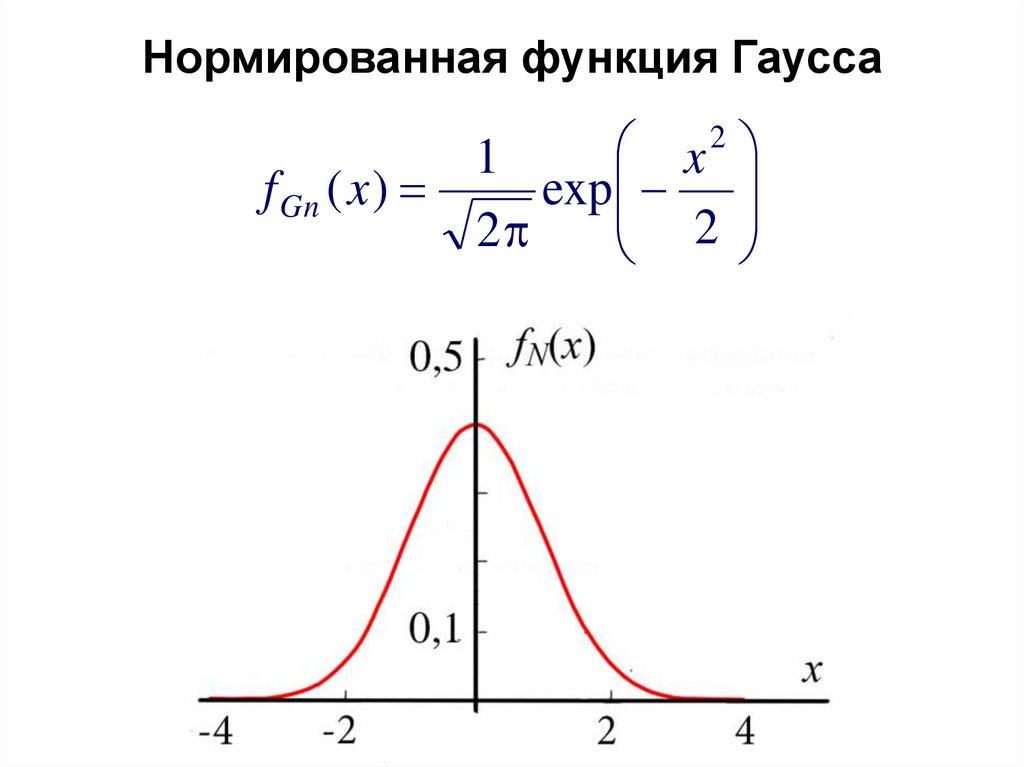
Нормированная функция Гаусса2
1
x
f Gn ( x )
exp
2
2
9. Случайная величина «хи-квадрат»
v2
2
i
i 1
где i – независимые случайные величины, каждая из
которых имеет нормальное нормированное
распределение вероятностей, имеющее плотность вида
2
1
x
f Gn ( x )
exp
2
2
10.
Вид распределения зависит от целочисленного параметра, который называется число степеней свободы и
принимает значения натурального ряда чисел.
1
f 2 ( x)
x
(v / 2)
v
x
1
2
2
e
2
v
2
x 0
Математическое ожидание и дисперсия
M( 2 ) = v
D( 2 ) = 2v
11.
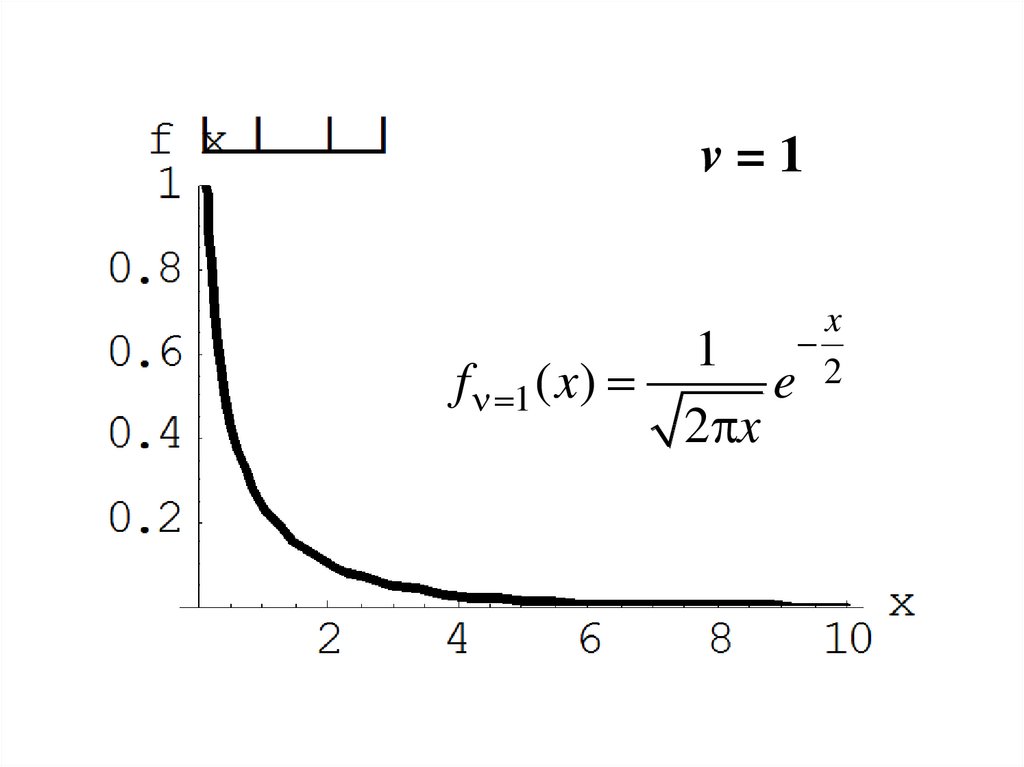
v=11
f 1 ( x)
2 x
x
e 2
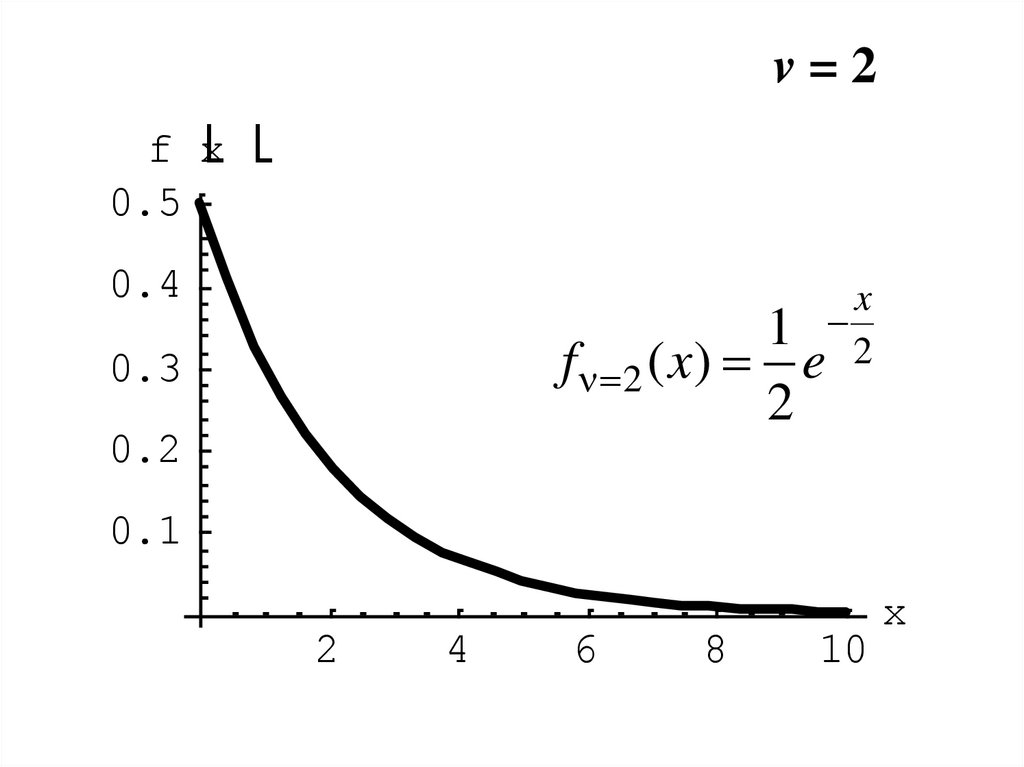
12.
v=2f x
0.5
0.4
f 2 ( x)
0.3
0.2
x
1 2
e
2
0.1
2
4
6
8
10
x
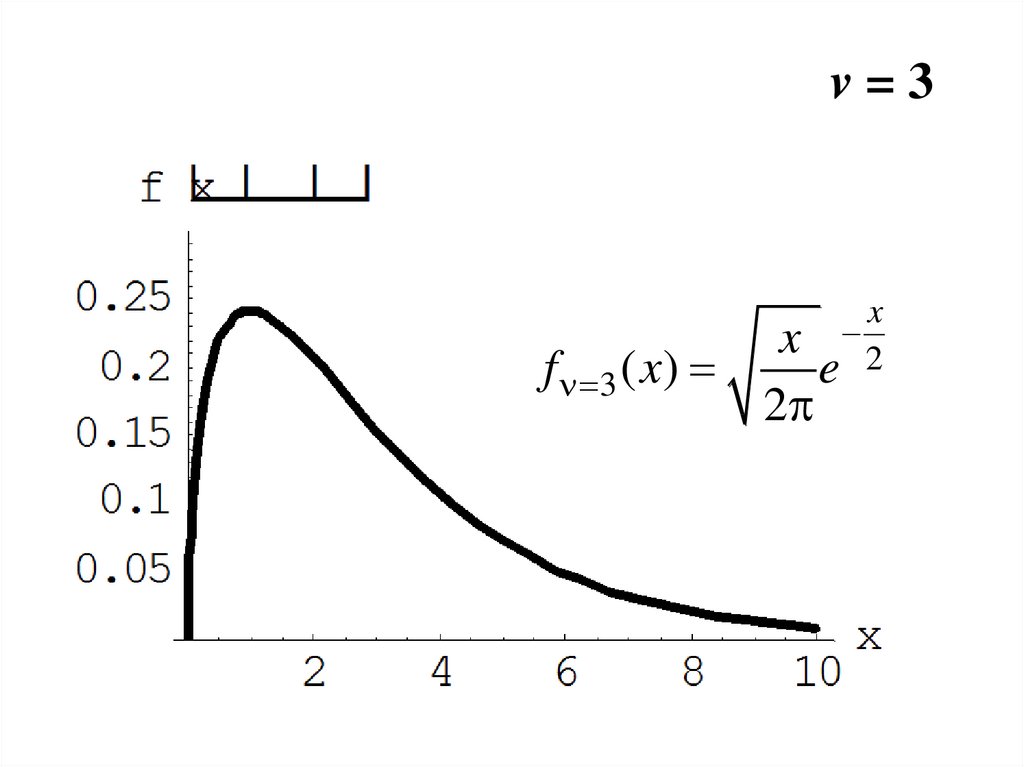
13.
v=3x
f 3 ( x)
2
x
e 2
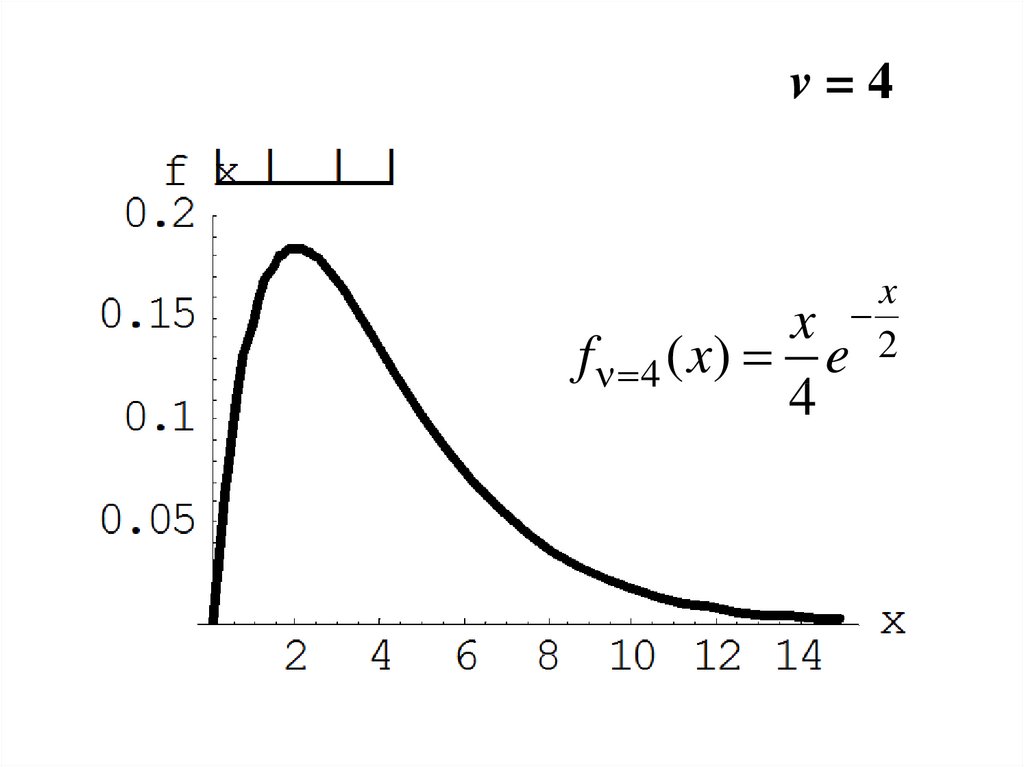
14.
v=4f 4 ( x)
x
x 2
e
4
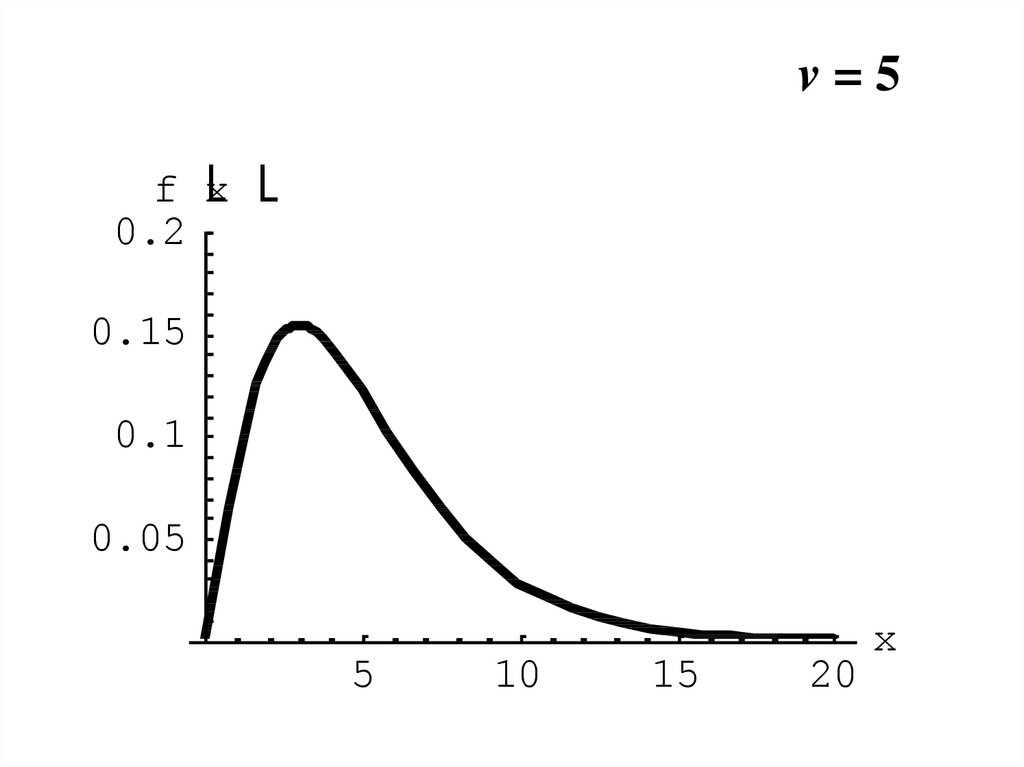
15.
v=5f x
0.2
0.15
0.1
0.05
5
10
15
20
x
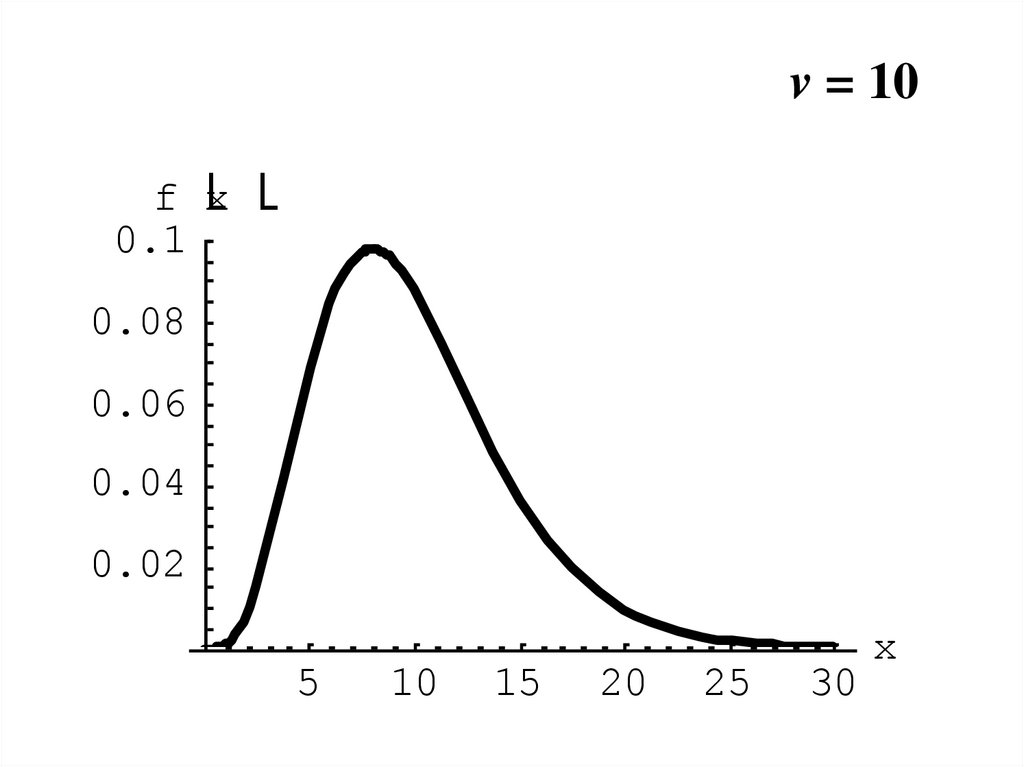
16.
v = 10f x
0.1
0.08
0.06
0.04
0.02
5
10
15
20
25
30
x
17.
v = 20f x
0.1
0.08
0.06
0.04
0.02
10
20
30
40
50
x
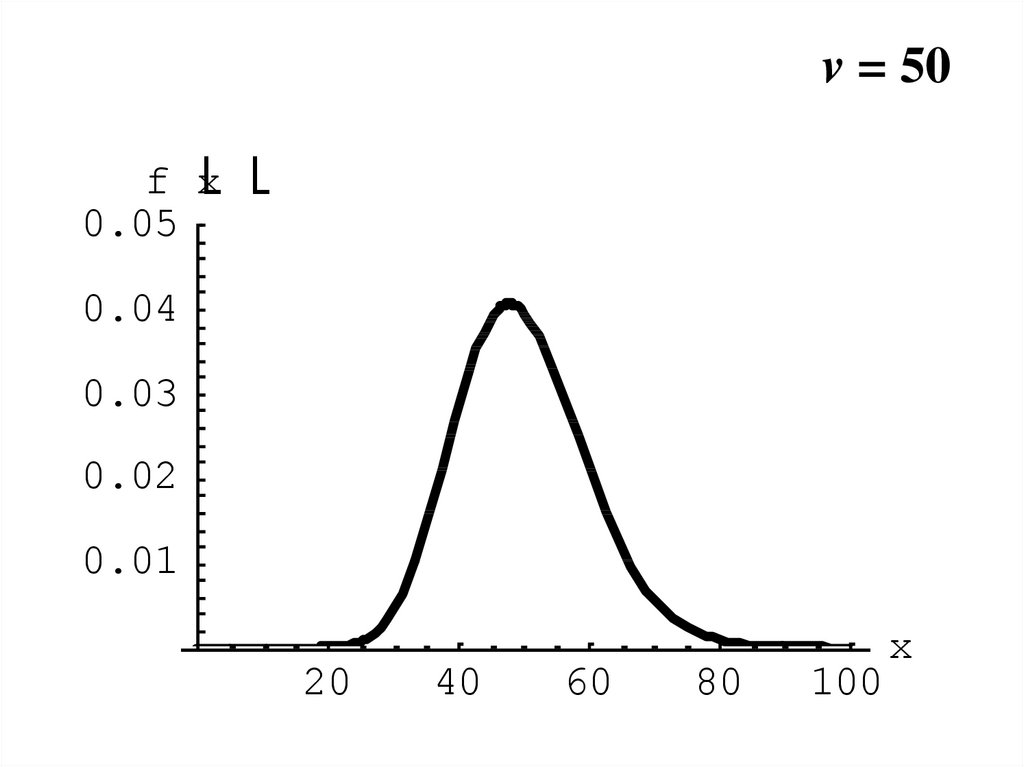
18.
v = 50f x
0.05
0.04
0.03
0.02
0.01
20
40
60
80
100
x
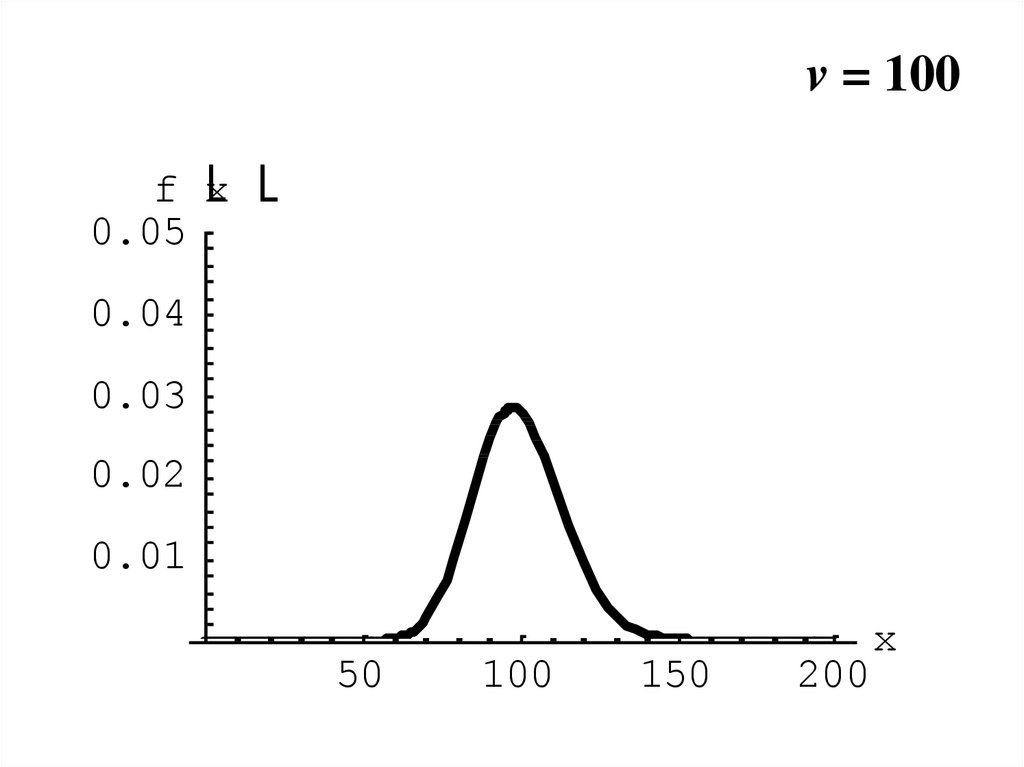
19.
v = 100f x
0.05
0.04
0.03
0.02
0.01
50
100
150
200
x
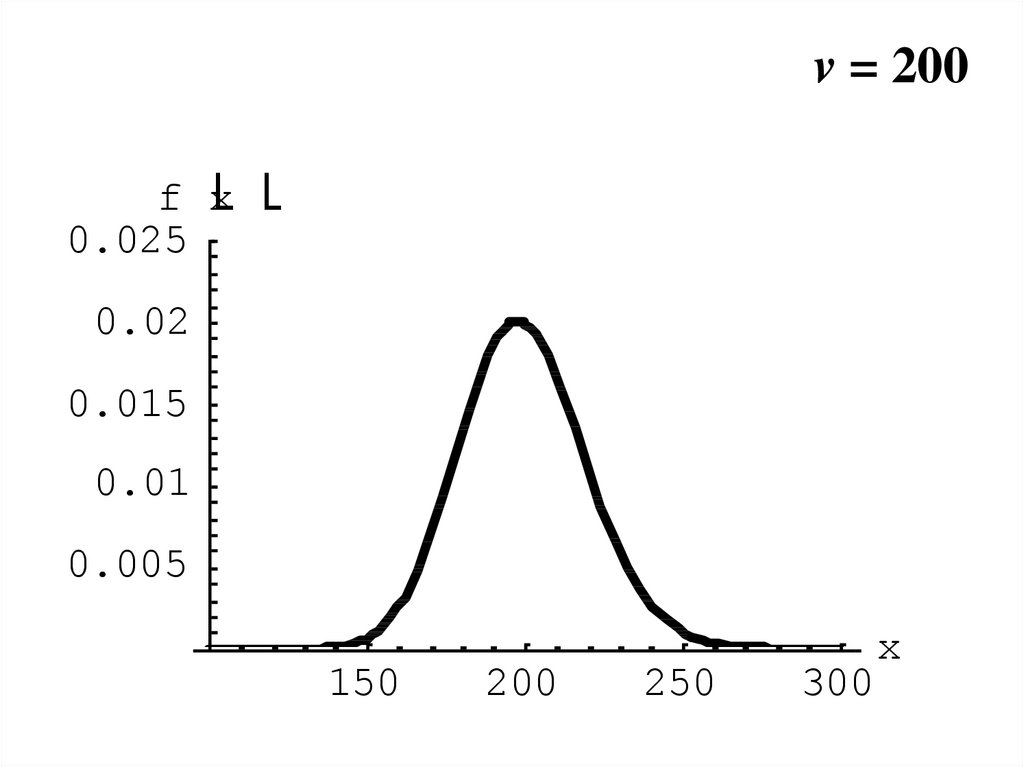
20.
v = 200f x
0.025
0.02
0.015
0.01
0.005
150
200
250
300
x
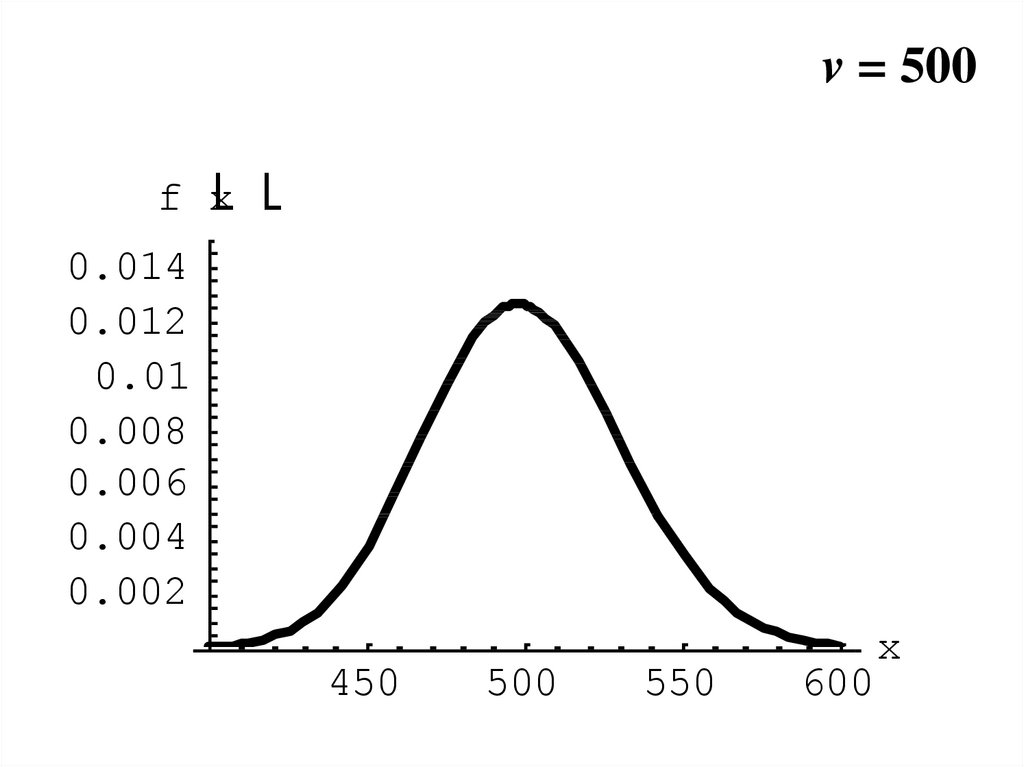
21.
v = 500f x
0.014
0.012
0.01
0.008
0.006
0.004
0.002
450
500
550
600
x
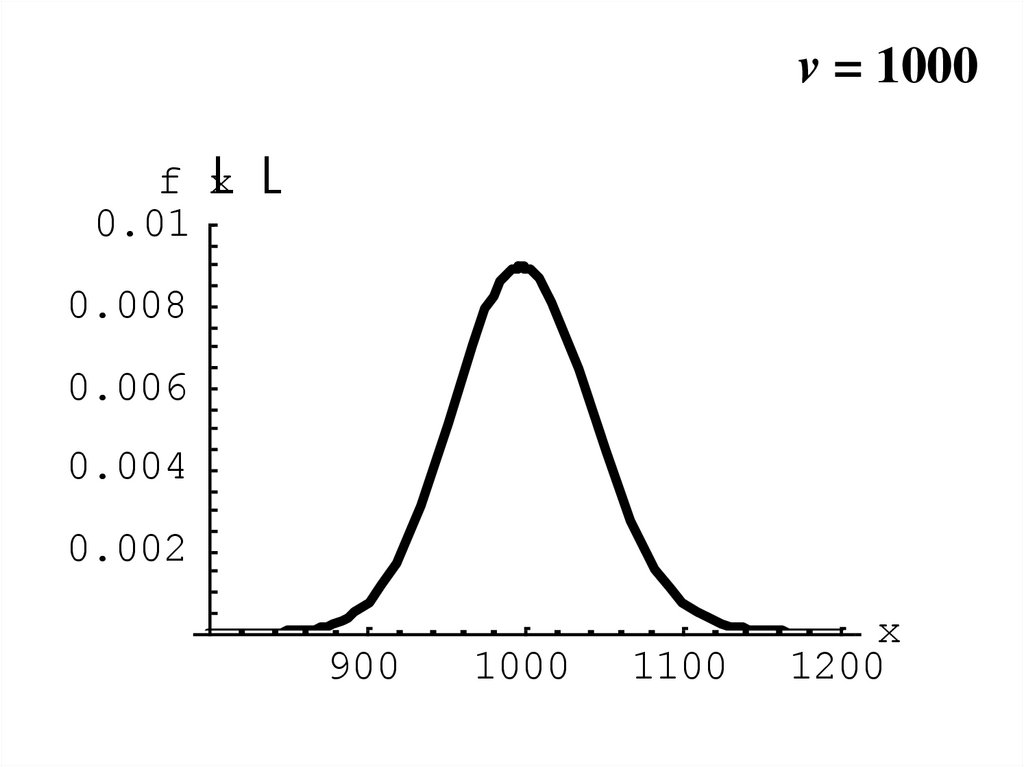
22.
v = 1000f x
0.01
0.008
0.006
0.004
0.002
900
1000
1100
x
1200
23.
2Случайная величина
v
2v
при v превращается в гауссову
нормированную случайную величину.
24. Случайная величина Стьюдента
Tv1
v
v
2
i
i 1
где все ( + 1) случайные величины i независимы и
имеют нормальное нормированное распределение
вероятностей.
Параметр называется числом степеней свободы
и принимает значения натурального ряда чисел.
25.
Плотность случайной величины Стьюдентаv 1
2 2
x
1 (( v 1) / 2)
f v ( x)
1
v
v (v / 2)
Вид распределения зависит от числа степеней свободы
Математическое ожидание и дисперсия
M(Tv) = 0
D (T )
2
26.
v=10.5
0.4
1
f 1 ( x)
2
(1 x )
0.3
0.2
0.1
4
2
2
4
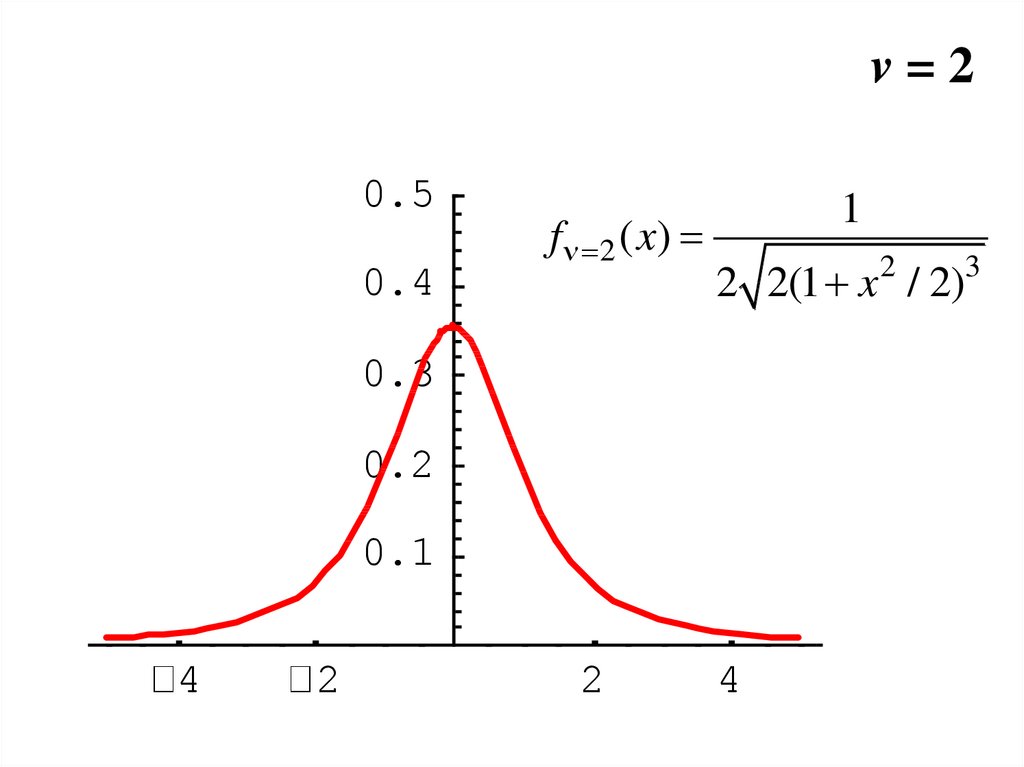
27.
v=20.5
0.4
f 2 ( x)
1
2 2(1 x / 2)
2
0.3
0.2
0.1
4
2
2
4
3
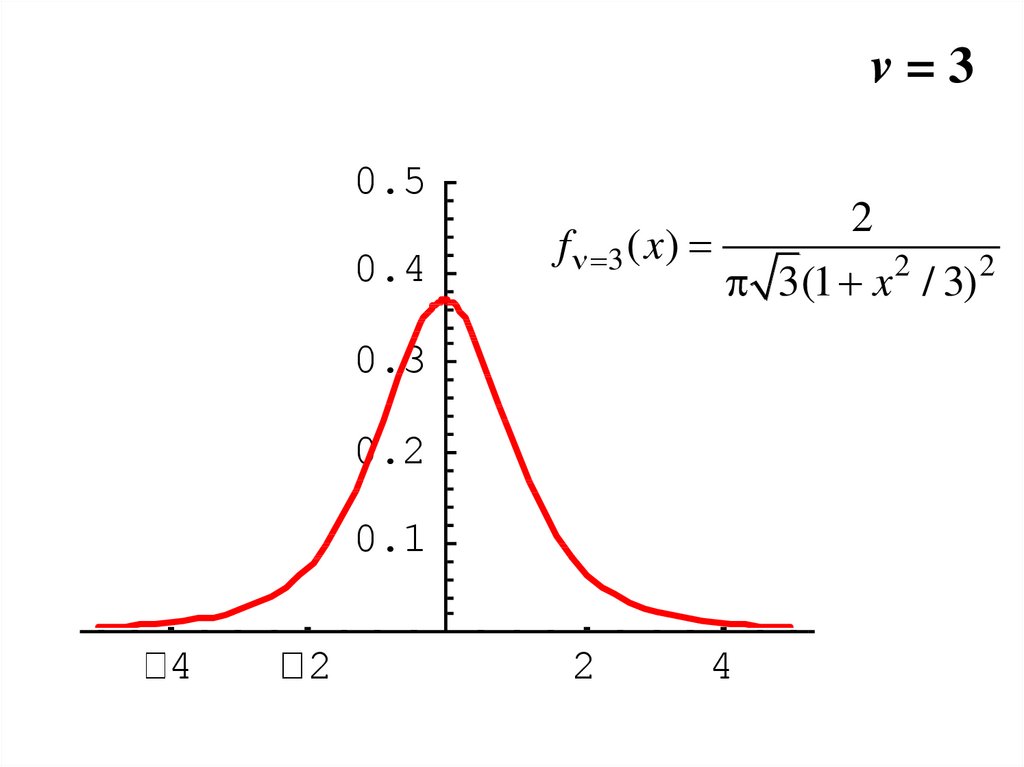
28.
v=30.5
0.4
2
f 3 ( x)
2
2
3(1 x / 3)
0.3
0.2
0.1
4
2
2
4
29.
v=50.5
0.4
0.3
0.2
0.1
4
2
2
4
30.
v = 100.5
0.4
0.3
0.2
0.1
4
2
2
4
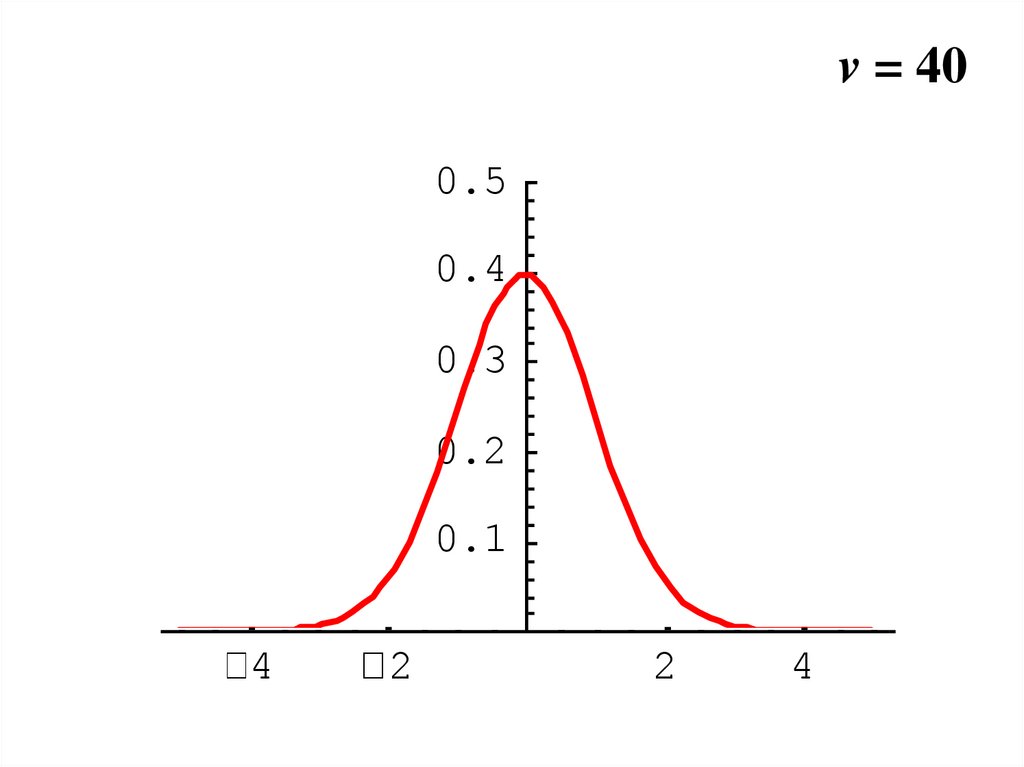
31.
v = 400.5
0.4
0.3
0.2
0.1
4
2
2
4
32. Нормированная функция Гаусса
33.
Случайная величина Стьюдентапри v превращается в гауссову
нормированную случайную величину.

















 Математика
Математика








